分部积分法与换元积分法
定积分的换元积分法与分部积分法

有
b
a f (x) dx f [(t)](t) dt
上式称为定积分的换元公式。
π
例1 计算 2 cos3 x sin x dx 。 0
解
设 t cos x ,则 dt sin x dx 。当 x 0 时,t 1 ;当
x π 时,t 1。 2
原式 0 t3dt 1 t3dt 1 t4计算
4 dx 。
0 1 x
解
令 x t ,x t2 ,则 dx 2tdt 。当 x 0 时,t 0 ;当
x 4 时,t 2。
原式 2 2t dt 2 2 t 1 1 dt 2 2 ln 1 t 2 4 2ln 3
0 1t
0 1t
0
例3 计算
高等数学
定积分的换元积分法与分 部积分法
一、定积分的换元积分法
定理 设函数 f (x) 在 [a ,b] 上连续,而 x (t) 是定义在 [ , ] 上的一个可微函数,并满足条件:
(1)(t)在区间 [a ,b] 上有连续的导数 (t) ;
(2)当t从α 变到β 时,(t) 从 ( ) a 单调地变到( ) b ,则
两边积分,得 移项,得 即
b
b
b
a (uv)dx a uvdx a uvdx
b uvdx
(uv)
b
b
vudx
a
a
a
b
b
b
udv uv vdu
a
a
a
这就是定积分的分部积分公式。
π
例6 计算 0 x cos x dx 。
解
原式
π
xd (sin
x)
x sin x
π
π
2.1.2换元微分法

例12 arctan xdx.
解
u
arctan
x,v
1, u
1
1 x2
,v
x,
arctan
xdx
x
arctan
x
1
x x2
dx
x arctan x 1 ln(1 x2 ) C 2
注 分部积分法适用于两类函数乘积的积分,也适用
于单个反三角函数,单个对数函数的积分.
a
x2 a2
ln x a
x2 a2 a
C ln x
x2 a2 C1,
其中 sec t 和 tan t 可借助辅助直角三角形求出.
例9
求
dx ( x2 a2 )2
(a 0).
解
x a tan t,
|
t
|
π 2
,
dx ( x2 a2 )2
a sec2 t a4 sec4 t
容易求出。那么如何选择变换呢?这往往与被积函数 的形式有关。 常用代换有无理代换,三角代换等.
1 无理代换
若被积函数是 x n1 , n2 x , , nk x 的无理式时,设n为
ni (1 i k) 的最小公倍数, 令 t n x即x t n.
例6
du u3u
6x5 x3x
2
dx
d( x a) xa
1 2a
d( x a) xa
1 2a
ln
|
x
a
|
1 2a
ln
|
x
a
|
1 ln x a C. 2a x a
凑微分法7: 分子分母需同时乘以(除以)某个因子
xk ,ex ,sin x,cos x,1 sin x,1 cos x 等然后再凑微分.
定积分的换元积分法和分部积分法

计算0
1
ln(1 x ) dx. 2 (2 x )
解
0
1
1 ln(1 x ) 1 dx 0 ln(1 x )d 2 (2 x ) 2 x
1
1 1 ln(1 x ) 0 2 x d ln(1 x ) 2 x 0
1 ln 2 1 1 1 1 dx 0 2 x 1 x 3 1 x 2 x ln 2 5 1 ln(1 x ) ln(2 x )0 ln 2 ln 3. 3 3
则 有 a f ( x )dx f [ ( t )] ( t )dt .
首页 上页
b
下页
证
设F ( x ) 是 f ( x ) 的一个原函数,
a f ( x )dx F (b) F (a ),
b
( t ) F [( t )],
dF dx f ( x ) ( t ) f [( t )]( t ), ( t ) dx dt
0 0
f (sin x )dx xf (sin x )dx, 0 0 xf (sin x )dx f (sin x )dx. 0 2 0
0
x sin x sin x dx dx 2 2 2 0 1 cos x 1 cos x
解
令 则
u x,
dv sinxdx,
du dx, v cos x ,
0
4 0
4 x sin xdx x cos x 0 4 cos xdx
2 sin x 8
4 0
2 2 2 8
5.3 定积分的换元法和分部积分法

= − න (π − )(sin(π − ))d
则 d = −d
0
0
π
= න (π − )(sin )d
0
π
π
= π න (sin )d − න (sin )d
0
π
0
π
= π න (sin )d − න (sin )d ,
0
+ න () d
0
= න [(−) + ()] d
0
2 න () d , (−) = (),
=
0
0,
− = − .
奇、偶函数在对称区间上的定积分性质 偶倍奇零
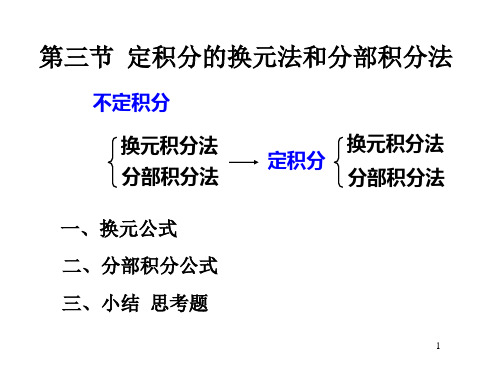
第三节 定积分的换元法和分部积分法
定积分
第五章
1
2 2 + cos
例6 计算 න
0
解
1
d.
( > 0)
π
令 = sin , d = cos d, = ⇒ = , = 0 ⇒ = 0.
2
π
2
cos
d
原式 = න
2
2
0 sin + (1 − sin )
=න
π
2
0
cos
1
d = න
sin + cos
1
=
6
6
1
อ
第三节 定积分的换元法和分部积分法
0
cos 5 sin d
= − න cos 5 d(cos )
= 0 ⇒ = 1.
原式 = − න
π
2
1
= .
数学分析8.2换元积分法与分部积分法(讲义)

第八章 不定积分2 换元积分法与分部积分法(讲义)一、换元积分法定理8.4:(换元积分法)设g(u)在[α,β]上有定义,u=φ(x)在[a,b]上可导,且α≤φ(x)≤β,x ∈[a,b],并记f(x)=g(φ(x))φ’(x), x ∈[a,b].1、(第一换元积分法)若g(u)在[α,β]上存在原函数G(u),则f(x)在[a,b]上也存在原函数F(x),且F(x)=G(φ(x))+C ,即 ∫f(x)dx=∫g(φ(x))φ’(x)dx=∫g(u )du=G(u)+C=G(φ(x))+C .2、(第二换元积分法)若φ’(x)≠0, x ∈[a,b],则命题1可逆,即f(x)在[a,b]上存在原函数F(x)时,g(u)在[α,β]上也存在原函数G(u),且G(u)=F(φ-1(u))+C, 即∫g(u )du=∫g(φ(x))φ’(x)dx=∫f(x)dx=F(x)+C=F(φ-1(u))+C. 证:1、∵dxdG(φ(x))=G ’(φ(x))φ’(x)=g(φ(x))φ’(x)=f(x), ∴∫f(x)dx=∫g(φ(x))φ’(x)dx=∫g(u )du=G(u)+C=G(φ(x))+C . (亦可简写为:∫g(φ(x))φ’(x)dx=∫g(φ(x))d φ(x)=G(φ(x))+C .) 2、若φ’(x)≠0, x ∈[a,b],则u=φ(x)有反函数x=φ-1(x),且du dx =(x)φx 1-(x)φ1=',∴dx d F(φ-1(u))=F ’(x)·(x)φ1'=f(x)·(x)φ1'=g(φ(x))φ’(x)·(x)φ1'=g(φ(x))=g(u). ∴∫g(u )du=∫g(φ(x))φ’(x)dx=∫f(x)dx=F(x)+C=F(φ-1(u))+C.例1:求∫tanxdx. 解:∫tanxdx=∫cosx sinx dx=-∫cosx1d(cosx). 令u=cosx ,则 ∫tanxdx=-∫u1du=-ln|u|+C=-ln|cosx|+C.例2:求∫22xa dx+(a>0). 解:∫22x a dx +=a 1∫2a x 1ax d ⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=a 1arctan a x +C.例3:求∫22x-a dx (a>0).解:∫22x -a dx =∫2a x -1a x d ⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=arcsin ax +C.例4:求∫22a -x dx(a ≠0). 解:∫22a -x dx =2a 1∫⎪⎭⎫⎝⎛+--a x 1a x 1dx=2a 1[∫a x 1-d(x-a)-∫a x 1+d(x+a)] =2a 1[ln|x-a|-ln|x+a|]+C=2a 1ln ax a-x ++C.例5:求∫secxdx.解法1:∫secxdx=∫cosxdx =∫2x sin 2x cos dx 22-=21∫⎪⎪⎪⎪⎭⎫⎝⎛+-+-+2x sin 2x cos 2x sin 2x cos 2x sin 2x cos 2x sin 2x cos dx =21(∫2x sin2x cos 2x sin 2x cos -+dx+∫2x sin 2x cos 2x sin 2x cos +-dx)= -∫2x sin 2x cos 2x sin 2x cos d -⎪⎭⎫ ⎝⎛-+∫2x sin 2x cos 2x sin 2x cos d +⎪⎭⎫ ⎝⎛+=-ln 2x sin 2x cos -+ln 2x sin 2x cos ++C=ln2x sin2x cos 2x sin2x cos -++C=ln cosx sinx 1++C. 解法2:∫secxdx=∫x cos cosx 2dx=∫xsin -112d(sinx)=21ln x sin 1sinx1-++C.解法3:∫secxdx=∫tanx secx tanx)secx(secx ++dx=∫tanxsecx tanx)d(secx ++=ln|secx+tanx|+C.例6:求∫3u-u du .解:令u=x 6,则x=6u ,原式=∫236x -x dx =6∫1-x x 3dx=6∫(1-x 1x 1-x 13-+)dx=6∫(1-x 1+x 2+x+1)dx=6[∫1-x 1d(x-1)+ ∫x 2dx+∫xdx+∫dx]=6(ln|x-1|+3x 3+2x 2+x)+C=6ln|x-1|+2x 3+3x 2+6x+C=6ln|6u -1|+2u +33u +66u +C.例7:求∫22x -a dx (a>0).解:令x=asint, |t|<2π,则t=arcsin ax ,原式=∫t sin a -a 222d(asint)=a 2∫cos 2tdt=4a 2∫(cos2t+1)d(2t)=4a 2[∫cos2td(2t)+∫d(2t)]=4a 2(sin2t+2t)+C =4a 2(2sinarcsin a x cosarcsin a x +2arcsin a x )+C=2a 2(ax2a x -1⎪⎭⎫⎝⎛+arcsin a x )+C.例8:求∫22a-x dx (a>0).解:令x=asect, 0<t<2π, 则t=arcsec ax , 原式=∫22a -)asect (d(asect)=∫ttan tantdtsect ⋅=∫sectdt=ln|sect+tant|+C 1 =ln|secarcsec a x +tanarcsec a x |+C 1=ln|a x +ax22xa -1|+C 1 =ln|a x +aa -x 22|+C 1=ln|x+22a -x |-lna+C 1=ln|x+22a -x |+C.例9:求∫222)a (x dx+(a>0). 解:令x=atant, |t|<2π, 则t=arctan ax ,原式=∫222]a )atant ([d(atant)+=3a 1∫t sec t sec 42dt=3a 1∫cos 2tdt=3a 1∫21cos2t +dt =34a 1∫(cos2t+1)d(2t)=34a 1[∫cos2td(2t)+∫d(2t)]=34a 1(sin2t+2t)+C =32a 1sintcost+32a t +C=)t tan 1(2a tant23++32a t +C=)ax1(2a a x223++32a a x arctan +C=32a 1(22a x ax ++arctan a x )+C.例10:求∫1-x xdx 22.解法1:(运用第一换元积分法)原式=∫23x1-1x dx =-∫2x 1-1)x 1d(x 1=2x 1-1+C=1-x x 12+C .解法2:(运用第二换元积分法)令x=sect, 则t=arcsecx. 原式=∫1-t sec t sec d(sect)22=∫tant t sec tant sect 2⋅⋅dt=∫costdt=sint+C=tsec 1-12+C =2x1-1+C=1-x x 12+C .二、分部积分法:定理8.5:(分部积分法)若u(x)与v(x)可导,不定积分∫u ’(x)v(x)dx 存在,则∫u(x)v ’(x)dx 也存在,并有∫u(x)v ’(x)dx=u(x)v(x)-∫u ’(x)v(x)dx. 可简写为:∫udv=uv-∫vdu. (分部积分公式) 证:由(u(x)v(x))’=u ’(x)v(x)+u(x)v ’(x),得∫(u(x)v(x))’dx=∫[u ’(x)v(x)+u(x)v ’(x)]dx=∫u ’(x)v(x)dx+∫u(x)v ’(x)dx ,即有 ∫u(x)v ’(x)dx=∫(u(x)v(x))’dx-∫u ’(x)v(x)dx=u(x)v(x)-∫u ’(x)v(x)dx.例11:求∫xcosxdx.解:∵∫sinxdx=-cosx+C ,∴∫xcosxdx=∫xdsinx=xsinx-∫sinxdx=xsinx+cosx+C.例12:求∫arctanxdx.解:∵∫xd(arctanx)=∫1x x 2+dx=21∫1x 12+d(x 2+1)=21ln(x 2+1)+C ,∴∫arctanxdx=xarctanx-∫xd(arctanx)=xarctanx-21ln(x 2+1)+C.例13:求∫x 3lnxdx.解:令t=lnx ,则x=e t ,∫x 3lnxdx=∫e 3t tde t =∫e 4t tdt=41∫tde 4t .∵∫e 4t dt=41e 4t +C ,∴41∫tde 4t =41(te 4t -∫e 4t dt)=161e 4t(4t-1)+C. ∴原式=161x 4(4lnx-1)+C.例14:求∫x 2e -x dx.解:∫x 2e -x dx=-∫x 2de -x ,又∫e -x dx 2=2∫x e -x dx=-2∫x de -x .∵∫e -x dx=-e -x +C ,∴∫xde -x =xe -x -∫e -x dx=xe -x +e -x +C ,∴∫e -x dx 2=-2(xe -x +e -x )+C , 原式=-(x 2e -x -∫e -x dx 2)=-x 2e -x -2(xe -x +e -x )+C=-x 2e -x -2xe -x -2e -x +C.例15:求I 1=∫e ax cosbxdx 和I 2=∫e ax sinbxdx.解:I 1=a1∫cosbxde ax =a1[e ax cosbx-∫e ax d(cosbx)]=a1(e ax cosbx+bI 2). I 2=a1∫sinbxde ax =a1[e ax sinbx-∫e ax d(sinbx)]=a1(e ax sinbx-bI 1).由此得方程组:⎩⎨⎧sinbx e =aI +bI coxbx e =bI -aI ax21ax 21. 解方程组得: I 1=22ax b a bsinbx)(acosbx e +++C ;I 2=22ax b a bcosbx)(asinbx e +-+C.。
定积分的换元法和分部积分法
2
0
1
1 cos2
x
d (cos
x)
arctan(cos
2
x )0
( ) 2 . 2 44 4
15
二、分部积分公式
设函数u( x) 、v( x)在区间 a,b 上具有
连续导数,则有
b
a udv
uv b a
b
a vdu
.
定积分的分部积分公式
推导
uv uv uv,
b
a (uv
第三节 定积分的换元法和分部积分法
不定积分
换元积分法 分部积分法
换元积分法 定积分
分部积分法
一、换元公式 二、分部积分公式 三、小结 思考题
1
一、换元公式
定理 假设 f ( x)在[a,b]上连续,函数x (t )
满足条件:
(1) ( ) a , ( ) b;
(2) (t)在[ , ](或 , )上具有连续导数, 且其值域R a, b;
14
0 xf (sin x)dx 0 f (sin t)dt 0 tf (sin t)dt
0 f (sin x)dx 0 xf (sin x)dx,
xf (sin x)dx
f (sin x)dx.
0
20
0
1
x
sin x cos2
x
dx
2
0
1
sin x cos2
x
dx
2) 必需注意换元必换限 , 原函数中的变量不必代回 .
3) 换元公式也可反过来使用 , 即
(t) (t)
b
f (x)d x
(令 x (t))
a
或配元
(t) (t)
定积分换元法与分部积分法
定积分换元法与分部积分法在微积分中,求解定积分是一个常见的问题。
为了解决这一问题,数学家们发展出了一系列的积分技巧和方法。
其中,定积分换元法和分部积分法是两种常用的方法。
1. 定积分换元法定积分换元法,也经常被称为反链式法或者u-置换法,是一种通过变量替换的方法来求解定积分的方法。
其基本思想是:将被积函数中的一个变量替换为一个新的变量,使得原来的被积函数在新的变量下形式简化。
换元法的一般步骤如下:1.选择一个合适的变量替换,通常使用一个新的变量来替换被积函数中的一个变量。
2.计算新的变量对应的微元变量,并求得其微分。
3.将原来的被积函数表示为新的变量的函数,并对其进行简化。
4.计算新的定积分,并将结果转换回原来的变量。
通过这种换元法,我们可以简化复杂的被积函数,从而更容易求解定积分。
下面通过一个实例来进一步说明定积分换元法的具体步骤。
示例:求解定积分 $I = \\int_{1}^{2} \\frac{1}{x^2} dx$步骤1:选择合适的变量替换。
我们选取新变量u=x2,则du=2xdx步骤2:计算新变量对应的微元变量。
由du=2xdx,可以得到 $dx =\\frac{du}{2x}$步骤3:将原被积函数表示为新的变量的函数,并进行简化。
将x表示为u的函数,则 $x = \\sqrt{u}$。
将被积函数 $\\frac{1}{x^2}$ 替换为 $\\frac{1}{u}\\cdot \\frac{1}{2\\sqrt{u}} = \\frac{1}{2u\\sqrt{u}}$步骤4:计算新的定积分,并转换回原变量。
将积分的上下限也用新的变量表示,则新的定积分为 $I = \\int_{1}^{4} \\frac{1}{2u\\sqrt{u}} \\cdot\\frac{du}{2x}$。
对新的定积分进行计算,得到 $I = \\frac{1}{4}\\left( \\frac{1}{\\sqrt{4}} - \\frac{1}{\\sqrt{1}} \\right) = \\frac{1}{8} -\\frac{1}{4} = -\\frac{1}{8}$通过定积分换元法,我们成功求解了该定积分的值。
定积分的换元积分法与分部积分法
解:对 p 1,
a
dx (a 0) p x
收敛或发散
b
1
1 1 1 p 1 p 1 ( b ) x dx x p 1 p 1 p 1
p
重要的问题是b的指数是正数还是负数. 假如是
负数, 则当b趋向无穷时, b–p+1趋向于0. 若指数为
正数,则b–p+1当b趋于无穷时无界增长. 因此, 若–
a
udv uv a vdu .
a
回忆::
定积分的分部积分公式
不定积分的分部积分公 式为 :
udv uv vdu .
例1. 计算
解: 原式 =
x arctan x
1 2
1 0
1
0
1 1 2 d (1 x ) 2 4 2 0 1 x
1 2 ln( 1 x ) 2 4 0 1 ln 2 2 4
当p>1时积分有值
1
b 1 1 1 1 p 1 b ) dx lim p dx lim ( p b p 1 b 0 x p 1 x
1 1 ( ) p 1 p 1
定理1 (比较判别法) [a,), g ( x) f ( x) 0, 设 且f ( x), ( x)于[a,)内有界, 则 g (1) 当 a g ( x)dx 收敛时,a f ( x)dx 也收敛 ; (2) 当
1
dx 增长且无界, x
y 1 x
dx 发散. y x
1
b
dx x
0
1
b
x
2. 其它情形意义
第4节 定积分的换元法与分部积分法
1 0
1 x
1 0
ax dx
a 4
4
即
a
1 0
f ( x )d x
3
7/9/2013 12:56 AM
第6章
函数的积分
7. 设
f (x)
F 是连续函数, ( x ) 是 f ( x ) 的原
函数,则( A )
(A) (B ) (C ) (D) F 当 f ( x ) 是奇函数时, ( x ) 必是偶函数 F 当 f ( x ) 是偶函数时, ( x ) 是奇函数
dx )
8(e 2e 2
7/9/2013 12:56 AM
x
) 8(e 2 )
第6章
函数的积分
例9 设
解
f (x)
x 1
2
sin t t
2 2
dt ,
2
求
2
1
x f ( x )d x
0
f ( x ) 2 x
x f ( x )d x
2 1 0
sin x x
,
x 1
3
f ( t ) d t ln x ,
求
x 1
3
f (e ) 。
3
解
ln x
3
1
3 ( t ) d t f ( x ) f (1 ) f ( x ) f
令
u x ,
得
f ( u ) ln
3
u
1 3
ln u
f (e )
3
思考 是否还有其它方法?
定积分的换元法与分部积分法
且其值域 R [a , b], 则有:
b
a
f ( x )dx f [ ( t )] ( t )dt
定积分换元公式
b
a
f ( x )dx f [ (t )] (t )dt
注 (1) 换 ( x )dx
三 个 变 化
(2) 公式特点 例1 计算 例2
b
a
b
b
a
udv uv a vdu
b b a
定积分的分部积分公式 注 使用分部积分公式应边积边代限 例14 计算
1 2
0
arcsin xdx 例15 计算 e x dx
0
1
例16 证明
n 1 n 3 3 1 , n n2 4 2 2
被积函数 f ( x ) 积分元素 dx 积分区间[a , b]
f [ ( t )] ( t )dt
f ( ( t )) ( t )dt [ , ] 或 [ , ]
变量不必回代
计算
a
换元必换限 必须注意积分限 上限对上限 下限对下限 注意简便算法
0
4
a 2 x 2 dx (a 0)
第三讲 定积分的换元法和分部积分法
定积分
牛-莱公式
换元积分法
不定积分 分部积分法
?
特点?
定积分的换元法与分部积分法
一、换元法
二、分部积分法
定积分的换元法与分部积分法
一、换元法
二、分部积分法
定理 假设f(x)在区间[a,b]上连续,函数 x ( t )满足条件:
( ) a, ( ) b ; (2) ( t )在[ , ](或[ , ])上具有连续导数,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
§7.2分部积分法与换元积分法 (一) 教学目的:熟练掌握第一、二换元积分法与分部积分法. (二) 教学内容:第一、二换元积分法;分部积分法. ————————————————————————
如何计算不定积分xdx2cos?我们知道,Cxxdxsincos,那么是否有
Cxxdx2sin2cos?显然不对。 计算不定积分,仅有直接积分法还是不行的。如xdx2cos、xdxln、xdxtan等积分就不能直接积分,下面探讨其它的计算不定积分的方法。 一、换元积分法 1.凑微分法
定理1(第一换元积分法)若函数)(xu在[a,b]可导,且)(x,],[u,有
)()(xfxF,则函数)()]([xxf存在原函数)]([xF,即 CxFdxxxf)]([)()]([ **具体应用此定理计算不定积分时,其过程是这样的: CxFCuFduufxdxfdxxxfxuxu)]([)()()()]([)()]([)()(
例7.求dxx35 分析:我们有公式Cxdxx34343,而上述积分中被积函数根号里面还要加5,不能直接用公式。为了能用公式计算,进行凑微分: )5(xddx 解:CxCuduuxdxdxxxuxu345343533)5(4343)5(55 例8.求dxx)85sin( 分析:为了能应用公式计算,进行凑微分:)85(51xddx 解:uduxdxdxxxusin51)85()85sin(51)85sin(85 CxCuxu)85cos(51cos5
185
一般地,在计算积分的时候,有时为了化为能用公式计算,我们常根据需要作下面的凑微分公式: (1))()(1)(baxdbaxfadxbaxf **计算熟练以后,就可以省略“设”的步骤,把所设的式子当作一个整体,在心里面想着它是一个变数,就可以使书写简化。如上面的例子,就可以简化为
Cxxdxdxx3433)5(43)5(55 Cxxdxdxx)85cos(51)85()85sin(51)85sin( 例9.求dxexx121 分析:注意到我们有xddxx112 解:Cexdedxexxxx111211 一般地,我们有凑微分公式: (2)duufkxdxfkdxxfxkkkk)(1)()(1)(1 特殊地,有
xdxfdxxf
x
1111
2,
xdxfdxxfx21,
2
2
1
xdxdx
等等。 除此以外,我们还可以写出许多凑微分公式:
(3);)(sin)(sincos)(sinduufxdxfxdxxf
(4);)(cos)(cossin)(cosduufxdxfxdxxf (5).)()(sec)(2duufdtgxtgxfxdxtgxf (6).)()()(duufdeefdxeefxxxx (7).)(ln)(ln)(lnduufxdxfxdxxf
(8);)(arcsin)(arcsin1)(arcsin2duufxdxfdxxxf (9)duufdarctgxarctgxfdxxarctgxf)()(1)(2 例10.求xdxx22)115( 分析:应用凑微分公式(2),有)115()115(101)115(22222xdxxdxx 解:(略) 例11.求dxxx3234
例12.求dxxa221 例13.求dxxa221 例14.求dxxxln1 例15.求xdxxsincos2 例16.求xdxxdxseccsc和 补充例题: dtgxxtgxdx2261sec
.secsec1secsecsecsec2222435xdxxdxtgxdxxtg
dttarctgtxdxxarctgdxxxxarctgxt21212
)1(
cxarctgcarctgttgtarctgtdarc22)()(2 2.第二换元法 这是一种与凑微分法的过程刚好相反的计算不定积分的方法。
定理2(第二换元积分法)若函数)(tx在],[可导,()atb,且0)(t,函数)(xf在
],[ba有定义,],[t,有 ).()]([)(ttftG 则函数)(xf在],[ba存在原函数,且 CxGdxxf)]([)(1
具体应用此定理计算不定积分时,其过程是这样的: CxGCtGdtttfdxxfxttx)]([)()()]([)(1)()(1
例17.求dxxa22 分析:被积函数带有根号,想办法去掉。联想到三角函数公式22cossin1,于是作变换
22sinttax,则tataaxacossin22222,根号去掉了。
解:设22sinttax,则tdtadxtaxacos,cos22,于是 Ctatatdtatdtatadxxa2sin42coscoscos222222
由taxsin,得221cosxaat,所以2222cossin22sinxaaxttt ∴ CxaxaxaCtatadxxa22222222arcsin22sin42 一般地,当被积函数是含有形如22xa)0(a的式子时,都可考虑作变量替换taxsin,目的是去掉根号。此时,cos22taxa ,costdtadx .arcsinaxt
例18.求22axdx 解:设22tanttax,则有taaxtdtadxsec,sec222,于是 Ctttdtdttataaxdxtanseclnsecsec
sec2
22
要将变量还原为x ,由axttan,可得aaxt22sec,于是 x
a t 22axCxaxCaxaaxCttaxdx222222lnlntansecln 一般地,当被积函数是含有形如22ax)0(a的式子时,都可考虑作变量替换taxtan,目的是去掉根号。此时taaxtdtadxsec,sec222,.arctanaxt
例19.求022aaxdx 解:设taxsec,则有tdttadxtansec,taataaxtansec22222 ∴dttattaaxdxtantansec22 当20t时, Ctttdtdttattaaxdxtanseclnsectan
tansec
22
由taxsec,得axtsec,aaxt22tan,于是 CaxxCttaxdx2222lntansecln 当 t2时, Ctttdtdttattaaxdxtanseclnsectan
tansec
22
由taxsec,axtsec,aaxt22tan CaxxCaxxCttaxdx222222lnlntansecln 综上所述,对任意,,aax,有 Caxxaxdx2222ln 一般地,当被积函数是含有形如22ax)0(a的式子时,都可考虑作变量替换taxsec,目的
t x a 22ax是去掉根号。此时tdttadxtansec,taataaxtansec22222 二、分部积分法 我们知道,
vuvuuv
即 vuuvvu 于是, vdxuuvdxvuuvdxvu 或 vduuvudv 这就是分部积分公式。 应用分部积分公式计算不定积分的过程一般为:
vdxuuvvduuvudvdxvu
在这里,主要是把不定积分dxvu的计算转化为不定积分vdxu计算。通过这样的转化,往往会达到化未知为已知,化繁为简,化难为易的目的。 在分部积分的过程中,还是要凑微分,
例1.求xdxxsin 分析:初看这道题,会感到无从下手。尝试一下使用分部积分。可以有两个凑微分的方向: )(sin21sin2xxdxdxx
或 xxdxdxxcossin
走哪条路好呢?通过尝试可以知道,第一种方法越算越复杂,无法得到结果。第二种方法刚好相反。 解:Cxxxdxxxxxdxdxxsincoscoscoscossin 从此例可以看到,原题中的积分可能有两种凑微分的方法,但选择那一种,有时是要认真考虑或尝试一下的。
一般地,形如xdxxksin、xdxxkcos的积分,都可以用分部积分法来计算,并且计算方法和例1的方法类似。 例2.求xdxxln
解:xdxxxxdxxxxxdxdxx21ln21)(ln21ln21ln21ln2222
例3.求dxxx3ln 解:)(ln1212ln1ln21ln2223xdxxxxxddxxx 一般地,形如xdxxkln的积分,都可以用分部积分法来计算,并且计算方法和例1、例2的方法类
