信号与系统习题解答(第1、2、3、4章)周昌雄主编
信号与系统习题解答 (1)

第一章作业参考答案: 1.18求下列积分值: (a )解:26242)2()2(2)()0()2()(2)()()]2(2)([)()]2(2)()[23(44444444442=+=-+=-+=-+=-+++⎰⎰⎰⎰⎰-----dtt x dt t x dtt t x dt t t x dtt t t x dt t t t t δδδδδδδδ(b) 解:6510)2()2()()0()5()5()2()()()()5()()]2()()5([)()]2()()5()[1(4444444444442=++=-+++-=-+++=-+++=-++++⎰⎰⎰⎰⎰⎰------dtt x dt t x dt t x dtt t x dt t t x dt t t x dtt t t t x dt t t t t δδδδδδδδδδδδ(C )解:1)2()cos 1()2()cos 1(2=--=--⎰⎰--ππππππδπδdt t dt t t(d )解:42312121231)(cos )23()(cos )2()(cos )2()(cos )23()(cos )1(200222=++++-+-=++-+-=+⎰⎰⎰⎰⎰-----ππππδπδπδπδπδππππππππdtt x dt t x dt t x dt t x dt t t 1.19解:1.21 判断下列每个信号是否周期的?如果是周期的,是求它的基波周期。
(a )解:32,/23)cos(2)43cos(200ππωϕωπ===+=+T T t t 基波周期为:是周期信号(b)解:e eeT e e et j T t j Tj T j t j T t j )1()1)(()1()1)((12--±±±--±====ππππππ,时,当 是周期信号,基波周期是 T 0=2(c)解:互质与是有理数,且74,742782)2cos()278cos(==Ω+Ω=+ππππn n 所以原式是周期信号,基波周期N 0=7.(d)解:不是有理数,,812412cos 4cos πππ==ΩΩ=nn所以原式不是周期信号(e )解:。
信号与系统--完整版答案--纠错修改后版本
1)
3)
5)
3.8、求下列差分方程所描述的离散系统的单位序列响应。
2)5)
3.9、求图所示各系统的单位序列响应。
(a)
(c)
3.10、求图所示系统的单位序列响应。
3.11、各序列的图形如图所示,求下列卷积和。
(1)(2)(3)(4)
4.34 某LTI系统的频率响应,若系统输入,求该系统的输出。
4.35 一理想低通滤波器的频率响应
4.36 一个LTI系统的频率响应
若输入,求该系统的输出。
4.39 如图4-35的系统,其输出是输入的平方,即(设为实函数)。该系统是线性的吗?
(1)如,求的频谱函数(或画出频谱图)。
(2)如,求的频谱函数(或画出频谱图)。
(1) (2) (3) (4) (5)
4.19 试用时域微积分性质,求图4-23示信号的频谱。
图4-23
4.20 若已知,试求下列函数的频谱:
(1)(3) (5)
(8)(9)
4下列方式求图4-25示信号的频谱函数 (1)利用xx和线性性质(门函数的频谱可利用已知结果)。
(1)
5-18 已知系统函数和初始状态如下,求系统的零输入响应。
(1),
(3),
5-22 如图5-5所示的复合系统,由4个子系统连接组成,若各子系统的系统函数或冲激响应分别为,,,,求复合系统的冲激响应。
5-26 如图5-7所示系统,已知当时,系统的零状态响应,求系数a、b、c。
5-28 某LTI系统,在以下各种情况下起初始状态相同。已知当激励时,其全响应;当激励时,其全响应。
(7)(8)
1-7 已知序列的图形如图1-7所示,画出下列各序列的图形。
《信号与系统》第二章作业题答案

第二章 连续时间系统的时域分析1.与()t δ相等的表达式为:A .1()4t δ B .2(2)t δ C .(2)t δ D .1(2)2t δ解:由()t δ函数的性质1()()t t δαδα=可得,选B2.()j tet dt ωδ∞--∞'=⎰。
解:运用性质0()()()(0)t f t t dt f t f δ∞=-∞'''=-≡-⎰,得到()()j tet dt j j ωδωω∞--∞'=--=⎰。
3.两个线性时不变系统的级联,其总的输入-输出关系与它们在级联中的次序没有关系。
(正确)解:以冲击响应为例。
因为级联时,系统总的冲击响应等于各子系统冲击响应的卷积,而卷积与顺序没有关系,所以冲击响应与子系统顺序没有关系。
4.若()()()y t x t h t =*,则()()()y t x t h t -=-*-。
(错误)解:由()()()y t x h t d τττ∞-∞=-⎰,得()()()y t x h t d τττ∞-∞-=--⎰。
而()()()()()x t h t x h t d y t τττ∞-∞-*-=--+≠-⎰5.已知(21)f t -+波形如图所示,试画出()f t 的波形。
解:根据1反2展36.用图解法求图中信号的卷积()()()t f t f t f 21*=。
(03北邮A,8分)解:当10t -<时,即1t <时,由图1所示,12()()*()0f t f t f t ==图1当1020t t ->⎧⎨-<⎩时,即12t <<时,由图2所示,11201()()*()sin()[cos()1]t f t f t f t d t πττππ-===+⎰图2当1220t t -<⎧⎨->⎩时,即23t <<时,由图3所示,11222()()*()sin()cos()t t f t f t f t d t πττππ--===⎰图3当1222t t ->⎧⎨-<⎩时,即34t <<时,由图4所示,21221()()*()sin()[cos()1]t f t f t f t d t πττππ-===-⎰图4当4t >时,如图5所示,12()()*()0f t f t f t ==图57.如图所示系统由几个子系统组成,各子系统的冲激响应为)()(1t u t h =,)1()(2-=t t h δ,)()(3t t h δ-=,试求此系统的冲激响应)(t h ;若以()()t u e t e t -=作为激励信号,用时域卷积法求系统的零状态响应。
信号与系统课后习题与解答第三章
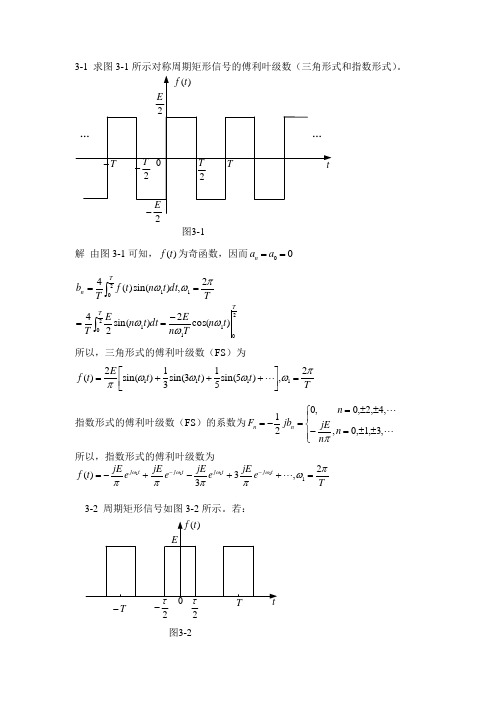
3-1 求图3-1所示对称周期矩形信号的傅利叶级数(三角形式和指数形式)。
图3-1解 由图3-1可知,)(t f 为奇函数,因而00==a a n2112011201)cos(2)sin(242,)sin()(4T T T n t n T n Edt t n E T T dt t n t f T b ωωωπωω-====⎰⎰所以,三角形式的傅利叶级数(FS )为T t t t E t f πωωωωπ2,)5sin(51)3sin(31)sin(2)(1111=⎥⎦⎤⎢⎣⎡+++=指数形式的傅利叶级数(FS )的系数为⎪⎩⎪⎨⎧±±=-±±==-= ,3,1,0,,4,2,0,021n n jE n jb F n n π所以,指数形式的傅利叶级数为T e jE e jE e jE e jE t f t j t j t j t j πωππππωωωω2,33)(11111=++-+-=--3-2 周期矩形信号如图3-2所示。
若:图3-22τT-2τ-重复频率kHz f 5= 脉宽 s μτ20=幅度 V E 10=求直流分量大小以及基波、二次和三次谐波的有效值。
解 对于图3-2所示的周期矩形信号,其指数形式的傅利叶级数(FS )的系数⎪⎭⎫⎝⎛=⎪⎭⎫ ⎝⎛====⎰⎰--22sin 12,)(1112212211τωττωππωττωωn Sa T E n n E dt Ee T T dt e t f T F tjn TT t jn n则的指数形式的傅利叶级数(FS )为∑∑∞-∞=∞-∞=⎪⎭⎫ ⎝⎛==n tjn n tjn n e n Sa TE eF t f 112)(1ωωτωτ其直流分量为TE n Sa T EF n ττωτ=⎪⎭⎫ ⎝⎛=→2lim100 基波分量的幅度为⎪⎭⎫ ⎝⎛⋅=+-2sin 2111τωπEF F 二次谐波分量的幅度为⎪⎭⎫ ⎝⎛⋅=+-22sin 122τωπEF F 三次谐波分量的幅度为⎪⎭⎫ ⎝⎛⋅=+-23sin 32133τωπE F F 由所给参数kHz f 5=可得s T s rad 441102,/10-⨯==πω将各参数的值代入,可得直流分量大小为V 110210201046=⨯⨯⨯--基波的有效值为())(39.118sin 210101010sin 210264V ≈=⨯⨯⨯- πππ二次谐波分量的有效值为())(32.136sin 251010102sin 21064V ≈=⨯⨯⨯- πππ三次谐波分量的有效值为())(21.1524sin 32101010103sin 2310264V ≈=⨯⨯⨯⨯- πππ3-3 若周期矩形信号)(1t f 和)(2t f 的波形如图3-2所示,)(1t f 的参数为s μτ5.0=,s T μ1= ,V E 1=; )(2t f 的参数为s μτ5.1=,s T μ3= ,V E 3=,分别求:(1))(1t f 的谱线间隔和带宽(第一零点位置),频率单位以kHz 表示; (2))(2t f 的谱线间隔和带宽; (3))(1t f 与)(2t f 的基波幅度之比; (4))(1t f 基波与)(2t f 三次谐波幅度之比。
信号与系统第三章习题部分参考答案

(7) (1 − t) f (1 − t) ;
(2) [1 + m f (t)]cosω0 t
(4) (t + 2) f (t); ( ) (6) e− jω0 t df t
dt
(8) f (t)∗ f (t − 3);
t
(9) ∫τ f (τ )dτ −∞
1−t / 2
(11) ∫ f (τ )dτ −∞
2π (sin π t )2 ↔ 2π (1− ⎜w⎜)[ε(w + 2π ) − ε(w − 2π )]
πt
2π
即 (sin π t )2 ↔ (1− ⎜w⎜)[ε(ω + 2π ) − ε(w − 2π )]
πt
2π
(3)双边指数信号
∵ e−a⎜t⎜
↔
2a a2 + w2
(−∞
<
t
<
+∞)
∴ 2a a2 + w2
(13) f (t)∗ Sa(2t) (15) t df (1 − t)
dt
t+5
(10) ∫ f (τ )dτ −∞
(12) df (t) + f (3t ) − 2 e− jt ;
dt
(14) f (t) u(t)
(16) (t − 2) f (t)e j2(t−3)
解:(1) f 2 (t) + f (t) = f (t). f (t) + f (t) ↔ 1 [F (w}* F (w)] + F (w)
又 f (t) = 2 + cos⎜⎛ 2πt ⎟⎞ + 4sin⎜⎛ 5πt ⎟⎞
⎝3⎠
信号与系统(应自炉)习题答案第1章 习题解重点

(222222j t k j t j t j k f t k e
e
e
e
f t π
π
π
πππ+++++==⨯==
∴原函数是周期函数,令1k =,则基波周期为2π。
1-2.
求信号( 14sin( 110cos(2--+=t t t f的基波周期。
解:cos(101 t +的基波周期为15
π,s i n (4
1-8.
用阶跃函数写出题图1-8所示各波形的函数表达式。
t
t
t
(a (
bc
题图1-8
解:(a)((((((3[31]2[11]f t t u t u t u t u t =++-+++-- (((3[13]t u t u t +-+---
(((((
(3 3(1 1(1 1(3 3f
t t u t t u t t u t t u t =+++--++-+-+--(b)([( (1]2[(1 (2]4(2 f t u t u t u t u t u t =--+---+-
1 t -的基波周期为
1
2
π二者的最小公倍数为π,故( 14sin( 110cos(2--+=t t t f的基波周期为π。
1-3.
设(3, 0<=tt f ,对以下每个信号确定其值一定为零的t值区间。
(1)(t f -1(2)((t f t f -+-21(3)((t f t f --21(4)(t f 3(5)(f
《信号与系统(第四版)》习题详解图文
故f(t)与{c0, c1, …, cN}一一对应。
7
3.3 设
第3章 连续信号与系统的频域分析
试问函数组{ξ1(t),ξ2(t),ξ3(t),ξ4(t)}在(0,4)区间上是否 为正交函数组,是否为归一化正交函数组,是否为完备正交函 数组,并用它们的线性组合精确地表示题图 3.2 所示函数f(t)。
题图 3.10
51
第3章 连续信号与系统的频域分析 52
第3章 连续信号与系统的频域分析 53
第3章 连续信号与系统的频域分析 54
第3章 连续信号与系统的频域分析 55
第3章 连续信号与系统的频域分析 56
第3章 连续信号与系统的频域分析 57
第3章 连续信号与系统的频域分析
题解图 3.19-1
8
第3章 连续信号与系统的频域分析
题图 3.2
9
第3章 连续信号与系统的频域分析
解 据ξi(t)的定义式可知ξ1(t)、ξ2(t)、ξ3(t)、ξ4(t)的波形如题 解图3.3-1所示。
题解图 3.3-1
10
不难得到:
第3章 连续信号与系统的频域分析
可知在(0,4)区间ξi(t)为归一化正交函数集,从而有
激励信号为f(t)。试证明系统的响应y(t)=-f(t)。
69
证 因为
第3章 连续信号与系统的频域分析
所以
即
70
系统函数
第3章 连续信号与系统的频域分析
故
因此
71
第3章 连续信号与系统的频域分析
3.23 设f(t)的傅里叶变换为F(jω),且 试在K≥ωm条件下化简下式:
72
第3章 连续信号与系统的频域分析 73
107
信号与系统课后习题与解答第一章
1-1分别判断图1-1所示各波形是连续时间信号还是离散时间信号,若是离散时间信号是否为数字信号?图1-1图1-2解 信号分类如下:图1-1所示信号分别为⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧--⎩⎨⎧--))(散(例见图数字:幅值、时间均离))(连续(例见图抽样:时间离散,幅值离散))(连续(例见图量化:幅值离散,时间))(续(例见图模拟:幅值、时间均连连续信号d 21c 21b 21a 21(a )连续信号(模拟信号);(b )连续(量化)信号;(c )离散信号,数字信号;(d )离散信号;(e )离散信号,数字信号;(f )离散信号,数字信号。
1-2 分别判断下列各函数式属于何种信号?(重复1-1题所示问)(1);)sin(t e at ω-(2);nT e -(3);)cos(πn (4);为任意值)(00)sin(ωωn (5)。
221⎪⎭⎫ ⎝⎛解由1-1题的分析可知:(1)连续信号;(2)离散信号;(3)离散信号,数字信号;(4)离散信号;(5)离散信号。
1-3 分别求下列各周期信号的周期T :(1);)30t (cos )10t (cos -(2);j10t e (3);2)]8t (5sin [(4)。
[]为整数)(n )T nT t (u )nT t (u )1(0n n ∑∞=-----解 判断一个包含有多个不同频率分量的复合信号是否为一个周期信号,需要考察各分量信号的周期是否存在公倍数,若存在,则该复合信号的周期极为此公倍数;若不存在,则该复合信号为非周期信号。
(1)对于分量cos (10t )其周期;对于分量cos (30t ),其周期。
由于5T 1π=15T 2π=为的最小公倍数,所以此信号的周期。
5π21T T 、5T π=(2)由欧拉公式)t (jsin )t (cos e t j ωωω+=即)10t (jsin )10t (cos e j10t +=得周期。
5102T ππ==(3)因为[])16t (cos 2252252)16t (cos 125)8t (5sin 2-=-⨯=所以周期。
信号与系统课后习题答案汇总
第一章习题参考解答1.1 绘出下列函数波形草图。
(1) ||3)(t et x -=(2) ()⎪⎪⎨⎧<≥=02021)(n n n x n n (3) )(2sin )(t t tx επ= (5) )]4()([4cos )(--=-t t t et x tεεπ(7) t t t t x 2cos)]2()([)(πδδ--=(9) )2()1(2)()(-+--=t t t t x εεε)5- (11) )]1()1([)(--+=t t dtdt x εε (12) )()5()(n n n x --+-=εε (13) ⎰∞--=td t x ττδ)1()((14) )()(n n n x --=ε1.2 确定下列信号的能量和功率,并指出是能量信号还是功率信号,或两者均不是。
(1) ||3)(t et x -=解 能量有限信号。
信号能量为:(2) ()⎪⎩⎪⎨⎧<≥=02021)(n n n x n n解 能量有限信号。
信号能量为:(3) t t x π2sin )(=解 功率有限信号。
周期信号在(∞-∞,)区间上的平均功率等于在一个周期内的平均功率,t π2sin 的周期为1。
(4) n n x 4sin)(π=解 功率有限信号。
n 4sin π是周期序列,周期为8。
(5) )(2sin )(t t t x επ=解 功率有限信号。
由题(3)知,在),(∞-∞区间上t π2sin 的功率为1/2,因此)(2sin t t επ在),(∞-∞区间上的功率为1/4。
如果考察)(2sin t t επ在),0(∞区间上的功率,其功率为1/2。
(6) )(4sin)(n n n x επ=解 功率有限信号。
由题(4)知,在),(∞-∞区间上n 4sin π的功率为1/2,因此)(4sinn n επ在),(∞-∞区间上的功率为1/4。
如果考察)(4sinn n επ在),0(∞区间上的功率,其功率为1/2。
信号与系统课后习题与解答第二章
2-1 对图2-1所示电路分别列写求电压)(0t v 的微分方程表示。
2(t ei )(t +-(e )(e )(t +-图2-1解 (a )对于图2-1(a )所示电路列写网孔电流方程,得[]⎪⎩⎪⎨⎧-=+-=-++⎰⎰⎰∞-∞-∞-t t t t v i d i i t e d i d i dt t di i )()()()()()()()(202122111ττττττττ 又 dtt di t v )(2)(20= 消元可得如下微分方程:)(3)(5)(5)(200022033t v t v dt dt v dtd t v dt d +++=2)(te dt d(b )对于图2-1(b )所示的双耦合电路,列写电路微分方程,得⎪⎪⎪⎩⎪⎪⎪⎨⎧=-=+++=+++⎰⎰∞-∞-)()(0)()()()(1)()()()()(10221221211t v t Ri t Ri dt t di M dt t di L d i Ct e t Ri dtt di M dt t di L d i C ttττττ 消元可得如下微分方程:)()(1)(2)(2)(2)()(22020022203304422t e dtd MR t v C t v dt d C R t v dtd R R L t v dtd RL t v dt d M L =++⎪⎭⎫ ⎝⎛+++- (c )对于图2-1(c )所示电路列写电路方程,得⎪⎪⎩⎪⎪⎨⎧=⎥⎦⎤⎢⎣⎡+++=⎰∞-)()()(1)()()()(10101011t v t v dt d C dt t v L R t v R t v t v dt d C t i t μ 消元可得如下微分方程:)()(1)(1)()(101011022110331t i dt dR t v RL t v dt d R R L C t v dt d R C R C t v dt d CC μ=+⎪⎪⎭⎫ ⎝⎛++⎪⎪⎭⎫ ⎝⎛++ (d )对图2-1(d )所示电路列写电路方程,电流)(t i 如图2-2所示,得⎪⎪⎩⎪⎪⎨⎧==+=++⎰∞-)()()()()()()()(1)(1011t v t v t e t v t Ri t e t v d i C t Ri t μμττ 消元可得如下微分方程:(t e )(t +-图2-2)()(1)()1(00t e Rt v R t v dt d Cμμ=+-2-2 图2-3所示为理想火箭推动器模型。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
信号与系统习题解答(第1章,p27))1-2.左上图: )2t ()1t (2)t ()t (f -ε+-ε-ε=右上图: ))2t ()1t ()(t 2()1t ()t ())t ()1t ()(1t ()t (f -ε--ε-+-ε-ε+ε-+ε+= 左下图: )2t ()1t ()1t ()2t ()t (f -ε--ε++ε-+ε=右下图: ⎩⎨⎧≤=其它,01t ,t )t (f 或))1t ()1t ((t )t (f -ε-+ε=1-3图(a): )2n ()n (f +ε=图(b): )7n ()3n ()n (f -ε--ε=图(c): )2n ()n (f +-ε= 图(d): )1n ()1()n (f n-ε-= 1-51-7(1) )t (x )0(q)t (y 22+=满足可分解性,),0(q )t (y 2zi=)t (x )t (y 2zs=均为非线性,故为非线性系统。
(2) )t (x lg )0(q )t (y =不满足可分解性, 故为非线性系统。
(3) ⎰λλ+=td )(x )0(q )t (y满足可分解性, ),0(q )t (y zi =⎰λλ=tzs d )(x )t (y 均为线性,故为线性系统。
(4) )t (x dtd)0(q lg )t (y += )0(q lg )t (y zi =为非线性,故为非线性系统。
ttt0 f(n)13 645 2 1 7 题1-3图(b)1-8(1) )t (f t )0(x 2)t (y 2+=满足可分解性, ),0(x 2)t (y zi =)t (f t )t (y 2zs =均为线性,故为线性系统。
(2) )t (f 3)0(x 4)t (y 2+=))t (f 3)t (y 2zi =为非线性,故为非线性系统。
(3) )t (f 5)0(x 3)t (y +=满足可分解性, ),0(x 3)t (y zi =)t (f 5)t (y zs =均为线性,故为线性系统。
(4) )t (f )3t 2()0(x )5t ()t (y 2+++=满足可分解性, ),0(x )5t ()t (y 2zi +=)t (f )3t 2()t (y zs +=均为线性,故为线性系统。
(5) ⎰∞-ττ+=td )(f t)0(x 3)t (y满足可分解性, ),0(x 3)t (y zi =⎰∞-ττ=tzs d )(f t )t (y 均为线性,故为线性系统。
(6) ⎰∞-ττ+=td )(f )t (f )0(x 2)t (y⎰∞-ττ=tzs d )(f )t (f )t (y 为非线性,故为非线性系统。
(7) )t (f 2)t (f )0(x )t (y += 不满足可分解性,故为非线性系统。
(8) )t (tf 3)t (f t )0(x 4)0(tx 2)t (y 2+++=满足可分解性, ),0(x 4)0(tx 2)t (y zi +=)t (tf 3)t (f t )t (y 2zs +=均为线性,故为线性系统。
1-11解: 根据线性系统的线性和微分特性可得:0t e 2)e 1(dtd)e 1(2)t (y t t t ≥-=-+-=---1-12 解: (1)t e 6e 17)e 2e 3(3)e 6e 4(2)t (y 3)t (y 2)t (y t4t 2t 4t 2t 4t 22x 1x 3x >+=-++=+=------(2)t )e 6e 15e 36)e 2e e 5(3)e 2e 3(3)e 6e 4(3)t (y 3)t (y 3)t (y 3)t (y t t 4t 2t t 4t 2t 4t 2t 4t 2f 2x 1x >++=+++-++=++=----------信号与系统习题解答(第2章,p72)) 2-1(提示:)t ()0(f )t ()t (f δ=δ;)t t ()t (f )t t ()t (f 000-δ=-δ;1dt )t t (),b ,a (t ba 00=-δ∈⎰) (1))1t ()1t (1)1t (t -δ=-δ⋅=-δ (3)21)3cos(dt )t ()3cos(dt )t ()3t cos(00=π-=δπ-=δπ-ω⎰⎰+∞+∞--2-2解:零输入响应为差分方程对应的齐次方程的解. 齐次方程为:0)2n (y 2)1n (y 3)n (y =-+-+特征方程: 0232=+λ+λ特征根: 2,121-=λ-=λ齐次方程的解为: n 2n 1zi )2(C )1(C )n (y -+-= 初始值:()421213)1(y 2)0(y 3)1(y 1452213)2(y 2)1(y 3)0(y =⎪⎭⎫⎝⎛-⨯--⨯-=---=-=⎪⎭⎫⎝⎛⨯-⎪⎭⎫ ⎝⎛-⨯-=----=由初始值确定齐次方程的解中常数C 1和C 2.4C 2C )1(y 1C C )0(y 2121zi =--=-=+=得C 1=2,C 2=-3.零输入响应:n n zi )2(3)1(2)n (y ---= 2-3解:(1)求零输入响应⎩⎨⎧-=-=-=-+-+5)2(y ,3)1(y 0)2n (y )1n (y 2)n (y特征方程: 0122=+λ+λ特征根: 121-=λ=λn 2n 1zi )1(C )1(n C )n (y -+-=初始值:()1312)1(y )0(y 2)1(y 1)5(32)2(y )1(y 2)0(y -=--⨯-=---=-=--⨯-=----=由初始值确定常数C 1和C 2.1C C )1(y 1C )0(y 212zi -=--=-==得C 1=2,C 2=-1. 零输入响应:)n ()1)(1n 2(0n ,)1()1(n 2)n (y nn n zi ε--=≥---=(2)求零状态响应⎪⎩⎪⎨⎧=-=-=-+-+0)2(y ,0)1(y )21(3)2n (y )1n (y 2)n (y n 初始值:29)21(332)21(3)1(y )0(y 2)1(y 3)21(3)2(y )1(y 2)0(y 0-=+⨯-=+---==+----= 特征根: 121-=λ=λ零状态响应: )n (y )1(C )1(n C )n (y p n 2n 1zs +-+-=)n (y p 为特解,由于,)21(3)n (f n =则设特解为n p )21(P )n (y =将代入方程得)2n (、y )1n (、y )n (y p p p --n 2n 1n n )21(3)21(P )21(P 2)21(P =++--得31p =n n 2n 1zs )21(31)1(C )1(n C )n (y +-+-=由初始值y(0)、y(1)确定常数C 1和C 2.29)21(31C C )1(y 331C )0(y 21zs 2zs -=+--==+=得C 1=2,C 2=8/3.零状态响应: )n ())21(31)1)(38n 2((0n ,)21(31)1(38)1(n 2)n (y n n n n n zs ε+-+=≥+-+-=(3) 全状态响应)n ())21(31)1)(35n 4(()n ())21(31)1)(38n 2(()n ()1)(1n 2()n (y )n (y )n (y n n n n n zs zi ε+-+=ε+-++ε--=+=2-6解: (1)阶跃响应s(t))t ()e 3231(0t ,e 3231)d e 1(e d e ))()((e d e ))(d )(d (e )t (s t 3t33t 0t 33t 0t 33t0t 3ε+=>+=τ+=ττε+τδ=ττε+ττε=--τ--τ--τ--⎰⎰⎰(2)冲激响应h(t))t (e 2)t ())t ()e 3231((dt d dt )t (ds )t (h t 3t3ε-δ=ε+==-- 2-7解:(1) (提示: 2t 1t t t 212211|)t (f *)t (f )t t (f *)t t (f ),t (t )t ()t (--→=--ε=ε*ε))2t ()2t (|)t (t |)t ()t ()5t (*)3t (2t t 2t t -ε-=ε=ε*ε=-ε+ε-→-→(3) (提示: )t (f *)t (f )t (f *)t (f ))t (f *)t (f (),t (f )t ()t (f 212121'='='=δ*))t ()te e ()t ()te ()t ()te e ()t ()te ()t ()te ())t (te ()t ())t (te ()t (*)t (te t t t t t t t t t t ε-=δ+ε-=ε'+ε'='ε=δ*'ε=δ'ε----------(5)[][])t (e 3)t ()]t (e [dtd)t ()]t (e [dt d )t (dt d )t (e )t (e dt d )t (e t 3t 3t 3t 3t t 3ε-δ=ε=δ*ε=δ*ε=δ*ε------(7) (提示: 2t 1t t t 2122112|)t (f *)t (f )t t (f *)t t (f ),t (t 21)t ()t (t --→=--ε=ε*ε)⎪⎪⎩⎪⎪⎨⎧≤≤>-<=-ε--ε=ε-ε=-ε*ε-εε=-ε-εε-→2t 0,t 212t ,2t 20t ,0)2t ()2t (21)t (t 21|)t (t 21)t (t 21)2t ()t (t )t (*)t (t )]2t ()t ([*)t (t 2222t t 22 2-8解:)t (e)t (y ))t ((*)t (h )t (y )t (y )t (y )t (e 3)t (y )t (*)t (h )t (y )t (y )t (y t3zi zi 2zi 2t 3zi zi 1zi 1ε=+ε-=+=ε=+ε=+=--由式(1)和(2)可得: )t (e )t (*)t (h t 3ε=ε- (3) 式(3)两边求导得:))t (e ())t (*)t (h (t 3'ε='ε-左边)t (h )t (*)t (h ))t (*)t (h (=δ='ε 右边)t (e 3)t ())t (e (t 3t 3ε-δ='ε-- 冲激响应:)t (e 3)t ()t (h t 3ε-δ=- 2-9解: (1) 单位响应(1) (2)⎩⎨⎧=-δ=--0)1(h )n ()1n (h 8.0)n (h 特征根8.0=λn )8.0(C )n (h =初值1)0()1(h 8.0)0(h =δ+-=1)8.0(C )0(h 0==得C=1, 单位响应为)n ()8.0()n (h 0n ,)8.0()n (h nn ε=≥=(2)阶跃响应)n ()8.01(5)8.0()i (h )n (s 1n ni in i ε-===+=-∞=∑∑(3)h(n)和s(n)图形 2-13解:)6n (*)n (a )n (*)n (a ))6n ()n ((*)n (a )n (f *)n (h )n (y n n n zs -εε-εε=-ε-εε==因为)n (a1a 1)n (*)n (a 1n nε--=εε+,所以 )6n (a1a 1)n (a 1a 1|)n (a1a 1)n (a 1a 1)6n (*)n (a )n (*)n (a )n (y 5n 1n 6n n 1n 1n nnzs -ε---ε--=ε---ε--=-εε-εε=-+-→++0 1 23nh(n )0.80.640.512…0 1 23ns(n)11.82.44…信号与系统习题解答(第3章,p103)) 3-1(1))4(F 41)t 4(f 1ω↔, )4(F d d 4j )]4(F 41[d d j)t 4(tf 11ωω=ωω↔*(2) )(F d d j )t (tf 1ωω↔, )(F )(F d dj )t (f )1t (11ω-ωω↔-* (3) ω-ω-↔--=-ω-↔-j 11e )(F ))1t ((f )t 1(f ),(F )t (f(4) )(F d d )(F )](F j [d d j)t (f t ),(F j )t (f 1111ωωω-ω-=ωωω↔'ωω↔' (5) 23j 1e )2(F 21))23t (2(f )3t 2(f ωω↔+=+3-2* (1) 根据傅氏变换的对称性质: )(f 2)t (F ),(F )t (f ω-π↔ω↔,及门函数的傅氏变换: )2(Sa )t (g ωττ↔τ,有 )(g 2)(g 2)2t (Sa ωτπ=ω-τπ↔ωττ π=τω=ωππ↔πππ4),(g 21)(g 42)t 2(Sa 44 则:⎩⎨⎧π>ωπ<ω=ω=ω↔-π=-π-π=ω-ω-πω-π2,02,e e )(g e )(g 22))2t (2(Sa 2)2t ()]2t (2sin[)t (f 2j 2j 42j 4(2) 根据傅氏变换的对称性质及单边指数函数的傅氏变换:ω+α↔εα-j 1)t (e t ,有 )](e [2jt1ω-επ↔+ααω,)](e [2jt 1ωεπ↔-ααω- 则:+∞<ω<-∞π=ωεπ+ω-επ↔-α++α=+ααωα-αω-αω,e 2)](e [2)](e [2jt 1jt 1t222* (1) π↔ωδ21)( )t sin(j )e e (21e 21e 21)()()(F 0t j t j t j t j 000000ωπ-=-π=π-π↔ω-ωδ-ω+ωδ=ωωω-ωω- (2) 解法1: )()()t cos(000ω-ωπδ+ω+ωπδ↔ω根据对称性质:)cos(2)cos(2)t ()t (0000ωωπ=ωω-π↔ω-πδ+ω+πδ))t ()t ((21)cos(000ω-δ+ω+δ↔ωω )5t ()5t ()5cos(2-δ++δ↔ω∴解法2: )t t (e ),t (10t j 0-δ↔δ↔ω-)5t ()5t (e e )5cos(25j 5j -δ++δ↔+=ω∴ω-ω3-4* (1) )t (f )t (y 2)t (y 3)t (y '=+'+'' 对微分方程两边取傅里叶变换2j 3)j (j )(F )(Y )(H )(F j )(Y )2j 3)j (()(F j )(Y 2)(Y j 3)(Y )j (222+ω+ωω=ωω=ωωω=ω+ω+ωωω=ω+ωω+ωω(2) )t (f 4)t (f )t (y 6)t (y 5)t (y +'=+'+'' 对微分方程两边取傅里叶变换6j 5)j (4j )(F )(Y )(H )(F )4j ()(Y )6j 5)j (()(F 4)(F j )(Y 6)(Y j 5)(Y )j (222+ω+ω+ω=ωω=ωω+ω=ω+ω+ωω+ωω=ω+ωω+ωω解法1:)]2(Sa )2(Sa [21)]()([*)2(Sa 21)]t [cos(F *)(G 21)]t (f [F )(F )t cos()t (g )t (f 1),2(Sa )2(Sa )]t (g [F )(G 000000ω-ω+ω+ω=ω-ωπδ+ω+ωπδωπ=ωωπ==ωω⨯==τω=ωττ==ωττττ 解法2:)]2(Sa )2(Sa [21)](G )(G [21)]t (f [F )(F )e e )(t (g 21)t cos()t (g )t (f 1),2(Sa )2(Sa )]t (g [F )(G 0000t j t j 000ω-ω+ω+ω=ω-ω+ω+ω==ω+=ω⨯==τω=ωττ==ωτωω-ττττ3-6ω++ω+=+ω+ω-ω+=ωj 11j 2123j 2j 3)(H 2,ω+α↔εα-j 1)t (e t)t ()e e (]j 11j 21[F )](H [F )t (h t t 211ε+=ω++ω+=ω=----)t ()e e (2)](Y [F )t (y j 22j 1223j 223j 2j 3j 5.11)(F )(H )(Y j 5.11)]t (e [F )(F t 2t ZS 1ZS 22ZS t 5.1ε-=ω=ω+-ω+=+ω+ω-=+ω+ω-ω+⨯ω+=ωω=ωω+=ε=ω----*3-7)2t ()e 1(2)t ()e 1(2)t (f *)t (f e )j 11j 1)((2)j 11j 1)((2j 11]e )j 1)((2)j 1)((2[)(F )(F )]t (f *)t (f [F j 11)(F ,e )j 1)((2)j 1)((2)(F )2t (t 21222121221-ε--ε-=ω+-ω+ωπδ-ω+-ω+ωπδ=ω+⨯ω+ωπδ+ω+ωπδ=ωω=ω+=ωω+ωπδ+ω+ωπδ=ω---ω-ω-ω-*3-8)t ()e 3e 2()](Y [F )t (y j 23j 12j 21j 1j 1)(F )(H )(Y j 21)]t (e [F )(F t 2t ZS 1ZS ZS t 2ε-=ω=ω+-ω+=ω+⨯ω+ω-=ωω=ωω+=ε=ω----3-9))sin()2(sin(2]e e [j 1]e e [j 1]e e e e [j 1)]t (f [F j 1)]t (f [F )(F e e e e )]t (f [F )2t ()1t ()1t ()2t ()t (f )2t ()1t ()1t ()2t ()t (f j j 2j 2j j 2j j 2j j 2j j 2j ω+ωω=-ω+-ω=--+ω='ω==ω--+='-δ+-δ-+δ++δ='-ε+-ε-+ε++ε=ω-ωω-ωω-ω-ωωω-ω-ωω信号与系统习题解答(第4章,p125))4-1(1) 2s 1s 2s 11)t (e )t (t 2++=+-↔ε-δ- (2) 3s 1)t (e t 3+↔ε-,根据复频域微分特性: 2t 3)3s (1)3S 1(ds d )t (te +=+-↔ε- (3) 1s s )t cos(2+↔,根据s 域平移性: 5s 4s 2s 1)2s (2s )t cos(e 2t2+++=+++↔- 4-4(1)解:2s 21s 222s 3s 222s 3s 6s 6s 2)s (F 222+-+++=++-=++++= )t ()e 2e 2()t (2]2s 2[L ]1s 2[L ]2[L )]s (F [L )t (f t 2t 1111ε-+δ=+-+++==∴------ (2)解:)t (e )3t 5()t (e 3)t (t e 5]1s 3[L ])1s (5[L ]1s 3)1s (5[L )]s (F [L )t (f 1s 3)1s (5)s (F 3|])1s )(s (F [dsd2k ,5|)8s 3(|)1s )(s (F 1k 1s 2k )1s (1k )1s (8s 3)s (F t tt 12121121s 21s 1s 222ε+=ε+ε=+++=+++==∴+++==+==+=+=+++=++=--------=-=-=4-52j 11|)2j 1s )(s (F k j 2j|)2j 1s )(s (F k 57|)2s )(s (F k 2j 1s k 2j 1s k 2s k )2j 1s )(2j 1s )(2s (3s )5s 2s )(2s (3s )s (F :解法12j 1s 32j 1s 22s 1321222+-=-+=+-=++==+=-++++++=-+++++=++++=+-=--=-=2j 1s 2j 112j 1s j 2j 2s 57)s (F -++-++++-++=t ),t 2sin 54t 2cos 52(e e 57)e 5j 2e 5j 2e 51e 51(e e 57)e 52j 1e 5j 21(e e 57e 2j 11e j 2j e 57)]s (F [F )t (f t t 2t 2j t 2j t 2j t 2j t t 2t 2j t 2j t t2t )2j 1(t )2j 1(t 21≥+-=-+++-=-++-=+-++-+==∴-----------+---)t ())t 2sin(e 2)t 2(cos(e 52e 57)t 2sin(e 54)t 2cos(e 52e 57)t (f 2)1s (2542)1s ()1s (522s 572)1s (58)1s (522s 575s 2s 2s 522s 57)s (F 2k ,52k ,57k :得3k 2k 50k k 2k 21k k 令)5s 2s )(2s (k 2k 5s )k k 2k 2(s )k k (5s 2s k s k 2s k )5s 2s )(2s (3s )s (F :解法2t t t 2t t t 222222223213132121231321221232122ε+-=--=∴++⨯-+++-+=++++-+=+++-+=-=-==⎪⎩⎪⎨⎧=+=++=++++++++++=+++++=++++=------4-6解:(1)零输入响应:⎩⎨⎧-='==+'+''--1)0(y ,1)0(y 0)t (y 6)t (y 5)t (y 对微分方程取拉氏变换,可得0)s (Y 6))0(y )s (sY (5)0(y )0(sy )s (Y s 2=+-+'----- 3s 12s 2)3s )(2s (4s 6s 5s 4s )s (Y 2+-++=+++=+++=)t ()e e 2()]s (Y [L )t (y t 3t 21si ε-==---(2)零状态响应:⎪⎩⎪⎨⎧='=ε=+'=+'+''--0)0(y ,0)0(y )t ()t cos(5)t (f )t (f 6)t (f 2)t (y 6)t (y 5)t (y 对微分方程取拉氏变换,可得)s (F 6)s (sF 2)s (Y 6)s (sY 5)s (Y s 2+=++1s s5)s (F 2+=)t ())6.26t cos(52e 4()t sin(2)t cos(4e 4)t (y 1s 21s s 42s 41s 2s 42s 4)1s )(2s (s 10)1s )(6s 5s (s 30s 106s 5s )s (F 6)s (sF 2)s (Y t 2t 2zs 22222222ε-+-=++-=+++++-=++++-=++=++++=+++=-- (3)全响应:)t ())6.26t cos(52e e 2()t (y )t (y )t (y t 3t 2zi zs ε-+--=+=--4-7解:对微分方程取拉氏变换,可得)s (sF 2)s (F s )s (Y 13)s (sY 6)s (Y s 22+=++13s 6s )s (F )s 2s ()s (Y 22+++= 系统函数为:22222)3s ()2s (s 13s 6s s 2s )s (F )s (Y )s (H +++=+++==零点为: 0,-2; 极点为: -3+j2,-3-j24-8 解:)t (f *)t (s )t (f *)t (h )t (y zs '==取拉氏变换,可得:)s (F )]t (s [L )s (Y zs ⨯'=σ2s s1)]t (s [sL )]t (s [L +-==',2zs )2s (12s 1s 1)s (Y +-+-=2s 5.0s 1s 4s 24s 2s s 1)2s (12s 1s 1)s )](t (s [L )s (Y )s (F 22zs ++=++=+-+-+-='= )t ()e 5.01()t (f t 2ε-=∴-4-9 (1)5s 2s 1s )s (H 2+++=解: 命05s 2s 2=++,得H(s)的二个极点为: p1=-1+j2, p2=-1-j2.由于p1、p2均位于s 平面左半面,故系统是稳定的.(2) )5s )(2s 3s (1s )s (H 22++++=解: 命0)5s )(2s 3s (2=+++,得H(s)的3个极点为: p1=-1, p2=-2, p3=-5.由于p1、p2、p3均位于s 平面左半面,故系统是稳定的.。
