河北省涞水县高中数学第二章点、直线、平面之间的位置关系2.1.2空间中直线与直线之间的位置关系课件新
高中数学《第二章点、直线、平面之间的位置关系2.1空间点、直线、平面之间的位置关系》19PPT课件

例题讲解
例:下列命题中正确的个数是( ) ① 若一条直线有无数个点不在一个平面内,则这条直
线与这个平面平行 ② 若一条直线与一个平面平行,则这条直线与这个平
面内的任意一条直线都平行 ③ 如果两条平行直线中的一条与一个平面平行,那么
另一条直线也与这个平面平行 ④ 若一条直线与一个平面平行,这这条直线与这个平
异面直线:不同在任何一个平面内,没有公共点
情境创设
问题1:把一支笔和一张纸分别看作一条直线和一 个平面,那么这条直线和这个平面会有怎样的位 置关系呢? 问题2:如图,线段A'B'所在直线与长方体ABCDA'B'C'D'的六个面所在平面有几种位置关系?
一、空间中直线与平面的位置关系
互动探究
平行于同一平面的两条直线一定平行吗? 过平面外一点可以作多少条直线与这个平面平行? 若一条直线平行一个平面,则这条直线与这个平
② 要证明直线与平面相交,只需说明直线与平面 只有一个公共点;
③ 要证明直线与平面平行,则必须说明直线与平 面没有公共点。
平面与平面位置关系的判断方法 ① 要证明两个平面平行,只要说明两个平面没有 公共点;
② 两个平面只要有一个公共点,那么它们就有一 条过该公共点的直线,这两个平面相交。
综合应用
面内的任意一条直线都没有公共点
A.0 B.1 C.2
D.3
针对训练
a 若直线 不平行于平面 ,且 a,则下
列结论成立的是( )
A. 内的所有直线与 a 异面 B. 内不存在与 a 平行的直线 C. 内存在唯一的直线与 a 平行 D. 内的直线与 a 都相交
情境创设
问题1:两张不重合的纸所在的平面可能有几种位 置关系?
高中数学《第二章点、直线、平面之间的位置关系2.1空间点、直线、平面之间的位置关系》100PPT课件

问位置关系?空间两直线有哪几 种位置关系?
2.就空间点、线、面位置关系而言, 还有哪几种类型有待分析?
复习: 空间中直线与平面有三种位置关系
(1)直线在平面内---有无数个公共 点;
(2)直线与平面相交---有且只有一个 公共点;
直线.
公共点; (3)直线与平面平行——没有公共点.
二、两个平面之间有两种位置关系:
课堂小结
一、直线与平面有三种位置关系: (1)直线在平面内——有无数个公共点; (2)直线与平面相交——有且只有一个
公共点; (3)直线与平面平行——没有公共点.
二、两个平面之间有两种位置关系: (1)两个平面平行——没有公共点; (2)两个平面相交——有且只有一条公共
C′ B′
C
A
B
思考3:由上面的观察和分析可知,两 个平面的位置关系只有两种,即两个平 面平行,两个平面相交.这两种位置关 系的基本特征是什么?
(1)两个平面平行---没有公共点; (2)两个平面相交---有一条公共直线.
思考4:下图表示两平面之间的两种位置, 如何用符号语言描述这两种位置关系?
β α
//
l
I l
课堂小结
一、直线与平面有三种位置关系: (1)直线在平面内——有无数个公共点; (2)直线与平面相交——有且只有一个
公共点; (3)直线与平面平行——没有公共点.
课堂小结
一、直线与平面有三种位置关系: (1)直线在平面内——有无数个公共点; (2)直线与平面相交——有且只有一个
(3)直线与平面平行---没有公共点.
a α
a
a
a
.P
α
α
高中数学第二章点、直线、平面之间的位置关系2.1空间点、直线、平面之间的位置关系2.1.3空间中直线

第十一页,共17页。
题型一
题型二
反思空间中直线与平面只有三种位置关系(guān xì):直线在平面内、直线 与平面相交、直线与平面平行.在判断直线与平面的位置关系(guān xì)时, 这三种情况都要考虑到,避免遗漏.正方体(长方体)是立体几何中的重要模 型,直线与平面的位置关系(guān xì)都可以在这个模型中得到反映,故我们 可以把要判断位置关系(guān xì)的直线、平面放在正方体(长方体)中,以 便正确作出判断,避免凭空臆断.
3.会用符号语言和图形语言表示直线和平面、平面和平面之间的位置关 系.
第二页,共17页。
1
2
1.空间中直线与平面(píngmiàn)的位置关系
位置 关系 公共 点
直线 a 在平面 α 内 直线 a 与平面 α 相交 直线 a 与平面 α平行
有无数个公共点
有且只有一个公共 点
没有公共点
图形 表示
符号 表示
是
.
答案:平行
第八页,共17页。
两个相交平面(píngmiàn)的画法 剖析:
第九页,共17页。
题型一
题型二
题型一 判断直线与平面的位置关系
【例1】 如图,A'B与长方体ABCD-A'B'C'D'的六个面所在的平面有什 么(shén me)位置解:因为直线A'B与平面ABB'A'有无数个公共(gōnggòng)点, 所以直线A'B在平面ABB'A'内. 因为直线A'B与平面ABCD,BCC'B'都有且只有一个公共(gōnggòng)点B, 所以直线A'B与平面ABCD,BCC'B'相交. 因为直线A'B与平面ADD'A',A'B'C'D'都有且只有一个公共(gōnggòng)点A',所 以直线A'B与平面ADD'A',A'B'C'D'相交. 因为直线A'B与平面DCC'D'没有公共(gōnggòng)点, 所以直线A'B与平面DCC'D'平行.
高中数学《第二章点、直线、平面之间的位置关系2.1空间点、直线、平面之间的位置关系》111PPT课件
A
A
(2)空间中线与线的位置关系
图形
b a
文字语言(读法)
两直线共面且无公 共点两直线平行
符号语言 a∥b
Ab a
两直线共面且有一个 aIb=A 公共点两直线相交
b a
两直线不共面且无 公共点两直线异面
a、b异面
(3)空间中线与面的位置关系
图形
a
文字语言(读法)
直线与平面无公共 点直线与平面平行
• ⑤用三种语言描述平面与平面之间的位置 关系.
两个平面的位置关系 有且只有两种:
位置关系 两平面平行
两平面相交
公共点 符号表示
没有公共点 α∥β
有一条公共直线
α∩β=a
图形表示
练习P50:1. 金版学案例题1, 2。 探究:思考?
2 如பைடு நூலகம்三个平面两两相交,那么它们的交线 有多少条?画出图形表示你的结论。 答:有可能1条,也有可能3条交线。
符号语言
a∥
a
A
直线与平面有一个公
共点直线与平面相交 aI =A
a 直线上所有的点都在
平面内直线在平面内
a
(4)空间中面与面的位置关系
图形
文字语言(读法)
符号语言
两个平面无公共点 两个平面平行
α∥β
β
两个平面有一公共直线 I l
α
两个平面相交
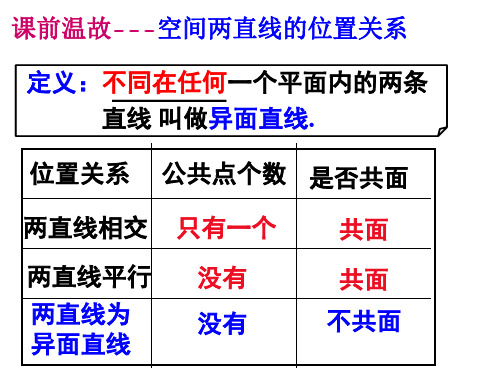
课前温故---空间两直线的位置关系
定义:不同在任何一个平面内的两条 直线 叫做异面直线.
位置关系 公共点个数 是否共面
两直线相交 只有一个 共面
两直线平行
两直线为 异面直线
没有 没有
共面 不共面
直线与平面的位置关系有且只有三种:
高中数学《第二章点、直线、平面之间的位置关系2.1空间点、直线、平面之间的位置关系》132PPT课件

图1
图2
两个平面相交画法
两个平面的位置关系
位置关系 公共点 符号表示
两平面平行 没有公共点
α∥β
两平面相交 有一条公共直线
α∩β=a
图形表示
教材第50页练习题
3个平面把空间分成几部分?
(1)
4
(2) 6
(3) 6
(4) 7
(5) 8
六、作业:
1.画出满足下列条件的图形。 a∥α,b∩α=A,a∩b=B
这两个平面互相平行.
(2)两个平面相交 如果两个平面有公共点,它们就相交于
一条过该公共点的直线,我们就说这两个平 面相交 . (3)两个平面的位置关系只有两种
①两个平面平行——没有公共点;记为 //
②两个平面相交——有一条公共直线,记为 I a
(4)两个平面平行的画法
画两个互相平行的平面时,要注意使表示 平面的两个平行四边形的对应边平行,如图1, 而不应画成图2那样.
学习目标
重难点
1.了解空间两个平面的位置关系。 2.会判断两个平面的位置关系。 3.空间中三个平面之间的位置关系。
探究平面与平面之间的位置关系
第一、二层的底面α和β无
论怎样延伸都没有公共点;
B
A
前、后两面房顶γ和δ则
有一条交线AB.
二层楼房示意图
一、两个平面的位置关系
(1)两个平面平行 如果两个平面没有公共点,我们就说
高中数学《第二章点、直线、平面之间的位置关系2.1空间点、直线、平面之间的位置关系》792PPT课件

(1) 这两条直线共面吗?
(2) 直线 a与平面相交吗?
a
b
直线与平面平行的判定定理:
直线与平面平行的判定定理:
平面外的一条直线与此平面内的一 条直线平行,则该直线与此平面平行.
直线与平面平行的判定定理: 平面外的一条直线与此平面内的一
条直线平行,则该直线与此平面平行.
a
b
直线与平面平行的判定定理:
(3)与直线AA1平行的 D1
平面是:
A1
D
A
C1 B1
C B
小试身手
例2. 如图,长方体的六个面都是矩形,则 (1)与直线AB平行的平面是:
平面A1C1和平面DC1
(2)与直线AD平行的平面是: 平面BC1和平面A1C1
(3)与直线AA1平行的 D1
平面是:
A1
D
C1 B1
C
A
B
小试身手
例2. 如图,长方体的六个面都是矩形,则
小试身手 例2. 如图,长方体的六个面都是矩形,则 (1)与直线AB平行的平面是:
(2)与直线AD平行的平面是:
(3)与直线AA1平行的 D1
平面是:
A1
D
A
C1 B1
C B
小试身手 例2. 如图,长方体的六个面都是矩形,则 (1)与直线AB平行的平面是:
平面A1C1和平面DC1
(2)与直线AD平行的平面是:
(1)与直线AB平行的平面是: 平面A1C1和平面DC1
(2)与直线AD平行的平面是: 平面BC1和平面A1C1
(3)与直线AA1平行的 D1
平面是:
A1
平面BC1和
D
平面DC1
A
C1 B1
高中数学必修2第二章点、线、面的位置关系知识点+习题+答案
D B A α 相交直线:同一平面内,有且只有一个公共点; ] ]; a 来表 a a 线线平行 A ·α C ·B · A · α P· αLβ 共面直线p线面平行 面面平行 作用:可以由平面与平面平行得出直线与直线平行叫做垂足。
叫做垂足。
的垂线,则这两个ba第 3 页 共 3 页aa b a b //,a a a ÞþýüË^^1、性质定理:垂直于同一个平面的两条直线平行。
符号表示:符号表示:b a b a //,Þ^^a a 2、性质定理:一条直线与一个平行垂直,那么过这条直线的平面也与此平面垂直 符号表示:b a b a ^ÞÌ^a a ,2.3.4平面与平面垂直的性质1、性质定理:、性质定理: 两个平面垂直,则一个平面内垂直于交线的直线与另一个平面垂直。
符号表示:b b a a b a ^Þïþïýü=^Ì^a l l a a ,2、性质定理:垂直于同一平面的直线和平面平行。
符号表示:符号表示:符号表示:一、异面直线所成的角一、异面直线所成的角1.已知两条异面直线,a b ,经过空间任意一点O 作直线//,//a a b b ¢¢, 我们把a ¢与b ¢所成的锐角(或直角)叫异面直线,a b 所成的角。
所成的角。
2.角的取值范围:090q <£°;垂直时,异面直线当b a ,900=q二、直线与平面所成的角二、直线与平面所成的角1. 定义:平面的一条斜线和它在平面上的射影所成的锐角,叫这条斜线和这个平面所成的角2.角的取值范围:°°££900q 。
三、两个半平面所成的角即二面角:三、两个半平面所成的角即二面角: 1、从一条直线出发的两个半平面所组成的图形叫做二面角。
高中数学《第二章点、直线、平面之间的位置关系2.1空间点、直线、平面之间的位置关系》59PPT课件
A.有限个 B.无数个 C.一个也,直线AB与直线CC1异面,平面ABCD与平面CDD1C1相交,有 无数个公共点;平面ABB1A1与平面CDD1C1平行,没有公共点.
答案:D
【变式训练2】 α、β是两个不重合的平面,在下列条件中,可判定 α∥β的 是( ) A.α、β都平行于直线l、m B.α内有三个不共线的点到β的距离相等 C.l、m是α内的两条 直线,且l∥β,m∥β D.l、m是两条异面直线,且l∥α、m∥α、l∥β,m∥β
题型一
反思判断两个平面之间的位置关系时,根据定义,只需判断这两个 平面是否有公共点即可.若有公共点,则它们相交,否则,它们平行.
【例2】如果三个平面两两相交,那么它们的交线有多少条? 画出图形表示你的结论.
解:三个平面两两相交,它们的交线有一 条或三条,如下图.
题型一
【变式训练1】 若两个平面内分别有一条直线,且这两条直线是 异面直线,则这两个平面的公共点的个数是( )
1
【做一做】 若平面α和平面β无公共点,则α和β的位置关系
是
.
答案:平行
两个相交平面的画法 剖析:
题型一
题型一 判断两个平面之间的位置关系
【例1】 如图,平面ABC与三棱柱ABC-A1B1C1的其他面所在平面之 间有什么位置关系?
解:因为平面ABC与平面A1B1C1无公共点, 所以平面ABC与平面A1B1C1平行. 因为平面ABC与平面ABB1A1有公共直线AB, 所以平面ABC与平面ABB1A1相交. 同理可得平面ABC与平面ACC1A1及平面BCC1B1均相交.
2.1.4 平面与平面之间的位置关系
1.了解平面与平面之间的两种位置关系,并能判断两个平面的位 置关系.
高中数学《第二章点、直线、平面之间的位置关系2.1空间点、直线、平面之间的位置关系》783PPT课件
××版 ×修×
公理3
文字 如果两个不重合的平面有一个__公__共__点____,那么它 语言 们有且只有一条过该点的公共___直__线_____
图形 语言
符号语言 (1)
作用 (2) (3)
P∈α∩β⇒α∩β=l且___P_∈__l____ 判定平面相交 证明点共线 证明线共点
××版 ×修×
• [名师点拨] 公理3反映了两个平面的位置关系,条件可简记 为“两面共一点”,结论是“两面共一线,且线过点,线唯 一”.
• (2)证明点线共面的常用方法 • ①纳入平面法:先由公理2或其推论确定一个平面,再由公理
1证明有关点线在此平面内.
• ②辅助平面法:先证明有关的点线确定平面α,再证明其余 元素确定平面β,最后证明平面α,β重合.
××版 ×修×
练习1
• 过直线l外一点P,引两条直线PA,PB和直线l分别交于A,B两 点,求证:三条直线PA,PB,l共面.
××版 ×修×
谢谢
• (2)公理2中“有且只有一个”的含义要准确理解,这里的“有 ”是说图形存在,“只有一个”是说图形唯一,强调的是存在 和唯一两个方面,因此“有且只有一个”必须完整地使用,不 能仅用“只有一个”来代替,否则就没有表达出存在性.确定 一个平面中的“确定”是“有且只有”的同义词,也是指存在 性和唯一性这两个方面,这个术语今后也会常常出现.
∵E,H 分别为 BC,AB 的中点,∴EH 綊12AC.
∵DF∶FC=1∶2,DG∶GA=1∶2, ∴FG∥AC,FG=13AC,∴EH∥FG 且 EH≠FG, ∴E,F,G,H 四点共面且 EF∥\ GH.∴EF 与 GH 相交.
××版 ×修×
• 设EF∩GH=O,则O∈GH,O∈EF. • ∵GH⊂平面ABD,EF⊂平面BCD, • ∴O∈平面ABD,O∈平面BCD. • ∵平面ABD∩平面BCD=BD,
高中数学 2.1 空间点、直线、平面之间的位置关系 2.1.
2.1.2 空间中直线与直线的位置关系教学目标1.知识与技能:(1)了解空间中两条直线的位置关系.(2)理解异面直线的概念、画法;(3)理解并掌握公理4、等角定理;(4)异面直线所成角的定义、范围及应用.2.过程与方法:培养学生的画图能力和空间想象能力;增强学生应用数学的意识,进一步培养学生将空间问题转化为平面问题的能力和逻辑思维能力,培养学生分析问题、解决问题的能力3.情感态度价值观:通过问题情境的设置,使学生认识到数学是从实际中来的,让学生感受到掌握空间两直线位置关系的必要性,进而增强学习的兴趣.培养学生主动探究知识、合作交流的意识,在体验数学美的过程中激发学生的学习兴趣,从而培养学生勤于思考、勤于动手的良好品质. 【重点难点】1.教学重点:1、异面直线的概念.2、公里4及等角定理.2.教学难点:异面直线所成角的计算.【教学策略与方法】1.教学方法:启发讲授式与问题探究式.2.教具准备:多媒体教学过程一、复习引入1.以长方体模型的12条棱所在直线的位置关系引入课题。
二、新课讲解1.异面直线的定义:不同在任何一个平面内的两条直线叫做异面直线。
注1:两直线异面的判别一 : 两条直线既不相交、又不平行.两直线异面的判别二 : 两条直线不同在任何一个平面内.2.空间两直线的位置关系a b 按平面基本性质分 (1)同在一个平面内:相交直线、平行直线(2)不同在任何一个平面内:异面直线按公共点个数分 (1)有一个公共点: 相交直线(2)无公共点:平行直线、异面直线例1:下图长方体中(1)说出以下各对线段的位置关系? ①EC 和BH 是 相交 直线 ②BD 和FH 是 平行 直线 ③BH 和DC 是 异面 直线 (2)与棱 A B 所在直线异面的棱共有 4 条?(3)与面对角线AF 所在直线异面的棱共有_6___条?(4)与体对角线AG 所在直线异面的棱共有_6___条?3.异面直线的画法说明: 画异面直线时 , 为了体现它们不共面的特点。
