压杆稳定实验报告数据处理
实验四在轴心受压荷载作用下钢结构柱整体压杆稳定试验

实验四 在轴心受压荷载作用下钢结构
柱整体压柱的轴心受压试验,加 深对受压杆件由于受长细比影响,而不 是由强度控制,而是随受压荷载的增加, 逐步弯曲失稳而失去承载力的认识。 2.验证钢柱轴心受压整体抗压稳定计算 公式。
二、试验内容和要求
1.量测在各级荷载下的钢柱中间断面的 应力—应变值; 2.量测在各级荷载下钢柱中间挠度值; 3.观察钢柱由于弯曲失稳而丧失承载力 的过程和特征; 4.记下钢柱失稳破坏荷载,并将试验值 与理论值进行比较。
四、试验方法
2.试验方法与试验步骤 1)试件安装:严格几何对中,试件初弯曲,初 偏心不大于3mm; 2)分级加载:按设计承载力的10%为一级,加 至80%时,减至5%为一级加荷; 3)每级荷载下测量其杆件中间挠度和应力—应 变值; 4)观察压杆整体失稳过程,记录失稳荷载。
五、注意事项
• 认真阅读试验指导书及相关参考资料, 明确本次试验的目的和要求。熟悉加载 装置和试件安装方法,了解试验方法和 测试内容。
三、试件和材料力学性能试验
1.采用圆形无缝钢管制 作,壁厚为4.5mm,总 高度为2.8m,如图所示。
2.钢材为Q235B.F。
3.设计整体失稳承载力 为165—195kN范围内。
四、试验方法
1.加载设备; 1)5000kN或2000kN压力试验机,直接加载试 验。 2)钢结构反力架,320kN油压千斤顶加载。 3)电阻应变仪,测量钢柱中间应力—应变值。 4)百分表或位移传感器测量中间挠度。
压杆稳定实验

《创新型力学实验》压杆稳定临界载荷测定综合实验一、实验目的1.熟悉动态应变仪的使用方法; 2.掌握振动信号的测量方法; 3.测量受压细长杆件失稳时的临界力; 4.讨论不同杆端约束条件对临界力的影响; 5.将材料力学方法与振动法测量结果进行比较,讨论两种方法的优缺点; 6.计算临界力,验证欧拉公式,并分析产生误差的原因。
二、实验仪器设备动态信号分析仪、压杆稳定综合实验装置、电阻应变片、电涡流传感器、力锤、力传感器读数器、电涡流读数器矩形截面钢制细长杆件(弹性模量E=180GPa )三、实验原理细长杆作垂直轴线方向的振动时,其主要变形形式是弯曲变形,通常称为横向振动或弯曲振动,简称梁的振动。
如果梁是直梁,而且具有对称面,振动中梁的轴线始终在对称面内。
忽略剪切变形和截面绕中心轴转动的影响,即所谓的欧拉梁。
它作横向振动时的偏微分方程为:()()()()()t x q t t x y x A x t x y x EI x ,,,222222=∂∂⋅+⎥⎦⎤⎢⎣⎡∂∂∂∂ρ (4-6) EI(x)为弯曲刚度(E 为纵向弹性模量,I(x)为截面惯性矩),()x ρ为密度,A(x)为截面积,q(x,t)为分布干扰力,y(x,t)为挠度。
若梁为均质、等截面时,截面积A(x)、弯曲刚度EI(x)、密度()x ρ均为与x 无关的常量,因此,式(4-6)可写成:()()()()t x q t t x y x A x t x y EI ,,,2244=∂∂⋅+∂∂ρ (4-7) 如果梁在两端轴向力T 0的作用下自由振动,其振动的偏微分方程为:()()()0,,,222202222=∂∂⋅+∂∂-⎥⎦⎤⎢⎣⎡∂∂∂∂t t x y A x t x y T x t x y EI x ρ (4-8)对于等截面梁,设:()()()ϕω+⋅=t x Y t x y n sin , (4-9)可得()()()0422244=-⋅-x Y k dxx Y d a dx x Y d (4-10) 式中 EI T a 0=, EIA k n ρω⋅=24 振型函数()x Dsh x Cch x B x A x Y 2211sin cos λλλλ+++= (4-11)式中 442142k a a ++-=λ, 442242k a a ++=λ (4-12) 设l k l i i =λ,0T 为轴向拉力,求得频率为:EIl k l T A EI l l k i i ni 22022)(1)(+=ρω (4-13) 此时相当于增加了梁的刚度。
压杆稳定小结
压杆稳定小结1、 压杆稳定的概念稳定平衡是指干扰撤去后可恢复的原有平衡;反之则为不稳定平衡。
压杆稳定性是指压杆保持或恢复原有平衡状态的能力。
压杆的临界压力是指压杆由稳定平衡转变为不稳定平衡时所受轴向压力的界限值,用cr F 来表示。
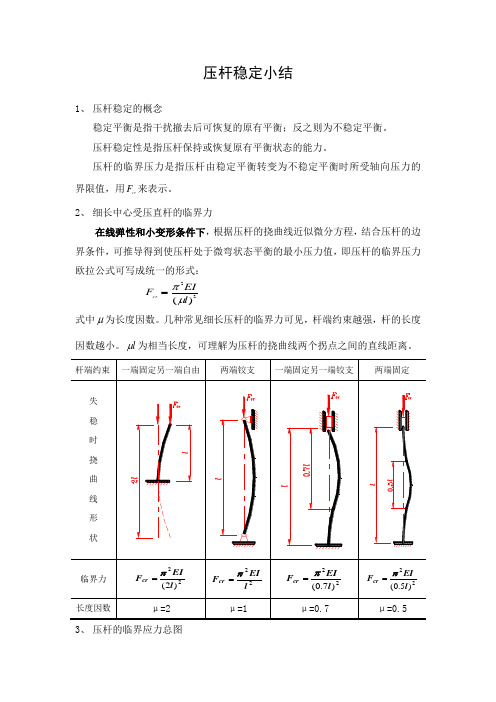
2、 细长中心受压直杆的临界力在线弹性和小变形条件下,根据压杆的挠曲线近似微分方程,结合压杆的边界条件,可推导得到使压杆处于微弯状态平衡的最小压力值,即压杆的临界压力欧拉公式可写成统一的形式:22)(l EIF crμπ=式中μ为长度因数。
几种常见细长压杆的临界力可见,杆端约束越强,杆的长度因数越小。
l μ为相当长度,可理解为压杆的挠曲线两个拐点之间的直线距离。
(d)(d)(d)3、 压杆的临界应力总图(1) 压杆的临界应力压杆在临界力作用下,其横截面上的平均应力称为压杆的临界应力, crcr F Aσ=(2) 欧拉公式的适用范围线弹性范围,()22cr cr p 22F EI E A l A ππσσλμ===≤ 即p λλ≥= 时,欧拉公式才能适用。
通常称p λλ≥的压杆为大柔度压杆或细长压杆。
(3) 压杆的柔度(或长细比)i l μλ=是一无量纲的量。
一般情况下,由于杆端约束(μ)或惯性半径(i )的不同,压杆在不同的纵向平面内具有不同的柔度值,压杆失稳首先发生在柔度最大的纵向平面内。
(4) 临界应力总图压杆的临界应力随柔度λ变化的λσ-cr 图称为临界应力总图。
大柔度杆p λλ≥,临界应力低于比例极限,可按欧拉公式计算,22λπσEcr= ;中柔度杆p s λλλ≤≤,临界应力超过比例极限,可按经验公式计算,如直线公式: λσb a cr -=,其中a 、b 为与材料有关的常数。
或钢结构设计中采用的抛物线公式,以及折减弹性模量理论进行计算;图13-12小柔度杆s λλ≤(或b λ),临界应力达极限应力:塑性材料s cr σσ=,脆性材料cr b σσ=,属于强度问题。
10压杆稳定解析

第十章压杆稳定30mm1m两根相同材料(松木)制成的杆,σb =20MPa ;A =10mm ×30mm短杆长:l =30mm ; FFFF长杆长:l =1000mm第一节 压杆稳定的概念一、稳定问题的提出若按强度条件计算,两根杆压缩时的极限承载能力均应为:F = σb A =6kN(1)短杆在压力增加到约为6kN时,因木纹出现裂纹而破坏。
(2)长杆在压力增加到约4kN时突然弯向一侧,继续增大压力,弯曲迅速增大,杆随即折断。
30mm1m FFFF压杆的破坏实验结果:• 短压杆的破坏属于强度问题;30mm1mFFFF• 长压杆的破坏则属于能否保持其原来的直线平衡状态的问题结论:短压杆与长压杆在压缩时的破坏性质完全不同压杆稳定性:压杆保持其原来直线平衡状态的能力。
压杆不能保持其原来直线平衡状态而突然变弯的现象,称为压杆的直线平衡状态丧失了稳定,简称为压杆失稳。
压杆失稳的严重后果:19世纪,瑞士的孟汗太因桥突然倒塌,造成200人遇难。
1907年加拿大的魁北克桥在建造时突然倒塌,其原因都是因为桥梁桁架中的受压杆失稳引起的。
1909年12月汉堡一个60万m3的大型贮气罐因一个受压构件失稳而突然倒塌。
研究压杆稳定性的意义:压杆因强度或刚度不足而造成破坏之前一般都有先兆;压杆由于失稳而造成破坏之前没有任何先兆,当压力达到某个临界数值时就会突然破坏,因此这种破坏形式在工程上具有很大的破坏性。
在建筑工程中的受压上弦杆、厂房的柱子等设计中都必须考虑其稳定性要求。
二、平衡状态的类型稳定平衡:干扰平衡的外力消失后,物体能自动恢复到原来的平衡位置的平衡不稳定平衡:即使干扰平衡的外力消失后,物体仍继续向远离原来平衡位置的方向继续运动的平衡。
随遇平衡:干扰平衡的外力消失后,物体可在任意位置继续保持平衡。
显然,随遇平衡是界于稳定平衡与不稳定平衡之间的状态,称为临界平衡状态。
F PF P 三、压杆临界力F crlF PF PF FF P F P F < F PcrF P F PF= F PcrF P F PF> F Pcr稳定直线平衡状态 不稳定平衡状态临界状态 压杆处于临界状态时的轴向压力称为压杆的临界力F cr 。
哈工大材力上机实验报告

材料力学电算实验压杆的临界力计算院系:机电工程学院班级:设计者:学号:指导教师:张桂莲软件要求:设计时间:一.概述:本程序使用Microsoft Visual Basic编写,可以对不同材料、不同约束类型、不同截面类型的压杆进行临界力的计算。
杆件的参数可以输入,得出结果之后也可以清零。
二、问题分析及相关公式:1、压杆稳定当短粗杆受压时(图1),在压力F由小逐渐增大的过程中,杆件始终保持原有的直线平衡形式,直到压力F达到屈服强度载荷F s(或抗压强度载荷F b),杆件发生强度破坏时为止。
但是,如果用相同的材料,做一根与图1a所示的同样粗细而比较长的杆件(图1b),当压力F比较小时,这一较长的杆件尚能保持直线的平衡形式,而当压力F逐渐增大至某—数值F1时,杆件将突然变弯,不再保持原有的直线平衡形式,因而丧失了承载能力。
我们把受压直杆突然变弯的现象,称为丧失稳定或失稳。
此时,F1可能远小于F s (或F b)。
可见,细长杆在尚未产生强度破坏时,就因失稳而破坏。
图1在研究压杆稳定时,我们用一微小横向干扰力使处于直线平衡状态的压杆偏离原有的位置,如图1所示。
当轴向压力F由小变大的过程中,可以观察到:1)当压力值F1较小时,给其一横向干扰力,杆件偏离原来的平衡位置。
若去掉横向干扰力后,压杆将在直线平衡位置左右摆动,最终将恢复到原来的直线平衡位置。
2)当压力值F2超过其一限度F cr时,平衡状态的性质发生了质变。
这时,只要有一轻微的横向干扰,压杆就会继续弯曲,不再恢复原状,。
3)界于前二者之间,存在着一种临界状态。
当压力值正好等于F cr时,一旦去掉横向干扰力,压杆将在微弯状态下达到新的平衡,既不恢复原状,也不再继续弯曲,。
临界状态是杆件从稳定平衡向不稳定平衡转化的极限状态。
压杆处于临界状态时的轴向压力称为临界力或临界载荷,用F cr表示。
2、两端铰支细长压杆的临界力图2为一两端为球形铰支的细长压杆,其临界力公式为:图222lEIF cr π=(1)式(1)又称为欧拉公式。
工程力学上册15压杆稳定

压杆的稳定性直接关系到这些结构物的安全性和可靠性,一旦发生失稳,可能会导致结构物的破坏和倒塌,造成严重的人员伤亡和财产损失。
因此,对压杆稳定性的研究和分析是工程力学中非常重要的一个方面,也是工程设计和安全评估的重要依据。
压杆稳定的重要性
02
压杆的分类与特性
总结词
长细比是描述压杆细长程度的重要参数,对临界力的影响显著。
工程力学上册15压杆稳定
目录
压杆稳定概述 压杆的分类与特性 压杆稳定的影响因素 压杆稳定的计算方法 压杆稳定的实验研究 工程实例分析
01
压杆稳定概述
01
02
压杆稳定的定义
当压杆受到的力小于其临界力时,压杆保持稳定平衡;当压杆受到的力大于其临界力时,压杆将发生屈曲失稳。
压杆稳定是指压杆在受到外力作用时,能够保持其原有平衡状态的能力。
03
压杆稳定的影响因素
压杆在制造过程中可能会产生弯曲,这种弯曲在受力时会进一步发展,导致压杆失稳。
为了提高压杆的稳定性,应尽量减小初始弯曲,可以通过提高制造精度和选用合适的材料来实现。
初始弯曲的影响
减小初始弯曲
初始弯曲
材料在加工过程中会形成残余应力,这些应力会在受力时对压杆的稳定性产生影响。
残余应力
结论应用
将实验结论应用于实际工程中,指导压杆结构的合理设计和应用。
实验结果与分析
06
工程实例分析
桥梁结构的压杆稳定分析
总结词:桥梁结构的压杆稳定分析是确保桥梁安全的重要环节,需要考虑多种因素,如材料特性、载荷分布和支撑条件等。
高层建筑的压杆稳定分析
总结词:高层建筑的压杆稳定分析是确保高层建筑安全的重要环节,需要考虑多种因素,如建筑高度、材料特性、风载荷和地震载荷等。
压杆稳定实验指导

t
=
Eε=Eεds/2。由弯矩产生的测点处的正应力可表达为:
t
i
上式可见, 在一定的荷载F作用下,应变仪读数εds的大小反映了压杆挠度δ的大 小。 所以可用电测应变的方法来确定临界载荷
t 。这只要在压杆中间截面两边贴 t。
ti
t
i
(3)
t
i
,所以
上电阻应变片按互补偿半桥接法接到应变仪上,随着荷载F的增加测得相应的应变 值ε,绘制F-ε曲线,根据实验曲线作渐近线即得临界载荷
二.实验原理
thh),压杆 根据欧拉小挠度理论,对于两端铰支的大柔度杆(低碳钢 u 保持直线平衡最大的载荷,保持曲线平衡最小载荷即为临界载荷 t,按照欧拉公式 可得: t (1) t t 式中E―材料的弹性模量,I―试件截面的最小轴惯性矩,l―压杆长度,μ―和 压杆端点支座情况有关的系数,两端铰支杆μ=1,两端固支μ=0.5,一端固支一段 铰支μ=0.7,一端固支一端自由μ=2。 当压杆所受的荷载F小于试件的临界力Fcr ,压杆在理论上应保持直线形状,压 杆处于稳定平衡状态;当F =Fcr 时,压杆处于稳定与不稳定平衡之间的临界状态,稍 有干扰,压杆即失稳而弯曲,其挠度迅速增加。若以载荷F为纵坐标,压杆中点挠度 δ为横坐标,按欧拉小挠度理论绘出的F-δ图形即为折线OAB,如图1 (b)所示。
图 1
由于试件可能有初曲率,荷载可能有微小的偏心,以及材料的不均匀等因素, 压杆在受力后就会发生弯曲,其中点挠度δ随荷载的增加而逐渐增大。当F<<Fcr 时, δ增加缓慢。当F接近Fcr 时,虽然载荷增加很慢,而δ却迅速增大,如OAB或OAB所 示。曲线OAB或OAB与折线OAB的偏离,就是由于初曲率载荷偏心等影响造成,此影响 越大,则偏离也越大。 i 处横截面上 若令杆件轴线为x坐标轴,杆件下端为坐标轴原点,则在 的内力如图2(a)所示,弯矩
压杆稳定实验

压杆稳定实验
根据欧拉公式,有
2 EI Pcr 2 l
压杆稳定实验
(二)细长压杆临界力测定 压杆稳定实验装置简图如图所示。
压杆稳定实验
1、实验值确定: 实验采用矩形截面薄钢杆6作为压杆试样,两端放 在V形槽内,相当于两端铰支。压力P通过加载杠杆4 、固定砝码2和移动砝码3加在压杆的A端,通过调节两 个砝码的重力和位置可以改变压力P。用两个涡流传感 器5和7对称的装在试样6中点E的两边,当试样6在轴向 力P作用下变弯时,用涡流传感器和计算机测出中点E 两边的位移。实验过程中一边加力一边注意监测变形 ,如果变形显著增加时,意味着试样有较大弯曲,这 时所对应的轴向力P即为临界力Pcr。 根据平衡条件,压力P与作用在B,C点砝码重力QB , QC及作用位置的关系为:
压杆稳定实验
QB BD QC CD P AD
根据实验记录的砝码重量和变形值按一定比例 绘制P- δ曲线图,从稳定图中确定临界力Pcr 。 2、理论计算: 图示约束和截面情况下,压杆的临界压力的理论值 为:
EI Eba Pcr 2 12l 2 l
2 2
3
压杆稳定实验
3、误差计算:
对杆件6的临界力Pcr计算相对误差:
Pcr Pcr e % Pcr
四、试验步骤 1、测量原始尺寸
将试样和传感器安装在相应的卡具中,测量并 记录有关数据。包括断面尺寸、位置尺寸。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
压杆稳定实验报告数据处理
压杆稳定实验的数据处理可以分为以下几个方面:
1. 数据采集与整理:将实验时用仪器采集得到的数据按照时间顺序整理在一起,可以使用Excel或其他数据处理软件完成;
2. 统计分析:计算得到稳定状态下压杆的平均值、标准差等统计数据指标,可以使用Excel 的函数或其他统计软件完成;
3. 数据可视化:使用图表展示实验数据,可以使用Excel的绘图工具或其他数据可视化软件。
可以绘制出随时间变化的曲线图,或者是不同试验条件下的对比图表。
4. 实验误差分析:计算实验数据的误差范围,包括仪器误差、人为误差等。
可以通过比较不同时间点的数据或者不同试验条件下的数据来评估实验误差并分析其来源。
5. 结论撰写:结合实验数据和误差分析,得出结论,总结实验内容和实验步骤。
结论应该简明扼要,并具有实验意义。
最终,可以根据以上数据分析,撰写完整的压杆稳定实验报告。
