一维多阶梯势垒的透射系数
16-3 一维势阱和势垒问题
]
ψ1 = A1 e + B1 e
ik1x
−ik1x
− ik 2 x
1
( x < 0)
( x > a)
U
通解: 通解
ψ 2 = A2 e
ik 2 x
1
+ B2 e
(0 ≤ x ≤ a )
U0
ψ 3 = A3 eik x + B3 e − ik x
处无反射波: 由 x > a 处无反射波: B 3 = 0 令 A1 = 1(以入射波强度为标准) 以入射波强度为标准) 由波函数的 标准条件得 O 可解得
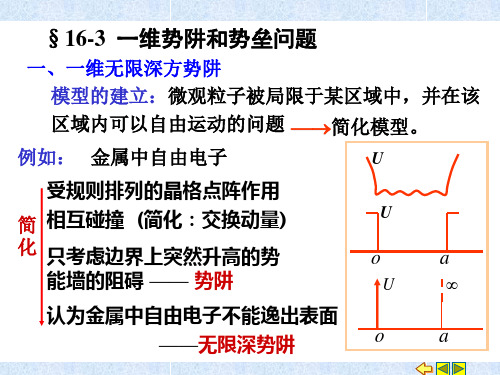
§16-3 一维势阱和势垒问题
一、一维无限深方势阱 模型的建立:微观粒子被局限于某区域中, 模型的建立:微观粒子被局限于某区域中,并在该 区域内可以自由运动的问题 →简化模型。 →简化模型 简化模型。 例如: 例如: 金属中自由电子 受规则排列的晶格点阵作用 简化:交换动量) 简 相互碰撞 (简化:交换动量) 化 只考虑边界上突然升高的势 能墙的阻碍 —— 势阱 认为金属中自由电子不能逸出表面 ——无限深势阱 无限深势阱
2 2πx p = ∫ |ψ | d x = ∫ sin dx a a 0 0
4 4 2 a a
2a πx 2 πx = ∫ sin d( ) aπ a a 0
4
a
1 πx 1 2 2 2π x = ( − sin ) π a 4 a
a
4
= 9.08 × 10 −2
0
练习: 练习
已知: 已知:
ψ = cx ( L − x )
A A2 ∞ 2 dx = ∫ dx = A arctg x − ∞ = A2π = 1 ∫∞ 1 + ix 1 + x2 − −∞
Tunneling Effect

故透射系数为:
而反射系数为:
由以上两式可见,一般情况下,透射系数 ,而反射系数 ,并且 。这表明,在量子力学中,即使粒子的能量大于势垒,粒子也并非能100%穿过势垒,而是一部分被反射回Ⅰ区,另一部分透射到Ⅲ区,但不会停留在势垒中。而在特定情况下,即 时,透射系数 ,此情况的透射现象被叫做共振透射。
◆当E < V0时, 是虚数,令 ,其中 是实数,把 代入上述式子中,再利用双曲函数 (双曲正弦)和 (双曲余弦),以及关系式 和 可将系数关系变化为:
则透射系数(T)和反射系数(R)变为:
由以上两式可以发现,即使在粒子能量小于势垒能量(即E < V0)的情况下,透射系数仍大于0(即T > 0),说明仍有部分粒子可以穿过比其自身能量高的势垒从而到达势垒的另一侧,这种现象便叫做隧穿效应(Tunneling Effect),这是围观粒子波动性的重要表现。
隧穿效应(Tunneling Effect)
假设 ,则 ,故 ,而
透射系数:
而
故
其中
上式表明,透射系数T随着势垒的高度V0和势垒的宽度a的增大而呈现指数减小,同时透射系数T也随粒子质量的增大而呈指数减小,如设 ,当势垒宽度 时,透射系数义,粒子概念过渡到经典。同理,若把质子与电子作比较(质子质量约为电子的1836多倍),则一定条件下,若电子的透射系数 ,则相同条件下,质子的透射系数仅为 。
一维中,粒子的定态薛定谔方程为:
其中,ℏ是约化普朗克常数(reduced Planck constant),亦称狄拉克常数(Dirac constant),
将V(x)的情况代入到方程中便可以得到:
势垒贯穿与应用解读

势垒贯穿与应用 势垒贯穿设一个质量为m 的粒子,沿x 轴正方向运动,其势能为: U(x)=0 x<0 和x>a U(x)=U 0 0≤x ≤a这种势能分布称为一维势垒。
粒子在 x < 0 区域里,若其能量小于势垒高度,经典物理来看是不能越过势垒达到 x > a 的区域。
在量子力学中,情况又如果呢?为讨论方便,我们把整个空间分成三个区域: 在各个区域的波函数分别表示为ψ1 ψ2 ψ3三个区间的薛定谔方程简化为:求出解的形式是)(),0(),0(a x a x x ≥I ∏≤≤∏≤I ),()(212122x E dx x d m ϕϕ=- 0≤x ),()()(22202222x E x U dxx d m ϕϕϕ=+- ax ≤≤0),()(232322x E dxx d m ϕϕ=- a x ≥222 mEk =2021)(2 E U m k -=,0)()(12212≤=+x x k dxx d ϕϕa x x k dxx d ≤≤=-0,0)()(221222ϕϕa x x k dxx d ≥=+,0)()(32232ϕϕikxikx e A Ae -'+=ψ1x ik Be 12+=ψikx Ce =ψ3O(1)E>U 0按照经典力学观点,在E>U 0情况下,粒子应畅通无阻地全部通过势垒,而不会在势垒壁上发生反射而在微观粒子的情形,却会发生反射。
(2)E<U 0从解薛定谔方程的结果来看,在势垒内部存在波函数ψ。
即在势垒内部找出粒子的概率不为零,同时,在x>a 区域也存在波函数,所以粒子还可能穿过势垒进入x>a 区域粒子在总能量E 小于势垒高度时仍能贯穿势垒的现象称为隧道效应定义粒子穿过势垒的贯穿系数是:透射波的概率密度与入射波概率密度的比值。
势垒高度U 0越低、势垒宽a 度越小,则粒子穿过势垒的概率就越大。
隧道效应是经典力学所无法解释的由于电子的隧道效应,金属中的电子并不完全局限于表面边界之内,电子密度并不在表面边界处突变为零,而是在表面以外呈指数形式衰减,衰减长度约为1nm只要将原子线度的极细探针以及被研究物质的表面作为两个电极,当样品与针尖的距离非常接近时,它们的表面电子云就可能重叠若在样品与针尖之间加一微小电压U b 电子就会穿过电极间的势垒形成隧道电流。
lecture7 一维散射问题(I)

( x) xa ( x) xa
ikx ( x ) Se , ( x a) 由7) x x ( x ) Ae Be , (0 x a) 由8)
Aea Be a Seika
13) 由于在 x a, U0 (有限势垒)
'( x) xa '( x) xa
1 a 在 a 1 近似下, sh a ch a e 1 2
S
2
4k (k 2 2 )2 sh 2 a 4k 2 2ch 2 a
2 2
S
2
16k 2 2 2 a 2 e (k 2 )2
k
2 E
2 (U 0 E )
( x) x0 ( x) x0
ikx ikx ( x ) Ae A ' e , ( x 0) 由20) i x i x 由21) ( x) Be B ' e , (0 x a)
A A' B B '
23) 由于在 x 0, U0 (有限势垒)
i * * b.对于一维体系:J ( ) 2 x x
ikx c.代表粒子从左向右运动的入射波: e
ikx ikx i k ikx e ikx e 得入射粒子流密度: Ji (e e ) v 2 x x
ikx d.对于反射波 Re 可得反射粒子流密度:J r | R |2 v
Jr
k
k
| A ' |2
ikx 29) 根据17),对于透射波 ( x) Ce 得透射粒子流密度:
Jt
§9势垒贯穿

但是,施加一个外电场,金属中 电子的所感受到的电势如图(b)所示。 金属中电子面对一个势垒,能量最大 的电子就能通过隧道效应穿过势垒漏 出,从而导致所谓场致电子发射。
图 (a)
图 (b)
三,扫描隧穿显微镜(STM) STM(Scanning Tunneling Microscope) I 是观察固体表面 原子情况的 A B S 超高倍显微镜。
用扫描隧穿显微镜拍摄的硅表面的象,每一个 隆起处是一个硅原子。
世界上最小的文字:
1990年1月,美国加利福尼亚州圣何塞IBM阿莫登 研
究中心的科学家宣称:他们利用扫描隧穿显微镜移动 并重新排列氙和镍表面的单个原子以便出其公司的开
头字母:IBM。
1993年美国加州 IBM Almaden 研究中心的研究人员,用 扫描隧穿显微镜(STM)操纵,将48个铁原子在铜的表面排 列成一个圆圈, 形成量子围栏(Quantum Corral) ,电子被 束缚在其中,其波函数形成同心圆状涟漪细浪。
2 2i ( k 12 k2 ) sin k2a
C
4k1k2e A 2 ik2a 2 ik2 a ( k1 k2 ) e ( k1 k2 ) e
ik1a
A
( k1 k2 ) e
2
ik2a
( k1 k2 ) e
2
ik2 a
A
4. 透射系数和反射系数
I 透射系数: 透射波几率流密度与入射波 几率流密度之比称为透射系数 D = JD/JI
1。原理 隧道电流 I 与 样品和针尖间 的距离S 关系极为敏感。
势能曲线
U U0
E
扫描探针A
S 10A
样品 B
定量关系:
第二章 一维势场中的粒子

第二章 一维势场中的粒子
本章要求 1. 掌握求解一维定态Schrödinger 方程的 基本步骤; 2. 掌握能量量子化,束缚态,宇称,隧道 效应,零点能,分立谱,连续谱等概念;
第二章 一维势场中的粒子
本章内容
§1 一维无限深势阱
§1
§2 势垒贯穿
§2
§3 一维谐振子
§3
§1 一维无限深方势阱
一维晶格中电子的势能曲线
L
x0
xa
x0
U
xa
无限深势阱
x0
xa
如果直接用此曲线表示的 势能带入薛定谔方程中,就形 成一个相当困难的数学问题。
第二次简化:
用平均势能代替晶格势能
( 这一步的实质是不考虑电子 间、电子与晶格离子间的相互 作用,这样的电子就相当于理 想气体分子-自由电子气。)
0;
x 0, x a
n(x)
2 sin nπ x aa
0 x a; n 1,2,...
n2 E1 16 E1
✓ 除端点(x=0 , a)外, 9E1
基态波函数无节点,第
一激发态有一个节点,
第二激发态有二个节点,
第m 激发态(量子数
4 E1
n=m+1)有m个节点。
E1
E) 2 ( x)
0
2
② 求解定态Schrödinger 方程
方程(2)的解 2 x 0 x 0; x a
理由: 因势阱壁无限高(V ),粒子不能穿透 势壁,故势阱外的波函数必定为0。
方程(1)中,令 k
2mE h2
,则方程(1)写为
d2 dx 2
1
Pˆ 2
曾谨言《量子力学教程》(第3版)笔记和课后习题(含考研真题)详解-一维势场中的粒子(圣才出品)
x)
xn
=
1
[
n2n−1 +
n
+ 2
1n+1
]
d dx
n
= [
n2n−1 −
n
+ 2
1n
+1
]
其中 =
。
2.2 课后习题详解
2.1 设粒子限制在矩形匣子中运动,即
求粒子的能量本征值和本征波函数,如 a=b=c,讨论能级的简并度。 解:在匣子内
,n
=
1,2,3,…
该本征能量表达式说明说明:并非任何 E 值所相应的波函数都满足本问题所要求的边
条件,一维无限深方势阱中粒子的能量是量子化的,即构成的能谱是离散的(disorete).
(2)无限深方势阱本证波函数
归一化波函数表示为
2.有限深对称方势阱 设
a 为阱宽,V0 为势阱高度.以下讨论束缚态(0<E<V0)情况. 束缚态能量本征函数(不简并)必具有确定宇称,因此只能取 sinkx 或 coskx 形式. (1)偶宇称态.
E
=
En
=
(n +
1)h, n 2
=
0,1, 2,…
此即谐振子的能量本征值.可以看出,谐振子的能级是均匀分布的,相邻的两条能级
的间距为 .
8 / 42
圣才电子书 十万种考研考证电子书、题库视频学习平台
2.一维谐振子本征波函数
一维谐振子波函数常用的关系式如下
n
=
− 1 2 x2
2.势阱中的束缚态 要求束缚能量本征态(不简并)具有确定字称.以下分别讨论. (1)偶宇称态 归一化的束缚能量本征态波函数可表示为(取 C 为实数)
专题3 势垒贯穿
2.8 势垒贯穿
E >U0时
平面波的几率流密度
1
iℏ J= (ψ∇ψ * −ψ *∇ψ ) 2µ
1
ψ = Aeik x + A′e −ik x
向右
向左
iℏ ik1 x d * − ik1 x * − ik1 x d J右 = [ Ae (A e ) − A e ( Aeik1x )] 2m dx dx iℏ ℏ ℏk1 2 2 2 * = [ AA (−ik1 ) + A k1 ] = 2 A k1 = A 2m 2m m − ℏk1 2 J左 = A′ 正值向右 m 负值向左
2.8 势垒贯穿
ℏ2 2 H不含时间,我们由定态薛方程 [− ∇ + U ]ψ = Eψ 不含时间, 不含时间 2µ 出发进行求解。 出发进行求解。
d 2ψ l 2m + 2 Eψ l = 0 2 ℏ dx d 2ψ r 2m + 2 Eψ r = 0 2 dx ℏ d 2ψ m 2m + 2 ( E − U 0 )ψ m = 0 2 dx ℏ
重点讨论
T 与 E,U0 ,a 的关系
T – a曲线 U0=2.0eV Ee=1.0eV Ee=1.5eV Ee=1.99eV Ee=2.2eV Ee=2.5eV Ee=3.0eV
2.8 势垒贯穿
探索思考
1 1
(2)
(3)
连续, 波函数及其微商在 x=0, x=a 连续,得到系数
ψ l (0) = ψ m (0) ψ 'l (0) = ψ 'm (0) ψ m (a) = ψ r (a) ψ 'm (a) = ψ 'r (a)
2ik1k3e − ik1a C= A 2 2 2ik1k3chk3 a + (k1 − k3 ) shk3 a (k12 + k32 ) s hk3 a A′ = A 2 2 2ik1k3chk3 a + (k1 − k3 ) shk3 a
波的反射率和透射率的统一形式规律
波的反射率和透射率的统一形式规律李楚元【摘要】本文系统研究了电磁波和机械波垂直入射时界面处的反射和透射规律,交流电在传输线上的反射率和透射率,最后比较了量子力学中的几率波,发现虽然不同类型波的界面边界条件不同,但是它们的反射率和透射率有相同的数学表达式.不同波的反射率和透射率的统一形式规律反映了波动有着统一的内在物理属性.【期刊名称】《物理与工程》【年(卷),期】2018(028)003【总页数】7页(P51-57)【关键词】波;反射;透射;统一性【作者】李楚元【作者单位】一诺仪器(中国)有限公司,上海 200233【正文语种】中文0 问题的提出声音、可见光、无线电波、地震波、物质波、引力波等是不同类型的波,波是自然界中最普遍的物质运动形式。
对波的研究和认识的加深,不仅推动着人类认知的不断前进,同时也改变了人们的生产生活方式,例如引力波的发现改变了人们对宇宙空间的认识[1],而无线电通信带来的移动通信革命深刻影响了人类社会的演进。
各种类型的波虽然各有特点,但也有着共同的特性,比如干涉、衍射和叠加效应。
除此之外波还有其他共同的特性。
本文以电磁波、机械波和传输线上的交流电为例,来探究波的反射率和透射率的共同特性。
发现虽然不同类型的波的传播有各自的载体和物理特征,但在垂直入射时它们的反射率和透射率有相同的数学形式。
电磁波是最常见的波。
无线电波、红外线、可见光、紫外线、X射线以及伽马射线等都是电磁波,区别仅是频率的不同。
19世纪物理学家麦克斯韦在总结前人工作的基础上,提出了位移电流假说并推广电流的含义,概括提出了一组描述电磁现象的方程。
这组方程称为麦克斯韦方程组[2]。
通过这组方程麦克斯韦预言了电磁波的存在,并预言光也是一种电磁波。
后来赫兹在实验上观测到了电磁波的存在。
现代无线通信技术的发展及各种电磁设备的运用完全证明了麦克斯韦方程和电磁理论的正确性。
物体机械振动的传播称之为机械波。
比如声音、水波以及地震波就是机械波。
高二物理竞赛课件:一维方势垒和隧道效应
Ⅰ区 Ⅱ区 Ⅲ区
d 2Ψ1 ( x) dx2
k12Ψ1 ( x)
0
d2Ψ2 (x) dx2
k22Ψ2
(
x)
0
d 2Ψ3 ( x) dx2
k12Ψ3
(x)
0
0a
k12
2mE 2
k22
2m(U 0 2
E)
k12
2mE 2
三个区域的波函数分别为
Ⅰ区 Ψ1(x) A1eik1x B1eik1x
U0 ⅠⅡ Ⅲ
一维方势垒和隧道效应
一维方势垒 隧道效应
一维方势垒
Ep ( x)
0, x 0, x a Ep(x) Ep0, 0 x a
Ep0
o ax
粒子的能量 E Ep0
d2
dx2
k 2
0
Ep
(x) Asin kx Bcoskx
o ax
波函数的标准条件:单值、有限和连续 .
x 0, 0, B 0
(2)E < U0 , T≠0, 虽然粒子总能量小于势垒高度,入射粒子仍 可能穿过势垒进入 III 区 — 隧道效应
(3) 透射系数T 随势垒宽度a、粒子质量m 和能量差变化, 随着势垒的加宽、加高透射系数减小。
粒子类型 粒子能量 势垒高度 势垒宽度 透射系数
1eV
2eV 5×10-10m 0.024
na
n4
(x) 2 2 sin 2 nπ x
a
a
n 2
16E1
n3
n2 n 1
x0
a x0
9E1
4E1 E1
a
Ep 0
四.隧道效应(势垒贯穿)
势垒 Ⅰ区 U ( x ) = 0 x ≤ 0
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1 一维多阶梯势垒的透射系数 甘肃省西和县何坝职校 胡来喜 742105 对于一般势垒,求解透射系数往往比方势垒复杂。应用W.K.B半经典近似法[1]可以精确推导出一般势垒的透射系数[1-3],只是在推导过程中要用到比较高深的数学知识。于是,有些文章将一般势垒分成多个宽度为ix的小方势垒,组成一维多阶
梯势垒,并有应用鲁阿德(Rouard)递推方法[4]和一维阶梯位势递推关系[5]分别得出一维多阶梯势垒透射系数的递推公式,这两种递推公式对于少数阶梯势垒很适用,但在阶梯势垒过多时要借助于计算机程序[6]才能完成。本文在参照了教科书[7]中求解方势垒透射系数方法的基础上,以连续函数势垒作为一般势垒的一个特例,将连续函数势垒分割成多个宽度为x的矩形势垒,如图1,对其过程应用相关数学处理,得出推导一维多阶梯势垒透射系数,再应用极限方法使阶梯势垒回归到连续函数势垒,推导出连续函数势垒的透射系数。最后,对推导过程中用到的近似处理进行了误差讨论,比较严密地证明了教科书[7,8]中关于势垒透射系数的结论。 1 一维多阶梯势垒透射系数 如图1所示,一般势垒U(x)的定态薛定谔方程为:
U(x) x 1x
2x
E
图1 x 2
22
2
dψ+Kxψx=0
dx, x (1)
式中 22EUxKxћ (2)令 kxKx (3)把粒子经过的区域分成n个小区域,每个小区域的U(x)近似为常数,成为“阶梯势垒”,从而每个区域的K(x)也近似为常数(图2)。 由(1)式解出的各区域的波函数具有相同形式,如第j区域和第n区域为: jjjjiKxiKxjjjxAeBe
,j=0,1,„,n-1 (4)
nniKx
nnxAe (5)
得到入射波的几率流密度为:
0000**02iћJ入入入入0200ћkx入0020
0
0
iKxћkAe (6)
透射波的几率流密度为: **2nnnDniћJn
2nnnћkx2nniKxn
n
n
ћkAe (7)
入射粒子从左到右经势垒后的透射系数为:
1jkj
k 1j
k
K(x)
x 图2 3
00220
0
0
nniKxn
n
nD
iKx
ћkAeJDћkJAe (8)
其中0n[5]。 若令 2jjiKxjjjIkAe,j=0,1,„,n 则(8)式可写为:
312001211jnnjnIIIIIIDIIIIII……
(9)
式中任一项的0jI。可以看出,引入很多jI相乘除,D值不变,只是一种数学处理。应用该处理是因为求相邻区域的1jjII比较容易,从而容易求出D。避开其中任一区域,即去掉其中一项jI,只要能求出11jjII,并不影响求D的值。所以,K=0的区域是可以避开的。 又令 1jjjIDI,j=1,2,„,n
即 11112221111jjjjjjjjiKxjjiKxKxjjjiKxjjjjkAekADekAkAe (10)则 1njjDD (11) 1.1 0jK,且左邻域10jK的第j区域的jD 由波函数及其微商在1jx点的连续条件得到: 111jjjjxxxx
得 11111111jjjjjjjjiKxiKxiKxiKxjjjjAeBeAeBe (12) 4
111jjjjxxxxdddxdx
得 1111111111jjjjjjjjiKxiKxiKxiKxjjjjjjjjkAekBekAekBe (13)由111213jjjkkk得:
1111111112jjjjjjiKxiKxiKxjjjjjjjjjjkkkAeAeBekkkk
(14)
(14)式有三个未知量1jA、jA、jB,由于K(x)是连续的,可以把区域取的很窄,使 1111jjjjjjjkkkkkkk
(15)
则(14)式中含jB的项可以忽略,得到: 111112jjjiKKxjjjjjAkeAkk
(16)
代入(10)式,并令1jjxxx,得: 21214jjiKxjjjjjkkDekk
(17)
而 2211122114jjjjjjjjjjkkkkkkkkkk 121111jjjkkkjjjkkk
所以 221 ,,jjjjiKxjkxEUxDeeEUx (18)
x K(x)
rk tk
qxrx
sx
tx
图3 5
1.2 0tK,而左邻域0sK的第t区域的tD 设rx、sx、tx三区域相邻(图3),由0sK得(sssxABC常数),则0sx。由波函数的连续性,在rx、sx点有:
rx点:0rrrrrrrriKxiKxrriKxiKxrrAeBeCAeBe和sx点:0tstststsiKxiKxttiKxiKxttCAeBeAeBe
解上面两个方程组得: 22rrtsiKxriKxtCAeCAe 则 rrtsikxkxtrAeA (19)将(19)式代入(10)式,因K(x)连续,故可取rtKK,得: ttrsttsiKxKxiKxxtttrrkADeekA
即 221 ,,ttttiKxtkxEUxDeeEUx (20)将(18)、(20)式代入(11)式,得: 12njjjkxDe (21)
该式即为服从连续函数的多阶梯势垒的透射系数。其中,EUx时,粒子很容
易穿过势垒,透射系数近似为1,这个结果是与事实相符的。 2连续函数势垒的透射系数
当多阶梯势垒的宽度jx无限小(jx→0)时,多阶梯势垒回归到一般势垒,
而1()2jkkxUxEћ,211112nnxjjjjxjjkxkxUxEdxћ, 6
于是(21)式可写成 2
1
2
exp2xxDUxEdxћ
(22)
上式就是连续函数势垒的透射系数,常数因子0D=1。其中1x,2x称为经典回转点,即12()()UxUxE。 对于一般势垒,可推得除常数因子01D外,透射系数与(22)式完全一致[8] 2
10
2
exp2xxDDUxEdxћ
(23)
3 结果讨论 在推导过程中用到一处近似处理,即忽略了(14)式含jB的项,0x时,0jD,,0nk区域的个数并不增加,故误差不能忽略(虽然每个小区域
的误差减小了,但这种小区域的个数n)。 由于做了近似计算,首先给(16)式的1jjAA带来误差,从而jD、D也有误
差。设与它们对应的准确值为AAjj-1、jD、D,又设1jjAA的相对误差为j。则0jx时,0j。
由 111jjjjjjjAAAAAA (24)得 1111jjjjjAAAA (25)
