1.4电场中的导体
合集下载
电磁学02静电场中的导体与介质

A q -q
-q+q
UA
q'
4 0 R0
q ' 4 0R1
q q '
4 0 R2
0
可得 q ( q) 1(9略)
例4 接地导体球附近有一点电荷,如图所示。
求:导体上感应电荷的电量
R
解: 接地 即 U0
o
感应电荷分布在表面,
l
q
电量设为:Q’(分布不均匀!)
由导体等势,则内部任一点的电势为0
选择特殊点:球心o计算电势,有:
1) Dds
S
1 (
r
1) q0内
l i mq内
V0V
1 (
r
1) limq0内 V0V
1 (
r
1)0
00 0。 40
[例2] 一无限大各向同性均匀介质平板厚度为 d
表明:腔内的场与腔外(包括壳的外表面)
物理 内涵
的电荷及分布无关。
在腔内 E 腔 外表 E 腔 面外 0带
电 量 的电 体 的
二.腔内有带电体时
q
① 带电量: Q腔内 q (用高斯定理易证)
表面
23
② 腔内的电场: 不为零。
由空腔内状况决定,取决于:
*腔内电量q;
*腔内带电体及腔内壁的 几何因素、介质。
平行放置一无限大的不带电导体平板。
0 1 2 求:导体板两表面的面电荷密度。
E2 • E1 解: 设导体电荷密度为 1、 2 ,
E0 电荷守恒: 1 + 2 = 0
(1)
导体内场强为零:E0 +E1‐E2 = 0
0 1 2 0 20 20 20
(1)、(2)解得:
静电场中的导体
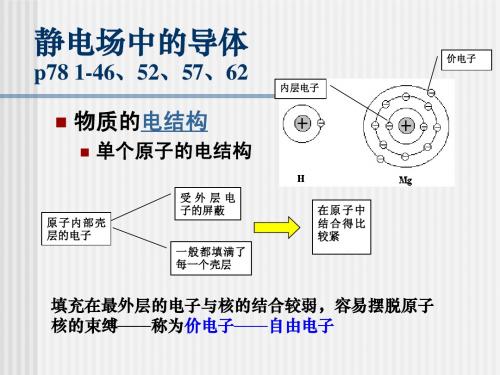
动的状态,从而电场分布不随时间变化。
说明:
一般情况表面有一定厚度,很复杂如:E=109V,则 感应电荷聚集在表面的厚度为10-10m,本课程不讨论 表面层电荷如何分布。 实际物质内部既有自由电子,又是电介质。如:气体 在一般情况下绝缘(电介质),但加高压气体会被击 穿(导体)——导体是一种理想模型。 对导体只讨论达到静电平衡以后的情况,不讨论加电 以后电荷的平衡过程。
S内
E
E d S 0
内表面不是等势面 ——导 体也不是等势体 ,矛盾
S面内 q 0
内 表面 电 荷代 数和 为 零? 内 表面 无 电荷
q 0
e内 0
空腔内部有带电体 q
导体内表面上所带电荷与腔内电荷的代数 和为零 证明:作Gauss面如图
E内=0 E
力学:只涉及物质的机械性质,对其本身研究甚 少。 电磁学:较多地讨论场,而对物质本身的电磁性 质也涉及得很少。 物质与场是物质存在的两种形式 物质性质非常复杂(要特别注意我们课程中讨论 这种问题所加的限制)
导体静电平衡条件
导体:有足够多的自由电子 ——受电场力会移动.
静电平衡状态:体是一个等势体,导体表 面是等势面 证明:
导体内部E=0
U ab E d l 0
a
b
导体内部任意两点间电势差为零 ——各点等电势——等势体 ——表面为等势面
场强分布
E内 0
表面附近:表 表面 E 表面 : σe 大小: E ε0
导体表面是等势 面,处处与电力 线正交 ?
S内
E d S 0
q 0 q x x q
说明:
一般情况表面有一定厚度,很复杂如:E=109V,则 感应电荷聚集在表面的厚度为10-10m,本课程不讨论 表面层电荷如何分布。 实际物质内部既有自由电子,又是电介质。如:气体 在一般情况下绝缘(电介质),但加高压气体会被击 穿(导体)——导体是一种理想模型。 对导体只讨论达到静电平衡以后的情况,不讨论加电 以后电荷的平衡过程。
S内
E
E d S 0
内表面不是等势面 ——导 体也不是等势体 ,矛盾
S面内 q 0
内 表面 电 荷代 数和 为 零? 内 表面 无 电荷
q 0
e内 0
空腔内部有带电体 q
导体内表面上所带电荷与腔内电荷的代数 和为零 证明:作Gauss面如图
E内=0 E
力学:只涉及物质的机械性质,对其本身研究甚 少。 电磁学:较多地讨论场,而对物质本身的电磁性 质也涉及得很少。 物质与场是物质存在的两种形式 物质性质非常复杂(要特别注意我们课程中讨论 这种问题所加的限制)
导体静电平衡条件
导体:有足够多的自由电子 ——受电场力会移动.
静电平衡状态:体是一个等势体,导体表 面是等势面 证明:
导体内部E=0
U ab E d l 0
a
b
导体内部任意两点间电势差为零 ——各点等电势——等势体 ——表面为等势面
场强分布
E内 0
表面附近:表 表面 E 表面 : σe 大小: E ε0
导体表面是等势 面,处处与电力 线正交 ?
S内
E d S 0
q 0 q x x q
大学物理静电场静电场中的导体课件

V
五.电场强度的计算 电偶极子 1.定义 (物理模型) P r 其距离较问 题涉及线度 –q l +q 小得多l<<r 的等量异号的点电荷系统. 2.电矩 (电偶极矩) p –q l +q p=ql p与l同向,l从负指向正. 3.电偶极子电场的电场强度 (1)延长线上的电场强度 E– A E+ 坐标如图 –q l +q A的坐标 O x 为x. E+=qi/[4πε0(x–l/2)2] E–=–qi/[4πε0(x+l/2)2] E=E++E–
四.电场叠加原理 4.点电荷系激发的电场 (由力的叠加原理得出) E = qiri/(4πε0ri3) 将带电体分成无数个点电荷. i 试验电荷受力为 5.连续带电体激发的电场 F =Fi= q0qiri/(4πε0ri3) E =q rdq/(4πε0r3) i i ρ=dq/dV E=F/q0 = q0 qiri/(4πε0ri3) q0 (1)体电荷 体电荷密度 i E = rρdV/(4πε0r3) E = qiri/(4πε0ri3) =Ei (2)线电荷截面尺寸远小于长 i i 1.独立性 任何电荷的电场不 度.也远小于问题所涉及线度 线电荷密度 λ=dq/dl 因其它电荷的存在而受影响; E = lrλdl/(4πε0r3) 2.叠加性 空间电场是所有电 (3)面电荷 厚度远小于表面尺 荷产生电场的矢量和. 3.求电场的基点 寸,也远小于问题所涉及线度 (1)点电荷激发的电场; 面电荷密度 σ=dq/dS (2)电场叠加原理. E = S rσdS/(4πε0r3)
2 1 2 ቤተ መጻሕፍቲ ባይዱ 2
1
讨论 1.中垂线上 1+2=π Ex=0 sin2=sin1 cos1=–cos2=(l/2)/(a2+l2/4)1/2 Ey=λcos1/(2πε0a) =(q/l)[(l/2)/(a2+l2/4)1/2]/(2πε0a) =q/[4πε0a)(a2+l2/4)1/2] (1)当l ≫ a 1=0 Ey=λ/(2πε0a) (2)当 Ey=q/(4πε0a2) 点电荷 (3)当a=0 带电体不再是线电荷 ≪a 2.延长线上 dl r bP x 所有电 O dE 荷元产 l
五.电场强度的计算 电偶极子 1.定义 (物理模型) P r 其距离较问 题涉及线度 –q l +q 小得多l<<r 的等量异号的点电荷系统. 2.电矩 (电偶极矩) p –q l +q p=ql p与l同向,l从负指向正. 3.电偶极子电场的电场强度 (1)延长线上的电场强度 E– A E+ 坐标如图 –q l +q A的坐标 O x 为x. E+=qi/[4πε0(x–l/2)2] E–=–qi/[4πε0(x+l/2)2] E=E++E–
四.电场叠加原理 4.点电荷系激发的电场 (由力的叠加原理得出) E = qiri/(4πε0ri3) 将带电体分成无数个点电荷. i 试验电荷受力为 5.连续带电体激发的电场 F =Fi= q0qiri/(4πε0ri3) E =q rdq/(4πε0r3) i i ρ=dq/dV E=F/q0 = q0 qiri/(4πε0ri3) q0 (1)体电荷 体电荷密度 i E = rρdV/(4πε0r3) E = qiri/(4πε0ri3) =Ei (2)线电荷截面尺寸远小于长 i i 1.独立性 任何电荷的电场不 度.也远小于问题所涉及线度 线电荷密度 λ=dq/dl 因其它电荷的存在而受影响; E = lrλdl/(4πε0r3) 2.叠加性 空间电场是所有电 (3)面电荷 厚度远小于表面尺 荷产生电场的矢量和. 3.求电场的基点 寸,也远小于问题所涉及线度 (1)点电荷激发的电场; 面电荷密度 σ=dq/dS (2)电场叠加原理. E = S rσdS/(4πε0r3)
2 1 2 ቤተ መጻሕፍቲ ባይዱ 2
1
讨论 1.中垂线上 1+2=π Ex=0 sin2=sin1 cos1=–cos2=(l/2)/(a2+l2/4)1/2 Ey=λcos1/(2πε0a) =(q/l)[(l/2)/(a2+l2/4)1/2]/(2πε0a) =q/[4πε0a)(a2+l2/4)1/2] (1)当l ≫ a 1=0 Ey=λ/(2πε0a) (2)当 Ey=q/(4πε0a2) 点电荷 (3)当a=0 带电体不再是线电荷 ≪a 2.延长线上 dl r bP x 所有电 O dE 荷元产 l
1、静电场中的导体-13
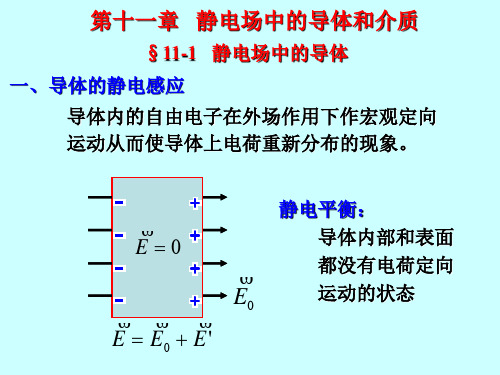
1= 4
P
3S + 4S = QB
又电荷守恒,所以有: 1S + 2S = QA
Q A QB 联立得: 1 4 2S QB Q A Q A QB 3 2 2S 2S
两板中间的场强为:
1 2 3 4 E 2 0 2 0 2 0 2 0 2 0 B 2 Q A QB U AB E dl Ed d d A 0 2 0 S
U ab
b
a
E dl
0
导体整体是等势体 导体表面是等势面
E0
三、静电平衡时导体上电荷的分布
导体的静电平衡条件; 根据:
1 静电场的高斯定理: E dS S 0
q
S内
i
(1)导体内部无净电荷,电荷分布在导体表面; 在导体内任作一高斯面S ,则:
1 SE dS 0
球A与壳B之间的电势差为:
q3 q2
q1
R3 R1 R2
U AB
R2
R1
q1 1 1 q1 ( ) dr 2 4 π 0 R1 R2 4 π 0 r
q3 q2
q1
R3 R1 R2
q1 q 2 0 q2 - q1
由电荷守恒定律:
q3 q q2 q q1
考虑电荷分布的对称性,由高斯定理得:
E 0 r R1
q1 E 2 4π 0 r
R1 r R2
E 0 R3 r R2 q1 q E r R3 2 4π o r
S内
q
S内
i
=0
S
qi 0 不存在净电荷
(2)导体表面上各处的面电荷密度与该处表面外 附近的场强大小成正比;
P
3S + 4S = QB
又电荷守恒,所以有: 1S + 2S = QA
Q A QB 联立得: 1 4 2S QB Q A Q A QB 3 2 2S 2S
两板中间的场强为:
1 2 3 4 E 2 0 2 0 2 0 2 0 2 0 B 2 Q A QB U AB E dl Ed d d A 0 2 0 S
U ab
b
a
E dl
0
导体整体是等势体 导体表面是等势面
E0
三、静电平衡时导体上电荷的分布
导体的静电平衡条件; 根据:
1 静电场的高斯定理: E dS S 0
q
S内
i
(1)导体内部无净电荷,电荷分布在导体表面; 在导体内任作一高斯面S ,则:
1 SE dS 0
球A与壳B之间的电势差为:
q3 q2
q1
R3 R1 R2
U AB
R2
R1
q1 1 1 q1 ( ) dr 2 4 π 0 R1 R2 4 π 0 r
q3 q2
q1
R3 R1 R2
q1 q 2 0 q2 - q1
由电荷守恒定律:
q3 q q2 q q1
考虑电荷分布的对称性,由高斯定理得:
E 0 r R1
q1 E 2 4π 0 r
R1 r R2
E 0 R3 r R2 q1 q E r R3 2 4π o r
S内
q
S内
i
=0
S
qi 0 不存在净电荷
(2)导体表面上各处的面电荷密度与该处表面外 附近的场强大小成正比;
静电场中的导体和电解质

Q + + + + ++ + + + + E= 0 S+ + + + + + + + ++
Q q + + + +++ + +-q + + - E= 0 S + 结论: 电荷分布在导体外表面, 导体 + q + + 内部和内表面没净电荷. + - - + + + + ++ 腔内有电荷q: E 0 q 0
i
结论: 电荷分布在导体内外两个表面,内表面感应电荷为-q. 外表面感应电荷为Q+q.
NIZQ
第 5页
大学物理学 静电场中的导体和电介质
结论: 在静电平衡下,导体所带的电荷只能分布在导体的 表面,导体内部没有净电荷. • 静电屏蔽 一个接地的空腔导体可以隔离内 外电场的影响. 1. 空腔导体, 腔内没有电荷 空腔导体起到屏蔽外电场的作用. 2. 空腔导体,腔内存在电荷 接地的空腔导 体可以屏蔽内、 外电场的影响.
NIZQ
第 3页
大学物理学 静电场中的导体和电介质
• 静电平衡时导体中的电场特性
E内 0
场强:
ΔVab
b
a
E dl 0
• 导体内部场强处处为零 E内 0 • 表面场强垂直于导体表面 E表面 // dS
• 导体为一等势体 V 常量 • 导体表面是一个等势面
S
0 E P dS qi
静电场中的导体

R2
R1
22
Vo
E dl
0 R3
0 R1
R2
E1 E3
dl
dl
R2
R3
E2
dl
R1 E4 dl
q (1 1 2)
4 π ε0 R3 R2 R1
2.31103 V
R1=10 cm,R2=7 cm R3=5 cm,q=10-8 C
2q
q
q
R3
R2 R1
23
S4
E4
dS
2q ε0
2q E4 4 π ε0r 2 (r R1)
S4
R1
2q
S3
qq
q
R33
rr
R2
R1111
R1
21
E1 0
(r R3 )
E2
4
q π ε0r 2
(R3 r R2 )
E3 0
(R1 r R2 )
E4
2q 4 π ε0r 2
(r R1)
2q
q
q
R3
电势也会受到影响 25
二 电介质的极化
电介质 无极分子:(氢、甲烷、石蜡等) 有极分子:(水、有机玻璃等)
26
电介质分子可分为有极和无极两类:
(1)分子中的正电荷等效中心 与负电荷等效
中心重合的称为无极分子(如H2、 CH4、CO2)
无极分子在电场中, 无极分子
E
正负电荷中心会被 拉开一段距离,产生 感应电偶极矩,这 称为位移极化。
1 CU 2 2
+++++++++
---------
+ dq
R1
22
Vo
E dl
0 R3
0 R1
R2
E1 E3
dl
dl
R2
R3
E2
dl
R1 E4 dl
q (1 1 2)
4 π ε0 R3 R2 R1
2.31103 V
R1=10 cm,R2=7 cm R3=5 cm,q=10-8 C
2q
q
q
R3
R2 R1
23
S4
E4
dS
2q ε0
2q E4 4 π ε0r 2 (r R1)
S4
R1
2q
S3
q
R33
rr
R2
R1111
R1
21
E1 0
(r R3 )
E2
4
q π ε0r 2
(R3 r R2 )
E3 0
(R1 r R2 )
E4
2q 4 π ε0r 2
(r R1)
2q
q
q
R3
电势也会受到影响 25
二 电介质的极化
电介质 无极分子:(氢、甲烷、石蜡等) 有极分子:(水、有机玻璃等)
26
电介质分子可分为有极和无极两类:
(1)分子中的正电荷等效中心 与负电荷等效
中心重合的称为无极分子(如H2、 CH4、CO2)
无极分子在电场中, 无极分子
E
正负电荷中心会被 拉开一段距离,产生 感应电偶极矩,这 称为位移极化。
1 CU 2 2
+++++++++
---------
+ dq
静电场中的导体和电介质
-
-
目录
静电场中的导体 和电介质
0
静电场中的导体和电介质
静电场中的导体和电介质
静电场是指在没有电流流动的情况下,电荷分布所产生的电场。在静电场中,导体和电介质 是两种不同的物质,它们的特性和作用也不同,本文将探讨导体和电介质在静电场中的性质 和应用 首先,我们需要了解导体和电介质的基本概念。导体是一种具有良好导电性能的物质,常见 的导体包括金属等。导体内的自由电子可以在外加电场的作用下移动,形成电流。而电介质 则是一种不良导电的物质,它的电导率远远低于导体。电介质在外加电场下无法形成连续的 电流,而是通过极化现象来响应电场的作用 在静电场中,导体和电介质的行为有很大的不同。对于导体来说,其特点是在静电平衡状态 下,内部电场为零。这是因为导体内的自由电子能够自由移动,它们会在外加电场的作用下 重新分布,直到达到平衡状态。这种现象被称为电荷运动的屏蔽效应。导体的另一个重要性 质是表面上的电荷分布是均匀的,这也是导体可以用来储存电荷的
与导体不同,电介质在静电场中的响应更加复杂。当外加电场作用于电介质时,电介 质分子会发生极化现象,即分子内部正、负电荷的分离。这种分离会导致电介质内部 产生电位移场,从而相应地改变电场分布。电介质的极化程度可以用极化强度来衡量 ,极化强度与外加电场的强度成正比。除了极化现象,电介质还可能发生击穿现象, 即在电场强度过高时,电介质内部的绝缘失效,导致电流的突然增加
0
静电场中的导体和电介质
导体在静电场中的一个重要应用 是电路中的导线。电路中的导线 由导体制成,它们能够有效地传 导电流。在电力系统中,导体连 接电源和电器设备,将电能传输 到目标地点。此外,在电子设备 制造中,导体用于制作电路板, 连接不同的电子元件,实现电信 号的传输和处理
-
目录
静电场中的导体 和电介质
0
静电场中的导体和电介质
静电场中的导体和电介质
静电场是指在没有电流流动的情况下,电荷分布所产生的电场。在静电场中,导体和电介质 是两种不同的物质,它们的特性和作用也不同,本文将探讨导体和电介质在静电场中的性质 和应用 首先,我们需要了解导体和电介质的基本概念。导体是一种具有良好导电性能的物质,常见 的导体包括金属等。导体内的自由电子可以在外加电场的作用下移动,形成电流。而电介质 则是一种不良导电的物质,它的电导率远远低于导体。电介质在外加电场下无法形成连续的 电流,而是通过极化现象来响应电场的作用 在静电场中,导体和电介质的行为有很大的不同。对于导体来说,其特点是在静电平衡状态 下,内部电场为零。这是因为导体内的自由电子能够自由移动,它们会在外加电场的作用下 重新分布,直到达到平衡状态。这种现象被称为电荷运动的屏蔽效应。导体的另一个重要性 质是表面上的电荷分布是均匀的,这也是导体可以用来储存电荷的
与导体不同,电介质在静电场中的响应更加复杂。当外加电场作用于电介质时,电介 质分子会发生极化现象,即分子内部正、负电荷的分离。这种分离会导致电介质内部 产生电位移场,从而相应地改变电场分布。电介质的极化程度可以用极化强度来衡量 ,极化强度与外加电场的强度成正比。除了极化现象,电介质还可能发生击穿现象, 即在电场强度过高时,电介质内部的绝缘失效,导致电流的突然增加
0
静电场中的导体和电介质
导体在静电场中的一个重要应用 是电路中的导线。电路中的导线 由导体制成,它们能够有效地传 导电流。在电力系统中,导体连 接电源和电器设备,将电能传输 到目标地点。此外,在电子设备 制造中,导体用于制作电路板, 连接不同的电子元件,实现电信 号的传输和处理
大学物理——静电场中的导体和电介质
v E
二、导体上电荷的分布 由导体的静电平衡条件和静电场的基本性 dV 质,可以得出导体上的电荷分布。 1.导体内部无静电荷 证明:在导体内任取体积元 dV
E内 = 0
r r 由高斯定理 E dS ⋅ = 0 ∫
S
∑q = ∫ ρ dV = 0
i i V
Q体积元任取 导体带电只能在表面!
ρ =0
证毕
A B σ1 σ 2σ 3
场 两板之间 强 分 布 两板之外
Q E = ε0S
r E
E=0
练习
已知: 两金属板带电分别为q1、q2 求:σ1 、σ2 、σ3 、σ4
q1
q2
q1 + q2 σ1 = σ 4 = 2S
σ1
σ2
σ3
σ4
q1 − q2 σ 2 = −σ 3 = 2S
2.导体表面电荷 表面附近作圆柱形高斯面
r r σΔS 0 ∫ E • dS = E ⋅ ΔS ⋅ cos 0 =
σ
r E
ΔS
ε0
σ ∴E = ε0
r σ ^ ^ E表 = n n :外法线方向
ε0
3.孤立带电导体表面电荷分布 一般情况较复杂;孤立的带电导体,电荷 分布的实验的定性的分布: 曲率较大,表面尖而凸出部分,电荷面密度较大 曲率较小,表面比较平坦部分,电荷面密度较小 曲率为负,表面凹进去的部分,电荷面密度最小
例3.已知:导体板A,面积为S、带电量Q,在其旁边 放入导体板B。 求:(1)A、B上的电荷分布及空间的电场分布 (2)将B板接地,求电荷分布
σ1 σ 2 σ 3 σ4 − − − =0 a点 2ε 0 2ε 0 2ε 0 2ε 0
A B σ1 σ 2σ 3 σ 4
大学物理-静电场中的导体
E内= 0 等势体
静电平衡时的导体
接地 :取得与无限远相同的电势 通常取为零)。 (通常取为零)。
6
半径为R的金属球与地相连接 的金属球与地相连接, 例1. 半径为 的金属球与地相连接,在与球心 相距d=2R处有一点电荷 处有一点电荷q(>0),问球上的 相距 处有一点电荷 , 感应电荷 q'=? q'?q =
q3
q2 q1
B
R1 R2
A
R3
22
解: (1)当球体和球壳为一般带电体时 ) 用高斯定理可求得场强分布为
r −R E3 = (q1 + 3 Q) ( R2 ≤ r ≤ R3 ) 2 4πε0r R3 − R 1
3 3 2 3 2
4πε0 R q1 E2 = 2 4πε0r
E1 =
q1
3 1
r
(r ≤ R1 )
E = σ / εo
1 3.面电荷密度正比于表面曲率 σ ∝ R 面电荷密度正比于表面曲率
31
例4-2 (3)如果外壳接地,情况如何? )如果外壳接地,情况如何? (4)如果内球接地,情况又如何? )如果内球接地,情况又如何? (3)如果外壳接地 ) 则: 外壳电势= 外壳电势= 无穷远处电势 =0 外壳带电量= 外壳带电量=Q’
S
ε0 V
S 是任意的。 是任意的。 令S→ 0,则必有ρ 内 = 0。 。
8
必为零。 2.导体壳: 外可不为零,但σ内 和 E内必为零。 导体壳: 可不为零, 导体壳 σ
σ内 = 0
E内 = 0
S内
σ外
理由: 理由: 在导体中包围空腔选取 高斯面S 高斯面 , 则:
S
r r ∫ E导内 ⋅ d s = 0
静电场中的导体
分布在导体的表面上。
4、导体以外,靠近导体表面附近处的场强大小与导 体表面在该处的面电荷密度 的关系
E 0
二
静电平衡时导体上电荷的分布
1、 实心导体
+
+ + + +
E 0
+
S
+ + +
+
q E dS 0
S
0
q 0
结论: 导体内部无电荷,电荷只能分布
q
+
q
+
+
q
+
实验验证
外表面所带感应电荷全部入地
总结: 空腔导体(无论接地与否)将使腔内不
受外场影响。
接地空腔导体将使外部空间不受腔内电
场的影响。
四 有导体存在时场强和电势的计算
电荷守恒定律 电荷分布
静电平衡条件
E U
例1、有一外半径R1,内半径为R2的金属球壳。在球壳 中放一半径为R3的金属球,球壳和球均带有电量10-8C的 正电荷。问:(1)两球电荷分布。(2)球心的电势。 (3)球壳电势。 + + + 解:(1)、电荷+q分布在内球表面。 + - + 球壳内表面带电-q。
S A+ +
A
+
+
B+ B +
+ +
+
b、空腔内有带电体
E dS 0
S1
q
i
0
电荷分布在表面上
思考: 内表面上有电荷吗?
E dS 0 qi 0
