互感自感磁场的能量2010
合集下载
第十五讲自感和互感磁场能量

2 互感系数 回路1 —— 电流 I1
21 —— 回路1的磁场在回路2产生的总的磁通量
回路2 —— 电流I2
12 —— 回路2的磁场
在回路1产生 总的磁通量
第十五讲 自感和互感 磁场能量_20160225 XCH
电磁学 -大学物理
穿过回路2总的磁通量 21 M 21I1 穿过回路1总的磁通量 12 M 12 I 2 M21 —— 回路1对2的互感系数 M12 —— 回路2对1的互感系数 —— 实验和理论表明
自感系数 L I
第十五讲 自感和互感 磁场能量_20160225 XCH
电磁学 -大学物理
d 自感电动势 E L dt
dL dI E L ( I L ) dt dt
—— 如果自感系数 L 为常数
LI
dI —— 总是和回路中电流的变化相反 E L L dt
自感 —— 具有保持原有电流不变的特性 自感系数 —— 电磁惯性(电磁惯量)
dI 2 E12 M dt
dI 一般表示 E M M dt
互感电动势总是反抗另外一个回路中电流的变化
第十五讲 自感和互感 磁场能量_20160225 XCH
电磁学 -大学物理
3 自感和互感的关系 两个同轴螺线管1和2同绕在一个半径为R的长磁介质棒上 绕向相同,截面积近似等于磁介质棒的截面积, 螺线管1和2的长度分别为l1和l2, 单位长度的匝数为n1和n2, 且l1,l2 >>R,证明 1) M 12 M 21 M 2) 两个线圈中的自感系数 和互感系数之间的关系
M 12 M 21 M
形状和大小 —— 与两个回路的匝数,几何 匝数 两个回路的相对位置,周围的 磁介质有关 相对位置 磁介质
磁场中的磁能与自感现象

实验验证方法
静态实验法
通过测量静态情况下两个线圈之间的互感系数来验证互感现象的存在。这种方法需要使用 精密的测量仪器和稳定的电源来提供恒定的电流。
动态实验法
通过改变线圈中的电流或线圈之间的相对位置来观察感应电动势的变化情况。这种方法需 要使用示波器、电流计等实验
汇报人:XX 2024-01-16
contents
目录
• 磁场与磁能基本概念 • 磁能计算与储存方式 • 自感现象及其产生原因 • 互感现象与自感现象关系 • 磁场中能量转换与传递过程 • 总结回顾与拓展延伸
01
磁场与磁能基本概念
磁场定义及性质
磁场定义
磁场是一种存在于磁体周围的特 殊物质,它对放入其中的磁体产 生磁力作用。
影响因素探讨:距离、角度等
距离
线圈之间的距离越近,互感作用越强。当两 个线圈紧密靠近时,它们之间的磁通量变化 会更加显著,从而导致更大的感应电动势。
角度
线圈之间的相对角度也会影响互感作用。当 两个线圈的法线方向相互平行时,它们之间 的磁通量变化最大,互感作用最强。随着相 对角度的增大,磁通量变化减小,互感作用 减弱。
互感和自感之间联系和区别
联系
自感和互感都是电磁感应现象,都遵循 法拉第电磁感应定律。在电路分析中, 自感和互感往往同时存在,相互影响。
VS
区别
自感是单个线圈中电流变化时产生的感应 电动势,而互感是两个或多个线圈之间相 互作用产生的感应电动势。此外,自感系 数仅与线圈本身的结构和电流变化率有关 ,而互感系数则与线圈之间的相对位置、 形状、大小以及周围介质有关。
超导线圈应用案例
超导线圈在磁共振成像(MRI)、粒子加速器等领域有重要 应用。例如,在MRI中,超导线圈产生的强磁场和梯度磁场 用于对人体进行成像。
第8章_静磁能1__磁场的能量和能量密度__20101227

0
0 dt
0
0
0
2
0
其中
T
∫ εidt
0
表示 0 → T中,电源所作的功;
1 Li2表示电源在0 → T中提供的转变为磁场的能量。 2
T
∫ i2Rdt
0
表示0 → T中,电流在电阻上作的功;
由此可见,电源所供给的能量,一部分转化为焦耳--楞茨热,另一部分用于反抗自感电动势所作的功,这将 是另一种形式的能量改变的量度。
0
0
注意积分上下限的变换以及M12 = M 21
和自感一样,两个线圈中电源抵抗互感电动势所作 的这部分额外功,也以磁能的形式储存起来,一旦电流中 止,这部分磁能便通过互感电动势作功全部释放出来。
定义:互感磁能
W12 = M12I1I2 = Φ12I2
其中Φ12是载流线圈1产生的磁场通过线圈2的磁通量。
=
1 2
r B1
⋅
r H1
=
1 2
B1H1
=
μ0I 2r2 8π 2a 4
∫ ∫ ∫ ∫ ∫ ∫ Wm1
=
a 0
2π l
ω m1rdϕdrdz
00
=
l 0
μ0I 2 8π 2a4
a
dz
0
2π
r 3dr dϕ
0
=
μ0I 2l 16π
注意
a. 在上面的积分中,根据对称性选取了柱坐标系。
b. 如果电流只分布在导线表面上,则此时 ∑ I = 0,
(rr2
)
⋅
r dS
其可以看成载流线圈2在外磁场 BrS12(由线圈1提供的)中
所具有的静磁能。其实这也就是线圈1和线圈2的互感磁能
大学物理-12第十二讲 感生电动势、自感、互感、磁场能量

3.按定义 L I
18
二、互感应
●由于一个载流回路中电流发生变化而引起邻近另 一回路中产生感生电流的现象称为“互感现象”, 所产生的电动势称为 “互感电动势”。
21N 2 21M 21I1 12N 1 12M 12I2
从能量观点可证明:
M12M21M
M称为互感系数简称互感 单位:亨利(H)
同理:
bo
ov r b E感dr0
ab oabo
o
E 感
L R2 L2 dB
2
4 dt
h
a
b
L
方向ab (Ub Ua )
9
vv
Байду номын сангаас法2: 用 LE感dl 求
vv
dE感dl
r 2
dB dt
cos
dl
h 2
dB dt
dl
vv
LE感dl
b h dB dl
a 2 dt 1 hL dB
缆单位长度的自感系数。
解: 两导体圆筒间磁场
B
I
2r
R2 R1
AB
通过单位长度一段的磁通量
I l 1
B vdS vR R 12Bldr2 IlnR R 1 2
DC
单位长度的自感系数 L lnR2 I 2 R1
17
总结L的计算方法 1.设回路电流为I,写出B的表达式(一般由安培
环路定理)
vv
2.计算磁通 B d S, N
LE库dvl
0
v
Ñ 感生电场是非保守力场 LE感dl 0
3
例:在半径为R 的长直螺线管中通有变化的电流,使
管内磁场均匀增强,求螺线管内、外感生电场的场强
18
二、互感应
●由于一个载流回路中电流发生变化而引起邻近另 一回路中产生感生电流的现象称为“互感现象”, 所产生的电动势称为 “互感电动势”。
21N 2 21M 21I1 12N 1 12M 12I2
从能量观点可证明:
M12M21M
M称为互感系数简称互感 单位:亨利(H)
同理:
bo
ov r b E感dr0
ab oabo
o
E 感
L R2 L2 dB
2
4 dt
h
a
b
L
方向ab (Ub Ua )
9
vv
Байду номын сангаас法2: 用 LE感dl 求
vv
dE感dl
r 2
dB dt
cos
dl
h 2
dB dt
dl
vv
LE感dl
b h dB dl
a 2 dt 1 hL dB
缆单位长度的自感系数。
解: 两导体圆筒间磁场
B
I
2r
R2 R1
AB
通过单位长度一段的磁通量
I l 1
B vdS vR R 12Bldr2 IlnR R 1 2
DC
单位长度的自感系数 L lnR2 I 2 R1
17
总结L的计算方法 1.设回路电流为I,写出B的表达式(一般由安培
环路定理)
vv
2.计算磁通 B d S, N
LE库dvl
0
v
Ñ 感生电场是非保守力场 LE感dl 0
3
例:在半径为R 的长直螺线管中通有变化的电流,使
管内磁场均匀增强,求螺线管内、外感生电场的场强
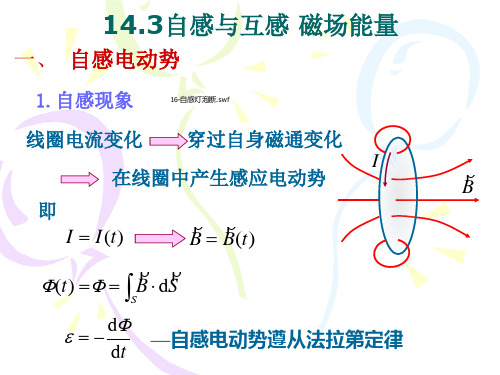
14.3自感与互感 磁场能量
例 2 在磁导率为 的均匀无限大的磁介质中, 一无限长直导线与一宽长分别为 b 和 l 的矩形线圈共 面,直导线与矩形线圈的一侧平行,且相距为 d . 求二者 的互感系数. 解 设长直导线通电流
I
b
B
I
2π x
I
d o x dx
l
x
I dΦ B ds ldx 2π x
0Leabharlann I0的功转化为磁场的能量
自感电动势所做的总功
A dA
L0
0
1 2 LI d I LI 0 2
Wm
(自感磁能公式)
(2) 与电容储能比较
1 2 Wm LI 2
2 Q0 We 2C
此公式适用于任何形状的自感线圈
自感线圈也是一个储能元件,自感系 数反映线圈储能的本领
2、 磁能的分布
2
均匀磁场:
Wm wmV
非均匀磁场:积分遍及磁场存在的空间
Wm wm dV
V
V
1 2 B dV 2
• 磁场能量密度与电场能量密度公式比较
wm
1 2 B 2
1 2 we E 2
例1: 一由 N 匝线圈绕成的螺绕环,通有电流 I ,其中 充有均匀磁介质 I 求: 磁场能量Wm 解: 根据安培环路定理,螺绕环内
若自感系数是一不变的常量
dI L L dt
dI dt
自感
L L
单位:1 亨利 ( H )= 1 韦伯 / 安培 (1 Wb / A)
1mH 10 H , 1μ H 10 H
讨论
自感具有使回路电流保持不变的性质 —— 电磁惯性
3
6
4.自感的计算方法 例1 如图的长直密绕螺线管,已知 l , S , N , , B
15-2-涡电流-自感和互感-磁场的能量-磁场能量密度1

Wm
1 2 LI (自感线圈) 2 Wm wm dV (已知磁场的分布)
V
能量存在 于场中 在电磁场中
we
1 D E 2
wm
1 BH 2
普遍适用各种
w we wm
1 1 电磁场 w D E B H 2 2
4
2012/5/30
三、磁场的能量
2. 磁场能量的分布
(2)磁场的能量密度
类比
三、磁场的能量
静电场 稳恒磁场
Wm 1 LI 2 2
器件中能量 We 1 CU 2 C 2 的表示
通过平板电容器 得出下述结论
wm
B 2
2
L
I
L
wm
1 1 H 2 BH 2 2
通过长直螺线管 得出下述结论
(3)磁场能量的计算
例2. 如图,在一柱形纸筒上绕有两组相同的线圈
AB,A’B’, 每个线圈的自感均为L。求:(1)A和A’ 相接时,B和B’间的自感L1; (2)A’和B相接时,A 和B’间的自感L2 。
S
L n 2V
l
E
A A’ B B’
L1 0
L2 4 L
例3 有两个同轴圆筒形导体 , 其半径分别为 R1 和 R2 , 通过它们的电流均为 I ,但电流的流向相反. 设在两圆筒间充满磁导率为 的均匀磁介质 , 求其 自感 L .
B
~
一、涡电流
2. 涡电流的应用
(1)电磁效应 金属探测器 (2)热效应
一、涡电流
2. 涡电流的应用
高频感应加热
B
I B
I
发射线圈
接收线圈
自感互感电磁能量
交变电压U=U0sint,求电容器极板间的: (1)位移电流;
(2)位移电流密度 Jd 的大小; (3)位移电流激发的磁场分布B(r) , r 为圆板的中心距离.
解: (1)由于l <<R , 故平板间
可作匀强电场处理, E U l
根据位移电流的定义:
Id
dF e dt
dDS
dt
0
dE R2
dt
(2) 位移电流与传导电流不同之处 • 产生机理不同 • 存在条件不同 位移电流可以存在于真空中、导体中、介质中
(3) 位移电流不产生焦耳热,传导电流产生焦耳热
相同点:
传导电流 I 0
位移电流 I d
激发涡旋磁场等效, 满足右手螺旋关系。
不同点:
自由电荷 定向运动
产生焦耳热
电场随时 间变化率
不产生焦耳热
解:对于长直螺线管,当有电流I通过时,可以把管内的磁场
看作是均匀的,其磁感应强度的大小为: 令V=Sl为螺线管的体积
B m N I mnI
l
L=mn2V
穿过螺线管的磁通量等于
增大L的方法:
F=NBS=NmnIS
(1)n大
自感系数为
L F =NmnS N mnSl
I
l
(2)m大
例 设一载流回路由两根平行的长直导线组成。 求 这一对导线单位长度的自感L 解 由题意,设电流回路 I
磁场能量密度的普遍计算公式
(适用于均匀与非均匀磁场)
磁场能量密度与电场能量密度公式的比较 在有限区域内
dV
w
V
磁场能量公式与电场能量公式具有完全对称的形式
例题.同轴电缆的磁能与自感
同轴电缆中金属 芯线的半径为R1, 金属圆筒半径为 R2,中间充满磁 导中为m的磁介质, 若芯线与圆筒分 别与电池两极相 连,芯线与圆筒 上的电流大小相 等,方向相反, 如略去金属芯线 内的磁场,求此 同轴芯线与圆筒 之间单位长度上 的磁能与自感系 数。
3.9互感和自感 3.10磁场能量
M12 M 21
诺伊曼公式
同理
由此可见
M 21
两个多匝回路的互感
dl dl M12 12 N1 N2 0 1 2 I1 4 c2 c1 R
N1为回路1匝数
N2为回路1匝数
单匝回路的自感
应用诺伊曼公式计算自感为
c2
I
dl1 dl2 0 L I 4 c2 c1 R
B
B
详解见例3-9
导线内的磁场
a
r
dr
I 2 H d l H 2 r 2 r c a 1 I H e H e 2 r 2 a
l
I
B 0 H e
0 I 2 r 2 a
c1
对于单匝回路,可将电流看作集中 于轴线回路c1上,而将计算磁通的回 路取作导线内侧的回路 c2 。
L
N匝回路的自感
dl dl N2 0 1 2 I 4 c2 c1 R
外自感
在导线内部的磁力线同样套链着电流,其磁链与电 流比值定义为内自感。
a a
r
dr
B
I
l
I
l
r
dr
x
dx
0
x
D
0 I D a 1 1 dx 2 a x ( D x) I Da 0 ln a
解:由 H dl I 得两导线在x处产生 的磁场分别为
I H1 ey , 2x
单位长度的外自感为
L
详解见例3-9、 I H 2 ey 3-7 单位长度的内自感为 2 D x
v
1 H BdV 2v
诺伊曼公式
同理
由此可见
M 21
两个多匝回路的互感
dl dl M12 12 N1 N2 0 1 2 I1 4 c2 c1 R
N1为回路1匝数
N2为回路1匝数
单匝回路的自感
应用诺伊曼公式计算自感为
c2
I
dl1 dl2 0 L I 4 c2 c1 R
B
B
详解见例3-9
导线内的磁场
a
r
dr
I 2 H d l H 2 r 2 r c a 1 I H e H e 2 r 2 a
l
I
B 0 H e
0 I 2 r 2 a
c1
对于单匝回路,可将电流看作集中 于轴线回路c1上,而将计算磁通的回 路取作导线内侧的回路 c2 。
L
N匝回路的自感
dl dl N2 0 1 2 I 4 c2 c1 R
外自感
在导线内部的磁力线同样套链着电流,其磁链与电 流比值定义为内自感。
a a
r
dr
B
I
l
I
l
r
dr
x
dx
0
x
D
0 I D a 1 1 dx 2 a x ( D x) I Da 0 ln a
解:由 H dl I 得两导线在x处产生 的磁场分别为
I H1 ey , 2x
单位长度的外自感为
L
详解见例3-9、 I H 2 ey 3-7 单位长度的内自感为 2 D x
v
1 H BdV 2v
3.大学物理-自感互感磁场能
K
ε
R
G
I1
变化
I2
线圈1 线圈1中产生 ε12 一个载流回路中电流变化,引起邻近另一回路中 一个载流回路中电流变化,引起邻近另一回路中 另一回路 互感现象. 产生感生电动势的现象 — 互感现象. 互感电动势
I1 变化
I 2 变化
ψ 12 变化
线圈2中产生 线圈 中产生 ε 21
2. 互感系数 (1)定义 (1)定义 当线圈几何形状,相对位置, 当线圈几何形状,相对位置, 周围介质磁导率均一定时
自感磁能: 自感磁能:
ε
R
1 2 WL = A = LI 2
o
t
*二. 互感磁能 二 如果有二个线圈,通以电流时, 如果有二个线圈,通以电流时,它们还有 二个线圈 互感磁能: 互感磁能: *三. 总磁能 三 二个线圈 二个线圈 多个线圈 多个线圈
W12 = MI1I 2
1 2 1 2 W = L1I1 + L2I2 + M12I2I1 m 2 2
R2
R1
l
I
I d Φ = B dr l = ldr 2π r R I Il R2 o r Ψ =Φ = ∫ l dr = ln R 2π r 2π R
2 1 1
I
电缆单位长度的自感: 电缆单位长度的自感
R2 Ψ ∴L = = ln lI 2π R1
五.互感 1. 互感现象
ψ12
1
2
ψ21
dI dI ε = ε1 + ε2 = (L1 + L2 + 2M) = L′ dt dt
L′ = L1 + L2 + 2M
L1
L2
L 1
L2
§10-3自感互感磁场能量讲解
讨论实际线路中的感生电动势问题。 一.自感现象 自感系数
i
K
dI 0 dt dI 0 dt
i
A
B
合上 K,支路中灯泡A先亮, 灯泡B后亮。
断开K ,A立即熄灭,B会瞬间闪亮再熄灭。 电路中电感元件具有阻交流、通直流的作用 。 电路中电容元件具有阻直流、通交流的作用 。
自感现象: 由于电路中的电流变化, 而在自己的线路 中产生感应电流的现象叫自感现象。 设电路中的电流为I 全磁通与回路的电流成正比:
L I
管内全磁通:
l
nN l
l V lS
S
L n V
2
自感系数 L 与螺线管体积V 、单位长度匝数 n、介质 有关
除线圈外,任何一个实际电路都存在电感,输电线相当 于单匝回路,回路中也分布电感。 例2 两根平行输电导线,中心距离为d,半径为a,求:两 导线单位长度上的分布电感(d >>a)。 解:设导线中有电流I
变 不变
C
例6 有两个长度均为l,半径分别为r1和r2( r1<r2 ),匝数分 别为N1和N2的同轴长直密绕螺线管.求它们的互感系数M. 解:设半径 r1 的线圈中通有电流 I1 ,则
N1 B1 0 I1 0 n1 I1 l
穿过半径为 r2 的线圈的全磁通
r2 r1
N2 N1
N2Φ21 N2 B1 (πr12 ) n2lB1 ( πr12 )
线圈2电流变化在线圈 1中产生感应电动势
1
2
电流 I 1 在2回路中所产生的全磁通
21 M 21I1
电流 I 2在1回路中所产生的全磁通
I1 (t )
N 1匝
N 2匝
1
i
K
dI 0 dt dI 0 dt
i
A
B
合上 K,支路中灯泡A先亮, 灯泡B后亮。
断开K ,A立即熄灭,B会瞬间闪亮再熄灭。 电路中电感元件具有阻交流、通直流的作用 。 电路中电容元件具有阻直流、通交流的作用 。
自感现象: 由于电路中的电流变化, 而在自己的线路 中产生感应电流的现象叫自感现象。 设电路中的电流为I 全磁通与回路的电流成正比:
L I
管内全磁通:
l
nN l
l V lS
S
L n V
2
自感系数 L 与螺线管体积V 、单位长度匝数 n、介质 有关
除线圈外,任何一个实际电路都存在电感,输电线相当 于单匝回路,回路中也分布电感。 例2 两根平行输电导线,中心距离为d,半径为a,求:两 导线单位长度上的分布电感(d >>a)。 解:设导线中有电流I
变 不变
C
例6 有两个长度均为l,半径分别为r1和r2( r1<r2 ),匝数分 别为N1和N2的同轴长直密绕螺线管.求它们的互感系数M. 解:设半径 r1 的线圈中通有电流 I1 ,则
N1 B1 0 I1 0 n1 I1 l
穿过半径为 r2 的线圈的全磁通
r2 r1
N2 N1
N2Φ21 N2 B1 (πr12 ) n2lB1 ( πr12 )
线圈2电流变化在线圈 1中产生感应电动势
1
2
电流 I 1 在2回路中所产生的全磁通
21 M 21I1
电流 I 2在1回路中所产生的全磁通
I1 (t )
N 1匝
N 2匝
1
