自感互感和磁场能量解读
合集下载
14电磁感应2(自感互感、磁场能量)

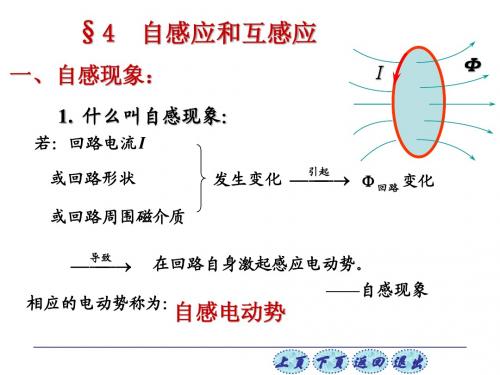
§14-3 自感和互感
I
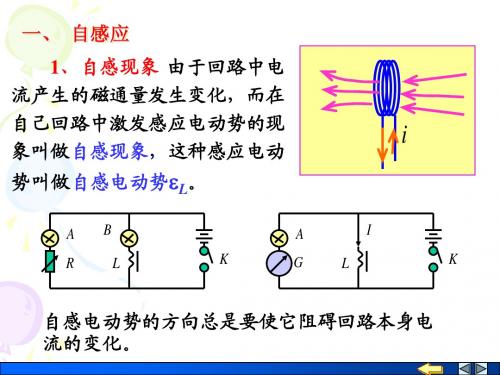
一、自感 1.当一线圈中的电流变化时,它所激发的磁 场通过线圈自身的磁通量也在变化,使线 圈自身产生感应电动势。 这种因线圈中电流变化而在线圈自身所引 起的感应现象叫做自感现象,所产生的电 动势叫做自感电动势。
R
L
S2 S1
S
L
闭合开关, 2比S1先亮 S
断开开关,S闪一下熄灭
电流增大时,dI 0 , L 0 ,即 L与电流反
向,阻碍电流增大;
dI 电流减小时, 0 , L 0 ,即 L与电流同 dt dt
向,阻碍电流减小
I
例1 、 试计算长直螺线管的自感。 已知:匝数N,横截面积S,长度l ,磁导率
μ
l
自感的计算步骤:
S
LH dl I B H B H
单位长度导线内磁能为:
R
P
Wm wm dV
V
R
0
I 2 r 2 I 2 2rdr 2 4 8 R 16
§14-5 位移电流 麦克斯韦方程组
一、电磁场的基本规律 静电场:
D dS q
S
E dl 0
l
(对真空或电介质都成立)
稳恒磁场:
例、如图,求同轴传输线之磁能及自感系数 R2 I I 解: H B dV 2rldr R 1 2r 2r 1 W V wdV V H 2 dV 2 R2 1 I 2 ( ) 2rldr R1 2 2r I 2 l R2 ln( ) 4 R1 I 2 l R2 1 2 LI W ln( ) 4 R1 2 l R2 可得同轴电缆 L ln( ) 的自感系数为 2 R1
I
一、自感 1.当一线圈中的电流变化时,它所激发的磁 场通过线圈自身的磁通量也在变化,使线 圈自身产生感应电动势。 这种因线圈中电流变化而在线圈自身所引 起的感应现象叫做自感现象,所产生的电 动势叫做自感电动势。
R
L
S2 S1
S
L
闭合开关, 2比S1先亮 S
断开开关,S闪一下熄灭
电流增大时,dI 0 , L 0 ,即 L与电流反
向,阻碍电流增大;
dI 电流减小时, 0 , L 0 ,即 L与电流同 dt dt
向,阻碍电流减小
I
例1 、 试计算长直螺线管的自感。 已知:匝数N,横截面积S,长度l ,磁导率
μ
l
自感的计算步骤:
S
LH dl I B H B H
单位长度导线内磁能为:
R
P
Wm wm dV
V
R
0
I 2 r 2 I 2 2rdr 2 4 8 R 16
§14-5 位移电流 麦克斯韦方程组
一、电磁场的基本规律 静电场:
D dS q
S
E dl 0
l
(对真空或电介质都成立)
稳恒磁场:
例、如图,求同轴传输线之磁能及自感系数 R2 I I 解: H B dV 2rldr R 1 2r 2r 1 W V wdV V H 2 dV 2 R2 1 I 2 ( ) 2rldr R1 2 2r I 2 l R2 ln( ) 4 R1 I 2 l R2 1 2 LI W ln( ) 4 R1 2 l R2 可得同轴电缆 L ln( ) 的自感系数为 2 R1
互感 自感和磁场能量

Li
L i
1mH=10-3H, 1m H=10-6H
单位:亨(利) H,
三、自感系数(自感)
2.性质:
L i
(1)L 决定于线圈的形状、尺寸、匝数和磁 介质的分布情况,与线圈是否通电流无关。
(2)L反映了回路反抗电流变化的能力
3.有关计算
Li
L i
di L L dt
已知:螺线管单位长度上n匝,圆环面积为S 求:螺线管与圆环的互感系数
思路: i1 B1 21 M
i1
B1
解: 设螺线管通有电流 i1
螺线管内磁场: B1 m0 ni1 通过圆环的全磁通
S
21 M i1
21 B1S m 0ni1 S m 0ni1 S m0 nS
设回路1通电流 i1,求 i1
i1
B1
变化时,回路2中的互感电动势
i2
M21:互感系数
B1 i1 21 i1 21 M 21i1
d21 di1 dM 21 di1 M 21 i1 M 21 21 dt dt dt dt
同理:
di2 12 M 12 dt
m 0 Il R2 ln 2 R1
L m0 ln R2 l = 2 R1
五、自感现象的应用与危害
•在许多电器设备中,常利用线圈的自感起稳 定电流的作用
例如,日光灯的镇流器就是一个带有铁芯的自感线圈
•通常在具有相当大的自 感和通有较大电流的电 路中,当扳断开关的瞬 时,在开关处将发生强 大的火花,产生弧光放电 现象,亦称电弧
m
L
I
L
i :I
0
自感电动势做的功=磁场能量变化
2 自感互感磁场能量
µI
1 µI 2 = ( ) 2µ 2 π r
2
第十三章电磁感应 第十三章电磁感应 电磁场 2
=
µI
8π r
2
2
8π r
2 2
dV
单位长度壳层体积
d V = 2π r d r ⋅ 1 2 R2 µI µ I 2 R2 ln Wm = ∫ dr = R1 4 π r 4π R1
µ
r dr
R2
µ R2 1 2 ln Wm = LI L = 2 π R1 2
dΦ dI2 12 ε12 = − = −M dt dt
dΦ21 dI1 ε21 = − = −M dt dt
假设一个线圈电流I分布 假设一个线圈电流 互感的计算 •假设一个线圈电流 分布
•计算该线圈产生的磁场在另一线圈产生的磁通量Φ 计算该线圈产生的磁场在另一线圈产生的磁通量Φ 计算该线圈产生的磁场在另一线圈产生的磁通量
I a b l
v
13 - 3 自感和互感
第十三章 电磁感应 电磁场
一长直螺线管,单位长度上的匝数为n,另一半经为r 例3、一长直螺线管,单位长度上的匝数为 ,另一半经为 的圆环放在螺线管内,圆环平面与管轴垂直。 的圆环放在螺线管内,圆环平面与管轴垂直。求螺线管与 圆环的互感系数。 圆环的互感系数。
I
I r
P
R2
l
S
dr
Φ = ∫ dΦ =
∫ R1
R2
µI
2π r
ld r
Φ = ∫ dΦ = ∫
即
R2 R1
µI
2π r
ld r
R1 Q
R
R2 Φ= ln 2π R1
Φ µl R2 L= = ln I 2π R1
自感互感磁场能量讲解

B2 n2I2
由于长直螺线管的端口外的磁感应强度为零,穿 过线圈1的总磁通量为
1 2 N '2 B 2 S n 1 l2 B 2 S n 1 n 2 l2 S 2 I
由 12M 得12I2
M 12 I2 12 n1n2l2S n1n2V2
两次计算证明 M 1 2M 2 1M n 1 n 2 V 2
设电路中的电流为I 全磁通与回路的电流成正比:
i B
I
dI 0
dt
回路中的磁通为 LI
自感系数:比例系数 L为该回路的自感系数 L
I
说明:
1、自感电动势
LI L
I
L
dLdI dt dt
自感系数的大小 L i dI dt
2、计算自感系数的方法
L I
或 L i dI dt
自感系数的大小与回路的形状、匝数、介质等因数有关
1
21M21I1
电流 I在2 1回路中所产生的全磁通
12M12I2
可以证明 M21M12M
12
N1匝
I1 (t )
N2匝
12
I (t ) N1匝
N2匝
2
M称为互感系数,和两个回路的大小、形状、匝数、 相对位置以及周围磁介质的性质有关。在没有铁磁质 时,M为常量。
互感电动势
2
1
M
dI1 dt
12
M
dI2 dt
Ldi iR
K2
dt
d t L d i id R t id L td ii i2 R d t
两边积分得 idtLdii2R dt
I Lidi 1LI2
0
2
0ti dt1 2L2I0ti2Rdt
由于长直螺线管的端口外的磁感应强度为零,穿 过线圈1的总磁通量为
1 2 N '2 B 2 S n 1 l2 B 2 S n 1 n 2 l2 S 2 I
由 12M 得12I2
M 12 I2 12 n1n2l2S n1n2V2
两次计算证明 M 1 2M 2 1M n 1 n 2 V 2
设电路中的电流为I 全磁通与回路的电流成正比:
i B
I
dI 0
dt
回路中的磁通为 LI
自感系数:比例系数 L为该回路的自感系数 L
I
说明:
1、自感电动势
LI L
I
L
dLdI dt dt
自感系数的大小 L i dI dt
2、计算自感系数的方法
L I
或 L i dI dt
自感系数的大小与回路的形状、匝数、介质等因数有关
1
21M21I1
电流 I在2 1回路中所产生的全磁通
12M12I2
可以证明 M21M12M
12
N1匝
I1 (t )
N2匝
12
I (t ) N1匝
N2匝
2
M称为互感系数,和两个回路的大小、形状、匝数、 相对位置以及周围磁介质的性质有关。在没有铁磁质 时,M为常量。
互感电动势
2
1
M
dI1 dt
12
M
dI2 dt
Ldi iR
K2
dt
d t L d i id R t id L td ii i2 R d t
两边积分得 idtLdii2R dt
I Lidi 1LI2
0
2
0ti dt1 2L2I0ti2Rdt
4-自感和互感 磁场的能量
磁能密度: 磁能密度: 单位体积内储存的磁场能量
1 wm = BH 2
(普适 普适) 普适
2. 磁场任意空间的磁能: Wm = ∫V wmdV 磁场任意空间的磁能:
上页 下页 返回 退出
上页 下页 返回 退出
例5:同轴电缆是由半径为 1 的铜芯线和半径为 2 筒状导体 用铜 :同轴电缆是由半径为R 的铜芯线和半径为R 筒状导体(用铜 线编成)组成 组成。 的绝缘介质。工作时, 线编成 组成。中间充满µ≈µ0 的绝缘介质。工作时,沿芯线 和外筒流过的电流大小相等、方向相反。略去导体内部磁场。 和外筒流过的电流大小相等、方向相反。略去导体内部磁场。 的磁能和自感。 求:无限长同轴电缆中一段长为 l 的磁能和自感。 由安培环路定理可得磁场分布: 解:由安培环路定理可得磁场分布:
dψ 12 dψ 21 M= = dI1 dI 2 上页 下页 返回 退出
3. 互感电动势: 互感电动势:
回路1 在回路2中引起的互感电动势 中引起的互感电动势: 回路 在回路 中引起的互感电动势:
ε 12
dψ 12 dI1 =− = −M dt dt
回路2 在回路1中引起的互感电动势 中引起的互感电动势: 回路2 在回路1中引起的互感电动势:
体现回路产生自感电动势来反抗电流改变 的能力,称为回路的自感系数 简称自感 自感系数, 自感。 的能力,称为回路的自感系数,简称自感。 它由回路的大小、形状、 它由回路的大小、形状、匝数以及周围磁 介质的性质决定,是一个由回路自身特征 介质的性质决定 是一个由回路自身特征 决定的电路参数 电路参数。 决定的电路参数。
引起
自感电动势
上页 下页 返回 退出
2. 自感系数: 自感系数:
r r0 r µ 0 I dl × r dB = 4π r2
第28讲 自感与互感 磁场能量

9.3 自感与互感
dB dI 感 dt dt
?
自感和互感现象
dI L L dt dI1 21 M dt
一 自感 1. 自感现象
当一个线圈中的电流发生变化时,它所激发的 磁场穿过线圈自身的磁通量发生变化,从而在 线圈本身产生感应电动势,这种现象称为自感 现象,相应的电动势称为自感电动势。
4. 自感系数的物理意义
dI const 时, 当线圈中的电流变化率为定值,即 dt L越大,产生的εL越大,因此线圈阻碍电流变化的能 力越强。所以线圈的自感系数L的物理意义为:
自感 L有维持原电路状态的能力, 自感系数L就是 这种能力大小的量度,它表征回路电磁惯性的大小。
dI L L dt
L0=L1+L2+2M =2L+2M
所以 L=L0/2-M < L0/2。
证毕。
9.4 磁场的能量
1 自感磁能 当电路中电流从 0 增加到稳定值 I0 时,电路附近 的空间逐渐建立起一定强度的磁场,磁场也具有 能量。 电源反抗自感电动势所做的功,就在建立磁场的 过程中转化为磁场的能量。 ─自感磁能
0 I 0 B 2 r 0 r R1 R1 r R2 r R2
I
R2 R1
l
取体积元为薄柱壳
d 2 rldr
1 B2 dV Wm wm dV V 2 V 0
r
dr
Wm wm dV
V
V
再根据
R2
R1
1 0 I 2 0 I 2 l R2 ( ) 2 rldr ln( ) 2 0 2 r 4 R1
5.自感的计算方法 • 假设线圈中电流为I; • 计算线圈中的全磁通Ψm ; m N B dS • 由L= Ψm / I, 求出L.
dB dI 感 dt dt
?
自感和互感现象
dI L L dt dI1 21 M dt
一 自感 1. 自感现象
当一个线圈中的电流发生变化时,它所激发的 磁场穿过线圈自身的磁通量发生变化,从而在 线圈本身产生感应电动势,这种现象称为自感 现象,相应的电动势称为自感电动势。
4. 自感系数的物理意义
dI const 时, 当线圈中的电流变化率为定值,即 dt L越大,产生的εL越大,因此线圈阻碍电流变化的能 力越强。所以线圈的自感系数L的物理意义为:
自感 L有维持原电路状态的能力, 自感系数L就是 这种能力大小的量度,它表征回路电磁惯性的大小。
dI L L dt
L0=L1+L2+2M =2L+2M
所以 L=L0/2-M < L0/2。
证毕。
9.4 磁场的能量
1 自感磁能 当电路中电流从 0 增加到稳定值 I0 时,电路附近 的空间逐渐建立起一定强度的磁场,磁场也具有 能量。 电源反抗自感电动势所做的功,就在建立磁场的 过程中转化为磁场的能量。 ─自感磁能
0 I 0 B 2 r 0 r R1 R1 r R2 r R2
I
R2 R1
l
取体积元为薄柱壳
d 2 rldr
1 B2 dV Wm wm dV V 2 V 0
r
dr
Wm wm dV
V
V
再根据
R2
R1
1 0 I 2 0 I 2 l R2 ( ) 2 rldr ln( ) 2 0 2 r 4 R1
5.自感的计算方法 • 假设线圈中电流为I; • 计算线圈中的全磁通Ψm ; m N B dS • 由L= Ψm / I, 求出L.
电磁感应 4-3 自感互感、磁场能量
任何磁场的能量
(不一定均匀磁场)
Wm
V wmdV
V
1 BHdV 2
电场 能量
磁场 能量
电场能量与磁场能量的对比
存储在器件中
存储在场中
We
1 2
CU
2
we
1 2
D
E
We V wedV
Wm
1 2
LI
2
wm
1 2
B
H
Wm V wmdV
若同时存在 电场和磁场
w
1
B
H
1
D
E
2
一、电感线圈存储的能量
前面演示自感的典型实验,当开关 突然断开后,灯泡会更亮地突闪。 这说明电感线圈中存储了某种形式 的能量,在开关断开后释放出来了
K
A
I
i
L
自感为 L 通有电流 I 的线圈所具有的磁能等于电流消 失过程中 (I → 0) 自感电动势所做的功,Wm = AL
dt 时间内通过灯泡的电量 q = i dt
的磁场中的,因此我们考虑磁场能量与磁感应强度之
间的关系。以长直螺线管为例,其自感 L = μn2V 忽略边缘效应,其内部的磁感应强度 B = μnI
Wm
1 2
LI 2
1 2
n2I 2V
1 2
B2
V
单位体积 磁场能量
wm
1 2
B2
1 2
BH
1 2
H 2
磁能 密度
wm
1 2
B
H
虽从长直螺线管特例推出,但对任何磁场均普遍适用
l
dr
穿过线框的磁通量为
2r
r
Φ
B dS
大学物理 12-4 自感和互感解读
设线圈1中通有电流 I1 若两回路几何形状、尺寸及相对 位置不变,周围无铁磁性物质,则第 二个线圈的磁通量为:
1
Φ21
I1
I2
2
Φ21 I1
Φ21 M 21I1
互感
同理,若线圈2中通有电流 I 2 若两回路几何形状、尺寸 及相对位置不变,周围无铁磁 性物质,则第一个线圈的磁通 量为:
I1
I2
Φm
Ψ NΦm
Ψ
Ψ LI
L
B
自感系数计算举例 解: B Φ Ψ L
NI B nI l
Ψ NΦ
NI S Φ B dS BS S l
N I
2 2
Ψ N L 2 lS I l 2 n V
l
S
μ
l
S
[补例] 求一环形螺线管的自感。
自感
2、 L的计算:可用上两式之一计算,一般由 L I 计算。 3、 L 的大小反映阻碍电流变化的能力,L 是电磁 惯性的一种表现。 4、利弊 1) 应用:镇流器,扼(抑)流圈,谐振电路,··· 2) 害处:上电迟延,断电影响,分布参数,···
自感
求自感电动势的关键,在于知道线圈的自感系数大小, 一般通过实验测得;规则线圈也可以计算得出。
自感
【讨论】: 1、 L 的定义:可用下两式之一定义 (1) Ψ LI L I dI L L (2) dI dt dt L 的意义:若I = 1A,则 L = Ψ
自感系数在数值上等于回路中通过单位电流 时,通过自身回路所包围面积的磁通链数。
★
自感系数是一个与线圈大小、形状及匝数有 关的量,与线圈内通有的电流 I无关,一般由实 验确定。
已知:R1 R2 h N H dl NI
1
Φ21
I1
I2
2
Φ21 I1
Φ21 M 21I1
互感
同理,若线圈2中通有电流 I 2 若两回路几何形状、尺寸 及相对位置不变,周围无铁磁 性物质,则第一个线圈的磁通 量为:
I1
I2
Φm
Ψ NΦm
Ψ
Ψ LI
L
B
自感系数计算举例 解: B Φ Ψ L
NI B nI l
Ψ NΦ
NI S Φ B dS BS S l
N I
2 2
Ψ N L 2 lS I l 2 n V
l
S
μ
l
S
[补例] 求一环形螺线管的自感。
自感
2、 L的计算:可用上两式之一计算,一般由 L I 计算。 3、 L 的大小反映阻碍电流变化的能力,L 是电磁 惯性的一种表现。 4、利弊 1) 应用:镇流器,扼(抑)流圈,谐振电路,··· 2) 害处:上电迟延,断电影响,分布参数,···
自感
求自感电动势的关键,在于知道线圈的自感系数大小, 一般通过实验测得;规则线圈也可以计算得出。
自感
【讨论】: 1、 L 的定义:可用下两式之一定义 (1) Ψ LI L I dI L L (2) dI dt dt L 的意义:若I = 1A,则 L = Ψ
自感系数在数值上等于回路中通过单位电流 时,通过自身回路所包围面积的磁通链数。
★
自感系数是一个与线圈大小、形状及匝数有 关的量,与线圈内通有的电流 I无关,一般由实 验确定。
已知:R1 R2 h N H dl NI
06自感互感磁场能量
dψ 21 dI1 dI1 ε 21 = = M 21 = M dt dt dt
电流变化在线圈1中产生的互感电动势 线圈2电流变化在线圈 中产生的互感电动势: 线圈 电流变化在线圈 中产生的互感电动势
dψ 12 dI 2 dI 2 ε 12 = = M 12 = M dt dt dt
互感系数的计算: 互感系数的计算: ①假设一个线圈中通有电流 I ; ②求另一个线圈中的磁链 ; 求另一个线圈中的磁链ψ 磁链 ③由定义求出互感系数 M. .
线圈中电流从 0 变化到 I 过程中电流作 的总功为: 的总功为:
0→I
A=∫
1 2 dA = ∫ Lidi= LI 2
I 0
根据功能原理,外力所作功全部转换为储存于线圈 根据功能原理,外力所作功全部转换为储存于线圈 中的磁能. 中的磁能. 因此,具有自感系数为 的线圈通有电流 的线圈通有电流I时所具有 因此,具有自感系数为L的线圈通有电流 时所具有 的磁场能量为: 的磁场能量为:
ψ 21 ∝ I1 ,
ψ 12 ∝ I 2
7
定义: 定义:回路的互感磁链与产生这个互磁链的电流的 比值,称为这两个路或线圈间的互感系数或互感量 互感系数或互感量. 比值,称为这两个路或线圈间的互感系数或互感量.
M21 =ψ21 / I1
M21 = M12 = M
M12 =ψ12 / I2
理论和实践证明对于两个给定的线圈有: 理论和实践证明对于两个给定的线圈有:
2
dWm = wmdV体
2)再计算体积V体内的磁场能量, )再计算体积 内的磁场能量, 内的磁场能量
Wm = ∫V dW = ∫V wmdV 体 m
n
I
Nφm NnIS L= = = I I I
§10-3自感互感磁场能量讲解
讨论实际线路中的感生电动势问题。 一.自感现象 自感系数
i
K
dI 0 dt dI 0 dt
i
A
B
合上 K,支路中灯泡A先亮, 灯泡B后亮。
断开K ,A立即熄灭,B会瞬间闪亮再熄灭。 电路中电感元件具有阻交流、通直流的作用 。 电路中电容元件具有阻直流、通交流的作用 。
自感现象: 由于电路中的电流变化, 而在自己的线路 中产生感应电流的现象叫自感现象。 设电路中的电流为I 全磁通与回路的电流成正比:
L I
管内全磁通:
l
nN l
l V lS
S
L n V
2
自感系数 L 与螺线管体积V 、单位长度匝数 n、介质 有关
除线圈外,任何一个实际电路都存在电感,输电线相当 于单匝回路,回路中也分布电感。 例2 两根平行输电导线,中心距离为d,半径为a,求:两 导线单位长度上的分布电感(d >>a)。 解:设导线中有电流I
变 不变
C
例6 有两个长度均为l,半径分别为r1和r2( r1<r2 ),匝数分 别为N1和N2的同轴长直密绕螺线管.求它们的互感系数M. 解:设半径 r1 的线圈中通有电流 I1 ,则
N1 B1 0 I1 0 n1 I1 l
穿过半径为 r2 的线圈的全磁通
r2 r1
N2 N1
N2Φ21 N2 B1 (πr12 ) n2lB1 ( πr12 )
线圈2电流变化在线圈 1中产生感应电动势
1
2
电流 I 1 在2回路中所产生的全磁通
21 M 21I1
电流 I 2在1回路中所产生的全磁通
I1 (t )
N 1匝
N 2匝
1
i
K
dI 0 dt dI 0 dt
i
A
B
合上 K,支路中灯泡A先亮, 灯泡B后亮。
断开K ,A立即熄灭,B会瞬间闪亮再熄灭。 电路中电感元件具有阻交流、通直流的作用 。 电路中电容元件具有阻直流、通交流的作用 。
自感现象: 由于电路中的电流变化, 而在自己的线路 中产生感应电流的现象叫自感现象。 设电路中的电流为I 全磁通与回路的电流成正比:
L I
管内全磁通:
l
nN l
l V lS
S
L n V
2
自感系数 L 与螺线管体积V 、单位长度匝数 n、介质 有关
除线圈外,任何一个实际电路都存在电感,输电线相当 于单匝回路,回路中也分布电感。 例2 两根平行输电导线,中心距离为d,半径为a,求:两 导线单位长度上的分布电感(d >>a)。 解:设导线中有电流I
变 不变
C
例6 有两个长度均为l,半径分别为r1和r2( r1<r2 ),匝数分 别为N1和N2的同轴长直密绕螺线管.求它们的互感系数M. 解:设半径 r1 的线圈中通有电流 I1 ,则
N1 B1 0 I1 0 n1 I1 l
穿过半径为 r2 的线圈的全磁通
r2 r1
N2 N1
N2Φ21 N2 B1 (πr12 ) n2lB1 ( πr12 )
线圈2电流变化在线圈 1中产生感应电动势
1
2
电流 I 1 在2回路中所产生的全磁通
21 M 21I1
电流 I 2在1回路中所产生的全磁通
I1 (t )
N 1匝
N 2匝
1
