09-2龙贝格算法
龙贝格积分法及其应用编程

龙贝格积分法及其应用编程龙贝格积分法是一种数值积分方法,可以用于计算具有一定复杂度的函数积分值,无需求解原函数。
它是由德国数学家卡尔·龙贝格和瑞士数学家约翰·贝格共同提出的。
其基本思想是将积分区间分成若干个小区间,然后通过不断加密网格及递归计算来达到精度要求,最终得到积分近似值。
在每次加密网格后,通过对新加入的点进行数值积分来增加计算精度。
下面我们就来看一下龙贝格积分法的具体步骤和应用。
一、龙贝格积分法的基本思路1、计算整个积分区间对应的函数值;2、将积分区间分成若干等份,计算每个小区间的积分值,并计算它们的平均值;4、重复以上步骤,直到达到预设精度或达到一定的迭代次数为止。
下面以MATLAB代码为例来实现龙贝格积分法的实现过程。
假设我们要计算函数f(x)=sin(x)在区间[0,pi/2]上的积分值。
步骤如下:a = 0; % 积分下限x = a: 0.1: b; % 将整个区间等分fx = sin(x); % 计算函数值b1 = (a+b)/2; % 分界点fb1 = sin(b1);I1 = (b-a)*(fa + 4*fb1 + fb)/6; % 计算整个区间的积分值Err = abs(I1 - I2); % 计算误差tol = 1e-10;n = 1;while Err > tol % 每循环一次,计算一个更细的区间h = (b-a)/2^(n-1);x1 = a+h/2:h:b-h/2;S = sum(fx1); % 求和计算for m = 1:n-1if Err1(n,m) < tolbreak; % 如果误差小于设定值,则跳出循环endI1 = I;Err = Err1(n-1, m-1);end输出结果为:I = 0.999999999845351,误差为2.6757E-14。
龙贝格积分法可以用于计算各种类型的函数积分值,例如:1、定积分:对于一般积分,如果不能求出原函数,就可以使用该方法进行数值计算。
龙贝格求 积分

龙贝格(Romberg )求积法1.算法理论Romberg 求积方法是以复化梯形公式为基础,应用Richardson 外推法导出的数值求积方法。
由复化梯形公式 )]()(2)([2222b f h a f a f h T +++=可以化为)]()]()([2[212112h a f h b f a f hT +++==)]([21211h a f h T ++一般地,把区间[a,b]逐次分半k -1次,(k =1,2,……,n )区间长度(步长)为kk m a b h -=,其中mk =2k -1。
记k T =)1(k T由)1(k T =]))12(([21211)1(1∑=---++km j k k k h j a f h T 从而⎰badxx f )(=)1(kT-)(''122k f h a b ξ- (1)按Richardson 外推思想,可将(1)看成关于k h ,误差为)(2k h O 的一个近似公式,因而,复化梯形公式的误差公式为⎰badxx f )(-)1(k T =......4221++kkh K h K =∑∞=12i i k i h K (2)取1+k h =k h 21有⎰badxx f )(-)1(1+k T=∑∞=+121221i i k iihK (3)误差为)(2jh O 的误差公式 )(j kT=)1(-j kT+141)1(1)1(------j j k j k T T 2.误差及收敛性分析(1)误差,对复化梯形公式误差估计时,是估计出每个子区间上的误差,然后将n 个子区间上的误差相加作为整个积分区间上的误差。
(2)收敛性,记h x i =∆,由于∑=++=ni i i n x f x f h f T 01))]()([2)(=))()((21101∑∑-==∆+∆n i ni i i i i x x f x x f上面两个累加式都是积分和,由于)(x f 在区间],[b a 上可积可知,只要],[b a 的分划的最大子区间的长度0→λ时,也即∞→n 时,它们的极限都等于积分值)(f I 。
龙贝格算法求数值积分程序说明及流程图
In(k,2)=4*In(k+1,1)/3-In(k,1)/3;
end
flag(2)=i+3;
for k=flag(3)+1:i+2
In(k,3)=16*In(k+1,2)/15-In(k,2)/15;
end
flag(3)=i+2;
for k=flag(4)+1:i+1
end
In(i+5,1)=In(i+5,1)/2^(i+5)+In(i+4,1)/2;
In(i+4,2)=4*In(i+5,1)/3-In(i+4,1)/3;
In(i+3,3)=16*In(i+4,2)/15-In(i+3,2)/15;
In(i+2,4)=64*In(i+3,3)/63-In(i+2,3)/63;
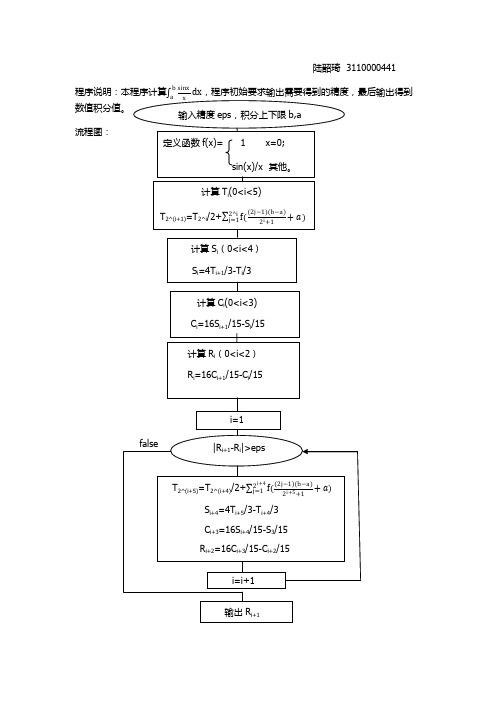
陆韶琦 3110000441
程序说明:本程序计算
数值积分值。
b sinx
a x
dx,程序初始要求输出需要得到的精度,最后输出得到
输入精度 eps,积分上下限 b,a
流程图:
定义函数 f(x)=
1
x=0;
sin(x)/x 其他。
计算 Ti(0<i<5)
T2^(i+1)=T2^i/2+
2j−1 b−a
2^i
j=1 f(
2 i +1
+ )
计算 Si(0<i<4)
Si=4Ti+1/3-Ti/3
计算 Ci(0<i<3)
龙贝格公式求数值积分算法的改进

龙贝格公式求数值积分算法的改进
1 龙贝格公式简介
龙贝格公式是一种数值积分算法,它采用的是分治思想,将待积
函数分割成若干段,然后对每一段使用欧拉公式和梯形公式进行数值
积分,最后将结果进行递推和加权,得到最终的数值积分结果。
龙贝
格公式的优点是计算准确度高,收敛速度快,但是对于高维或者复杂
函数的计算效率比较低。
2 龙贝格公式的改进
针对龙贝格公式计算效率低这个问题,专家们不断的提出了各种
改进方法。
其中比较有代表性的是以下两种方法:
2.1 自适应龙贝格公式
自适应龙贝格公式的基本思想是将龙贝格公式对于不同段的递推
次数进行调整,将计算的精度根据函数局部的性质进行调整,从而减
少计算次数,提高计算效率。
这种方法常常和迭代算法和递归算法组
合使用,能够对于大部分函数的积分计算精确度和效率得到有效的提升。
2.2 并行计算龙贝格公式
另外一种方法是采用并行计算方法,将函数的不同部分交给不同
的处理器进行计算,最后将结果进行融合,得到最终的数值积分结果。
这种方法可以有效的利用多核处理器的计算能力,将计算时间大大缩短,计算效率得到提升。
3 总结
龙贝格公式是一种数值积分算法,虽然在准确度上表现出色,但是在计算效率上存在一定的局限性。
通过自适应龙贝格公式和并行计算龙贝格公式等方法对其进行改进,可以提高算法的计算效率和精确度,尤其是针对高维或者复杂函数的积分计算,效果更加显著。
这些改进方法不仅为龙贝格公式的使用提供了更多的选择,同时也为数值积分算法的发展带来了新的思路和创新。
数值分析63 复化求积公式龙贝格求积公式讲解

只增加了一个分点
1 xk?1/ 2 ? 2 ( xk ? xk?1)
设hn=(b? a)/n, xk=a+kh n (k=0,1,? ,n),在[xk, xk+1] 上用梯形公式得
T1 ?
hn 2
?f
(
xk
)
?
f ? ( xk ? 1 )
复化求积的基本想法 :
将积分区间 [a, b]n等分, 步长
h?
b
? n
a
,
分点为
xk=a+kh (k=0,1,…,n) , 则由定积分性质知
? ? ? I ?
b
n?1
f ( x )dx ?
xk?1 f ( x )d x
a
k ? 0 xk
每个子区间 上的积分
?xk?1 f ( x )dx xk
用低阶求积公式 , 然后把所有区间的 计算结果求和 ,
注2: 同样也可用 | S4m-S2m |<ε 来控制计算的精度 . 这就是下面要介绍的 龙贝格求 积公式 .
6.4 龙贝格求积公式
6.4.1 梯形公式的递推化
复化求积方法可提高求积精度,实际计算时若
精度不够可将步长逐次分半 . 设将区间 [a, b]分为n等
分,共有 n+1个分点,如果将求积区间再分一次,则 分点增至 2n+1个,我们将二分 前后两个积分值 联系
果T8=0.9456909 只有2位有效数字,而应用复化辛普 森公式计算的结果 S4= 0.9460832 却有6位有效数字 .
注:为了利用余项公式估计误差,要求 f(x)=sin x/x 的高阶导数,由于
龙贝格算法

龙贝格算法1.通过二分次数,确定精度 #include #include double f(double x) { return exp(x); } void Romberg(double a, double b, double e) { double h = b - a; int k = 0, j=0; double T[10][10]; T[0][0] = ( f(a) + f(b) ) * h / 2; cout<<'\t'<<"k\t"<<"T\t"<<"S\t"<<"C\t"<<"R\n"; cout<<'\t'<>b; cout<<"输入下限:"; cin>>a; cout<<"输入二分次数:"; cin>>e; Romberg(a, b, e); } 2.通过指定误差,确定精度 #include #include
double f(double x) { return sqrt(x); }
void Romberg(double a, double b, double e) { double h = b - a; int k = 0, j; double T[10][10]; T[0][0] = ( f(a) + f(b) ) * h / 2; cout<<'\t'<<"k\t"<<"T\t"<<"S\t"<<"C\t"<<"R\n"; cout<<'\t'
龙贝格算法应用
龙贝格算法应用目录一(试验名称 (2)二(试验目的 (2)三(方法原理 (2)四(算法设计 (4)五(实例分析 (6)六(总结 (6)七(附录 (9)1一(试验名称龙贝格算法的应用二(试验目的要求学生运用龙贝格算法解决实际问题(塑料雨篷曲线满足函数y(x)=sin(tx),l则给定雨篷的长度后,求所需要平板材料的长度)。
三(方法原理(1)实际计算中常采用变步长的计算方案,即在步长逐步减半(即步长二分)的过程中,反复利用复化求积公式进行计算,直到所求得的积分值满足精度要求为止。
1.梯形法的递推化我们在变步长的过程中探讨梯形法的计算规律。
设将求积区间[a,b]分为ba,h,n等分,则一共有n+1个等分点,,k=0,1...,n。
这里用表示用xakh,,Tknn复化梯形法求得的积分值,其下标n表示等分数。
11x,xx先考虑一下子段[],其中点=,,在该子段上二分前后xx,,,kkk,1kk,122的两个积分值h,,,,Tfxfx ,,,,11kk,,,2h,,2 ,,,Tfxfxfx,,,,211kk,,,k,,,24,,显然有下列关系1h,, TTfx 211,,k,222将这一关系式关于k从0到n-1累加求和,即可导出下列递推公式n,11h,, TTfx,,21nn,k,222k,0ba,h,需要强调指出的是,上式中的代表二分前的步长,而 n1,,xakh ,,,1,,k,22,,22.龙贝格公式梯形法的算法简单,单精度低,收敛的速度缓慢。
2 根据梯形法的计算公式(21),积分值的截断误差大致与成正比,因hTn1此步长减半后误差将减至,既有 41,T12n ,14,Tn将上式移项整理,知1,,,TTT (25) 1,,22nnn3与相当接近,就可以保证计算结由此可见,只要二分前后两个积分值TT2nn果的误差很小。
T2n1TT,按式(25),积分值的误差大致等于,如果用这个误差值作为TT,,2nn2n2n3的一种补偿,可以期望,所得的141TTTTTT,,,,, (26) ,,222nnnnn333应当是更好的结果。
龙贝格求积公式
Romberg积分公式正是由此思想产生 积分公式正是由此思想产生
类似于梯形加速公式的处理方法,得到: 类似于梯形加速公式的处理方法,得到: 加速公式的处理方法
2 1 4 S2 n − Sn I ≈ S2 n + 2 ( S2 n − Sn ) = 2 4 −1 4 −1 2 4 S2 n − Sn Simpson加速公式: C n = 加速公式 加速公式: 2 4 −1 3 1 4 C2n − Cn I ≈ C 2 n + 3 (C 2 n − C n ) = 3 4 −1 4 −1
求出f(1/4)
f(3/4) 进而求得
T4=1/2{T2+1/2[f(1/4)+f(3/4)]} =3.131176471 S2=1/3(4T4-T2)=3.141568628 C1=1/15(16S2-S1)=3.142117648 计算f(1/8) f(3/8) f(5/8) f(7/8)进而求得 T8=1/2{T4+1/4[f(1/8)+f(3/8)+f(5/8)+f(7/8)]} =3.138988495 S4=1/3(4T3-T4)=3.141592503 C2=1/15(16S4-S2)=3.141594095 R1=1/63(64C2-C1)=3.141585784
梯形值序列
4个积分值序列: 个积分值序列: 个积分值序列
T2k
S 2k =
C 2k =
4T2k +1 − T2k 4 −1 2 4 S2k +1 − S2k
4 −1
2
2k
2k 2k
R2k =
4 C 2k +1 − C 2k
3
4 −1
3
5.3龙贝格(Romberg)算法
一、复合梯形公式的递推化
将定积分I = ∫ f ( x )dx的积分区间[ a , b ]分割为n等份 a b−a xk = a + jh , j = 0 ,1,L , n 各节点为 h= n 复合梯形(Trapz)公式为
n−1 b−a Tn = [ f ( a ) + 2 ∑ f ( x j ) + f (b )] 2n j =1
k −3
if(fabs(t3[k-3]-t2[k-2])<0.000000001) // 若 | R2 { printf("k=%3d,I=%12.9f\n",k,t3[k-3]); break; } } } double f(double x) { double y; y=sqrt(1.0+x*x); return y; }
13
其中外推加速公式可简化为
1 Tm ( k − 1) = m [ 4 m Tm − 1 ( k ) − Tm − 1 ( k − 1)] 4 −1
--------(11)
并且m可以推广到 m = 1,2 ,L
Romberg算法求解步骤
k = 1 , 2 ,L
Romberg算法的代 数精度为m的两倍 Romberg算法的收敛 阶高达m+1的两倍
第6章 数值积分与数值微分
龙贝格(Romberg)算法 算法 龙贝格
1
龙贝格(Romberg)算法 算法 龙贝格
综合前几节的内容,我们知道 梯形公式,Simpson公式,Cotes公式的代数精度分别为 1次,3次和5次 复合梯形、复合Simpson、复合Cotes公式的收敛阶分别为 2阶、4阶和6阶 无论从代数精度还是收敛速度,复合梯形公式都是较差的 有没有办法改善梯形公式呢?
龙贝格求积法.
的基础上,若将T
与 Tn
按(4.4.6)作线性组合就可产生收敛速度较快的Simpson序列:
S :S
2
k
1
S4 ... 、S2 、
关于(4.4.3.6)的证明:由(4.4.1)可知:
4T2 n Tn ba n 1 b a 1 Tn 2 f a 2k 1 3 n k 1 2 n 3
§4.4 外推原理与Romberg求积方法
4.4.1 外推原理 在科学与工程计算中,很多算法与步长h有关,特别是数值 积分、数值微分和微分方程数值解的问题。对于这些算法,我 们可以通过外推技巧提高计算精度。 例1 计算的近似值。 由函数 sin x 的Taylor展开式有
n sin
n
3
F (h) F (0) ap h p O(hs ), s p,
a p 与h无关。如果我们用h和h/q (q>1)两种步长分别计算 其中, h h p F(h)和F(h /q),则有 F ( ) F (0) a p ( ) O(h s ), q q
削去截断误差的主项,得新的算法 h q p F ( ) F ( h) q s F1 (h) F (0) O ( h ), p q 1 我们称这个计算过程为Richardson外推法。 F1(h)逼近F(0)的截 断误差是 O(hs ).
可见计算的近似值的算法F(h)的截断误差是O (h2), 而算法F1(h)的截断误差是O (h4)。外推一次,精度就提 高了。这就是外推法的基本思想。若重复以上过程,不 断外推,即不断折半步长h, 得到计算的算法序列 {Fk(h)}。随着k的增加,算法的截断误差阶越来越高,计 算精度越来越好。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2013-2014(1)专业课程实践论文
题目:龙贝格算法
一、算法理论
龙贝格求积公式也称为逐次分半加速法。它是在梯形公式、辛卜生公式和
柯特斯公式之间的关系的基础上,构造出一种加速计算积分的方法。 作为一
种外推算法, 它在不增加计算量的前提下提高了误差的精度。
在等距基点的情况下,用计算机计算积分值通常都采用把区间逐次分半的方法
进行。这样,前一次分割得到的函数值在分半以后仍可被利用,且易于编程。
具体实现为:对区间,ab,令hab构造梯形值序列2kT。
1
[()()]/2Thfafb
把区间二等分,每个小区间长度为 /2()/2hba,于是
21
/2/2(/2)TThfah
把区间四(2)等分,每个小区间长度为/2()/4hba,于是
42
/2(/2)(/4)(3/4)TThfahfah
.....................
把,ab 2等分,分点()/(2*)ixabai 0,1,2....2ik每个小
区间长度为()/2ba
二、算法框图
开始
输入a, b ,e
b-a=> h
h/2[f(a)+f(b)]=>T
0 => s
a + h/2 => x
X < b?
t/2 + h/2 *s =>T
It1-t2I < ε?
输出 T2
结束
h/2 => h
T2 => T1
S +f(x) =>s
X + h =>x
三、算法程序
#include
#include
using namespace std;
const int MAXRepeat = 100; //最大允许重复
double function(double x)//被积函数,根据自己的需要手工输入
{
double s;
s = 1.0 / (1 + x);//此为被积函数,积哪个就换哪个
return s;
}
void Romberg(double a, double b, double epsion, double f(double x))
{
int m = 1;
int n = 1;
int k;
double h;
double ep;
double p;
double xk;
double s;
double q;
double T[MAXRepeat];
h = b - a;
T[0] = 0.5 * h * (f(a) + f(b));
ep = epsion + 1.0;
while ((ep >= epsion) && (m < MAXRepeat))
{
p = 0.0;
for (k = 0; k < n; k++)
{
xk = a + (k + 0.5) * h; // n-1
p = p + f(xk); //计算∑f(xk+h/2),T
} // k=0
p = (T[0] + h * p) / 2.0; //T`m`(h/2),变步长梯形求积公式
s = 1.0;
for (k = 1; k <= m; k++)
{
s = 4.0 * s;
//[pow(4,m)T`m`(h/2)-T`m`(h)]/[pow(4,m)-1],2m阶牛顿柯斯特公式,即龙
贝格公式
q = (s * p - T[k - 1]) / (s - 1.0);
T[k-1] = p;
p = q;
}
ep = fabs(q - T[m - 1]);
m++;
T[m - 1] = q;
n++; // 2 4 8 16
h /= 2.0;
}
for (int i = 0; i < m; i++)
{
int j;
if (!(i % j))
{
cout<
else
{
cout<
j++;
}
}
int main()
{
double a;
double b;
double epsion;
cout<<"Please input the lower limit: ";
cin>>a;
cout<<"Please input the upper limit: ";
cin>>b;
cout<<"Please input the precision : ";
cin>>epsion;
Romberg( a, b, epsion, function);
return 0;
}
四、算法实现
例1.
求积分101/(1)xdx在精度为0.01下的积分值。
解:把上页代码编译运行后,输入被积函数的上下线和被要求精度,即可求得
如下结果
例2.
求积分3221/(1)xdx在精度为0.02下的积分值。
解:在代码中标注被积函数的地方把原被积函数换成21/(1)x,然后重新编译
运行
