10-3毕奥-萨伐尔定律
毕奥-萨伐尔定律

1.若 ,(无限长的 无限长的) 1.若 l >>R ,(无限长的)螺线管的中心处
β1 = π , β2 = 0
2.若 在管端口处: 2.若 l >>R ,在管端口处:
B = µ0nI
1 B = µ0nI 2
µ 0 nI
2
β1 = π/2 , β2 = 0 ; β1 = π, β2 = π/2
B
µ 0 nI
第五章 稳恒电流的磁场
17
v r
P
v dB
v r
v dB
v dB
v Idl
r
v I vdl
磁场为: 对任何一载流导线在某点产生的磁场为:
v B=
v ∫ dB
v v ˆ µ0 Idl × er B=∫ 4π r 2 L
先化为分量式后分别积分。 先化为分量式后分别积分。
3 µ0I 2 π 3µ0I B2 = ⋅ = 2R 2π 8R
I 1 3
方向垂直纸面向外
B3 =
µ0I
4πR
3µ0I µ0I + 8R 4πR
方向垂直纸面向外
B = B1 + B2 + B3 =
方向垂直纸面向外
12
第五章 稳恒电流的磁场
例4:载流螺旋管在其轴上的磁场。 :载流螺旋管在其轴上的磁场。 求半径为R,总长度 求半径为 ,总长度l ,导线电 流为I,单位长度上的匝数为n 流为 ,单位长度上的匝数为 的 螺线管在其轴线上一点的磁场? 螺线管在其轴线上一点的磁场? 解:采用“并排圆电流”模型简化。 采用“并排圆电流”模型简化。
4π r2
P
方向为垂直向里。且所有电流元在 点的磁感应强 方向为垂直向里。且所有电流元在P点的磁感应强 度方向相同(垂直向里)。 度方向相同(垂直向里)。
毕奥萨伐尔定律推导

“毕奥.萨伐尔”定律推导
毕奥·萨伐尔定律:
其中是从电流元指向参考点方向的单位矢量,是真空磁导率。
电流元产生的磁场的磁感应强度dB垂直Idl与e r组成的平面,并满足右手螺旋定则。
电流元
定义:Idl为电流元。
大小为Idl,的方向由线元所在处电流的流向来确定。
目的:用积分法来求出任意形状的磁场分布。
电流元的磁场
大小:
载流直导线的磁场
长为的载流直导线,其中电流为I,计算距离直导线为r0的P点的磁感应强度。
涉及到的数学公式
磁感应强度的积分推导
所以:
无限长载流直导线
则,
扩展知识:
磁现象
一切磁现象都源于电荷的运动。
一切磁力本质上都是电荷之间的作用力。
宇宙间四种基本作用力
1、引力又称重力,是四个基本相互作用中最弱的,但是同时又
是作用范围最大的。
而广义相对论中说引力是由于弯曲的空间和时间。
2、电磁力:世上大部分物质都具有电磁力,而磁与电是电磁力其中的一种表现模式。
3、强相互作用力又称为强核力,所有存在宇宙中的物质都是由原子构成,原子由电子和原子核组成,而原子核是由中子和质子组成。
4、弱相互作用力又称为弱核力,可以说是核能的另一种来源,主要是核子产生的天然辐射,四种相互作用力中,弱相互作用只比引力强一点。
毕奥萨伐尔定律介绍课件

定律的物理意义
物理意义
毕奥-萨伐尔定律揭示了电流在空间 中产生磁场的基本规律,对于电磁场 理论的发展和应用具有重要意义。
应用举例
在电磁学、电机学、变压器、电磁铁 等领域中,毕奥-萨伐尔定律被广泛应 用于分析和计算磁场分布。
Part
02
毕奥萨伐尔定律的推导
毕奥萨伐尔的生平与贡献
毕奥出生于1774年,是 法国物理学家和数学家。
在物理学中的应用
01
02
03
描述磁场分布
毕奥-萨伐尔定律可以用来 描述磁场在空间中的分布 ,特别是在电流和磁铁附 近产生的磁场。
计算磁场力
根据毕奥-萨伐尔定律,可 以计算磁场对电流和磁铁 的作用力,即洛伦兹力和 安培力。
解决电磁问题
在解决电磁学问题时,毕 奥-萨伐尔定律常与其他电 磁学定律一起使用,以完 整地描述电磁场的行为。
毕奥萨伐尔定律介绍 课件
• 毕奥萨伐尔定律概述 • 毕奥萨伐尔定律的推导 • 毕奥萨伐尔定律的应用 • 毕奥萨伐尔定律的实验验证 • 毕奥萨伐尔定律的扩展与展望
目录
Part
01
毕奥萨伐尔定律概述
定义与公式
定义
毕奥-萨伐尔定律描述了电流在空间中产生的磁场分布,特别是电流元在空间中产生的磁 场。
公式
毕奥和萨伐尔通过实验观 测到电流在空间中产生磁 场的现象。
毕奥萨伐尔定律的数学表达形式
毕奥萨伐尔定律可以用数学公式 表示,描述了电流产生的磁场的
大小和方向。
这个定律在电磁学中非常重要, 是研究电磁场和电磁力的基础。
通过应用毕奥萨伐尔定律,可以 解决许多与电流和磁场相关的问
题。
Part
03
毕奥萨伐尔定律的应用
毕奥-萨伐尔定律

几何关系的确定
把电流分割成 许多电流元
df Idl
还和几何因素如
r, 有关
毕奥-萨伐尔定律
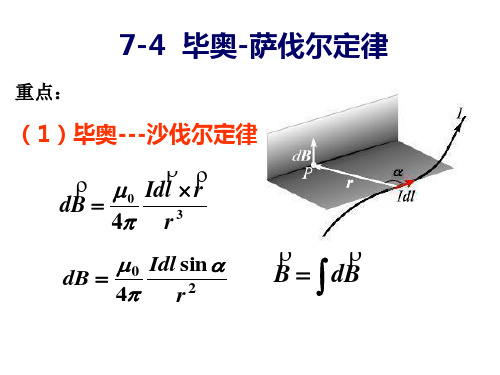
• 任一电流元Idl 在空间某点P处产生的磁 感应强度 dB 的大小与电流元Idl 的大小 成正比,与电流元Idl 所在处到 P点的矢 径r和电流元Idl 之间的夹角的正弦成正比, 而与电流元Idl 到P点的距离的平方成反 比 。 dB的方向垂直于dl和矢径r所组成的 平面,指向由电流元Idl 经小于180°的角 转向r时右螺旋前进的方向。
奥斯特的实验 装置:
电流方向
直导线
电流方向
结论:
1. 通电导体周围存在 着磁场
2. 电流的磁场方向跟 电流方向有关
奥斯特实验意义
• 揭示了电现象与磁现象的联系 • 宣告电磁学作为一个统一学科诞
生 • 历史性的突破 • 此后迎来了电磁学蓬勃发展的高
潮
• 二、毕奥-萨伐尔定律的发现
奥斯特做了有关的实验,于1820年7月21日发现了电流 的磁效应。随后实验物理学家毕奥和萨伐尔根据奥斯特 的发现提出了自己的想法,并通过两个相关的实验验证 了他们有关电流磁效应的假设。在1820年,毕奥和萨伐 尔,通过实验测量了长直电流线附近小磁针的受力规律, 发表了题为“运动中的电传递给金属的磁化力”的论文, 在数学家拉普拉斯的帮助下,将电流载体转换为电流元 的情况,并得出了毕奥-萨伐尔定律的数学表达式。因
磁 场: 取 Idl
dB
B 4
Idl
r
3
r
dB
方向:右螺旋法则
P
r
Idl
大小:
dB
0
4
Idl sin r2
毕奥-萨伐尔定律 磁通量 磁场的高斯定理
解:(1)判断电流元产生 每个电流元产生磁场同方向
磁场的方向是否一致
z
D
2
z r 0 cot
dz
I
z
1
r
r0
x
C
o
r0 dz d 2 sin dB r0 又r * y P sin 0 Idl sin (1) 大小 dB 2 4 r
B
0 I
2πr
I
B
I
X
B
电流与磁感强度成右手螺旋关系
2013-7-5
10
[例14-2] 圆电流轴线上的磁场。
0 Idl 解: dB sin 90 2 4 r 0 Idl B dB sin 90 2 4 r
x 因为圆线圈上各个电流元在P点产生的磁感应强度 的方向是不同的,所以只能用它的矢量表示:
第五版
四.运动电荷的磁场
7-4
毕奥-萨伐尔定律
考虑一段导体,其截面积为S,其 中载流子的密度为n,载流子带电 q,以漂移速度 v 运动。
毕奥—萨伐尔定律:
0 Idl r dB 4 π r3 0 nSdlqv r dB 3 4π r
P r dB Idl j Sdl nSdlqv
z
o
r
Idl
y
R
0 I dl sin x 2 2 2 r2 r R z 4 2 2 R 0 IR 0 I sin dl 3 2 0 2 2 4 r 2( R z ) 2
B
0 IR
2
2 2 32
2( R z )
毕奥萨伐尔定律

在静磁学中,毕奥-萨伐尔定律(英文:Biot-Savart Law)描述电流元在空间任意点P处所激发的磁场。
定律文字描述:电流元Idl 在空间某点P处产生的磁感应强度 dB 的大小与电流元Idl 的大小成正比,与电流元Idl 所在处到 P点的位置矢量和电流元Idl 之间的夹角的正弦成正比,而与电流元Idl 到P点的距离的平方成反比。
该定律在静磁近似中是有效的,并且与Ampère的电路规律和磁性高斯定律一致,以Jean-Baptiste Biot和FélixSavart命名。
定义在静磁学中,毕奥-萨伐尔定律(英文:Biot-Savart Law)描述电流元在空间任意点P处所激发的磁场。
定律文字描述:电流元Idl 在空间某点P处产生的磁感应强度dB 的大小与电流元Idl 的大小成正比,与电流元Idl 所在处到 P点的位置矢量和电流元Idl 之间的夹角的正弦成正比,而与电流元Idl 到P点的距离的平方成反比。
该定律在静磁近似中是有效的,并且与Ampère的电路规律和磁性高斯定律一致,以Jean-Baptiste Biot和FélixSavart命名。
电流(沿闭合曲线)毕奥-萨伐尔定律适用于计算一个稳定电流所产生的磁场。
这电流是连续流过一条导线的电荷,电流量不随时间而改变,电荷不会在任意位置累积或消失。
采用国际单位制,用方程表示:电流(整个导体体积)当电流可以近似为穿过无限窄的电线时,上面给出的配方工作良好。
如果导体具有一定厚度,则适用于Biot-Savart定律(再次以SI为单位):Biot-Savart:毕奥萨伐尔定律定律是实验定律,以一些简单的典型的载流导体产生的磁场为基础,经分析、归纳出的定律,而不是由电流元直接得出的,实际上不可能得到单独的电流元。
毕奥萨伐尔定律的数学表达式
毕奥萨伐尔定律的数学表达式
毕奥萨伐尔定律是描述一个重要物理现象的重要定律。
1853年,德国物理学家威廉·毕奥萨·伐尔提出了这一定律,他指出,磁体周围存在一种旋转电流,磁体正在试图引导这种旋转电流。
由此,如果磁体不能无限循环这种电流,那么磁场强度就会减弱,直到磁体消失。
毕奥萨·伐尔定律的数学表达式是用来描述磁体的磁场的变化的重要理论,其定律如下:B⃗={μ⃗0 ·(I⃗·r̂)/4πr2}r̂, 其中B⃗是磁场,μ⃗0是真空磁导率,I⃗是电流,r̂是相对于磁片的单位向量。
从这个公式可以看出,磁场强度随着距离的增加而减弱,磁场强度和电流强度之间存在着内在联系。
毕奥萨·伐尔定律非常重要,它不仅在物理上解释了磁场的结构,而且是研究电磁相关问题的基础。
在电工学中广泛应用,例如在线圈的设计中,用伐尔定律可以迅速计算线圈的磁场,确定绕线的线圈,以及测量电压、电流和功率。
总之,毕奥萨·伐尔定律是一个重要及有效的定律,它可以解释磁体所受到的影响,而且它在电磁学中被广泛应用。
它的数学表达式让研究变得简单、快速,也显示出物理系统中物体与环境之间微妙的相互作用。
毕奥-萨伐尔定律
同 学 们 好§11-2历史之旅:毕奥-萨伐尔定律1820 年4月: 丹麦物理学家奥斯特(1777~1851)发 现电流的磁效应。
“猛然打开了科学中一个黑暗领域的大门。
” ——法拉第历史之旅:1820 年8月: 法国物理学家阿拉果在瑞士得到消息,并于9月向 法国科学院介绍了奥斯特实验,引起极大反响。
1820年10月: 法国物理学家毕奥和沙伐尔发表《运动的电传递给金属 的磁化力》,提出直线电流对磁针作用的实验规律。
法国数学、物理学家拉普拉斯由实验规律推出载流线段 元(电流元)磁场公式。
毕奥和沙伐尔用实验验证了该 公式。
一 毕奥—萨伐尔定律 (电流元在空间产生的磁场)v Idlv dBv 电流元:IdlI d l sin α dB ∝ k 2 rv dBP *v rαv IdlIdB =µ0 Idl sin α4π r2−7v r−2真空磁导率 µ0 = 4π ×10 N ⋅ A方向v Idlv dBv v v µ0 Idl × r dB = 3 4π rv dBP *v rαv IdlIv r任意载流导线在点 P 处的磁感应强度 磁感强度叠加原理v v v v µ 0 I dl × r B = ∫ dB = ∫ 3 4π r试比较点电荷电场公式与电流元毕奥—萨伐尔定律r dE =1 dq v ⋅ 3 r 4 πε0 rr v r µ0 I d l × r ⋅ dB = 4π r3毕—萨定律:电流元产生磁场的规律, 与点电荷电场公式作用地位等价。
二 毕奥—萨伐尔定律的应用 求解电流磁场分布基本思路: 将电流视为 电流元的集合 电流元磁场公式 磁场叠加原理电流磁场分布1.载流长直导线的磁场 已知: I , a , α1 , α2 求:r B 分布r 解:取电流元 I d lµ 0 I d l sin α dB = 4π r 2lBIα2; 方向 ⊗r 各电流元在 P 点 d B同向µ 0 Idl sin α B = ∫ dB = ∫ 4πr 2 ABor I dlaαr rr dB ⊗P统一变量:l = − actgα a dα dl = sin 2α a r= sinαα1Aµ0I α B= ∫α sin α d α 4π a µ0I = (cos α 1 − cos α 2 ) 4π a2 1方向⊗µ0I B= (cos α 1 − cos α 2 ) 4π a方向 ⊗µ0I (cos α 1 − cos α 2 ) B= 讨论: 4π a α1 = 0 , α 2 = π (1)无限长直电流:Iµ0I B = 2π aIr B内密外疏(2)导线半无限长,场点与一端的连线垂 直于导线 µ0IB = 4π a(3)直导线及其延长线上点 r α = 0 或 π , dB = 0r B=02.载流圆线圈轴线上的磁场(I,R)r Id lRr rθr dBPr 解:在圆电流上取电流元 IdlxIoµ 0 I d l sin 90 o µ Id l dB = = 0 2 4π r 2 4π r方向如图各电流元在 P 点r IdlRr dB大小相等,方向不同,由对称性:zr dBr rθr dBPB⊥ = ∫ dB⊥ = 0yIoxr' dBPr Idl ′r IdlRr rθr dBPB = B// = ∫ dB sin θ =x2πR∫0µ0 Idl R 4πr 2 r23 2Ior' Id lr' dBµ0 IR = 4πr 32πR∫ dl = 2( R0µ 0 IR 22+x )方向 :+ x (右螺旋法则)轴线上r B=µ 0 IR 22( R 2 + x 2 )3 2r i讨论: (1) 定义电流的磁矩v v m = IS e nr Pmr nS : 电流所包围的面积规定正法线方向: 圆电流磁矩:r n与 I 指向成右旋关系v 2v m = Iπ R enSI圆电流轴线上磁场:r B=µ 0 IR 22( R + x )2 23 2r i =µ0 m2π ( R + x )2 23 2vr B=µ 0 IR 22( R + x )2 23 2r i =µ0 m2π ( R + x )2 23 2v(2)圆心处磁场x=0Nµ0 I B0 = ; N匝 : B0 = 2R 2R(3)在远离线圈处µ0 Ix >> R, x ≈ rµ 0 IS µ 0 IS B = = 3 2π x 2π r 3 v r µ0 m B = 3 2π r(4)画 B− x曲线 2 r r µ0 IR B= 3 i 2 2 2( R + x ) 2 练习:BoBo = ?xIRoR o⊗IB0 =µ0 I8R3µ 0 I µ 0 I B0 = + 8R 4π R⋅(1) I (2 )v R B x 0 µ0I o B0 = 2RI R o+(4)BA =d (5) I *AR1µ0 I4π dB0 =µ0 I4RR2(3) I R o*oB0 =µ0 I8RB0 =µ0 I4 R2−µ0 I4 R1−µ0 I4π R1亥姆霍兹圈:两个完全相同的N匝共轴密绕短线圈,其 中心间距与线圈半径R相等,通同向平行等大电流 I。
毕奥萨伐尔定律公式
毕奥萨伐尔定律公式毕奥萨伐尔定律公式,简称毕伐尔定律,是一个用于计算细胞及其组件信息含量的公式,是全球最大的基因组学家和生物信息学家使用的公式之一。
该公式由毕奥萨伐尔(Pio A.V.A. Valfle)于1962年提出,他用它计算了英国人群中个体谱系学词汇的信息含量。
毕奥萨伐尔定律公式是一种分类法,它可用来描述一个系统中的不同元素之间的关系,用于衡量一个系统的复杂性。
它的基本思想是,一个系统的复杂性可以用该系统中的元素之间的差异性来衡量。
毕奥萨伐尔(Pio A.V.A. Valfle)定律公式的表达形式如下:I=logN/NlogM其中,I表示系统的信息含量,N表示每个元素的数量,M表示每个元素的种类数。
毕奥萨伐尔公式能用来度量生物体在进化上获得了多少信息,因为不同物种的基因组大小、基因数量和特定基因的表达水平可能会有所不同,这些就可以用毕奥萨伐尔公式来计算。
例如,研究人员可以使用毕奥萨伐尔定律公式来计算双螺杆菌和大肠杆菌的基因组中的基因数量之间的差别。
双螺杆菌有4,288个基因,而大肠杆菌有4,996个基因,根据毕奥萨伐尔定律公式,可以计算出这两者之间的信息含量差异为0.41。
毕奥萨伐尔定律公式还可用于评估两个不同物种间的基因组大小之间的不同,以及用于计算某一物种基因组大小的变化。
此外,毕奥萨伐尔定律公式的应用范围不仅限于生物领域,还可用于研究计算机中的软件、图形和图像处理。
比如,可以使用毕奥萨伐尔定律公式来计算某种软件的数据结构的复杂性,以及执行特定任务时所需要的算法复杂性。
毕奥萨伐尔定律公式的发展为研究基因组差异提供了一个有用工具,为基因组学研究者提供了重要信息,帮助他们理解基因组变异和生物多样性之间的关系,使人类对每一个物种有更深入的了解。
因此,毕奥萨伐尔定律公式非常有用,它提供了一种快速、有效的方法来衡量和研究某个系统中的不同元素之间的差异,在生物领域和计算机领域都发挥了重要作用。
电磁学 毕奥-萨伐尔定律 课件
2 π x3
10
(1)
R
B0
x
推
Io
广 (2)
I
R
组
o×
合 (3) I
R ×o
11
B0
0I
2R
B0
0I
4R
B0
0I
8R
(4)
(5) I
d *A
R1
R2
*o
12
BA
0I
4πd
B0
0I
4R2
0I
4R1
0I
4 π R1
三 磁偶极矩
m ISen
B
0 IR 2
2x3
B
0m
2 π x3
B
0m
2 π x3
Idl
2
例 判断下列各点磁感强度的方向和大小.
1
8
2
×
7
Idl × 3
R
6
×
4
dB
5
0
4π
Idl
r
r3
1、5点 :dB 0
3、7点
:dB
0 Idl
4π R2
2、4、6、8 点 :
dB
0 Idl
4π R2
sin
450
毕奥-萨伐尔定律
3
二 毕奥-萨伐尔定律应用举例
例1 载流长直导线的磁场.
一 毕奥-萨伐尔定律
(电流元在空间产生的磁场)
dB
0
4π
Idl sin
r2
dB
0
4π
Idl
r
r3
真空磁导率
Idl
dB
r
I
dB
