正切函数的性质与图象
合集下载
《正切函数的图像与性质》公开课课件

2
2
y cos x : 定义域为R,值域[1,1]
最大值1,此时x 2k ;最小值-1, 此时x 2k .(k Z )
-6 -5
-4 -3
-2 -
y y=sinx
1 o
-1
2 3
4 5
6 x
y y=cosx
1
-6 -5 -4 -3 -2
- -1
2 3 4
5
6 x
六.对称轴和对称点:
y sin x的对称轴:x k , 对称点: (k ,0);
4
4
5
5
2
2
5
42
tan( 2 ) tan( ),
5
4
即 tan( 13 ) tan( 17 )
4
5
例3.求函数y tan x 1 的定义域 3 tan x
例4.试讨论函数y loga tan x的单调性
例3.解:由tan x 1 0和 3 - tan x 0k x k , k Z
2
y cos x的对称轴:x k , 对称点: (k ,0);
2
七.y sin x和y cos x的图像性质的研究思想:
(1)充分利用图像 - - - -数形结合的思想
(2) y sin x, y cos x与y Asin(x ), y Acos(x )间的换元思想
正切函数的性质与图象
-6 -5 -6 -5
-4 -3 -4 -3
-2 -
-2
-
y y=sinx
1 o
-1
y y=cosx
1
-1
2 3
4 5
2
3
4
5
6 x 6 x
正切函数图象与性质课件.ppt

x 2k 时, ymax 1 x 2k 时,ymin 1
x[ 2k , 2k ] 增函数
x[2k , 2k ]
偶函数
2
减函数
对称轴: x
2
k
,
k
Z
对称中心: (k , 0) k Z
对称轴: x k , k Z 对称中心:(2 k , 0) k Z
探究
一、你能否根据研究正弦、余弦函数的图 象和性质的经验 以同样的方法研究正切函数 的图像和性质?
函数 图形 定义域 值域 最值
单调性 奇偶性
周期 对称性
y
1
2
0
-1
y=sinx
3
2
2
xR
2 5 x
2
y=cosx
y
1
0
2
3 2
2
5 2
x
-1
xR
y [1,1]
y [1,1]
x
2
2k 时, ymax
1
x
2
2k 时,ymin
1
x[-
2
2k
,
2
2k
]
增函数
x[2
2k ,
3
2
2k
]
减函数
奇函数
2
4
例题分析
例 4 解不等式:tan x 3
解:
y
3
0 x
32
由图可知:x
k
3
,
k
2
(k
Z
)
反馈演练
1、 解不等式 1+tanx 0
2、解不等式:1- tan x 0
3、解不等式:tan(x ) 3
正切函数的性质与图像 -公开课PPT课件

kπ)
,k
Z
内都是增函数。
强调:
a.不能说正切函数在整个定义域内是增函数;
b.正切函数在每个单调区间内都是增函数;
c. 每个单调区间都跨两个象限:四、一或 二、三。
图像特征: 1、间断性:正切曲线是被互相平行的直线 x k , k Z
2
所隔开的无穷多支曲线组成的。
2、在每一个开区间 ( k , k ), k Z 内,图像自左向
23
23
tan[ (x 2) ] f (x 2)
2
3
因此函数的周期为2.
由
k x k K∈Z 解得
2
2 32
5 2k x 1 2k K∈Z
3
3
因此,函数的单调递增区间是 ( 5 2k, 1 2k), k Z
33
提高练习
求函数
的定义域、值域,并指出它的
有最大值、最小值
O
x
因此,正切函数的值域是
实数集R
问题、如何利用正切线画出函数 的图像?
y tan x
,x
2
,
2
角 的终边 Y
T3
(
3
,ta
n3)
A
0
X
3
作图 利用正切线画出函数 y tan x,x , 的图像: 2 2 作法: (1) 等分:把单位圆右半圆分成8等份。
(2) 作正切线 (3) 平移
22 右呈上升趋势,向上与直线 x
k , k Z
无限接近但
永不相交;向下与直线
x
2
k
,k
Z无限接近但永不
2
相交。
将 x k , k Z 称为正切曲线的渐近线。
2
(完整版)正切函数的性质与图像.ppt

2
2
正
渐
切
近 线
函
数
渐
图
近 线
像
性质 :
渐近线方程: x k , k Z 2
对称中心
( kπ,0) 2
正切函数有对称轴吗? 无对称轴
问题5: (1)正切函数是整个定义域上的增函数吗?为什么? (2)正切函数会在某一区间内是减函数吗?为什么?
A
B
在每一个开区间
(-π+ kπ,π+ kπ) ,kZ 内都是增函数。
5、周期性
最小正周期是
3
小结:正切函数的图像和性质
1、正切曲线是先利用平移正切线得y tan x, x ( , )的图象, 22
再利用周期性把该段图象向左、右扩展得到。
2 、y tan x 性质:
⑴ 定义域: {x | x k, k Z}
⑵ 值域: R 2 ⑶ 周期性:
⑷ 奇偶性:奇函数,图象关于原点对称。
22 右呈上升趋势,向上与直线 x
k
,k
Z
无限接近但
永不相交;向下与直线
x
2
k , k
Z无限接近但永不
2
相交。
将 x k , k Z 称为正切曲线的渐近线。
2
题型一 求与正切函数有关的函数的定义域
例1.求下列函数的定义域.
(1) y tan(x );
3 (2) y lg tan x 16 x2 .
x 2k 时, ymax 1 x 2k 时,ymin 1
x[ 2k , 2k ] 增函数
x[2k , 2k ]
偶函数
2
减函数
对称轴: x
2
k
,
正切函数的图象与性质

故T不存在 不存在 综上:正切函数的最小正周期为π 综上:正切函数的最小正周期为
二:几何法作图: 几何法作图:
π π 1、画出正切函数在一个周期 − , 内的图象 、 2 2
y
−
π
2
0
π
2
x
三点两线
2、利用周期性,把上述图象向x轴两边扩展, 、利用周期性,把上述图象向 轴两边扩展 轴两边扩展, 得到正切曲线; 得到正切曲线;
使得 f (α 1 ) > f (α 2 )成立,求实数 a 的取值范围
π π y = cot x = tan − x = − tan x − 2 2
y
−π
3 − π 2 1 − π 2
π
2π
3 π 2
0
1 π 2
x
我今天的收获: 我今天的收获:
知识点:_________________ 知识点:_________________ 智慧群: ★智慧群: _________________ _________________ _________________ 我易错: ★我易错:_________________ 其他感悟: 其他感悟:_______________ Good!
1
1
0 π 4
A 0 x
π x
2
问题3 问题3:
1 3 1)比大小:tan( − ), cot , tan π 5 10 10
π
拓展提高
π tan x ( 0 < x < 2 ) 2) f ( x ) = cot x ( π < x < π ) 2 若有 α 1 = 1 - 2 a ) π , α 2 = 2 a π (
正切函数的图象和性质
f ( x ) tan(x ) tan x f ( x)
所以 y=tanx 是周期函数, 是它的一个周期
类似正弦曲线的作法,我们先作正切函数在一 个周期上的图象。
y tan x, x (
, ) 的图象 2 2
y
利用正切线画图
3
2
4
6
1
A
2
课堂作业
课本P80 习题 4.10 1. 3.
所以函数
y tan(x ) 4
的定义域是
{x | x
4
k , k Z }
四:小 结
(1)图象:
y
3 2
2
0
2
3 2
x
(2)性质: 1. 定义域: 2. 值 域: 3. 周期性: 4. 奇偶性: 5. 单调性:
x x
k , k Z 正切函数的值域是实数集R 正切函数是周期函数,周期是 奇函数, 它的图象关于原点 对称. ( k , k ), k Z 增函数 2 2
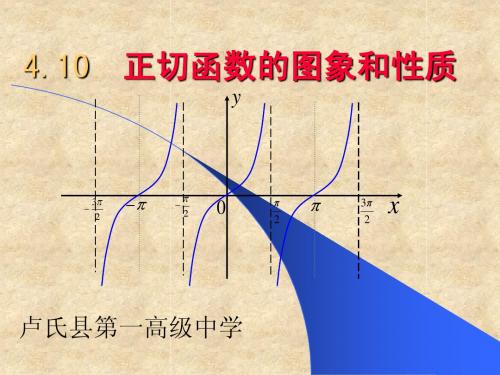
4.10 正切函数的图象和性质
y
3 2
2
0
2
3 2
x
卢氏县第一高级中学
知识回顾:
1. 什么是正切线?y
P
O
T
A
x
2. 什么是周期函数?
f ( x) f ( x T )
3. 如何利用单位圆中的正弦线作出
正弦函数图象?
一:用正切线作正切函数的图象
首先我们一起分析一下正切函数y=tanx 是否为 周期函数? 因为
正切函数图象与性质PPT课件
(6)单调性:在每一个开区2间
(-π+ kπ,π+ kπ) ,k Z
2
2
(7)渐近线方程: x k , k Z
2
内都是增函数。
3.数学思想方法:数形结合的思想
❖ 1.必做题:习题1.4 A组 6、8 B组 2 ❖ 2.选做题:
(1)解不等式1 tan x 0
(2)解不等式:tan x 3
2
R
T=
奇函数
增区间 (k , k )k Z
2
2
二、图象 正切曲线
是被相互平行的直线 x k , k z
2
所隔开的无穷多支曲线组成的.
渐近线 渐近线
3
0
2
渐近线 渐近线
正 切 函 数 图 像
性质
⑴
:
定义域:
{x
|
x
k, k Z}
⑵ 值域: R
2
⑶ 周期性:
⑷ 奇偶性: 奇函数,图象关于原点对称.
2
2
基础练习
1.关于正切函数 y tan x , 下列判断不正确的是(B )
A 是奇函数 B 在整个定义域上是增函数 C 在定义域内无最大值和最小值
D 平行于 x 轴的的直线被正切曲线各支所截线
段相等
2.函数 y tan(3x)的一个对称中心是( C )
A
.
(
, 0)
9
B. ( , 0)
4
C.
⑸(6)渐单近调线性(方:2程:在kx每,k2一个k2开,)区k 间,kZ Z
内都是增函数。
(7)对称中心
(
kπ,0) 2
问题讨论:
(1)正切函数是整个定义域上的增函数吗?为什么? (2)正切函数会不会在某一区间内是减函数?为什么?
(-π+ kπ,π+ kπ) ,k Z
2
2
(7)渐近线方程: x k , k Z
2
内都是增函数。
3.数学思想方法:数形结合的思想
❖ 1.必做题:习题1.4 A组 6、8 B组 2 ❖ 2.选做题:
(1)解不等式1 tan x 0
(2)解不等式:tan x 3
2
R
T=
奇函数
增区间 (k , k )k Z
2
2
二、图象 正切曲线
是被相互平行的直线 x k , k z
2
所隔开的无穷多支曲线组成的.
渐近线 渐近线
3
0
2
渐近线 渐近线
正 切 函 数 图 像
性质
⑴
:
定义域:
{x
|
x
k, k Z}
⑵ 值域: R
2
⑶ 周期性:
⑷ 奇偶性: 奇函数,图象关于原点对称.
2
2
基础练习
1.关于正切函数 y tan x , 下列判断不正确的是(B )
A 是奇函数 B 在整个定义域上是增函数 C 在定义域内无最大值和最小值
D 平行于 x 轴的的直线被正切曲线各支所截线
段相等
2.函数 y tan(3x)的一个对称中心是( C )
A
.
(
, 0)
9
B. ( , 0)
4
C.
⑸(6)渐单近调线性(方:2程:在kx每,k2一个k2开,)区k 间,kZ Z
内都是增函数。
(7)对称中心
(
kπ,0) 2
问题讨论:
(1)正切函数是整个定义域上的增函数吗?为什么? (2)正切函数会不会在某一区间内是减函数?为什么?
高二数学正切函数的性质与图象
复习:怎样利用单位圆中的正弦线作出 y sin x 的图象?
思考:能否用正切线作正切函数图像呢?
y
3 8 4 8O
O1
A
x
8
4
3 8
2
用光滑曲线 将这些正切线的终 端连结起来
tan(x+π)=tanx 即 :T= π
y
3 2
1
2
o
2
3 2
强调:
a.不能说正切函数在整个定义域内是增函数; b.正切函数在每个单调区间内都是增函数;
c. 每个单调区间都跨两个象限:四、一域: R
1、 定 义 域 : x | x k , k Z 2
3、周期性: T
4、奇偶性 : 奇函数
R
3.函数y tan(2 x )的图象是将tan 2 x的图象 3 左平移 ____ 向 ___ . 6 个单位而得到的
; 汇添富娱乐,汇添富娱乐官网,汇添富娱乐开户,汇添富娱乐注册
vgd69wjw
平凡,我的家族过于强大,我的一生已经被定死,使我没有任何动力去想象属于我自己的生活,因为我必须活在责任与情义当 中。姐姐深知我将来的路会变成这样一条险路,假如我不做出改变的话。于是就要我学会做人、学会负责,学会走自己的人生 之路;于是我来到了姐姐的单位实习;于是我要每晚做公务员的真题;于是对了,我们家的灯烧坏了。想到这,我猛地惊了一 番,“啊,痛,好强的光。”心想,这屋里的灯有这么强吗?不对,这不是灯光,是带有自然气息的太阳光。“哥哥,你没事 吧?”一陌生的声音在耳边响起。我顿时心头一惊,这是谁的声音,听起来就是个十来岁的小伙的声音,奇怪这声音怎么这么 优美。我正想要睁开眼睛,却发现强光过于刺眼,我没能成功。而且身体也像是在沉睡一样,动不了。这时的我,隐约感受到 背部有一种软软的感觉,也断续闻到有一股带有草原气息的气味,难道我这是躺在内蒙古的广阔的草原上吗?又蓦地,我被自 己的想法惊了一下,我这不是昏过去躺在我姐姐的出租屋里的冷冰冰的地板上的吗?“哥哥,你不打紧吧?要不我去找你来帮 你吧?”又来了,这小正太究竟是谁啊?过了这么一段时间,眼睛稍微适应了强光,于是我就努力试着睁开眼睛,因为不这样 做的话就根本没办法行动,心中就会担心自己继续待下去会遇到什么危险,因为我已经感觉到了,这根本不是出租屋;我这个 人对于一些未知的领域,总会自动有一种想逃跑的危机感,也许是我那胆小怕事的性格衍生出来的吧。对了,从前试过睡觉睡 到脑瓜子醒了但是身子却动不了的情况,是俗话说的鬼压身吧?其实我知道那是大脑醒了身体还在休息的一种生理现象罢了。 好,我试试用尽全身的力去唤醒我的身体吧!“哥哥”那小男孩貌似对我不离不弃;很好,等我醒过来好好表扬你一番这关爱 陌生人的情操吧!我集中了所有精力,用尽全身能感受到的力气去努力“扒开”眼皮,终于我能稍稍地睁开了眼睛;蓦地,映 入眼帘的是一张俊俏的小脸蛋;不行,还是受不了这突如其来的强光,难道我还是个怕光的软蛋,头很痛,我又一次昏了过去。 等我真正醒来的时候,我震惊了。这哪是什么姐姐的破出租屋啊,这是一间破旧的木屋,怎么看都像是我们家族在山区老家那 祖屋啊!托着沉重而稍带晕眩的脑瓜,我仔细打量了一下这木屋。它的格局确实不像我那老祖屋,而且一些房屋建造的关键之 处甚是薄弱,明显不是专业木匠搭建起来的,而且我有一种直觉,那就是这里缺少我们现代所有的气息,难道,我穿越了?正 想着这不可思议的问题,门外蹦进了一个小男孩,他冲着我叫到:“哥哥,你醒啦?”这声音有点熟耶,对了,是那个我做梦 时在与鬼压身战斗时所听到的小正太的声音。我还
正切函数的图象和性质
∵f x +π = tan x +π = tanx f x
∴ y 期.
= tanx
是周期函数,
是它的一个周
我们先来作一个周期内的图象。 想一想:先作哪个区间上的图象好呢?
ππ (- , ) 2 2
为什么?
y tan x 利用正切线画出函数 ,x , 的图像: 2 2
1、 正 切 曲 线 是 先 利 用 移 平正 切 线 得 y tan x, x ( , )的 图 象 , 2 2 再 利 用 周 期 性 把 该 段象 图向 左 、 右 扩 展 得 到 。
2 、y tan x 性质: ⑴ 定义域⑷ 奇偶性:
x k (6)渐近线方程: 2 , kZ
(7)对称中心
kπ ( ,0) 2
π 例1,求函数y = tan(x + ) 4 的定义域,值域,周期和单调性。
例 2:
(1)正切函数是整个定义域上的增函数吗?为什么?
(2)正切函数会不会在某一区间内是减函数?为什么?
A
B
π π (- + kπ, + kπ) ,k Z 2 2
o
3 0 2 8 4 8
8
4
3 8
2
正 切 函 数 图 像
⑴ 定义域: {x | x k, k Z} 2 ⑵ 值域: R
⑶ 周期性:
⑷ 奇偶性: 奇函数,图象关于原点对称。
⑸ 单调性: 在每一个开区间 ( k , k ) ,k Z 内都是增函数。 2 2
13π 17π > (2)tan()_____tan() 4 5
2、求函数y=tan3x的定义域,值域,单调性。
正切函数的图象与性质优秀课件
( , ) 2 2
的情形, 再拓展到整个定义域.
作业:P45练习:2,3,4,6.
19、一个人的理想越崇高,生活越纯洁。 20、非淡泊无以明志,非宁静无以致远。 21、理想是反映美的心灵的眼睛。 22、人生最高之理想,在求达于真理。 便有了文明。 24、生当做人杰,死亦为鬼雄。 25、有理想的、充满社会利益的、具有明确目的生活是世界上最美好的和最有意义的生活。 26、人需要理想,但是需要人的符合自然的理想,而不是超自然的理想。 27、生活中没有理想的人,是可怜的。 28、在理想的最美好的世界中,一切都是为美好的目的而设的。 29、理想的人物不仅要在物质需要的满足上,还要在精神旨趣的满足上得到表现。 30、生活不能没有理想。应当有健康的理想,发自内心的理想,来自本国人民的理想。 31、理想是美好的,但没有意志,理想不过是瞬间即逝的彩虹。 32、骐骥一跃,不能十步;驽马十驾,功在不舍;锲而舍之,朽木不折;锲而不舍,金石可镂。——荀况 33、伟大的理想只有经过忘我的斗争和牺牲才能胜利实现。 34、为了将来的美好而牺牲了的人都是尊石质的雕像。 35、理想对我来说,具有一种非凡的魅力。 36、扼杀了理想的人才是最恶的凶手。 37、理想的书籍是智慧的钥匙。 人生的旅途,前途很远,也很暗。然而不要怕,不怕的人的面前才有路。—— 鲁 迅 2 人生像攀登一座山,而找寻出路,却是一种学习的过程,我们应当在这过程中,学习稳定、冷静,学习如何从慌乱中找到生机。 —— 席慕蓉 3 做人也要像蜡烛一样,在有限的一生中有一分热发一分光,给人以光明,给人以温暖。—— 萧楚女 4 所谓天才,只不过是把别人喝咖啡的功夫都用在工作上了。—— 鲁 迅 5 人类的希望像是一颗永恒的星,乌云掩不住它的光芒。特别是在今天,和平不是一个理想,一个梦,它是万人的愿望。—— 巴 金 6 我们是国家的主人,应该处处为国家着想。—— 雷 锋 7 我们爱我们的民族,这是我们自信心的源泉。—— 周恩来 8 春蚕到死丝方尽,人至期颐亦不休。一息尚存须努力,留作青年好范畴。—— 吴玉章 9 学习的敌人是自己的满足,要认真学习一点东西,必须从不自满开始。对自己,“学而不厌”,对人家,“诲人不倦”,我们应取这种态度。—— 毛泽东 10 错误和挫折教训了我们,使我们比较地聪明起来了,我们的情就办得好一些。任何政党,任何个人,错误总是难免的,我们要求犯得少一点。 犯了错误则要求改正,改正得越迅速,越彻底,越好。—— 毛泽东 38、理想犹如太阳,吸引地上所有的泥水。 9.君子欲讷于言而敏于行。 ——《论语》 译:君子不会夸夸其谈,做起事来却敏捷灵巧。 10.二人同心,其利断金;同心之言,其臭如兰。 ——《周易》 译:同心协力的人,他们的力量足以把坚硬的金属弄断;同心同德的人发表一致的意见,说服力强,人们就像嗅到芬芳的兰花香味,容易接受。 11.君子藏器于身,待时而动。 ——《周易》 译:君子就算有卓越的才能超群的技艺,也不会到处炫耀、卖弄。而是在必要的时刻把才能或技艺施展出来。 12.满招损,谦受益。 ——《尚书》 译:自满于已获得的成绩,将会招来损失和灾害;谦逊并时时感到了自己的不足,就能因此而得益。 13.人不知而不愠,不亦君子乎? ——《论语》 译:如果我有了某些成就,别人并不理解,可我决不会感到气愤、委屈。这不也是一种君子风度的表现吗?知缘斋主人 14.言必信 ,行必果。 ——《论语》 译:说了的话,一定要守信用;确定了要干的事,就一定要坚决果敢地干下去。 15.毋意,毋必,毋固,毋我。 ——《论语》 译:讲事实,不凭空猜测;遇事不专断,不任性,可行则行;行事要灵活,不死板;凡事不以“我”为中心,不自以为是,与周围的人群策群力,共同完成任务。 16.三人行,必有我师焉,择其善者而从之,其不善者而改之。——《论语》 译:三个人在一起,其中必有某人在某方面是值得我学习的,那他就可当我的老师。我选取他的优点来学习,对他的缺点和不足,我会引以为戒,有则改之。 17.君子求诸己,小人求诸人。 ——《论语》 译:君子总是责备自己,从自身找缺点,找问题。小人常常把目光射向别人,找别人的缺点和不足。很多人(包括我自己)觉得面试时没话说,于是找了一些名言,可以在答题的时候将其穿插其中,按照当场的需要或简要或详细解释一番,也算是一种应对的方法吧 1.天行健,君子以自强不息。 ——《周易》 译:作为君子,应该有坚强的意志,永不止息的奋斗精神,努力加强自我修养,完成并发展自己的学业或事业,能这样做才体现了天的意志,不辜负宇宙给予君子的职责和才能。 2.勿以恶小而为之,勿以善小而不为。 ——《三国志》刘备语 译:对任何一件事,不要因为它是很小的、不显眼的坏事就去做;相反,对于一些微小的。却有益于别人的好事,不要因为它意义不大就不去做它。 3.见善如不及,见不善如探汤。 ——《论语》 译:见到好的人,生怕来不及向他学习,见到好的事,生怕迟了就做不了。看到了恶人、坏事,就像是接触到热得发烫的水一样,要立刻离开,避得远远的。 4.躬自厚而薄责于人,则远怨矣。 ——《论语》 译:干活抢重的,有过失主动承担主要责任是“躬自厚”,对别人多谅解多宽容,是“薄责于人”,这样的话,就不会互相怨恨。 5.君子成人之美,不成人之恶。小人反是。 ——《论语》 译:君子总是从善良的或有利于他人的愿望出发,全心全意促使别人实现良好的意愿和正当的要求,不会用冷酷的眼光看世界。或是唯恐天下不乱,不会在别人有失败、错误或痛苦时推波助澜。小人却相反,总是“成人之恶,不成人之美”。 6.见贤思齐焉,见不贤而内自省也。 ——《论语》 译:见到有人在某一方面有超过自己的长处和优点,就虚心请教,认真学习,想办法赶上他,和他达到同一水平;见有人存在某种缺点或不足,就要冷静反省,看自己是不是也有他那样的缺点或不足。 7.己所不欲,勿施于人。 ——《论语》 译:自己不想要的(痛苦、灾难、祸事……),就不要把它强加到别人身上去。 8.当仁,不让于师。 ——《论语》 译:遇到应该做的好事,不能犹豫不决,即使老师在一旁,也应该抢着去做。后发展为成语“当仁不让”。 18.君子坦荡荡,小人长戚戚。 ——《论语》 译:君子心胸开朗,思想上坦率洁净,外貌动作也显得十分舒畅安定。小人心里欲念太多,心理负担很重,就常忧虑、担心,外貌、动作也显得忐忑不安,常是坐不定,1.书到用时方恨少,事非经过不知难。 ——陈廷焯 译:知识总是在运用时才让人感到太不够了,许多事情如果不亲身经历过就不知道它有多难。 72、笨鸟先飞早入林,笨人勤学早成材。 ——《省世格言》 译:飞得慢的鸟儿提早起飞就会比别的鸟儿早飞入树林,不够聪明的人只要勤奋努力,就可以比别人早成材。 73.书山有路勤为径,学海无涯苦作舟。 ——《增广贤文》 译:勤奋是登上知识高峰的一条捷径,不怕吃苦才能在知识的海洋里自由遨游。 74.学如逆水行舟,不进则退。 ——《增广贤文》 译:学习要不断进取,不断努力,就像逆水行驶的小船,不努力向前,就只能向后退。 75.吾生也有涯,而知也无涯。 ——《庄子》 译:我的生命是有限的,而人类的知识是无限的。 76.天下兴亡,匹夫有责。 ——明•顾炎武 译:国家的兴旺、衰败,每一个人都负有很大的责任。 77.生于忧患,死于安乐。 ——孟子 译:逆境能使人的意志得到磨炼,使人更坚强。相反,时常满足于享受,会使人不求上进而逐渐落后。 78.位卑未敢忘忧国。 ——陆游《病起书怀》 译:虽然自己地位低微,但是从没忘掉忧国忧民的责任。 79.人生自古谁无死,留取丹心照汉青。 ——宋•文天祥《过零丁洋》 译:自古以来,谁都难免会死的,那就把一片爱国的赤胆忠心留在史册上吧! 80.先天下之忧而忧,后天下之乐而乐。 ——宋•范仲淹《岳阳楼记》 译:为国家分忧时,比别人先,比别人急;享受幸福,快乐时,却让别人先,自己居后。知缘斋主人 81.小来思报国,不是爱封侯。 ——唐•岑参《关人赴安西》 译:从小就想着报效祖国,而不是想着要封侯当官。) 82.有益国家之事虽死弗避。 ——明•吕坤《呻吟语•卷上》 译:对国家有利的事情要勇敢地去做,就算有死亡的危险也不躲避 译:风声、雨声、琅琅读书声,都进入我们的耳朵,所以,作为一个读书人,家事、国事,天下的事情,各种事情都应该关心,不能只是死读书。 87.生当作人杰,死亦为鬼雄。 ——宋•李清照《夏日绝句》 译:活着的时候要做英雄,死后也要当英雄。 88.利于国者爱之,害于国者恶之。 ——《晏子春秋》 译:对于国家有利的事就要热心地去做,对国家有害的事就要憎恶它,远离它。 89.读书本意在元元。 ——宋•陆游 译:读书的目的应该是掌握了知识后为社会和大众服务,而不是为了自己的升官发财。 90.时穷节乃现,一一垂丹青。 ——宋•文天祥 译:历史上许多忠臣义士,在国家有难时,他们的节操就显现出来,一个个名垂史册。 91.哀哀父母,生我劬劳。 ——《诗经》 译:想起父母,做子女的是多么为他们感到心痛啊!他们生我育我,花费了多少辛勤的劳动啊! 92.报国之心,死而后已。——宋•苏轼 译:报效祖国的志向到死都不会变。 93.忧国忘家,捐躯济难,忠臣之志也。 ——三国•曹植《求自诚表》 译:忧虑国家大事忘记小家庭,为拯救国家危难而捐躯献身,这都是忠臣的志向。 94.大丈夫处世,当扫除天下,安事一室乎? ——汉•陈蕃语 译:有志气的人活在世上,应当敢于跟各种不利于国家的行为作斗争,哪能只满足于处理好自己小家的小事呢? 95.君子之交淡如水,小人之交甘若醴。 ——《庄子》 译:君子之间的交往,像水一样的平淡、纯净,这样的友谊才会持久;往小人之间的交像甜酒一样的又浓又稠,但不会长久。 96.老吾老,以及人之老;幼吾幼,以及人之幼。 ——《孟子》 译:尊敬、爱戴别人的长辈,要像尊敬、爱戴自己长辈一样;爱护别人的儿女,也 97.见侮而不斗,辱也。 ——《公孙龙子》 译:当正义遭到侮辱、欺凌却不挺身而出,是一种耻辱的表现。 98.天下皆知取之为取,而莫知与之为取。 ——《后汉书》 译:人们都认为只有获取别人的东西才是收获,却不知道给予别人也是一种收获。 99.人固有一死,或重于泰山,或轻于鸿毛。 ——汉•司马迁《史记》 译:人终究免不了一死,但死的价值不同,为了人民正义的事业而死就比泰山还重,而那些自私自利,损人利已的人之死就比鸿毛还轻。知缘斋主人 100.羊有跪乳之恩,鸦有反哺之义。 ——《增广贤文》 译:羊羔有跪下接受母乳的感恩举动,小乌鸦有衔食喂母鸦的情义,做子女的更要懂得孝顺父母
的情形, 再拓展到整个定义域.
作业:P45练习:2,3,4,6.
19、一个人的理想越崇高,生活越纯洁。 20、非淡泊无以明志,非宁静无以致远。 21、理想是反映美的心灵的眼睛。 22、人生最高之理想,在求达于真理。 便有了文明。 24、生当做人杰,死亦为鬼雄。 25、有理想的、充满社会利益的、具有明确目的生活是世界上最美好的和最有意义的生活。 26、人需要理想,但是需要人的符合自然的理想,而不是超自然的理想。 27、生活中没有理想的人,是可怜的。 28、在理想的最美好的世界中,一切都是为美好的目的而设的。 29、理想的人物不仅要在物质需要的满足上,还要在精神旨趣的满足上得到表现。 30、生活不能没有理想。应当有健康的理想,发自内心的理想,来自本国人民的理想。 31、理想是美好的,但没有意志,理想不过是瞬间即逝的彩虹。 32、骐骥一跃,不能十步;驽马十驾,功在不舍;锲而舍之,朽木不折;锲而不舍,金石可镂。——荀况 33、伟大的理想只有经过忘我的斗争和牺牲才能胜利实现。 34、为了将来的美好而牺牲了的人都是尊石质的雕像。 35、理想对我来说,具有一种非凡的魅力。 36、扼杀了理想的人才是最恶的凶手。 37、理想的书籍是智慧的钥匙。 人生的旅途,前途很远,也很暗。然而不要怕,不怕的人的面前才有路。—— 鲁 迅 2 人生像攀登一座山,而找寻出路,却是一种学习的过程,我们应当在这过程中,学习稳定、冷静,学习如何从慌乱中找到生机。 —— 席慕蓉 3 做人也要像蜡烛一样,在有限的一生中有一分热发一分光,给人以光明,给人以温暖。—— 萧楚女 4 所谓天才,只不过是把别人喝咖啡的功夫都用在工作上了。—— 鲁 迅 5 人类的希望像是一颗永恒的星,乌云掩不住它的光芒。特别是在今天,和平不是一个理想,一个梦,它是万人的愿望。—— 巴 金 6 我们是国家的主人,应该处处为国家着想。—— 雷 锋 7 我们爱我们的民族,这是我们自信心的源泉。—— 周恩来 8 春蚕到死丝方尽,人至期颐亦不休。一息尚存须努力,留作青年好范畴。—— 吴玉章 9 学习的敌人是自己的满足,要认真学习一点东西,必须从不自满开始。对自己,“学而不厌”,对人家,“诲人不倦”,我们应取这种态度。—— 毛泽东 10 错误和挫折教训了我们,使我们比较地聪明起来了,我们的情就办得好一些。任何政党,任何个人,错误总是难免的,我们要求犯得少一点。 犯了错误则要求改正,改正得越迅速,越彻底,越好。—— 毛泽东 38、理想犹如太阳,吸引地上所有的泥水。 9.君子欲讷于言而敏于行。 ——《论语》 译:君子不会夸夸其谈,做起事来却敏捷灵巧。 10.二人同心,其利断金;同心之言,其臭如兰。 ——《周易》 译:同心协力的人,他们的力量足以把坚硬的金属弄断;同心同德的人发表一致的意见,说服力强,人们就像嗅到芬芳的兰花香味,容易接受。 11.君子藏器于身,待时而动。 ——《周易》 译:君子就算有卓越的才能超群的技艺,也不会到处炫耀、卖弄。而是在必要的时刻把才能或技艺施展出来。 12.满招损,谦受益。 ——《尚书》 译:自满于已获得的成绩,将会招来损失和灾害;谦逊并时时感到了自己的不足,就能因此而得益。 13.人不知而不愠,不亦君子乎? ——《论语》 译:如果我有了某些成就,别人并不理解,可我决不会感到气愤、委屈。这不也是一种君子风度的表现吗?知缘斋主人 14.言必信 ,行必果。 ——《论语》 译:说了的话,一定要守信用;确定了要干的事,就一定要坚决果敢地干下去。 15.毋意,毋必,毋固,毋我。 ——《论语》 译:讲事实,不凭空猜测;遇事不专断,不任性,可行则行;行事要灵活,不死板;凡事不以“我”为中心,不自以为是,与周围的人群策群力,共同完成任务。 16.三人行,必有我师焉,择其善者而从之,其不善者而改之。——《论语》 译:三个人在一起,其中必有某人在某方面是值得我学习的,那他就可当我的老师。我选取他的优点来学习,对他的缺点和不足,我会引以为戒,有则改之。 17.君子求诸己,小人求诸人。 ——《论语》 译:君子总是责备自己,从自身找缺点,找问题。小人常常把目光射向别人,找别人的缺点和不足。很多人(包括我自己)觉得面试时没话说,于是找了一些名言,可以在答题的时候将其穿插其中,按照当场的需要或简要或详细解释一番,也算是一种应对的方法吧 1.天行健,君子以自强不息。 ——《周易》 译:作为君子,应该有坚强的意志,永不止息的奋斗精神,努力加强自我修养,完成并发展自己的学业或事业,能这样做才体现了天的意志,不辜负宇宙给予君子的职责和才能。 2.勿以恶小而为之,勿以善小而不为。 ——《三国志》刘备语 译:对任何一件事,不要因为它是很小的、不显眼的坏事就去做;相反,对于一些微小的。却有益于别人的好事,不要因为它意义不大就不去做它。 3.见善如不及,见不善如探汤。 ——《论语》 译:见到好的人,生怕来不及向他学习,见到好的事,生怕迟了就做不了。看到了恶人、坏事,就像是接触到热得发烫的水一样,要立刻离开,避得远远的。 4.躬自厚而薄责于人,则远怨矣。 ——《论语》 译:干活抢重的,有过失主动承担主要责任是“躬自厚”,对别人多谅解多宽容,是“薄责于人”,这样的话,就不会互相怨恨。 5.君子成人之美,不成人之恶。小人反是。 ——《论语》 译:君子总是从善良的或有利于他人的愿望出发,全心全意促使别人实现良好的意愿和正当的要求,不会用冷酷的眼光看世界。或是唯恐天下不乱,不会在别人有失败、错误或痛苦时推波助澜。小人却相反,总是“成人之恶,不成人之美”。 6.见贤思齐焉,见不贤而内自省也。 ——《论语》 译:见到有人在某一方面有超过自己的长处和优点,就虚心请教,认真学习,想办法赶上他,和他达到同一水平;见有人存在某种缺点或不足,就要冷静反省,看自己是不是也有他那样的缺点或不足。 7.己所不欲,勿施于人。 ——《论语》 译:自己不想要的(痛苦、灾难、祸事……),就不要把它强加到别人身上去。 8.当仁,不让于师。 ——《论语》 译:遇到应该做的好事,不能犹豫不决,即使老师在一旁,也应该抢着去做。后发展为成语“当仁不让”。 18.君子坦荡荡,小人长戚戚。 ——《论语》 译:君子心胸开朗,思想上坦率洁净,外貌动作也显得十分舒畅安定。小人心里欲念太多,心理负担很重,就常忧虑、担心,外貌、动作也显得忐忑不安,常是坐不定,1.书到用时方恨少,事非经过不知难。 ——陈廷焯 译:知识总是在运用时才让人感到太不够了,许多事情如果不亲身经历过就不知道它有多难。 72、笨鸟先飞早入林,笨人勤学早成材。 ——《省世格言》 译:飞得慢的鸟儿提早起飞就会比别的鸟儿早飞入树林,不够聪明的人只要勤奋努力,就可以比别人早成材。 73.书山有路勤为径,学海无涯苦作舟。 ——《增广贤文》 译:勤奋是登上知识高峰的一条捷径,不怕吃苦才能在知识的海洋里自由遨游。 74.学如逆水行舟,不进则退。 ——《增广贤文》 译:学习要不断进取,不断努力,就像逆水行驶的小船,不努力向前,就只能向后退。 75.吾生也有涯,而知也无涯。 ——《庄子》 译:我的生命是有限的,而人类的知识是无限的。 76.天下兴亡,匹夫有责。 ——明•顾炎武 译:国家的兴旺、衰败,每一个人都负有很大的责任。 77.生于忧患,死于安乐。 ——孟子 译:逆境能使人的意志得到磨炼,使人更坚强。相反,时常满足于享受,会使人不求上进而逐渐落后。 78.位卑未敢忘忧国。 ——陆游《病起书怀》 译:虽然自己地位低微,但是从没忘掉忧国忧民的责任。 79.人生自古谁无死,留取丹心照汉青。 ——宋•文天祥《过零丁洋》 译:自古以来,谁都难免会死的,那就把一片爱国的赤胆忠心留在史册上吧! 80.先天下之忧而忧,后天下之乐而乐。 ——宋•范仲淹《岳阳楼记》 译:为国家分忧时,比别人先,比别人急;享受幸福,快乐时,却让别人先,自己居后。知缘斋主人 81.小来思报国,不是爱封侯。 ——唐•岑参《关人赴安西》 译:从小就想着报效祖国,而不是想着要封侯当官。) 82.有益国家之事虽死弗避。 ——明•吕坤《呻吟语•卷上》 译:对国家有利的事情要勇敢地去做,就算有死亡的危险也不躲避 译:风声、雨声、琅琅读书声,都进入我们的耳朵,所以,作为一个读书人,家事、国事,天下的事情,各种事情都应该关心,不能只是死读书。 87.生当作人杰,死亦为鬼雄。 ——宋•李清照《夏日绝句》 译:活着的时候要做英雄,死后也要当英雄。 88.利于国者爱之,害于国者恶之。 ——《晏子春秋》 译:对于国家有利的事就要热心地去做,对国家有害的事就要憎恶它,远离它。 89.读书本意在元元。 ——宋•陆游 译:读书的目的应该是掌握了知识后为社会和大众服务,而不是为了自己的升官发财。 90.时穷节乃现,一一垂丹青。 ——宋•文天祥 译:历史上许多忠臣义士,在国家有难时,他们的节操就显现出来,一个个名垂史册。 91.哀哀父母,生我劬劳。 ——《诗经》 译:想起父母,做子女的是多么为他们感到心痛啊!他们生我育我,花费了多少辛勤的劳动啊! 92.报国之心,死而后已。——宋•苏轼 译:报效祖国的志向到死都不会变。 93.忧国忘家,捐躯济难,忠臣之志也。 ——三国•曹植《求自诚表》 译:忧虑国家大事忘记小家庭,为拯救国家危难而捐躯献身,这都是忠臣的志向。 94.大丈夫处世,当扫除天下,安事一室乎? ——汉•陈蕃语 译:有志气的人活在世上,应当敢于跟各种不利于国家的行为作斗争,哪能只满足于处理好自己小家的小事呢? 95.君子之交淡如水,小人之交甘若醴。 ——《庄子》 译:君子之间的交往,像水一样的平淡、纯净,这样的友谊才会持久;往小人之间的交像甜酒一样的又浓又稠,但不会长久。 96.老吾老,以及人之老;幼吾幼,以及人之幼。 ——《孟子》 译:尊敬、爱戴别人的长辈,要像尊敬、爱戴自己长辈一样;爱护别人的儿女,也 97.见侮而不斗,辱也。 ——《公孙龙子》 译:当正义遭到侮辱、欺凌却不挺身而出,是一种耻辱的表现。 98.天下皆知取之为取,而莫知与之为取。 ——《后汉书》 译:人们都认为只有获取别人的东西才是收获,却不知道给予别人也是一种收获。 99.人固有一死,或重于泰山,或轻于鸿毛。 ——汉•司马迁《史记》 译:人终究免不了一死,但死的价值不同,为了人民正义的事业而死就比泰山还重,而那些自私自利,损人利已的人之死就比鸿毛还轻。知缘斋主人 100.羊有跪乳之恩,鸦有反哺之义。 ——《增广贤文》 译:羊羔有跪下接受母乳的感恩举动,小乌鸦有衔食喂母鸦的情义,做子女的更要懂得孝顺父母
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
f ( x ) tan( x ) tan( x ) tan[ ( x 2) ] f ( x 2) 2 3 2 3 2 3
因此函数的周期为2.带入正切的单调区间可解得函 数得单调区间
5 1 ( 2k , 2k ), k Z 3 3
(1)1 tan x 0;
y 3
(2) tan x 3 0;
4
3
y 1
小结
正切函数的周期性,奇偶
性,单调性,值域.
作业
课本45页练习
4、值域
正切函数的值域是实数 R. 集
举例
π π 例1 求函数y tan ( x )的定义域, 周 2 3 期和单调区间.
解:
x k 2 3 2
即
所以函数的定义域是 由于
1 { x | x 2k , k Z }. 3
1 x 2k , k Z 3
y A sin( x ), x R.( A 0, 0) y A cos(x ), x R.( A 0, 0)
y A tan( x ).( A 0, 0)
T
2
T
例2 求使下列不等式成立的 的集合: x
§ 1.4.3 正切函数的 性质与图象
引入
正切函数:
y tan x , x k , k Z 2
新课
正切函数图像:
FLASH
1、周期性
正切函数是周期函数, 周期是π.
2、奇偶性
正切函数是奇函数.
3、单调性
π π 在每一个开区间 , kπ ), k Z上都是增函数 (kπ . 2 2
