2015年春季新版北师大版七年级数学下学期2.4、用尺规作角同步练习7
数学:2.4 用尺规作角 课件(北师大版七年级下)

范O’
C’
A’
∠A’O’B’就是所求的角.
随堂练习
请用没有刻度的直尺和圆规, 在课本的图 2-23中, 过点C作AB的平行线. 分析:若以点C为顶 点作一个角∠FCE 与∠BAC 相等, 则∠FCE的边CF 所在的直线即为所求
.
B F D
H
A
G
C
G’ E
随堂练习
已知: ∠AOB。 利用尺规作: ∠A’O’B’ 使∠A’O’B’=2∠AOB。
(2) 如果你只有一
个圆规和一把没有 刻度的直尺,你能 解决这个问题吗?
A
C
探索发现
B
D
A
C
E
上述问题:用尺规(无刻度的直尺和圆规)
“过直线外一点作已知直线的平行线”
相当于 “过点C作∠ECD等于已知∠CAB.”
已知: ∠AOB。 求作: ∠A’O’B’ 使∠A’O’B’=∠AOB。
作 法 示
(1) 作射线O’A’; (2) 以点O为圆心, 任意长为半径 画弧, 交OA于点C, 交OB于点D; (3) 以点O’为圆心, 同样(OC)长为半径画弧, 交O’A’于点C’; (4) 以点C’为圆心, CD长为半径画弧, 交前面的弧于点D’ , (5) 过点D’作射线O’B’. D B
4 用尺规作角
回顾与思考
怎样利用没有刻度的直尺和圆规作一条 线段等于已知线段? 已知线段a,b,c,作一条线段m,使得m=a+b-c a b c
如图2—23,要在长方形木板上截一个平 用直尺 与三角板你 行四边形,使它的一组对边在长方形木板 画得出来吗 ? 的边缘上,另一组对边中的一条边为 AB。 试一试. (1)请过C点画出与 B AB平行的另一条边。
北师大版七年级数学下册2.4 用尺规作图1 同步练习

《用尺规作角》习题一、选择题1.下列关于作图的语句中正确的是()A.画直线AB=10厘米B.画射线OB=10厘米C.已知A,B,C三点,过这三点画一条直线D.过直线AB外一点画一条直线和直线AB平行2.下列属于尺规作图的是()A.用刻度尺和圆规作△ABC B.用量角器画一个300的角C.用圆规画半径2cm的圆D.作一条线段等于已知线段3.尺规作图的画图工具是()A.刻度尺、量角器B.三角板、量角器C.直尺、量角器 D.没有刻度的直尺和圆规4.下列作图语句正确的是()A.以点O为顶点作∠AOB B.延长线段AB到C,使AC=BC C.作∠AOB,使∠AOB=∠αD.以A为圆心作弧5.图中的尺规作图是作()A.线段的垂直平分线 B.一条线段等于已知线段C.一个角等于已知角 D.角的平分线6.下列作图语句正确的是()A.作射线AB,使AB=a B.作∠AOB=∠aC.延长直线AB到点C,使AC=BC D.以点O为圆心作弧7.下列叙述中,正确的是()A.以点O为圆心,以任意长为半径画弧,交线段OA于点B B.以∠AOB的边OB为一边作∠BOCC.以点O为圆心画弧,交射线OA于点BD.在线段AB的延长线上截取线段BC=AB8.下列尺规作图的语句错误的是()A.作∠AOB,使∠AOB=3∠αB.作线段AB,使线段AB=aC.以点O为圆心画弧D.作∠ABC,使∠ABC=∠α+∠β9.下列属于尺规作图的是()A.用量角器画∠AOB的平分线OPB.利用两块三角板画15°的角C.用刻度尺测量后画线段AB=10cmD.在射线OP上截取OA=AB=BC=a10.下列关于作图的语句正确的是()A.作∠AOB的平分线OE=3 cmB.画直线AB=线段CDC.用直尺作三角形的高是尺规作图D.已知A、B、C三点,过这三点不一定能画出一条直线11.下列作图属于尺规作图的是()A.画线段MN=3cmB.用量角器画出∠AOB的平分线C.用三角尺作过点A垂直于直线L的直线D.已知∠α,用没有刻度的直尺和圆规作∠AOB,使∠AOB=2∠α12.下列尺规作图的语句错误的是()A.作∠AOB,使∠AOB=3∠αB.以点O为圆心作弧C.以点A为圆心,线段a的长为半径作弧D.作∠ABC,使∠ABC=∠α+∠β二、填空题13.作图题的书写步骤是、、,而且要画出和,保留.14.下列语句表示的图形是(只填序号)①过点O的三条直线与另条一直线分别相交于点B、C、D三点:.②以直线AB上一点O为顶点,在直线AB的同侧画∠AOC和∠BOD:.③过O点的一条直线和以O为端点两条射线与另一条直线分别相交于点B、C、D三点:.15.下列语句是有关几何作图的叙述.①以O为圆心作弧;②延长射线AB到点C;③作∠AOB,使∠AOB=∠1;④作直线AB,使AB=a;⑤过三角形ABC的顶点C作它的对边AB的平行线.其中正确的有.(填序号即可)参考答案一、选择题1.答案:D解析:【解答】A、直线没有长度,故A选项错误;B、射线没有长度,故B选项错误;C、三点有可能在一条直线上,可画出一条直线,也可能不在一条直线上,此时可画出三条直线,故选项错误;D、正确.故选:D.【分析】根据基本作图的方法,逐项分析,从而得出正确的结论.2.答案:D解析:【解答】A、用刻度尺和圆规作△ABC,而尺规作图中的直尺是没有长度的,错误;B、量角器不在尺规作图的工具里,错误;C、画半径2cm的圆,需要知道长度,而尺规作图中的直尺是没有长度的,错误;D、正确.故选:D.【分析】根据尺规作图的定义分别分析得出即可.3.答案:D解析:【解答】尺规作图的画图工具是没有刻度的直尺和圆规.故选D.【分析】根据尺规作图的定义可知.4.答案:C解析:【解答】A、画角既需要顶点,还需要角度的大小,错误;B、延长线段AB到C,则AC>BC,即AC=BC不可能,错误;C、作一个角等于已知角是常见的尺规作图,正确;D、画弧既需要圆心,还需要半径,缺少半径长,错误.故选C.【分析】根据画角的条件判断A;根据线段延长线的等腰判断B;根据基本作图判断C;根据确定弧的条件判断D.5.答案:A解析:【解答】根据图象是一条线段,它是以线段的两端点为圆心,作弧,进而作出垂直平分线,故做的是:线段的垂直平分线,故选:A.【分析】根据图象以及做线段垂直平分线的作法,即可得出答案.6.答案:B解析:【解答】A、射线是不可度量的,故选项错误;B、正确;C、直线是向两方无线延伸的,故选项错误;D、需要说明半径的长,故选项错误.故选B.【分析】根据射线、直线的延伸性以及确定弧的条件即可作出判断.7.答案:D解析:【解答】A、以点O为圆心,以任意长为半径画弧,交线段OA于点B,任意长为半径,不一定与线段AO相交,故此选项错误;B、以∠AOB的边OB为一边作∠BOC,∠BOC的度数不确定,故此选项错误;C、以点O为圆心画弧,交射线OA于点B,没有半径长,故此选项错误;D、在线段AB的延长线上截取线段BC=AB,正确.故选:D.【分析】分别利用尺规作图的定义,结合能否画出图形进而分析得出即可.8.答案:C解析:【解答】A、作一个角等于已知角的倍数是常见的尺规作图,语句正确;B、作一条线段等于已知线段是常见的尺规作图,语句正确;C、画弧既需要圆心,还需要半径,缺少半径长,这样的弧可以画出无数条,语句错误;D、作一个角等于两个已知角的和是基本作图,语句正确.故选C.【分析】分别利用尺规作图的定义,结合能否画出图形进而分析得出即可.9.答案:D解析:【解答】根据尺规作图的定义可得:在射线OP上截取OA=AB=BC=a,属于尺规作图,故选:D.【分析】根据尺规作图的定义:是指用没有刻度的直尺和圆规作图可直接选出答案.10.答案:D解析:【解答】A、作∠AOB的平分线OE=3 cm,角平分线是射线,故此选项错误;B、画直线AB=线段CD,直线没有长度,故此选项错误;C、用直尺作三角形的高是尺规作图,尺规应有圆规,故此选项错误;D、已知A、B、C三点,过这三点不一定能画出一条直线,此选项正确;故选:D.【分析】射线、直线具有延伸性,不能画出其长度;尺规作图需用圆规和无刻度的直尺;若A、B、C三点不共线,则无法过这三点画出一条直线,即A、B、C错误,D项正确.11.答案:D解析:【解答】A、画线段MN=3cm,需要知道长度,而尺规作图中的直尺是没有长度的,错误;B、用量角器画出∠AOB的平分线,量角器不在尺规作图的工具里,错误;C、用三角尺作过点A垂直于直线L的直线,三角尺也不在作图工具里,错误;D、正确.故选D.【分析】根据尺规作图的定义可知.12.答案:B解析:【解答】A、作一个角等于已知角的倍数是常见的尺规作图,正确;B、画弧既需要圆心,还需要半径,缺少半径长,错误.C、以点A为圆心,线段a的长为半径作弧,正确;D、作∠ABC,使∠ABC=∠α+∠β,正确故选B.【分析】根据基本作图的方法,逐项分析,从而得出结论.二、填空题13.答案:已知、求作、作法,图形,结论,作图痕迹.解析:【解答】作图题的书写步骤是已知、求作、作法,而且要画出图形和结论,保留作图痕迹.【分析】根据作图题的书写步骤和尺规作图的要求作答.14.答案:(3),(2),(1).解析:【解答】①过点O的三条直线与另一条直线分别相交于点B、C、D三点的图形为(3);②以直线AB上一点O为顶点,在直线AB的同侧画∠AOC和∠BOD的图形为(2);③过O点的一条直线和以O为端点两条射线与另一条直线分别相交于点B、C、D三点的图形为(1).【分析】图(1)为过点O有两条射线OC、OD,一条直线AB;图(2)为以直线AB上一点O为顶点,在直线AB的同侧画∠AOC和∠BOD,图(3)为过点O的三条直线AB、OC、OD与另一条直线分别相交于点B、C、D三点.根据语句及图形特征进行选择.15.答案:③⑤.解析:【解答】①以O为圆心作弧可以画出无数条弧,因为半径不固定,所以叙述错误;②射线AB是由A向B向无限延伸,所以叙述错误;③根据作一个角等于已知角的作法,可以作一个角∠AOB,使∠AOB等于已知∠1,所以叙述正确;④直线可以向两方无限延伸,所以叙述错误;⑤根据平行公理:过直线外一点有且只有一条直线与已知直线平行,可以过三角形ABC的顶点C 作它的对边AB的平行线,所以叙述正确.所以正确的有③⑤.【分析】①根据确定圆的两个条件:圆心和半径判断即可;②根据射线的性质判断即可;③根据基本作图:作一个角等于已知角判断即可;④根据直线的性质判断即可;⑤根据平行公理判断即可.。
七年级数学下册2.4《用尺规作角》典型例题素材北师大版(new)
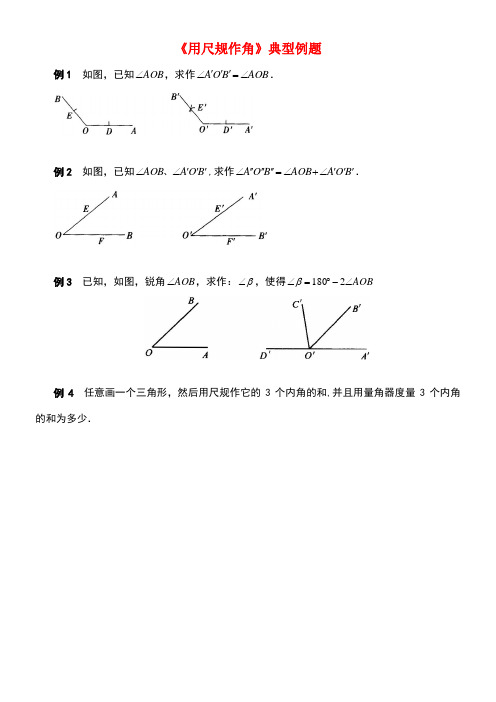
《用尺规作角》典型例题例1 如图,已知AOB ∠,求作AOB B O A ∠='''∠.例2 如图,已知B O A AOB '''∠∠、,求作B O A AOB B O A '''∠+∠=''''''∠.例3 已知,如图,锐角AOB ∠,求作:β∠,使得AOB ∠-︒=∠2180β例4 任意画一个三角形,然后用尺规作它的3个内角的和,并且用量角器度量3个内角的和为多少.参考答案例1 分析:要作AOB B O A ∠='''∠,可以先作A O '',在此基础上我们再来确定B O ''的位置.作法:(1)作射线A O ''.(2)以O 为圆心,以任意长为半径画弧交OA 于D ,OB 于E .(3)以O '为圆心,以OE 为半径画弧交A O ''于D .(4)以D '为圆心,以DE 为半径画弧和前弧交于E '点.(5)过E '作射线B O '',则B O A '''∠就是所要求的角.说明:在进行第2步时,以“任意长为半径",要注意这个“任意"要适当,否则就都会给作图带来不必要的麻烦.例 2 分析:我们可以先作出一个角等于AOB ∠,再在这个角的外边,以这个角的一边为边作一个角等B O A '''∠,这就作出了这两个角的和,这个过程可以简化成如下过程.作法:(1)作射A O ''''.(2)以O 为圆心任意长为半径画弧交OA 于E ,OB 于F ;再以O '为圆心同样长为半径画弧交A O ''于E ',B O ''于F '.(3)以O ''为圆心,以OE 为半径画弧交A O ''''于E ''.(4)以E ''为圆心,以EF 为半径画弧,于前弧交于D 点;再以D 点为圆心,以F E ''为半径画弧,交E ''、D 所同在的弧为F ''点.(5)作射线F O '''',则B O A ''''''∠就是所求的角.说明:中间连结D O ''这一步直接省略即可.例3 分析:首先作出AOB ∠2,再求AOB ∠2的补角即是所求的角.作法:1.作AOB B O A ∠='''∠,2.以B O ''为始边作AOB C O B ∠='''∠3.反向延长射线A O ''到D '.β∠为图中所示的D O C '''∠例4 分析:首先根据题目叙述写出已知、求作,然后再作图.解:已知:如图,已知三角形ABC .求作:DOG ∠,使C B A DOG ∠+∠+∠=∠.作法:(1)作A DOE ∠=∠;(2)以OE 为一边,在A DOE ∠=∠的外部作B EOF ∠=∠;(3)以OF 为一边,在EOF ∠的外部作C GOF ∠=∠.DOG ∠就是所求作的角(如图).用量角器量得︒=∠180DOG .尊敬的读者:本文由我和我的同事在百忙中收集整编出来,本文档在发布之前我们对内容进行仔细校对,但是难免会有不尽如人意之处,如有疏漏之处请指正,希望本文能为您解开疑惑,引发思考。
北师大版七年级数学下册2.4用尺规作角(23张PPT)

2.4 用尺规作角
1 课堂讲解 尺规作图
作一个角等于已知角
2 课时流程
逐点 导讲练
课堂 小结
作业 提升
复习回顾
我们学过的作图: 1.作一条线段等于已知线段 (尺规第一个基本作图); 2.经过一点画已知直线的垂线; 3.经过直线外一点作已知直线的平行线 .
新知探究
如图,要在长方形木板上截一个平行四边形,使它的一组对边在长方
D.以点E为圆心,DM为半径的弧
C可.根以据点“同E为位圆角心相,则等O,∠D为两C半直径A线的D平弧行就”作是图,所也求可 的角.
经过一点画已知直线的垂线;
位角相等或内错角相等,使m∥l,且m经过点P.
如图,∠AOB为所求作的角.
本题应用作图法,利用尺规作∠CAD等于∠1与
位角相等或内错角相等,使m∥l,且m经过点P.
(4) 以点C’为圆心, CD长为半径 画弧, 交前面的弧于点D’ ,
(5) 过点D’作射线O’B’.
示
范
DB
O
CA
D’ B’
O’
C’
A’
∠A’O’B’就是所求的角.
尺规作角过程中应注意哪些细节?
1 . 作一个角等于已知角可以归纳为“一线三弧”. 2 . 先画一条射线,再作三次弧 . 其中前两次弧半径 相同,而第三次以原角的两边与弧的交点之间的距离 为半径 .
O′A′于点C′;(4)以点C′为圆心,以CD长为半径画弧,交
前弧于点D′,再以点D′为圆心,以CD长为半径画弧,交
前弧于点E′;(5)过点E′作射线O′B′.∠A′O′B′就是所求作
的角.
1 已知∠AOB,利用尺规作∠A′O′B′,使∠A′O′B′
七年级数学下册2.4用尺规作角教你用尺规作角素材北师大版(new)

教你用尺规作角刚学习了用尺规作角,不知同学们掌握得怎样了,为了加深对尺规作图的掌握,请看下面几例:例1 如图,已知∠AOB和射线O′B′.求作:∠A′O′B′=∠AOB.(要求保留作图痕迹)解:如下图.作法:(1)以点O为圆心,以任意长为半径画弧,交OA于点C,交OB于点D。
(2)以点O′为圆心,以OD的长为半径画弧,交O′B′于点D′.(3)以点D′为圆心,以DC的长为半径画弧,交前面的弧于点C′。
(4)过点C′作射线O′A′.则∠A′O′B′就是所求作的角.评注:(1)尺规作图题一般不要求写作法,但要保留作图痕迹。
切记:不要用“手画弧线”代替“圆规画弧线”,这种懒偷不得,这种小聪明耍不得,因为这种画法显然是错误的,而且很容易就能看出来.(2)因为不需要写作法,所以图中C,D,C′,D′这几个字母不标也可以.但A′必须标注,且最后要交代一句“∠⨯⨯⨯就是所求作的角”。
跟踪训练1 如图,已知∠COD和射线O′D′.求作:∠C′O′D′=∠COD.(要求保留作图痕迹)例2 如图,已知∠α,∠β,求作:∠AOB,使∠AOB=∠α+∠β .解:如下图.作法:(1)作射线OA.(2)以射线OA为一边作∠AOC=∠α。
(3)以O为顶点,以射线OC为一边,在∠AOC的外部作∠COB=∠ .则∠AOB就是所求作的角.评注:本题同样是两次运用基本作图“作一个角等于已知角”而得到所求,值得注意的是作∠COB时,应在∠AOC的外部,否则就不是作两个角的和了。
跟踪训练2 已知:如图,∠AOB为已知角。
求作:∠A′O′B′,使∠A′O′B′=2∠AOB.答案1.略.2.略.尊敬的读者:本文由我和我的同事在百忙中收集整编出来,本文档在发布之前我们对内容进行仔细校对,但是难免会有不尽如人意之处,如有疏漏之处请指正,希望本文能为您解开疑惑,引发思考。
文中部分文字受到网友的关怀和支持,在此表示感谢!在往后的日子希望与大家共同进步,成长。
北师大版七年级下册数学《用尺规作角》典型例题 含答案
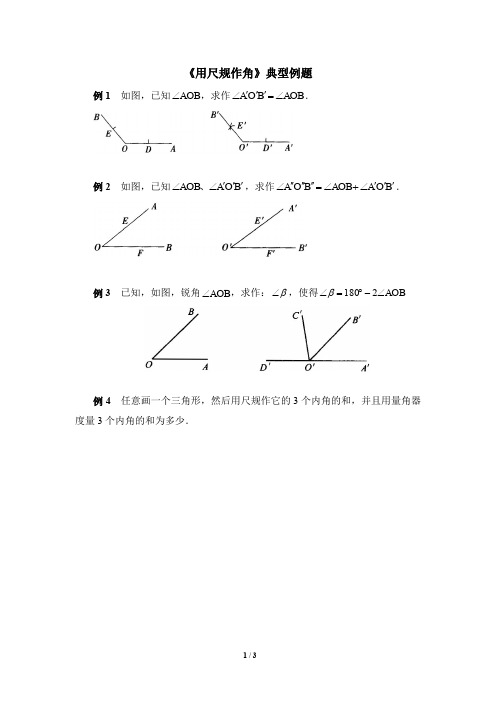
《用尺规作角》典型例题例1 如图,已知AOB ∠,求作AOB B O A ∠='''∠.例2 如图,已知B O A AOB '''∠∠、,求作B O A AOB B O A '''∠+∠=''''''∠.例3 已知,如图,锐角AOB ∠,求作:β∠,使得AOB ∠-︒=∠2180β例4 任意画一个三角形,然后用尺规作它的3个内角的和,并且用量角器度量3个内角的和为多少.参考答案例1 分析:要作AOB B O A ∠='''∠,可以先作A O '',在此基础上我们再来确定B O ''的位置.作法:(1)作射线A O ''.(2)以O 为圆心,以任意长为半径画弧交OA 于D ,OB 于E .(3)以O '为圆心,以OE 为半径画弧交A O ''于D .(4)以D '为圆心,以DE 为半径画弧和前弧交于E '点.(5)过E '作射线B O '',则B O A '''∠就是所要求的角.说明:在进行第2步时,以“任意长为半径”,要注意这个“任意”要适当,否则就都会给作图带来不必要的麻烦.例2 分析:我们可以先作出一个角等于AOB ∠,再在这个角的外边,以这个角的一边为边作一个角等B O A '''∠,这就作出了这两个角的和,这个过程可以简化成如下过程.作法:(1)作射A O ''''.(2)以O 为圆心任意长为半径画弧交OA 于E ,OB 于F ;再以O '为圆心同样长为半径画弧交A O ''于E ',B O ''于F '.(3)以O ''为圆心,以OE 为半径画弧交A O ''''于E ''.(4)以E ''为圆心,以EF 为半径画弧,于前弧交于D 点;再以D 点为圆心,以F E ''为半径画弧,交E ''、D 所同在的弧为F ''点.(5)作射线F O '''',则B O A ''''''∠就是所求的角.说明:中间连结D O ''这一步直接省略即可.例3 分析:首先作出AOB ∠2,再求AOB ∠2的补角即是所求的角. 作法:1.作AOB B O A ∠='''∠,2.以B O ''为始边作AOB C O B ∠='''∠3.反向延长射线A O ''到D '.β∠为图中所示的D O C '''∠例4 分析:首先根据题目叙述写出已知、求作,然后再作图. 解:已知:如图,已知三角形ABC .求作:DOG ∠,使C B A DOG ∠+∠+∠=∠.作法:(1)作A DOE ∠=∠;(2)以OE 为一边,在A DOE ∠=∠的外部作B EOF ∠=∠;(3)以OF 为一边,在EOF ∠的外部作C GOF ∠=∠.DOG ∠就是所求作的角(如图).用量角器量得︒=∠180DOG .。
2024-2025学年七年级数学下册同步讲义(北师大版)专题2.4用尺规作角(原卷版)
(1)在射线 EM 的上方,作 NEM B ; (2)在射线 EN 上作线段 DE ,在射线 EM 上作线段 EF ,使得 DE AB , EF BC ; (3)连接 DF ,观察并猜想: DF 与 AC 的数量关系是 DF ______ AC ,填(“>”、“<”或“=”)
知识点 02 用尺规作一个角等于已知角
③以点 P 为圆心, MN 的长为半径作弧,交上一段弧于点 Q;
④以点 C 为圆心, OM 的长为半径作弧,交 OB 于点 P.下列排序正确的是( )
A.①②③④
B.②④③①
C.③②④①
D.④③①②
3.实践课上,张老师给同学们出了这样一道题:已知,如图点 C 在 AOD 的边上,用尺规作出 CN / /OA.小
颖进行如图所示的操作,从作图的痕迹可以发现, FG 是( )
A.以点 C 为圆心, OM 为半径的弧
B.以点 C 为圆心, DM 为半径的弧
C.以点 E 为圆心, OM 为半径的弧
D.以点 E 为圆心, DM 为半径的弧
4.如图所示,过点 P 画直线 a 的平行线 b 的作法的依据是( )
A.两直线平行,同位角相等
(2)如图 2 所示:
【点拨】此题主要考查了基本作图,关键是熟练掌握作一个角等于已知角的方法.
巩固练习
1.尺规作图的画图工具是( ) A.刻度尺、圆规
B.三角板和量角器
C.直尺和量角器
D.没有刻度的直尺和圆规
2.如图,已知三角形 ABC 和射线 EM ,用直尺和圆规按下列步骤作图(保留作图痕迹,不写作法):
1. 尺规作图:如图,作一个角等于已知角.(要求:写出已知、求作,保留作图痕迹,不写作法) 2.已知∠AOB,利用尺规作∠A'O'B',使∠A'O'B' = 2∠AOB.
北师大版七年级数学下册用尺规作角(共15张)
4 用尺规作角
用尺规作一个角等于已知角 利用尺规作一个角等于已知角,是一个尺规基本作图,因为一个角 的大小只与角的两边___张__开___的大小有关,而与两边的___长__短___无关, 因此可利用尺规作图作一个角等于已知角.
1.在上学期我们已经学习了一个尺规基本作图,你还记得那个尺 规基本作图的内容吗?
解:方法一:把∠A移到∠B上,如图1,得∠A<∠B; 方法二:把∠B移到∠A上,如图2,得∠A<∠B.
5 cm.其中,属于尺规作图的有
(A )
A.1个
B.2个
C.3个
D.4个
2.下列关于尺规功能的说法不正确的是
(B )
A.直尺的功能:在两点间连接一条线段或将线段向两方向延长
B.直尺的功能:可作平角和直角
C.圆规的功能:以任意长为半径,以任意点为圆心作一个圆
D.圆规的功能:以任意长为半径,以任意点为圆心作一段弧
答:那个尺规基本作图内容是:“作一条线段等于已知线段.”
知识点 用尺规作一个角等于已知角 例 如图,已知直线m与直线m外一点M,请你利用尺规过点M作 一条直线与直线m平行.说出作图方法,保留作图痕迹.
解:作法如下: (1)过点M任意画一条直线OM与直线m交于点O; (2)以点O为圆心,任意长为半径画弧交直线OM于点A,交直线m于 点B; (3) 以 点 M 为 圆 心 , OA 为 半 径 画 弧 交 直 线 OM 于 点 C , 以 点 C 为 圆 心,AB为半径画弧交前弧于点D;
(4)过点M,D画直线,则直线MD即为所求,如图.
2.本题利用尺规作直线MD与直线m平行,平行的根据是 ( B ) A.平行公理 B.同位角相等,两直线平行 C.内错角相等,两直线平行 D.同旁内角互补,两直线平行 3.本题中,弧OA的半径产生变化时,作出的∠CMD的度数一定 ___不__会___变化.(填“会”或“不会”)
北师大版数学七年级下册第二章相交线与平行线第4节用尺规做角课后练习
第二章相交线与平行线第4节用尺规做角课后练习学校:___________姓名:___________班级:___________考生__________ 评卷人 得分一、单选题1.如图,点C 在∠AOB 的边OB 上,用尺规作出了∠BCN =∠AOC ,作图痕迹中,弧FG 是( )A.以点C 为圆心,OD 为半径的弧 B .以点C 为圆心,DM 为半径的弧 C .以点E 为圆心,OD 为半径的弧 D .以点E 为圆心,DM 为半径的弧2.如图,在ABC ∆中,90ACB ∠=,按如下步骤操作:∠以点A 为圆心,任意长为半径作弧,分别交AC ,AB 于D ,E 两点;∠以点C 为圆心,AD 长为半径作弧,交AC 的延长线于点F ;∠以点F 为圆心,DE 长为半径作弧,两弧交于点G ;∠作射线CG ,若50FCG ∠=,则B 为( )A .40B .50C .60D .703.如图,不是B ∠的同旁内角是( )A .1∠;B .2∠;C .3∠;D .BCD ∠;4.下列属于尺规作图的是( ) A .用量角器画∠AOB 的平分线OP B .利用两块三角板画15°的角 C .用刻度尺测量后画线段AB =10cm D .在射线OP 上截取OA =AB =BC =a5.下列作图语句正确的是()A.以点O为顶点作∠AOBB.延长线段AB到C,使AC=BCC.作∠AOB,使∠AOB=∠αD.以A为圆心作弧6.如图所示,过点P画直线a的平行线b的作法的依据是()A.两直线平行,同位角相等B.同位角相等,两直线平行C.两直线平行,内错角相等D.内错角相等,两直线平行7.如图,点C在∠AOB的边OB上,用尺规作出了∠BCN=∠AOC,作图痕迹中,弧FG是()A.以点C为圆心,OD为半径的弧B.以点C为圆心,DM为半径的弧C.以点E为圆心,OD为半径的弧D.以点E为圆心,DM为半径的弧8.如图,用尺规法作∠DEC=∠BAC,作图痕迹MN的正确画法是()A.以点E为圆心,线段AP为半径的弧B.以点E为圆心,线段QP为半径的弧C.以点G为圆心,线段AP为半径的弧D.以点G为圆心,线段QP为半径的弧评卷人得分二、填空题9.阅读下面材料:在数学课上,老师提出如下问题:作图:过直线外一点作已知直线的平行线.已知:直线l及其外一点A.求作:l的平行线,使它经过点A.小凡利用两块形状相同的三角尺进行如下操作:如图所示:(1)用第一块三角尺的一条边贴住直线l,第二块三角尺的一条边紧靠第一块三角尺;(2)将第二块三角尺沿第一块三角尺移动,使其另一边经过点A,沿这边作出直线AB.所以,直线AB即为所求.老师说:“小凡的作法正确.”请回答:小凡的作图依据是________.10.已知,∠AOB .求作:∠A′O′B′,使∠A′O′B′=∠AOB .作法:∠以________为圆心,________为半径画弧.分别交OA,OB于点C,D .∠画一条射线O′A′,以________为圆心,________长为半径画弧,交O′A′于点C′,∠以点________为圆心________长为半径画弧,与第2步中所画的弧交于点D′.∠过点________画射线O′B′,则∠A′O′B′=∠AOB .11.下列语句表示的图形是(只填序号)∠过点O的三条直线与另条一直线分别相交于点B、C、D三点:_____.∠以直线AB上一点O为顶点,在直线AB的同侧画∠AOC和∠BOD:_______.∠过O点的一条直线和以O为端点两条射线与另一条直线分别相交于点B、C、D三点:_________.12.尺规作图“作一个角等于已知角“的依据是三角形全等的判定方法_______.13.下列作图中:∠用量角器画出90AOB∠=︒;∠作AOB∠,使2AOBα∠=∠;∠连接AB;∠用直尺和三角板作AB的平行线CD,属于尺规作图的是__________.(填序号)14.在几何里,把只用_________和_________画图的方法称为尺规作图.15.完成作图步骤:已知∠α,∠β(∠β>∠α),求作一个角,使它等于∠β-∠α.作法:(1)作∠AOB=_______;(2)以OA为一边,在∠AOB的内部作∠AOC=___,则∠BOC就是所求作的角(如图).16.阅读下面材料:数学课上,老师提出如下问题:小明解答如右图所示,其中他所画的弧MN是以E为圆心,以CD长为半径的弧老师说:“小明作法正确.”请回答小明的作图依据是:_______________________________________.评卷人得分三、解答题17.已知平面内有α∠,如图(1).(1)尺规作图:在图(2)AOB∠的内部作AODα∠=∠(保留作图痕迹,不需要写作法);(2)已知(1)中所作的40AOD∠=︒,OE平分BOC∠,2AOE BOE∠=∠,求BOD∠.18.如图,已知线段40mmAB=,60BAM∠=︒,请你用量角器和刻度尺按下列要求画图:(1)以B为顶点,BA为一边,在BAM∠同侧画30ABN∠=︒,AM与BN相交于点C;(2)取线段AB的中点G,连接CG;(3)用量角器得ACB=∠;(4)用刻度尺测得线段CG=mm,AC的长为mm.(结果保留整数),图中与线段相等的线段有.19.尺规作图,不写作法,保留作图痕迹已知:线段a和∠α求作:∠ABC,使得AB=a,BC=2a,∠ABC=∠α.20.如图,一块大的三角板ABC,D是AB上一点,现要求过点D割出一块小的三角板ADE,使∠ADE=∠ABC,(1)尺规作出∠ADE.(不写作法,保留作图痕迹,要写结论)(2)判断BC与DE是否平行,如果是,请证明.参考答案:1.D【解析】【分析】运用作一个角等于已知角可得答案.【详解】解:根据作一个角等于已知角可得弧FG是以点E为圆心,DM为半径的弧.故选:D.【点睛】本题主要考查了尺规作图——作一个角等于已知角,熟练掌握作一个角等于已知角是解题的关键.2.A【解析】【分析】利用基本作图得到∠FCG=∠CAB=50°,然后利用互余计算∠B的度数.【详解】解:由作法得∠FCG=∠CAB,∠∠FCG=50°,∠∠CAB=50°,∠∠ACB=90°,∠∠B=90°-50°=40°.故选:A.【点睛】本题考查了作图-复杂作图-作一个角等于已知角,复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作,也考查了直角三角形的两锐角互余.3.C【解析】【分析】按照同旁内角的概念逐一判断即可.【详解】解:从图形可以判断,∠1,∠2,∠BCD都是∠B的同旁内角,但∠3不是;故答案为C.【点睛】本题考查了同旁内角的概念,熟知同旁内角概念的模型(如图的∠1和∠2)是解题的关键.4.D【解析】【详解】解:根据尺规作图的定义可得:在射线OP上截取OA=AB=BC=a,属于尺规作图,故选D.5.C【解析】【详解】解:选项A,画角既需要顶点,还需要角度的大小,错误;选项B,延长线段AB到C,则AC>BC,即AC=BC不可能,错误;选项C,作一个角等于已知角是常见的尺规作图,正确;选项D,画弧既需要圆心,还需要半径,缺少半径长,错误.故选C.6.D【解析】【详解】试题解析:如图所示,根据图中直线a、b被c所截形成的内错角相等,可得依据为内错角相等,两直线平行.故选D.7.D【解析】运用作一个角等于已知角可得答案.【详解】解:根据作一个角等于已知角可得弧FG是以点E为圆心,DM为半径的弧.故选:D.【点睛】本题主要考查了尺规作图——作一个角等于已知角,熟练掌握作一个角等于已知角是解题的关键.8.D【解析】【分析】根据作一个角等于已知角的作法即可得出结论.【详解】先以点A为圆心,以任意长为半径画弧,分别交AC,AB于点Q,P;再以点E为圆心,AQ的长为半径画弧,交AC于点G,再以点G为圆心,PQ的长为半径画弧.故选D.【点睛】本题考查的是作图-基本作图,熟知作一个角等于已知角的基本步骤是解答此题的关键.9.内错角相等,两直线平行【解析】【分析】根据平行线的判定方法即可解决问题;【详解】解:如图所示:∠两块形状、大小相同的三角尺,将第二块三角尺沿第一块三角尺移动,使其另一边经过∠∠1=∠2,∠AB∠直线l(内错角相等,两直线平行),故答案为:内错角相等,两直线平行.【点睛】本题主要考查的是平行线的判定定理、尺规作图,依据作图过程发现∠1=∠2是解题的关键.10.O任意长O′OC C CD D′【解析】【分析】根据作一个角等于已知角的作图方法解答即可.【详解】∠以O为圆心,任意长为半径画弧.分别交OA,OB于点C、D .∠画一条射线O′A′,以O′为圆心,OC长为半径画弧,交O′A′于点C′,∠以点C为圆心CD长为半径画弧,与第2步中所画的弧交于点D′.∠过点D′画射线O′B′,则∠A′O′B′=∠AOB.故答案为:(1). O;(2). 任意长;(3). O′;(4). OC;(5). C ;(6). CD ;(7). D′【点睛】本题主要考查了作一个角等于已知角,是基本作图,需熟练掌握.11.(3)(2)(1)【解析】【详解】解:观察图形,根据所给的信息可得:∠过点O的三条直线与另一条直线分别相交于点B、C、D三点的图形为(3);∠以直线AB上一点O为顶点,在直线AB的同侧画∠AOC和∠BOD的图形为(2);∠过O点的一条直线和以O为端点两条射线与另一条直线分别相交于点B、C、D三点的图形为(1).故答案为:(3);(2);(1).【点睛】本题考查了直线、射线与线段的知识,注意掌握三者的特点,给出图形应该能判断出是哪一个.12.SSS【解析】【详解】在尺规作图中,作一个角等于已知角是通过构建三边对应相等的全等三角形来证, 因此由作法知其判定依据是SSS ,即边边边公理.故答案为SSS.13.∠∠【解析】【详解】尺规作图的定义:只能用没有刻度的直尺和圆规作图,因此属于尺规作图的是∠、∠. 故答案为∠∠.14. 没有刻度的直尺 圆规【解析】【分析】根据尺规作图的概念进行回答即可.【详解】在几何里,把只用没有刻度的直尺和圆规画图的方法称为尺规作图.故答案为没有刻度的直尺,圆规.【点睛】牢记尺规作图的概念,尺规作图只允许使用两种工具:没有刻度的直尺和圆规. 15. ∠β; ∠α【解析】【详解】试题解析:(1)作,AOB β∠=∠(2)以OA 为一边,在AOB ∠的内部作,AOC α∠=∠ 则BOC ∠ 就是所求作的角(如图). 故答案为,.βα∠∠16.边边边定理证明两个三角形全等,则它们的对应角相等【解析】【分析】由作图过程可知,BE BM OC OD EM CD ====,根据边边边定理证明∆OCD∠∆BME ,可得FBE AOB ∠=∠.【详解】解:以B 点为圆心,OC 为半径画弧EM 交BO 于E,以E 点为圆心,DC 为半径画弧交弧EM 于N, 由此过程可知,BE BM OC OD EM CD ====∴ ∆OCD∠∆BME (SSS )∴FBE AOB ∠=∠故答案为边边边定理证明两个三角形全等,则它们的对应角相等【点睛】本题考查了作一个角等于已知角的作图依据,正确理解作图过程是解题的关键. 17.(1)图见解析;(2)20°.【解析】【分析】(1)按照要求进一步画出图形即可; (2)利用角平分线性质结合2AOE BOE ∠=∠得出==60COE BOE ∠∠°,然后进一步求解即可.【详解】(1)如图所示:(2)∠OE 平分BOC ∠,∠∠COE=∠BOE ,∠2AOE BOE ∠=∠,∠2AOE COE ∠=∠,∠+=180AOE COE∠∠°,∠2+=180COE COE∠∠°,∠==60COE BOE∠∠°,∠60AOB∠=︒,∠40AOD∠=︒,∠=604020BOD∠︒︒︒=-.【点睛】本题主要考查了角度的计算,熟练掌握相关概念是解题关键.18.(1)如图,见解析;(2)如图,见解析;(3)90°(4)20mm,20mm,相等的线段有AC=CG=AG=GB【解析】【分析】(1)按照题中要求用量角器作角;(2)按照题中要求用刻度尺作G点;(3)用量角器测量∠ACB的度数;(4)用刻度尺测量线段CG,AC的长,通过测量结果及已知条件找到图中相等的线段.【详解】解:(1)以B为顶点,BA为一边,在∠BAM同侧用量角器画∠ABN=30°,AM与BN相交于点C,如图;(2)用刻度在线段AB上取点G,使AG=20mm,点G即为AB的中点,如图;(3)用量角器测量∠ACB的度数,得∠ACB=90°;(4)用刻度尺测量线段CG=20mm,AC的长为20mm,∠AB=40mm,G为AB中点,∠AG=BG=20mm,∠AC=CG=AG=GB,即AC=CG=AG=GB.本题考查用量角器和刻度尺画图,掌握线段的比较与图形的作法是解答此题的关键. 19.见解析【解析】【分析】先作∠B=∠α,分别在∠B的两边上截取BA=a,BC=2a,连接AC,则△ABC即为所作.【详解】如图,先作∠B=∠α,分别在∠B的两边上截取BA=a,BC=2a,连接AC,则△ABC即为所求作.【点睛】考查了复杂作图,解题关键是掌握作一个角等于已知角的方法.20.(1)详见解析;(2)BC∠DE【解析】【分析】(1)利用基本作图作∠ADE=∠ABC,交AC于点E;(2)根据平行线的判断方法进行判断.【详解】解:(1)如图,∠ADE为所作;(2)BC∠DE.理由如下:∠∠ADE=∠ABC,∠BC∠DE.本题考查了作图-基本作图,解题的关键是熟练掌握基本作图(作一条线段等于已知线段;作一个角等于已知角;作已知线段的垂直平分线;作已知角的角平分线;过一点作已知直线的垂线).。
北师大版七年级下2.4用尺规作角 课件
范
OD’Βιβλιοθήκη C A B’O’C’
A’
∠A’O’B’就是所求的角.
随堂练习
请用没有刻度的直尺和圆规, 在课本的图 2-23中, 过点C作AB的平行线. 分析:若以点C为顶 点作一个角∠FCE 与∠BAC 相等, 则∠FCE的边CF 所在的直线即为所求
.
B F D
H
A
G
C
G’ E
随堂练习
已知: ∠AOB。 利用尺规作: ∠A’O’B’ 使∠A’O’B’=2∠AOB。
学习目标
1.能按照作图语言来完成作图动作,能用尺 规作一个角等于已知角,并了解它在尺规 作图中的简单应用. 2.能利用尺规作角的和、差、倍. 3.能够通过尺规设计并绘制简单的图案. 4.在尺规作图过程当中,积累数学活动经 验,培养动手能力和逻辑分析能力.
回顾与思考
怎样利用没有刻度的直尺和圆规作一条 线段等于已知线段? 已知线段a,b,c,作一条线段m,使得m=a+b-c a b c
A
C
E
上述问题:用尺规(无刻度的直尺和圆规)
“过直线外一点作已知直线的平行线”
相当于 “过点C作∠ECD等于已知∠CAB.”
已知: ∠AOB。 求作: ∠A’O’B’ 使∠A’O’B’=∠AOB。
作 法 示
(1) 作射线O’A’; (2) 以点O为圆心, 任意长为半径 画弧, 交OA于点C, 交OB于点D; (3) 以点O’为圆心, 同样(OC)长为半径画弧, 交O’A’于点C’; (4) 以点C’为圆心, CD长为半径画弧, 交前面的弧于点D’ , (5) 过点D’作射线O’B’. D B
用直尺 如图2—23,要在长方形木板上截一个平 与三角板你 行四边形,使它的一组对边在长方形木板 画得出来吗? 试一试 . 的边缘上,另一组对边中的一条边为 AB。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
- 1 -
知能提升作业(十九) 2.4 用尺规作角
(30分钟 50分)
一、选择题(每小题4分,共12分)
1.下列关于尺规的功能说法不正确的是( )
(A)直尺的功能是:在两点间连接一条线段,将线段向两方延长
(B)直尺的功能是:可作平角和直角
(C)圆规的功能是:以任意长为半径,以任意点为圆心作一个圆
(D)圆规的功能是:以任意长为半径,以任意点为圆心作一段弧
2.(2012·河北中考)如图,点C在∠AOB的边OB上,用尺规作出了CN∥OA,作图痕迹中,弧FG是( )
(A)以点C为圆心,OD为半径的弧
(B)以点C为圆心,DM为半径的弧
(C)以点E为圆心,OD为半径的弧
(D)以点E为圆心,DM为半径的弧
3.只用无刻度直尺就能作出的是( )
(A)延长线段AB至C,使BC=AB
(B)过直线l上一点A作l的垂线
(C)作已知角的平分线
(D)从点O再经过点P作射线OP
二、填空题(每小题4分,共12分)
4.尺规作图的画图工具是_____.
5.如图所示,求作一个角等于已知角∠AOB.
作法:(1)作射线_____.
(2)以_____为圆心,以_____为半径画弧,交OA于点C,交OB于点D.
(3)以_____为圆心,以_____为半径画弧,交O ′B ′于点D ′.
(4)以点D ′为圆心,以_____为半径画弧,交前面的弧于点C ′.
(5)过_____作射线O ′A ′.∠A ′O ′B ′就是所求作的角.
6.画线段AB;延长线段AB到点C,使BC=2AB;反向延长线段AB到点D,使AD=AC,则线段CD=_____AB.
三、解答题(共26分)
7.(8分) 已知,如图,∠AOB及其两边上的点C,D,过点C作CE∥OB,过点D作DF∥OA,使CE,
- 2 -
DF交于点P.
8.(8分)已知:线段a,∠α,∠β.
求作:作一个三角形,使其两角分别等于∠α,∠β,且两角所夹的边长为a.
【拓展延伸】
9.(10分)已知:线段a,如图,直线AB与CD相交于点O.利用尺规,按下
列要求作图:
(1)在射线OA,OB,OC,OD上作线段OA′,OB′,
OC′,OD′,使它们都与线段a相等.
(2)依次连接A′,C′,B′,D′,A′.你会得到一个什么图形?
答案解析
1.【解析】选B.尺规作图中的直尺不含单位长度和角度,不能用直尺作直角,直尺的功能是作直线、射线或
线段.
2.【解析】选D.根据尺规作图中作一个角等于已知角的作图方法,可知D正确.
3.【解析】选D.使用的是无刻度的直尺,作图时不能作出BC=AB,所以A不能选;过直线l上一点A作
l的垂线时,要有直角三角板或量角器、圆规,只用直尺是不能作出垂线的,所以不能选B;作已知角的
平分线,需用圆规,只用直尺是作不出角平分线的,所以不能选C;从点O再经过点P作射线OP,可以
只用无刻度直尺就能作出,故选D.
4.【解析】尺规作图的画图工具是没有刻度的直尺和圆规.
答案:没有刻度的直尺和圆规
5.【解析】(1)作射线O ′B ′.
(2)以点O为圆心,以任意长为半径画弧,交OA于点C,交OB于点D.
(3)以点O′为圆心,以线段OD的长为半径画弧,交O′B′于点D′.
(4)以点D′为圆心,以线段CD的长为半径画弧,交前面的弧于点C′.
(5)过点C′作射线O′A′.∠A′O′B′就是所求作的角.
- 3 -
答案:(1)O ′B ′ (2)点O 任意长
(3)点O′ 线段OD的长
(4)线段CD的长 (5)点C′
6.【解析】此题要先根据题意画出图形,
如图,设AB=x,则BC=2x,AC=AD=3x,
所以CD=AC+AD=6x,所以CD=6AB.
答案:6
7.【解析】在图中作∠ACE=∠O,∠BDF=∠O即可,作图痕迹略.
【归纳整合】要过C,D两点作OB和OA的平行线,根据平行线的条件可知:同位角相等,两直线平行.
所以分别作∠ACE=∠O;∠BDF=∠O即可.本题体现了数学知识的应用理念,基本作图的目的是培养学生
综合画图的能力.
8.【解析】作法:①作线段AB=a;②过点A作∠CAB=∠α,过点B作∠CBA=∠β,两边交于点C.则△ABC
就是要求作的图形.
9.【解析】(1)如图,
- 4 -
(2)长方形.
