工程力学第11讲 拉压：许用应力与强度条件
合集下载
轴向拉压应力与力学性能
2
s max = s a =0 = s 0 s0 t max = s a =45 =
2
圣维南原理
杆端应力分布
应力均匀区
圣维南原理 “ 力作用于杆端的分布 方式，只影响杆端局部范围 的应力分布，影响区约距杆 端 1~2 倍杆的横向尺寸”
（杆端镶入底座, 横向变形受阻）
例 题
例1
已知：F = 50 kN，A = 400 mm2 试求： 截面 m-m 上的应力
s ts s cs
愈压愈扁
灰口铸铁压缩
s cb= 3~4s tb
断口与轴线约成45o
温度对力学性能的影响
钢的强度、塑性随温度变化的关系
钢的弹性常数随温度变化的关系
E E,G/GPa
G
T/C
世贸中心塌毁
（点击画面，可重复点击）
大厦受撞击后，为什麽沿铅垂方向塌毁 ？
据分析，由于大量飞机燃油燃烧，温度高达1200 C，组 成大楼结构的钢材强度急剧降低，致使大厦铅垂塌毁
横截面上 的正应力 均匀分布
横截面间 的纤维变 形相同
斜截面间 的纤维变 形相同
斜截面上 的应力均 匀分布
2. 应力 pa
A Fx = 0, pa cosa F = 0
Fcosa pa = = s 0cosa A
3. 应力sa 、ta与最大应力
s a = pa cosa = s 0cos 2a s0 t a = pa sina = sin2a
切应变概念
切应变（shear strain）定义 微体相邻棱边所夹直 角的改变量 g ，称为 切应变（剪应变） 切应变为无量纲量 切应变单位为 rad
例 题
例2 解：
s max = s a =0 = s 0 s0 t max = s a =45 =
2
圣维南原理
杆端应力分布
应力均匀区
圣维南原理 “ 力作用于杆端的分布 方式，只影响杆端局部范围 的应力分布，影响区约距杆 端 1~2 倍杆的横向尺寸”
（杆端镶入底座, 横向变形受阻）
例 题
例1
已知：F = 50 kN，A = 400 mm2 试求： 截面 m-m 上的应力
s ts s cs
愈压愈扁
灰口铸铁压缩
s cb= 3~4s tb
断口与轴线约成45o
温度对力学性能的影响
钢的强度、塑性随温度变化的关系
钢的弹性常数随温度变化的关系
E E,G/GPa
G
T/C
世贸中心塌毁
（点击画面，可重复点击）
大厦受撞击后，为什麽沿铅垂方向塌毁 ？
据分析，由于大量飞机燃油燃烧，温度高达1200 C，组 成大楼结构的钢材强度急剧降低，致使大厦铅垂塌毁
横截面上 的正应力 均匀分布
横截面间 的纤维变 形相同
斜截面间 的纤维变 形相同
斜截面上 的应力均 匀分布
2. 应力 pa
A Fx = 0, pa cosa F = 0
Fcosa pa = = s 0cosa A
3. 应力sa 、ta与最大应力
s a = pa cosa = s 0cos 2a s0 t a = pa sina = sin2a
切应变概念
切应变（shear strain）定义 微体相邻棱边所夹直 角的改变量 g ，称为 切应变（剪应变） 切应变为无量纲量 切应变单位为 rad
例 题
例2 解：
工程力学第十一章 组合变形
土建工程中的混凝土或砖、石偏心受压柱，往往不 允许横截面上出现拉应力。这就是要求偏心压力只能作 用在横截面形心附近的截面核心内。
要使偏心压力作用下杆件横截面上不出现拉应力， 那么中性轴就不能与横截面相交，一般情况下充其量只能 与横截面的周边相切，而在截面的凹入部分则是与周边外 接。截面核心的边界正是利用中性轴与周边相切和外接时 偏心压力作用点的位置来确定的。
解：拉扭组合:
7kNm T
50kN FN
安全
例11-8 直径为d的实心圆轴，
·B
P 若m=Pd，指出危险点的位置， 并写出相当应力 。
x
m
解：偏拉与扭转组合
z
C P P 例11-9 图示折角CAB，ABC段直径
d=60mm，L=90mm，P=6kN，[σ]＝
BA
60MPa，试用第三强度理论校核轴 x AB的强度。
例11-6 图示圆轴.已知,F=8kN,Me=3kNm,［σ］=100MPa, 试用第三强度理论求轴的最小直径.
解：(1) 内力分析
4kNm M
3kNm T
(2)应力分析
例11-7 直径为d=0.1m的圆杆受力如图，T=7kNm，P=50kN， []=100MPa，试按第三强度理论校核此杆的强度。
至于发生弯曲与压缩组合变形的杆件，轴向压力 引起的附加弯矩与横向力产生的弯矩为同向，故只有 杆的弯曲刚度相当大（大刚度杆）且在线弹性范围内 工作时才可应用叠加原理。
A M
F FN
+ ql2/8
+
B
+
=
C 10kN
A 1.6m
1.6m
10kN
1.2m
例11-3 两根无缝钢管焊接 而成的折杆。钢管外径 D=140mm，壁厚t=10mm。求 危险截面上的最大拉应力和 B 最大压应力。
结构力学 拉压 课件
31
目录
低碳钢的 20 — 30% 60% 为塑性材料
§2-4 材料拉伸时的力学性质
三 卸载定律及冷作硬化
e P
d
e
b
f
即材料在卸载过程中 应力和应变是线形关系， 这就是卸载定律。
b
a c
s
材料的比例极限增高， 延伸率降低，称之为冷作硬 化或加工硬化。
f h
o
d g
目录
3
目录
§2-1
概述
4
§2-1
目录
§2-1
概述
5
目录
§2-1
概述
6
目录
§2-1
概述
7
目录
§2-1
概述
8
目录
§2-1
概述
特点：
作用在杆件上的外力合力的作用线与 杆件轴线重合，杆件变形是沿轴线方向的伸 长或缩短。
杆的受力简图为 拉伸
F
压缩
F F
F
9
目录
§2-1
概述
10
目录
§2-2 轴力和轴力图
厦门理工学院土木工程与建筑系 陈昌萍
Email: cpchen@
1
第二章
拉伸与压缩
2
目录
第二章
•§2-1 •§2-2
轴向拉伸与压缩
概 轴 力 和 轴 述 力 图
•§2-3 •§2-4
•§2-5 •§2-6 •§2-7 •§2-8 •§2-9
截
面
上
的
应
力
材料拉伸时的力学性质
材料压缩时的力学性质 拉 压 杆 的 强 度 条 件 拉压杆的变形 胡克定律 拉、 压 超 静 定 问 题 应 力 集 中 的 概 念
目录
低碳钢的 20 — 30% 60% 为塑性材料
§2-4 材料拉伸时的力学性质
三 卸载定律及冷作硬化
e P
d
e
b
f
即材料在卸载过程中 应力和应变是线形关系， 这就是卸载定律。
b
a c
s
材料的比例极限增高， 延伸率降低，称之为冷作硬 化或加工硬化。
f h
o
d g
目录
3
目录
§2-1
概述
4
§2-1
目录
§2-1
概述
5
目录
§2-1
概述
6
目录
§2-1
概述
7
目录
§2-1
概述
8
目录
§2-1
概述
特点：
作用在杆件上的外力合力的作用线与 杆件轴线重合，杆件变形是沿轴线方向的伸 长或缩短。
杆的受力简图为 拉伸
F
压缩
F F
F
9
目录
§2-1
概述
10
目录
§2-2 轴力和轴力图
厦门理工学院土木工程与建筑系 陈昌萍
Email: cpchen@
1
第二章
拉伸与压缩
2
目录
第二章
•§2-1 •§2-2
轴向拉伸与压缩
概 轴 力 和 轴 述 力 图
•§2-3 •§2-4
•§2-5 •§2-6 •§2-7 •§2-8 •§2-9
截
面
上
的
应
力
材料拉伸时的力学性质
材料压缩时的力学性质 拉 压 杆 的 强 度 条 件 拉压杆的变形 胡克定律 拉、 压 超 静 定 问 题 应 力 集 中 的 概 念
工程力学第十一章
11.5 压杆的稳定计算
与强度设计一样，在压杆稳定 设计时，同样需要留有保证杆 的稳定性的安全储备。
稳定性条件：
引入稳定许用安全系数nst，则许用压力为 [Fst]=Fcr/nst，稳定性条件是
或
第11章 压杆稳定
承受轴向压力的杆，称为压杆。对 于一些受轴向压力作用的细长杆， 在满足强度条件的情况下，却会出 现弯曲变形。杆在轴向载荷作用下 发生的弯曲，称为屈曲，构件由屈 曲引起的失效，称为失稳(丧失稳定 性)。本章研究细长压杆的稳定。
11.1 稳定的概念
物体的平衡存在有稳定与不稳定的问 题。物体的平衡受到外界干扰后，将 会偏离平衡状态。若在外界的微小干 扰消除后，物体能恢复原来的平衡状 态，则称该平衡是稳定；若在外界的 微小干扰消除后，物体仍不能恢复原 来的平衡状态，则称该平衡是不稳定 的。
直杆在轴向载荷作用下发生的弯 曲称为屈曲，发生了屈曲就意味 着构件失去稳定(失稳)。压杆保持 稳定与发生屈曲间的力Fcr称为压 杆的临界载荷或临界压力。
11.2 两端铰支细长压杆的 临界载荷
二端铰支压杆稳定临界载荷的欧拉公式
欧拉公式指出：压杆稳定的临界载荷与杆长 的平方成反比，与杆的抗弯刚度成正比。
不同支承情况下，用欧拉公式的一般形式确 定临界载荷时的相当长度系数μ为：
μ=1
二端铰支
μ固定
μ=0.5 二端固定
可见，杆端支承对于压杆的临界载荷有显著 影响。
11.4 中小柔度杆的临界应力
11.4.1 临界应力与杆的柔度
压杆的柔度或细长比
11.4.2 临界应力总图
λ>λP的杆，称为大柔度杆，前面讨论中的 所说的细长杆，就是指大柔度杆，其破坏 形式是弹性屈曲失稳，临界应力可由欧拉 公式确定。
拉伸和压缩
解 （1）计算AB杆和BC杆的轴力
d
A
B
30
取结点B为研究对象，其受力如图所示。由 平衡方程
Fx 0, FNBC cos 30 FNAB 0
Fy 0, FNBC sin 30 F 0
C aa FNAB
F
B AB
FNAB
3F，FNBC
2F
（2）校核AB杆和BC杆的强度
FNAB AAB
3F d2 /4
3
二、内力与应力
1、内力
杆件在外力作用下产生变形，其内部相互间的 作用力称为内力。这种内力将随外力增加而增 大。当内力增大到一定限度时，杆件就会发生 破坏。内力是与构件的强度密切相关的，拉压
杆上的内力又称为轴力。
F
FN
2、求内力的方法—截面法
将受外力作用的杆件假想地 切开，用以显示内力的大 小，并以平衡条件确定其 合力的方法，称为截面法。 它是分析杆件内力的唯一 方法。具体求法如下：
例 图示支架中，杆①的许用应力[]1＝100MPa，杆②的许用 应力[]2＝160MPa，两杆的面积均为A=200mm2,求结构的许
可载荷[F]。
解 （1）计算AC杆和BC杆的轴力
B 取C铰为研究对象，受力如图所示。列平衡
方程
A ① 45 30 ②
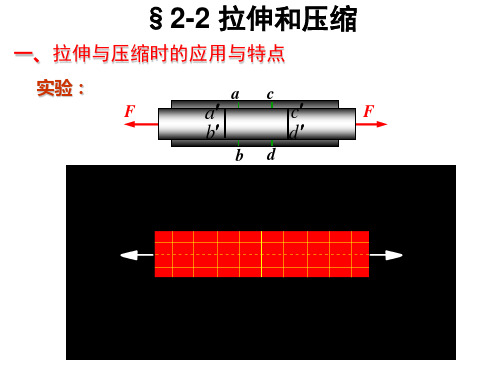
§2-2 拉伸和压缩
一、拉伸与压缩时的应用与特点
实验：
F
ac
a
c
F
b
d
bd
1.变形现象
横向线ab和cd仍为直线，且仍然垂直于轴线;
结论：各纤维的伸长相同，所以它们所受的力 也相同。 2.平面假设
变形前原为平面的横截面，在变形后仍保
持为平面，且仍垂直于轴线。
第11、12章 材料力学的基本概念和杆件拉压
18 §9-2
目录
A
1 B
1 F2
2 C
2
3 D
例题
F1
F1 F1
F3 3
FN2
F4
FN1 F2
10
已知F1=10kN；F2=20kN； F3=35kN；F4=25kN;试画 出图示杆件的轴力图。 解：1、计算各段的轴力。
AB段
0 FN1 F1 10kN
x x
F
FN3
FN kN
25
F4
BC段
x
F
0 FN 2 F2 F1
FN 2 F1 F2
10
CD段
10 20 10kN Fx 0
FN 3 F4 25kN
2、绘制轴力图。
19
练习 一等直杆及受力情况如图（a）所示，试作杆的轴 力图。如何调整外力，使杆上轴力分布得比较合理。
F
F
F
F
F
F
拉杆
压杆
16
二、拉压杆的轴力及轴力图
1、轴力：横截面上的内力
m F m F FN FN F
F
2、截面法求轴力 截: 假想沿m-m横截面将杆切开
取: 留下左半段或右半段
代: 将抛掉部分对留下部分的作 用用内力代替 平: 对留下部分写平衡方程求出 内力即轴力的值
F
x
0 FN F 0 FN F
F m F FN
F
4）平——对保留段列平衡方程 ，即可求得相应的内力。
F
x
0
FN F 0
FN F
11
§11、12-2 轴向拉伸与压缩内力计算
§9-1
目录
A
1 B
1 F2
2 C
2
3 D
例题
F1
F1 F1
F3 3
FN2
F4
FN1 F2
10
已知F1=10kN；F2=20kN； F3=35kN；F4=25kN;试画 出图示杆件的轴力图。 解：1、计算各段的轴力。
AB段
0 FN1 F1 10kN
x x
F
FN3
FN kN
25
F4
BC段
x
F
0 FN 2 F2 F1
FN 2 F1 F2
10
CD段
10 20 10kN Fx 0
FN 3 F4 25kN
2、绘制轴力图。
19
练习 一等直杆及受力情况如图（a）所示，试作杆的轴 力图。如何调整外力，使杆上轴力分布得比较合理。
F
F
F
F
F
F
拉杆
压杆
16
二、拉压杆的轴力及轴力图
1、轴力：横截面上的内力
m F m F FN FN F
F
2、截面法求轴力 截: 假想沿m-m横截面将杆切开
取: 留下左半段或右半段
代: 将抛掉部分对留下部分的作 用用内力代替 平: 对留下部分写平衡方程求出 内力即轴力的值
F
x
0 FN F 0 FN F
F m F FN
F
4）平——对保留段列平衡方程 ，即可求得相应的内力。
F
x
0
FN F 0
FN F
11
§11、12-2 轴向拉伸与压缩内力计算
§9-1
《材料力学》课件2-7强度条件.安全因数.许用应力
多尺度分析
随着科学技术的发展，材料力学的尺度效应越来越受到关 注。强度理论正朝着多尺度方向发展，以更好地描述不同 尺度下材料的力学行为。
非线性分析
随着复杂载荷和极端环境的应用，材料的非线性行为越来 越突出。强度理论正朝着非线性方向发展，以更好地描述 材料的复杂力学行为。
智能化分析
随着人工智能和大数据技术的应用，强度理论的智能化分 析成为新的发展趋势。通过数据挖掘和机器学习等技术， 实现对材料力学行为的智能预测和优化。
在土木工程中，安全因数 用于评估结构的稳定性和 安全性。
安全因数还可以用于评估 现有结构的剩余寿命和可 靠性。
03
许用应力
许用应力的定义
许用应力是指在一定条件下，材料能 够承受的最大应力，以保证结构在使 用过程中的安全性和可靠性。
它通常由材料的机械性能和结构的使 用条件共同决定，是结构设计时的一 个重要参数。
通过应用材料力学，工程师 可以预测结构在各种载荷下 的响应，从而预防潜在的失 效模式。
尽管材料力学在许多情况下 都能提供有用的指导，但它 也有局限性。例如，它通常 不能考虑非线性行为、疲劳 、磨损等复杂因素。因此， 在某些情况下，可能需要更 详细和专业的分析方法。
05
强度理论的应用和发展趋 势
强度理论的应用
土木工程
在土木工程中，强度条件用于评估桥梁、房屋、道路等结构的安全性和稳定性。通过满足 强度条件，可以确保结构在使用过程中不会发生破坏或过度的变形。
航空航天
在航空航天领域，由于对安全性和可靠性的要求极高，强度条件的应用尤为重要。飞机和 航天器的结构和零部件需要进行严格的强度分析和测试，以确保在各种极端条件下都能保 持安全和稳定。
1 2
机械设计
拉伸、压缩时的强度条件_汽车机械基础（第2版）_[共2页]
汽车机械基础（第2版）（附微课视频） 30 正比。
五、许用应力通过前面分析可知，拉（压）杆横截面上的正应力N A σ=。
此应力称为工作应力，是拉（压）杆工作时由载荷引起的应力。
构件材料所允许承受的应力是有一定限度的，超过某一限度，构件就不能正常工作，甚至破坏，我们把构件材料在保证安全工作的条件下允许承受的最大应力，称为许用应力，用[σ ]（表示许用拉、压应力）、[τ ]（表示许用切应力）表示。
许用应力是通过对材料进行试验和考虑各有关因素来确定的。
为了保证构件正常的工作，一般不允许它在受力后发生断裂或者发生过量的塑性变形。
所以我们不能将材料破坏时的极限应力作为许用应力。
同时还要考虑到外力计算的误差和工作中可能出现超负荷等情况，故一般只能取极限应力的几分之一作为许用应力。
具体许用应力值可查阅有关手册。
塑性材料的许用应力 []s n σσ= （2-5） 脆性材料的许用应力 []b nσσ= （2-6） 式中，σs —塑性材料的屈服点应力；σb —脆性材料的强度极限应力；n —安全系数，它反映了构件必要的强度储备。
在工程实际中，静载时塑性材料一般取n = 1.2～2.5，脆性材料一般取n = 2～3.5。
安全系数也反映了经济与安全之间的矛盾关系。
取值过大，许用应力过低，造成材料浪费。
反之，取值过小，安全得不到保证。
六、拉伸、压缩时的强度条件为保证构件安全可靠的正常工作，必须使构件最大工作应力不超过材料的许用应力[σ ]，即 []max N A σσ=≤ （2-7） 式中，σmax —拉、压时，构件的最大工作应力；[σ ]—材料的许用应力。
式（2-7）称为拉伸或压缩的强度条件。
利用强度条件可进行以下3类运算。
（1）强度校核。
当已知杆件的截面面积A 、材料的许用应力[σ ]，以及所受的载荷F N ，即可以用强度条件判断杆件是否能够安全工作，即N []F Aσσ=≤。
（2）选择截面尺寸。
若已知杆件所受载荷和所用材料，根据强度条件，可以确定该杆件所需的横截面面积，其值A ≥F N /[σ ]。
轴向拉压应力与力学性能
大厦受撞击后，为什麽沿铅垂方向塌毁 ？
据分析，由于大量飞机燃油燃烧，温度高达1200 C，组 成大楼结构的钢材强度急剧降低，致使大厦铅垂塌毁
§6 应力集中与材料疲劳
应力集中概念 交变应力与材料疲劳概念
应力集中对构件强度的影响
应力集中概念
应力集中 由于截面急剧变化引起应力局部增大现象
解：1. 接头受力分析
当各铆钉的材料与直径均相同，且外力作用线在
铆钉群剪切面上的投影，通过铆钉群剪切面形心时， 通常即认为各铆钉剪切面上的剪力相等
2. 强度校核
剪切强度：
FS 4FS F 99.5 MPa < [ ] 2 2 πd πd F 4
挤压强度：
bs
Fb FS 125 MPa < [ bs ] d d
轴力
轴力定义：通过截面形心并沿杆件轴线的内力 符号规定：拉力为正,压力为负
轴力计算
试分析杆的轴力 （F1=F，F2=2F）
FR F2 F1 F
AB 段： FN1 F
BC 段： FN2 F 0
FN2 F
要点：逐段分析轴力；设正法求轴力
轴力图
FN1 F
2
max a 0 0 0 max a 45
2
圣维南原理
杆端应力分布
应力均匀区
圣维南原理 “ 力作用于杆端的分布 方式，只影响杆端局部范围 的应力分布，影响区约距杆 端 1~2 倍杆的横向尺寸”
（杆端镶入底座, 横向变形受阻）
例 题
例1
已知：F = 50 kN，A = 400 mm2 试求： 截面 m-m 上的应力
材料力学(拉压、剪切、扭转、弯曲)
拉伸实验
实验结果观察：
① 纵向线伸长、横向线缩短； ② 横向线保持直线，仍与纵向线垂直； ③ 每根纵向线的伸长都相等。
天津大学材料力学
平截面假设
轴向拉、压杆件，变形前原为平面的横截面，变形后仍保 持为平面，且仍垂直于轴线。
横截面上应力均匀分布
FN
FN
A
正应力（法向应力）：沿截面法线方向。
天津大学材料力学
天津大学材料力学
§1.4 工程材料的力学性能简介
工程材料的力学性能指标要通过实验测定。 影响工程材料力学性能的因素
与材料的成份、组织结构密切相关的，同时还与工作 条件，如受力方式，加载速度，工作温度等因素有关。 在常温、静载（缓慢加载）下的力学行为。 构件变形包括——弹性变形、塑性变形 根据材料破坏前产生的塑性变形的大小，将材料分为
2F
F
A
D
FN图：
120 kN
2F
F
C B
60 kN
60 kN
天津大学材料力学
解： 1．确定杆各段的轴力。
2．计算杆各段的应力
AD段：
AD
FNAD A1
FNAD
π
d
2 1
4
4 120 103 π 402 106
95.5M Pa
BC段：
BC
FNBC A2
FNBC
π
d
2 2
4
4 60 103 π 202 106
0 .7 2 m m
LBC
FNBC LBC E A2
4 60 103 2 π 202 106 200 109
1.91m m
3．计算杆的总变形
LAC LAD LDB LBC 1.91 0.48 0.72 0.71m m
实验结果观察：
① 纵向线伸长、横向线缩短； ② 横向线保持直线，仍与纵向线垂直； ③ 每根纵向线的伸长都相等。
天津大学材料力学
平截面假设
轴向拉、压杆件，变形前原为平面的横截面，变形后仍保 持为平面，且仍垂直于轴线。
横截面上应力均匀分布
FN
FN
A
正应力（法向应力）：沿截面法线方向。
天津大学材料力学
天津大学材料力学
§1.4 工程材料的力学性能简介
工程材料的力学性能指标要通过实验测定。 影响工程材料力学性能的因素
与材料的成份、组织结构密切相关的，同时还与工作 条件，如受力方式，加载速度，工作温度等因素有关。 在常温、静载（缓慢加载）下的力学行为。 构件变形包括——弹性变形、塑性变形 根据材料破坏前产生的塑性变形的大小，将材料分为
2F
F
A
D
FN图：
120 kN
2F
F
C B
60 kN
60 kN
天津大学材料力学
解： 1．确定杆各段的轴力。
2．计算杆各段的应力
AD段：
AD
FNAD A1
FNAD
π
d
2 1
4
4 120 103 π 402 106
95.5M Pa
BC段：
BC
FNBC A2
FNBC
π
d
2 2
4
4 60 103 π 202 106
0 .7 2 m m
LBC
FNBC LBC E A2
4 60 103 2 π 202 106 200 109
1.91m m
3．计算杆的总变形
LAC LAD LDB LBC 1.91 0.48 0.72 0.71m m