计量经济学:时间序列模型习题与解析
伍德里奇《计量经济学导论》(第5版)笔记和课后习题详解-第11章 OLS用于时间序列数据的其他问题【

第11章OLS 用于时间序列数据的其他问题11.1复习笔记一、平稳和弱相关时间序列1.平稳和非平稳时间序列平稳时间序列过程,就是概率分布在如下意义上跨时期稳定的时间序列过程:如果从这个序列中任取一个随机变量集,并把这个序列向前移动h 个时期,那么其联合概率分布仍然保持不变。
(1)平稳随机过程对于随机过程{ 1 2 }t x t =:,,…,如果对于每一个时间指标集121m t t t ≤<<⋅⋅⋅<和任意整数h≥1,()12m t t t x x x ⋅⋅⋅,,,的联合分布都与()12 m t h t h t h x x x ++⋅⋅⋅+,,,的联合分布相同,那么这个随机过程就是平稳的。
这种平稳经常称为严平稳,它是从概率分布的角度去定义的。
其含义之一是(取m=1和t 1=1):对所有t=2,3,…,x 1与x t 都有相同的分布。
序列{ 1 2 }t x t =:,,…是同分布的。
不平稳的随机过程称为非平稳过程。
因为平稳性是潜在随机过程而非其某单个实现的性质,所以很难判断所搜集到的数据是否由一个平稳过程生成。
但是,要指出某些序列不是平稳的却很容易。
(2)协方差平稳过程(宽平稳,弱平稳)对于一个具有有限二阶矩()2t E x ⎡⎤∞⎣⎦<的随机过程{ 1 2 }t x t =:,,…,若:(i)E(x t )为常数;(ii)Var(x t )为常数;(iii)对任何t,h≥1,Cov(x t ,x t+h )仅取决于h,而不取决于t,那它就是协方差平稳的。
协方差平稳只考虑随机过程的前两阶矩:这个过程的均值和方差不随着时间而变化,而且,x t 和x t+h 的协方差只取决于这两项之间的距离h,与起始时期t 的位置无关。
由此立即可知x t 与x t+h 之间的相关性也只取决于h。
如果一个平稳过程具有有限二阶矩,那么它一定是协方差平稳的,但反过来未必正确。
由于严平稳的条件比较苛刻,在实际中从概率分布的角度去验证是无法实现的,所以在实际运用中所指的平稳都是指宽平稳,即协方差平稳。
(李子奈计量经济学配套课件)2.5 实例:时间序列(Eviews简介)

采用Eviews软件 软件进行回归分析的结果见下表 软件
的回归( 表 2.5.2 中国居民人均消费支出对人均 GDP 的回归(1978~2000) ) LS // Dependent Variable is CONSP Sample: 1978 2000 Included observations: 23 Variable C GDPP1 Coefficient 201.1071 0.386187 Std. Error 14.88514 0.007222 t-Statistic 13.51060 53.47182 Prob. 0.0000 0.0000 905.3331 380.6428 7.092079 7.190818 2859.235 0.000000
R-squared 0.992709 Adjusted R-squared 0.992362 S.E. of regression 33.26711 Sum squared resid 23240.71 Log likelihood -112.1945 Durbin-Watson stat 0.550288
表 2.5.1 中国居民人均消费支出与人均 GDP(元 /人) ( 人 年份 人均居民消费 CONSP 395.8 437.0 464.1 501.9 533.5 572.8 635.6 716.0 746.5 788.3 836.4 779.7 人均GDP GDPP 675.1 716.9 763.7 792.4 851.1 931.4 1059.2 1185.2 1269.6 1393.6 1527.0 1565.9 年份 人均居民消费 CONSP 797.1 861.4 966.6 1048.6 1108.7 1213.1 1322.8 1380.9 1460.6 1564.4 1690.8 人均GDP GDPP 1602.3 1727.2 1949.8 2187.9 2436.1 2663.7 2889.1 3111.9 3323.1 3529.3 3789.7
时间序列计量经济学模型

时间序列计量经济学模型经济分析中所用到的三大类重要数据中,时间序列数据是其中最常见,也是最重要的一类数据。
迄今为止,对时间序列的分析是通过建立因果关系为基础的结构模型。
时间序列模型反映动态特征,通常是运用时间序列的过去值、当期值及滞后扰动项的加权和建立模型来“解释”时间序列的变化规律。
时间序列资料具有相关性,大部分资料具有非平稳性,而无论是单方程计量经济学模型还是联立方程计量经济学模型,这种分析背后有一个隐含的假设,即这些数据是平稳的(stationary)。
------目录-------一.简介1.时间序列数据处理二.时间序列的平稳性及其检验1.非平稳时间序列简介2.单位根检验3.非平稳时间序列的平稳化三.平稳时间序列模型1.AR(P)过程2.MA(q)过程3.ARIMA模型四.协整与误差修正模型五.条件异方差六.向量自回归模型(VAR)一、简介1时间序列数据的处理1.1cd C:\stata10\Net_course\ B6_TimeS1)声明时间序列:tsset 命令use gnp96.dta, clearlist in 1/20gen Lgnp = L.gnptsset datelist in 1/20gen Lgnp = L.gnp2)检查是否有断点:tsreport, reportuse gnp96.dta, cleartsset datetsreport, reportdrop in 10/10list in 1/12tsreport, reporttsreport, report list /*列出存在断点的样本信息*/3)填充缺漏值:tsfilltsfilltsreport, report listlist in 1/124)追加样本:tsappenduse gnp96.dta, cleartsset datelist in -10/-1sumtsappend , add(5) /*追加5个观察值*/list in -10/-1sum5)应用:样本外预测: predictreg gnp96 L.gnp96predict gnp_hatlist in -10/-16)清除时间标识: tsset, cleartsset, clear1.2变量的生成与处理1)滞后项、超前项和差分项 help tsvarlistuse gnp96.dta, cleartsset dategen Lgnp = L.gnp96 /*一阶滞后*/gen L2gnp = L2.gnp96gen Fgnp = F.gnp96 /*一阶超前*/gen F2gnp = F2.gnp96gen Dgnp = D.gnp96 /*一阶差分*/gen D2gnp = D2.gnp96list in 1/10list in -10/-12)产生增长率变量: 对数差分gen lngnp = ln(gnp96)gen growth = D.lngnpgen growth2 = (gnp96-L.gnp96)/L.gnp96gen diff = growth - growth2 /*表明对数差分和变量的增长率差别很小*/ list date gnp96 lngnp growth* diff in 1/101.3日期的处理日期的格式 help tsfmt基本时点:整数数值,如 -3, -2, -1, 0, 1, 2, 3 .... 1960年1月1日,取值为 0;显示格式:1)使用 tsset 命令指定显示格式use B6_tsset.dta, cleartsset t, dailylistuse B6_tsset.dta, cleartsset t, weeklylist2)指定起始时点cap drop monthgenerate month = m(1990-1) + _n - 1format month %tmlist t month in 1/20cap drop yeargen year = y(1952) + _n - 1format year %tylist t year in 1/203)自己设定不同的显示格式日期的显示格式 %d (%td) 定义如下:%[-][t]d<描述特定的显示格式>具体项目释义:“<描述特定的显示格式>”中可包含如下字母或字符c y m l nd j h q w _ . , : - / ' !cC Y M L ND J W定义如下:c and C 世纪值(个位数不附加/附加0)y and Y 不含世纪值的年份(个位数不附加/附加0)m 三个英文字母的月份简写(第一个字母大写)M 英文字母拼写的月份(第一个字母大写)n and N 数字月份(个位数不附加/附加0)d and D 一个月中的第几日(个位数不附加/附加0)j and J 一年中的第几日(个位数不附加/附加0)h 一年中的第几半年 (1 or 2)q 一年中的第几季度 (1, 2, 3, or 4)w and W 一年中的第几周(个位数不附加/附加0)_ display a blank (空格). display a period(句号), display a comma(逗号): display a colon(冒号)- display a dash (短线)/ display a slash(斜线)' display a close single quote(右引号)!c display character c (code !! to display an exclamation point)样式1:Format Sample date in format-----------------------------------%td 07jul1948%tdM_d,_CY July 7, 1948%tdY/M/D 48/07/11%tdM-D-CY 07-11-1948%tqCY.q 1999.2%tqCY:q 1992:2%twCY,_w 2010, 48-----------------------------------样式2:Format Sample date in format----------------------------------%d 11jul1948%dDlCY 11jul1948%dDlY 11jul48%dM_d,_CY July 11, 1948%dd_M_CY 11 July 1948%dN/D/Y 07/11/48%dD/N/Y 11/07/48%dY/N/D 48/07/11%dN-D-CY 07-11-1948----------------------------------clearset obs 100gen t = _n + d(13feb1978)list t in 1/5format t %dCY-N-D /*1978-02-14*/list t in 1/5format t %dcy_n_d /*1978 2 14*/list t in 1/5use B6_tsset, clearlisttsset t, format(%twCY-m)list4)一个实例:生成连续的时间变量use e1920.dta, clearlist year month in 1/30sort year monthgen time = _ntsset timelist year month time in 1/30generate newmonth = m(1920-1) + time - 1 tsset newmonth, monthlylist year month time newmonth in 1/301.4图解时间序列1)例1:clearset seed 13579113sim_arma ar2, ar(0.7 0.2) nobs(200)sim_arma ma2, ma(0.7 0.2)tsset _ttsline ar2 ma2* 亦可采用 twoway line 命令绘制,但较为繁琐twoway line ar2 ma2 _t2)例2:增加文字标注sysuse tsline2, cleartsset daytsline calories, ttick(28nov2002 25dec2002, tpos(in)) ///ttext(3470 28nov2002 "thanks" ///3470 25dec2002 "x-mas", orient(vert))3)例3:增加两条纵向的标示线sysuse tsline2, cleartsset daytsline calories, tline(28nov2002 25dec2002)* 或采用 twoway line 命令local d1 = d(28nov2002)local d2 = d(25dec2002)line calories day, xline(`d1' `d2')4)例4:改变标签tsline calories, tlabel(, format(%tdmd)) ttitle("Date (2002)")tsline calories, tlabel(, format(%td))二、时间序列的平稳性及其检验时间序列分析中首先遇到的问题是关于时间序列数据的平稳性问题,假定某个时间序列是由某一个随机过程(stochastic process)生成的,即假定时间序列{X_t}(t=1,2,3…)的每一个数值都是从一个概率分布中随机得到,如果X_T满足下列条件:(1)均值E(X_t)=μ,与时间t无关的常数;(2)方差Var(X_t)=б^2,与时间t无关;(3)协方差Cov(X_t X_t+k)只与时期间隔k有关,与时间t无关的常数。
时间序列分析与预测课后习题答案

22 7336 18 0766 20 2040
第八章 时间序列分析与预测
练习题第五题答案
2000
季度 销售量
长期趋势
一季度 13 1
9 3324
二季度 13 9
9 9722
三季度 79
10 6121
四季度 86
11 2519
2001
Y/T 销售量 长期趋势
1 4037 10 8
11 8918
1 3939 11 5
9
2 10
10
2 50
Y 1 1 = 0 . 3 6 5 3 3 3 + 0 . 1 9 2 6 4 8 1 1 = 2 . 4 8 6 6 6 7
2024/1/18
第八章 时间序列分析与预测
练习题第五题
某县2000—2003年各季度鲜蛋销售量如表所示单位:万公斤 1用移动平均法消除季节变动 2拟合线性模型测定长期趋势 3预测2004年各季度鲜蛋销售量
13 95 0 987174
2024/1/18
第八章 时间序列分析与预测
练习题第五题答案
2用线形趋势模型法测定时间序列的长期趋势
年份 2000 2001 2002 2003
季度 一 二 三 四 一 二 三 四 一 二 三 四 一 二 三 四
2024/1/18
销售量
13 1 13 9
t 1 3 6 , t= 8 .5 , t2 = 1 4 9 6
0 9177 17 5
15 0910 1 1596
20 0 17 6504 1 1331 1 1511 1 1472 20 2099
0 7364 16 0
15 7309 1 0171
16 9 18 2903 0 9240 0 8555 0 8526 20 8497
伍德里奇《计量经济学导论》(第5版)笔记和课后习题详解-第10章 时间序列数据的基本回归分析【圣才出

第10章时间序列数据的基本回归分析10.1复习笔记一、时间序列数据的性质时间序列数据与横截面数据的区别:(1)时间序列数据集是按照时间顺序排列。
(2)时间序列数据与横截面数据被视为随机结果的原因不同。
①横截面数据应该被视为随机结果,因为从总体中抽取不同的样本,通常会得到自变量和因变量的不同取值。
因此,通过不同的随机样本计算出来的OLS估计值通常也有所不同,这就是OLS统计量是随机变量的原因。
②经济时间序列满足作为随机变量是因为其结果无法事先预知,因此可以被视为随机变量。
一个标有时间脚标的随机变量序列被称为一个随机过程或时间序列过程。
搜集到一个时间序列数据集时,便得到该随机过程的一个可能结果或实现。
因为不能让时间倒转重新开始这个过程,所以只能看到一个实现。
如果特定历史条件有所不同,通常会得到这个随机过程的另一种不同的实现,这正是时间序列数据被看成随机变量之结果的原因。
(3)一个时间序列过程的所有可能的实现集,便相当于横截面分析中的总体。
时间序列数据集的样本容量就是所观察变量的时期数。
二、时间序列回归模型的例子1.静态模型假使有两个变量的时间序列数据,并对y t和z t标注相同的时期。
把y和z联系起来的一个静态模型(staticmodel)为:10 1 2 t t t y z u t nββ=++=⋯,,,,“静态模型”的名称来源于正在模型化y 和z 同期关系的事实。
若认为z 在时间t 的一个变化对y 有影响,即1t t y z β∆=∆,那么可以将y 和z 设定为一个静态模型。
一个静态模型的例子是静态菲利普斯曲线。
在一个静态回归模型中也可以有几个解释变量。
2.有限分布滞后模型(1)有限分布滞后模型有限分布滞后模型(finitedistributedlagmodel,FDL)是指一个或多个变量对y 的影响有一定时滞的模型。
考察如下模型:001122t t t t ty z z z u αδδδ--=++++它是一个二阶FDL。
时间序列计量经济学模型案例(宁大刘慧宏)讲解
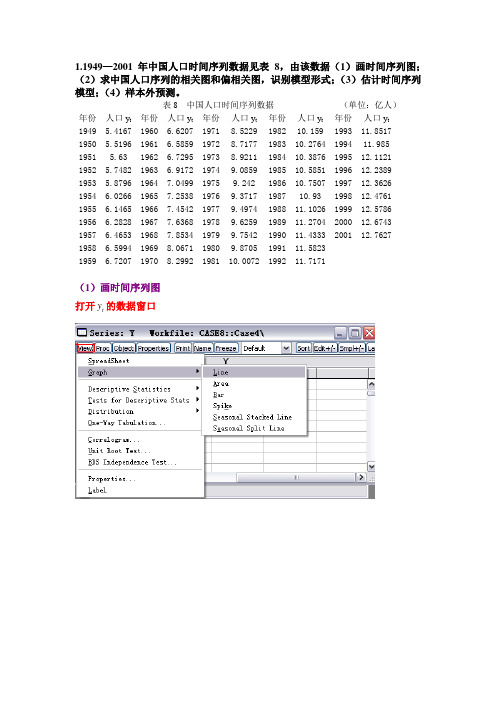
1.1949—2001年中国人口时间序列数据见表8,由该数据(1)画时间序列图;(2)求中国人口序列的相关图和偏相关图,识别模型形式;(3)估计时间序列模型;(4)样本外预测。
表8 中国人口时间序列数据(单位:亿人)年份人口y t年份人口y t年份人口y t年份人口y t年份人口y t1949 5.4167 1960 6.6207 1971 8.5229 1982 10.159 1993 11.85171950 5.5196 1961 6.5859 1972 8.7177 1983 10.2764 1994 11.9851951 5.63 1962 6.7295 1973 8.9211 1984 10.3876 1995 12.11211952 5.7482 1963 6.9172 1974 9.0859 1985 10.5851 1996 12.23891953 5.8796 1964 7.0499 1975 9.242 1986 10.7507 1997 12.36261954 6.0266 1965 7.2538 1976 9.3717 1987 10.93 1998 12.47611955 6.1465 1966 7.4542 1977 9.4974 1988 11.1026 1999 12.57861956 6.2828 1967 7.6368 1978 9.6259 1989 11.2704 2000 12.67431957 6.4653 1968 7.8534 1979 9.7542 1990 11.4333 2001 12.76271958 6.5994 1969 8.0671 1980 9.8705 1991 11.58231959 6.7207 1970 8.2992 1981 10.0072 1992 11.7171(1)画时间序列图y的数据窗口打开t求中国人口差分图:从人口序列图和人口差分序列图可以看出我国人口总水平除在1960年和1961年两年出现回落外,其余年份基本上保持线性增长趋势。
时间序列计量经济学模型讲义PPT课件(275页)
3)协方差Cov(Xt,Xt+k)=k 是只与时期间隔k有 关,与时间t 无关的常数;
则称该随机时间序列是平稳的(stationary), 而该随机过程是一平稳随机过程 (stationary stochastic process)。
Xt= 1Xt-1+2Xt-2…+kXt-k 该随机过程平稳性条件将在第二节中介绍。
三、平稳性检验的图示判断
• 给出一个随机时间序列,首先可通过该序列 的时间路径图来粗略地判断它是否是平稳的。
• 一个平稳的时间序列在图形上往往表现出一 种围绕其均值不断波动的过程。
• 而非平稳序列则往往表现出在不同的时间段 具有不同的均值(如持续上升或持续下降)。
易知,随着k的增加,样本自相关函数下 降且趋于零。但从下降速度来看,平稳序列 要比非平稳序列快得多。
rk
rk
1
1
0
k
0
k
(a)
(b)
图9.1.2 平稳时间序列与非平稳时间序列样本相关图
• 注意:
确定样本自相关函数rk某一数值是否足够 接近于0是非常有用的,因为它可检验对应的自 相关函数k的真值是否为0的假设。
该统计量近似地服从自由度为m的2分布 (m为滞后长度)。
因此:如果计算的Q值大于显著性水平为 的临界值,则有1-的把握拒绝所有k(k>0)同 时为0的假设。
例9.1.3: 表9.1.1序列Random1是通过一 随机过程(随机函数)生成的有19个样本的随 机时间序列。
表 9.1.1
一个纯随机序列与随机游走序列的检验
0.059 3.679 4.216 6.300 7.297 11.332 12.058 15.646 17.153 18.010 22.414 22.481 24.288 25.162 26.036 26.240 26.381
计量经济学习题及参考答案解析详细版
计量经济学(第四版)习题参考答案潘省初第一章 绪论试列出计量经济分析的主要步骤。
一般说来,计量经济分析按照以下步骤进行:(1)陈述理论(或假说) (2)建立计量经济模型 (3)收集数据 (4)估计参数 (5)假设检验 (6)预测和政策分析 计量经济模型中为何要包括扰动项?为了使模型更现实,我们有必要在模型中引进扰动项u 来代表所有影响因变量的其它因素,这些因素包括相对而言不重要因而未被引入模型的变量,以及纯粹的随机因素。
什么是时间序列和横截面数据? 试举例说明二者的区别。
时间序列数据是按时间周期(即按固定的时间间隔)收集的数据,如年度或季度的国民生产总值、就业、货币供给、财政赤字或某人一生中每年的收入都是时间序列的例子。
横截面数据是在同一时点收集的不同个体(如个人、公司、国家等)的数据。
如人口普查数据、世界各国2000年国民生产总值、全班学生计量经济学成绩等都是横截面数据的例子。
估计量和估计值有何区别?估计量是指一个公式或方法,它告诉人们怎样用手中样本所提供的信息去估计总体参数。
在一项应用中,依据估计量算出的一个具体的数值,称为估计值。
如Y就是一个估计量,1nii YY n==∑。
现有一样本,共4个数,100,104,96,130,则根据这个样本的数据运用均值估计量得出的均值估计值为5.107413096104100=+++。
第二章 计量经济分析的统计学基础略,参考教材。
请用例中的数据求北京男生平均身高的99%置信区间NS S x ==45= 用=,N-1=15个自由度查表得005.0t =,故99%置信限为x S t X 005.0± =174±×=174±也就是说,根据样本,我们有99%的把握说,北京男高中生的平均身高在至厘米之间。
25个雇员的随机样本的平均周薪为130元,试问此样本是否取自一个均值为120元、标准差为10元的正态总体? 原假设 120:0=μH备择假设 120:1≠μH 检验统计量()10/2510/25XX μσ-Z ====查表96.1025.0=Z 因为Z= 5 >96.1025.0=Z ,故拒绝原假设, 即 此样本不是取自一个均值为120元、标准差为10元的正态总体。
第八章 时间序列分析书上答案 经济计量学 教学课件
2007 43 52 45 41 48 65 79 86 64 60 45 41
2008 40 64 58 56 67 74 84 95 76 68 56 52
2009 55 72 62 60 70 86 98 ## 87 78 63 58
试分别用同期平均法和移动平均剔除法计算季节比例
(1)直接按月平均法:
1月
2006
40
2007
43
2008
40
2009
55
各年同月平均 44.50
季节比率 0.7255
2月 50 52 64 72 59.50 0.9701
3月 41 45 58 62 51.50 0.8397
4月 39 41 56 60 49.00 0.7989
5月 45 48 67 70 57.50 0.9375
12月 0.7755 0.7354 0.7899 0.7759 0.7692
月 量 一次 1月 40 2月 50 3月 41 4月 39 5月 45 6月 53 49.00 7月 68 49.25 8月 73 49.42 9月 50 49.75 10月 48 49.92 11月 43 50.17 12月 38 51.17
8255
逐期增长量 累积增长量 定基发展速度 环比发展速度 定基增长速度 环比增长速度 增长 1%的绝对值
2004
2005 1328 1328 119.2% 119.2% 19.2% 19.2% 82.55
2006 1602 2730 133.1% 117.1% 33.1% 17.1% 93.83
2007 1253 3983 148.2% 111.4% 48.2% 11.4% 109.85
计量经济学习题与解答3
第四章经典单方程计量经济学模型:放宽基本假定的模型一、内容提要本章主要介绍计量经济模型的二级检检验问题,即计量经济检验。
主要讨论对回归模型的若干基本经典假定是否成立进行检验、当检验发现不成立时继续采用OLS估计模型所带来的不良后果以及如何修正等问题。
具体包括异方差性问题、序列相关性问题、多重共线性问题以及随机解释变量这四大类问题。
异方差是模型随机扰动项的方差不同时产生的一类现象。
在异方差存在的情况下,OLS 估计尽管是无偏、一致的,但通常的假设检验却不再可靠,这时仍采用通常的t检验和F检验,则有可能导致出现错误的结论。
同样地,由于随机项异方差的存在而导致的参数估计值的标准差的偏误,也会使采用模型的预测变得无效。
对模型的异方差性有若干种检测方法,如图示法、Park与Gleiser检验法、Goldfeld-Quandt检验法以及White检验法等。
而当检测出模型确实存在异方差性时,通过采用加权最小二乘法进行修正的估计。
序列相关性也是模型随机扰动项出现序列相关时产生的一类现象。
与异方差的情形相类似,在序列相关存在的情况下,OLS估计量仍具无偏性与一致性,但通常的假设检验不再可靠,预测也变得无效。
序列相关性的检测方法也有若干种,如图示法、回归检验法、Durbin-Watson检验法以及Lagrange 乘子检验法等。
存在序列相关性时,修正的估计方法有广义最小二乘法(GLS)以及广义差分法。
多重共线性是多元回归模型可能存在的一类现象,分为完全共线与近似共线两类。
模型的多个解释变量间出现完全共线性时,模型的参数无法估计。
更多的情况则是近似共线性,这时,由于并不违背所有的基本假定,模型参数的估计仍是无偏、一致且有效的,但估计的参数的标准差往往较大,从而使得t-统计值减小,参数的显著性下降,导致某些本应存在于模型中的变量被排除,甚至出现参数正负号方面的一些混乱。
显然,近似多重共线性使得模型偏回归系数的特征不再明显,从而很难对单个系数的经济含义进行解释。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第九章 时间序列计量经济学模型的理论与方法 练习题 1、 请描述平稳时间序列的条件。 2、 单整变量的单位根检验为什么从DF检验发展到ADF检验?
3、设,10,sincostttxt其中,是相互独立的正态分布N(0, 2)随机变
量,是实数。试证:{10,txt}为平稳过程。 4、 用图形及LBQ法检验1978-2002年居民消费总额时间序列的平稳性,数据如下: 年份 居民消费总额 年份 居民消费总额 年份 居民消费总额 1978 1759.1 1987 5961.2 1995 26944.5 1979 2005.4 1988 7633.1 1996 32152.3 1980 2317.1 1989 8523.5 1997 34854.6 1981 2604.1 1990 9113.2 1998 36921.1 1982 2867.9 1991 10315.9 1999 39334.4 1983 3182.5 1992 12459.8 2000 42895.6 1984 3674.5 1993 15682.4 2001 45898.1 1985 4589 1994 20809.8 2002 48534.5 1986 5175
5、 利用4中数据,用ADF法对居民消费总额时间序列进行平稳性检验。 6、 利用4中数据,对居民消费总额时间序列进行单整性分析。 7、 根据6中的结论,对居民消费总额的差分平稳时间序列进行模型识别。 8、 用Yule Walker法和最小二乘法对7中的居民消费总额的差分平稳时间序列进行时间序列模型估计,并比较估计结果。 9、 有如下AR(2)随机过程:
ttttXXX2106.01.0 该过程是否是平稳过程? 10、求MA(3)模型3213.05.08.01tttttuuuuy的自协方差和自相关函数。
11、设动态数据,92.0,82.0,74.0,9.0,7.0,8.0654321xxxxxx,78.07x ,84.0,72.0,86.01098xxx求样本均值x,样本方差
0
ˆ
,样本自协方差1ˆ、2ˆ和样
本自相关函数1ˆ、2
ˆ
。
12、判断如下ARMA过程是否是平稳过程: 12114.01.07.0tttttxxx 13、以tQ表示粮食产量,tA表示播种面积,tC表示化肥施用量,经检验,他们取对数后都是I(1)变量且相互之间存在CI(1,1)关系。同时经过检验并剔除了不显著的变量(包括滞后变量),得到如下粮食生产模型:
ttttttCCAQQ1432110lnlnlnlnln
推导误差修正模型的表达式,并指出误差修正模型中每个待估参数的经济意义。 14、固定资产存量模型tttttIIKK132110中,经检验,
)1(~),2(~IIIKtt,试写出由该ADL模型导出的误差修正模型的表达式。
15、以下是天津食品消费相关数据,试完成误差修正模型的建立 年份 人均食物年支出 人均年生活费收入 职工生活费用定基价格指数 1950 92.28 151.2 1 1951 97.92 165.6 1.145 1952 105 182.4 1.16332 1953 118.08 198.48 1.254059 1954 121.92 203.64 1.275378 1955 132.96 211.68 1.275378 1956 123.84 206.28 1.272827 1957 137.88 225.48 1.295738 1958 138 226.2 1.281485 1959 145.08 236.88 1.280203 1960 143.04 245.4 1.296846 1961 155.4 240 1.445984 1962 144.24 234.84 1.448875 1963 132.72 232.68 1.411205 1964 136.2 238.56 1.344878 1965 141.12 239.88 1.297807 1966 132.84 239.04 1.287425 1967 139.2 237.48 1.2797 1968 140.76 239.4 1.27842 1969 133.56 248.04 1.286091 1970 144.6 261.48 1.274516 1971 151.2 274.08 1.271967 1972 163.2 286.68 1.271967 1973 165 288 1.277055 1974 170.52 293.52 1.273224 1975 170.16 301.92 1.274497 1976 177.36 313.8 1.274497 1977 181.56 330.12 1.278321 1978 200.4 361.44 1.278321 1979 219.6 398.76 1.291104 1980 260.76 491.76 1.35695 1981 271.08 501 1.374591 1982 290.28 529.2 1.381464 1983 318.48 552.72 1.388371 1984 365.4 671.16 1.413362 1985 418.92 811.8 1.598512 1986 517.56 988.44 1.707211 1987 577.92 1094.64 1.823301 1988 665.76 1231.8 2.131439 1989 756.24 1374.6 2.44476 1990 833.76 1522.2 2.518103
参考答案 1、如果时间序列{tX}满足下列条件: 1)均值)(tXE 与时间t 无关的常数; 2)方差2σ)var(tX 与时间t 无关的常数; 3)协方差kkttXX)cov( 只与时期间隔k有关,与时间t 无关的常数。 则称该随机时间序列是平稳的。
2、在使用DF检验时,实际上假定了时间序列是由具有白噪声随机误差项的一阶自回归过程(AR(1))生成的。但在实际检验中,时间序列可能是由更高阶的自回归过程生成的,或者随机误差项并非是白噪声,这样用OLS法进行估计均会表现出随机误差项出现自相关,导致DF检验无效。另外,如果时间序列包含有明显的随时间变化的某种趋势(如上升或下降),则也容易导致上述检验中的自相关随机误差项问题。为了保证DF检验中随机误差项的白噪声特性,Dicky和Fuller对DF检验进行了扩充,形成了ADF检验。
3、E(tx)=0)(sin)(costEtE
ktkttkttEkttEkttEkttEktttktktExxErtktkcos]sin)(sincos)([cos)(cos)(sin)(sin)(cos)(sin)(sin)(cos)(cos]}sincos)][(sin)(cos{[)(2222
20)var(rXt
所以{10,txt}为平稳过程 4、居民消费总额时间序列图: 01000020000300004000050000
78808284868890929496980002X 序列图表现出了一个持续上升的过程,即在不同的时间段上,其均值是不同的,因此可初步判断是非平稳的。
居民消费总额时间序列相关图及相关系数、LBQ统计量:
从图中可以看出,样本自相关系数是缓慢下降的,表明了该序列的非平稳性。滞后12期的LBQ统计量计算值为75.18,超过了显著性水平5%时的临界值21.03,因此进一步否定了该
时间序列的自相关系数在滞后一期之后的值全部为0的假设。这样,结论是1978~2002年间居民消费总额时间序列是非平稳序列。
5、经过偿试,模型3取了3阶滞后: 321123.078.024.106.014.19585.894tttttXXXXTX
(-1.37) (2.17) (-1.68) (5.17 ) (-2.33) (0.94) DW值为2.03,可见残差序列不存在自相关性,因此该模型的设定是正确的。
从1tX的参数值看,其t统计量的绝对值小于临界值绝对值,不能拒绝存在单位根的 零假设。同时,由于时间T的t统计量也小于ADF分布表中的临界值,因此不能拒绝不存在趋势项的零假设。需进一步检验模型2 。 经试验,模型2中滞后项取3阶:
321130.095.043.101.061.401tttttXXXXX (1.38) (0.33) (5.84) (-2.62) (1.14) DW值为2.01,模型残差不存在自相关性,因此该模型的设定是正确的。从1tX的参数值看,其t统计量为正值,大于临界值,不能拒绝存在单位根的零假设。同时,常数项的t统计量也小于ADF分布表中的临界值,因此不能拒绝不存常数项的零假设。需进一步检验模型1。 经试验,模型1中滞后项取3阶:
321135.002.153.101.0tttttXXXXX (0.63) (6.35) (-2.77) (1.29) DW值为1.99,残差不存在自相关性,因此模型的设定是正确的。从1tX的参数值看,其t统计量为正值,大于临界值,不能拒绝存在单位根的零假设。 至此,可断定居民消费总额时间序列是非平稳的。
6、利用ADF检验,经过试算,发现居民消费总额是2阶单整的,适当的检验模型为:
13123471.0854.0tttXXX (-3.87) (2.30) Correlogram-Q-Statistics检验证明随机误差项已不存在自相关。从12tX的参数值看,其t统计量绝对值3.87大于临界值的绝对值,所以拒绝零假设,认为居民消费总额的二阶差分是平稳的时间序列,即居民消费总额是2阶单整的。
7、居民消费总额经二阶差分后的新序列X2的样本自相关函数图与偏自相关函数图及数据如图所示:
