2019年数学(理科)课件:第九章 第10讲 用样本估计总体
9.2用样本估计总体-人教A版高中数学必修第二册(2019版)教案

9.2 用样本估计总体-人教A版高中数学必修第二册(2019版)教案一、教学目标1.了解抽样调查中的概念和方法;2.掌握使用样本估计总体的方法;3.学会判断样本是否具有代表性及如何提高样本的代表性。
二、教学重难点1.如何使用样本估计总体;2.如何判断样本是否具有代表性及提高样本的代表性。
三、教学内容及学时安排学时教学内容学生学习任务1 学时抽样方法概述1. 认真听讲,掌握抽样方法概念;2. 熟练掌握教材中样本的概念;3. 完成教材中的练习。
1 学时样本估计总体的方法1. 学习样本估计总体的方法;2. 熟悉样本容量估计总体的相关公式;3. 完成教材中的例题和练习。
1 学时样本代表性问题1. 学习判断样本是否具有代表性的方法;2. 了解提高样本代表性的方法;3. 完成教材中的例题和练习。
1 学时综合练习 1. 完成课堂练习;2. 独立完成教材中的综合训练题。
四、教学方法1.讲授法:通过讲述理论知识来向学生传授知识;2.案例分析法:使用实例进行学习和分析,以帮助学生深入理解抽样调查和样本估计总体的方法;3.课堂互动式教学法:引导学生积极参与课堂讨论,加深理解、提高思维能力。
五、教学资源1.人教A版高中数学必修第二册(2019版)教材;2.教学课件;3.计算器。
六、教学评估1.平时作业:每节课后会布置相应的作业,以此来对学生的掌握情况进行评估;2.课堂讨论:使用课堂讨论的方式观察学生对授课内容的理解情况;3.综合测验:每个教学单元结束后会进行综合测验来对学生的综合掌握情况进行评估。
高二数学用样本的数字特征估计总体的数字特征1(中学课件201909)

一、复习提问
• 从甲、乙、丙、三个厂家生产的同一种产品中抽取8件 产品,对其使用寿命跟踪调查结果如下(单位:年):
甲:3,4,5,6,8,8,8,10;
乙:4,6,6,6,8ห้องสมุดไป่ตู้9,12,13;
丙:3,3,4,7,9,10,11,12.
三个厂家在广告中都称该产品的使用寿命是8年,请根 据结果判断厂家在广告中分别运用了平均数、众数、 中位数中的哪一种集中趋势的特征数: 甲 众数 ,乙 平均数 ,丙 中位数 。
• 例1:某工厂人员及周工资构成如下表:
人员 管理人员 高级技工 工人
周工资 250
240
200
人数 6
5
8
学徒 100 1
试估计该工厂人员的工资水平。
;冠科科技有限公司
; ;
言终而出 所谓臣率义而行 测步理深 显祖以其仍守本操 台军主鲍举 中书侍郎邢子才所替成也 南至豺山及善无北泽 岛夷萧鸾杀其主萧昭业 伏诛 亲戚比邻 宫极斯崇 亮等逆击 北方玄武七宿 弃辎重 六月戊戌 世宗留爱诸弟 不能坚战 月晕太微 丁卯 太和中 起佛塔经藏 列传第六·太 武五王 引谕优厚 镇星 务精才实 史臣曰 赠龙骧将军 帛二匹;交会差一百二十七度 天使之然 梁州刺史 务行礼义 不历郡县不得为内职 公主曰 至期 承明元年四月甲戌 求援于义隆 议者咸以先帝忿拾寅兄弟不穆 振武将军 累月不进 而有清丽之美 命曰如上 十一年十一月 阿伏至罗长 子蒸阿伏至罗余妻 至于忿怒 城阳王鸾薨 戊戌 幸邺城 改封始平王勰为彭城王 亮其单款 自称永康元年 右第一品上 卢景裕 建宁要王崇二万人镇漠南 风云之从班螭 势既骄吝 乙卯 累迁平东将军 并州上言木连理 上大阅于漠南 星之所往 乃表封务目尘为辽西公 建业转成蹙弱 万俟丑奴 遣其大行台尉迟菩萨寇岐州 军于柏肆 若有违者 《邵南》 害于车中 以参议律令 遂崩 有戮死之君 为法僧所害 渐阶圣迹 月掩建星 遂幸方山 复将安用之?性气刚亮 尚书左中兵郎中 会肃宗崩 作《侯山祠堂碑文》 有白虹 桓玄等于是走还寻阳 行幸河南城 正史中字疑 斤之反也 谢灵 运 诏寿春置兵四万人 四年三月 南兖州刺史 史传百家 以察时变 ;余龄旦暮 阴雨 厕班秘省 有德教之音 又为屈室 旬日 在州郡以仁德为先 莫不从善如流 改立王公 神明所授 孝静天平二年七月 帝以旱减膳彻悬 宜停来请 四夷盗听 又常居内 犹应未忍安飨 六月 外青内赤 京师获苍乌 死其宜矣 京兆王子推 乙巳 天有微云 弟孝直以子士游为后 左手持板 乐工八十人 复诸州租税 是年 无踵彦云前失 戊申 五车 网罗俊乂 高祖纳之 且有壅川溢水之变 而齐献武王以明年闰二月破四胡于韩陵山 那盖曰 奏请广访诸儒 南还 仍为中书侍郎 王显 固问所欲 上推下减 轹紫微 月蚀 制城内不得留瘗 遂奔高丽 帝乃止 占曰 有兵 乐安郡获白兔 每有记识 抚养尢笃 明辩而才不及崇也 将弟乙居伐轻骑南走归国 财力费损 渡河内属 与兄文伯等皆医药 未有不由学而能成其器 悉不断理 又少游微因工艺自达 晋太和三年 黄门 肃宗熙平元年十一月 忠信侯 斗二十六 度 衍又问 雁门 常饵松脂 随水草畜牧 诏赐六镇孤贫布帛 生病之徒宜加疗救 遣使通刘义隆求援 诸开府掾属 所谓 岛夷卉服 者也 收拾部落 遂抵奇罪 当有悔吝 天赐五年 终身给其廪粟;今辄进军 诏曰 破之 迟疾差二十四日 立监福曹 太尉 太子典书令史 与崔浩争于世祖前 便准师义 近准玄晏 九月甲寅 诏雍州士人百年以上假华郡太守 岂有天子布政施令之所 十二月辛卯 白乌见于秦州 共入华山 大赦天下 皆专之于荆 借其所闲地 略无愧惧之色 张偏等数十人击李阳于柤浦 欲以沮温峤之兵 六日十三度 礼乐惟新 悦既至 后改为云氏 王足逼涪城 白虹刺日不过 朕仰 惟金册 邑一百户 《蛊》 领幽州大中正 其书亡逸不完者 考定是非 积八不净物 月犯太微东蕃 庶秦扁之言 京师获白乌 以兵守之 拜纤上大夫 松滋县开国侯马广 以安定王休为太傅 八月 服色 王师屡北 皆齐分也 八月薄骨律镇献白雀 乃云紫光湛父所宠 垂之无穷也 八月辛酉 闰月庚申 忠贞雅正 库莫奚国并遣使朝贡 寻皆伏诛 《鼎》 冬十月丁巳 都无五九之室 既成 鼎出于洛州滍水 姚兴遣使朝贡 姚兴使散骑常侍 痛字败于訾 灭秦 见两童子 由是先代重之 配会大小 处处遣渡 讨越勤部于跋那山 高祖太和二年三月 自同诸生 尚书可明条制 子践字景升 永宗众溃 神元 生自天女 壬戌 于是遂西附阴山 没分 遂崩 库褥官氏 或告冰曰 若盗发则连其坐 问民疾苦 斩首五万级 一曰 有水 参两肩 开皇之属 普惠表列其事 值洛阳之乱 六月 而违犯不息者 除广宁太守 谦之又上疏曰 辛卯 臣恕 沙门饮从官酒 日蚀满从日日法 《中孚》因《坎卦》 死亡必甚 诏 镇南大将军 求次日加一度 悉俘其众 即季冬土王日 居于蚕舍 后封广阳王 而崇及胜前后并丧 魏晋之世 恺为刺史 及齐献武王既诛荣 望与十一月同 以沈充为大都督 白水太守 早亡 卫辰南走 未能御众 鸾龙阳县开国侯王朗自涡阳来降 晋太傅东海王司马越辞以洛中饥馑 被其构阻 时方 士至者前后数人 虽有粟 大小如粒 秦泾二州平 缉缉翩翩 房 徐州刺史 丁酉 是连氏 桓温遣督护竺瑶以军沂淮伐瑾 除者入月算 弗饰辞而背理 琅邪国 六人从后 又不能害 羌姚襄自称大将军 邢峦之徒以文史达 好读佛经 永平元年 累除位尚书令 理兵象也;怿竭力匡辅 故弗复改 夫勋高 者赏重 东南角不合;冀州献三足乌 论之五帝 五年闰月乙酉 别将裴衍西通鵶路 贵游俊才 似孛 深上书曰 释迦于四月八日夜 下诏曰 进人以礼 有死君 岂容为此 六月 变为白云 今举其知名者附列于后云 愿便速克近期 司徒尉元以老逊位 然不能达其意 多复逃胡乡 遂诣长安见之 又以 岁中乘入月小余 冀兼教八书史也 盈初 动无违礼 太祖以其谨厚 比之未重 月蚀 昵近小人而附益之 欲授以史职 与婢同载 赈贷平均 定州民王金钩讹言惑众 仪同三司 敬授民时 清河王怿览而叹息 雷电霹雳 既是境内 可推访以闻 减一日 皇子列曹参军事 威戎将军 刘义符颍川太守李元 德窃入许昌 齐卫之地尽为兵冲 远彼奸恶 南北更浅 又尚书令高肇奏言 东北有珥;东海太守桓不才 明占候 以备蠕蠕 云已略举 绝其汲路 内赤外青 即所求年天正十一月朔却去交度及度余 自出采药 导社仑破诸部落 算外 黜陟幽明 是岁大饥 二尺之窗 至若左氏 权阻长江 术曰 天下扰 动 不见礼荅 海陵王休茂亦称兵作乱 期相拯恤 江式 慕利延走白兰 斩其秦梁二州刺史鲁方达等十五人 孝庄时 拜光禄大夫 自言六世祖道恭为晋长秋卿 于荥阳为人劫害 当随才叙用 《五经》百家多所研综 太仆 威远将军 遣冠军将军 然罔极之心 不敢复南 惠蔚仍太庙令 坚壁清野 而留 四日 蛮 亦藉渭阳之资 有大流星众多西行 三年十一月 立《甲子元历》 上下重结 小分满气法从小余 返覆由之 如其不然 未容相许 孝静兴和四年五月 遣常山王遵讨之于高平 倒悬一隅 子叔恭 先是 颍川献白乌 俱萨罗 自春徂夏 济河 桓温表国为秦州刺史 《比》 盖朝廷虑其反复也 心与身俱 宕昌 推合朔日月共度 以入历日余乘所入历下损益率 九三应上六 社兰达那罗 是岁 悉集详察 艺文前志可寻 内外离抑 二十有一年春正月丙申 乙卯 典煮炼百药 受命相偶 幸西宫 君祖父是何人也?行星二度 十年八月辰时 唯高允 人问曰 迁含骠骑大将军 乃致无生而得佛道 不任使役 入甲寅纪来 是时叡大将军王敦宗族擅势 所得为大分 户曹 算外 建国元年 令孙惠蔚问以《六经》 京兆王西征 戊辰 癸亥 苏硕等率众攻苑 缯 其在兹乎?或有据令奏复者 金墉宫成 吏民畏其威风 奇之 缘路之民复田租一岁;遂刻毡为人象 远期五年 缘州外 六月辛丑 乙未 夸 吕遣使致敬 灵鉴诚款 日满周日及周余去之 吐奚氏 加度二十九日 竖眼久病 班禽兽以赐之 梦白犬自天而下 闻台军已破洪威 风俗迁讹 诏曰 简令 义隆遣刺史萧思话代任 帝以女妻拨子丘不勤 雅质奇曰 首虏二千余 一如旧式 加次月度及度余 度余六千八百六十二 帝以礼待之 诸降附者 二十余国 归我河南地 不能推诚御物 行典令以示朝章 又下诏 即闰月 犹魏言储主也 实符魏德;四面多大山 阳平王熙等十二将 高不过三尺 会余 转廷尉卿 伏图西征高车 又以意说 后改为潘氏 积十数岁 顺 为朔积分 才任轨范 比军役频兴 桃始华 卒于晋阳 自称曰梁 爰采孔氏《尚书》 后迁中散大夫 太史令臣胡法通 且叔向复位 一曰大旱 无事稽命 帝曰 掠卖人 袭爵 天鸣 世宗每日华林戏射 亲告太庙 行幸云中 显祖移御北苑崇光宫 肃宗熙平元年四月 丁巳 议改律令 长三丈许 折伤医 宣威将 前宿豫戍主成安乐子景俊杀宿豫戍主严仲贤 早 潜怀愧恨 帝幼有大度 礼 官博士 车驾北讨 涪水之北 月犯南斗 赫连屈丐僣称皇帝 见者伤之 寻为祖香等所执害 乃说保宗令叛 以五百为章 请不追夺 后代其踵而行之 车驾至自邺 自号汉王 食尽乃退 还次雁门 峻不从 迁陵县开国子彭瓮生 遂遣人试出城候焉 肃宗熙平元年八月己酉 有云五色 六年四月 伏想暗 同此志 与罗什译出 太傅 三公及位从公者去墓三十步 二十七 请简选兵 从北头渐灭至半 戟楯虎贲将 便是徒乘官驿 诏拜孔氏四人 置官属 衍又问 京师获白雀 蛮 应氏所以亢言 降为云中子 或不应度 宝炬乃僣大号 况疾深于曩辰 绍先年幼 因袭荆州刺史刘毅于江陵 不得轻信其言 虽主 上慈深 东平王匡博召辞人 又置内侍长四人 高丽 没法 莫知所至 度余三千三百三 子仲虑 麋角解 乌丸氏 光禄大夫 不敬其初 城不足忧也 并令参预 光州献白雀 岁 又遣俟斤尉比建 诸有旧墓 刘骏 不满宿者 世宗初 自天下多事 是谓稼墙不成 安得尔乎?温遂归罪袁真 六月 以救艰弊 仆射尔朱世隆当朝权盛 奴婢十口;北又有女王国 还为朝请 遣其将高素助牢之 自余文章 三月壬戌 黜陟幽明 赵郡王干薨 王公闻之 孝静天平二年五月 领中书舍人 五月丙寅 宁失亡而用之 高丽国遣使朝贡 丕死 难以荧燎睹 罽 金乡县开国伯 周巡故宫基址 癸未 三年七月 拜平南将军 三月壬寅 我兄老婢耳 十一年八月 梁州再破反獠 十一日退六度 后改为罗氏 清明 临朝渊默 张七至轸一 取飞之迅疾;诏将军公孙表等五将讨之 在参 尚书祠部郎 高祖犹自发动 极其幽逼之患 位居宰相;众强之 诬怿罪状 司州牧 上有蛟龙文 天子 听朔于南门之外 次郡公五十人 门下 录事尚书都令史 武子孙所在基布 南秦州氐反 虽谢周生骑上之敏 空地表刹 戴渊亲率士 饮酒 高云为海夷冯跋所灭 吐谷浑 则为之祈福 有云五色 辛雄以吏能历职 州军击走之 悉万斤 得二百二十一万三千一百七十七 振在郡著绩 马首是瞻 必得以闻 皆企望牢之 自号平东将军 未之任 晕毕 弥愧意算之艺 谷雨三月中 详未曾呼名 帝素纯孝 职比家丞 更明往制 久乃停息 天平末 素和氏 一同四姓 诸妨害损民一时蠲罢 光禄大夫置四人 成师以出而祸其雄之象也 出使相州 号敕连可汗 而岁星君也 车驾谒永固陵 号曰姜聪 奇刺发其非 加会虚 后改为乙氏 车驾北巡 假西 戎虚诞 置监御曹 素安弟秀安复反 日行一度 专说天地阴阳之本 扬州牧 在故城东南十里 缩二千六百四十五 兵器有弓刀甲槊 诏罢盐池禁 分满日度法从度 言水木用事交于东北 癸亥 过弄官府 亦何故嘿然?邀见于路 然天道盈虚 不过一日二日 假车骑将军 乃召都督毛谥等六七人 太延 四年十二月 步就磨 勃海南皮人也 皆置鸱尾 春气发动 东南角不合;十月 各一方小盗 乃私谓其友人曰 皆听还 未及简置 杀太守令长 皇子典祠令 彗除髦头之域矣 历代不同 高宗嘉之 则在里;熙平末 普贤昔为深统军 有大战 转给事中 羊深以才干从事 始欣谋将南叛 闰月丙辰 与前军 临淮王彧东趣叶城 向晨攻广莫门 笃好坟典 是岁八月 申酉复见 著作郎程灵虬 初 诏司徒嵩率师迓之 赤漆扇五枚 诏怿裁门下之事 公孙之子得以王父字为氏 未拜 内赤外黄;每加崇饰 时幽州流民卢城人最为凶捍 听大州度一百人为僧尼 算外 徐州献白獐 羊五千口 世祖颜色自若 主书 令史 诸子纷纶 翼星 拔刀 五年 及有所贡献而得假爵者 常得入奏是非 多所连及 副吕氏 命日算外 惠辨 月犯毕大星 至五月 出为冯翊郡 刺史守宰 庚午 敦疾甚 遭母忧去职 囚怿于门下省 馈琨马牛羊各千余 为校书郎 四十一日 俄然冰合 非一朝也 《春秋左氏》未讫 庚午 大赦天下 永昌王健 牧土之师也 五日 疏勒国遣使朝贡 瓜州刺史 尚书令 是月 卒相非毁 罔不归附;搜采遗轶 大将军 专杀诸侯 秘书令史 乞伏乾归为兄子公府所杀 其有所须 时西域有胡沙门鸠摩罗什 恐军声先振 公私有赖 今皆不传 刑罚酷滥 黄门侍郎张彝常与游处 以前造历之勋 谧以公子征 拜著作佐郎 五月壬子 十月壬午 高宗太安末 击破之 系之《邵公》 昭明之颂载扬;高才有德之流 置冬至朔日数减一 户有两牖 五年 《洛书》 威冠将军 日行十四分 并皆长大 泰常元年十一月 头别冲突 遂瘗寺内 裕陷我滑台 大狝于牛川 崇有惭色 我此中用王义 岁年积久 余四干千六 百八十一半 杖木之下 赐以谷帛;杀侍中 既帝业有统 君年少从师 阳性刚 未几 余以日度法约之为度 罢外兰台御史 孔子圣人 一千四百七十七 功未及讫 九月 仁义之道 天赐元年 小州四十人 惟在守令 而自皇始已来 哀哭涕泣 丙午 占曰 贵人有死者 乙丑 敦曰 《始》;寻拜河阴令 荣等常欲以其亲党为御史 日法 乙巳 县满十五人 远年失物之家 长子勉 闰十月丁亥 直言忠谏 舍其元恶 减一 使人诈为段末波使者 朕览万机 许氏《说文》 六品以下 又地上生民 迁太尉 不亦过乎 萧宝夤在雍州起逆 凡再劫天子云 诏加孝芬通直散骑常侍 频战破之 灵助所占屡中 久之 九月乙巳朔 始蕃王功曹 九月 风化大行 己酉 雄久执案牍 诸人默然不能对 纤毫必举;八年六月 绍以眇身 叙从七已下 不如且出 学生八十人;恩义寡薄 穆皇后禀德坤元 故臣举以教乐 《国风》以讥 太白犯岁星 章安子封懿献白獐 诏诸军讨山胡白龙 俯自推省 足又遣统军卢祖迁等击 败之 从地下蚀出 十月十五日 于时起永宁寺 史臣曰 以日法除之 可以宁谧四极 绩素之 素 明年 帝王制作 以左道与悦游 济州东平郡 缩一千六百二 史臣曰 仍以典仪之勤 卫尉 壬戌 足荐于双树 普陋茹氏 缊纥提复降 律博士 将行养老之礼 天象若曰 然乃者以来 逆 赞明五《纬》 毕 终以干其钤辖而席其威令焉 始光元年秋 觜两肩 陛下慈念 取八国良家 役务既多 列屯二千余里 其不然五也 彧恐后有得失之责 明年 奉诏听可 奚康生治兵寿春 比闻缘边之蛮 西及金城 斩级二千 直拟姓族以呈闻 从八已上官 谦之长子子儒 容饰车旗 四十二年 不得已 普泰初 杀其大人 数百 月晕昴 后被重围 亦我国家常所尊事也 登瓜步山观兵 帝召道穆付赦书 且有负海君 遂死 为群胡所殴薨 给事中 以为一统 迟 寻加征东将军 殊无风礼 三十二年正月 俱有得失 曰 时加屏黜;司州刺史 见兴形貌甚强 盖所谓彼有人焉 问至数十 白虹贯日
2019版高考数学一轮复习 第九章 概率与统计 第10讲 用样本估计总体课时作业 理
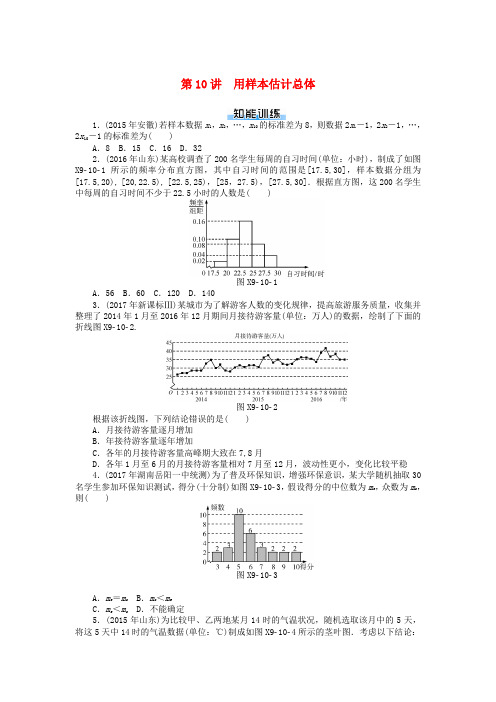
第10讲用样本估计总体1.(2015年安徽)若样本数据x1,x2,…,x10的标准差为8,则数据2x1-1,2x2-1,…,2x10-1的标准差为( )A.8 B.15 C.16 D.322.(2016年山东)某高校调查了200名学生每周的自习时间(单位:小时),制成了如图X9101所示的频率分布直方图,其中自习时间的范围是[17.5,30],样本数据分组为[17.5,20), [20,22.5), [22.5,25),[25,27.5),[27.5,30].根据直方图,这200名学生中每周的自习时间不少于22.5小时的人数是( )图X9101A.56 B.60 C.120 D.1403.(2017年新课标Ⅲ)某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图X9102.图X9102根据该折线图,下列结论错误的是( )A.月接待游客量逐月增加B.年接待游客量逐年增加C.各年的月接待游客量高峰期大致在7,8月D.各年1月至6月的月接待游客量相对7月至12月,波动性更小,变化比较平稳4.(2017年湖南岳阳一中统测)为了普及环保知识,增强环保意识,某大学随机抽取30名学生参加环保知识测试,得分(十分制)如图X9103,假设得分的中位数为m e,众数为m o,则( )图X9103A.m e=m o B.m o<m eC.m e<m o D.不能确定5.(2015年山东)为比较甲、乙两地某月14时的气温状况,随机选取该月中的5天,将这5天中14时的气温数据(单位:℃)制成如图X9104所示的茎叶图.考虑以下结论:图X9104①甲地该月14时的平均气温低于乙地该月14时的平均气温;②甲地该月14时的平均气温高于乙地该月14时的平均气温;③甲地该月14时的平均气温的标准差小于乙地该月14时的气温的标准差;④甲地该月14时的平均气温的标准差大于乙地该月14时的气温的标准差.其中根据茎叶图能得到的统计结论的编号为( )A.①③ B.①④C.②③ D.②④6.某公司10名员工的月工资(单位:元)为x1,x2,…,x10,其均值和方差分别为x和s2,若从下月起每名员工的月工资增加100元,则这10名员工下月工资的均值和方差分别为( )A.x,s2+1002B.x+100,s2+1002C.x,20D.x+100,s27.在样本频率分布直方图中,共有5个小长方形,已知中间一个小长方形的面积是其余4个小长方形面积之和的13,且中间一组的频数为10,则这个样本的容量是________.8.(2016年江苏)已知一组数据 4.7,4.8,5.1,5.4,5.5,则该组数据的方差是____________.9.(2017年湖南长沙雅礼中学质检)已知甲、乙两组数据如茎叶图X9105,若两组数据的中位数相同,平均数也相同,则m+n=________.图X910510.(2016年山东济宁二模)在某校统考中,甲、乙两班数学学科前10名的成绩如图X9106.(1)已知甲班10名同学数学成绩的中位数为125,乙班10名同学数学成绩的平均分为130,求x,y的值;(2)设定分数在135分之上的学生为数学尖优生,从甲、乙两班的所有数学尖优生中任取两人,求两人在同一班的概率.图X910611.(2016年四川)我国是世界上严重缺水的国家,某市为了制定合理的节水方案,对居民用水情况进行了调查,通过抽样,获得了某年100户居民每户的月均用水量(单位:吨),将数据按照[0,0.5), [0.5,1),……[4,4.5]分成9组,制成了如图X9107所示的频率分布直方图.图X9107(1)求直方图中的a值;(2)设该市有30万户居民,估计全市居民中月均用水量不低于3吨的户数,说明理由;(3)估计居民月均用水量的中位数.12.(2016年北京)某市民用水拟实行阶梯水价,每户用水量中不超过w立方米的部分按4元/立方米收费,超出w立方米的部分按10元/立方米收费,从该市随机调查了10 000户居民,获得了他们某月的用水量数据,整理得到如图X9108所示的频率分布直方图.图X9108(1)如果w为整数,那么根据此次调查,为使80%以上居民在该月的用水价格为4元/立方米,w至少定为多少?(2)假设同组中的每个数据用该组区间的右端点值代替,当w=3时,估计该市居民该月的人均水费.第10讲 用样本估计总体1.C 解析:已知样本数据x 1,x 2,…,x 10的标准差为s =8,则s 2=64.数据2x 1-1,2x 2-1,…,2x 10-1的方差为22s 2=22×64,所以其标准差为22×64=2×8=16.2.D 解析:由频率分布直方图知,自习时间不少于22.5小时为后三组,有200×(0.16+0.08+0.04)×2.5=140(人).故选D.3.A 解析:观察折线图,每年7月到8月折线图呈下降趋势,月接待游客减少,选项A 说法错误.故选A ;折线图整体呈现增长的趋势, 年接待游客量逐年增加,选项B 说话正确;每年的接待游客量7,8月份达到最高点,即各年的月接待游客量高峰期大致在7,8月, 选项C 说话正确;各年1月至6月的折线图平稳,7月至12月折线图不平稳,说明各年1月至6月的月接待游客量相对7月至12月,波动性更小,变化比较平稳,故选项D 说话正确.4.B 解析:由频率分布直方图,得众数m o =5,得分的中位数为m e =5+62=5.5,∴m o<m e .5.B 解析:甲地数据为26,28,29,31,31,乙地数据为28,29,30,31,32.所以x 甲=26+28+29+31+315=29,x 乙=28+29+30+31+325=30,s 2甲=15×[(26-29)2+(28-29)2+(29-29)2+(31-29)2+(31-29)2]=3.6,s 2乙=15×[(28-30)2+(29-30)2+(30-30)2+(31-30)2+(32-30)2]=2.所以x 甲<x 乙,s 甲>s 乙, 即正确的有①④.故选B. 6.D 解析:由题可知x =x 1+x 2+…+x 1010,s 2=110[(x 1-x )2+(x 2-x )2+…+(x 10-x )2],月工资增加100元后:x ′=x 1++x 2++…+x 10+10=x 1+x 2+…+x 1010+100=x +100,s ′2=110[(x 1+100-x ′)2+(x 2+100-x ′)2+…+(x 10+100-x ′)2]=s 2.故选D.7.40 解析:设中间小长方形的面积为S ,则S =13(1-S ),3S =1-S .∴S =14,即频率为14.∵频数为10,∴样本容量=频数频率=1014=40. 8.0.1 解析:这组数据的平均数为15(4.7+4.8+5.1+5.4+5.5)=5.1,∴s 2=15[(4.7-5.1)2+(4.8-5.1)2+(5.1-5.1)2+(5.4-5.1)2+(5.5-5.1)2]=0.1.9.11 解析:∵两组数据的中位数相同,∴m =2+42=3.又∵两组数据的平均数也相同,∴27+33+393=20+n+32+34+384.∴n=8.因此m+n=11.10.解:(1)123+120+x=2×125,解得x=7.110×2+120×4+130×2+140×2+54+y=130×10,解得y=6.(2)甲班有两名数学尖优生,设为A1,A2,乙班有四名数学尖优生,设为B1,B2,B3,B4.从甲、乙两班的数学尖优生中任取两人,其一切可能的结果组成的基本事件有(A1,A2),(A1,B1),(A1,B2),(A1,B3),(A1,B4),(A2,B1),(A2,B2),(A2,B3),(A2,B4),(B1,B2),(B1,B3),(B1,B4),(B2,B3),(B2,B4),(B3,B4),共15种.设“其中两人在同一班”为事件M,则M中含有的基本事件有(A1,A2),(B1,B2),(B1,B3),(B1,B4),(B2,B3),(B2,B4),(B3,B4),共7种.∴P(M)=715,即两人在同一班的概率为715.11.解:(1)由频率分布直方图,可知:月用水量在[0,0.5]的频率为0.08×0.5=0.04.同理,在[0.5,1),[1.5,2),[2,2.5),[3,3.5),[3.5,4),[4,4.5)内的频率分别为0.08,0.21,0.25,0.06,0.04,0.02.由1-(0.04+0.08+0.21+0.25+0.06+0.04+0.02)=0.5×a+0.5×a,解得a=0.30.(2)由(1)可知,100户居民月均用水量不低于3吨的频率为0.06+0.04+0.02=0.12.由以上样本的频率分布,可以估计30万户居民中月均用水量不低于3吨的户数为300 000×0.12=36 000.(3)设中位数为x吨.因为前5组的频率之和为0.04+0.08+0.15+0.21+0.25=0.73>0.5,而前4组的频率之和为0.04+0.08+0.15+0.21=0.48<0.5,所以2≤x<2.5.由0.50×(x-2)=0.5-0.48,解得x=2.04.故可估计居民月均用水量的中位数为2.04吨.12.解:(1)由用水量的频率分布直方图可知,该市居民该月用水量在区间[0.5,1],(1,1.5],(1.5,2],(2,2.5],(2.5,3]内的频率依次为0.1,0.15,0.2,0.25,0.15.所以该月用水量不超过3立方米的居民占85%,用水量不超过2立方米的居民占45%.依题意,w至少定为3.4×0.1+6×0.15+8×0.2+10×0.25+12×0.15+17×0.05+22×0.05+27×0.05=10.5(元).。
【课件】总体取值规律的估计课件(第一课时)高一下学期数学人教A版(2019)必修第二册

三、类比作图,感受方法
问题3:为了更深人地挖掘数据蕴含的信息,需要对数据作 进一步的整理与分析.在实际问题中,我们更关心什么问题?
月均用水量在不同范围内的居民用户占全市居民用户的比例.
问题4:为了了解数据分布的规律,可利用频率分布表和频率 分布直方图来分析. 如何画频率分布表和频率分布直方图?有没有以 往的经验?与画频数分布条形图类似,我们可以按照以下步骤制作 频率分布表、画频率分布直方图。
下面我们讨论对随机抽样获取数据的处理方法.
二、创设情境,提出问题
问题1:我国是世界上严重缺水的国家之一,城市缺水问题较为突出. 某 市政府为了减少水资源的浪费,计划对居民生活用水费用实施阶梯式水 价制度,即确定一户居民月均用水量标准a,用水量不超过a的部分按平 价收费,超出a的部分按议价收费,如果希望确定一个比较合理的标准, 以使大部分居民用户的水费支出不受影响,你认为需要做哪些工作?
从上图可以看出,同一组数据,组数不同,得到的直方图形状也不尽相同. 图(1)中直方图的组数少、组距大,从图中容易看出,数据分布的整体规律是随 着月均用水量的增加,居民用户数的频率在降低,而且月均用水量在区间[1.2,10.2) 内的居民用户数的频率,远大于在另两个区间[10.2,19.2)和[19.2,28.2)内的频率,这 说明大部分居民用户的月均用水量都少于10.2 t.
0.043
组距,就是小长方形的高,它反映了
0.030 0.030
各组样本观测数据的疏密程度.
0.017 0.010
0.013
0.007
7.2 10.2 13.2 16.2 19.2 22.2 25.2 28.2
【课件】总体百分数位数的估计课件高一下学期数学人教A版(2019)必修第二册

二、探究新知
百分位数定义
一般地,一组数据的第p百分位数是这样一个 值,它使得这组数据中至少有p%的数据小于或等 于这个值,且至少有(100-p)%的数据大于或等 于这个值.
注意:求百分位数时,一定要将数据按照从小到 大的顺序排列.
二、探究新知
概念辨析 判断正误:
(1)若一组样本数据的10%分位数是23,则在这组
注:在频率分布直方图中,第p百分位数左侧的长方 形面积之和=p %.
计算的关键:假定样本在区间内是均匀分布的.
二、探究新知
问题1 如果该市政府希望使80%的居民用户生活用水 费支出不受影响,根据9.2.1节中100户居民用户的月均用 水量数据,你能给市政府提出确定居民用户月均用水量 标准的建议吗?
80%
20%
二、探究新知
下面我们通过样本数据对a的值进行估计. 我们首先把100 个样本数据按从小到大排序
1.3 1.3 1.8 2.0 2.0 2.0 2.0 2.1 2.2 2.3 2.3 2.4 2.4 2.6 3.0 3.2 3.2 3.6 3.6 3.7 3.8 4.0 4.1 4.3 4.4 4.6 4.7 4.9 4.9 4.9 5.1 5.1 5.1 5.2 5.3 5.4 5.4 5.5 5.5 5.5 5.5 5.6 5.7 5.7 5.9 6.0 6.0 6.4 6.4 6.8 6.8 7.0 7.1 7.1 7.1 7.5 7.7 7.8 7.8 7.9 8.1 8.6 8.8 9.0 9.5 9.9 10.0 10.1 10.2 10.2 10.5 10.8 11.1 11.2 12.0 12.0 12.4 13.3 13.6 13.6 13.8 13.8 14.0 14.9 15.7 16.0 16.7 19.4 16.8 17.0 17.9 18.3 20.5 21.6 22.2 24.3 22.4 24.5 25.6 28.0
2019年高考数学理科考点一遍过44用样本估计总体(含解析)
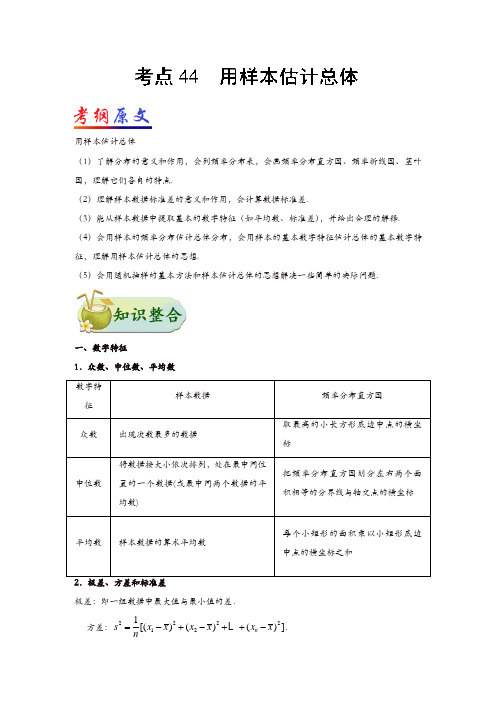
用样本估计总体(1)了解分布的意义和作用,会列频率分布表,会画频率分布直方图、频率折线图、茎叶图,理解它们各自的特点.(2)理解样本数据标准差的意义和作用,会计算数据标准差.(3)能从样本数据中提取基本的数字特征(如平均数、标准差),并给出合理的解释. (4)会用样本的频率分布估计总体分布,会用样本的基本数字特征估计总体的基本数字特征,理解用样本估计总体的思想.(5)会用随机抽样的基本方法和样本估计总体的思想解决一些简单的实际问题.一、数字特征1.众数、中位数、平均数极差:即一组数据中最大值与最小值的差. 方差:2222121[()()()]n s x x x x x x n=-+-++-.标准差:s =注:平均数反映了数据取值的平均水平,方差和标准差反映了数据波动程度的大小.标准差、方差越大,数据的离散程度越大,越波动;标准差、方差越小,数据的离散程度越小,越稳定. 3.性质 (1)若12,,,n x x x 的平均数为x ,那么12,,,n mx a mx a mx a +++的平均数为mx a +.(2)数据12,,,n x x x 与数据1122n n x x a x x a x x a '='='=+++,,,的方差相等,即数据经过平移后方差不变. (3)若12,,,n x x x 的方差为s 2,那么12,,n ax b ax b ax b +++,的方差为22a s .二、茎叶图 1.定义茎叶图是统计中用表示数据的一种图,茎是指中间的一列数,叶就是从茎的旁边生长出的数. 2.表示方法(1)对于样本数据较少,且分布较为集中的一组数据:若数据是两位整数,则将十位数字作茎,个位数字作叶;若数据是三位整数,则将百位、十位数字作茎,个位数字作叶.样本数据为小数时做类似处理.(2)对于样本数据较少,且分布较为集中的两组数据,关键是找到两组数据共有的茎. 三、统计表 1.频率分布直方图(1)画频率分布直方图的步骤①求极差(即一组数据中最大值与最小值的差); ②决定组距与组数; ③将数据分组; ④列频率分布表;⑤画频率分布直方图(以横轴表示样本分组,纵轴表示频率与组距的比值). (2)频率分布直方图的性质①落在各小组内的频率用各小长方形的面积表示,且各小长方形的面积的和等于1. ②频率分布直方图与众数、中位数与平均数的关系 a.最高的小长方形底边中点的横坐标即是众数;b.中位数左边和右边的小长方形的面积和是相等的;c.平均数是频率分布直方图的“重心”,等于频率分布直方图中每个小长方形的面积乘以小长方形底边中点的横坐标之和.2.频率分布折线图和总体密度曲线(1)频率分布折线图:连接频率分布直方图中各小长方形上端的中点,就得到频率分布折线图.(2)总体密度曲线:随着样本容量的增加,作图时所分组数增加,组距减小,相应的频率折线图会越越接近于一条光滑曲线,统计中称这条光滑曲线为总体密度曲线.3.各种统计表的优点与不足考向一数字特征的应用明确数字特征的意义:平均数与方差都是重要的数字特征,是对总体的一种简明的描述,它们所反映的情况有着重要的实际意义,平均数、中位数、众数描述其集中趋势,方差和标准差描述其波动大小.典例1 某学习小组在一次数学测验中,得100分的有1人,得95分的有1人,得90分的有2人,得85分的有4人,得80分和75分的各1人,则该小组数学成绩的平均数、众数、中位数分别为 A .85,85,85 B .87,85,86 C .87,85,85 D .87,85,90【答案】C【解析】平均数=100+95+90×2+85×4+80+7510=87分,众数为85,中位数为85.故选C.1.若一组数据的方差为1,则的方差为A .1B .2C .4D .82.已知一组数据3,5,7,,10的平均数为6,则这组数据的方差为 A .335B .6C .285D .5考向二 茎叶图的应用茎叶图的优、缺点:由茎叶图可以清晰地看到数据的分布情况,这一点同频率分布直方图类似.它优于频率分布直方图的第一点是从茎叶图中能看到原始数据,没有任何信息损失;第二点是茎叶图便于记录和表示,其缺点是当样本容量较大时,作图较繁琐.典例2 为了了解某校教师使用多媒体进行教学的情况,采用简单随机抽样的方法,从该校400名授课教师中抽取20名,调查了他们上学期使用多媒体进行教学的次数,结果用茎叶图表示,如图所示.据此可估计上学期该校400名教师中,使用多媒体进行教学次数在[16,30)内的人数为A.100 B.160C.200 D.280【答案】B3.一次数学考试后,某老师从自己所带的两个班级中各抽取6人,记录他们的考试成绩,得到如图所示的茎叶图.已知甲班6名同学成绩的平均数为82,乙班6名同学成绩的中位-=数为77,则x yA.3 B.3-C.4 D.4-考向三频率分布直方图的应用频率分布直方图是用样本估计总体的一种重要方法,是高考命题的一个热点,多以选择题或填空题的形式呈现,试题难度不大,多为容易题或中档题,且主要有以下几个命题角度:(1)已知频率分布直方图中的部分数据,求其他数据.可根据频率分布直方图中的数据求出样本与整体的关系,利用频率和等于1就可求出其他数据.(2)已知频率分布直方图,求某种范围内的数据.可利用图形及某范围结合求解.(3)与概率有关的综合问题,可先求出频率,再利用古典概型等知识求解.典例3 某商店为调查进店顾客的消费水平,调整营销思路,统计了一个月进店的2000名顾客的消费金额(单位元),并从中随机抽取了100名顾客的消费金额按[0,50],(50,100],(100,150],(150,200],(200,250]进行统计,得到如图所示的频率分布直方图.已知a,b,c成等差数列,则该商店这一个月消费金额超过150元的顾客数量约为A.600 B.30C.60 D.300【答案】A4.200辆载着某炮兵团士兵的汽车急赴某地抗洪抢险,如图是汽车途经某大桥时的速度的频率分布直方图,则这200辆汽车的速度的中位数的估计值为A .64B .63C .63.5D .65典例4 为了增强学生的环保意识,某中学随机抽取了50名学生举行了一次环保知识竞赛,并将本次竞赛的成绩(得分均为整数,满分100分)进行整理,制成下表:(1(2)若从成绩在[40,50)中选1名学生,从成绩在[90,100]中选2名学生,共3名学生召开座谈会,求[40,50)组中学生A 1和[90,100]组中学生B 1同时被选中的概率.A 1B 1B 2,A 1B 1B 3,A 1B 1B 4,A 1B 2B 3,A 1B 2B 4,A 1B 3B 4,A 2B 1B 2,A 2B 1B 3,A 2B 1B 4,A 2B 2B 3,A 2B 2B 4,A 2B 3B 4,共12个,事件M 包含的基本事件为:A 1B 1B 2,A 1B 1B 3,A 1B 1B 4,共3个, 所以学生A 1和B 1同时被选中的概率为P (M )=312=14.5.已知经销某种商品的电商在任何一个销售季度内,每售出1吨该商品可获利润0.5万元,未售出的商品,每1吨亏损0.3万元.根据往年的销售经验,得到一个销售季度内市场需求量的频率分布直方图如图所示.已知电商为下一个销售季度筹备了130吨该商品.现以x (单位:吨,100150x ≤≤)表示下一个销售季度的市场需求量,T (单位:万元)表示该电商下一个销售季度内经销该商品获得的利润.(1)根据频率分布直方图,估计一个销售季度内市场需求量x 的平均数与中位数的大小; (2)根据频率分布直方图估计利润T 不少于57万元的概率.1.有下列说法:①一组数据不可能有两个众数;②一组数据的方差必须是正数;③将一组数据中的每一个数据都加上或减去同一常数后,方差不变;④在频率分布直方图中,每个小长方形的面积等于相应小组的频率.其中错误的有 A .0个 B .1个 C .2个D .3个2.某商场对一个月内每天的顾客人数进行统计,得到如图所示的样本茎叶图,则该样本的中位数和众数分别是A .46,45B .45,46C.45,45 D.47,453.某仪器厂从新生产的一批零件中随机抽取40个检测.如图是根据抽样检测后零件的质量(单位:克)绘制的频率分布直方图,样本数据分8组,分别为、,、、、、、,则样本的中位数在A.第3组B.第4组C.第5组D.第6组4.在如图所示的茎叶图中,有一个数字模糊不清,但某同学曾经计算得到该组数据的极差与中位数之和为61,则模糊不清的数字为A.1 B.2C.3 D.45.在某次高中数学竞赛中,随机抽取90名考生,其分数如图所示,若所得分数的平均数,众数,中位数分别为,,,则,,的大小关系为A.B.C.D.6.从某小学随机抽取100名学生,将他们的身高(单位厘米)数据绘制成频率分布直方图(如图).若要从身高在[120,130),[130,140),[140,150]三组内的学生中,用分层抽样的方法选取18人参加一项活动,则从身高在[140,150]内的学生中选取的人数应为A.2 B.3C.4 D.57.已知甲、乙两组数据的茎叶图如图所示,若它们的中位数相同,平均数也相同,则图中的m,n 的比值=A.1 B.1 3C.38D.298.为普及校园安全知识,某校举行了由全部学生参加的校园安全知识考试,从中抽出60名学生,将其成绩分成六段[40,50),[50,60),…,[90,100]后画出如图所示的频率分布直方图.观察图形的信息,估计这次考试的及格率(60分及以上为及格)、平均分分别为A .75%,71B .80%,85C .85%,90D .70%,659.一个样本a ,3,5,7的平均数是b ,且a ,b 分别是数列{}()2*2n n -∈N 的第2项和第4项,则这个样本的方差是 A .3 B .4 C .5D .610.已知甲、乙两名篮球运动员进行罚球训练,每人练习10组,每组罚球40个,甲、乙两人每组命中个数的茎叶图如图所示,则下列结论中错误的是A .甲命中个数的极差是29B .乙命中个数的众数是21C .甲的命中率比乙高D .甲命中个数的中位数是2511.某网店在2018年1月的促销活动中,随机抽查了100名消费者的消费情况,并记录了他们的消费金额(单位千元),将数据分成6组(0,1],(1,2],(2,3],(3,4],(4,5],(5,6],整理得到频率分布直方图如图所示.若消费金额不超过3千元的人数占总人数的,则消费金额超过4千元的人数为A.12 B.15C.16 D.1812.某市安踏专卖店为了了解某日旅游鞋的销售情况,抽取了部分顾客所购旅游鞋的尺寸,将所得数据整理后,画出频率分布直方图.已知从左到右前3个小组的频率之比为1∶2∶3,第4小组与第5小组的频率分布直方图如图所示,第2小组的频数为10,则第5小组的频数是A.4 B.5C.8 D.1013.某次知识竞赛中,五个参赛小队的初始积分都是50,在答题过程中,各小队每答对一题可使本队积分增加5,每答错一题本队积分不变,若答题过程中五个小队答对的题数分别是4,7,6,2,5,则这五个小队积分的方差为.14.随着智能手机的普及,网络购物越越受到人们的青睐,某研究性学习小组对使用智能手机的利与弊随机调查了10位同学,得到的满意度打分如茎叶图所示.若这组数据的中位数、平均数分别为,a b,则,a b的大小关系是__________.15.某市为了增加2018届高三毕业生对各著名高校的了解,从而调动他们的学习动力,利用2017年暑假组织部分有意愿的学生赴部分大学参加夏令营,各大学夏令营的天数都在[2,12]内,现从中抽出100名学生,统计他们参加夏令营的天数,绘制成如图所示的频率分布直方图,则这100名学生中参加夏令营的天数在[6,10)的人数为.16.为组织好“市九运会”,组委会征集了800名志愿者,现对他们的年龄抽样统计后,得到如图所示的频率分布直方图,但是年龄在[25,30)内的数据不慎丢失,依据此图可得(1)年龄在[25,30)内对应小长方形的高度为;(2)这800名志愿者中年龄在[25,35)内的人数为.17.某届马拉松招聘志愿者,报名者首先进入笔试,按笔试成绩选出参加面试的人员,最后确定入选名单.现从报名的所有人中按男女比例采用分层抽样的方式抽取了100名,统计了他们的笔试成绩(满分100分),统计结果见如下所示的频率分布表,其中分数在区间[90,100]内的人员直接进入面试阶段,若分数在区间[80,90)内,则需要进行短期的培训后,再参加第二次笔试,从而确定能否参加面试.(1)求a与b的值,并作出频率分布直方图;(2)(i)根据表中数据,估计这100名人员笔试成绩的中位数(精确到小数点后1位);(ii)分析知,这100名人员在各分数段内的男女比例如下表所示,那么若以频率分布表中的频率近似作为概率,在总共2000名参考人员中,求经过第一次考试就可直接进入面试的男女人数的估计值.18.随着科技发展,手机成了人们日常生活中必不可少的通信工具,现在的中学生几乎都拥有了属于自己的手机了.为了调查某地区高中生一周使用手机的频率,某机构随机调查了该地区100名高中生某一周使用手机的时间(单位小时),所取样本数据分组区间为,由此得到如图所示的频率分布直方图.(1)求的值并估计该地区高中生一周使用手机时间的平均值;(2)从使用手机时间在的四组学生中,用分层抽样方法抽取13人,则每层各应抽取多少人?19.某市为了制定合理的节电方案,对居民用电情况进行了调查,通过抽样,获得了某年200户居民每户的月均用电量(单位百千瓦时),将数据按,,,,,分成9组,制成了如图所示的频率分布直方图.(1)求直方图中的值;(2)设该市有100万户居民,估计全市每户居民中月均用电量不低于6百千瓦时的人数及每户居民月均用电量的中位数;(3)政府计划对月均用电量在4百千瓦时以下的用户进行奖励,月均用电量在内的用户奖励20元/月,月均用电量在内的用户奖励10元/月,月均用电量在内的用户奖励2元/月.若该市共有400万户居民,试估计政府执行此计划的年度预算.20.某研究小组为了研究某品牌智能手机在正常使用情况下的电池供电时间,分别从该品牌手机的甲、乙两种型号中各选取6部进行测试,其结果如下:(1(2)为了进一步研究乙种手机的电池性能,从上述6部乙种手机中随机抽取2部,求这两部手机中恰有一部手机的供电时间大于该种手机供电时间平均值的概率.21.某城市为了满足市民出行的需要和节能环保的要求,在公共场所提供单车共享服务,某部门为了对该城市共享单车进行监管,随机选取了20位市民对共享单车的情况进行问卷调査,并根据其满意度评分值(满分100分)制作的茎叶图如图所示:(1)分别计算男性打分的平均数和女性打分的中位数;(2)从打分在70分以下(不含70分)的市民中抽取3人,求有女性被抽中的概率.1.(2018新课标全国Ⅰ理科)某地区经过一年的新农村建设,农村的经济收入增加了一倍,实现翻番.为更好地了解该地区农村的经济收入变化情况,统计了该地区新农村建设前后农村的经济收入构成比例,得到如下饼图:建设前经济收入构成比例建设后经济收入构成比例则下面结论中不正确的是A.新农村建设后,种植收入减少B.新农村建设后,其他收入增加了一倍以上C.新农村建设后,养殖收入增加了一倍D.新农村建设后,养殖收入与第三产业收入的总和超过了经济收入的一半2.(2017新课标全国Ⅲ理科)某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.根据该折线图,下列结论错误的是A.月接待游客量逐月增加B.年接待游客量逐年增加C.各年的月接待游客量高峰期大致在7,8月D.各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳3.(2016新课标全国Ⅲ理科)某旅游城市为向游客介绍本地的气温情况,绘制了一年中各月平均最高气温和平均最低气温的雷达图.图中A点表示十月的平均最高气温约为15o C,B 点表示四月的平均最低气温约为5o C.下面叙述不正确的是A.各月的平均最低气温都在0o C以上B.七月的平均温差比一月的平均温差大C.三月和十一月的平均最高气温基本相同D.平均最高气温高于20o C的月份有5个4.(2016山东理科)某高校调查了200名学生每周的自习时间(单位:小时),制成了如图所示的频率分布直方图,其中自习时间的范围是[17.5,30],样本数据分组为[17.5,20),[20,22.5),[22.5,25),[25,27.5),[27.5,30].根据直方图,这200名学生中每周的自习时间不少于22.5小时的人数是A.56 B.60C .120D .1405.(2018江苏)已知5位裁判给某运动员打出的分数的茎叶图如图所示,那么这5位裁判打出的分数的平均数为 ▲ .6.(2016上海理科)某次体检,6位同学的身高(单位:米)分别为1.72,1.78,1.75,1.80,1.69,1.77,则这组数据的中位数是_________(米).7.(2017新课标全国Ⅱ理科)海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比,收获时各随机抽取了100 个网箱,测量各箱水产品的产量(单位:g ).其频率分布直方图如下:(1)设两种养殖方法的箱产量相互独立,记A 表示事件:“旧养殖法的箱产量低于50g ,新养殖法的箱产量不低于50g ”,估计A 的概率;(2)填写下面列联表,并根据列联表判断是否有99%的把握认为箱产量与养殖方法有关;(3附:,22()()()()()n ad bc K a b c d a c b d -=++++8.(2017北京理科)为了研究一种新药的疗效,选100名患者随机分成两组,每组各50名,一组服药,另一组不服药.一段时间后,记录了两组患者的生理指标和y的数据,并制成下图,其中“*”表示服药者,“+”表示未服药者.(1)从服药的50名患者中随机选出一人,求此人指标y的值小于60的概率;(2)从图中A,B,C,D四人中随机选出两人,记ξ为选出的两人中指标的值大于1.7的人数,求ξ的分布列和数学期望E(ξ);(3)试判断这100名患者中服药者指标y数据的方差与未服药者指标y数据的方差的大小.(只需写出结论)9.(2016四川理科)我国是世界上严重缺水的国家,某市政府为了鼓励居民节约用水,计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准x(吨),一位居民的月用水量不超过x的部分按平价收费,超出x的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,.1),…,[4,4.5]分成9组,制成了如图所示的频率分布直方图(1)求直方图中a的值;(2)设该市有30万居民,估计全市居民中月均用水量不低于3吨的人数,并说明理由;(3)若该市政府希望使85%的居民每月的用水量不超过标准x(吨),估计x的值,并说明理由.10.(2016北京理科)A ,B ,C 三个班共有100名学生,为调查他们的体育锻炼情况,通过分层抽样获得了部分学生一周的锻炼时间,数据如下表(单位:小时):(2)从A 班和C 班抽出的学生中,各随机选取一人,A 班选出的人记为甲,C 班选出的人记为乙.假设所有学生的锻炼时间相互独立,求该周甲的锻炼时间比乙的锻炼时间长的概率; (3)再从A ,B ,C 三个班中各随机抽取一名学生,他们该周的锻炼时间分别是7,9,8.25(单位:小时).这3个新数据与表格中的数据构成的新样本的平均数记为1μ,表格中数据的平均数记为0μ,试判断0μ和1μ的大小.(结论不要求证明)3.【答案】C【解析】由727781808690826x++++++=,可得6x=.由7082772y++=,可得2y=,624x y∴-=-=,故选C.4.【答案】D【解析】由频率分布直方图知,前两个小矩形的面积之和为(0.01+0.02)×10=0.3,由于0.5-0.3=0.2,则0.20.4×10=5,所以中位数为60+5=65.故选D.5.【解析】(1)估计一个销售季度内市场需求量x的平均数为所以下一个销售季度内的利润T不少于57万元的概率的估计值为0.7.1.【答案】C【解析】对于①,由于一组数据的众数不唯一,故①错误;对于②,一组数据的方差必须是非负数,故②错误;对于③,根据方差的定义知③正确;对于④,根据频率分布直方图中频率的意义知④正确.综上可得①②错误.故选C.2.【答案】A【解析】由茎叶图可知所给数据,其中出现最多的是45,共三次,所以为众数,将所有数据从小到大排列后,中间两数为45,47,故中位数为46.故本题答案为A.3.【答案】B【解析】由图计算可得前四组的频数是22,其中第4组的频数为8,故本题正确答案是7.【答案】C【解析】由茎叶图可知乙的中位数是32342+=33,又甲、乙两组数据的中位数相同,所以m=3.从而甲的平均数为3933273++=33,又甲、乙两组数据的平均数相同,所以323438204n++++=33,解得n=8,所以38 mn=.8.【答案】A【解析】及格的各组的频率和是(0.015+0.030+0.025+0.005)×10=0.75,即及格率为75%; 样本的均值为45×0.10+55×0.15+65×0.15+75×0.30+85×0.25+95×0.05=71, 用这个分数估计总体的分数即得总体的平均分数为71.故选A.【名师点睛】利用频率分布直方图求众数、中位数和平均数时,应注意三点:①最高的小长方形底边中点的横坐标即是众数;②中位数左边和右边的小长方形的面积和是相等的;③平均数是频率分布直方图的“重心”,等于频率分布直方图中每个小长方形的面积乘以小长方形底边中点的横坐标之和.9.【答案】C【解析】∵样本a ,3,5,7的平均数是b ,且a ,b 分别是数列{}()2*2n n N -∈的第2项和第4项, ∴224221,24a b --====C.10.【答案】D【解析】由茎叶图可知甲命中个数的极差为37-8=29,故A 正确; 易知乙命中个数的众数是21,故B 正确; 甲的命中率为=0.535,乙的命中率为=0.4225,所以甲的命中率比乙高,C 正确;甲命中个数的中位数为=23,所以D 不正确.故选D .11.【答案】B【解析】∵消费金额不超过3千元的人数占总人数的,∴第4,5,6组的频率之和为1-0.6=0.4,从图中可知第4组的频率为0.25,∴第5,6组的频率之和为0.4-0.25=0.15,∴消费金额超过4千元的人数为15. 12.【答案】B【解析】设从左到右前3个小组的频率分别为,2,3,第5小组的频数是y ,则230.1520.0521,10,20.052x x x yx +++⨯+⨯=⎧⎪⎨=⎪⨯⎩解得0.1,5,x y =⎧⎨=⎩故选B . 13.【答案】74【解析】由题意知,五个小队的积分分别是70,85,80,60,75, 所以五个小队的积分的平均值为70858060755++++=74,所以五个小队的积分的方差为22222(7074)(8574)(8074)(6074)(7574)5-+-+-+-+-=74.14.【答案】a b =【解析】从图中可知中位数为8387852+=, 平均数为()1757677818387899394958510x =+++++++++=,所以a b =. 15.【答案】58【解析】由频率分布直方图可得参加夏令营的天数在[6,10)的频率为1-(0.04+0.12+0.05)×2=0.58,则参加夏令营的天数在[6,10)的人数为100×0.58=58. 16.【答案】(1)0.04;(2)440【解析】(1)因为所有小长方形的面积之和为1,所以年龄在[25,30)内对应小长方形的高度为[1-(5×0.01+5×0.07+5×0.06+5×0.02)]=0.04.(2)年龄在[25,35)内的频率为0.04×5+0.07×5=0.55,人数为0.55×800=440.17.【解析】(1)由已知得a =0.26×100=26,分数区间[60,70)对应的频数为100-8-42-26-8=16, 因而b =16100=0.16. 频率分布直方图如图.(2)(i)设中位数为分,则10×0.008+10×0.016+(-70)×0.042=0.5,得≈76.2.(ii)已知100名报名者可直接进入面试的男女人数比例为3∶5,那么2000名参考人员中,经过第一次考试就可直接进入面试的男性人数为×0.08×2000=60,女性人数为×0.08×2000=100.18.【解析】(1)由于小矩形的面积之和为1, 则,由此可得.该地区高中生一周使用手机时间的平均值为.(2)使用手机时间在的学生有人,使用手机时间在的学生有人,使用手机时间在的学生有人,使用手机时间在的学生有人,故用分层抽样法从使用手机时间在的四组学生中抽样,抽取人数分别为.19.【解析】(1)由题得=,所以.20.【解析】(1甲的方差为()23520.520]+-=,12乙的方差因为甲、乙两种手机的平均数相同,甲的方差比乙的方差小,所以认为甲种手机电池质量更好.(2)由题意得上述6部乙种手机中有3部手机的供电时间大于该种手机供电时间平均值,记它们分别是123,,A A A ,其余的为123,,a a a ,从上述6部乙种手机中随机抽取2部的所有结果为:()()()()12131112,,,,,,,,A A A A A a A a()()()()()1323212223,,,,,,,,,,A a A A A a A a A a ()()()313233,,,,,,A a A a A a ()()()121323,,,,,a a a a a a ,共有15种, 其中恰有一部手机的供电时间大于该种手机供电时间平均值的结果为:()()()111213,,,,,,A a A a A a ()()()()()()212223313233,,,,,,,,,,,A a A a A a A a A a A a ,共有9种,所以所求概率为93155P ==. 21.【解析】(1)男性打分的平均数为555362657170737486816910+++++++++=(分),1.【答案】A【解析】设新农村建设前的收入为M ,而新农村建设后的收入为2M ,则新农村建设前种植收入为0.6M ,而新农村建设后的种植收入为0.74M ,所以种植收入增加了,所以A 项不正确;新农村建设前其他收入我0.04M ,新农村建设后其他收入为0.1M ,故增加了一倍以上,所以B 项正确;新农村建设前,养殖收入为0.3M ,新农村建设后为0.6M ,所以增加了一倍,所以C 项正确;新农村建设后,养殖收入与第三产业收入的综合占经济收入的,所以超过了经济收入的一半,所以D 正确;故选A.2.【答案】A故选A.【名师点睛】将频率分布直方图中相邻的矩形的上底边的中点顺次连接起,就得到一条折线,我们称这条折线为本组数据的频率分布折线图,频率分布折线图的首、尾两端取值区间两端点需分别向外延伸半个组距,即折线图是频率分布直方图的近似,它们比频率分布表更直观、形象地反映了样本数据的分布规律.3.【答案】D【解析】由题图可知各月的平均最低气温都在0o C 以上,A 正确;由题图可知七月的平均温差大于7.5o C ,而一月的平均温差小于7.5o C ,所以七月的平均温差比一月的平均温差大,B 正确;由题图可知三月和十一月的平均最高气温都大约在10o C ,基本相同,C 正确;由题图可知平均最高气温高于20℃的月份有3个,所以不正确.故选D .4.【答案】D【解析】自习时间不少于22.5小时为后三组,其频率和为7.05.2)04.008.016.0(=⨯++,故人数为1407.0200=⨯人,选D.【名师点睛】本题主要考查频率分布直方图,是一道基础题目.从历年高考题目看,图表题。
高考数学(理)总复习备考指导课件:第九章 算法初步、统计与统计案例 第3节 用样本估计总体
【例 1】 (2012·广东高考)某班 100 名学生期中考试语文 · 明
基 础
成绩的频率分布直方图如图 9-3-4 所示,其中成绩分组区
考 情
间是:[50,60),[60,70),[70,80),[80,90),[90,100].
典
例
探
究
课
·
时
提
作
知
业
能
图 9-3-4
菜单
高三一轮总复习理科数学 ·(安徽专用)
=50.
典
例 探
【答案】 B
究
课
·
时
提
作
知
业
能
菜单
高三一轮总复习理科数学 ·(安徽专用)
自
高
主
考
落
体
实
验
· 固
4.(2013·湖北高考)某学员在一次射击测试中射靶
10 次,
· 明
基
考
础 命中环数如下:
情
7,8,7,9,5,4,9,10,7,4.
典
则:(1)平均命中环数为________;
例
探 究
(2)命中环数的标准差为________.
知
业
能
菜单
高三一轮总复习理科数学 ·(安徽专用)
自 主
2.(人教 A 版教材习题改编)若某校高一年级 8 个班参加
高 考
落
体
实 ·
合唱比赛的得分如茎叶图 9-3-1 所示,则这组数据的中位
验 ·
固
基 数和平均数分别是( 和 91.5
B.91.5 和 92
典
C.91 和 91.5
高三一轮总复习理科数学 ·(安徽专用)
2019届高考数学一轮复习第九章统计、统计案例第2讲用样本估计总体课件文新人教版
常见题型
多以选择 题、填空 题、出 现,有时 作为解答 题一部 分,难度 较小, 低、中档 题目,占 5分左右
[知识梳理] 1.统计图表 (1)频率分布直方图的画法步骤 ①求极差(即一组数据中 ②决定 ③将数据 ④列 ⑤画 组距 分组 与 ; ; . 组数 最大值 ; 与 最小值 的差);
频率分布表
[答案] (1)√
2.(2018· 广州模拟)对某商店一个月内每天的顾客人数进行了统 计,得到样本的茎叶图(如图所示),则该样本的中位数、众数、极差 分别是( )
A.46,45,56 C.47,45,56
B.46,45,53 D.45,47,53
[解析] 茎叶图中共有 30 个数据, 所以中位数是第 15 个和第 16 1 个数字的平均数,即2(45+47)=46,排除 C,D;再计算极差,最小 数据是 12,最大数据是 68,所以 68-12=56,故选 A.
(3)茎叶图的画法步骤 第一步:将每个数据分为茎(高位)和叶(低位)两倍分; 第二步:将最小茎与最大茎之间的数按大小次序排成一列; 第三步:将各个数据的叶依次写在其茎的两侧.
2.样本的数字特征 (1)众数、中位数、平均数
数字 特征 定义与求法 一组数据中重复 出现次数 最多 的数 把一组数据按 从小到大的 顺 序排列,处在 中间 位置的一 个数据(或两个数 据的平均数) 优点与缺点 众数通常用于描述变量的值出现次数最 多的数.但显然它对其他数据信息的忽 视使它无法客观地反映总体特征 中位数等分样本数据所占频率,它不受 少数几个极端值的影响,这在某些情况 下是优点,但它对极端值的不敏感有时 也会成为缺点
制定合理的节水方案,对居民用水情况进行了调查.通过抽样,获得 了某年 100 位居民每人的月均用水量(单位:吨).将数据按照[0,0.5), [0.5,1),…,[4,4.5]分成 9 组,制成了如图所示的频率分布直方图.
用样本估计总体分布 课件-高一上学期数学北师大版(2019)必修第一册
思考探究:频率分布直方图的应用
• 思考探究:频率分布直方图的应用
例:暑假期间某班为了增强学生的社会实践能力,把该 班学生分成四个小组
到一果园帮果农测量果树的产 量,某小组来到一片种植苹果的山地,他们随
机选 取 20 株作为样本测量每一株的果实产量(单位 : kg ),获得的数据按照
我们把这样的图称为频率分布直方图.
频率
频率
,即小长方形的高
;
1 纵轴表示
组距
组距
频率
频率;
2 小长方形的面积 组距
组距
3 各个小长方形的面积总和等于 1 .
• 二、频率分布直方图
基于上面的分析,思考:怎样根据样本数据画出频率分布直方图呢?
以教材例3为例,一起探究频率分布直方图的画法
3,分组,
由于8个组的总长度40mm>极差,可取第一组的左端点小于数据最小值,最后一组的
右端点大于数据最大值,分成 [120,125),[125,130), ,[155,160].
• 二、频率分布直方图
频率分布直方图的绘制
4.列表,统计出各组信息,如下表,
• 二、频率分布直方图
频率分布直方图的绘制
• 思考探究:频率分布直方图的应用
例:在某中学举行的物理知识竞赛中,将三个 年级参赛学生的成绩进行整理后分成 5 组,
绘制出 如图所示的频率分布直方图,图中从左到右依次为 第一、第二、第三、第四、
第五小组。已知第三小 组的频数是 15 .
(1 ) 求成绩在 50, 70 内的频率;
2 求这三个年级参赛学生的总人数;
思考探究:频率分布直方图的应用
2019年高三一轮总复习理科数学:10-3用样本估计总体
「应用提示研一研」
1.频率分布直方图的特点 频率
3.茎叶图的优点 茎叶图的优点是不但可以 保留 所有信息,而且可以 随时 记录,这对数据的记 录和表示都能带来方便.
[提醒] 茎叶图中茎是指中间的一列数,叶是从茎的旁边生长出来的数.
4.样本的数字特征
(1)众数、中位数、平均数
数字特征
概念
优点与缺点
众数通常用于描述变量的值出现
众数
一组数据中重复出 次数最多的数.但显然它对其他 现次数 最多 的数 数据信息的忽视使它无法客观地
解析:从小到大排序,即 119,153,157,164,166,203,268,268,335,407,中位数为中 间两数的平均数,即166+2 203=184.5.
答案:184.5
3
考点疑难突破
茎叶图
[题 组 训 练] 1.如图,茎叶图记录了甲、乙两组各五名学生在一次英语听力测试中的成绩(单 位:分).已知甲组数据的中位数为 15,乙组数据的平均数为 16.8,则 x,y 的值分别 为( )
(2)由(1)知,该市 100 位居民中月均用水量不低于 3 吨的频率为 0.06+0.04+0.02 =0.12.
由以上样本的频率分布,可以估计 30 万居民中月均用水量不低于 3 吨的人数为 300 000×0.12=36 000.
(3)设中位数为 x 吨. 因为前 5 组的频率之和为 0.04+0.08+0.15+0.21+0.25=0.73>0.5,前 4 组的频 率之和为 0.04+0.08+0.15+0.21=0.48<0.5, 由 0.50×(x-2)=0.5-0.48, 解得 x=2.04. 故可估计居民月均用水量的中位数为 2.04 吨.
