新北师大版初中九年级数学下册1.4 解直角三角形1公开课优质课教学设计
九年级数学初三下册:1.4 解直角三角形1教案 教学设计

1.4 解直角三角形1.正确运用直角三角形中的边角关系解直角三角形;(重点)2.选择适当的关系式解直角三角形.(难点)一、情境导入如图,美丽的徒骇河宛如一条玉带穿城而过,沿河两岸的滨河大道和风景带成为该市的一道新景观.在数学课外实践活动中,小亮在河西岸滨河大道一段AC 上的A ,B 两点处,利用测角仪分别对东岸的观景台D 进行了测量,分别测得∠DAC =60°,∠DBC =75°.又已知AB =100米,根据以上条件你能求出观景台D 到徒骇河西岸AC 的距离吗?二、合作探究探究点:解直角三角形【类型一】 利用解直角三角形求边或角已知在Rt △ABC 中,∠C =90°,∠A 、∠B 、∠C 的对应边分别为a 、b 、c ,按下列条件解直角三角形.(1)若a =36,∠B =30°,求∠A 的度数和边b 、c 的长;(2)若a =6,b =6,求∠A 、∠B 的度数和边c 的长.解析:(1)已知直角边和一个锐角,解直角三角形;(2)已知两条直角边,解直角三角形.解:(1)在Rt △ABC 中,∵∠B =30°,a =36,∴∠A =90°-∠B =60°,ac =cosB ,即c =a cosB =3632=243,∴b =12c=12×243=123; (2)在Rt △ABC 中,∵a =6,b =6,∴c =62,∠A =∠B =45°.方法总结:解直角三角形时应求出所有未知元素,尽可能地选择包含所求元素与两个已知元素的关系式求解. 变式训练:见《学练优》本课时练习“课堂达标训练” 第6题【类型二】构造直角三角形解决长度问题一副直角三角板如图放置,点C在FD 的延长线上,AB ∥CF ,∠F =∠ACB =90°,∠E =30°,∠A =45°,AC =122,试求CD 的长.解析:过点B 作BM ⊥FD 于点M ,求出BM 与CM 的长度,然后在△EFD 中可求出∠EDF =60°,利用解直角三角形解答即可.解:过点B 作BM ⊥FD 于点M ,在△ACB 中,∠ACB =90°,∠A =45°,AC =122,∴BC =AC =12 2.∵AB ∥CF ,∴BM =sin45°BC =122×22=12,CM =BM =12.在△EFD 中,∠F =90°,∠E =30°,∴∠EDF =60°,∴MD =BMtan60°=43,∴CD =CM -MD =12-4 3.方法总结:解答此类题目的关键是根据题意构造直角三角形,然后利用所学的三角函数的关系进行解答.变式训练:见《学练优》本课时练习“课后巩固提升” 第7题【类型三】 构造直角三角形解决面积问题在△ABC 中,∠B =45°,AB =2,∠A =105°,求△ABC 的面积.解析:过点A 作AD ⊥BC 于点D ,根据勾股定理求出BD 、AD 的长,再根据解直角三角形求出CD 的长,最后根据三角形的面积公式解答即可.解:过点A 作AD ⊥BC 于点D ,∵∠B =45°,∴∠BAD =45°,∴AD =BD =22AB =22×2=1.∵∠A =105°,∴∠CAD =105°-45°=60°,∴∠C =30°,∴CD =AD tan30°=133=3,∴S △ABC =12(CD +BD)·AD =12×(3+1)×1=3+12.方法总结:解答此类题目的关键是根据题意构造直角三角形,然后利用所学的三角函数的关系进行解答.变式训练:见《学练优》本课时练习“课堂达标训练” 第7题三、板书设计 解直角三角形1.解直角三角形的概念2.解直角三角形的基本类型及其解法 3.解直角三角形的简单应用本节课的设计,力求体现新课程理念.给学生自主探索的时间,给学生宽松和谐的氛围,让学生学得更主动、更轻松,力求在探索知识的过程中,培养探索能力、创新能力、合作能力,激发学生学习数学的积极性、主动性.。
北师大版九年级数学下册1.4 :解直角三角形 教案设计

1.在直角三角形中,由已知元素求出所有未知元素的过程,叫做解直角三角形.
2.解直角三角形的依据
(1)三边之间的关系:a2+b2=c2(勾股定理)
(2)锐角之间的关系:∠A+∠B=900;
(3)边角之间的关系:
(4)面积公式:
四、例题讲解:
例1.在Rt△ABC中,∠C=90°,AC= 6 ,BC = ,解这个直角三角形.
(1)……………
(2)……………
(3)……………
(4)……………
例1.
解:
例2.
解:
教学设 计
学科:数学
教师:
年级:九年级
课题
1.4解直角三角形
授课人
教
学
目
标
1、理解直角三角形中,除直角外其余五个元素之间的关系,了解确定一个三角形和解直角三角形所需条件的一致性.
2、经历对满足什么条件可解直角三角形的问题分析过程,体会从一般到特殊的思考方法.
3、会解直角三角形;会选择合理的算法.
4、通过师生共同探索,体验独立思考与合作交流的学习过程;渗透分类讨论、化归等数学思想,激发学生探索数学的热情和兴趣.
(2)已知∠A﹣∠B=30°,b+c=30,解这个直角三角形.
(3) 已知∠A=60°,△ABC的面积S= ,解这个三角形.
学生根据自己完成《导学案》内容,并回答,为本课的学习提供理论依据.
通过复习特殊角的三角函数值,为下面解直角三角形提供数据支持
通过学生自主探究,发现直角三角形中除直角外,再至少需要两个元素,才能求出其它元素,并且这两个元素中至少有一条是边.
培养学生自主探究能力和对知识的应用能力
通过对定义的认识,寻找解直角三角形的理论依据,通过这一活动,将新的知识与所学知识有机结合起来.
初中北师大版数学九年级下册1.4【教学设计】《解直角三角形》

《解直角三角形》教学设计解直角三角形是义务教育课程标准实验教科书(北师版)《数学》九年级下册第一章第四节内容,本章主要研究直角三角形的边角关系;本节要求知道解直角三角形的概念、理解直角三角形中五个元素的关系。
通过综合运用勾股定理,掌握解直角三角形,逐步形成分析问题、解决问题的能力。
渗透数形结合的数学思想,养成良好的学习习惯。
能够用计算器辅助解决含三角函数值计算的实际问题。
因此本节的重点是掌握利用直角三角形边角关系解直角三角形【知识与能力目标】1.知道解直角三角形的概念、理解直角三角形中五个元素的关系。
2.通过综合运用勾股定理,掌握解直角三角形,逐步形成分析问题、解决问题的能力。
3.渗透数形结合的数学思想,养成良好的学习习惯。
【过程与方法目标】1.利用解三角形的知识,解决含三角函数的实际问题,提高用现代工具解决实际问题的能力。
2.发现实际问题中的边角关系,提高学生有条理地思考和表达的能力。
【情感态度价值观目标】1.积极参与数学活动,体会解决问题后的快乐。
2.形成实事求是的态度。
【教学重点】 掌握利用直角三角形边角关系解直角三角形【教学难点】锐角三角比在解直角三角形中的灵活运用教师准备课件、多媒体;学生准备;练习本;一、创设情景引入新课:如图所示,一棵大树在一次强烈的地震中倒下,树干断处离地面3米且树干与地面的夹角是30°。
大树在折断之前高多少米?由30°直角边等于斜边的一半就可得AB=6米。
分析树高是AB+AC=9米。
由勾股定理容易得出BC的长为3 米。
当然对于特殊锐角的解题用几何定理比较简单,也可以用锐角三角函数来解此题。
二、知识回顾问题:1.在一个三角形中共有几条边?几个内角?(引出“元素”这个词语)2.直角三角形ABC中,∠C=90°,a、b、c、∠A、∠B这五个元素间有哪些等量关系呢?讨论复习师白:Rt△ABC的角角关系、三边关系、边角关系分别是什么?总结:直角三角形的边、角关系(板书)(PPT)(1)两锐角互余∠A+∠B=90°;(2)三边满足勾股定理a2+b2=c2;(3)边与角关系sinA=cosB=,cosA=sinB=,tanA=cotB=,cotA=tanB=。
新北师大版九年级数学下册第一章1.4解直角三角形教案

另外,在实践活动环节,虽然大多数同学都能够积极参与,但在操作过程中,还是有一些同学对测量和计算步骤不够熟悉。这说明我在教学中还需要加强对学生动手能力的培养,让他们在实际操作中更好地理解和掌握知识。
(2)勾股定理的运用:在讲解解题过程时,强调勾股定理的应用,提醒学生注意检查计算结果是否符合勾股定理;
(3)实际问题解决:教授学生如何从实际问题中提取关键信息,建立数学模型,运用锐角三角函数求解。如:在测量电线杆高度的问题中,引导学生通过画图、列方程等方式,将实际问题转化为数学问题,从而解决问题。
四、教学流程
(一)导入新课(用时5分钟)
同学们,今天我们将要学习的是《解直角三角形》这一章节。在开始之前,我想先问大家一个问题:“你们在日常生活中是否遇到过需要测量物体高度或距离的情况?”(如测量树的高度)这个问题与我们将要学习的内容密切相关。通过这个问题,我希望能够引起大家的兴趣和好奇心,让我们一同探索解直角三角形的奥秘。
新北师大版九年级数学下册第一章1.4解直角三角形教案
一、教学内容
新北师大版九年级数学下册第一章1.4节,主要围绕解直角三角形展开,本节课将涵盖以下内容:
1.锐角三角函数的定义及其互化关系;
2.解直角三角形的两种情况:已知两直角边求斜边和一直角边;已知斜边及一直角边求另一直角边;
3.运用勾股定理与锐角三角函数解决实际问题;
3.成果展示:每个小组将向全班展示他们的讨论成果和实验操作的结果。
(四)学生小组讨论(用时10分钟)
1.讨论主题:学生将围绕“解直角三角形在实际生活中的应用”这一主题展开讨论。他们将被鼓励提出自己的观点和想法,并与其他小组成员进行交流。
北师大版九年级下册 1.4 解直角三角形 教案
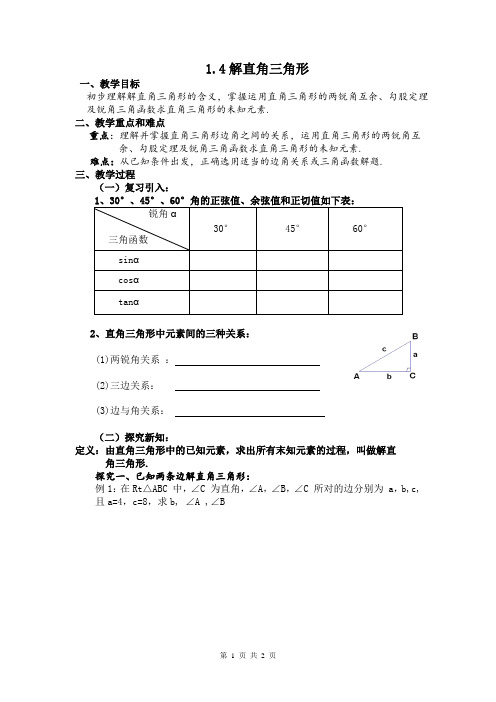
1.4解直角三角形一、教学目标初步理解解直角三角形的含义,掌握运用直角三角形的两锐角互余、勾股定理及锐角三角函数求直角三角形的未知元素.二、教学重点和难点重点:理解并掌握直角三角形边角之间的关系,运用直角三角形的两锐角互余、勾股定理及锐角三角函数求直角三角形的未知元素.难点:从已知条件出发,正确选用适当的边角关系或三角函数解题.三、教学过程(一)复习引入:2、直角三角形中元素间的三种关系:定义:由直角三角形中的已知元素,求出所有末知元素的过程,叫做解直角三角形.探究一、已知两条边解直角三角形:例1:在Rt△ABC 中,∠C 为直角,∠A,∠B,∠C 所对的边分别为 a,b,c, 且a=4,c=8,求b, ∠A ,∠B练习1:在Rt△ABC中,∠C=90°,∠A,∠B,∠C所对的边分别为a, b, c,根据下列条件求出直角三角形的其他元素:(1)19,a c==(2)a b==探究二、已知一条边和一个锐角(两个已知元素中至少有一条边)解直角三角形:例2:在Rt△ABC 中,∠C为直角,∠A,∠B,∠C所对的边分别为a,b,c,且b=30,∠B=30°求这个三角形的其他元素(边长精确到1)。
练习2:在Rt△ABC 中,∠C为直角,∠A,∠B,∠C所对的边分别为a,b,c,且c=8,∠A=370,解直角三角形。
(参考数据:tan370≈0.75,sin370≈0.6,cos370≈0.8)(三)中考链接:1、如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,则下列结论不正确的是()A、sinADBAB= B、sinACBBC=C、sinADBAC= D、sinCDBAC=2、在Rt△ACB中,∠C=90°,AB=10,4sin5A=,3cos5A=,3tan A=4,则BC的长为()A、6B、7.5C、8D、12.5(四)、课堂小结:1、解直角三角形除直角外,至少要知道两个元素(这两个元素中至少有一条边)2、解直角三角形的条件可分为两大类:①、已知一锐角、一边(一锐角、一直角边或一斜边)②、已知两边(一直角边,一斜边或者两条直角边)。
北师大版数学九年级下册1.4《解直角三角形》说课稿

北师大版数学九年级下册1.4《解直角三角形》说课稿一. 教材分析北师大版数学九年级下册1.4《解直角三角形》是本册教材中的重要内容。
本节课主要介绍了解直角三角形的方法和应用。
在学习本节课之前,学生已经掌握了勾股定理和直角三角形的性质,这为学习本节课奠定了基础。
教材通过引入直角三角形的边长关系,引导学生探索解直角三角形的方法,进而运用到实际问题中。
本节课的内容在高考和日常生活中都有广泛的应用,对于培养学生的数学素养和解题能力具有重要意义。
二. 学情分析九年级的学生在数学方面已经有了一定的基础,对于勾股定理和直角三角形的性质已经有了初步的认识。
但是,学生在解直角三角形方面可能还存在一些困难,如对解题方法的掌握不熟练,应用能力较弱等。
因此,在教学过程中,需要关注学生的这些实际情况,有针对性地进行教学。
三. 说教学目标1.知识与技能目标:使学生掌握解直角三角形的方法,能够熟练运用勾股定理和直角三角形的性质解决实际问题。
2.过程与方法目标:通过自主探究、合作交流,培养学生的动手操作能力和解决问题的能力。
3.情感态度与价值观目标:激发学生学习数学的兴趣,培养学生的耐心和自信心,使学生感受到数学在生活中的应用。
四. 说教学重难点1.教学重点:解直角三角形的方法和应用。
2.教学难点:如何引导学生掌握解直角三角形的思路,以及如何将所学知识应用于实际问题中。
五. 说教学方法与手段在本节课的教学过程中,我将采用自主探究、合作交流、讲授法等多种教学方法。
同时,利用多媒体课件和实物模型等教学手段,帮助学生更好地理解和掌握解直角三角形的方法。
六. 说教学过程1.导入:通过复习勾股定理和直角三角形的性质,引出本节课的主题——解直角三角形。
2.自主探究:让学生独立思考,探索解直角三角形的方法,引导学生发现解题规律。
3.合作交流:学生分组讨论,分享解题方法和心得,互相学习,提高解题能力。
4.讲解与演示:教师对解直角三角形的方法进行讲解,并通过多媒体课件和实物模型进行演示,帮助学生更好地理解和掌握。
《解直角三角形》示范公开课PPT教学课件【九年级数学下册北师大版】
(1)由“直角三角形的两个锐角互余”求出另一个锐角;
已知一边和一锐角解直角三角形的方法:
例1 在Rt△ABC中,已知∠C=90°,a=35,b=28,求∠A,∠B的度数(结果精确到1°)和c的长(结果精确到1).
至少知道几个元素,就可以求出其他的元素?
在Rt△ABC中,如果已知其中两边的长,你能求出这个三角形的其他元素吗?
如图,在Rt△ABC中,已知∠C=90°,a=4,c=8.解这个直角三角形.
a
b
c
也可以换成其他两边试一试!
在Rt△ABC中,a=4,c=8,
由勾股定理求直角边b,
再由∠A+∠B=90°求出∠B.
A
B
C
35°
4.如图,一个长为 10 m 的梯子斜靠在墙上,梯子的顶端距地面的垂直距离为 8 m.分别求梯子的底端距墙多少米,梯子与墙和梯子与地面的夹角(精确到1°)?
解:如图,依题Байду номын сангаас知,在Rt△ABC中, ∠C=90°,AB=10 m,BC=8 m.
∴ ∠A ≈37°,
所以,梯子的底端距墙6米,梯子与墙和梯子与地面的夹角分别为53°和37°.
a
b
c
在Rt△ABC中,∠C=90°,其他边角关系如下:
(2) 三边之间的关系: a2+b2=_____;
(1) 锐角之间的关系:∠A+∠B=_____;
(3) 边与角之间的关系:sinA=cosB=_____,cosA=sinB=_____, tanA=_____,tanB=_______.
由“直角三角形两个锐角互余”可得∠B,
北师大版九年级下册数学教案设计:1.4解直角三角形
1.4解直角三角形教学目标:1、知识技能:了解解直角三角形的含义,并能熟练地根据题目中的已知条件解直角三角形.2、数学思考:通过综合运用直角三角形的相关知识解直角三角形,逐步培养学生分析问题、解决问题的能力.3、问题解决:掌握解直角三角形所用的边角关系,能适当地选择锐角三角函数解直角三角形.4、情感态度:在教学中逐步培养学生分析问题、解决问题的能力,渗透数形结合的数学思想和分类的数学思想.教学重点:根据条件解直角三角形.教学难点:三角函数在解直角三角形中的灵活运用.教学方法:引导演示法课堂讨论法学习方法:自主探究合作交流教具准备:课件教师用的含60°的直角三角板学生用的含60°的直角三角板教学过程:第一环节:复习引入1、(1)在直角三角形中,除直角外共有几个元素?(2)如图,在Rt△ABC 中∠C=90°,a、b、c、∠A、∠B这五个元素间有哪些等量关系呢?图一三边之间的关系锐角之间的关系边角之间的关系(以∠A为例)第二环节:探究新知1、在上面引入课题的基础上教师直接给出解直角三角形的定义:由直角三角形中的已知元素,求出所有末知元素的过程,叫做解直角三角形2、提问 问题:(1)、解直角三角形至少需要几个条件?(2)、解直角三角形的条件可分为哪几类? 目的:通过以上两个问题让学生明白,除了直角外,已知一个元素没法解直角三角形,到底两个元素行不行?给后面的内容做铺垫,我们抱着试一试的心态去解决问题,当然,已知两个元素时,我们要对元素进行分类: 类 别 :①角角AA②边边 SS ③边角 SA3、例题讲解探究一、已知两个锐角解直角三角形例1、 在Rt △ABC 中,∠C=90°,∠A, ∠B ,∠C 所对的对边分别为a,b,c,且∠A=30 ,∠B= 60° ,你能求出a,b,c 的值吗?教法:演示法,教师用直角三角板引导学生,发现含30°,60°角的直角三角形不唯一结论:在直角三角形中已知两个锐角,不能解直角三角形。
北师大版九年级数学下册:第一章1.4《解直角三角形》精品说课稿
北师大版九年级数学下册:第一章 1.4《解直角三角形》精品说课稿一. 教材分析北师大版九年级数学下册第一章《相似三角形》的1.4节《解直角三角形》是本节课的重点内容。
本节内容是在学生已经掌握了直角三角形的性质、勾股定理以及相似三角形的基础知识的基础上进行学习的。
通过本节课的学习,使学生能够掌握解直角三角形的方法,提高解决实际问题的能力。
二. 学情分析九年级的学生已经具备了一定的数学基础,对于直角三角形、勾股定理和相似三角形的相关知识有一定的了解。
但是,对于如何运用这些知识解决实际问题,部分学生可能还存在一定的困难。
因此,在教学过程中,要注重引导学生将理论知识与实际问题相结合,提高解决问题的能力。
三. 说教学目标1.知识与技能目标:让学生掌握解直角三角形的方法,能够运用勾股定理和相似三角形的知识解决实际问题。
2.过程与方法目标:通过观察、操作、思考、讨论等过程,培养学生的动手操作能力、思维能力和合作能力。
3.情感态度与价值观目标:让学生体验数学在生活中的应用,提高学生学习数学的兴趣和自信心。
四. 说教学重难点1.教学重点:让学生掌握解直角三角形的方法,能够运用勾股定理和相似三角形的知识解决实际问题。
2.教学难点:如何引导学生将理论知识与实际问题相结合,提高解决问题的能力。
五. 说教学方法与手段1.教学方法:采用问题驱动法、案例教学法、合作学习法等,引导学生主动探究、合作交流。
2.教学手段:利用多媒体课件、实物模型、黑板等辅助教学,提高教学效果。
六. 说教学过程1.导入:通过复习直角三角形、勾股定理和相似三角形的相关知识,引出本节课的主题——解直角三角形。
2.探究:让学生观察、分析直角三角形的特点,引导学生发现解直角三角形的方法,并通过小组合作,总结出解直角三角形的步骤。
3.应用:教师提出一些实际问题,让学生运用所学的知识解决,巩固解直角三角形的方法。
4.拓展:引导学生思考如何解决更复杂的直角三角形问题,激发学生的求知欲。
1.4解直角三角形(教案)2023-2024学年北师大版九年级数学下册
(三)实践活动(用时10分钟)
1.分组讨论:学生们将分成若干小组,每组讨论一个与解直角三角形相关的实际问题。
2.实验操作:为了加深理解,我们将进行一个简单的实验操作,如使用三角板和尺子来实际测量并计算物体的高度。
四、教学流程
(一)导入新课(用时5分钟)
同学们,今天我们将要学习的是《解直角三角形》这一章节。在开始之前,我想先问大家一个问题:“你们在日常生活中是否遇到过需要测量高度或距离的情况?”(如测量树的高度)这个问题与我们将要学习的内容密切相关。通过这个问题,我希望能够引起大家的兴趣和好奇心,让我们一同探索解直角三角形的奥秘。
3.成果分享:每个小组将选择一名代表来分享他们的讨论成果。这些成果将被记录在黑板上或投影仪上,以便全班都能看到。
(五)总结回顾(用时5分钟)
今天的学习,我们了解了直角三角形的基本概念、三角函数的重要性和应用,以及勾股定理的实际运用。同时,我们也通过实践活动和小组讨论加深了对解直角三角形原理的理解。我希望大家能够掌握这些知识点,并在日常生活中灵活运用。最后,如果有任何疑问或不明白的地方,请随时向我提问。
3.能够运用勾股定理求解直角三角形的各边长。
二、核心素养目标
本章节的核心素养目标旨在培养学生以下能力:
1.理解直角三角形概念,提高空间观念和几何直观;
2.掌握三角函数的计算及应用,发展学生的数据分析与数学抽象能力;
3.应用勾股定理解决问题,加强学生的逻辑推理和数学建模能力;
4.通过解决实际生活中的直角三角形问题,提高学生的数学应用意识和解决实际问题的能力;
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1
1.4 解直角三角形
1.正确运用直角三角形中的边角
关系解直角三角形;(重点)
2.选择适当的关系式解直角三角
形.(难点)
一、情境导入
如图,美丽的徒骇河宛如一条玉
带穿城而过,沿河两岸的滨河大道和
风景带成为该市的一道新景观.在数
学课外实践活动中,小亮在河西岸滨
河大道一段AC上的A,B两点处,利
用测角仪分别对东岸的观景台D进行
了测量,分别测得∠DAC=60°,∠
DBC=75°.又已知AB
=100米,根据
以上条件你能求出观景台D到徒骇河
西岸AC的距离吗?
二、合作探究
探究点:解直角三角形
【类型一】 利用解直角三角形求
边或角
已知在Rt△ABC中,∠C=
90°,∠A、∠B、∠C的对应边分别
为a、b、c,按下列条件解直角三角形.
(1)若a=36,∠B=30°,求∠
A
的度数和边b、c的长;
(2)若a=6,b=6,求∠A、∠B的
度数和边c的长.
解析:(1)已知直角边和一个锐角,
解直角三角形;(2)已知两条直角边,
解直角三角形.
解:(1)在Rt△ABC中,∵∠B=
30°,a=36,∴∠A=90°-∠B=
60°,ac =cosB,即c=acosB=3632=
2
243,∴b=12c=12×243=123;
(2)在Rt△ABC中,∵a=6,b=6,
∴c=62,∠A=∠B=45°.
方法总结:解直角三角形时应求
出所有未知元素,尽可能地选择包含所求元素与两个已知元素的关系式求解. 变式训练:见《学练优》本课时练习“课堂达标训练” 第6题 【类型二】 构造直角三角形解决长度问题 一副直角三角板如图放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,∠E=30°,∠A=45°,AC=122,试求CD的长. 解析:过点B作BM⊥FD于点M,求出BM与CM的长度,然后在△EFD中可求出∠EDF=60°,利用解直角三角形解答即可. 解:过点B作BM⊥FD于点M,在△ACB中,∠ACB=90°,∠A=45°,AC=122,∴BC=AC=122.∵AB∥CF,∴BM=sin45°BC=122×22=12,CM=BM=12.在△EFD中,∠F=90°,∠E=30°,∴∠
EDF
=60°,∴MD=BMtan60°=43,∴
CD
=CM-MD=12-43.
方法总结:解答此类题目的关键
是根据题意构造直角三角形,然后利
用所学的三角函数的关系进行解答.
变式训练:见《学练优》本课时
练习“课后巩固提升” 第7题
【类型三】 构造直角三角形解决
面积问题
在△ABC中,∠B=45°,
AB=2,∠A=105°,求△ABC
的面
积.
解析:过点A作AD⊥BC于点D,
根据勾股定理求出BD、AD的长,再
3
根据解直角三角形求出CD的长,最后
根据三角形的面积公式解答即可. 解:过点A作AD⊥BC于点D,∵∠B=45°,∴∠BAD=45°,∴AD=BD=22AB=22×2=1.∵∠A=105°,∴∠CAD=105°-45°=60°,∴∠C=30°,∴CD=ADtan30°=133=3,∴S△ABC=12(CD+BD)·AD=12×(3+1)×1=3+12. 方法总结:解答此类题目的关键是根据题意构造直角三角形,然后利用所学的三角函数的关系进行解答. 变式训练:见《学练优》本课时练习“课堂达标训练” 第7题 三、板书设计 解直角三角形 1.解直角三角形的概念 2.解直角三角形的基本类型及其解法 3.解直角三角形的简单应用 本节课的设计,力求体现新课程理
念.给学生自主探索的时间,给学生
宽松和谐的氛围,让学生学得更主动、
更轻松,力求在探索知识的过程中,
培养探索能力、创新能力、合作能力,
激发学生学习数学的积极性、主动性.
