2011学年度高三一模考试数学试卷文理合卷

合集下载

上海市2011届高三数学一模试卷(浦东新区)

上海市2011届高三数学一模试卷(浦东新区)浦东新区2010学年度第一学期期末质量抽测高三数学试卷（文科）注意：1. 答卷前，考生务必在试卷上指定位置将学校、班级、姓名、考号填写清楚. 2. 本试卷共有23道试题，满分150分，考试时间120分钟.一、填空题（本大题共有14题，满分56分）只要求直接填写结果，每个空格填对得4分，否则一律得零分.1．函数yx 1的定义域为__________________. 2 x2．函数y log3(x 1)的反函数是__________________.3．若五个数a,0,1,2,3的平均数为1，则这五个数的方差等于__________________. 4．方程cosxsinx0的解为__________________.sinxcosx5．若“条件：2 x 4”是“条件：3m 1 x m”的充分条件，则m的取值范围是__________________.6．从一个底面半径和高都是R的圆柱中，挖去一个以圆柱的上底为底,下底面的中心为顶点的圆锥，得到一个如图（1）所示的几何体，那么这个几何体的体积是__________________.7．在等差数列{an}中，则数列{an}a1 a2 a3 0,a4 a5 a6 18，的通项公式为__________________.8．在ABC中，AB ,BC 4, ACB 60 ，则AC的长等于__________________. 9．已知[26,3]，则sin 的取值范围是__________________.图（2）10．执行如图（2）所示的程序框图，若输入x 0，则输出y的值为__________________.11．方程x2 (4 i)x 4 2i 0有实数根b，则b __________________.12．世博期间，5人去某地铁站参加志愿者活动，该地铁站有4个出口，要求一号出口必须安排2个人，其余每个出口都要有志愿者服务，不同安排方法有__________________种（用数值表示）.(n为奇数) n13．设定义N上的函数f(n) n，an f(1) f(2) f(3) f(2n)，f()(n为偶数) 2那么a3 a2 __________________.14．在某条件下的汽车测试中，车驾驶员在一次加满油后的连续行驶过程中从汽车仪表盘得到如下信息：注：油耗=加满油后已用油量加满油后已行驶距离，可继续行驶距离=汽车剩余油量当前油耗，平均油耗指定时间内的用油量.指定时间内的行驶距离从上述信息可以推断在10∶00―11∶00这1小时内_________(填上所有正确判断的序号)① 向前行驶的里程为80公里；② 向前行驶的里程不足80公里；③ 平均油耗超过9.6升/100公里；④ 平均油耗恰为9.6升/100公里；⑤ 平均车速超过80公里/小时．二、选择题(本大题共有4题，满分16分) 每小题都给出四个选项，其中有且只有一个选项是正确的，选对得4分，否则一律得零分.15．若函数f(x) sin(x )是偶函数，则可取的一个值为（）A．B．2C．4D．816．关于数列{an}有以下命题，其中错误的命题为（）A．若n 2且an 1 an 1 2an，则{an}是等差数列B．设数列{an}的前n项和为Sn，且2Sn 1 an，则数列{an}的通项an ( 1)n 1 C．若n 2且an 1an 1 an，则{an}是等比数列D．若{an}是等比数列，且m，n，k N,m n 2k，则aman ak22b，17．一颗骰子连续掷两次，朝上的点数依次为a、使a 2b的概率是（）A．13 B．14 C．16D．11218．点O在ABC所在平面内，给出下列关系式：（1）；（2）；（3）0；（4）( ) ( ) 0．则点O依次为ABC的（A．内心、外心、重心、垂心B．重心、外心、内心、垂心C．重心、垂心、内心、外心D．外心、内心、垂心、重心三、解答题（本大题共有5题，满分78分）解答下列各题必须写出必要的步骤．19．（本小题满分14分，第1小题满分6分，第2小题满分8分）已知向量m (ax, a),n (ax,a),，其中a 0且a 1，（1）当x为何值时，；（2）解关于x的不等式 .）20．（本小题满分14分，第1小题满分6分，第2小题满分8分）野营活动中，学生在平地上用三根斜杆搭建一个正三棱锥形的三脚支架P ABC（如图3）进行野炊训练，将炊事锅看作一个点Q，用吊绳PQ将炊事锅吊起烧水（锅的大小忽略不计）. 已知PC 130cm，A、B 两点间距离为3cm.（1）设PQ的延长线与地面ABC的交点为O，求cos PCO的值；（2）若使炊事锅Q到各条斜杆的距离都等于30cm，试求吊绳PQ的长.图（3）21．（本小题满分16分，第1小题满分6分，第2小题满分10分）已知f(x) x（1）b 2时，求f(x)的值域；b3,x [1,2] x（2）b 2时，f(x)0恒成立，求b的取值范围．22．（本小题满分16分，第1小题满分4分，第2小题满分5分，第3小题满分7分）（1）若对于任意的n N，总有n 2AB成立，求常数A,B的值；n(n 1)nn 1（2）在数列{an}中，a1n 211} ，an 2an 1 （n 2，n N），求证{an2n 1n(n 1)是等比数列，并求通项an；（3）在（2）题的条件下，设bn n 1，从数列{bn}中依次取出第k1项，第k2项，2(n 1)an 21？若存在，求出m的值；不存7第kn项，按原来的顺序组成新的数列{cn}，其中cn bkn，其中kn 1 kn k1 m N .试问是否存在正整数m，使lim(c1 c2 cn) n在，说明理由.23．（本题满分18分，第1小题满分6分，第2小题满分6分，第3小题满分6分）已知函数f(x)，如果存在给定的实数对（a,b），使得f(a x) f(a x) b 恒成立，则称f(x)为“S-函数”.（1）判断函数f1(x) x,f2(x) 3x是否是“S-函数”；（2）若f3(x) tanx是一个“S-函数”，求出所有满足条件的有序实数对(a,b)；（3）若定义域为R的函数f(x)是“S-函数”，且存在满足条件的有序实数对(0,1)和(1,1)，,2012]时函数f(x)的值域. 当x [0,1]时，f(x)的值域为[1,2]，求当x [ 2012浦东新区2010学年度第一学期期末质量抽测高三数学试卷（文科）注意：1. 答卷前，考生务必在试卷上指定位置将学校、班级、姓名、考号填写清楚. 2. 本试卷共有23道试题，满分150分，考试时间120分钟.一、填空题（本大题共有14题，满分56分）只要求直接填写结果，每个空格填对得4分，否则一律得零分.1．函数yx 1的定义域为______[1,2) (2, )_______. 2 x2．函数y log3(x 1)的反函数是____y 3x 1 （x R）____. 3．若五个数a,0,1,2,3的平均数为1，则这五个数的方差等于_____2______. 4．方程cosxsinxk,k Z______. 0的解为_____x 24sinxcosx5．若“条件：2 x 4”是“条件：3m 1 x m”的充分条件，则m的取值范围是___( , 4]___.6．从一个底面半径和高都是R的圆柱中，挖去一个以圆柱的上底为底,下底面的中心为顶点的圆锥，得到一个如图（1）所示的几何体，那么这个几何体的体积是____2 3R_____. 37．在等差数列{an}中，a1 a2 a3 0,a4 a5 a6 18，则数列{an}的通项公式为____an 2n 4_____.8．在ABC中，AB ,BC 4, ACB 60 ，则AC的长等于_____1或3_______. 9．已知[26,1]，则sin 的取值范围是____[,1]_____. 32图（2）10．执行如图（2）所示的程序框图，若输入x 0，则输出y的值为_____3______. 211．方程x2 (4 i)x 4 2i 0有实数根b，则b _____ 2______.12．世博期间，5人去某地铁站参加志愿者活动，该地铁站有4个出口，要求一号出口必须安排2个人，其余每个出口都要有志愿者服务，不同安排方法有____60____种（用数值表示）.(n为奇数) n13．设定义N上的函数f(n) n，an f(1) f(2) f(3) f(2n)，f()(n为偶数) 2那么a3 a2 ____16_____.14．在某条件下的汽车测试中，车驾驶员在一次加满油后的连续行驶过程中从汽车仪表盘得到如下信息：注：油耗=加满油后已用油量加满油后已行驶距离，可继续行驶距离=汽车剩余油量当前油耗，平均油耗指定时间内的用油量.指定时间内的行驶距离从上述信息可以推断在10∶00―11∶00这1小时内__②③__(填上所有正确判断的序号)①行使了80公里；②行使不足80公里；③平均油耗超过9.6升/100公里；④平均油耗恰为9.6升/100公里；⑤ 平均车速超过80公里/小时．解题过程：实际用油为7.38，行驶距离为7.38100 76.875，所以①错误，②正确. 9.6设L为已用油量，△L为一个小时内的用油量，S为已行驶距离，△S为一个小时内已行的距离LS 9.5得V V 9.6S 9.6 S L L9.6 S S9.5S V 9.6S 9.6 S，V 0.1S 9.6 S，所以③正确，④错误.⑤由②知错误.V0.1S9.6 9.6. S S二、选择题(本大题共有4题，满分16分) 每小题都给出四个选项，其中有且只有一个选项是正确的，选对得4分，否则一律得零分.15．若函数f(x) sin(x )是偶函数，则可取的一个值为（B ）A．B．2C．4D．816．关于数列{an}有以下命题，其中错误的命题为（C ）A．若n 2且an 1 an 1 2an，则{an}是等差数列B．设数列{an}的前n项和为Sn，且2Sn 1 an，则数列{an}的通项an ( 1)n 1 C．若n 2且an 1an 1 an，则{an}是等比数列D．若{an}是等比数列，且m，n，k N ,m n 2k，则aman ak22b，17．一颗骰子连续掷两次，朝上的点数依次为a、使a 2b的概率是（D ）1111B．C．D．***-*****．点O在ABC所在平面内，给出下列关系式：A．（1）；（2）；0；（3）（4）( ) ( ) 0．则点O依次为ABC的（C ）A．内心、外心、重心、垂心B．重心、外心、内心、垂心C．重心、垂心、内心、外心D．外心、内心、垂心、重心三、解答题（本大题共有5题，满分78分）解答下列各题必须写出必要的步骤．19．（本小题满分14分，第1小题满分6分，第2小题满分8分）已知向量m (ax, a),n (ax,a),，其中a 0且a 1，（1）当x为何值时，m n；（2）解关于x的不等式m n m n.解：（1）因为,所以0, 2分得a2xa2 0，即a2x a2. 4分所以2x 2，即x 1，∴当x 1时， . 6分（2，∴( )2 ( )2，0.所以a a 0，即a a. 10分当0 a 1时，x 1，当a 1时，x 1, 综上，当0 a 1时，不等式的解集为(1, );当a 1时，不等式的解集为( ,1). 14分2x22x220．（本小题满分14分，第1小题满分6分，第2小题满分8分）野营活动中，学生在平地上用三根斜杆搭建一个正三棱锥形的三脚支架炊事锅吊起烧水（锅的大小忽略不计）. 已知PC 130cm，A、B 两点间距离为3cm. （1）设PQ的延长线与地面ABC的交点为O，求cos PCO的值；（2）若使炊事锅Q到各条斜杆的距离都等于30cm，试求吊绳PQ的长. 解：（1）设P点在平面ABC上的射影为点O，连接CO，CO50在Rt△POC中，cos PCOP ABC（如图3）进行野炊训练，将炊事锅看作一个点Q，用吊绳PQ将5. 5分135即cos PCO的值为. 6分13（2）在Rt△POC中，解得PO 120，作QD PC交PC于D点，由QD 30，得PQQD3078. 12分sin QPD13故吊绳PQ的长78cm. 14分21．（本小题满分16分，第1小题满分6分，第2小题满分10分）已知f(x) x（1）b 2时，求f(x)的值域；b3,x [1,2] x（2）b 2时，f(x)0恒成立，求b的取值范围．解：（1）当b=2时，f(x) x23,x [1,2] . x因为f(x)在[1,2]上单调递减，在[2,2]上单调递增, ２分所以f(x)的最小值为f(2) 22 3. ４分又因为f(1) f(2) 0, ５分所以f(x)的值域为[22 3,0]．6分（2）（。

2011年高考一模试卷(三)数学试题(文)人教A版

2011年高考一模试卷(三)数学试题(文)人教A版D束A ．2B ．1C ．23 D ．135．如图所示程序框图，标平面中一点P a b c ()，，，输出相应的点 Q a b c ()，， 2 3 1()，，，则 P Q ，间的距离为） “←”或“：=” ） A ．0 BC D ．6．已知条件p ：不等式210xmx ++>条件q ：指数函数()(3)xf x m =+则p 是q 的（）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件7．设平面区域D 是由双曲线2214y x-=的两条渐近线和直线680x y --=所围成三角形的边界及内部．当,x y D ∈()时，222x y x++的最大值为（） A ．24B ．25C ．4D ．78．已知函数f x ()的定义域为 1 5-[，]，部分对应值如下表．f x ()的导函数y f x '=()的图象如图所示．下列关于函数f x ()的命题： ①函数y f x =()是周期函数； ②函数f x ()在0 2[，]是减函数；③如果当 1 x t ∈-[，]时，f x ()的最大值是2，那么t 的最大值为4；④当12a <<时，函数y f x a =-()有4个零点．其中真命题的个数有（）A ．4个B ．3个C ．2个D ．1个9．如图所示的方格纸中有定点 O P Q E F G H ,,,,,,，则OP OQ +=（）A ．OHB ．OGC ．FOD ．EO 10．设22)1(则,3005满足约束条件,y x x y x y x y x ++⎪⎩⎪⎨⎧≤≥+≥+-的最大值为（）A ． 80 B．C ． 25D ． 17211．有三个命题：①垂直于同一个平面的两条直线平行；②过平面α的一条斜线l 有且仅有一个平面与α垂直；③异面直线a 、b 不垂直，那么过a 的任一个平面与b 都不垂直。

2011年高三数学一模试题(15)：算法初步分类解析

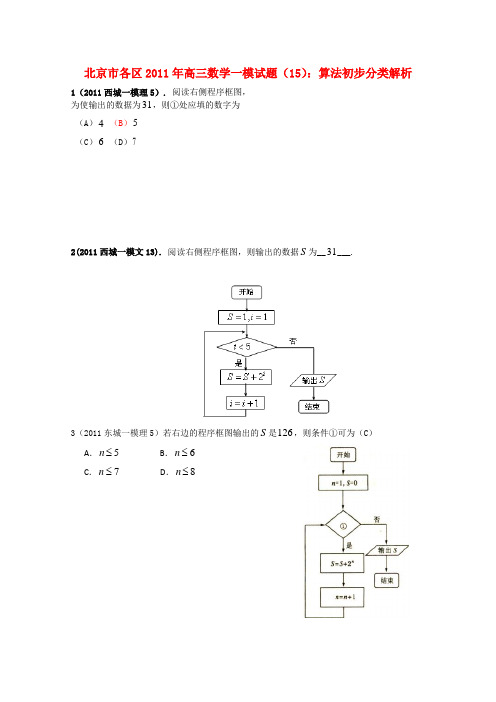
北京市各区2011年高三数学一模试题（15）：算法初步分类解析1（2011西城一模理5）. 阅读右侧程序框图，为使输出的数据为31，则①处应填的数字为（A ）4 （B ）5 （C ）6 （D ）72(2011西城一模文13). 阅读右侧程序框图，则输出的数据S 为__31___.3（2011东城一模理5）若右边的程序框图输出的S 是126，则条件①可为（C ） A ．5n ≤ B ．6n ≤ C ．7n ≤ D ．8n ≤4（2011东城一模文6）若右边的程序框图输出的S 是126，则条件①可为（A ）5n ≤ （B ）6n ≤ （C ）7n ≤ （D ）8n ≤6（2011朝阳一模理12）．执行右图所示的程序框图，若输入 5.2x =-，则输出y 的值为 0.8 ．开始输入x是 ?i ≥5输出y结束 x y =|2|y x =-否0, 0y i ==1i i =+7(2011海淀一模理4)．执行如图所示的程序框图，若输出x的值为23，则输入的x值为 CA．0B．1 C．2D．118（2011石景山一模理10）. 阅读如图所示的程序框图，运行该程序后输出的k的值是______4_________．9(2011朝阳一模文13)．执行右图所示的程序框图，若输入 5.2x=，则输出y的值为0.8．21x x=+是否3n≤1n n=+x输入开始1n=x输出结束10(2011海淀一模文4). 执行如图所示的程序框图，若输入x 的值为2，则输出的x 值为 CA. 25 B ．24 C. 23 D ．2211(2011门头沟一模文11).右上图所示为一个判断直线0=++C By Ax 与圆222)()(r b y a x =-+-的位置关系的程序框图的一部分，在？处应该填上C Bb Aa ++ .11题图）12(2011石景山一模文10).阅读如图所示的程序框图，运行该程序后输出的k的值是________4_______．。

2011丰台区高三一模数学试题(含答案)理科

y C y x2y x =(1,1)B丰台区2011年高三年级第二学期统一练习（一）数学（理科）2011.3 一、本大题共8小题，每小题5分，共40分．在每小题列出的四个选项中，选出符合题目要求的一项． 1．已知集合U =R ，2{560}A x x x =-+≥，那么U A =ð(A) {2x x <或3}x > (B) {23}x x << (C) {2x x ≤或3}x ≥ (D) {23}x x ≤≤2．6的展开式中常数项是 (A) -160(B) -20(C) 20(D) 1603．已知平面向量a ，b 的夹角为60°，=a ，||1=b ，则|2|+=a b(A) 2(C)(D)4．设等差数列{}n a 的公差d ≠0，14a d =．若k a 是1a 与2k a 的等比中项，则k = (A) 3或-1 (B) 3或1(C) 3 (D) 1 5．设m ，n 是两条不同的直线，α，β，γ是三个不同的平面．有下列四个命题： ① 若m β⊂，αβ⊥，则m α⊥； ② 若α//β，m α⊂，则m //β；③ 若n α⊥，n β⊥，m α⊥，则m β⊥； ④ 若αγ⊥，βγ⊥，m α⊥，则m β⊥．其中正确命题的序号是 (A) ①③ (B) ①②(C)③④ (D) ②③6．已知函数3,0,()ln(1),>0.x x f x x x ⎧≤=⎨+⎩ 若f (2-x 2)>f (x )，则实数x 的取值范围是(A) (,1)(2,)-∞-⋃+∞ (B) (,2)(1,)-∞-⋃+∞ (C) (1,2)-(D) (2,1)-7．从如图所示的正方形OABC 区域内任取一个点(,)M x y ，则点M 取自阴影部分的概率为(A)12(B)13(C) 14(D)168．对于定义域和值域均为[0，1]的函数f (x )，定义1()()f x f x =，21()(())f x f f x =，…，1()(())n n f x f f x -=，n =1，2，3，…．满足()n f x x =的点x ∈[0，1]称为f 的n 阶周期点．设12,0,2()122,1,2x x f x x x ⎧≤≤⎪⎪=⎨⎪-<≤⎪⎩ 则f 的n 阶周期点的个数是(A) 2n(B) 2(2n -1)(C) 2n(D) 2n 2二、填空题：本大题共6小题，每小题5分，共30分．9．如图所示，在平面直角坐标系xOy 中，角α的终边与单位圆交于点A ，点A 的纵坐标为45，则cos α= ． 10．双曲线的焦点在x 轴上，实轴长为4，离心率为3，则该双曲线的标准方程为，渐近线方程为．11．已知圆M ：x 2+y 2-2x -4y +1=0，则圆心M 到直线43,31,x t y t =+⎧⎨=+⎩（t 为参数）的距离为．12．如图所示，过⊙O 外一点A 作一条直线与⊙O 交于C ，D 两点，AB 切⊙O 于B ，弦MN 过CD 的中点P ．已知AC =4，AB =6，则MP ·NP = ． 13．对某种花卉的开放花期追踪调查，调查情况如下：则这种卉的平均花期为___天．14．将全体正奇数排成一个三角形数阵： 1 3 5 7 9 11 1315 17 19 …… 按照以上排列的规律，第n 行（n ≥3）从左向右的第3个数为．三、解答题：本大题共6小题，共80分．解答应写出文字说明，演算步骤或证明过程． 15.（本小题共13分）在△ABC 中，a ，b ，c 分别为内角A ，B ，C 的对边，且b 2+c 2-a 2=bc ．BAαxy O（Ⅰ）求角A 的大小；（Ⅱ）设函数2cos 2cos 2sin 3)(2x x x x f +=，当)(B f 取最大值23时，判断△ABC的形状．16.（本小题共14分）如图，在四棱锥P -ABCD 中，底面ABCD 为直角梯形，AD //BC ，∠ADC =90°，平面P AD ⊥底面ABCD ，Q 为AD 的中点，M 是棱PC 上的点，P A =PD =2，BC =12AD =1，CD（Ⅰ）若点M 是棱PC 的中点，求证：P A // 平面BMQ ；（Ⅱ）求证：平面PQB ⊥平面P AD ；（Ⅲ）若二面角M -BQ -C 为30°，设PM =tMC ，试确定t 的值．17.（本小题共13分）某商场在店庆日进行抽奖促销活动，当日在该店消费的顾客可参加抽奖．抽奖箱中有大小完全相同的4个小球，分别标有字“生”“意”“兴”“隆”．顾客从中任意取出1个球，记下上面的字后放回箱中，再从中任取1个球，重复以上操作，最多取4次，并规定若取出“隆”字球，则停止取球．获奖规则如下：依次取到标有“生”“意”“兴”“隆”字的球为一等奖；不分顺序取到标有“生”“意”“兴”“隆”字的球，为二等奖；取到的4个球中有标有“生”“意”“兴”三个字的球为三等奖．（Ⅰ）求分别获得一、二、三等奖的概率；（Ⅱ）设摸球次数为ξ，求ξ的分布列和数学期望．PABCD QM18.（本小题共13分）已知函数3211()(0)32f x x ax x b a =+++≥，'()f x 为函数()f x 的导函数．（Ⅰ）设函数f (x )的图象与x 轴交点为A ，曲线y =f (x )在A 点处的切线方程是33y x =-，求,a b 的值；（Ⅱ）若函数()'()ax g x e f x -=⋅，求函数()g x 的单调区间．19.（本小题共14分）已知点(1,0)A -，(1,0)B ，动点P 满足||||PA PB +=P 的轨迹为W ．（Ⅰ）求W 的方程；（Ⅱ）直线1y kx =+与曲线W 交于不同的两点C ，D ，若存在点(,0)M m ，使得CM DM =成立，求实数m 的取值范围．20.（本小题共13分）已知123{(,,,,)n n S A A a a a a ==，0i a =或1，1,2,,}i n =(2)n ≥，对于,n U V S ∈，(,)d U V 表示U 和V 中相对应的元素不同的个数．（Ⅰ）令(0,0,0,0,0)U =，存在m 个5V S ∈，使得(,)2d U V =，写出m 的值；（Ⅱ）令0(0,0,0,,0)n W =个，若,n U V S ∈，求证：(,)(,)(,)d U W d V W d U V +≥；（Ⅲ）令123(,,,,)n U a a a a =，若n V S ∈，求所有(,)d U V 之和．（考生务必将答案答在答题卡上，在试卷上作答无效）丰台区2011年高三年级第二学期数学统一练习（一）数学（理科）参考答案一、选择题：本大题共8小题，每小题5分，共40分．二、填空题：本大题共6小题，每小题5分，共30分．9．35- 10．221432x y -=，y =± 11．212．25413．16天（15.9天给满分） 14．n 2-n +5 注：两个空的填空题第一个空填对得3分，第二个空填对得2分．三、解答题：本大题共6小题，共80分．解答应写出文字说明，演算步骤或证明过程． 15.（本小题共13分）解：（Ⅰ）在△ABC 中，因为b 2+c 2-a 2=bc ，由余弦定理 a 2= b 2+c 2-2bc cos A 可得cos A =12．(余弦定理或公式必须有一个，否则扣1分) ……3分∵ 0<A <π ，（或写成A是三角形内角） ……………………4分∴3A π=． ……………………5分（Ⅱ）2cos 2cos 2sin 3)(2x x x x f +=11cos 22x x =++ ……………………7分1sin()62x π=++， ……………………9分∵3A π= ∴2(0,)3B π∈ ∴5666B πππ<+< （没讨论，扣1分） …………………10分∴当62B ππ+=，即3B π=时，()f B 有最大值是PABCD QM23． ……………………11分又∵3A π=， ∴3C π=∴△ABC 为等边三角形． ……………………13分16.（本小题共14分）证明：（Ⅰ）连接AC ，交BQ 于N ，连接MN ． ……………………1分∵BC ∥AD 且BC =12AD ，即BC //AQ ． ∴四边形BCQA 为平行四边形，且N 为AC 中点，又∵点M 在是棱PC 的中点，∴ MN // P A ……………………2分 ∵ MN ⊂平面MQB ，P A ⊄平面MQB ，…………………3分 ∴ P A // 平面MBQ ． ……………………4分（Ⅱ）∵AD // BC ，BC =12AD ，Q 为AD 的中点，∴四边形BCDQ 为平行四边形，∴CD//BQ ． ……………………6分∵∠ADC =90° ∴∠AQB =90° 即QB ⊥AD ．又∵平面P AD ⊥平面ABCD 且平面P AD ∩平面ABCD=AD ， ……………………7分∴BQ ⊥平面P AD ． ……………………8分∵BQ ⊂平面PQB ， ∴平面PQB ⊥平面P AD ． ……………………9分另证：AD // BC ，BC =12AD ，Q 为AD 的中点 ∴ BC // DQ 且BC = DQ ，∴ 四边形BCDQ 为平行四边形，∴CD // BQ ． ∵ ∠ADC =90° ∴∠AQB =90°即QB ⊥AD ． ……………………6分∵ P A =PD ， ∴PQ⊥AD ． ……………………7分∵ PQ ∩BQ =Q ，∴AD ⊥平面PBQ ． ……………………8分∵ AD ⊂平面P AD ， ∴平面PQB ⊥平面P AD ． ……………………9分（Ⅲ）∵P A =PD ，Q 为AD 的中点， ∴PQ ⊥AD ．C∵平面P AD ⊥平面ABCD ，且平面P AD ∩平面ABCD=AD ， ∴PQ ⊥平面ABCD ．……………10分（不证明PQ ⊥平面ABCD 直接建系扣1分）如图，以Q 为原点建立空间直角坐标系．则平面BQC 的法向量为(0,0,1)n =；(0,0,0)Q ，P ，B，(1C -分设(,,)M x y z ，则(,,PM x y z =，(1,)MC x y z =---， ∵PM tMC =，∴(1))(x t x y ty z t z =--⎧⎪=⎨⎪=-⎩）， ∴1t x t y z ⎧=-⎪+⎪⎪=⎨⎪⎪=⎪⎩……………………12分在平面MBQ 中，QB =，(1t QM t =-+， ∴平面MBQ法向量为(3,0,)m t =．……………………13分∵二面角M -BQ -C 为30°， c o s 303n m n m︒⋅===+ ∴3t =． …………………14分17.（本小题共13分）解：（Ⅰ）设“摸到一等奖、二等奖、三等奖”分别为事件A ，B ，C ． ……1分则P (A )=111114444256⨯⨯⨯=，（列式正确，计算错误，扣1分） ………3分P (B )33341-A =2565= （列式正确，计算错误，扣1分） ………5分三等奖的情况有：“生，生，意，兴”；“生，意，意，兴”；“生，意，兴，兴”三种情况．P (C )222444111*********()()()444444444444A A A =⨯⨯⨯⨯+⨯⨯⨯⨯+⨯⨯⨯⨯964=．…7分（Ⅱ）设摸球的次数为ξ，则1,2,3ξ=． ……8分1(1)4P ξ==， 313(2)4416P ξ==⨯=，3319(3)44464P ξ==⨯⨯=，27(4)1(1)(2)(3)64P P P P ξξξξ==-=-=-==．（各1分）故取球次数ξ的分布列为139271234 2.754166464E ξ=⨯+⨯+⨯+⨯=．(约为2.7) …13分18.（本小题共13分）解：（Ⅰ）∵3211()(0)32f x x ax x b a =+++≥， ∴2'()1f x x ax =++． (1)分∵()f x 在(1,0)处切线方程为33y x =-， ∴'(1)3(1)0f f =⎧⎨=⎩， ……………………3分∴1=a ，611-=b ．（各1分） ……………………5分（Ⅱ）'()()ax f x g x e =21axx ax e ++=()x R ∈．'()g x =22(2)(1)()ax ax ax x a e a x ax e e +-++2[(2)]axx ax a e -=-+-． ……………………7分①当0a =时，'()2g x x =，()g x 的单调递增区间为(0,)+∞，单调递减区间为(,0)-∞． ……………………9分②当a >时，令'(g x =，得x =或2x a a=- ……………………10分（ⅰ）当20a ->，即0a <时，()g x 的单调递增区间为22(0,)a a -，单调递减区间为(,0)-∞，22(,)a a-+∞；……11分（ⅱ）当20a a-=，即a ='()g x =2220x x e -=-≤，故()g x 在(,)-∞+∞单调递减； ……12分（ⅲ）当20a a-<，即a >()g x 在22(,0)a a-上单调递增，在(0,)+∞，22(,)a a --∞上单调递 ………13分综上所述，当0a =时，()gx 的单调递增区间为(0,)+∞，单调递减区间为(,0)-∞；当0a <时，()g x 的单调递增区间为22(0,)a a-，单调递减区间为(,0)-∞，当a =()g x 的单调递减区间为(,)-∞+∞；当a >()g x 的单调递增区间为22(,0)a a-，单调递减区间为(0,)+∞，22(,)a a--∞．（“综上所述”要求一定要写出来）19.（本小题共14分）解：（Ⅰ）由椭圆的定义可知，动点P 的轨迹是以A ，B 为焦点，长轴长为……2分∴1c =，a =22b =． ……3分W 的方程是22132x y +=． …………4分（另解：设坐标1分，列方程1分，得结果2分）（Ⅱ）设C ，D 两点坐标分别为11(,)C x y 、22(,)D x y ，C ，D 中点为00(,)N x y ．由221132y kx x y =+⎧⎪⎨+=⎪⎩ 得 22(32)630k x kx ++-=． ……6分所以122632kx x k +=-+ …………7分∴12023232x x k x k +==-+，从而0022132y kx k =+=+． ∴MN 斜率2002232332MN y k k k x m m k +==---+． ………9分又∵CM DM =， ∴CD MN ⊥， ∴222132332k k k m k +=---+ 即 232k m k =-+ …10分当0k =时，0m =； ……11分当0k ≠时，212323k m k k k=-=-++]126,0()0,126[⋃-∈． ……13分故所求m 的取范围是]126,126[-． ……14分（可用判别式法）20.（本小题共13分）解：（Ⅰ）2510C =； ………3分（Ⅱ）证明：令123(,,)n u a a a a =……，123(,,)n v b b b b =……∵0i a =或1，0i b =或1；当0i a =，0i b =时，||i a +||0i b =||i i a b =-当0i a =，1i b =时，||i a +||1i b =||i i a b =-当1i a =，0i b =时，||i a +||1i b =||i i a b =-当1i a =，1i b =时，||i a +||2i b =||0i i a b ≥-=故||i a +||i b ||i i a b ≥-∴(,)(,)d u w d v w +=123()n a a a a ++++123()n b b b b +++++123(||||||)n a a a a =++|++|123(||||||)n b b b b +++|++|112233(||||||)n n a b a b a b a b ≥-+-+--|++|(,)d u v = ………8分（Ⅲ）解：易知n S 中共有2n 个元素，分别记为(1,2,,2)n k v k =123(,,)n v b b b b =…… ∵0i b =的k v 共有12n -个，1i b =的k v 共有12n -个． ∴21(,)nk k d u v =∑ =1111111122(2|0|2|1|2|0|2|120|21|)n n n n n n n n a a a a a a -------+-+-+---|++|+| =12n n - ……13分∴21(,)n kk d u v =∑=12n n -．法二：根据（Ⅰ）知使(,)k d u v r =的k v 共有r n C 个∴21(,)nk k d u v =∑=012012n n n n n C C C n C ++++ 21(,)n k k d u v =∑=120(1)(2)0n n n n n n nn Cn C n C C --+-+-++ 两式相加得 21(,)n kk d u v =∑=12n n -（若用其他方法解题，请酌情给分）。

2011年北京市海淀区高三一模数学(理)试题Word版带答案

海淀区高三年级第二学期期中练习数学（理科） 2011。

4选择题（共40分）一、选择题:本大题共8小题,每小题5分，共40分。

在每小题列出的四个选项中,选出符合题目要求的一项。

1、已知集合{}30<<∈=x x A R ，{}42≥∈=x x B R ，则=B A A. {}32<<x x B 。

{}32<≤x x C. {}322<≤-≤x x x 或 D 。

R2．已知数列{}n a 为等差数列，n S 是它的前n 项和。

若21=a ，123=S ，则=4S A ．10 B ．16 C ．20 D ．243. 在极坐标系下，已知圆C 的方程为2cos ρθ=，则下列各点在圆C 上的是 A ．1,3π⎛⎫- ⎪⎝⎭B ． 1,6π⎛⎫⎪⎝⎭C．34π⎫⎪⎭D ．54π⎫⎪⎭4．执行如图所示的程序框图，若输出x 的值为23,则输入的x 值为A ．0B ．1C ．2D ．11 5．已知平面l =αβ，m 是α内不同于l 的直线,那么下列命题中错．误．的是 A ．若β//m ，则l m // B ．若l m //，则β//m C ．若β⊥m ,则l m ⊥ D ．若l m ⊥,则β⊥m6。

已知非零向量,,a b c 满足++=a b c ０，向量,a b 的夹角为120，且||2||=b a ,则向量a 与c 的夹角为 A ．︒60 B ．︒90 C ．︒120D ． ︒1507。

如果存在正整数ω和实数ϕ使得函数)(cos )(2ϕω+=x x f （ω,ϕ为常数)的图象如图所示(图象经过点（1,0）），那么ω的值为A ．1B ．2C ． 3D 。

4 8．已知抛物线M ：24yx ，圆N ：222)1(r y x =+-（其中r 为常数，0>r ）.过点（1，0）的直线l 交圆N 于C 、D 两点，交抛物线M 于A 、B 两点，且满足BD AC =的直线l 只有三条的必要条件是A ．(0,1]r ∈B ．(1,2]r ∈C ．3(,4)2r ∈ D ．3[,)2r ∈+∞非选择题（共110分）二、填空题：本大题共6小题，每小题5分,共30分。

2011丰台区高三一模数学试题及答案(文).doc

北京市丰台区2011年高三年级第二学期统一练习（一）数学试题（文）注意事项：1．答题前，考生务必将答题卡上的学校、年级、班级、姓名、准考证号用黑色字迹签字笔填写清楚，并认真核对条形码上的准考证号、姓名，在答题卡上的“条形码粘贴区”贴好条形码。

2．本次考试所有答题均在答题卡上完成。

选择题必须用2B 铅笔以正确的填涂方式将各小题对应选项涂黑，如需改动，用橡皮擦干净后再选涂其它选项。

非选择题区域使用标准黑色字迹签字笔书写，要求字体工整、字迹清楚。

3．请严格按照答题卡上题号在相应答题区内作答，超出答题区域书写的答案无效，在试题、草稿纸上答题无效。

4．请保持答题卡卡面清洁，不要装订、不要折叠、不要破损。

一、本大题共8小题，每小题5分，共40分。

在每小题给出的四个选项中，选出符合题目要求的一项。

1．已知集合2,{|560},U U R A x x x C A ==-+≥那么=（）A ．(|23)x x x <>或B ．{|23}x x <<C ．{|23}x x x ≤≥或D ．{|23}x x ≤≤2．“a=2”是“直线2010ax y x y +=++=与直线平行”的（）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件3．已知平面向量,a b 的夹角为60,||4,||3,||a b a b ︒==+则= （）A ．37BC ．13D 4．记集合22{(,)|4}{(,)|20,0}A x y x y B x y x y y =+≤=+-≤≥和集合表示的平面区域分别为12,ΩΩ，若在区域1Ω内任取一点(,)M x y ，则点M 落在区域2Ω内的概率为（）A ．12πB ．1πC ．14D ．24ππ- 5．如图所示，O 是正方体ABCD —A 1B 1C 1D 1对角线A 1C 与AC 1的交点，E 为棱BB 1的中点，则空间四边形OEC 1D 1在正方体各面上的正投影不可能．．．是（）6．程序框图如图所示，若输入a 的值是虚数单位i ，则输出的结果是（） A ．-1 B ．i-1 C ．0 D ．-i7．设m ，n 是两条不同的直线，α，β，γ是三个不同的平面。

2011年高三数学一模试题(10)：平面向量分类解析

十、平面向量1（2011西城一模理4）．设向量(1,sin )θ=a ，(3sin ,1)θ=b ，且//a b ，则cos2θ等于（A ）31-（B ）32-（C ）32（D ）31 2（2011西城一模文10）.设向量(1,sin )θ=a ，b (1,cos )θ=，若35⋅=a b ，则θ2sin =___45-___. 3（2011东城一模理4）已知平面上不重合的四点P ，A ，B ，C 满足0PA PB PC ++=，且AB AC mAP +=，那么实数m 的值为（C ）（A ）2 （B ）3（C ）4 （D ）54（2011东城一模文11）已知向量a ，b ，c 满足-+=20a b c ，且⊥a c ，||2=a ，||1=c ，则||=b5（2011朝阳一模理11）．如右图，在三角形ABC 中，D ，E 分别为BC ，AC 的中点，F 为AB 上的点，且B 4A AF =. 若AD x AF y AE =+ ，则实数x = 2 ，实数y = 1 .6（2011丰台一模理3．）、已知平面向量a ，b的夹角为60°，=a ，||1=b ，则|2|+=a b(C) (A) 2(C)(D)7（2011海淀一模理6.）、已知非零向量,,a b c 满足++=a b c ０，向量,a b 的夹角为120，且||2||=b a ，则向量a 与c 的夹角为 B A ．︒60 B ．︒90 C ．︒120D ． ︒150 8（2011门头沟一模理6）、．直线:(2)2l y k x =-+ 将圆22:220C x y x y +--=平分，则直线l 的方向向量是 A BC D E ··F（A ）(2,2)-（B ）(2,2) （C ）(3,2)- （D ）(2,1)9（2011石景山一模理5）、．已知O 是ABC △所在平面内一点，D 为BC 边中点，且02=++OC OB OA ，那么（）A ．AO OD =B ．2AO OD =C ．3AO OD = D ．2AO OD =10(2011朝阳一模文11). 已知两点(3, 2)A --，(3,6)B ，点C 满足AC CB =，则点C 的坐标是 (0, 2) ，AB AC ⋅= 50 .11(2011丰台文3)．已知平面向量a ，b 的夹角为60°，||4=a ，||3=b ，则||+a b 等于(B)(A) 37 (B) (C) 1312(2011海淀一模文13). 已知向量(,2),(1,)a x b y ==，其中,0x y ≥.若4≤a b ，则y x -的取值范围为[4,2]- .13(2011门头沟一模文9).向量)4,3(-=a ，，若5-=⋅，那么向量b a ,的夹角是 32π 14(2011石景山一模文5)．已知O 是ABC △所在平面内一点，D 为BC 边中点，且2=++，那么（）A ．AO OD =B ．2AO OD =C ．3AO OD = D ．2AO OD =15(2011石景山一模文12)．已知向量(1,)a n =，(1,)b n =-，若b a +2与b 垂直，则n =_________．。

2011丰台区高三一模数学试题(含答案)理科.doc

xy OAC y x=2y x =(1,1)B丰台区2011年高三年级第二学期统一练习（一）数学（理科）2011.3 一、本大题共8小题，每小题5分，共40分．在每小题列出的四个选项中，选出符合题目要求的一项． 1．已知集合U =R ，2{560}A x x x =-+≥，那么U A =ð(A) {2x x <或3}x > (B) {23}x x << (C) {2x x ≤或3}x ≥ (D) {23}x x ≤≤2．6的展开式中常数项是 (A) -160(B) -20(C) 20(D) 1603．已知平面向量a ，b 的夹角为60°，=a ，||1=b ，则|2|+=a b(A) 2(C)(D)4．设等差数列{}n a 的公差d ≠0，14a d =．若k a 是1a 与2k a 的等比中项，则k = (A) 3或-1 (B) 3或1(C) 3 (D) 1 5．设m ，n 是两条不同的直线，α，β，γ是三个不同的平面．有下列四个命题： ① 若m β⊂，αβ⊥，则m α⊥； ② 若α//β，m α⊂，则m //β；③ 若n α⊥，n β⊥，m α⊥，则m β⊥； ④ 若αγ⊥，βγ⊥，m α⊥，则m β⊥．其中正确命题的序号是 (A) ①③ (B) ①②(C)③④ (D) ②③6．已知函数3,0,()ln(1),>0.x x f x x x ⎧≤=⎨+⎩ 若f (2-x 2)>f (x )，则实数x 的取值范围是(A) (,1)(2,)-∞-⋃+∞ (B) (,2)(1,)-∞-⋃+∞ (C) (1,2)-(D) (2,1)-7．从如图所示的正方形OABC 区域内任取一个点(,)M x y ，则点M 取自阴影部分的概率为(A)12(B)13(C) 14(D)168．对于定义域和值域均为[0，1]的函数f (x )，定义1()()f x f x =，21()(())f x f f x =，…，1()(())n n f x f f x -=，n =1，2，3，…．满足()n f x x =的点x ∈[0，1]称为f 的n 阶周期点．设12,0,2()122,1,2x x f x x x ⎧≤≤⎪⎪=⎨⎪-<≤⎪⎩ 则f 的n 阶周期点的个数是(A) 2n(B) 2(2n -1)(C) 2n(D) 2n 2二、填空题：本大题共6小题，每小题5分，共30分．9．如图所示，在平面直角坐标系xOy 中，角α的终边与单位圆交于点A ，点A 的纵坐标为45，则cos α= ． 10．双曲线的焦点在x 轴上，实轴长为4，离心率为3，则该双曲线的标准方程为，渐近线方程为．11．已知圆M ：x 2+y 2-2x -4y +1=0，则圆心M 到直线43,31,x t y t =+⎧⎨=+⎩（t 为参数）的距离为．12．如图所示，过⊙O 外一点A 作一条直线与⊙O 交于C ，D 两点，AB 切⊙O 于B ，弦MN 过CD 的中点P ．已知AC =4，AB =6，则MP ·NP = ． 13．对某种花卉的开放花期追踪调查，调查情况如下：则这种卉的平均花期为___天．14．将全体正奇数排成一个三角形数阵： 1 3 5 7 9 11 1315 17 19 …… 按照以上排列的规律，第n 行（n ≥3）从左向右的第3个数为．三、解答题：本大题共6小题，共80分．解答应写出文字说明，演算步骤或证明过程． 15.（本小题共13分）在△ABC 中，a ，b ，c 分别为内角A ，B ，C 的对边，且b 2+c 2-a 2=bc ．BAαxy O（Ⅰ）求角A 的大小；（Ⅱ）设函数2cos 2cos 2sin 3)(2x x x x f +=，当)(B f 取最大值23时，判断△ABC的形状．16.（本小题共14分）如图，在四棱锥P -ABCD 中，底面ABCD 为直角梯形，AD //BC ，∠ADC =90°，平面P AD ⊥底面ABCD ，Q 为AD 的中点，M 是棱PC 上的点，P A =PD =2，BC =12AD =1，CD．（Ⅰ）若点M 是棱PC 的中点，求证：P A // 平面BMQ ；（Ⅱ）求证：平面PQB ⊥平面P AD ；（Ⅲ）若二面角M -BQ -C 为30°，设PM =tMC ，试确定t 的值．17.（本小题共13分）某商场在店庆日进行抽奖促销活动，当日在该店消费的顾客可参加抽奖．抽奖箱中有大小完全相同的4个小球，分别标有字“生”“意”“兴”“隆”．顾客从中任意取出1个球，记下上面的字后放回箱中，再从中任取1个球，重复以上操作，最多取4次，并规定若取出“隆”字球，则停止取球．获奖规则如下：依次取到标有“生”“意”“兴”“隆”字的球为一等奖；不分顺序取到标有“生”“意”“兴”“隆”字的球，为二等奖；取到的4个球中有标有“生”“意”“兴”三个字的球为三等奖．（Ⅰ）求分别获得一、二、三等奖的概率；（Ⅱ）设摸球次数为ξ，求ξ的分布列和数学期望．PABCD QM18.（本小题共13分）已知函数3211()(0)32f x x ax x b a =+++≥，'()f x 为函数()f x 的导函数．（Ⅰ）设函数f (x )的图象与x 轴交点为A ，曲线y =f (x )在A 点处的切线方程是33y x =-，求,a b 的值；（Ⅱ）若函数()'()axg x e f x -=⋅，求函数()g x 的单调区间．19.（本小题共14分）已知点(1,0)A -，(1,0)B ，动点P 满足||||PA PB +=P 的轨迹为W ．（Ⅰ）求W 的方程；（Ⅱ）直线1y kx =+与曲线W 交于不同的两点C ，D ，若存在点(,0)M m ，使得CM DM =成立，求实数m 的取值范围．20.（本小题共13分）已知123{(,,,,)n n S A A a a a a ==，0i a =或1，1,2,,}i n =(2)n ≥，对于,n U V S ∈，(,)d U V 表示U 和V 中相对应的元素不同的个数．（Ⅰ）令(0,0,0,0,0)U =，存在m 个5V S ∈，使得(,)2d U V =，写出m 的值；（Ⅱ）令0(0,0,0,,0)n W =个，若,n U V S ∈，求证：(,)(,)(,)d U W d V W d U V +≥；（Ⅲ）令123(,,,,)n U a a a a =，若n V S ∈，求所有(,)d U V 之和．（考生务必将答案答在答题卡上，在试卷上作答无效）丰台区2011年高三年级第二学期数学统一练习（一）数学（理科）参考答案一、选择题：本大题共8小题，每小题5分，共40分．二、填空题：本大题共6小题，每小题5分，共30分．9．35- 10．221432x y -=，y =± 11．2 12．25413．16天（15.9天给满分） 14．n 2-n +5 注：两个空的填空题第一个空填对得3分，第二个空填对得2分．三、解答题：本大题共6小题，共80分．解答应写出文字说明，演算步骤或证明过程． 15.（本小题共13分）解：（Ⅰ）在△ABC 中，因为b 2+c 2-a 2=bc ，由余弦定理 a 2= b 2+c 2-2bc cos A 可得cos A =12．(余弦定理或公式必须有一个，否则扣1分) ……3分∵ 0<A <π ，（或写成A是三角形内角） ……………………4分∴3A π=． ……………………5分（Ⅱ）2cos 2cos 2sin 3)(2xx x x f +=11cos 22x x =++ ……………………7分1sin()62x π=++， ……………………9分∵3A π= ∴2(0,)3B π∈ ∴5666B πππ<+< （没讨论，扣1分） …………………10分∴当62B ππ+=，即3B π=时，()f B 有最大值是PABCD QM23． ……………………11分又∵3A π=， ∴3C π=∴△ABC 为等边三角形． ……………………13分16.（本小题共14分）证明：（Ⅰ）连接AC ，交BQ 于N ，连接MN ． ……………………1分∵BC ∥AD 且BC =12AD ，即BC //AQ ． ∴四边形BCQA 为平行四边形，且N 为AC 中点，又∵点M 在是棱PC 的中点，∴ MN // P A ……………………2分 ∵ MN ⊂平面MQB ，P A ⊄平面MQB ，…………………3分 ∴ P A // 平面MBQ ． ……………………4分（Ⅱ）∵AD // BC ，BC =12AD ，Q 为AD 的中点，∴四边形BCDQ 为平行四边形，∴CD//BQ ． ……………………6分∵∠ADC =90° ∴∠AQB =90° 即QB ⊥AD ．又∵平面P AD ⊥平面ABCD 且平面P AD ∩平面ABCD=AD ， ……………………7分∴BQ ⊥平面P AD ． ……………………8分∵BQ ⊂平面PQB ， ∴平面PQB ⊥平面P AD ． ……………………9分另证：AD // BC ，BC =12AD ，Q 为AD 的中点 ∴ BC // DQ 且BC = DQ ，∴ 四边形BCDQ 为平行四边形，∴CD // BQ ． ∵ ∠ADC =90° ∴∠AQB =90°即QB ⊥AD ． ……………………6分∵ P A =PD ， ∴PQ⊥AD ． ……………………7分∵ PQ ∩BQ =Q ，∴AD ⊥平面PBQ ． ……………………8分∵ AD ⊂平面P AD ， ∴平面PQB ⊥平面P AD ． ……………………9分（Ⅲ）∵P A =PD ，Q 为AD 的中点， ∴PQ ⊥AD ．C∵平面P AD ⊥平面ABCD ，且平面P AD ∩平面ABCD=AD ， ∴PQ ⊥平面ABCD ．……………10分（不证明PQ ⊥平面ABCD 直接建系扣1分）如图，以Q 为原点建立空间直角坐标系．则平面BQC 的法向量为(0,0,1)n =；(0,0,0)Q ，P ，B ，(C -分设(,,)M x y z ，则(,,PM x y z =，(1,)MC x y z =---， ∵PM tMC =，∴(1))(x t xy t y z t z =--⎧⎪=⎨⎪=-⎩）， ∴11t x t y t z ⎧=-⎪+⎪⎪=⎨+⎪⎪=⎪⎩……………………12分在平面MBQ 中，QB =，(,,)111t QM t t t=-+++， ∴平面MBQ法向量为(3,0,)m t =．……………………13分∵二面角M -BQ -C 为30°， c o s 303n m n m︒⋅===+ ∴3t =． …………………14分17.（本小题共13分）解：（Ⅰ）设“摸到一等奖、二等奖、三等奖”分别为事件A ，B ，C ． ……1分则P (A )=111114444256⨯⨯⨯=，（列式正确，计算错误，扣1分） ………3分P (B )33341-A =2565= （列式正确，计算错误，扣1分） ………5分三等奖的情况有：“生，生，意，兴”；“生，意，意，兴”；“生，意，兴，兴”三种情况．P (C )222444111*********()()()444444444444A A A =⨯⨯⨯⨯+⨯⨯⨯⨯+⨯⨯⨯⨯964=．…7分（Ⅱ）设摸球的次数为ξ，则1,2,3ξ=． ……8分1(1)4P ξ==， 313(2)4416P ξ==⨯=，3319(3)44464P ξ==⨯⨯=，27(4)1(1)(2)(3)64P P P P ξξξξ==-=-=-==．（各1分）故取球次数ξ的分布列为139271234 2.754166464E ξ=⨯+⨯+⨯+⨯=．(约为2.7) …13分18.（本小题共13分）解：（Ⅰ）∵3211()(0)32f x x ax x b a =+++≥， ∴2'()1f x x ax =++． (1)分∵()f x 在(1,0)处切线方程为33y x =-， ∴'(1)3(1)0f f =⎧⎨=⎩， ……………………3分∴1=a ，611-=b ．（各1分） ……………………5分（Ⅱ）'()()ax f x g x e=21ax x ax e ++=()x R ∈．'()g x =22(2)(1)()ax axax x a e a x ax e e +-++2[(2)]ax x ax a e -=-+-． ……………………7分①当0a =时，'()2g x x =，()g x 的单调递增区间为(0,)+∞，单调递减区间为(,0)-∞． ……………………9分②当a >时，令'(g x =，得x =或2x a a=- ……………………10分（ⅰ）当20a ->，即0a <<时，()g x 的单调递增区间为22(0,)a a -，单调递减区间为(,0)-∞，22(,)a a-+∞；……11分（ⅱ）当20a a-=，即a ='()g x =2220x x e -=-≤，故()g x 在(,)-∞+∞单调递减； ……12分（ⅲ）当20a a-<，即a >()g x 在22(,0)a a-上单调递增，在(0,)+∞，22(,)a a --∞上单调递 ………13分综上所述，当0a =时，()gx 的单调递增区间为(0,)+∞，单调递减区间为(,0)-∞；当0a <<时，()g x 的单调递增区间为22(0,)a a-，单调递减区间为(,0)-∞，当a =()g x 的单调递减区间为(,)-∞+∞；当a >()g x 的单调递增区间为22(,0)a a-，单调递减区间为(0,)+∞，22(,)a a--∞．（“综上所述”要求一定要写出来）19.（本小题共14分）解：（Ⅰ）由椭圆的定义可知，动点P 的轨迹是以A ，B 为焦点，长轴长为……2分∴1c =，a =22b =． ……3分W 的方程是22132x y +=． …………4分（另解：设坐标1分，列方程1分，得结果2分）（Ⅱ）设C ，D 两点坐标分别为11(,)C x y 、22(,)D x y ，C ，D 中点为00(,)N x y ．由221132y kx x y =+⎧⎪⎨+=⎪⎩ 得 22(32)630k x kx ++-=． ……6分所以122632kx x k +=-+ …………7分∴12023232x x k x k +==-+，从而0022132y kx k =+=+． ∴MN 斜率2002232332MN y k k k x m m k +==---+． ………9分又∵CM DM =， ∴CD MN ⊥， ∴222132332k k k m k +=---+ 即 232k m k =-+ …10分当0k =时，0m =； ……11分当0k ≠时，212323k m k k k=-=-++]126,0()0,126[⋃-∈． ……13分故所求m 的取范围是]126,126[-． ……14分（可用判别式法）20.（本小题共13分）解：（Ⅰ）2510C =； ………3分（Ⅱ）证明：令123(,,)n u a a a a =……，123(,,)n v b b b b =……∵0i a =或1，0i b =或1；当0i a =，0i b =时，||i a +||0i b =||i i a b =-当0i a =，1i b =时，||i a +||1i b =||i i a b =-当1i a =，0i b =时，||i a +||1i b =||i i a b =-当1i a =，1i b =时，||i a +||2i b =||0i i a b ≥-=故||i a +||i b ||i i a b ≥-∴(,)(,)d u w d v w +=123()n a a a a ++++123()n b b b b +++++ 123(||||||)n a a a a =++|++|123(||||||)n b b b b +++|++|112233(||||||)n n a b a b a b a b ≥-+-+--|++|(,)d u v = ………8分（Ⅲ）解：易知n S 中共有2n 个元素，分别记为(1,2,,2)n k v k =123(,,)n v b b b b =…… ∵0i b =的k v 共有12n -个，1i b =的k v 共有12n -个．∴21(,)nk k d u v =∑ =1111111122(2|0|2|1|2|0|2|120|21|)n n n n n n n n a a a a a a -------+-+-+---|++|+|=12n n - ……13分∴21(,)nk k d u v =∑=12n n -．法二：根据（Ⅰ）知使(,)k d u v r =的k v 共有rn C 个∴21(,)nk k d u v =∑=012012nn n n n C C C n C ++++21(,)nk k d u v =∑=12(1)(2)0nn n n n n n n C n C n C C --+-+-++两式相加得 21(,)nk k d u v =∑=12n n -（若用其他方法解题，请酌情给分）。

(2011烟台一模)山东省烟台市2011届高三第一次模拟考试(数学理)word版

山东省烟台市2011届高考模拟试卷数学（理）注意事项：1.本试题满分150分，考试时间为120分钟。

2.使用答题纸时，必须使用0.5毫米的黑色墨水签字笔书写，作图时，可用2B铅笔.要字迹工整，笔迹清晰.超出答题区书写的答案无效；在草稿纸，试题卷上答题无效.3.答卷前将密封线内的项目填写清楚.一、选择题：本大题共12小题；每小题5分，共60分.在每小题给出的四个选项中，只有一个选项是符合题目要求的，把正确选项的代号涂在答题卡上.1.已知R是实数集，，则A.（1，2）B. [0，2]C.D. [1，2]2.幂函数y=f(x)的图象经过点（4，），则f()的值为A.1B.2C.3D.43.在平行四边形ABCD中，AC为一条对角线，A.（2，4）B.（3，5）C.（—3，—5）D.（—2，—4）4.如图，水平放置的三棱柱的侧棱长和底边长均为2，且侧棱AA1⊥面A1B1C1，正视图是边长为2的正方形，俯视图为一个等边三角形，该三棱柱的左视图面积为A.B.C.D.45.设a，b为两条直线，为两个平面，则下列结论成立的是A.若且B.若C.若D.若6.等比数列{a n}中，a3=6，前三项和，则公比q的值为A.1B.C.1或D.或7.函数y=ln(1-x)的图象大致为8.已知双曲线的一个焦点与抛物线的焦点重合，且双曲线的离心率等于，则该双曲线的方程为A. B. C. D.9.设曲线在点（3，2）处的切线与直线垂直，则A.2B.C.D.10.函数的部分图象如图所示，则的值分别为A.2，0B.2，C.2，-D.2，11.设是从-1，0，1这三个整数中取值的数列，若，则中数字0的个数为A.11B.12C.13D.1412.设函数内有定义，对于给定的正数K，定义函数：取函数在下列区间上单调递减的是A. B. C. D.二、填空题.本大题共有4个小题，每小题4分，共16分.把正确答案填在答题卡的相应位置.13.若14.在等腰直角三角形ABC中，D是斜边BC的中点，如果AB的长为2，则的值为15.设变量x,y满足约束条件则目标函数的最大值为16.椭圆的左、右焦点分别是F1，F2，过F2作倾斜角为的直线与椭圆的一个交点为M，若MF1垂直于x轴，则椭圆的离心率为三、解答题.本大题共6个小题，共74分.解答应写出文字说明、证明过程或推演步骤.17.（本小题满分12分）已知向量，其中A，B，C是△ABC的内角，a,b,c分别是角A，B，C的对边.（1）求角C的大小；（2）求的取值范围.18.（本小题满分12分）设数列的前项和为，且b n=2-2S n；数列{a n}为等差数列，且a5=14，a7=20.（1）求数列的通项公式；（2）若 (=1,2,3…)，为数列的前项和.求.19.（本小题满分12分）如图，在底面为直角梯形的四棱锥P—ABCD中，，平面（1）求证：平面PAC；（2）求二面角的大小.20.（本小题满分12分）某商店预备在一个月内分批购入每张价值为20元的书桌共36台，每批都购入x台（x 是正整数），且每批均需付运费4元，储存购入的书桌一个月所付的保管费与每批购入书桌的总价值（不含运费）成正比，若每批购入4台，则该月需用去运费和保管费共52元，现在全月只有48元资金可以用于支付运费和保管费.（1）求该月需用去的运费和保管费的总费用（2）能否恰当地安排每批进货的数量，使资金够用？写出你的结论，并说明理由.21.（本小题满分12分）如图，平面上定点F到定直线l的距离|FM|=2，P为该平面上的动点，过P作直线l 的垂线，垂足为Q，且（1）试建立适当的平面直角坐标系，求动点P的轨迹C的方程；（2）过点F的直线交轨迹C于A、B两点，交直线于点N，已知为定值.22.（本小题满分14分）已知（1）求函数上的最小值；（2）对一切恒成立，求实数的取值范围；（3）证明：对一切，都有成立.高三数学（理）参考答案及评分标准一、BBCAD CCDBD AD二、13. 14. 4 15. 5 16.三、17.解：（1）由得……2分由余弦定理得 ……………………………………4分……………………………………………………6分（2）2π2π2πsin sin sin sin()sin sin cos cos sin 333A B A A A A A ∴+=+-=+- …………………………………………………9分即. ………………………………………………………12分18.解：（1）由，令，则，又所以………………………………………………………………2分当时，由，可得即…………………………………………………………………………4分所以是以为首项，为公比的等比数列，于是……………………………………………………………………6分（2）数列为等差数列，公差,可得…………7分从而，………………11分. ………………………………………………………12分19.解：（1）如图，建立坐标系，则，，……………………………2分，又， . ……………………………………6分（2）设平面的法向量为，设平面的法向量为，则…………………8分解得，令，则……………………………………………………10分二面角的大小为. …………12分20.解：（1）设题中比例系数为，若每批购入台，则共需分批，每批价值为20元，由题意………………………………………………4分由时，得………………………………………………6分……………………………………………8分（2）由（1）知（元）………………………………………………10分当且仅当，即时，上式等号成立.故只需每批购入6张书桌，可以使资金够用. ………………………………………12分21.解：（1）方法一：如图，以线段的中点为原点，以线段所在的直线为轴建立直角坐标系.则，.…………2分设动点的坐标为，则动点的坐标为，，……………3分由·，得. ………5分方法二：由. ………2分所以，动点的轨迹是抛物线，以线段的中点为原点，以线段所在的直线为轴建立直角坐标系，可得轨迹的方程为：. ………………………………………………………………………5分（2）方法一：如图，设直线的方程为，，……6分则. ………………………………………………………………………………7分联立方程组消去得，，，…………………………………………………8分故…………………………………………………………………………9分由，得，，，………………………………………………………10分整理得，，·. ……………………12分方法二：由已知，，得. ……………………………7分于是，，①…………………………………………………8分如图，过、两点分别作准线的垂线，垂足分别为、，则有== ，②…………………………………………………10分由①、②得. ……………………………………………………………………12分22.解：（1），……………………………………………………………1分当单调递减，当单调递增……2分①，没有最小值；………………………………………………3分②，即时，；……………………………………………………4分③，即时，上单调递增，；5分所以…………………………………………………………6分（2），则，………………………………………7分设，则，①单调递减，②单调递增，所以，对一切恒成立，所以；…………………………………………………………10分（3）问题等价于证明，………………………………11分由（1）可知的最小值是，当且仅当时取到，设，则，易知，当且仅当时取到，……………………………………13分从而对一切，都有成立……………………………14分。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

中国中学生联盟网：www.cando100.com 中国中学生联盟网：www.cando100.com 黄浦区2010学年度第一学期期终基础学业测评高三数学试卷(文理合卷) (2011年1月12日) 考生注意： 1．每位考生应同时收到试卷和答题卷两份材料，解答必须在答题卷上进行，写在试卷上的解答一律无效； 2．答卷前，考生务必将姓名、准考证号等相关信息在答题卷上填写清楚； 3．本试卷共23道试题，满分150分；考试时间120分钟．

一．填空题(本大题满分56分) 本大题共有14题，考生应在答题卷的相应编号的空格内直接填写结果，每题填对得4分，否则一律得零分．

1．函数lg(1)xyx的定义域是．

2．已知函数1()()yfxyfx与函数互为反函数，若函数1()xafxxa ()xaxR，的图像过点(23)，，则(4)f＝． 3．已知命题A：若431586212xxxxx，则且成立．命题A的逆否命题是；该逆否命题是．(填“真命题”或“假命题”)

4．已知全集21012U，，，，，集合221|log()12AxxxR，， |43220xxBxxR，，则()UACB＝．

5．不等式||52||1xx的解集是． 6．方程sincos1xx的解集是． 7．已知角的顶点在原点，始边与平面直角坐标系x轴的正半轴重合，点

(23)P，在角的终边上，则sin()3＝．

8．(理科)如图1所示，正三棱柱111ABCABC的所有棱的长度都为4，则异面直线11ABBC与所成的角是 (结果用反三角函数值表示)．中国中学生联盟网：www.cando100.com 中国中学生联盟网：www.cando100.com A B C

图1

图1 A B C C1 A

(文科) 如图1所示，正三棱柱111ABCABC的所有棱的长度都为4，点11DBC是的中点，则异面直线11ABAD与所成的角是 (结果用反三角函数值表示)．

9．已知某圆锥体的底面半径3r，沿圆锥体的母线把侧面展开后可得到圆心角为23的扇形，则该圆锥体的体积是．

10．已知12ee、是两个不共线的平面向量，向量12122()aeebeeR，，若//ab，则＝．

11．(理科)一副扑克牌(有四色，同一色有13张不同牌)共52张．现随机抽取3张牌，则抽出的3张牌有且仅有2张花色相同的概率为 (用数值作答)． (文科) 一副扑克牌(有四色，同一色有13张不同牌)共52张．现随机抽取3张牌，则抽出的3张牌花色各不相同的概率为 (用数值作答)．

12．下面是用区间二分法求方程2sin10xx在[01]，内的一个近似解(误差不超过0.001)的算法框图，如图2所示，则判断框内空白处应填入，才能得到需要的解．中国中学生联盟网：www.cando100.com

中国中学生联盟网：www.cando100.com 13．(理科)在数列*211nnnnnaaanNpaa中，如果对任意都有(p为常数)，则称数列na为“等差比”数列，p叫数列na的“公差比”．现给出如下命题： (1) 等差比数列na的公差比p一定不为零； (2) 若数列na*()nN是等比数列，则数列na一定是等差比数列； (3) 若等比数列na是等差比数列，则等比数列na的公比与公差比相等．则正确命题的序号是．

(文科) 计算22222343limnnCCCCn＝．中国中学生联盟网：www.cando100.com 中国中学生联盟网：www.cando100.com 14．(理科)若关于x的方程2||3xkxx有四个不同的实数根，则实数k的取值范围是． (文科) 若*1112()1nnnnaaaanNa数列满足，，则可得该数列的前2011项的

乘积12320102011aaaaa ．二．选择题(本大题满分16分) 本大题共有4题，每题有且只有一个正确答案，考生应在答题卷的相应编号上，将代表答案的小方格涂黑，选对得4分，否则一律得零分．

15．函数22()cossinfxxx(xR)的最小正周期T= [答]( )

A．2． B．． C．4． D．2．

16．已知关于x、y的二元一次线性方程组的增广矩阵是13122，则该线性方程组有无穷多组解的充要条件是＝ [答]( ) A．2． B．1或2． C．1． D．0． 17．给出下列命题：

(1)函数sin3cossinyxxyx的图像可由的图像平移得到；

(2) ||bababab



已知非零向量、，则向量在向量的方向上的投影可以是；

(3)在空间中，若角的两边分别与角的两边平行，则； (4)从总体中通过科学抽样得到样本数据123nxxxx、、、、(*2nnN，)，则数

值22212()()()1nxxxxxxSn(x为样本平均值)可作为总体标准差的点估计值．则上述命题正确的序号是 [答]( ) A．(1)、(2)、(4)． B．(4)． C．(2)、(3)． D．(2)、(4)．

18．(理科)若*1112()1nnnnaaaanNa数列满足，，则该数列的前2011项的乘中国中学生联盟网：www.cando100.com 中国中学生联盟网：www.cando100.com 积12320102011aaaaa [答]( ) A．3． B．-6． C．1． D．23． (文科) (文科)若函数4||yyxax和的图像有三个不同的公共点，则实数a的取值范围是 [答]( ) A．4a． B．4a． C．4a． D．4a．

三．解答题(本大题满分78分)本大题共有5题，解答下列各题必须在答题卷的相应编号规定区域内写出必要的步骤．

19．(本题满分14分)本题共有2个小题，第1小题满分7分，第2小题满分7分．

如图3所示，已知三棱锥ABCD-中，ADBCD^平面，点MNGH、、、分别是 ABADDCCB棱、、、的中点．

(1)求证MNGH、、、四点共面； (2)已知126DCCBADABM===，，，是球的大圆直径，点C在球面上，求球M的体积V．

20．(本题满分14分)本题共有2个小题，第1小题满分7分，第2小题满分7分．定义：如果函数00()[]yfxabxax

A C B · ·

· ·

M N

G H

图3 中国中学生联盟网：www.cando100.com

中国中学生联盟网：www.cando100.com 0()()()fbfafxba

，则称函数()yfx是[]ab，上的“平均值函数”，0x是它的一个

均值点．如4[11]yx是，上的平均值函数，0就是它的均值点． (1)判断函数2()4fxxx在区间[09]，上是否为平均值函数？若是，求出它的均值点；若不是，请说明理由； (2)若函数2()1[11]fxxmx是区间，上的平均值函数，试确定实数m的取值范围．

21．(本题满分16分)本题共有2个小题，第1小题满分7分，第2小题满分9分．

已知12((1)abRexebx、，向量，1)，，，?=--urur121()||fxaee函数=-×urur是偶函数． (1) 求b的值； (2) 若在函数定义域内总存在区间[]mn，(m

函数值组成的集合也是[]mn，，求实数a的取值范围． 22．(本题满分16分)本题共有3个小题，第1小题满分5分，第2小题满分6分，

第3小题满分5分．如图4,某市拟在长为16km的道路OP的一侧修建一条自行车赛道，赛道的前一

部分为曲线OSM，该曲线段为函数sin(00[08])yAxAx，，，的图像，且图

像的最高点为(643)S，.赛道的后一段为折线段MNP，为保证参赛队员的安全，限定120MNP.

(1)求实数A和的值以及M、P两点之间的距离；中国中学生联盟网：www.cando100.com

中国中学生联盟网：www.cando100.com (2)联结MP，设NPMyMNNP，，试求出用y表示的解析式； (3)(理科)应如何设计，才能使折线段MNP最长？ (文科)求函数y的最大值．

23．(本题满分18分)本题共有3个小题，第1小题满分6分，第2小题满分7分，

第3小题满分5分． (理科)已知各项都为正数的数列*1111()2nnnnaaSaanN满足，，其中nnSa是数列的前n项的和．

(1)nnaa求数列的通项公式；

(2)已知p(2)是给定的某个正整数，数列1111kkkkbkpbbba满足， (1231kp，，，，)，求kb； (3)化简123pbbbb．

(文科) 在数列*211nnnnnaaanNpaa中，如果对任意都有(p为非零常数)，则称数列na为“等差比”数列，p叫数列na的“公差比”． (1) 已知数列na满足*325()nnanN，判断该数列是否为等差比数列？ (2) 已知数列nb*()nN是等差比数列，且1224bb，，公差比2p，求数列nb

的通项公式nb； (3)记nS为(2)中数列nb的前n项的和，证明数列nS*()nN也是等差比数列，并求出公差比p的值．