一元二次方程根的分布练习及答案
一元二次方程及根的分布

ax 2 + bx + c = 0(a ≠ 0)
T1:如何判断方程实数解的个数? T1:如何判断方程实数解的个数? 如何判断方程实数解的个数 T2:根系关系(韦达定理)? T2:根系关系(韦达定理)? 注: (1)前提条件 两根同号; (2)两根同号;两根异号 两根同正; (3)两根同正;两根同负 一正一负,且正根的绝对值大; (4)一正一负,且正根的绝对值大; 一正一负, 一正一负,且负根的绝对值大 (5)常见的恒等变形
�
2
与线段AB : x + y = 3,0 ≤ x ≤ 3,有1个交点; 2个交点;以及没有交点?
例3 :已知关于x的方程3x 2 5x + a = 0的 一根大于 2而小于0,另一根大于1而 小于3,求a的取值范围.
例4 :已知函数f ( x ) = (m - 2) x 2 4mx + 2m - 6 的图像与x轴的负半轴有交点,求实数m 的取值范围.
(6)k1 < x1 ≤ x2 < k 2 a>0 a<0 ≥0 ≥0 b b < k 2 或k1 < < k2 k1 < 2a 2a f (k1 ) > 0 f (k1 ) < 0 f (k 2 ) > 0 f (k 2 ) < 0
注: (1)开口向上出现负值时,不写判别式 )开口向上出现负值时,不写判别式. (2)对称轴位置不确定时,不写 )对称轴位置不确定时,不写. (3)注意开口方向对根的分布的影响 )注意开口方向对根的分布的影响. (4)若不等号改为等号,则需要把所求 )若不等号改为等号, 出的范围的端点值加以检验( 出的范围的端点值加以检验(一定要单 独检验); 独检验); (5)若能直接把方程的根求出来,则无 )若能直接把方程的根求出来, 需讨论,直接求解. 需讨论,直接求解.
初高衔接知识第二讲 :一元二次方程与韦达定理(含练习+参考答案)

第二讲:一元二次方程与韦达定理班级:______姓名:__________问题一、一元二次方程的基本知识定义: 判别式: 求根公式:两根差的绝对值:例1 若x 1和x 2分别是一元二次方程2x 2+5x -1=0的两根,求| x 1-x 2|的值.问题二、韦达定理如果ax 2+bx +c =0(a ≠0)的两根分别是x 1,x 2,那么x 1+x 2=b a -,x 1·x 2=c a.这一关系也被称为韦达定理.例1 已知方程2560x kx +-=的一个根是2,求它的另一个根及k 的值.例2 已知关于x 的方程x 2+2(m -2)x +m 2+4=0有两个实数根,并且这两个实数根的平方和比两个根的积大21,求m 的值.例3 已知两个数的和为4,积为-12,求这两个数.例4 若x 1和x 2分别是一元二次方程x 2+x -1=0的两根.(1)求| x 1-x 2|的值; (2)求221211x x 的值; (3)x 13+x 23.问题三、韦达定理与根的分布问题例1 若关于x 的一元二次方程x 2-x +a -4=0的(1)一根大于零、另一根小于零,求实数a 的取值范围;(2)两个根都大于零,求实数a 的取值范围.例2.若关于x 的方程x 2+x +a =0的(1)一个大于1、零一根小于1,求实数a 的取值范围;(2)两根都小于1,求实数a 的取值范围.例3 若一元二次方程x 2-(m +1)x+4=0的两个根都落在[0,3]内,求实数m 的取值范围.参考答案定义:一般的,把形如20ax bx c ++=()0a ≠的方程叫做一元二次方程判别式:240b ac =-≥求根公式:2b x a -±=两根差的绝对值:12||x x a -=问题一例1.122x x -===问题二例1. 解:由题意得121212355675k x x x x x x -⎧+=⎧⎪=-⎪⎪⇒⎨⎨⎪⎪=-=-⎩⎪⎩例2. 解:由题意得()()22212120401171021m b ac m m m x x x x ≤⎧⎧-≥⎪⎪⇒⇒=-⎨⎨-+=+-=⎪⎪⎩⎩例3 解:由题意得24120x x --=解得126,2x x ==-例4 解:(1)12x x -===(2)()()()2212122222212122121131x x x x x x x x +--++===- (3)()()()()()233221212112212121234x x x x x x x x x x x x x x +=+-+=++-=-问题三例1解:(1)1240x x a =-<,4a <(2)由题意得1220174440x x a b ac <⎧⇒<≤⎨-≥⎩例2解:(1)由题意得()()12110x x --<()121210x x x x -++<2a ∴<(2)由题意得122b a -=- ∴()()12211012440x x a b ac ⎧-->⎪⇒-<≤⎨-≥⎪⎩例3解:由题意得 ()()()()21212121240010033330330b ac x x x x m x x x x ⎧-≥⎪+≥⎪⎪≥⇒≤≤⎨⎪-+-≤⎪⎪--≥⎩高一数学衔接知识讲义二练习班级:________姓名:_________1. 若关于x 的方程mx 2+ (2m +1)x +m =0有两个不相等的实数根,则实数m 的取值范围是 ( )(A )m <14 (B )m >-14 (C )m <14,且m ≠0 (D )m >-14,且m ≠0 2.已知关于x 的方程x 2+kx -2=0的一个根是1,则它的另一个根是 ( )(A )-3 (B )3 (C )-2 (D )23.若关于x 的方程x 2+(k 2-1) x +k +1=0的两根互为相反数,则k 的值为 ( )(A )1,或-1 (B )1 (C )-1 (D )04.已知a ,b ,c 是ΔABC 的三边长,那么方程cx 2+(a +b )x +4c =0的根的情况是 ( ) (A )没有实数根 (B )有两个不相等的实数根(C )有两个相等的实数根 (D )有两个异号实数根5.已知一个直角三角形的两条直角边长恰好是方程2x 2-8x +7=0的两根,则斜边长等于 ( )(A(B )3 (C )6 (D )96.若方程x 2-3x -1=0的两根分别是x 1和x 2,则1211x x = ; 7.以-3和1为根的一元二次方程是 ;8.若方程x 2-8x +m =0的两根为x 1,x 2,且3x 1+2x 2=18,则m =_____________;9.写一个一元二次方程,使它的两根分别是方程x 2-7x -1=0各根的相反数_________________________.10.若一元二次方程x 2+2(m -1)x+2m +6=0有两个实数根,且都比1大,求实数m 的取值范围.11.若方程(m +3)x 2-4mx+2m +1=0的两个实数根异号,且负根的绝对值较大,求实数m 的取值范围.12.若一元二次方程x 2-2ax+a+2=0的两根都在区间(1,3)内,求实数a 的取值范围.参考答案1-5 D C C B B6-9 3-;(3)(1)0x x +-=;12;2710x x +-= 10 解: ,则51540m m m m ≥≤-⎧⎪⎪>-⎨⎪<⎪⎩∴514m -<≤-11 解:121200300x x x x m ⋅<⎧⎪+<⎪⎨+≠⎪⎪∆>⎩ ,则2(21)(3)04(m 3)03828-12>0m m m m m m ++<⎧⎪+<⎪⎨≠-⎪⎪∆=-⎩∴132m -<<- 12 解:法一:24480(1,3)2(1)30(3)1150a ab a a f a f a ⎧∆=--≥⎪⎪-=∈⎪⎨⎪=->⎪=->⎪⎩ ∴1125a ≤< 法二:利用韦达定理12121212(1)(1)0(1)(1)0(3)(3)0(3)(3)00x x x x x x x x -->⎧⎪-+->⎪⎪-+-<⎨⎪-->⎪⎪∆≥⎩ ∴1125a ≤< 2416200(1)4502(m 1)122m m f m b a ⎧⎪∆=--≥⎪=+>⎨⎪-⎪-=->⎩。
默写(10-12):二次方程根的分布(答案)
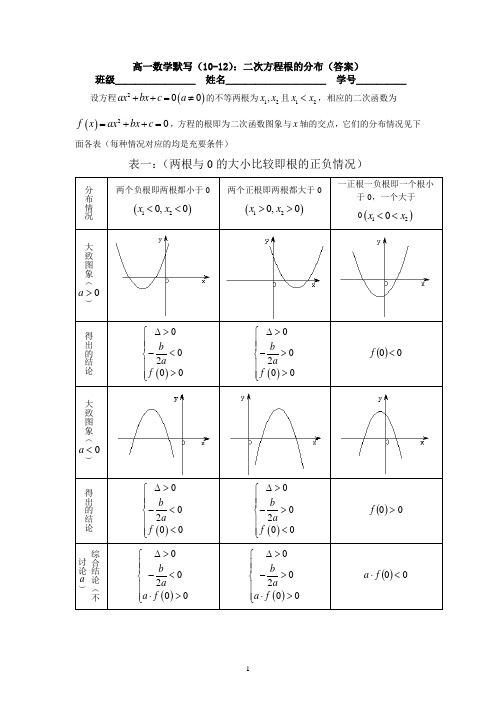
高一数学默写(10-12):二次方程根的分布(答案)班级________ 姓名__________ 学号_____设方程()200ax bx c a ++=≠的不等两根为12,x x 且12x x <,相应的二次函数为()20f x ax bx c =++=,方程的根即为二次函数图象与x 轴的交点,它们的分布情况见下面各表(每种情况对应的均是充要条件)表一:(两根与0的大小比较即根的正负情况)k k k根在区间上的分布还有一种情况:两根分别在区间()n m ,外,即在区间两侧12,x m x n <>,(图形分别如下)需满足的条件是(1)0a >时,()()00f m f n <⎧⎪⎨<⎪⎩; (2)0a <时,()()0f m f n >⎧⎪⎨>⎪⎩对以上的根的分布表中一些特殊情况作说明: (1)两根有且仅有一根在()n m ,内有以下特殊情况:1︒ 若()0f m =或()0f n =,则此时()()0f m f n <不成立,但对于这种情况是知道了方程有一根为m 或n ,可以求出另外一根,然后可以根据另一根在区间()n m ,内,从而可以求出参数的值。
如方程()2220mx m x -++=在区间()1,3上有一根,因为()10f =,所以()()()22212mx m x x mx -++=--,另一根为2m,由213m <<得223m <<即为所求;2︒ 方程有且只有一根,且这个根在区间()n m ,内,即0∆=,此时由0∆=可以求出参数的值,然后再将参数的值带入方程,求出相应的根,检验根是否在给定的区间内,如若不在,舍去相应的参数。
如方程24260x mx m -++=有且一根在区间()3,0-内,求m 的取值范围。
分析:①由()()300f f -<即()()141530m m ++<得出15314m -<<-;②由0∆=即()2164260m m -+=得出1m =-或32m =,当1m =-时,根()23,0x =-∈-, 即1m =-满足题意;当32m =时,根()33,0x =∉-,故32m =不满足题意;综上分析,得出15314m -<<-或1m =-。
二次函数图像解题——根的分布

其交点横坐标便是方程的解,由图知: k 4时, 无解; k = 4或k 3时,有两解; 4 k 3时有四个解; k 3时有三个解.
3
4
y
x
结论: 一元二次方程 ax2 bx c 0(a 0) 在区间上的
实根分布问题.
() 1 一元二次方程有且仅有一个实根属于(m, n)的 充要条件是: f (m) f (n) 0. b 2 4ac 0 a f ( m) 0 a f ( n) 0 m b n 2a
(6) x1,x2有且只有一个根在(k1 , k2)内
k1
k2
f (k1 ) f (k2 ) 0
k1
k2
0 或 b k1 k2 2a
k1
k2
f ( k1 ) 0 或 b k1 k2 k1 2a 2
k1
f ( k2 ) 0 或 k1 k2 b 2 2a k2 k2
(2) 一元二次方程两个实根都属于(m, n)的充要条件是:
(3) 一元二次方程两个实根分别在(m, n)两侧的
a f ( m) 0 充要条件是: a f ( n) 0 (4)一元二次方程两个实根分别在(m, n)同一侧的 充要条件是: 分两类: b 2 4ac 0 () 在(m, n)右侧 a f (n) 0 b n 注:前提 m,n 2a 不是方程(1) b 2 4ac 0 () 在(m, n)左侧 a f (m) 0 b m 2a
不等式组
2 x 变式题:m为何实数值时,关于x的方程 mx (3 m) 0
有两个大于1的根.
根的个数判定及一元二次方程根的分布

0 0
(1)已知方程 x2 (m 2)x 2m1 0 有一实根在0和1之间
练 另一实根在之外,求 m 的取值范围。 习 (2)已知关于 x 的方程 x2 (m 2)x 2m 0
的两根为 、 且满足 0 1 ,求 m的取值
范围。
(3)若方程 x2 (k 2)x k 0 的两实根均在区间
练习
已知关于x的一元二次 x2 2m x 2m 1 0
(1)若方程两根均为正,求m的取值范围; (2)若方程两根均为负,求m的取值范围; (3)若方程的一根为正另一根为负,求m范围;
(二)k分布
1.两根均大于k的条件
b2 4ac 0
b 2a
k
af (k ) 0
3.一根大于k一根小于k
比2小,求 m 的取值范围。
(三)区间分布
1. 一个根在区间内另一根在区间外
f (k1) f (k2) 0
2.两根均在区间内
b2 4ac 0
af (k1) 0
Байду номын сангаас
af k1
(k2) 0 b
2a
k2
3.两根分别位于两区间内
f f
(k1 ( p1
) )
f f
(k2 ) ( p2 )
2.两根均小于k的条件呢?
的条件
af (k) 0
练习
(1)已知方程 x2 11x m 2 0 的两实根都大于1,求
m 的取值范围。
(2)若一元二次方程 mx2 (m 1)x 3 0 的两实根都小于2,求 m 的取值范围。
(3)已知方程 x2 2m x 2m2 3 0 有一根大于2,另一根
在[-1,3]内有实根,求a的取值范围;
二、一元二次方程的根的分布
专题二次函数根的分布问题、含参数一元二次不等式(原卷版)

专题09 二次函数根的分布问题、含参数一元二次不等式【考点预测】1、实系数一元二次方程20(0)ax bx c a ++=≠的实根符号与系数之间的关系 (1)方程有两个不等正根12,x x ⇔212124000b ac b x x a c x x a ⎧⎪∆=->⎪⎪+=->⎨⎪⎪=>⎪⎩(2)方程有两个不等负根12,x x ⇔212124000b ac b x x a c x x a ⎧⎪∆=->⎪⎪+=-<⎨⎪⎪=>⎪⎩(3)方程有一正根和一负根,设两根为12,x x ⇔120cx x a=< 2、一元二次方程20(0)ax bx c a ++=≠的根的分布问题 一般情况下需要从以下4个方面考虑: (1)开口方向;(2)判别式;(3)对称轴2bx a=-与区间端点的关系;(4)区间端点函数值的正负.设12,x x 为实系数方程20(0)ax bx c a ++=>的两根,则一元二次20(0)ax bx c a ++=>的根的分布与其限定条件如表所示. 根的分布图像限定条件12m x x <<2()0b m a f m ∆>⎧⎪⎪->⎨⎪⎪>⎩ 12x m x <<()0f m <12x x m <<02()0b m a f m ∆>⎧⎪⎪-<⎨⎪⎪>⎩ 在区间(,)m n 内 没有实根0∆<12120x x m x x m∆==≤=≥或02()0b m a f m ∆>⎧⎪⎪-<⎨⎪⎪≥⎩02()0b n a f n ∆>⎧⎪⎪->⎨⎪⎪≥⎩()0()0f m f n ≤⎧⎨≤⎩ Onm yxOnmyxOnm yxOnm yxOnm yx在区间(,)m n 内 有且只有一个实根()0()0f m f n >⎧⎨<⎩()0()0f m f n <⎧⎨>⎩在区间(,)m n 内 有两个不等实根02()0()0b m n a f m f n ∆>⎧⎪⎪<-<⎪⎨⎪>⎪>⎪⎩ 3、解含参数的一元二次不等式需要对字母的取值进行分类讨论,常用的分类方法有以下三种:(1)按二次项系数a 的符号分类,即0,0,0a a a >=<; (2)按判别式的符号分类,即0,0,0∆>∆=∆<;(3)按方程20ax bx c ++=的根1x 、2x 的大小分类,即121212,,x x x x x x >=<. 【典型例题】例1.(2022·辽宁·营口市第二高级中学高一期末)已知关于x 的不等式2320(R)ax x a ++>∈. (1)若2320ax x ++>的解集为{}1x b x <<,求实数,a b 的值; (2)求关于x 的不等式2321ax x ax -+>-的解集.例2.(2022·全国·高一专题练习)已知关于x 的不等式ax 2﹣x +1﹣a <0.OnmyxOn m yxOn myx(1)当a =2时,解关于x 的不等式; (2)当a >0时,解关于x 的不等式.例3.(2022·河南·高一阶段练习)(1)若不等式210ax bx +-<的解集是113x x ⎧⎫-<<⎨⎬⎩⎭∣,求,a b的值;(2)若31b a =--,且关于x 的方程210+-=ax bx 有两个不同的负根,求a 的取值范围.例4.(2022·全国·高一课时练习)已知关于x 的方程220x x a -+=. (1)当a 为何值时,方程的一个根大于1,另一个根小于1?(2)当a 为何值时,方程的一个根大于1-且小于1,另一个根大于2且小于3? (3)当a 为何值时,方程的两个根都大于0?例5.(2022·全国·高一单元测试)求实数m 的范围,使关于x 的方程()221?260.x m x m +-++= (1)有两个实根,且一个比2大,一个比2小; (2)有两个实根 αβ,,且满足014αβ<<<<; (3)至少有一个正根.【过关测试】一、单选题1.(2022·湖北·华中师大一附中高一开学考试)关于x 的方程()2290ax a x a +++=有两个不相等的实数根12,x x ,且121x x ,那么a 的取值范围是( ) A .2275a -<<B .25a > C .27a <-D .2011a -<<2.(2022·全国·高一课时练习)关于x 的方程()22210x m x m +-+-=恰有一根在区间()0,1内,则实数m 的取值范围是( ) A .13,22⎡⎤⎢⎥⎣⎦B .12,23⎛⎤ ⎥⎝⎦C .1,22⎡⎫⎪⎢⎣⎭D .{}12,6723⎛⎤⋃- ⎥⎝⎦3.(2022·江苏·高一专题练习)关于x 的方程222(1)0x m x m m +-+-=有两个实数根α,β,且2212αβ+=,那么m 的值为( ) A .1-B .4-C .4-或1D .1-或44.(2022·江苏·高一)已知关于x 的方程230x kx k -++=有两个正根,那么两个根的倒数和最小值是( ) A .-2B .23C .89D .15.(2022·全国·高一专题练习)已知方程240x x a -+=的两根都大于1,则a 的取值范围是( ) A .34a <≤ B .14a <≤ C .1a >D .4a ≤6.(2022·全国·高一期中)若关于x 的不等式()2330x m x m -++<的解集中恰有3个整数,则实数m 的取值范围为( ) A .(]6,7B .[)1,0-C .[)(]1,06,7-⋃D .[]1,7-7.(2022·上海·高一专题练习)关于x 的不等式2320ax x -+>的解集为{|1x x <或}x b >,则关于x 的不等式2()0ax ac b x bx -++>,以下结论正确的是( ) A .当0c >时,解集为{}|0x x c << B .当0c 时,解集为R C .当0c <时,解集为{|x x c <或0}x >D .以上都不正确8.(2022·全国·高一课时练习)若关于x 的不等式()210x a x a -++<的解集中恰有两个整数,则实数a 的取值范围是 A .{}34a a << B .{|21a a -<<-或}34a << C .{}34a a < D .{|21a a -<-或}34a <二、多选题9.(2022·湖南·株洲二中高一开学考试)已知关于x 的不等式组222802(27)70x x x k x k ⎧-->⎨+++<⎩仅有一个整数解,则k 的值可能为( ) A .5-B .3-C .πD .510.(2022·江苏·高一专题练习)已知函数23y ax bx =+-,则下列结论正确的是( )A .关于x 的不等式230ax bx +-<的解集可以是{}3x x >B .关于x 的不等式230ax bx +->的解集可以是∅C .函数23y ax bx =+-在()0,∞+上可以有两个零点D .“关于x 的方程230ax bx +-=有一个正根和一个负根”的充要条件是“0a >”11.(2022·湖南·长沙市实验中学高一期中)已知关于x 的方程x 2+(m -3)x +m =0,下列结论正确的是( )A .方程x 2+(m -3)x +m =0有实数根的充要条件是m ∈{m |m <1或m >9}B .方程x 2+(m -3)x +m =0有一正一负根的充要条件是m ∈{m |m <0}C .方程x 2+(m -3)x +m =0有两正实数根的充要条件是m ∈{m |0<m ≤1}D .方程x 2+(m -3)x +m =0无实数根的必要条件是m ∈{m |m >1}12.(2022·湖南·新化县教育科学研究所高一期末)已知a Z ∈,关于x 的一元二次不等式x 2-8x +a ≤0的解集中有且仅有3个整数,则a 的值可以是( ) A .13 B .14 C .15 D .17三、填空题13.(2022·全国·高一单元测试)方程()2250x a x a --+-=的两根都大于2,则实数a 的取值范围是_____.14.(2022·全国·高一专题练习)方程()2110mx m x --+=在区间()0,1内有两个不同的根,m 则的取值范围为__.15.(2022·全国·高一专题练习)已知方程()()22110x a x a a -+++=的两根分别在区间()0,1,()1,3之内,则实数a 的取值范围为______.16.(2022·安徽·泾县中学高一开学考试)记关于x 的不等式220x x a a -+-≤的解集为A ,集合{}12B x x =-≤<,若A B ,则实数a 的取值范围为___________. 四、解答题17.(2022·四川成都·高一期末)设函数()()()3f x x x a =--,R a ∈. (1)解关于x 的不等式()0f x <;(2)当()3x ∈+∞,时,不等式()9f x ≥-恒成立,求a 的取值范围.18.(2022·全国·高一课时练习)已知函数()()21f x x x a a =++-,(1)当2a =时,求不等式()0f x <的解集.(2)求不等式()2f x x <的解集.19.(2022·江苏省天一中学高一期末)已知二次函数()()222,R f x ax bx b a a b =++-∈,当()1,3x ∈-时,()0f x >;当()(),13,x ∈-∞-⋃+∞,()0f x <. (1)求a ,b 的值;(2)解关于x 的不等式:()()220R ax b c x c c +-+>∈.20.(2022·湖南·高一课时练习)当k 为何值时,关于x 的方程()22340x k x k +-+=分别满足:(1)无实数根? (2)有两正实根?21.(2022·全国·高一单元测试)关于x 的方程2220x mx m +++=分别满足下列条件: (1)当4m =时,两根分别为1x 、2x ,求2212x x +的值; (2)m 为何值时,有一正根一负根; (3)m 为何值时,有两个不相等的正根.22.(2022·全国·高一专题练习)已知关于x 的方程2(21)70x m x m -+++=有两个不等的实根1x ,2x .(1)两根一个根大于1,一个根小于1,求参数m 的取值范围; (2)113x <<,24x >,求参数m 的取值范围.。
一元二次方程与根的分布
一元二次方程根的分布设一元二次方程02=++c bx ax (0≠a )的两实根为1x ,2x ,且21x x ≤。
k 为常数。
则一元二次方程根的k 分布(即1x ,2x 相对于k 的位置)有以下若干定理。
【定理1】21x x k ≤<⇔⎪⎪⎩⎪⎪⎨⎧>->≥-=∆k ab k af ac b 20)(042【定理2】kx x <≤21⇔⎪⎪⎩⎪⎪⎨⎧<->≥-=∆k ab k af ac b 20)(042。
【定理3】21x k x <<⇔0)(<k af 。
推论1 210x x <<⇔0<ac 。
推论2 211x x <<⇔0)(<++c b a a 。
【定理4】有且仅有11x k <(或2x )2k <⇔0)()(21<k f k f【定理5】221211p x p k x k <<≤<<⇔⎪⎪⎪⎩⎪⎪⎪⎨⎧><<>>0)(0)(0)(0)(02121p f p f k f k f a 或⎪⎪⎪⎩⎪⎪⎪⎨⎧<>><<0)(0)(0)(0)(02121p f p f k f k f a此定理可直接由定理4推出,请读者自证。
【定理6】2211k x x k <≤<⇔⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧<-<>>>≥-=∆2121220)(0)(004k a b k k f k f a ac b 或⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧<-<<<<≥-=∆2121220)(0)(004k a b k k f k f a ac b三、例题与练习【例1】 已知方程02112=-+-m x x 的两实根都大于1,求m 的取值范围。
(412912<<m )(2)若一元二次方程03)1(2=++-x m mx 的两个实根都大于-1,求m 的取值范围。
高一数学一元二次方程根的分布
一元二次方程根的分布一.知识要点二次方程02=++c bx ax 的根从几何意义上来说就是抛物线c bx ax y ++=2与x 轴交点的横坐标,所以研究方程02=++c bx ax 的实根的情况,可从c bx ax y ++=2的图象上进行研究.若在),(+∞-∞内研究方程02=++c bx ax 的实根情况,只需考察函数c bx ax y ++=2与x 轴交点个数及交点横坐标的符号,根据判别式以及韦达定理,由c bx ax y ++=2的系数可判断出2121,,x x x x +∆的符号,从而判断出实根的情况.若在区间),(n m 内研究二次方程02=++c bx ax ,则需由二次函数图象与区间关系来确定.分布情况 两根都小于k 即 k x k x <<21, 两根都大于k 即 k x k x >>21, 一个根小于k ,一个大于k 即 21x k x <<大致图象(0>a )得出的结论()020b k a f k ∆>⎧⎪⎪-<⎨⎪>⎪⎩ ()020b k a f k ∆>⎧⎪⎪->⎨⎪>⎪⎩ ()0<k f分布情况两根都在()n m ,内 两根有且仅有一根在()n m ,内 (图象有两种情况,只画了一种) 一根在()n m ,内,另一根在()q p ,内,q p n m <<<kk k大致图象(>a )得出的结论 ()()0002f m f n b m n a ∆>⎧⎪>⎪⎪>⎨⎪⎪<-<⎪⎩ ()()0<⋅n f m f ()()()()0000f m f n f p f q ⎧>⎪<⎪⎨<⎪⎪>⎩或()()()()00f m f n f p f q <⎧⎪⎨<⎪⎩ 根在区间上的分布还有一种情况:两根分别在区间()n m ,外,即在区间两侧12,x m x n <>,(图形分别如下)需满足的条件是 (1)0a >时,()()00f m f n <⎧⎪⎨<⎪⎩; (2)0a <时,()()00f m f n >⎧⎪⎨>⎪⎩ 对以上的根的分布表中一些特殊情况作说明: (1)两根有且仅有一根在()n m ,内有以下特殊情况:1︒ 若()0f m =或()0f n =,则此时()()0f m f n <不成立,但对于这种情况是知道了方程有一根为m 或n ,可以求出另外一根,然后可以根据另一根在区间()n m ,内,从而可以求出参数的值。
一元二次方程根的分布情况归纳(完整版)
二次方程根的分布与二次函数在闭区间上的最值归纳1、一元二次方程ax 2 +bx +c = 0根的分布情况设方程ax 2+bx +c =0(a 0)的不等两根为x ,x 且x x ,相应的二次函数为 f (x )=ax 2+bx +c =0,方程的 根即为二次函数图象与 x 轴的交点,它们的分布情况见下面各表(每种情况对应的均是充要条件)表一:(两根与 0 的大小比较即根的正负情况)分布情况小)都根2根x 1大)都根2,根x 1)2小0 一x 1即(根负于一负大根个正一 一大致图象()a得出的结论00b 2a()0-f00b 2a()0-f0 ) (0 (f大致图象()a得出的结论00b 2a()0-f00b 2a ()0-f0 ) (0 f综合结论(不讨论a)0 0 0)b -a2(f 0a0 0 0)b -a2(f 0a0 ) (0 f a表二:(两根与k的大小比较)表三:(根在区间上的分布)两根有且仅有一根在(m , n )内 (图象有两种情况,只画了一种)一根在 (m ,n )内,另一根在(p ,q ) 内, mn p qf (m )f (n ) 0f (p )f (q )根在区间上的分布还有一种情况:两根分别在区间(m ,n )外,即在区间两侧x 1m ,x 2 n ,(图形分别如下)需满 足的条件是大致图象(a得出的结f (m ) 0 f (n ) 0bm - n2af (m ) f (n ) 0或0 00 )m )n )p )q f (m ) f (n ) 0 f (p ) f (q ) 0 0大致图象(a得出的结f (m ) 0 f (n ) 0bm - n2af (m ) f (n ) 0f (m )f (n)0 f (m ) f (n )0 f (p )0 f (p ) f (q )f (q ) 0 分布情况两根都在(m , n )内综合结论(不讨论af (m ) f (n )2g2 f (0)(m +1) - 8mm - 1mm 3-2 2或m 3+2 2m对以上的根的分布表中一些特殊情况作说明:1)两根有且仅有一根在(m ,n )内有以下特殊情况: 若 f(m )=0或 f (n )=0,则此时 f (m )g f (n )0不成立,但对于这种情况是知道了方程有一根为m 或n ,可以 求出另外一根,然后可以根据另一根在区间(m ,n )内,从而可以求出参数的值。
一元二次方程根的分布情况归纳(完整版)
二次方程根的分布与二次函数在闭区间上的最值归纳1、一元二次方程02=++c bx ax 根的分布情况 设方程()200ax bx c a ++=≠的不等两根为12,x x 且12x x <,相应的二次函数为()20f x ax bx c =++=,方程的根即为二次函数图象与x 轴的交点,它们的分布情况见下面各表(每种情况对应的均是充要条件)表一:(两根与0的大小比较即根的正负情况)分布情况两个负根即两根都小于0()120,0x x << 两个正根即两根都大于0()120,0x x >>一正根一负根即一个根小于0,一个大于0()120x x <<大致图象(>a )得出的结论()00200b a f ∆>⎧⎪⎪-<⎨⎪>⎪⎩ ()00200b a f ∆>⎧⎪⎪->⎨⎪>⎪⎩ ()00<f大致图象(<a )得出的结论()00200b a f ∆>⎧⎪⎪-<⎨⎪<⎪⎩ ()00200b a f ∆>⎧⎪⎪->⎨⎪<⎪⎩ ()00>f综合结论(不讨论a)()00200b a a f ∆>⎧⎪⎪-<⎨⎪⋅>⎪⎩ ()00200b a a f ∆>⎧⎪⎪->⎨⎪⋅>⎪⎩ ()00<⋅f a分布情况两根都小于k 即 k x k x <<21, 两根都大于k 即 k x k x >>21, 一个根小于k ,一个大于k 即21x k x <<大致图象(>a )得出的结论()020b k a f k ∆>⎧⎪⎪-<⎨⎪>⎪⎩ ()020b k a f k ∆>⎧⎪⎪->⎨⎪>⎪⎩ ()0<k f大致图象(<a )得出的结论()020b k a f k ∆>⎧⎪⎪-<⎨⎪<⎪⎩ ()020b k a f k ∆>⎧⎪⎪->⎨⎪<⎪⎩ ()0>k f综合结论(不讨论a)()020b k a a f k ∆>⎧⎪⎪-<⎨⎪⋅>⎪⎩ ()020b k a a f k ∆>⎧⎪⎪->⎨⎪⋅>⎪⎩ ()0<⋅k f akkk分布情况两根都在()n m ,内两根有且仅有一根在()n m ,内(图象有两种情况,只画了一种) 一根在()n m ,内,另一根在()q p ,内,q p n m <<<大致图象(>a )得出的结论()()0002f m f n b m na ∆>⎧⎪>⎪⎪>⎨⎪⎪<-<⎪⎩()()0<⋅n f m f()()()()0000f m f n f p f q ⎧>⎪<⎪⎨<⎪⎪>⎩或()()()()00f m f n f p f q <⎧⎪⎨<⎪⎩ 大致图象(<a )得出的结论()()0002f m f n b m na ∆>⎧⎪<⎪⎪<⎨⎪⎪<-<⎪⎩()()0<⋅n f m f()()()()0000fm f n f p f q ⎧<⎪>⎪⎨>⎪⎪<⎩或()()()()00f m f n f p f q <⎧⎪⎨<⎪⎩综合结论(不讨论a)——————()()0<⋅n f m f()()()()⎪⎩⎪⎨⎧<<00q f p f n f m f 根在区间上的分布还有一种情况:两根分别在区间()n m ,外,即在区间两侧12,x m x n <>,(图形分别如下)需满足的条件是(1)0a >时,()()00f m f n <⎧⎪⎨<⎪⎩; (2)0a <时,()()0f m f n >⎧⎪⎨>⎪⎩对以上的根的分布表中一些特殊情况作说明: (1)两根有且仅有一根在()n m ,内有以下特殊情况:若()0f m =或()0f n =,则此时()()0f m f n <g 不成立,但对于这种情况是知道了方程有一根为m 或n ,可以求出另外一根,然后可以根据另一根在区间()n m ,内,从而可以求出参数的值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一元二次方程根的分布 一.一元二次方程根的基本分布——零分布 所谓一元二次方程根的零分布,指的是方程的根相对于零的关系。比如二次方程有一正根,有一负根,其实就是指这个二次方程一个根比零大,一个根比零小,或者说,这两个根分布在零的两侧。 设一元二次方程02cbxax(0a)的两个实根为1x,2x,且21xx。
【定理1】01x,02x
(两个正根)212124000bacbxxacxxa,
推论:01x,02x00)0(0042bcfaacb或00)0(0042bcfaacb
上述推论结合二次函数图象不难得到。
【例1】 若一元二次方程0)1(2)1(2mxmxm有两个正根,求m的取值范围。
分析:依题意有24(1)4(1)02(1)0101mmmmmmm0
【定理2】01x,02x
000421212acxxabxx
acb,
推论:01x,02x00)0(0042bcfaacb或00)0(0042bcfaacb
由二次函数图象易知它的正确性。 【例2】 若一元二次方程0332kkxkx的两根都是负数,求k的
取值范围。(512k或k>3) 【定理3】210xx
0
a
c
【例3】 k在何范围内取值,一元二次方程0332kkxkx有一个正根和一个负根?
分析:依题意有3kk<0=>0
【定理4】 ○101x,02x0c且0ab;
○201x,02x0c且0ab。
【例4】 若一元二次方程03)12(2kxkkx有一根为零,则另一根是正根还是负根? 分析:由已知k-3=0,∴k=3,代入原方程得32x+5x=0,另一根为负。
二.一元二次方程的非零分布——k分布 设一元二次方程02cbxax(0a)的两实根为1x,2x,且21xx。k为常数。则一元二次方程根的k分布(即1x,2x相对于k的位置)有以下若干定理。
【定理1】21xxk
kabkafacb2
0)(042
【定理2】kxx21
kabkafacb2
0)(042。 【定理3】21xkx
0)(kaf
。
推论1 210xx
0ac
。
推论2 211xx
0)(cbaa
。
【定理4】有且仅有11xk(或2x)2k0)()(21kfkf
【定理5】221211pxpkxk
0)(0)(0)(0)(02121pfpfkfkfa或
0)(0)(0)(0)(02121pfpfkfkfa
此定理可直接由定理4推出,请读者自证。 【定理6】2211kxxk
2121220)(0)(004kabkkfkfaacb或
2121220)(0)(004kabkkfkfaacb 三、例题与练习 【例5】 已知方程02112mxx的两实根都大于1,求m的取值范围。(412912m)
(2)若一元二次方程03)1(2xmmx的两个实根都大于-1,求m的取值范围。 (6252mm或) (3)若一元二次方程03)1(2xmmx的两实根都小于2,求m的取值范围。
(62521mm或) 【例6】 已知方程032222mmxx有一根大于2,另一根比2小,求m的取值范围。 (221221m) (2)已知方程012)2(2mxmx有一实根在0和1之间,求m的取值范围。 (3221m)
(3)已知方程012)2(2mxmx的较大实根在0和1之间,求实数m的取值范围。 变 式:改为较小实根 (不可能;221m)
(4)若方程0)2(2kxkx的两实根均在区间(1、1)内,求k的取值范围。 (21324k) (5)若方程012)2(2kxkx的两根中,一根在0和1之间,另一根在1和2之间,求k的取值范围。 (3221k) (6)已知关于x的方程062)1(22mmmxxm的两根为、且满足10
,求m的取值范围。 (73m或72m)
【例7】 已知关于x的二次方程x2+2mx+2m+1=0. (1)若方程有两根,其中一根在区间(-1,0)内,另一根在区间(1,2)内,求m的范围. (2)若方程两根均在区间(0,1)内,求m的范围. 本题重点考查方程的根的分布问题,解答本题的闪光点是熟知方程的根对于二次函数性质所具有的意义. 技巧与方法:设出二次方程对应的函数,可画出相应的示意图,然后用函数性质加以限制. 解:(1)条件说明抛物线f(x)=x2+2mx+2m+1与x轴的交点分别在区间(-1,0)和(1,2)内,画出示意图,得
65,21,21056)2(,024)1(,02)1(,012)0(mmRmmmfmffmf
∴2165m.
(2)据抛物线与x轴交点落在区间(0,1)内,列不等式组10,0,0)1(,0)0(mff
.01,2121,21,21mmmmm或(这里0<-m<1是因为对称轴x=-m应在区间(0,1)内通过)
练习: 1. 若方程4(3)20xxmm•有两个不相同的实根,求m的取值范围。 提示:令2x=t转化为关于t的一元二次方程有两个不同的正实根。答案:02. 若关于x的方程2lg(20)lg(863)0xxxa有唯一的实根,求实数a的取值范围。
提示:原方程等价于2220020863xxxxxa即2200 12630xxxxa或……①……② 令()fx=2x+12x+6a+3 (1) 若抛物线y=()fx与x轴相切,有△=144-4(6a+3)=0即a=112。
将a=112代入式②有x=-6不满足式①,∴a≠112。 (2) 若抛物线y=()fx与x轴相交,注意到其对称轴为x=-6,故交点的横坐标有且仅有一个满足式①的充要条件是 (20)0(0)0ff
解得163162a。
∴当163162a时原方程有唯一解。 另法:原方程等价于2x+20x=8x-6a-3(x<-20或x>0)……③ 问题转化为:求实数a的取值范围,使直线y=8x-6a-3与抛物线y=2x
+20x(x<-20或x>0)有且只
有一个公共点。 虽然两个函数图像都明确,但在什么条件下它们有且只有一个公共点却不明显,可将③变形为2x
+12x+3=
-6a(x<-20或x>0),再在同一坐标系中分别也作出
O x
y
-20 -6
O x
y -20 -6 163 3 抛物线y=2x+12x+3和直线y=-6a,如图,显然当3<-6a≤163即
1631
62a
时直线y=-6a与抛物线有且只有一个公共点。 3. 已知()fx=(x-a)(x-b)-2(a(<),则实数a,b,、的大小关系是( ) A、
4. 方程()fx=2axbxc=0(a>0)的两个根都大于1的充要条件是( ) A、 △≥0且f(1)>0
B、 f(1)>0且-ab>2
C、 △≥0且-ab>2,ca>1 D、 △≥0且f(1)>0,-ab>2。
