12.2过渡态理论_图文.ppt
化学反应中的过渡态理论分析

化学反应中的过渡态理论分析化学反应的过程涉及反应物的相互转化以及化学键的形成和断裂。
而过渡态理论,则是解释和描述了化学反应中的过程中,产生的临时生成物——过渡态。
本文将对过渡态理论进行分析,探讨其在化学反应研究中的应用和意义。
一、过渡态的定义与性质在化学反应中,过渡态是反应物转变为产物的过程中的中间稳定状态。
它是在活化能垒上的高点,具有较短的存在时间,不是反应物也不是产物,但对研究反应机理起到了重要的作用。
过渡态具有以下几个特性:1. 能量最高:过渡态的活化能最高,是反应过程中的能垒。
2. 结构变化性:过渡态的结构中包含了反应物和产物之间的中间状态,具有中间结构的特征。
3. 不稳定性:过渡态相对于反应物和产物来说,非常不稳定,容易解离或重新结合。
二、过渡态理论的基本原理1. 高斯-赛德尔理论:高斯与赛德尔提出,过渡态可以通过控制分子的构象来实现。
在过渡态过程中,分子将沿着反应坐标可逆地延展和收缩,从而形成整个过渡态的路径。
2. 键级别的描述:通过分析化学键的能量和取向变化,可以确定过渡态的结构与性质。
在反应过程中,不同化学键的生成和断裂导致了丰富的过渡态形成。
3. 光谱学解释:通过光谱学方法,可以对过渡态的结构和能级进行研究。
通过分析过渡态的振动光谱和电子吸收光谱,可以揭示其分子结构和能量变化。
三、过渡态理论在反应机理研究中的应用1. 反应速率的解释:过渡态理论提供了理解反应速率的重要依据。
根据过渡态的能垒高低,可以预测反应的速率常数,进而解释和优化反应条件。
2. 催化剂设计与应用:过渡态理论可以帮助理解催化剂在反应中的作用机理,进而指导催化剂的设计和优化。
通过降低反应的能垒,催化剂可以加速反应速率。
3. 反应机理的揭示:通过研究并确定过渡态的结构和性质,可以深入理解反应的机理。
这对于合成新的化合物、优化反应条件以及实现可控合成等方面具有重要意义。
四、过渡态理论的局限性与发展方向尽管过渡态理论在化学反应研究中具有重要意义,但也存在一些局限性:1. 考虑不充分:过渡态理论忽略了许多其他因素对反应的影响,如溶剂效应、温度变化等。
物理化学12章_化学动力学基础(二)
Eb。Eb。是活化络合物与反应物最 低势能之差,E0是两者零点能
之间的差值。
这个势能垒的存在说明了实验活化能的实质。
上一内容 下一内容 回主目录
返回
2021/1/16
势能面剖面图
上一内容 下一内容 回主目录
返回
2021/1/16
三原子系统振动方式
式中r0是分子中双原子分子间的平衡核间 距,De是势能曲线的井深,a为与分子结构有 关的常数.
上一内容 下一内容 回主目录
返回
2021/1/16
双原子分子的莫尔斯势能曲线
AB双原子分子根据该公式 画出的势能曲线如图所示。
当r>r0时,有引力,即化学键力。 当r<r0时,有斥力。 0时的能级为振动基态能级,E0为零点能。
物理化学12章_化学动力学基础(二 )
上一内容 下一内容 回主目录
返回
物理化学电子教案—第十二章
上一内容 下一内容 回主目录
返回
2021/1/16
第十二章 化学动力学基础(二)
§12.1 碰撞理论 *§12.2 过渡态理论
§12.3 单分子反应理论 * §12.4 分子反应动态学简介
§12.5 在溶液中进行的反应 * §12.6 快速反应的几种测试手段
Ea≈ E
上一内容 下一内容 回主目录
返回
2021/1/16
概率因子(probability factor)
由于简单碰撞理论所采用的模型过于简单, 没有考虑分子的结构与性质,所以用概率因子 来校正理论计算值与实验值的偏差。
P=k(实验)/k(理论)
概率因子又称为空间因子或方位因子。
上一内容 下一内容 回主目录
最新第十二章化学动力学基础二

P
0.16 510-2 2.510-3
4.8
举例
1. 根据碰撞理论,温度增加反应速率提高的主要原因是:( ) (A) 活化能降低 (B) 碰撞频率提高 (C) 活化分子所占比例增加 (D) 碰撞数增加
2.在简单硬球碰撞理论中,有效碰撞的定义是:
()
(A) 互撞分子的总动能超过Ec (B) 互撞分子的相对动能超过Ec (C) 互撞分子的相对平动能在连心线上的分量超过Ec (D) 互撞分子的内部动能超过Ec
(C)反应分子数未知,不能比较; (D)相等
2. 有一单分子重排反应AP,实验测得在393K时的速率常数为 1.806×10-4 s-1, 413K时为9.14×10-4 s-1。试计算该基元反应的实验 活化能、393 K时的活化熵和活化焓。
作业:6,7,15
12.5 在溶液中进行的反应
笼效应 原盐效应
102.1
硝基甲烷
3.13
13.5
102.5
溴
4.27
13.3
100.4
反应分子在溶剂分子形成的笼中进行多次反复的 碰撞,其碰撞频率并不低于气相反应中的碰撞频率, 这种现象称为笼效应。
表12.3.2 不同溶剂中季胺盐(C2H5)4NI形成反应的动力学参数(100℃ )
溶剂
k/(10-5mol-1dm3 s-1)
k lg
k0
2z A zBA
I
(1)ZA ZB >0,离子强度增大,k增大,正原盐效应。 (2)ZA ZB <0,离子强度增大,k下降,负原盐效应。 (3)ZA ZB =0,离子强度不影响k值,无原盐效应。
(1) S2O32-+3I -P (2) [Co(NH3)5Br]2++Hg2++H2OP (3) CH3COOC2H5+OH-P (4) [ O2N-NCO2Et]-+OH-P (5) H++ Br-+H2O2P (6) [Co(NH3)5Br]2++OH-P
§112 过渡态理论

§11.2 过渡态理论一、过渡态理论(transition state theory)过渡态理论是1935年由Eyring ,Evans 和Polanyi 等人在统计热力学和量子力学的基础上提出来的。
他们认为由反应物分子变成生成物分子,中间一定要经过一个过渡态,而形成这个过渡态必须吸取一定的活化能,这个过渡态就称为活化络合物,所以又称为活化络合物理论。
用该理论,只要知道分子的振动频率、质量、核间距等基本物性,就能计算反应的速率常数,所以又称为绝对反应速率理论。
二、势能面该理论认为反应物分子间相互作用的势能是分子间相对位置的函数:莫尔斯(Morse)公式是对双原子分子最常用的计算势能E p 的经验公式:式中r 0是分子中原子间的平衡核间距,D e 是势能曲线的井深,a 为与分子结构特性有关的常数。
AB 双原子分子根据该公式画出的势能曲线见教材P236图12.4所示。
当r>r 0时有引力,即化学键力;当r<r 0时,有斥力;v=0时的能级为振动基态能级, E 0 称为零点能;D 0 是为把基态分子解离为孤立原子所需的能量,它的值可从光谱数据得到。
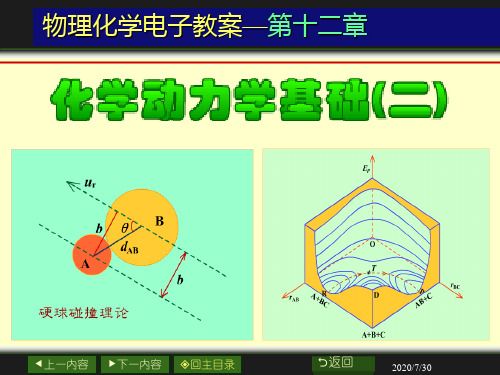
以三原子反应为例:当A 原子与双原子分子BC 反应时,首先形成三原子分子的活化络合物,该络合物的势能是3个内坐标的函数:这要用四维图表示;见教材P236图12.5三原子系统的核间距现在令∠ABC=180°,即A 与BC 发生共线碰撞,活化络合物为线型分子。
随着核间距r AB 和r BC 的变化,势能也随之变化。
这些不同点在空间构成高低不平的曲面,称为势能面。
见教材P237图12.6三原子反应的势能面示意图在势能面上,活化络合物所处的位置T 点称为马鞍点。
该点势能与反应物和生成物所处的稳定态能量R 点和P 点相比是最高点,但与坐标原点一侧和D 点的势能相比又是最低点。
如把势能面比作马鞍的话,则马鞍点处在马鞍的中心。
从反应物到生成物必须越过一个能垒。
陕西师范大学考研物理化学资料PPT课件
在硬球碰撞示意图上,A
和B两个球的碰撞直径d AB 与
相对速度 u r 之间的夹角为 。
通过A球质心画平行于 u r
的平行线,两平行线间的距离
ur
b
B
d AB A
b
就是碰撞参数b 。
硬球碰撞理论
bdABsin bmax dAB
b 值愈小碰撞愈激烈, b 0 迎头碰撞,最激烈。
上一内容 下一内容 回主目录
上一内容 下一内容 回主目录ຫໍສະໝຸດ 返回2020/7/30
两个分子的一次碰撞过程
v
v
b
o
上一内容 下一内容 回主目录
返回
2020/7/30
有效碰撞直径和碰撞截面
运动着的A分子和B分子,两者质心的投影落在
半径为 d AB的圆截面之内,都有可能发生碰撞。
d A B 称为有效碰撞直
径(两个分子的质心在碰
撞时所能达到的最短距 离),数值上等于A分子 和B分子的半径之和。
互碰频率为:
ZAB
dA 2B
NA V
NB V
8RT
uA
8RT πM A
uB
8 RT πM B
上一内容 下一内容
或ZABdA 2BL2 8RT[A][B]
式中 MAMB
MA MB
NA[A]L NB[B]L
V
V
回主目录
返回
2020/7/30
两个A分子的互碰频率
当体系中只有一种A分子,两个A分子互碰的相对
12.1 碰撞理论 12.2 过渡态理论 12.3 单分子反应理论 12.4 分子反应动态学简介 12.5 在溶液中进行的反应 12.6 快速反应的测试 12.7 光化学反应 12.8 化学激光简介 12.9 催化反应动力学
化学动力学基础(二)

§12.2
势能面
过渡态理论
由过渡态理论计算反应速率常数 *活化络合物的活化能Ea和指前因子A与 诸热力学函数之间的关系
过渡态理论(transition state theory)
过渡态理论是1935年由Eyring,Evans和
Polany 等人在统计热力学和量子力学的基础上
提出来的。 他们认为由反应物分子变成生成物分子,中 间一定要经过一个过渡态,而形成这个过渡态必
设有反应
ABP
若每次碰撞都能起反应,则反应速率为 dnA Z AB dt 改用物质的浓度表示(单位体积) dnA dcA L
8RT dcA dnA 1 Z AB 2 d AB L cA cB dt dt L L
dcA kcA cB dt
k d L
但必须越过势能垒 Eb
Eb是活化络合物与反 应物最低势能之差,E0是
势 能
Eb E0
A B C ≠
两者零点能之间的差值。
这个势能垒的存在说 明了实验活化能的实质。
AB+C
A+BC
反应坐标
势能剖面图
势能面投影图
将三维势能面投影到平面上,就得到势能面的
投影图。 图中曲线是相同
势能的投影,称为等
NA NB V V
8RT
或 Z AB d L
2 2 AB
8 RT
[A][B]
MAMB 式中 MA MB
NA [A]L V
NB [B]L V
两个A分子的互碰频率
当系统中只有一种A分子,两个A分子互碰 的相对速度为: u (2 8 RT )1/ 2
r
MA
化学动力学
RT
1
k2dA 2BLRT Me
2
eEa
RT
1
A2dA2BLRTMe 2
1
A2dA2BLRM T 2
kkB hTcθ1nexp R Sm θ exp R H Tm θ
适用范围:凝聚相反应
kkB h T R pT 1nexp R Sm θ exp R H Tm θ
Carbon Dioxide Fixation into Chemicals Methyl Formate at High Yields by Surface Coupling over a Pd/Cu/ZnO Nanocatalyst
Gm θRTlnKcθ
G m θRTlnKc
cθ
n1
Gm θ RT
lnKc
cθ
n1
cθ
K n1 c
expRG Tm θ
Kc cθ 1nexpRG Tm θ
k
kBT h
K
c
kkBT h
cθ
1nexpR G Tm θ
G
m
标准摩尔反应活化Gibbs自由能变
G m θ H m θT Sm θ
kkB h Tcθ1nexp R Sm θ exp E aR T R T
kkB hTcθ1nexp R Sm θ exp R T R TE a
kkBTcθ h
1nexp R Sm θexp1R E T a
kkBTecθ h
1nexp R Sm θexp R E Ta
rk2KccAcBC
根据过渡状态理论的假设活化络合物只 进行一次非对称伸缩振动就能断裂发生 反应因此反应速率为
k2
rr K cccAcBC
第十二章.化学动力学基础(二)
2013-7-26
Shenming
24
第十二章 化学动力学基础 2
根据量子力学理论, =/h,h为Planck常数, 是一个振动自由度的能量。 按照能量均分原理有, = h = kBT 则 kB——玻兹曼常数 = kBT/ h 代入 (a) 式得:
k BT k K c ——过渡状态理论的基本公式 h
2 AB
1/ 2
式中V为体积,dAB称为有效碰撞直径,MA、MB分别 为其摩尔质量,NA、NB分别为反应物分子的个数,nA 、 nB为则1立方厘米中的分子个数。
2013-7-26
Shenming
3
第十二章 化学动力学基础 2
A与B分子碰撞的激烈程度,不是取决于两个分子 的总动能,而是与A、B两分子在质心连线方向上的相 对平动能有关。当这种相对平动能超过化学反应的临界 能c (又称阈能)时,才能发生化学反应。化学反应不 同, c值不同,在碰撞理论中,把c ×L=Ec称为反应 的活化能, L为阿佛加德罗常数。 也就是说,只有相对平动能在 质心连心线上的分量大于阈能的碰 撞才是有效的,而绝大部分的碰撞 是无效的。因此应在碰撞频率项上 乘以有效碰撞分数q。
Ec q exp( ) RT
4
2013-7-26
Shenming
第十二章 化学动力学基础 2
反应阈能又称为反应临界能。两个分子相撞, 相对平动能在质心连心线上的分量必须大于一个 临界值 Ec,这种碰撞才有可能引发化学反应, 这个临界值Ec也称为反应阈能,它是反应物反应 生成产物时所必须越过的一个能垒。
Shenming
8
第十二章 化学动力学基础 2
但是由于简单碰撞理论所采用的模型过于简单, 没有考虑分子的结构与性质,所以要用概率因子来校 正理论计算值与实验值的偏差。
11-2 过渡态理论
三原子体系振动方式
对于稳定分子,这四种振动方式都不会使分子破坏。 但对于过渡态分子,不对称伸缩振动没有回收 力,会导致它越过势垒分解为产物分子。所以这种不 对称伸缩振动每发生一次,就使过渡态分子分解, 显然,分解频率f应该为不对称伸缩振动频率的2 倍,
k v Kc
统计热力学方法计算速率常数 过渡态理论假设:
k BT f E0 n-1 k n exp L h RT fi
的几率穿越势垒而出现在势阱之外。
吸引型势能面
早垒(吸引型势垒)
排斥型势能面
晚垒(排斥型势垒)
统计热力学方法计算速率常数
Eyring等以势能面为基础,建立了过渡态理论 (Transition State Theory, TST),通过引入适当的假 设,将问题简化,最后结合统计力学,原理上可以不借助宏 观动力学实验,而仅根据分子的微观性质及势能面的计算得 到宏观速率常数,因而有时也被称为绝对速率理论 (Absolute Reaction Rate Theory,ART)。 假设1. 任何跨过势能垒的活化络合物必将继续向前生成产物, 而不会重新调头再次跨越势垒,变回反应物,也即过渡态是反 应物向产物过渡的一个无返回点(point of no return)。
Ep
H2 基态势能曲线图
0
r0
D0
v =2 v =1 v =0
De
r
莫尔斯(Morse)公式是对双原子分子最常 用的计算势能Ep的经验公式:
Ep (r ) De [exp{2a (r r0 )} 2 exp{ a (r r0 )}]
式中r0是分子中双原子分子间的平衡核间 距,De是势能曲线的井深,a为与分子结构有关 的常数.
过渡态理论
过渡态理论假设:过渡态分解为生成物的步骤是 整个反应的速率控制步。速率常数
k=vK ≠
v为导致过渡态分解为生成物的键振动频率;K ≠ 为生成过渡态的平衡常数。 过渡态中,A、B、C处在同一直线上,振动方式 有四种 只有第二种可能造成过渡态分解而成为生成物。 由量子学理论知,振动频率
v=k B T/h=RT/Lh
由量子学理论知振动频率摩尔气体常量t热力学温度统计热力学中grtlnk表示活化吉布斯自由能把35代入1中求得krtlhexps在气体中需要做相应的校正
7.5化学反应速率理论
7.5.1 碰撞理论 7.5.2 过渡态理论
过渡态理论是在量子力学和统计力学的 基础上提出来的。
内容:该理论认为,在化学反应过程中,反 应物需要经过一个过渡态,再转化为产物。 在此过程中存在着化学键的重新排布和能 量的重新分配。对于反应
K ≠ =exp(ΔS ≠ /R- Δ H ≠ /RT)
把(3)(5)代入(1)中求得
(5)
k=RT/Lh exp(ΔS ≠ /R- Δ H ≠ /RT)(6)
在固体和液体反应中Δ H ≠可以近似代替Ea, 在气体中需要做相应的校正。得到 k=RT/Lh exp(ΔS ≠ /R- Ea /RT) (7) 在碰撞理论中 k=PAexp[-E/RT] (8) 联立(7)(8)得到 PA=RT/Lh exp( ΔS ≠ /R)
• 对于复杂的反应体系,过渡态的结构难以确 定,计算的数值准确性很差,而量子力学对多质 点体系的计算也尚未解决。所以使得过渡态理论 在实际反应体系中应用困难。
A与BC反应时,A与B接近并产生一定的作 用力,同时B与C之间的键减弱,生成不稳 定的[A…B…C] ≠,成为过渡态,又称为活性 复合物。此时旧键还没完全断裂,新键还 未完全建立。
