用直方图描述数据
《直方图》参考课件

问题1解答
3.列频数分布表 对落在各个小组内的数据进行累计,得到各 个小组内的数据的个数(叫做频数).整理可以 得到频数分布表,见下表.
表10-3 频数分布表
从表中可以看出,身高在155≤x<158,158≤x<161,161≤x<164 三个组的人数最多,一共有41人,因此可以从身高在155cm至164 cm(不含164 cm)的学生中选队员.
5.4 5.5 6.0 7.0 5.7 6.3 6.7 5.7 5.2 5.8
4.6 5.8 5.5 6.4 7.4 5.6 6.0 5.7 6.0 6.3
列出样本的频数分布表,画出频数分布直方 图,从图表中可以得到什么信息?
解:(1)计算最大值和最小值的差
在样本数据中,最大值是 7.4 ,最小值是 4.0 , 它们的差是 7.4-4.0=3.4(cm) (2)决定组距和组数 最大值与最小值的差是3.4 cm,若取组距为 0.3 cm,那么由于
我们已经学习了用哪些方法来描述数据? 统计表;条形图;折线图;扇形图. 各方法有什么特点?
问题1
为了参加全校各个年级之间的广播操比赛, 七年级准备从63名同学中挑出身高相差不多的40 名同学参加比赛.为此收集到这63名同学的身高 (单位:cm)如下:
158 158 160 168 159 159 151 158 159 168 158 154 158 154 169 158 158 158 159 167 170 153 160 160 159 159 160 149 163 163 162 172 161 153 156 162
4.画频数分布直方图 为了更直观形象地看出频数分布的情况,可 以根据表格中的数据画出频数分布直方
149 152 155 158 161 164 167 170 173 身高/㎝
频率分布直方图的平均数

频率分布直方图的平均数
频率分布直方图是用来描述一组数据的分布情况的图表。
它将数据的取值范围划分成一些区间,统计每个区间内数据出现的次数,然后将这些次数用纵向的条形图表示出来。
频率分布直方图的平均数是指所有数据的平均数。
如果数据有n个,则平均数计算公式为:
平均数= Σ(数据值× 频率) / Σ频率
其中,Σ(数据值× 频率)表示所有数据值乘以对应的频率的总和,Σ频率表示所有数据的频率的总和。
例如,对于如下的频率分布直方图:
数据值频率
0-10 3
10-20 5
20-30 2
30-40 4
40-50 1
则平均数计算如下:
平均数= (0 × 3 + 10 × 5 + 20 × 2 + 30 × 4 + 40 × 1) / (3 + 5 + 2 + 4 + 1)
= 270 / 15
= 18
频率分布直方图的平均数可以反映出数据的中位数,即大多数数据取值的中间值。
初中数学频数直方图画法举例

初中数学频数直方图画法举例频数散布直方图是描述数据的一种重要统计图。
利用其描述数据,可清楚看出每一个数据段所占的数据个数的多少。
咱们不仅要能从频数直方图中获取正确的信息,而且还要正确绘制频数直方图,下面举例说明如何画频数直方图呢。
例1 七。
五(1)班40个学生某次数学考试成绩如下:63,84,91,53,69,81,61,69,91,78,75,81,80,67,76,81,79,94,61,69,89,70,70,87,81,86,90,88,85,67,71,82,87,75,87,95,53,65,74,77(1)请你按10分的组距分段,算出每一个分数段学生成绩显现的频数,填入频数散布表:请把频数散布表及频数散布直方图补充完整;(2)请你统计一下这次数学考试的合格率(60分以上含60分为合格)及优秀率(90分以上含90分为优秀);(3)请说明哪个分数段的学生最多?哪个分数段的学生最少?分析制作频数散布直方图,需要对所给的数据进行正确的整理分组,统计出每一个分数段的人数,列出频数散布表,再依照频数散布表绘制频数散布直方图。
解制作频数散布表(表1):表1成绩x(分)划记频数50≤x<60 260≤x<70 正970≤x<80 正正1080≤x<90 正正1490≤x<100 正 5(1)依照频数散布表画频数直方图。
(如图1)(2)合格率(40-2)÷40=95%;优秀率5÷40=%。
(3)从图中能够清楚地看出80到90那个分数段的学生数最多,50分到60分那个分数段的学生数最少。
例2 育才中学为了了解本校学生的躯体发育情形,对同年龄的40名女生的身高进行了测量,结果如下(数据均为整数,单位:cm):168,160,157,161,158,153,158,164,158,163,158,157,167,154,159,166,159,156,162,158,159,160,164,164,170,163,162,154,151,146,151,160,165,158,149,157,162,159,165,157.请将上述的数据整理后,列出频数散布表,画出频数直方图,并依照所画的直方图说明:大部份同窗处于哪个身高段?身高的整体散布情形如何?分析由于有40个数据,最小的数据为146cm,最大数据为170cm,其差为24cm,可将数据分成5组,整理数据列出散布表,画出频数直方图,可从整体上把握数据的散布情形。
10.2直方图1
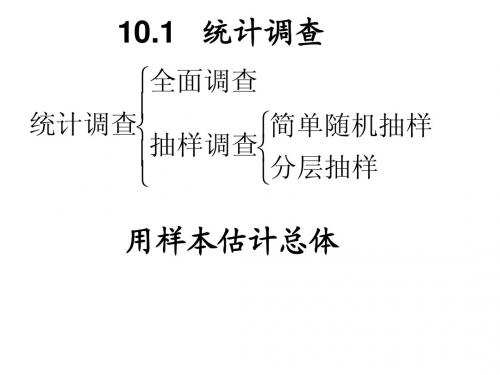
3. 某中学九年级部分同学参加全国初中数学竞赛,指 导老师统计了所有参赛同学的成绩(成绩都是整数,试 题满分120分),并且绘制了频数分布直方图,如图所 示,请根据直方图回答下列问题: (1)该中学参加本次数学竞赛的有多少名同学? (2)如果成绩在90分以上(含90分)的同学获奖,那 么该中学参赛同学的获奖率是多少? (3)图中还提供了其他信息,例如该中学没有获得满 分的同学等等。请再写出两条信息。
149
152
155
158
161
164
167
170
173
身高
(厘米)
小长方形的面积是什么?
4.画频数分布直方图
频数 (学生人数)
20
15
10 5 0
149 152 155 158 161 164 167 170 173
身高/㎝
频数折线图
频数(学生人数)
20
将直方图中每个小 长方形上面一条边 的中点顺次连结起 来,即可得到频数 折线图
注意:一般情况 在样本数据中,最大值是7.4,最小 值是4.0,它们的差是 (1)可以由组距来求组数; 7.4-4.0=3.4(cm) (2)当数据个数小于40时,组数 为6-8组; (2)决定组距和组数 当数据个数40—100个时,组 最大值与最小值的差是3.4 cm,若 数为7-10组; 取组距为0.3 cm,那么由于 3.4 11 1
频数(学生人数)
16 14 12 10 8 6 4 2 0
130 135 140 145 150 155 160 165 170
2.根据直方图回答问题:
脉搏次数 (次/分)
(1)脉搏在 155~160 范围的学生最多,有 14 个人。 (2)脉搏在135---140有 2 人,160---165有 11 人, (3) 全班有 49 人。
直方图
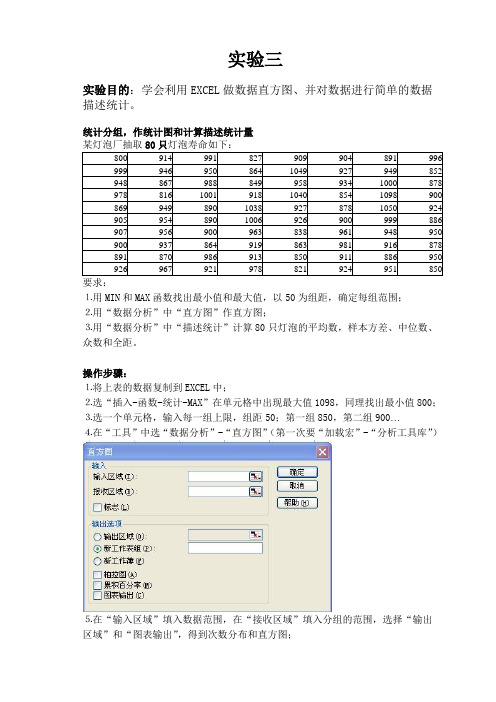
实验三实验目的:学会利用EXCEL做数据直方图、并对数据进行简单的数据描述统计。
统计分组,作统计图和计算描述统计量800914991827909904891996 9999469508641049927949852 9488679888499589341000878 978816100191810408541098900 86994989010389278781050924 9059548901006926900999886 907956900963838961948950 900937864919863981916878 891870986913850911886950 926967921978821924951850要求:⒈用MIN和MAX函数找出最小值和最大值,以50为组距,确定每组范围;⒉用“数据分析”中“直方图”作直方图;⒊用“数据分析”中“描述统计”计算80只灯泡的平均数,样本方差、中位数、众数和全距。
操作步骤:⒈将上表的数据复制到EXCEL中;⒉选“插入-函数-统计-MAX”在单元格中出现最大值1098,同理找出最小值800;⒊选一个单元格,输入每一组上限,组距50;第一组850,第二组900…⒋在“工具”中选“数据分析”-“直方图”(第一次要“加载宏”-“分析工具库”)⒌在“输入区域”填入数据范围,在“接收区域”填入分组的范围,选择“输出区域”和“图表输出”,得到次数分布和直方图;⒍对直方图进行编辑:在直方图上按右键,选“数据系列格式-选项”,将“分类间隔”设置为0⒎在“数据分析”中选“描述统计”,选择“输入区域”、“输出区域”和“汇总统计”,练习2:某车间100个工人本月生产某种产品的产量资料如下:(单位:件)要求:根据以上资料,作直方图和计算描述统计量。
(平均数,样本方差、中位数、众数和全距。
)1。
基本统计直方图知识点总结

基本统计直方图知识点总结直方图是统计学中一种常用的数据可视化工具,它能够清晰地展示数据的分布情况,帮助我们快速了解数据的特征和规律。
直方图常用于描述数据的频数分布和概率密度分布,是数据分析和可视化中的重要工具。
在本文中,我们将总结直方图的基本概念、构造方法、应用场景以及注意事项,帮助读者更好地理解和运用直方图。
一、直方图的基本概念1.1 直方图的定义直方图是一种用于显示数据频率分布的图表,它将数据按照数值范围分组,并用柱状图的形式展示每个组的频数或频率。
通常情况下,直方图的横轴表示数据的取值范围,纵轴表示数据的频数或频率。
通过直方图,我们可以直观地看出数据的分布情况,包括中心位置、散布程度、异常值等。
1.2 直方图与柱状图的区别直方图和柱状图在外观上很相似,但它们的用途和展示内容却有所不同。
柱状图用于比较不同类别或组的数据,每个柱子代表一个类别或组,而直方图则主要用于展示连续型数据的分布情况,每个柱子表示数据的范围。
1.3 直方图的特点直方图具有以下几个特点:(1)展示数据分布:直方图可以直观地展示数据的分布情况,包括中心位置、离散程度和形态特征。
(2)非负性:直方图中每个柱子的高度代表数据的频数或频率,因此必须是非负的。
(3)相对宽度:直方图中每个柱子的宽度表示数据范围,相邻柱子之间没有间隙,以突出数据的连续性。
(4)面积相等:直方图中每个柱子的面积代表数据的频数或频率,因此相等宽度的柱子面积应当相等。
1.4 直方图的应用直方图在统计学和数据分析中有着广泛的应用,主要包括以下几个方面:(1)数据分布展示:直方图可以清晰地展示数据的分布情况,包括正态分布、偏态分布、离散分布等。
(2)异常值检测:直方图可以帮助我们快速发现数据中的异常值,通常异常值会在直方图中呈现为孤立的柱子。
(3)数据分组分析:直方图可以帮助我们合理地对数据进行分组,并分析不同组的分布情况和特征。
(4)统计规律验证:直方图可以用于验证数据的统计规律,比如频率分布是否符合某个特定分布模型。
第十章课件第三课时10.2直方图
(2)通话时间不足10分的有多少次? 43
(3)哪个时间范围的通话最多? 通话时间在1~5分钟的次数最多, 通话时间在10~15分钟的次数最少. 哪个时间范围的通话最少?
25 18 10 16 8
许昌市医院出生的20名新生婴 儿的体重如下:(单位:kg)
140 145
16 9 5 .
150
5
0
.
.
.
165
2 . .
170 175
155 160
身高cm
频数分布直方图是以小长方形 的面积来反映数据落在各个小组内 的频数的大小。
小长方形的高表示: 但是等距分组时,为了画图、 看图的方便,通常直接用小长方形 的高表示频数。
某同学统计了他家10月份的长途电 话细清单,并按通话时间画出直方图。
新人教版七年级数学(下册)第十章
你知道几种描述数据的统计图?
(条形统计图、扇形统计图)
今天我们在来学习一种常用的描述
数据的方法---直方图.
问 题
为了参加全校各个年级之间的 广播操比赛,七年级准备从我班63
名同学中挑出身高相差不多的40名
同学参加比赛.为此收集到这63名 同学的身高(单位:cm)如下:
②所有的频率之和等于数字1。
4、画频数分布直方图: 以组距为底长,以频数为高,画 出各组的矩形图。
步 骤:
①画平面直角坐标系的第一象限; ②在横轴上取与组数相同的等分数;
每一线段对应一个组的组距; ③将纵轴分成适当的等分数;
④以各组的频数为高画矩形.
直方图
学生人数
20
15 10
6 9 3 . .
问题1:身高的变化范围是?
直方图(精)
将所有的数都加起来除以数据总个数。用公式表示为:
②、标准偏差S的计算
虽然极差R也能反映分散程度,但是它只考虑数据最大值和最小值的影响,没有考虑其余中间数据分布的影响,因此极差反映实际情况的能力较差。因此,实际工作中,就有必要运用另一个较为准确反映分散程度的统计特征值,即标准偏差:
③、直方图的定量表示
图9
②、平均值偏低,部份产品超规格下限有不良发生,但分配正常(常态)。
对策:调平均值(往右)。
图10
③、平均值偏高,部份产品超规格上限有不良发生,但分配正常(常态)。
对策:调平均值(往左)。
图11
④、制品虽成常态公配,但产品变异大,超出规格范围,品质不均。
对策:应缩小变异或放宽规格。
图12
⑤、制程呈常态分布,品质过剩,变异太小。
图2直方图
F、在图上标出图名,记入搜集数据的时间和其他必要的记录。总次数(频数)、统计特征值(平均值)与S(标准偏差)是直方图上的重要数据,一定要标出。
3、直方图的作用
①、由图形可以比较容易掌握制程的全貌(如:中心趋势,离散趋势,分配形状);
②、可了解制程的安定或异常状况;
③、与规格进行比较可判断制程能力。
直方图
1、概念
直方图是指:将某期间所收集的计量值数据(如:尺寸、重量、硬度……等)经分组整理成次数分配表,并以柱形予以图形化,以掌握这些数据所代表的情报。
直方图主要应用于:展示过程的分布情况。
图1表示了直方图的基本形状。
图1直方图的基本形状
2、直方图的制作步骤
A、收集数据,至少要收集50~100个数据;
(d)、制作次数分配表。如下表:
表2次数分配表
组号
