09讲 最优控制-极小值-时间最短
合集下载
第六章最优控制-PPT精品
最优控 u*(制 t)：满足上述条作 件用 u的 (t)。 控制 最优轨 x*(t线 )：在 u*(t)作用下状态方程的解。 最优指 J*： 标沿最优x*(轨 t)，线使性能J所 指达 标到的最
6.2 静态最优控制问题的解 （多元普通函数极值的解法）
静态最优化：J是一个多元普通函数
一、一元函数的极值：
第六章 最优控制
着重介绍最优控制系统的基本概念、基 本理论及其应用。
要点： 1 最优控制的概念 2 变分法 3 极小值原理 4 动态规划 5 线性最优控制器的设计
难点： 线性最优控制器的设计
6.1最优控制问题概述
一、最优控制
（一）最优控制目的
设计一个就某种性能指标或设计指标而言 是最好的系统。即利用u(t)使x(t)选择一条达到 目标的最好途径，即最优轨线。
（二）最优控制问题 一个系统在某些约束条件下寻找它的最好
的控制过程u(t)的问题。
最优控制问题包括：
1、描述受控系统的状方态程
x(t) f x(t),u(t),t
2、评价性能指标目 好标 坏泛 的函数
J＝[x(tf
)]
tf t0
L[x(t),u(t),t]dt
式中x(： t),u(t)是t的函数 J是， x(t),u(t)的函数
H
x H
u
H
f x f u
(g x
(g u
g (x,u
)T )T )0
0 0
[例 6－ 2]求J使 f(x,u)12xTQ1x12uTQ2u取极x值 *和 u的 *。 它满足约 g(x束 ,u)条 x件 Fud0，其 Q1， 中 Q2均为正 矩阵 F为 ，任意矩阵。
f x2
10 x2
2 x3
6.2 静态最优控制问题的解 （多元普通函数极值的解法）
静态最优化：J是一个多元普通函数
一、一元函数的极值：
第六章 最优控制
着重介绍最优控制系统的基本概念、基 本理论及其应用。
要点： 1 最优控制的概念 2 变分法 3 极小值原理 4 动态规划 5 线性最优控制器的设计
难点： 线性最优控制器的设计
6.1最优控制问题概述
一、最优控制
（一）最优控制目的
设计一个就某种性能指标或设计指标而言 是最好的系统。即利用u(t)使x(t)选择一条达到 目标的最好途径，即最优轨线。
（二）最优控制问题 一个系统在某些约束条件下寻找它的最好
的控制过程u(t)的问题。
最优控制问题包括：
1、描述受控系统的状方态程
x(t) f x(t),u(t),t
2、评价性能指标目 好标 坏泛 的函数
J＝[x(tf
)]
tf t0
L[x(t),u(t),t]dt
式中x(： t),u(t)是t的函数 J是， x(t),u(t)的函数
H
x H
u
H
f x f u
(g x
(g u
g (x,u
)T )T )0
0 0
[例 6－ 2]求J使 f(x,u)12xTQ1x12uTQ2u取极x值 *和 u的 *。 它满足约 g(x束 ,u)条 x件 Fud0，其 Q1， 中 Q2均为正 矩阵 F为 ，任意矩阵。
f x2
10 x2
2 x3
最优控制课件第3章
第三章 极小值原理及应用
经典变分法局限性： 1、应用前提： a ）控制量 u(t)的取值无约束。 b ） f、L、Φ等函数对其自变量二次连续可微，要求哈密 尔顿函数关于控制变量的偏导数存在 。 2、实际控制要求：
a ）控制量u受不等式约束，如：M i (u ) 0 ，i=1,2,3……
b ）性能指标有时关于u并不可微，要求哈密尔顿函数 关于控制变量的偏导数不存在 。
一般:对于实际系统根据物理意义有最优解 极小值原理 有唯一解－－ 最优解
－－－－－－－－
－－－－－－－－
但是，对于线性系统可以证明极小值原理既是泛函取最小 值的必要条件，也是充分条件。
Optimal Control Theory
Dong Jie 2014. All rights reserved.
Date: File:
05.04.2015 OC_CH3.6
Optimal Control Theory & its Application
②在最优轨线上，与最优控制u*相对应的H函数取绝对极小 值，即 或 沿最优轨线
③H函数在最优轨线终点满足
Optimal Control Theory
Dong Jie 2014. All rights reserved.
Optimal Control Theory & its Application
取哈密尔顿函数为
则实现最优控制的必要条件是，最优控制u*、最优轨线x* 和最优协态矢量λ*满足下列关系式： ①沿最优轨线满足正则方程
当g中不含x时
Optimal Control Theory
Dong Jie 2014. All rights reserved.
经典变分法局限性： 1、应用前提： a ）控制量 u(t)的取值无约束。 b ） f、L、Φ等函数对其自变量二次连续可微，要求哈密 尔顿函数关于控制变量的偏导数存在 。 2、实际控制要求：
a ）控制量u受不等式约束，如：M i (u ) 0 ，i=1,2,3……
b ）性能指标有时关于u并不可微，要求哈密尔顿函数 关于控制变量的偏导数不存在 。
一般:对于实际系统根据物理意义有最优解 极小值原理 有唯一解－－ 最优解
－－－－－－－－
－－－－－－－－
但是，对于线性系统可以证明极小值原理既是泛函取最小 值的必要条件，也是充分条件。
Optimal Control Theory
Dong Jie 2014. All rights reserved.
Date: File:
05.04.2015 OC_CH3.6
Optimal Control Theory & its Application
②在最优轨线上，与最优控制u*相对应的H函数取绝对极小 值，即 或 沿最优轨线
③H函数在最优轨线终点满足
Optimal Control Theory
Dong Jie 2014. All rights reserved.
Optimal Control Theory & its Application
取哈密尔顿函数为
则实现最优控制的必要条件是，最优控制u*、最优轨线x* 和最优协态矢量λ*满足下列关系式： ①沿最优轨线满足正则方程
当g中不含x时
Optimal Control Theory
Dong Jie 2014. All rights reserved.
最优控制特点
切换一次，设切换
2t
时间为ts，则令
0
为了求出ts，必须
首先找出状态在
1
平面上的转移轨线。
0
1
ts
tf
t
t
由 则：
设u=1，则
其中
如图(a)所示，为一组抛物线， 当K=0时经过原点[pos]
X2 s
0
t
p
若u=-1，则
X2 N
o
X1
T u=-1
为一组抛物线，如图(b)，当K1=0时过原点[NOT]
j =1，2…r
u 最优控制 *(t)是使
为极小，则：
＋１ －１ 不定
u*(t) +1
-1
奇异
t
可见：当 当
时， 时，
有确定值，正常情况 不定， 奇异情况
我们仅研究正常情况
u*(t)写成符号函数sgn{ }形式
则
j =1，2…r
向量形式：u*(t)=-sgn{q*(t)}
=-sgn{
}
⑶根据规范方程：
在证明过程中：
与H得符号与这里所定义的相反。
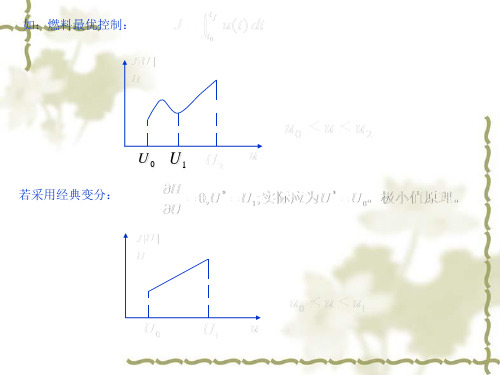
∴所以有的文献中也称为“极大值原理”。 3、H对u没有可微要求，因此应用拓宽。 4、 极小值原来是求取最优控制的必要条件，非充分条件。 即：满足极小值原理不一定J取极小值,需进一步判断。
一般:对于实际系统
有最优解
有唯一解
最优解
三、几种边界条件得讨论：
上面所讨论的是
控制向量约束条件: 末端状态：
g：p ×1维函数向量
目标函数：
: 自由
问题：寻求最优控制u*(t)，使系统由初态到终态， 目标函数J 为最小
❖ 步骤：应用最小值原理进行问题的求解
最短时间和最少燃料控制
(3 17) （由两个积分环节构成）
定义u(t)=f(t)/m , 则（3-16）式变为： y(t) u(t) (3 18)
取状态变量 x1(t) y(t), x2 (t) y(t) 则有 xx12((tt))xu2((tt))
(3 19)
矩阵形式为：
x(t)
0 0
1 0
x(t)
10u(t
)
(3 20)
第3章 最短时间和最少燃料的最优控制
3.1 非线性系统旳最短时间控制问题
最短时间控制问题旳提法：
设受控系统状态方程为
x(t) f [x(t),t] B[x(t),t]u(t)
(3 1)
给定终端约束条件为
x(t0 ) x0
[x(t f ),t f ] 0 (3 2)
谋求m维有界闭集中旳最优控制u*(t)，满足不等式约束
[x(t f ),t f ] 0 (3 2)
谋求m维有界闭集中旳最优控制u*(t)，满足不等式约束
u j (t) 1 ( j 1,2,..., m) (3 3) 使系统从已知初始状态 x(t0 ) 转移到目的集中某一状态 x(t f ) 时，如
下目的泛函取极小值，其中 t f 未知
J[u(t)]
x1 (t ) x2 (t)
x2 (t) u(t)
(1) (2)
(1) dx1 x2 x2 , 1 (2) dx2 u(t)
dx1 x2dx2
x1
2
x2 2
c
(3 26)
为抛物线
第3章 最短时间和最少燃料的最优控制
{(x1,
x2 ) :
x1
1 2
x22 ,
x2
0}
x2
14 最优控制4
x2 u
x1 x 2 x2 u
x 2 (0 ) x 20
x1 ( 0 ) x1 0 x1 ( t f ) 0
x 2 (0 ) x 20 x2 (t f ) 0
x2 (t f ) 0
第四章 二次型性能指标的线性 系统最优控制
如果所研究的系统为线性，所取的性能 指标为状态变量与控制变量的二次型函 数，则这种动态系统的最优化问题，称 为线性二次型问题。
§4.1 线性二次型问题
(t ) A (t ) x (t ) B (t )u (t ) x y (t ) C (t ) x (t )
e (t ) y d (t ) y (t )
J 1 2 e ( t f ) Fe ( t f )
T
1 2
t
f
[e (t )Q (t )e (t ) u
T
T
( t ) R ( t ) u ( t )] dt
t0
二次型性能指标的物理含义
（1）末值项
对系统末态跟踪误差的要求 对动态跟踪误差加权平方和的积分要求
（2）第一过程项
（3）第二过程项
对系统加权后的控制能量消耗的总度量
几种重要的特殊情形
（1）状态调节器问题
J 1 2 x ( t f ) Fx ( t f )
T
*
T
*
b2 ( x, t)
bm ( x, t )
g i (t ) b i ( x , t ) (t )
1 , g i ( t ) 0 u i ( t ) sgn{ g i ( t )} 1, g i ( t ) 0
时间最优控制
其 中x(t ) Rn，u(t ) Rm，f ()和B()的 各 元 对x(t )和t连 续 可 微 ，
g() R p， 其 各 元 对x(t f )和t f 连 续 可 微 ，t f 是 状 态 轨 线 首 次 与 目标集相遇的时刻。
为 统 一 起 见 ， 时 间 最 优控 制 问 题 的 性 能 指 标 取为 积 分 型
为奇异区间。
7
定 理4.4.1 Bang Bang控 制 原 理 设u*(t )是 问 题4.4.1的 时 间 最 优 控 制 ， 且 问题4.4.1是 正 常 的 ， 则最优控制
u*(t ) sgnq(t ) sgn BT ( x(t ),t )(t )
或
u*j (t )＝ sgn q j (t ) sgn bTj ( x(t ),t )(t )
j 1,2, , m; t t0 , t f
因 此 时 间 最 优 控 制 的 各个 分 量u*j (t )都 是 时 间t的 分 段 常 值 函 数 ， 在q j (t )＝0的 诸 点 上 ，u*j (t )由 一 个 边 界 值 切 换到另一个边界值。
8
4.4.2 线 性 定 常 系 统 的 时 间 最优 控 制 问 题 4.4.2 已 知 线 性 定 常 系 统x(t ) Ax(t ) Bu(t ) 是 完 全 能 控 的 ， 求 满 足约 束
u j (t ) 1
设 q(t) BT (x(t),t)(t)
或 q j (t) bTj (x(t),t)(t), j 1,2, , m
其中bj (x(t),t)是矩阵B的第j个列向量，于是(1)式可写为
m
m
T (t)B(x*(t),t)u*(t)
最优控制系统设计
* 另一方面，近年来，由于对系统控制质量的要 求越来越高，和计算机在控制领域的应用越来越 广泛，所以最优控制系统受到很大重视。
* 最优控制的目的是使系统的某种性能 指标达到最佳，也就是说，利用控制作 用可按照人们的愿望选择一条达到目标 的最佳途径（即最优轨线），至于哪一 条轨线为最优，对于不同的系统有不同 的要求。而且对于同一系统，也可能有 不同的要求。
下面介绍什么是二次型性能指标的最优 控制
给定一个n阶线性控制对象，其状态方程是 X(t) A(t)X(t) B(t)u(t), X(t0 ) X0 (4.4)
寻求最优控制u(t)，使性能指标
J
1 2
XT
(t f
)SX(t f
)
(4.5)
1 tf [XT (t)Q(t)X(t) uT (t)R(t)u(t)]dt
求解的一种方法是: 先解状态方程， 求出 1, 2, , 再将其代入 J中求解，此 种方法非常繁琐。
另一种方法是:组成新的泛函 J，求 考虑约束的极值问题，即拉格朗日乘子法。
它的具体步骤如下：
①用一个向量拉格朗日乘子λ(t) ，将 约束即系统的状态方程加到原来的性能指
标J中去，得到新的性能指J标 为:
性能指标J在数学上称为泛函，而在控 制系统术语中称为损失函数。通常，在实 际系统中，特别是在工程项目中，损失函 数的确定很不容易，需要多次反复。
性能指标的选择:
性能指标J是一个标量，在最优控 制中它代替了传统的设计指标，如最大 超调量、阻尼比、幅值裕度和相位裕度。 适当选择性能指标，使系统设计符合物 理上的标准。////
例如在机床加工中可要求加工成本最低为最优； 在导弹飞行控制中可要求燃料消耗最少为最优； 在截击问题中可选时间最短为最优等等。 因此，最优是以选定的性能指标最优为依据的。 * 一般来讲，达到一个目标的控制方式很多， 但实际上的经济、时间、环境、制造等方面有各 种限制，因此可实行的控制方式是有限的。
* 最优控制的目的是使系统的某种性能 指标达到最佳，也就是说，利用控制作 用可按照人们的愿望选择一条达到目标 的最佳途径（即最优轨线），至于哪一 条轨线为最优，对于不同的系统有不同 的要求。而且对于同一系统，也可能有 不同的要求。
下面介绍什么是二次型性能指标的最优 控制
给定一个n阶线性控制对象，其状态方程是 X(t) A(t)X(t) B(t)u(t), X(t0 ) X0 (4.4)
寻求最优控制u(t)，使性能指标
J
1 2
XT
(t f
)SX(t f
)
(4.5)
1 tf [XT (t)Q(t)X(t) uT (t)R(t)u(t)]dt
求解的一种方法是: 先解状态方程， 求出 1, 2, , 再将其代入 J中求解，此 种方法非常繁琐。
另一种方法是:组成新的泛函 J，求 考虑约束的极值问题，即拉格朗日乘子法。
它的具体步骤如下：
①用一个向量拉格朗日乘子λ(t) ，将 约束即系统的状态方程加到原来的性能指
标J中去，得到新的性能指J标 为:
性能指标J在数学上称为泛函，而在控 制系统术语中称为损失函数。通常，在实 际系统中，特别是在工程项目中，损失函 数的确定很不容易，需要多次反复。
性能指标的选择:
性能指标J是一个标量，在最优控 制中它代替了传统的设计指标，如最大 超调量、阻尼比、幅值裕度和相位裕度。 适当选择性能指标，使系统设计符合物 理上的标准。////
例如在机床加工中可要求加工成本最低为最优； 在导弹飞行控制中可要求燃料消耗最少为最优； 在截击问题中可选时间最短为最优等等。 因此，最优是以选定的性能指标最优为依据的。 * 一般来讲，达到一个目标的控制方式很多， 但实际上的经济、时间、环境、制造等方面有各 种限制，因此可实行的控制方式是有限的。
ppt第四章极小值原理及其应用
1 (t) c1
（4-30）
2 (t) c2 c1t
其中，c1 、c2 是积分常数。
（4-31）
由的表达式（4-27）可见，若要选择 u(t) 使 H 取极小，只要使 2(t)u(t) 越负越好，而 u(t) 1 ， 故当 u(t) 1 ，且 u(t) 与 2(t) 反号时， H 取极小， 即最优控制为
取极小的最优控制。
（4-24） （4-25） （4-26）
解 ； 因为控制作用有限制（属于有界闭集），故要用
极小值原理求解。取哈密顿函数
H F T f 1 1(t)x2 (t) 2 (t)u(t) 协态方程为
（4-27）
1
H
x1
0
2
H x2
1
（4-28） （4-29）
积分上面两个方程可得
H
H
H
u*
u u* u0
u u*
u
(a)
(b)
(c)
图4-1有界闭集内函数的几种形状
对于图4-1（a） H / u 0 仍对应最优解 u 。对于
图4-1(b) H / u 0 所对应的解 u0不是最优解，最优 解 u 在边界上。对于图4-1（c）H / U 常数，由这个
方程解不出最优控制 u 来（这种情况称为奇异情
G X (t f ),t f 0 （4-18）
3 横截条件
(t
f
)
X (t
f
)
G T X (t f
)
（4-19）
4 最优终端时刻条件
H
(t
f
)
t f
G T
t f
（4-20）
5 在最优轨线 X * (t) 和最优控制 U * (t) 上哈密 6 顿函数取极小值
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
18
最优控制——极小值原理 3.4 极小值原理的典型应用
能源与动力学院系统控制与仿真研究室
19
最优控制——极小值原理 3.4 极小值原理的典型应用
能源与动力学院系统控制与仿真研究室
20
最优控制——极小值原理 3.4 极小值原理的典型应用
能源与动力学院系统控制与仿真研究室
21
最优控制——极小值原理 3.4 极小值原理的典型应用
能源与动力学院系统控制与仿真研究室
24
最优控制——极小值原理 3.4 极小值原理的典型应用
能源与动力学院系统控制与仿真研究室
25
最优控制——极小值原理 3.4 极小值原理的典型应用
1 u sgn x1 x2 x2 2
能源与动力学院系统控制与仿真研究室
26
最优控制——极小值原理 3. 连续系统极小值原理
x1 0 1 x1 t f 0 , 0 x t x2 0 1 f 2 u 1
能源与动力学院系统控制与仿真研究室 11
最优控制——极小值原理 3.4 极小值原理的典型应用
能源与动力学院系统控制与仿真研究室
能源与动力学院系统控制与仿真研究室
9
最优控制——极小值原理 3.4 极小值原理的典型应用
能源与动力学院系统控制与仿真研究室
10
最优控制——极小值原理 3.4 极小值原理的典型应用
双积分环节时间最优控制问题
min J tf 1 0 1 x1 0 x u x 2 0 0 x2 1
线性定常系统时间最优控制问题的提法
能源与动力学院系统控制与仿真研究室
6
最优控制——极小值原理 3.4 极小值原理的典型应用
能源与动力学院系统控制与仿真研究室
7
最优控制——极小值原理 3.4 极小值原理的典型应用
能源与动力学院系统控制与仿真研究室
8
最优控制——极小值原理 3.4 极小值原理的典型应用
x2 t 1, u 1 3 x t 1 2 , u 1 2 2
能源与动力学院系统控制与仿真研究室
23
最优控制——极小值原理 3.4 极小值原理的典型应用
对于二阶系统，开关切换次数最多为1次， 如果初始状态位于PO曲线上，则不需要切 换（切换次数为0），即可转移到原点。 对于n阶可控系统的快速控制，开关切换次 数最多为n-1次。
12
最优控制——极小值原理 3.4 极小值原理的典型应用
能源与动力学院系统控制与仿真研究室
13
最优控制——极小值原理 3.4 极小值原理的典型应用
能源与动力学院系统控制与仿真研究室
14
最优控制——极小值原理 3.4 极小值原理的典型应用
1 2 x1 x2 k1 2
能源与动力学院系统控制与仿真研究室
能源与动力学院系统控制与仿真研究室
22
最优控制——极小值原理 3.4 极小值原理的典型应用
t2 x1 t 1, u 1 2 2 3 7 3 x t 1 2 t 2 , u 1 1 2 2 2 2
15
最优控制——极小值原理 3.4 极小值原理的典型应用
能源与动力学院系统控制与仿真研究室
16
最优控制——极小值原理 3.4 极小值原理的典型应用
1 2 x1 x2 k2 2
能源与动力学院系统控制与仿真研究室
17
最优控制——极小值原理 3.4 极小值原理的典型应用
能源与动力学院系统控制与仿真研究室
肖玲斐 lf i @ lfxiao@ d
最优控制 最 控制 前次课程回顾——极小值
离散系统的极小值原理 •离散系统基本概念 •离散极小值原理 •离散极小值原理与连续极小值原理的比较
能源与动力学院系统控制与仿真研究室
2
最优控制——极小值原理 3.4 极小值原理的典型应用
能源与动力学院系统控制与仿真研究室
4
最优控制——极小值原理 3.4 极小值原理的典型应用
时间最优控制问题的基本特征是
• 在满足一定约束条件前提下， • 取一控制作用（最优控制）， • 使系统以最短的时间从初始状态转移到给
定的终态。
能源与动力学院系统控制与仿真研究室
5
最优控制——极小值原理 3.4 极小值原理的典型应用
重点掌握
1.双积分环节的时间最优 控制求解步骤及结果分析
能源与动力学院系统控制与仿真研究室
27
思考题
3.2 电梯最速上升最优控制
能源与动力学院系统控制与仿真研究室
28
思考题
3.3 简谐振动系统的时间最优控制
能源与动力学院系统控制与仿真研究室
29
肖玲斐 lf i @ lfxiao@ d
时间最优控制 燃料最优控制 时间-燃料最优控制 能量最优控制
能源与动力学院系统控制与仿真研究室
3
最优控制——极小值原理 3.4 极小值原理的典型应用
时间最优控制问题
• 也称为最短时间控制又称为问题或最速控
制问题 • 其性能指标简单，有实用价值，因而研究 得最早 • 这类问题的研究结果也最为成熟。