牛头刨床MATLAB运动仿真
机械毕业设计1157牛头刨床六杆机构运动分析程序设计

摘要在工程技术领域,经常会遇到一些需要反复操作,重复性很高的工作,如果能有一个供反复操作且操作简单的专用工具,图形用户界面就是最好的选择。
如在本设计中对于牛头刨床平面六杆机构来说,为了保证结构参数与运动参数不同的牛头刨床的运动特性,即刨刀在切削过程中接近于等速运动从而保证加工质量和延长刀具寿命,以及刀具的急回性能从而提高生产率,这样的问题如果能够通过设计一个模型平台,之后只需改变参量就可以解决预期的问题,这将大大的提高设计效率。
本设计中正是通过建立牛头刨床六杆机构的数学模型,然后用MA TLAB程序设计出一个友好的人机交互的图形界面,并将数学模型参数化,使用户只需改变牛头刨床的参数就可以方便的实现运动分析和运动仿真,用户可以形象直观地观察到牛头刨床的运动轨迹、速度变化及加速度变化规律。
关键词:牛头刨床六杆机构MA TLAB 运动仿真程序开发AbstractIn the engineering area, often repeatedly encountered some operational needs, repetitive highly, and if the operation can be repeated for a simple operation and dedicated tool graphical user interface is the best choice. As in the planer graphic design for six pole bodies, and campaigns to ensure the structural parameters of different parameters planer movement characteristics, planning tool in the process of cutting close to equal campaign to ensure processing quality and extended life cutlery and cutlery rush back to the performance enhancing productivity, If such issues can be adopted to design a model platform parameter can be changed only after the expected settlement, which will greatly enhance the efficiency of the design. It is through the establishment of this design planer six pole bodies mathematical model, and then use MATLAB to devise procedures of a friendly aircraft in the world graphics interface, and mathematical models of the parameters, so that users only need to change the parameters planer can facilitate the realization of movement analysis and sports simulation, Users can visual image observed in planer movement trajectories, speed changes and acceleration changes.Keywords:Planer 6 pole bodies MATLAB Campaign simulation Procedure development.目录1 绪论 (4)2牛头刨床六杆机构运动分析程序设计2.1 MA TLAB介绍 (5)2.2 MA TLAB的特点 (6)2.3 用MA TLAB处理工程问题优缺点 (7)3牛头刨床运动分析的模型3.1 基本概念与原理 (9)3.2 牛头刨床六杆机构的数学模型 (9)4 图形用户界面GUI4.1界面设计的原则 (13)4.2 功能要求 (16)4.3界面结构设计 (17)4.4 程序框图的设计 (19)5运动仿真程序界面设计与编程实现5.1 句柄图形体系 (21)5.1.1 图形对象、对象句柄和句柄图形树结构 (22)5.1.2 对象属性 (23)5.1.3 对象句柄的获取方法 (23)5.1.4 对象句柄的获取和设置 (25)5.2 主界面参数含义 (27)5.3 界面制作步骤 (27)6总结 (49)7致谢 (50)8参考书目 (51)9附录程序源代码 (52)1 绪论1.1本课题的意义机构运动分析是不考虑引起机构运动的外力的影响,而仅从几何角度出发,根据已知的原动件的运动规律(通常假设为匀速运动),确定机构其它构件上各点的位移、速度、加速度,或构件的角位移、角速度、角加速度等运动参数。
牛头刨机构的运动分析
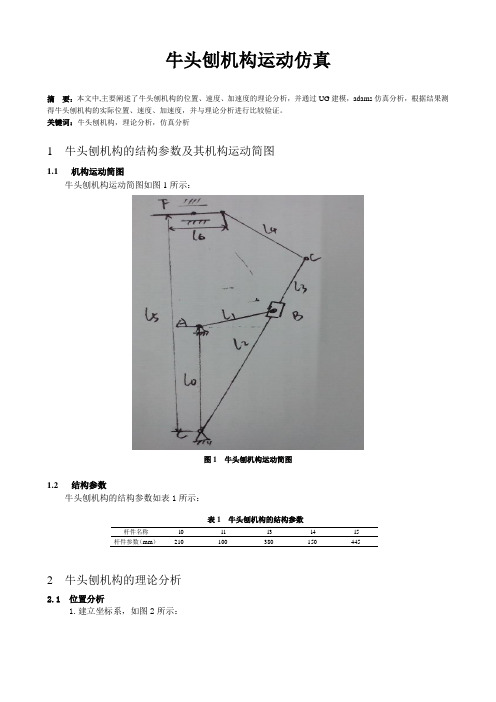
牛头刨机构运动仿真摘 要:本文中,主要阐述了牛头刨机构的位置、速度、加速度的理论分析,并通过UG 建模,adams 仿真分析,根据结果测得牛头刨机构的实际位置、速度、加速度,并与理论分析进行比较验证。
关键词:牛头刨机构,理论分析,仿真分析1 牛头刨机构的结构参数及其机构运动简图1.1 机构运动简图牛头刨机构运动简图如图1所示:图1 牛头刨机构运动简图1.2 结构参数牛头刨机构的结构参数如表1所示:表1 牛头刨机构的结构参数2 牛头刨机构的理论分析2.1 位置分析1.建立坐标系,如图2所示:杆件名称 l0 l1l3l4 l5 杆件参数(mm ) 210 100 380 150 445图2 牛头刨机构运动简图2.建立矢量方程由封闭图形ABCA 可写出机构一个封闭矢量方程:CA AB CB += (1-1)其分量形式为: 12121cos 2cos 01sin 2sin l l l l l θθθθ⋅=⋅⎧⎨+⋅=⋅⎩ (1-2)由封闭图形CDEFC 可写出机构另一个 封闭矢量方程:C D D EC F F E +=+ (1-3)其分量形式为:23233cos 4cos 63sin 4sin 5l l l l l l θθθθ⋅+⋅=⎧⎨⋅+⋅=⎩(1-4)3.求解未知参数2l (1-5) 21arccos(1cos /2)l l θθ=⋅ (1-6)32arcsin((53sin /)4)l l l θθ=-⋅ (1-7)2363cos 4cos l l l θθ=⋅+⋅ (1-8)2.2 速度分析将式(1-2)和式(1-4)对时间t 求一次导数,得速度关系:1122221122221sin 2sin cos 1cos 2cos sin l l l l θωθωνθθωθωνθ⋅⋅=⋅⋅-⋅⎧⎨⋅⋅=⋅⋅+⋅⎩ (1-9) 2233622333sin 4sin 3cos 4cos 0l l l l θωθωνθωθω⋅⋅+⋅⋅=-⎧⎨⋅⋅+⋅⋅=⎩(1-10) 若用矩阵形式来表示,则上式可写为:222122211233236cos 2sin 001sin sin 2cos 001cos 03sin 4sin 1003cos 4cos 00l v l l l l l l l θθθθθωθωθθωθθν--⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦ (1-11)2.3 加速度分析将式(1-9)和(1-10)对时间t 求二次导数,可得加速度关系表达式。
哈工大机械原理大作业1 连杆机构运动分析 牛头刨床 学号5号

大作业1 连杆机构运动分析运动分析题目图1-13 牛头刨床机构简图一、按比例画出机构运动简图见A3图纸二、机构的结构分析及基本杆组的划分(1)机构的结构分析该机构为平面连杆机构,活动构件数n=5;有A、B、C、E、F五个转动副和B、F两个移动副,没有高副,故低副数PL=7,高副数PH=0。
机构的自由度F=3n-2PL-PH=3*5-2*7=1。
机构有确定运动轨迹。
(2)基本杆组的划分图1-13中,原动件构件1为Ⅰ级杆组,移除之后按照拆杆组法对机构进行拆分,可得由滑块2和杆3组成的RPRⅡ级杆组,以及由杆4和滑块5组成的RRPⅡ级杆组。
拆分图如下:图1-13-1 Ⅰ级杆组图1-13-2 RPRⅡ级杆组图1-13-3 RRPⅡ级杆组三、各杆组的运动分析数学模型图1-13-1 Ⅰ级杆组 x B =x A +l AB cos ϕy B =y A +l AB sin ϕ图1-13-2 RPR Ⅱ级杆组 x E =x B +(l CE -s)cos ϕj y E =y B +(l CE -s)sin ϕjϕj =arctan(B 0/A 0)A 0=xB -x CB 0=y B -y CS =2020B A + 图1-13-3 RRP Ⅱ级杆组F 的位置 x F =x E -l EF cos ϕiy F =y E +l EF sin ϕi ϕi =arcsin(A 1/l EF )A 1=H-H 1-y EF 的速度F 的加速度四、建立坐标系以A 为原点建立坐标系,则A (0,0)五、编程使用MATLAB 编写程序如下lAB=108;lCD=620;lEF=300;H1=350;H=635;xC=0;yC=-350;syms t;f=(255*pi/30)*t;xB=lAB*cos(f);yB=lAB*sin(f);A0=xB-xC;B0=yB-yC;S=sqrt(A0^2+B0^2);f1=atan(B0/A0);xE=xB+(lAB-S)*cos(f1);yE=yB+(lAB-S)*sin(f1);A1=H-H1-yE;f2=asin(A1/lEF);xF=xE-lEF*cos(f2);yF=yE+lEF*sin(f2);a=0:0.001:0.5;xF=subs(xF,t,a);plot(a,xF)title('位移x随时间t变化图像') xlabel('t(s)'),ylabel(X')lAB=108;lCD=620;lEF=300;H1=350;H=635;xC=0;yC=-350;syms t;f=(255*pi/30)*t;xB=lAB*cos(f);yB=lAB*sin(f);A0=xB-xC;B0=yB-yC;S=sqrt(A0^2+B0^2);f1=atan(B0/A0);xE=xB+(lAB-S)*cos(f1);yE=yB+(lAB-S)*sin(f1);A1=H-H1-yE;f2=asin(A1/lEF);xF=xE-lEF*cos(f2);yF=yE+lEF*sin(f2);vF=diff(xF,t);a=0:0.001:0.5;vF=subs(vF,t,a);plot(a,vF)title('速度v随时间t变化图像') xlabel('t(s)'),ylabel(V')lAB=108;lCD=620;lEF=300;H1=350;H=635;xC=0;yC=-350;syms t;f=(255*pi/30)*t;xB=lAB*cos(f);yB=lAB*sin(f);A0=xB-xC;B0=yB-yC;S=sqrt(A0^2+B0^2);f1=atan(B0/A0);xE=xB+(lAB-S)*cos(f1);yE=yB+(lAB-S)*sin(f1);A1=H-H1-yE;f2=asin(A1/lEF);xF=xE-lEF*cos(f2);yF=yE+lEF*sin(f2);aF=diff(xF,t,2);a=0:0.001:0.5;aF=subs(aF,t,a);plot(a,aF)title('加速度a随时间t变化图像') xlabel('t(s)'),ylabel(A')六、位移、速度、加速度图像位移xE随时间t变化图像速度vE随时间t变化图像加速度aE随时间t变化图像七、运动分析由MATLAB编程后绘制所得图线分析可知,牛头刨床的刨头F行程约为500mm,在0.06s~0.17s之间速度和加速度波动较大,在0.17s~0.29s 之间速度和加速度波动较小,这就保证了刨头在空行程时有急回运动,而在工作行程是由较均匀的切削速度,运动连续,且运动性能良好稳定。
牛头刨床的连杆机构运动分析

牛头刨床的连杆机构运动分析0 前言机构运动分析的任务是对于结构型式及尺寸参数已定的具体机构,按主动件的位置、速度和加速度来确定从动件或从动件上指定点的位置、速度和加速度。
许多机械的运动学特性和运动参数直接关系到机械工艺动作的质量,运动参数又是机械动力学分析的依据,所以机构的运动分析是机械设计过程中必不可少的重要环节。
以计算机为手段的解析方法,由于解算速度快,精确度高,程序有一定的通用性,已成为机构运动分析的主要方法。
连杆机构作为在机械制造特别是在加工机械制造中主要用作传动的机构型式,同其他型式机构特别是凸轮机构相比具有很多优点。
连杆机构采用低副连接,结构简单,易于加工、安装并能保证精度要求。
连杆机构可以将主动件的运动通过连杆传递到与执行机构或辅助机构直接或间接相连的从动件,实现间歇运动,满足给定的运动要求,完成机器的工艺操作。
牛头刨床是一种利用工作台的横向运动和纵向往复运动来去除材料的一种切削加工机床。
工作台的纵向往复运动是机床的主运动,实现工件的切削。
工作台的横向运动即是进给运动,实现对切削精度的控制。
本文中只分析纵向运动的运动特性。
牛头刨床有很多机构组成,其中实现刨头切削运动的六连杆机构是一个关键机构。
刨床工作时,通过六杆机构驱动刨刀作往复移动。
刨刀右行时,当刨刀处于工作行程时;要求刨刀的速度较低且平稳,以减小原动机的容量和提高切削质量。
当刨刀处于返回行程时,刨刀不工作,称为空行程,此时要求刨刀的速度较高以提高生产率。
由此可见,牛头刨床的纵向运动特性对机床的性能有决定性的影响。
1 牛头刨床的六连杆机构牛头刨床有很多机构组成,其中实现刨头切削运动的六杆机构是一个关键机构。
图1所示的为一牛头刨床的六连杆机构。
杆1为原动件,刨刀装在C点上。
假设已知各构件的尺寸如表1所示,原动件1以等角速度ω1=1rad/s沿着逆时针方向回转,要求分析各从动件的角位移、角速度和角加速度以及刨刀C点的位移、速度和加速度的变化情况。
基于Pro-E牛头刨床变速箱虚拟装配和运动仿真

基于Pro/E的牛头刨床变速箱的虚拟装配和运动仿真摘要:利用pro/e设计软件,建立牛头刨床变速箱各零件三维模型,并对其进行虚拟装配和运动仿真,缩短了产品的开发周期,提高了产品的设计效率,其设计方法可以借鉴到其他产品的的设计。
关键词:牛头刨床变速箱 pro/engineer 虚拟装配运动仿真中图分类号:th12 文献标识码:a 文章编号:1674-098x(2012)06(b)-0056-011 牛头刨床变速箱的基本结构牛头刨床变速箱是滑移齿轮变速机构,通过排挡杠杆带动变速制动轴上的叉子来实现变速。
b665牛头刨床变速箱的变速机构如图1所示,轴ⅰ为输入轴,有电动机直接驱动。
轴ⅲ为输出轴,在轴ⅰ上安装齿数为20(2019)-30(2021)-25(2022)的三联滑移齿轮,轴ⅲ上安装齿数为30(2028)-48(2031)的双联滑移齿轮,与各固定齿轮组成滑移齿轮变速机构。
改变各滑移齿轮的位置,就可以改变该轮系的传动比,满足变速要求。
2 变速箱虚拟装配的实现2.1 零件的三维建模牛头刨床变速箱的零件大概共有180多个,其中很多的建模方式大致相同,利用pro/e的零件模块,通过必要的草绘,进行拉伸,旋转,镜像,阵列等建模方式得到零件的三维模型。
标准件可以到标准件网站下载获得或者自己按照要求进行三维建模。
变速箱中有很多齿轮,以渐开线圆柱直齿轮为例说明齿轮建模。
已知齿轮模数m=4mm,齿数z=35,齿轮厚b=28mm。
按照齿轮的孔和齿顶圆的直径的尺寸绘制胚体;再通过草绘,绘制齿顶圆和齿根圆,并通过“曲线”→“从方程”输入渐开线的方程,保存形成渐开线曲线;利用“镜像”生成另外一条渐开线,把镜像得到的渐开线阵列;利用“拉伸”→“边创建图元”,生成第一个齿槽;选择生成的齿槽,利用“阵列”设置数量和角度生成齿轮。
2.2 牛头刨床变速箱零件的虚拟装配虚拟装配就是把各个实体模型通过一定的约束关系组装成一个个子组件,再将各个子组件组装起来形成一个完整组件的过程,在装配过程中,设计人员可以及时发现和处理装配过程中的各种问题。
牛头刨床刨刀的往复运动机构

机械原理课程设计令狐采学计算说明书课题名称:牛头刨床刨刀的往复运动机构姓名:院别:工学院学号:专业:机械设计制造及其自动化班级:机设1201指导教师:2014年6月7日工学院课程设计评审表目录一.设计任务书 (4)1.1 设计题目 (4)1.2 牛头刨床简介 (4)1.3 牛头刨床工作原理 (4)1.4 设计要求及设计参数 (6)1.5 设计任务 (7)二.导杆机构的设计及运动分析 (8)2.1 机构运动简图 (8)2.2 机构运动速度多边形 (9)2.3 机构运动加速度多边形 (11)三.导杆机构动态静力分析 (14)3.1 静态图 (14)3.2 惯性力及惯性力偶矩 (14)3.3 杆组拆分及用力多边形和力矩平衡求各运动反力和曲柄平衡力 (15)心得与体会 (21)参考文献 (22)一、设计任务书1.1 设计题目:牛头刨床刨刀的往复运动机构1.2 牛头刨床简介:牛头刨床是用于加工中小尺寸的平面或直槽的金属切削机床,多用于单件或小批牛头刨床外形图量生产。
为了适用不同材料和不同尺寸工件的粗、精加工,要求主执行构件—刨刀能以数种不同速度、不同行程和不同起始位置作水平往复直线移动,且切削时刨刀的移动速度低于空行程速度,即刨刀具有急回现象。
刨刀可随小刀架作不同进给量的垂直进给;安装工件的工作台应具有不同进给量的横向进给,以完成平面的加工,工作台还应具有升降功能,以适应不同高度的工件加工。
1.3 牛头刨床工作原理:牛头刨床是一种刨削式加工平面的机床,图1所示为较常见的一种机械运动的牛头刨床。
电动机经皮带传动和两对齿轮传动,带动曲柄2和曲柄相固结的凸轮转动,由曲柄2驱动导杆2-3-4-5-6,最后带动刨头和刨刀作往复运动。
当刨头右行时,刨刀进行切削,称为工作行程。
当刨头左行时,刨刀不切削,称为空回行程。
当刨头在工作行程时,为减少电动机容量和提高切削质量,要求刨削速度较低,且接近于匀速切削。
在空回行程中,为节约时间和提高生产效率,采用了具有急回运动特性的导杆机构。
牛头刨的运动分析
大作业---牛头刨的运动分析一、题目机构运动简图如下, 其中12800,360,120,200,960AB CD h mm h mm h mm l mm l mm =====160DE l mm =,1=5rad /s ω,逆时针方向回转。
求:(1)推导出刨头上C 点的111(),()()c c c c c c s s v v a a ϕϕϕ===和的数学表达式;(2)打印出10~36010,c c c s v a ϕ︒︒由每变化时的和的数值,并绘出相应的曲线; (3)打印计算程序及其说明。
(4)利用ADAMS 建立该机构的虚拟样机,并测量,c c cs v a 和解:(1)根据题意可得:令;S ;;;3431b d de cd ab l l l l l l l ==== S 5是C 点的位移则: 刨头上C 点的位移方程为:⎪⎪⎩⎪⎪⎨⎧=-+=++=--+=--+-0sin sin 0cos cos 0sin sin sin 0cos cos cos 53344334433441123344111S l l h l l S l l h S l l h ϕϕϕϕϕϕϕϕϕϕ刨头上C 点的速度方程为:⎪⎪⎩⎪⎪⎨⎧=-+=+=---=+-+-0cos cos 0sin sin 0cos sin cos cos 0sin cos sin sin 53334443334443333344411133333444111v l l l l S v l l S v l l ϕωϕωϕωϕωϕωϕϕωϕωϕωϕϕωϕω刨头上C 点的加速度方程为:⎪⎪⎩⎪⎪⎨⎧=-+-+-=+++=+----+-=+++-++-0cos sin cos sin 0sin cos sin cos 0sin cos cos 2sin cos sin sin 0cos sin sin 2cos sin cos cos 533333234444424333332344444243323333333334444424112133233333333344444241121αϕαϕωϕαϕωϕαϕωϕαϕωϕωϕαϕωϕϕαϕωϕωϕωϕαϕωϕϕαϕωϕωl l l l l l l l S S v a l l l S S v a l l l(1)图像:数据表格:(3)Matlab 程序:位移函数:(其中)4();3();2();1(5334th S th th S th ====ϕϕ)function f=myfun1(th,th1)h=0.8; h1=0.36; h2=0.12; l1=0.2; l3=0.96; l4=0.16;f=[-h1+l1*cos(th1)-l4*cos(th(1))-th(2)*cos(th(3)); h2+l1*sin(th1)-l4*sin(th(1))-th(2)*sin(th(3)); l4*cos(th(1))+l3*cos(th(3))+h;l4*sin(th(1))+l3*sin(th(3))-th(4)];速度函数:(其中)4();3();2();1(5334ωωωωωω====v v )function f=myfun2(w,th,th1) l1=0.2; l3=0.96; l4=0.16; w1=5;f=[-w1*l1*sin(th1)+w(1)*l4*sin(th(1))-w(2)*cos(th(3))+w(3)*th(2)*sin(th(3)); w1*l1*cos(th1)-w(1)*l4*cos(th(1))-w(2)*sin(th(3))-w(3)*th(2)*cos(th(3)); w(1)*l4*sin(th(1))+w(3)*l3*sin(th(3));w(1)*l4*cos(th(1))+w(3)*l3*cos(th(3))-w(4)];加速度函数:(其中)4();3();2();1(5334a a a a a a ====αα)function f=myfun3(a,w,th,th1) l1=0.2; l3=0.96; l4=0.16; w1=5;f=[-(w1)^2*l1*cos(th1)+(w(1))^2*l4*cos(th(1))+a(1)*l4*sin(th(1))-a(2)*cos(th (3))+2*w(2)*w(3)*sin(th(3))+a(3)*th(2)*sin(th(3))+(w(3))^2*th(2)*cos(th(3));-(w1)^2*l1*sin(th1)+(w(1))^2*l4*sin(th(1))-a(1)*l4*cos(th(1))-a(2)*sin(th(3))-2*w(2)*w(3)*cos(th(3))-a(3)*th(2)*cos(th(3))+(w(3))^2*th(2)*sin(th(3));(w(1))^2*l4*cos(th(1))+a(1)*l4*sin(th(1))+(w(3))^2*l3*cos(th(3))+a(3)*l3*sin(th(3));-(w(1))^2*l4*sin(th(1))+a(1)*l4*cos(th(1))-(w(3))^2*l3*sin(th(3))+a(3)*l3*co s(th(3))-a(4)];主函数:x=zeros(37,4);y=zeros(37,4);z=zeros(37,4);th=0:pi/18:2*pi;th1=180/pi*th;x1=[0,0,0,0];y1=[0,0,0,0];z1=[0,0,0,0];for i=1:1:37xx1=fsolve(@myfun1,x1,optimset('fsolve'),th(i));x(i,1)=xx1(1,1);x(i,2)=xx1(1,2);x(i,3)=xx1(1,3);x(i,4)=xx1(1,4);x1=xx1;yy1=fsolve(@myfun2,y1,optimset('fsolve'),xx1,th(i));y(i,1)=yy1(1,1);y(i,2)=yy1(1,2);y(i,3)=yy1(1,3);y(i,4)=yy1(1,4);y1=yy1;zz1=fsolve(@myfun3,z1,optimset('fsolve'),yy1,xx1,th(i));z(i,1)=zz1(1,1);z(i,2)=zz1(1,2);z(i,3)=zz1(1,3);z(i,4)=zz1(1,4);z1=zz1;endsubplot(2,2,1)plot(th1,x(:,4),'-k');hold on;title('\phi1与C点位移之间的关系');xlabel('\phi1');ylabel('Sc');axis([0 360 -0.2 0.6])grid;subplot(2,2,2)plot(th1,y(:,4),'-k');hold on; title('\phi1与C点速度之间的关系'); xlabel('\phi1');ylabel('Vc');axis([0 360 -2 2.5])grid;subplot(2,2,3)plot(th1,z(:,4),'-k');hold on; title('\phi1与C点加速度之间的关系'); xlabel('\phi1');ylabel('ac');axis([0 360 -15 10])grid;(4)ADAMS建立ADAMS模型:经过ADAMS计算,可得到C点的位移、速度、加速度的图像:。
牛头刨床
实战篇
工程图
两个建模软件的机构设计
两一个不断犯 错,反复尝试的过程,对于现在的一些软件尤 其是这样,只有在错误中才能真正学到难忘的 知识;此次研究中,不管是设计机构,还是 solidedge仿真以及mathematica仿真,都体现出 了在尝试中学习是必须经历的学习方法,有了 99次失败的尝试,才会迎来第100次得成功。 此外,此次学习中我们也感到向有经验的前辈 学习能够节省不少的时间和精力,大大地提高 了学习的效率。在以后的学习中我们会继续保 持高度的积极性,勇敢地去尝试。
机构结构分析
深入学习
急回机构的设计和仿真分析
Auto CAD画图
A杆长度为55cm,B杆长度为96cm,最大压力角 γmax=62°
Solidworks进行建模和仿真分析
Solidworks中的滑块的速度
Solidworks中的滑块的速度
working model中的建模与分析
牛头刨床相关设计和仿真分析
组员:周子航(10223058) 邵 剑(10223018) 高 翔(10223003)
牛头刨床相关设计和仿真分析
摘要:本次项目是牛头刨床的相关设计及 仿真分析。此次设计首先通过一个平面四连杆 机构床架作为学习使用Mathematica、 SolidEdge 、AutoCAD、Solidworks、以及 Working Model等相关软件材料。之后设计一 个符合相关要求的牛头刨床机构,进行相关的 软件仿真分析。
主要难点
1,如何将一个竖直面经过运动转化为一个水平面; 2,在何处设定基准点,以便计算与设计; 3,杆长关系如何确定; 4,床尾的支撑腿应该选用何种机构。通过working model 进行相关的仿真,可以确定基本方案,在符合机 构运动要求的情况下,使用了等长的杆,产生了自锁的 效果,避免了由于重力作用而倾倒。使床尾的支撑腿实 现90°的转向,在水平时要保证不会由于外力作用而向 内倾倒,故选择了带有死点自锁的一个简单机构。为了 能将床得到充分的利用,还将床与一个衣柜结合在一起 ,在不使用床的时候可以将床作为柜门,在使用时衣柜 也可以为床提供水平方向的约束,避免了床向一边倾斜
机械原理牛头刨床课程设计----运动分析
3的角位移l1=120;l6=240;x=-pi/6:2*pi/36:11*pi/6;y=atan((l6+l1*sin(x))./(l1*cos(x))); for i=14:1:31y(i)=pi+y(i);end>> plot(x*180/pi,y*180/pi)E的位移l1=120;l6=240;x=-pi/6:2*pi/36:11*pi/6;y=atan((l6+l1*sin(x))./(l1*cos(x))); for i=14:1:31y(i)=pi+y(i);endl=466.507;l3=500;l4=97.929;a=pi-asin((l-l3*sin(y))./l4);b=l3*cos(y)+l4*cos(a);plot(x*180/pi,b)4的角位移l1=120;l6=240;x=-pi/6:2*pi/36:11*pi/6;y=atan((l6+l1*sin(x))./(l1*cos(x))); for i=14:1:31y(i)=pi+y(i);endl=466.507;l3=500;l4=97.929;a=pi-asin((l-l3*sin(y))./l4);>> plot(x*180/pi,a*180/pi)3的角速度l1=120;l6=240;x1=-pi/6:2*pi/36:11/6*pi;y1=l1*2*pi*(l1+l6*sin(x1))./(l6*l6+l1*l1+2*l6*l1*sin(x1)); plot(x1*180/pi,y)4的角速度l1=120;l6=240;>> x=-pi/6:2*pi/36:11*pi/6;>> y=atan((l6+l1*sin(x))./(l1*cos(x)));>> for i=14:1:31y(i)=pi+y(i);end>> l=466.507;l3=500;l4=97.929;>> a=pi-asin((l-l3*sin(y))./l4);>> y1=l1*2*pi*(l1+l6*sin(x))./(l6*l6+l1*l1+2*l6*l1*sin(x)); >> y4=(y1.*l3.*cos(y))./(l4.*cos(a));>> plot(x*180/pi,y4)E的速度l1=120;l6=240;x=-pi/6:2*pi/36:11*pi/6;y=atan((l6+l1*sin(x))./(l1*cos(x)));for i=14:1:31y(i)=pi+y(i);endl=466.507;l3=500;l4=97.929;a=pi-asin((l-l3*sin(y))./l4);y1=l1*2*pi*(l1+l6*sin(x))./(l6*l6+l1*l1+2*l6*l1*sin(x)); >> v=-(y1.*l3.*sin(y+a))./cos(a);>> plot(x*180/pi,v)3的角加速度l1=120;l6=240;x=-pi/6:2*pi/36:11*pi/6;y3=(l6.*l6-l1.*l1).*l6.*l1.*2.*2.*pi.*pi.*cos(x)./((l6.*l6+l1.*l1+2.*l6.*l1.*sin(x)).*(l6.*l6+l1.*l1 +2.*l6.*l1.*sin(x)));>>plot(x*180/pi,y3)4的角加速度>> l1=120;l6=240;x=-pi/6:2*pi/36:11*pi/6;y=atan((l6+l1*s in(x))./(l1*cos(x)));for i=14:1:31y(i)=pi+y(i);endl=466.507;l3=500;l4=97.929;a=pi-asin((l-l3*sin(y))./l4);y1=l1*2*pi*(l1+l6*sin(x))./(l6*l6+l1*l1+2*l6*l1*sin(x));y4=-(y1.*l3.*cos(y))./(l4.*cos(a));>>y3=(l6.*l6-l1.*l1).*l6.*l1.*2.*2.*pi.*pi.*cos(x)./((l6.*l6+l1.*l1+2.*l6.*l1.*sin(x)).*(l6.*l6+l1.*l1 +2.*l6.*l1.*sin(x)));a4=((y3.*l3.*cos(y)-y1.*y1.*l3.*sin(y)).*l4.*cos(a)+y1.*l3.*l4.*cos(y).*sin(a).*y4)./((l4.*cos(a)). *(l4.*cos(a)));>> plot(x*180/pi,a4)E的加速度l1=120;l6=240;x=-pi/6:2*pi/36:11*pi/6;y=atan((l6+l1*sin(x))./(l1*cos(x)));for i=14:1:31y(i)=pi+y(i);endl=466.507;l3=500;l4=97.929;a=asin((l-l3*sin(y))./l4);y1=l1*2*pi*(l1+l6*sin(x))./(l6*l6+l1*l1+2*l6*l1*sin(x));y4=-(y1.*l3.*cos(y))./(l4.*cos(a));y3=(l6.*l6-l1.*l1).*l6.*l1.*2.*2.*pi.*pi.*cos(x)./((l6.*l6+l1.*l1+2.*l6.*l1.*sin(x)).*(l6.*l6+l1.*l1 +2.*l6.*l1.*sin(x)));>>e=-((y3.*l3.*sin(y-a)+y1.*l3.*cos(y+a).*(y1+y4)).*cos(a)+y1.*l3.*sin(y+a).*sin(a).*y4)./(cos(a). *cos(a));>> plot(x*180/pi,e)。
牛头刨床机构设计
机械原理设计说明书设计题目:牛头刨床机构设计学生:汪在福班级:铁车二班学号:******** 指导老师:**机械原理设计说明书设计题目:牛头刨床机构设计学生姓名汪在福班级铁车二班学号 20116473一、设计题目简介牛头刨床是用于加工中小尺寸的平面或直槽的金属切削机床,多用于单件或小批量生产。
为了适用不同材料和不同尺寸工件的粗、精加工,要求主执行构件—刨刀能以数种不同速度、不同行程和不同起始位置作水平往复直线移动,且切削时刨刀的移动速度低于空行程速度,即刨刀具有急回现象。
刨刀可随小刀架作不同进给量的垂直进给;安装工件的工作台应具有不同进给量的横向进给,以完成平面的加工,工作台还应具有升降功能,以适应不同高度的工件加二、? 设计数据与要求电动机轴与曲柄轴2平行,刨刀刀刃D点与铰链点C的垂直距离为50mm,使用寿命10年,每日一班制工作,载荷有轻微冲击。
允许曲柄2转速偏差为±5%。
要求导杆机构的最大压力角应为最小值;凸轮机构的最大压力角应在许用值[α]之内,摆动从动件9的升、回程运动规律均为等加速等减速运动。
执行构件的传动效率按0.95计算,系统有过载保护。
按小批量生产规模设计题号导杆机构运动分析导杆机构动态静力分析凸轮机构设计转机工行连工导滑导从从许推远回6三、? 设计任务1、根据牛头刨床的工作原理,拟定2~3个其他形式的执行机构(连杆机构),并对这些机构进行分析对比。
2、根据给定的数据确定机构的运动尺寸。
并将设计结果和步骤写在设计说明书中。
3、用软件(VB、MATLAB、ADAMS或SOLIDWORKS等均可)对执行机构进行运动仿真,并画出输出机构的位移、速度、和加速度线图。
4、导杆机构的动态静力分析。
通过参数化的建模,细化机构仿真模型,并给系统加力,写出外加力的参数化函数语句,打印外加力的曲线,并求出最大平衡力矩和功率。
5、凸轮机构设计。
根据所给定的已知参数,确定凸轮的基本尺寸(基圆半径ro、机架lO2O9和滚子半径rr),并将运算结果写在说明书中。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
[MATLAB机械运动仿真] [牛头刨床机构运动仿真分析] [摘要:通常机械运动学、动力学分析是比较繁琐的事情,稍不注意就可能出错,更改起来更是麻烦。而MATLAB作为强有力的计算分析工具,将之运用到机械运动、动力仿真分析方面,不仅可以减轻工作量,缩短设计时间,而且可以得到比较精确的分析结果。本文借助MATLAB的SIMULINK模块,对牛头刨床机构进行运动仿真分析。] 牛头刨床机构简图 二、运动方程的求解
(1)对如右图所示的矢量三角形
矢量方程为: .321RRR (*)
将上述矢量方程分别向水平、竖直方向投影,得:
.sinsin;coscos332213322rrrrr
(1-1)
上式分别对时间 t 求导,得:
.cossincos;sincossin3333322233333222rrrrrr
(1-2)
上式写成关于3 、3r的矩阵方程,为: .cossinsincoscossin22222233333333
rrrrr
(1-3)
将(2)式分别对时间 t 求导,得:
.sincoscos2sinsincos;cossinsin2coscossin33233333333322222223323333333332222222rrrrrrrrrrrr
(1-4)
上式写成关于3 、3r的矩阵方程,为:
一、牛头刨床机构简介: 牛头刨床是一种常用的平面切削加工机床。电动机经皮带传动、齿轮传动最后带动曲柄1(见右图)转动。刨床工作时,是由导杆机构1-2-3-4-5带动刨头和刨刀做往复直线运动刨头5右行时,刨头切断,称为工作行程,此时要求速度较低且均匀;刨头左行时,不进行切削,称为空行程,此时速度较高,以节省时间提高生产率。为此刨床采用有急回作用的导杆机构。 这里给出各构件的长度,以供下面的仿真使用。
.88.210,92.702,72315102.133DECDABlll .sincos2sincoscossin2cossinsincoscossin332333322222223323333222222233333333
rrrrrrrrrrr
(1-5)
(2)对如右图所示的矢量三角形 矢量方程为: .7654RRRR (**)
将上述矢量方程分别向水平、竖直方向投影,得:
.sinsin;coscos6554475544rrrrrr
(2-1)
上式分别对时间 t 求导,得:
.0sincos;sinsin5554447555444rrrrr
(2-2)
将(2)式分别对时间 t 求导,得:
.0sincossincos;cossincossin55255554424444755255554424444rrrrrrrrr
(2-3)
上式写成关于5 、7r的矩阵方程,为: .sinsincoscossin0cos1sin552544244444424444755555
rrrrrrrr
(2-4)
三、构建SIMULINK方框图 a) 构建速度方框图并仿真 1. 首先对方程(1-3)的常变量分析:
已知常量有:2,2r;变量有:2,3,3,3r,3r。但2,3,3r可分别由2,3,3r导出。因此,系统输入量为
3,2,2,3r,输出量为3,3r。
2. 用到的模块有:
3. 将各模块按次序连接起来 omega2theta2theta3r3omega3dotr34Out4
3Out3
2Out2
1Out1
theta3
r3omega3
dor r3MATLAB
Function
MATLAB Fcn
1s
Integrator21sIntegrator11sIntegrator-C-Constant
4. 设置各模块初值如下:(注意:各模块初值必须正确设置,否则运行结果会出错!)
%myfun11.m function [out]=myfun11(u) %u(1)=theta3 %u(2)=theta2 %u(3)=omega2 %u(4)=r3 % r2=.13372315102; % a=[-u(4)*sin(u(1)) cos(u(1));u(4)*cos(u(1)) sin(u(1))]; b=[-u(3)*r2*sin(u(2));u(3)*r2*cos(u(2))]; out=inv(a)*b;
5. 仿真: 仿真时间设置为60/89 s,即一个周期。 在MATLAB的Command Window窗口输入命令:plot(tout,yout) 仿真输出结果如下图所示: 00.10.20.30.40.50.60.7-4-3-2-101233
3
r3dotr3
Results of simulition
time(s)3(rad)
r3(m)3(rad/s)
dotr3(m/s)
b).构建加速度方框图并仿真 1.对方程(1-5)分析,它有7个输入,2个输出。详见系统方框图。 2.用到的模块与前面的一样。 3.将方框图连接起来:
alpha2omega2theta2
alpha3omega3theta3ddot r3dot r3
omega3theta3theta2omega2alpha2 r3dot r3Created byZhang Haizhong12.26.20114Out43Out32Out21Out11stheta21sr3omega_31somega31somega2MATLABFunctionfun1dot r_31sdot r3alpha30alpha21s
Theta-3
4.设置各模块初值:(这里只说明新添加模块的初值,其他的与前面的相同。) %fun1 function [y]=fun1(x) % %x(1)=omega3 %x(2)=theta3 %x(3)=theta2 %x(4)=omega2 %x(5)=alpha2 %x(6)=r3 %x(7)=dot r3 % % constant r2 % %y(1)=alpha3 %y(2)=ddotr3 % r2=.13372315102; % a=[-x(6)*sin(x(2)),cos(x(2));x(6)*cos(x(2)),sin(x(2))]; b=[-x(5)*r2*sin(x(3))-x(4)*x(4)*r2*cos(x(3))+2*x(7)*x(1)*sin(x(2))+x(1)*x(1)*x(6)*cos(x(2)) x(5)*r2*cos(x(3))-x(4)*x(4)*r2*sin(x(3))-2*x(7)*x(1)*cos(x(2))+x(1)*x(1)*x(6)*sin(x(2))]; y=inv(a)*b; 5.仿真: 仿真时间同样设置为60/89 s,即一个周期。 在MATLAB的Command Window窗口输入命令:plot(tout,yout) 仿真输出结果如下图所示:
00.10.20.30.40.50.60.7-40-30-20-100102030403
3
dotr3
ddotr3
time(s)
Results of simulation3(rad/s2)
3(rad/s)
ddotr3(m/s2)dotr3(m/s)
C).前面运动方程求解过程中,虽然将方程(*)与方程(**)分开来写,但两者是有联系的。即: .;;434343
