宏微复合平台的微运动动态模型研究
工程机械驾驶模拟器运动平台多体动力学分析

M ul ib dy d t- o yna i ala l i n m o i na m c na ys s o to l
Fi 3 Va ito n lngh o e swh l b l g. ra in i e t flg iemo i e
p a f r t - x st a l to l t o m wih Y a i r nsa i n
当动平 台沿 方 向平动 时 , 杆行 程 的变化 如 图 4所示 . 各 由于 6根杆 对称 安装 , 假设 平 台结构 质 量对 称 , 6杆 位移 相 同. 则 当动平 台绕 轴转动 时 , 杆行 程 的变 化如 图 5所示 . 各
速度 为 1 O ; 大角 加速 度绕 , 轴 均 为 1 0 ・ ~. .g 最 Y, 8。 S
根 据 结构 尺寸 和连 接关 系 , 立 系统模 型 . 建
1 1 刚体 模 型 的建立 .
对 于刚体模 型 , 多体 动 力学分 析 需要 的参 数是 零件 的质心 、 量 和转 动 惯 量 . 质 通过 精 确建 立 零 件 的三 维 实体 模 型 , 以获得其 准确 的动力 学分 析参 数 . 设计 初期 , 以简化 零 部件 的细节 结构 . 可 在 可 本文 对运 动平
p at or f r d i i i ul t l f m r v ng s m o a or
DU AN u—i g .Z Xi b n HU h —h S is un
一种滚动隔震平台动力学建模及实验研究

一种滚动隔震平台动力学建模及实验研究刁建超;谢溪凌;凌华;张志谊【摘要】针对振动敏感型设备地震响应隔离问题,研究一种滚动隔震平台,并给出凹形复位板曲面轮廓.建立隔震平台的运动微分方程,通过数值仿真对El-Centro地震波响应进行分析,结果表明隔震平台可消减地震加速度向其承载设备的传递,并且曲面轮廓限制了设备的相对位移.在仿真分析的基础上,对滚动隔震平台的隔震性能进行实验验证,结果显示滚动隔震平台水平方向共振频率在0.5 Hz~1 Hz之间,对于0~16 Hz内的随机激励,隔震后的加速度RMS值下降90%以上;在隔震区,对单频激励也有较好的衰减效果.%In order to protect vibration-sensitive equipment from seismic excitation, a rolling platform is presented for vibration isolation and its concave surface profile is investigated. The nonlinear kinematic equation of the platform is established and its response to the El-Centro earthquake is analyzed. Numerical simulation of the platform is carried out to analyze its response to the EL-Centro seismic wave. Numerical results show that this isolation platform can eliminate the transmission of seismic acceleration to the equipment and the concave profile can limit the relative displacement of the equipment. Experiments are also conducted to verify the vibration isolation performance of the platform. The test results demonstrate that the horizontal resonance frequency of the rolling isolation platform is within 0.5 Hz-1 Hz. For random excitation in the frequency range of 0-16 Hz, the RMS value of acceleration is reduced by more than 90%. And for periodical excitation in the isolation area, the platform can also have better attenuation effect.【期刊名称】《噪声与振动控制》【年(卷),期】2017(037)005【总页数】5页(P13-17)【关键词】振动与波;振动敏感型设备;地震响应;滚动隔震平台;凹形复位板【作者】刁建超;谢溪凌;凌华;张志谊【作者单位】上海交通大学振动、冲击、噪声研究所,上海 200240;上海交通大学机械系统与振动国家重点实验室,上海 200240;上海交通大学振动、冲击、噪声研究所,上海 200240;上海交通大学机械系统与振动国家重点实验室,上海 200240;华为技术有限公司,广东深圳 518129;上海交通大学振动、冲击、噪声研究所,上海200240;上海交通大学机械系统与振动国家重点实验室,上海 200240【正文语种】中文【中图分类】TB535目前数据中心和电信网络影响着国家经济的稳定性,重大应急响应中心(医院,消防和救援)也严重依赖这些高度灵敏的通信网络[1–3]。
1.2017年度河南省高等学校重点科研项目资助计划

混杂纤维增强粉煤灰陶粒混凝土配合比设计及 安阳师范学院 耐久性试验研究 河南省中医药资源及其旅游开发研究 安阳师范学院
基于‚双赢‛视角的河南粮食主产区土地流转 安阳师范学院 长效机制研究 有界线性算子在推广框架中的应用 安阳学院
分布阶分数阶偏微分方程的高效快速算法研究 河南财经政法大学 忆阻动态耦合神经网络的动力学分析及应用 河南财经政法大学
钢管混凝土空间桁架结构在大型螺旋咬边钢板 安阳工学院 仓开发中的应用研究 郑州航空港临空物流与区域经济联动发展研究 安阳工学院 平面调和映射与极小曲面中的若干问题研究 安阳师范学院
阿尔茨海默病早期诊断与药物开发的基础应用 安阳师范学院 研究 镧锰氧化合物基层状复合薄膜中的磁电耦合机 安阳师范学院 制研究 蜂窝-VANET 异构无线网络中无线资源协同管理 安阳师范学院 的研究 甲骨文大规模语义关联数据的构建方法研究 CPS 系统行为的可执行建模与自动分析方法 安阳师范学院 安阳师范学院
— 3 —
17A310014 17A310015 17A320019 17A320020 17A320021 17A320022 17A320023 17A320024 17A330001 17A330003 17A413001 17A430012 17A530001 17A630008 17A630009 17A630010 17A790009 17A790010 17A790011 17A790012 17A790013 17A790014 17A790015 17A880005 17A110017
柠檬醛抑制 Clostridium Perfringens 的机理 河南城建学院 研究 基于微观分析的混凝土干缩及自收缩变形研究 河南城建学院 再生骨料塑性混凝土力学变形性能试验研究 河南城建学院
六自由度微重力模拟平台研究

六自由度微重力模拟平台研究
杨平;吴洪涛;杨小龙;陈柏
【期刊名称】《机械设计与制造》
【年(卷),期】2015(000)003
【摘要】太空环境与地面环境有着很大的不同,根据地面环境下动力学特性设计而成的机械系统在太空零重力环境下作业时会产生“动力过冲”的现象,因此太空机械系统在进入太空工作之前需要进行严格的地面微重力模拟实验以对系统的设计进行验证.针对大型昂贵空间实验目标的地面测试问题,提出了一种基于Stewart机构的混合驱动的六自由度微重力模拟实验平台,基于Kane方法建立了该实验平台的动力学方程,据此设计了面向该平台运动控制的计算力矩控制方法,并利用MATLAB/Simulink与ADAMS进行联合仿真,验证了所提出的控制方法的正确性.【总页数】5页(P5-9)
【作者】杨平;吴洪涛;杨小龙;陈柏
【作者单位】南京航空航天大学机电学院,江苏南京210016;南京航空航天大学机电学院,江苏南京210016;南京航空航天大学机电学院,江苏南京210016;南京航空航天大学机电学院,江苏南京210016
【正文语种】中文
【中图分类】TH16;TH113
【相关文献】
1.微重力模拟育种平台运动轨迹的规划研究 [J], 吕雨鑫;李伟凯;董晓威
2.气电联合的六维微重力模拟平台自抗扰控制研究 [J], 王灵禺;吴洪涛;张学祥;刘艳梨;杨小龙
3.基于六自由度运动平台的大型空间结构低频力学环境模拟研究 [J], 于新战;肖勇;黄超;方永刚;雷艳妮
4.飞行模拟器六自由度运动平台的仿真研究 [J], 王辉;陈学森
5.基于六自由度运动平台的潜艇模拟器的研究与仿真 [J], 陈雪丽;张成义
因版权原因,仅展示原文概要,查看原文内容请购买。
【国家自然科学基金】_stewart_基金支持热词逐年推荐_【万方软件创新助手】_20140801

2009年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52
科研热词 stewart平台 并联机构 六维力传感器 鲁棒控制 隔振 轨迹跟踪 自适应控制 动力学 位置正解 主动隔振 sylvester结式 鼓式 飞毯 预紧 隔振控制 遗传算法 车辆 超静定 解析方法 自适应模糊 自适应控制系统 自适应交互pid 脉冲 耦合衰减 绳牵引 矩阵 直线音圈电机 特征 滑模控制 深海采矿 测量误差 模态分析 模型试验 模型不确定性 标定 柔性支撑 权系数 机构 机器人 有限元法 旋转矩阵 数据采集 推力矢量喷管 拓扑 性能指标 径向基神经网络 应力应变 并联机器人 并联 干扰抑制 干扰力补偿8 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78
工作空间 封闭解 大射电望远镜 多维运动补偿器 土工离心机 固有频率 各向同性 反馈线性化 反步法 动力学方程 动力学与控制 加速度量程 加速度前馈 加权函数 力/位置控制 内模原理 六维加速度传感器 修船技术 优化设计 仿真 任务空间控制 stewart液压平台 stewart机构 stewart fast 6-sps结构stewart平台
科研热词 stewart平台 工作空间 鲁棒控制 饱和控制 雅克比矩阵 道路模拟振动台 运动学正解 运动学 资产经济价值 财务管理系统 虚拟重力 自适应交互 耦合控制 绳索牵引机器人 符号计算 税后净营业利润 监督控制 激励报酬制度 机能训练 机器人 有限时间稳定 数值方法 收敛性 控制方法 控制 振动 并联机构 并联机器人 并串联机床 射电望远镜 宏微并联机器人 多体动力学 咨询公司 可达空间 动力学 力控制 六自由度并联机器人 位置反解 估价模型 企业并购 仿真平台 二维搜索 stewart机构 pd控制 newton-raphson法 mathematica软件 eva方法 5自由度
(完整word版)平面双连杆机械臂动态模型 (2)(word文档良心出品)
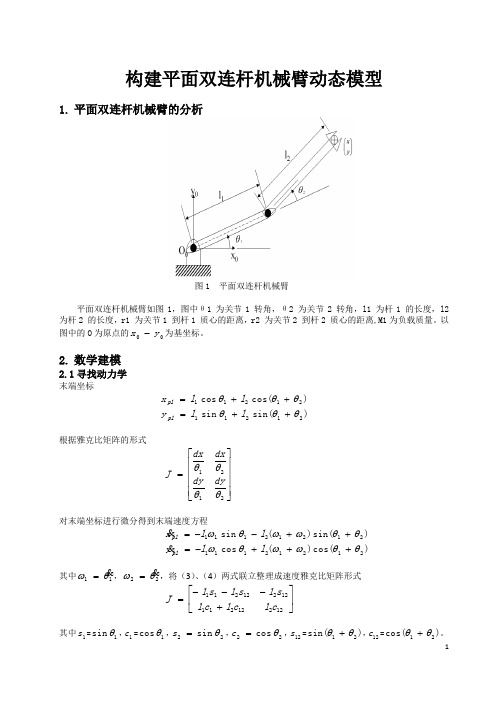
构建平面双连杆机械臂动态模型1. 平面双连杆机械臂的分析图1 平面双连杆机械臂平面双连杆机械臂如图1,图中θ1 为关节1 转角,θ2 为关节2 转角,l1 为杆1 的长度,l2为杆2 的长度,r1 为关节1 到杆1 质心的距离,r2 为关节2 到杆2 质心的距离,M1为负载质量。
以图中的O 为原点的00y x -为基坐标。
2. 数学建模2.1寻找动力学末端坐标)cos(cos 21211θθθ++=l l x pl )sin(sin 21211θθθ++=l l y pl根据雅克比矩阵的形式⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=2121θθθθdy dy dx dx J对末端坐标进行微分得到末端速度方程)sin()(sin 21212111θθωωθω++--=l l x pl & )cos()(cos 21212111θθωωθω+++-=l l y pl &其中11θω&=,22θω&=,将(3)、(4)两式联立整理成速度雅克比矩阵形式 ⎥⎦⎤⎢⎣⎡+---=1221221112212211c l c l c l s l s l s l J其中1s =1sin θ,1c =1cos θ,22sin θ=s ,22cos θ=c ,12s =)sin(21θθ+,12c =)cos(21θθ+。
在机器人基础坐标系中的速度与各关节速度间的关系以及手部与外界接触力与对应各关节间的关系可以利用雅克比矩阵来建立。
对机械臂末端速度方程(3) 、方程(4) 进行求导得到末端加速度方程如下[]1221222122211221121221122112)()(c l c l c l c l s l s l s l x pl ωωωωαα+++-=+++&& []1221222122211221121221122112)()(s l s l s l sl s l s l s l y pl ωωωωαα+++-=+++&&其中1α=1θ&&,2α=2θ&&,上述推导的方程构成了进行动力学仿真的基础,它们表明了有效负荷的加速度与 两节点处电动机的角速度和角加速度之间的关系。
华北工学院力学学科的发展战略
力学学科的发展战略一、本学科发展现状及趋势作为我国七大基础学科之一的力学具有很强的基础性,又有广泛的应用性。
力学的基础研究,不断深化和丰富人类对基本自然规律的认识,不断为其他学科的发展提供认识工具。
目前,力学正在突破经典的力学概念和范畴,进入一个新的发展阶段,力学的物理内容在深化,力学在与其他学科交缘处迅速发展。
力学的发展总趋势是:①致力于力学界公认的几个基本现象和规律的研究,如湍流运动,固体介质的本构、实效理论,传统连续介质力学的改造,使之可以刻划非均匀、多尺度、宏微细观多层次。
②将继续以应用基础研究为重点,同时大力发展应用力学。
力学学科通常有如下几个分支:一般力学、固体力学、流体力学及交叉学科,其研究前沿为:(1)一般力学①非线性动力学:有限维系统的分岔与混沌,②运动稳定性:力学系统、控制系统、大系统、分布参数系统稳定性和鲁棒稳定性,③多柔体系统动力学:刚体运动与柔体变形的耦合、柔体姿态稳定性等,④随机振动,⑤近代分析力学:“几何动力学理论”等。
(2)固体力学①以非线性力学为核心的力学与数学的结合,②以宏微细观力学为核心的力学与物理学的结合,③岩土力学,④实验固体力学,⑤计算固体力学⑥流固耦合问题。
(3)流体力学①湍流,②流动稳定性,③混沌,④水波动力学,⑤涡动力学,⑥复杂流场计算,⑦多相流,⑧非平衡流。
(4)力学中的交叉学科①物理力学,②电磁力学,③爆炸力学,④地球动力学⑤生物力学,等等。
作为力学的重要分支,固体力学兼具技术科学与基础科学的双重属性。
虽然固体力学经过长期发展,在宏观力学上取得了一系列成果,形成了固体力学的近代理论。
尽管固体力学已呈现出一个高度发达学科的某些特征,但仍有一些基本问题尚未解决,如固体本构理论在宏观连续介质层次上未能实现封闭,破坏的发生和传播机制并不很清楚,疲劳行为的机制远未得到阐明,有生命的固体与无生命的固体在本构响应的不同也远不清楚,等等。
上述问题仅仅是固体力学尚未解决问题的极小部分,其学科进展是永无止境的。
【国家自然科学基金】_大行程_基金支持热词逐年推荐_【万方软件创新助手】_20140802
科研热词 高精度 驱动电源 精密定位 大行程柔性铰链 大行程 大功率 复合放大 压电陶瓷 pa93 间接测量 闭环控制 转角柔度 转动精度 超声电机 超声波直线电机 超声波电动机 角度误差补偿 螺旋理论 自动定位 纳米定位 柔性铰链 柔性机构 柔度矩阵 构型综合 有限元法 快速刀具伺服 工具显微镜 射影变换 宏微驱动 宏微二级驱动 大行程柔性机构 垂直轴 刚度模型 刚度 刀具轨迹跟踪控制算法 刀具路径 六自由度工作台 光栅 光学自由曲面 交叉轴解耦 二维细分 xy柔性并联微定位平台 psoc3 cortex-m4 cmac
2008年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45
科研热词 精密定位 显微视觉 力解耦 主从控制 逐步回归 运动规划 运动控制 运动平台 超精密工件台 超精密 自动标定 细分 纳米工作台 纳米 精度 磁悬浮导轨 硅片台 研究现状 直线电机 直线度 直线导向机构 电液振动台 正交实验法 柔性铰链 柔性机构 有限元分析 摩擦建模 摩擦力补偿 摩擦 惯性驱动 微驱动器 尺蠖运动 宏微双重驱动 宏/微双重驱动 双衍射光栅 压电陶瓷拨爪电机 压电旋转机构 压电技术 压电微动台 光栅 伺服阀 仪器仪表技术 二维位移工作台 两级驱动 roberts机构
2012年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32
科研热词 高分辨率 超磁致伸缩驱动器 膝关节 组合驱动器 纳米定位 箝位机构 移动策略 柔顺性 柔性铰链放大机构 柔性铰链 有限元法 最大应力 显微图像 数据采集处理 拼接 微位移检测 康复 尺蠖运动 大行程驱动器 大行程 多模式 参数辨识 压电驱动器 压电陶瓷驱动 前馈控制 刚度 伪刚体模型 串联柔性机构 三维位移系统 pid控制 labview ccd标定
弹道中段微动目标宽带回波模拟
0 引 言
动 目标 的 回波 中蕴含 了 目标 的电磁散 射特性 和运 动 特性 , 为雷 达 目标识 别 提 供 了重要 依 据 J 。导 弹 防 御系 统 中的 目标 识别 方法 已由上 世纪 六十 年代 的窄
近 年来 , 道导 弹的攻 防技 术得 到 了快 速 发展 , 弹
其攻防对抗主要集 中在弹道 中段 。 中段 目标运 动形式复杂 , 除了高速 的质心运动外 , 还伴有 自旋 、
( col f l t ncSineadE g er g ai a U iesyo ees eh o g , hn sa4 0 7 , hn ) Sho o e r i c c n ni e n ,N t nl nvri f f eT cnl y C agh 10 3 C ia E co e n i o t D n o
第 3 3卷 第 3期
21 0 2年 3月
五自由度气浮仿真试验台的动力学建模
架构 的嵌 入式 计算 机 。计 算 机能 够 对 A P平 台 的姿
态及位 置信 息进 行 测 量 处 理 , 过 相应 的控 制 算 法 通 控制 其上 冷气 推进装 置工 作产 生相 应 的控制 力或 控
制力矩 。控 制 力 经 球 面 气 浮 轴 承 间 气 膜 的传 递 作
用, 推动 T P及 A P平 台 一 起 在 工 作 台面 上 实 现 X Y 平 面 2个 自由度 的 平移 运 动 。 同时 A P平 台在 控 制
冷气推进装置作 为执 行器的实 际工作 情况 , 建立了相 应 的状 态方程 , 为下一步气浮 台模 拟航天器 自治轨 道 及姿态飞行提供了重要的理论基础。
气体 , 在轴 承下表 面 与 大理 石 工 作 台面 间形 成 一层 气垫, 能够 浮起整 个 试验 台并 形 成低 摩擦 的气 体 润
中 图分 类 号 :V 4 .5 4 8 2 文献 标 识 码 :A 文 章 编 号 :10 .3 8 2 1 ) 1 0 00 0 0 12 (0 0 0 . 6 — 0 5
DOI:0. 8 3 iis 1 0 1 2 2 0. 1. 0 1 3 7 / .s n.00 — 3 8.01 0 0 9
验的多 自由度气 浮台 , 通过平 面及球 面气浮 轴承的作
用, 能够 在地 面模 拟 微小 卫 星 的轨道 及 姿态 运 动 。
图 1 五 自由度 气 浮 仿 真 试 验 台 月 片 强
Fg. P oo o h —do i e tn p c ca i ltr i 1 h t fte5— farb a g s a e rf smu ao i t
( 尔滨 工 业 大 学 气 动技 术 中心 ,哈 尔滨 10 8 ) 哈 500
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
宏微复合平台的微运动动态模型研究高健;陈小国;张揽宇;周志强【摘要】宏微复合平台常应用于大行程运动和高精度定位的场合.基于对宏微复合驱动技术的的分析及研究,提出了一种音圈电机与压电陶瓷复合驱动的宏微复合运动平台结构,其中微运动平台采用压电陶瓷驱动和弹簧预紧,具有结构简单、分辨率高、刚度高和响应速度快等优点.针对微运动平台的主动控制问题,考虑压电陶瓷驱动器驱动电路以及滑块与摩擦复合作用的影响,建立微运动平台动态模型.通过微运动平台动态特性的实验研究,分析滑块与摩擦复合作用对微运动平台平稳性的影响.结果表明,该模型可快速缩短平台到达稳定的时间,满足平台精密定位要求.【期刊名称】《机械设计与制造》【年(卷),期】2017(000)002【总页数】5页(P62-66)【关键词】宏微复合平台;微运动平台;压电陶瓷驱动器;动态模型【作者】高健;陈小国;张揽宇;周志强【作者单位】广东工业大学机电工程学院机械装备制造与控制技术教育部重点实验室,广东广州510006;广东工业大学机电工程学院机械装备制造与控制技术教育部重点实验室,广东广州510006;广东工业大学机电工程学院机械装备制造与控制技术教育部重点实验室,广东广州510006;广东工业大学机电工程学院机械装备制造与控制技术教育部重点实验室,广东广州510006【正文语种】中文【中图分类】TH1620世纪80年代中后期,国内外学者相继提出了宏微双重驱动技术的初步想法[1-2],并在20多年的探索中证明了宏微双重驱动技术是实现大行程高精度定位的一种有效手段[3-5]。
结合宏、微驱动技术,宏动台以地面为参照物,实现运动平台大范围移动和粗定位,微动台附着于宏动台上,并以宏动台为参照物,实现平台的微小位移,补偿宏动台大行程粗定位产生的位移精度误差。
宏微双重驱动精密定位系统具体可描述为:宏动部分由高精度的伺服电动机或者直线电机和丝杠组成,宏动台由宏动台导轨导向;由压电驱动器和弹性铰链构成的微动台附着于宏动台上,压电驱动器输出位移,微动台由微动台导轨导向[6]。
宏微两级运动的点位控制具有先后顺序,是分离进行控制的[7]。
宏动台的运动行程通常可达数百毫米,速度也可达上百毫米每秒,微动台在宏动台运动结束后,对测得的定位误差做补偿进给,定位控制只对始末两点间的位置精度有要求,而对中间位置的定位精度及运动轨迹则无要求,利用反馈进行控制[8-9]。
微运动行程可达数百微米,精度可达数十个纳米[10]。
面向微电子制造的高速高精度运动要求,介绍了一类新型宏微复合平台的结构设计,阐述了这类一维微运动平台的机构特点。
针对微运动平台的主动控制问题,建立了微运动平台的动态模型,并实验研究了微运动平台动态特性,验证了微运动平台所建模型的正确性。
提出的宏微复合平台由宏运动与微运动构成。
其中宏运动由音圈电机驱动,实现平台的高加速度和大行程粗定位;微运动由压电陶瓷驱动,实现对宏运动大行程粗定位产生的位移精度误差进行补偿,以实现高速高精度的设计目标。
宏微复合平台结构,如图1所示。
由大理石基座、音圈电机、工作台、直线导轨、压电陶瓷、预紧弹簧以及绝对式光栅尺等组成。
音圈电机主轴驱动工作台以高加速度(最大加速度为15g)实现大行程的宏运动,并由嵌入在音圈电机中的增量式光栅尺实现自身的闭环控制,该运动能可达到微米级运动精度;嵌入在套筒内的压电陶瓷与预紧弹簧组合驱动工作台产生微运动,并由绝对式光栅尺实现精定位位置检测以补偿音圈电机宏运动造成的定位误差。
本宏微复合平台采用宏微串接的设计方式,微运动采用将压电陶瓷安装在工作台上,直接与音圈电机主轴末端接触,由弹簧和预紧螺母对压电陶瓷进行预紧的新型设计结构,实现平台运动的精确定位。
微运动平台结构,如图2所示。
主要由压电陶瓷驱动器、弹簧、工作台、套筒、导轨、预紧螺母等部分组成。
其中关键部件压电陶瓷驱动器选用德国Physik Instrumente(PI)公司制造,型号为PSt150/7/7VS12。
该压电陶瓷名义伸长量为13μm,分辨率1nm,轴向刚度为120N/μm,最大推力1800N。
压电陶瓷驱动器的一端通过预紧螺钉安装在微定位平台上,另一端与音圈电机主轴末端顶杆接触。
由于压电陶瓷驱动器属于脆性材料,其抗弯性能和抗扭性能较差。
为了防止压电陶瓷驱动器在平台运动过程中受到弯矩和扭矩的作用,同时也为了避免压电陶瓷驱动器在微运动过程中高速响应使压电陶瓷驱动器与电机主轴末端顶杆脱离,影响微运动平台的动态性能,因此,压电陶瓷驱动器通过套在顶杆上的弹簧和预紧螺母进行预紧,可通过调节预紧螺母的进给来调整预紧力的大小。
此外,采用XE-501D驱动电源控制压电陶瓷驱动器自身闭环反馈回路,消除压电陶瓷驱动器自身非线性对微运动平台动态特性的影响,提高微运动平台的动态性能。
所设计的微运动平台结构具有占用空间小、结构紧凑、工作台负载小、易于嵌入到其他平台中。
同时结合平台导轨侧面的绝对式光栅尺进行整体闭环位置反馈控制,达到对平台精密定位的目标。
压电陶瓷驱动器采用将多片压电陶瓷片粘结共烧而成,在电路上可等效为一个容性负载,其等效电路,如图3所示。
基于Kirchhoff laws有如下等式:式中:kamp—驱动电源内部放大器的放大系数;vd(t)—输入驱动电源放大器的控制电压信号;R—等效电阻;C—压电陶瓷驱动器的等效电容;vpzt(t)—实际施加在压电陶瓷驱动器两端的电压。
基于等式(1),如果vd(t)输入阶跃信号vd0,则实际施加在压电陶瓷驱动器两端的电压可以表示为:式中:RC—压电陶瓷等效电路的时间常数,。
基于等式(2),基于阶跃信号vd0的压电陶瓷驱动器的瞬态位移ypzt(t)可以表示为:式中:d33—压电常数;n—压电陶瓷片片数。
由于微运动平台结构中存在预紧弹簧压缩的影响,故等式(3)调整为:式中:kpzt—压电陶瓷驱动器的等效刚度;ks—预紧弹簧的刚度。
考虑到压电陶瓷驱动器受预紧弹簧刚度的影响,压电陶瓷瞬态力可描述为:上述等式可简化为:上述式子描述了压电陶瓷驱动器瞬态力与输入电压的关系。
从式(6)中可以看出,压电陶瓷瞬态力受时间常数RC的影响,不是一个简单的线性函数,即施加给微运动平台的力也不是一个简单的线性函数。
微运动平台由工作台、预紧弹簧以及压电陶瓷驱动器等组成,压电陶瓷驱动器在机构上可以等价为质量-弹簧-阻尼系统,微运动平台瞬态位移模型,如图4所示。
微运动平台系统的微分方程表达如式(7):式中:Fpzt(t)—压电陶瓷驱动器产生的瞬态力;u—平台与导轨的摩擦系数;y(t)—微平台移动的位移;y0—稳定时平台的位移;mm—工作台的质量;mpzt—压电陶瓷驱动器的质量;cpzt—压电陶瓷驱动器的等效阻尼;cs—预紧弹簧的等效阻尼。
为了探究微运动平台对阶跃信号的动态响应,由等式(6)和(7),可得到基于阶跃信号vd0的微运动平台位移等式:式中:ζ—阻尼系数;ωn—自然角频率,有如下的计算方法:应用Laplace变换以及Laplace反变换对(8)式进行求解。
针对输入驱动电源放大器的阶跃控制信号电压的无摩擦(u=0)微运动平台的动态响应可描述如下:由于导轨滑块在工作台运动过程中,以紧靠状态使用,滑块受力矩和安装面精度的影响,难以得到均匀的载荷分布导致摩擦力受力不均,且在高速往复运动过程中,伴有振动和冲击,故上述式(9)需调整为:在等式(10)中,第一项为输入驱动电源放大器的阶跃控制电压信号对微运动平台的影响,第二项和第三项表示时间常数RC、阻尼系数ζ以及自然角频率ωn对平台的影响。
为了验证宏、微复合微运动平台瞬态位移模型的正确性,对宏、微复合平台的微运动特性进行了实验。
所搭建的实验平台测试装置如图5所示。
实验中,将平台置于隔震平台上,以便消除外界振动对测试的干扰。
同时将音圈电机上电(此时由音圈电机内部的电磁力作用而形成一个最大扭转力,最大扭力由电机指令SQ设定(SQ=30000N),压电陶瓷的最大推力为1800N(<<30000N)。
此时,只要音圈电机上电,音圈电机在最大扭转力的作用下,不会产生位移移动,在微运动实验时可当做静止物体)。
由置于平台前方的激光干涉仪进行数据采集,最终的数据通过PC机的自带软件查看。
测试装置中的激光干涉仪动态测量范围高达50kHz,最大位移分辨率为1nm。
因压电陶瓷驱动器自身非线性将影响宏、微复合微运动平台位移输出特性。
为了测量平台的迟滞特性,利用PC机通过NI卡给微运动平台输出控制电压由0V线性增加到10V,然后线性减少至0V。
利用激光干涉仪测量微运动平台输出位移,得到微运动平台的迟滞特性曲线,如图6所示。
由图可知,压电陶瓷驱动器作用10V的控制电压时,微运动平台的输出位移为9.717um,开环的升压、降压曲线最大相差0.96um,最大迟滞率为19.2%。
利用XE-501D驱动电源自身闭环控制可以消除迟滞特性,使输出位移与控制电压成线性。
将阶跃信号(2V、9V)施加于微运动平台,测量得到动态响应如图7、图8所示。
可以得到微运动平台阶跃信号的上升时间约为1.5ms,稳定时间为(30~40)ms。
自然频率约为428.3Hz,系统的阻尼系数为0.056。
由压电陶瓷驱动器的技术资料可知:d33= 635×10-12m/V,电容C=0.7uF,其他参数为:mpzt=50g,Kamp=13,RC= 0.2ms,压电陶瓷驱动器的刚度Kpzt=120N/μm。
微运动平台工作台的质量为mm=0.6kg,预紧弹簧的刚度为104N/m,滑块系数影响k1=0.35,k2=4。
将所得参数带入所建方程(9)、方程(10)得到平台在2V、9V控制电压分别作用下无摩擦和有摩擦与滑块复合作用下的阶跃响应仿真曲线,如图9、图10和图7、图8某线所示。
2V比较图7、图8仿真结果与实验结果,如表1所示。
从表1可以得出:(1)2V时仿真的稳定值为1.845μm,实验稳定最低值为1.815μm,两者的相对误差为1.65%;9V时仿真的稳定值为8.788μm,实验稳定最低值为8.729μm,两者的相对误差0.67%。
(2)振动频率和最大超调量,从图中可看出振动频率几乎一致。
2V仿真和实验的最大超调量分别为2.541μm和2.562μm,相对误差为-0.82%;9V仿真和实验的最大超调量分别为11.37μm和11.23μm,相对误差为1.24%。
实验结果与仿真结果基本一致,从而验证所建模型的正确性。
比较图9、图10有/无摩擦时平台仿真结果比较,如表2所示。
从中可以得出:(1)相同电压下有/无摩擦的最终稳定值结果相差极小,证明摩擦和滑块的复合作用对平台输出的最终稳定值无太大影响。
(2)有摩擦到达稳定所需时间明显小于无摩擦到达稳定时间,证明摩擦和滑块的复合作用可快速缩短平台到达稳定的时间。
