十年(2010-2019)高考数学真题分类汇编(试卷版+解析版):直线与圆
理科数学高考真题分类汇编 直线与圆答案

c = 5 ,故所求直线的方程为2x + y + 5 = 0 或 2x + y − 5 = 0 .
8.C【解析】设过 A, B,C 三点的圆的方程为 x2 + y2 + Dx + Ey + F = 0 ,
D + 3E + F +10 = 0 则 4D + 2E +F +20 = 0 ,解得 D = −2, E = 4, F = −20 ,
专题九 解析几何
第二十五讲 直线与圆
答案部分
2019 年
1.解析 由直线 l 的参数方程消去 t,可得其普通方程为 4x − 3y + 2 = 0 .
则点(1,0)到直线 l 的距离是 d = 41− 3 0 + 2 = 6 .故选 D.
42 + (−3)2 5
2.
解析
解法一:由
y=
x+ 4 x
(x
D − 7 E + F + 50 = 0 所求圆的方程为 x2 + y2 − 2x + 4 y − 20 = 0 ,令 x = 0 ,得 y2 + 4 y − 20 = 0 ,
设 M (0, y1) ,N (0, y2 ) ,则 y1 + y 2 = −4 , y1 y2 = −20 , 所以 | MN |=| y1 − y2 |= ( y1 + y2 )2 − 4 y1 y2 = 4 6 . 9.C【解析】圆 C 标准方程为 (x − 2)2 + ( y −1)2 = 4 ,圆心为 C(2,1) ,半径为 r = 2,
2 2 = 1. 22
3.C【解析】由题意可得 d = | cos − msin − 2 | = | msin − cos + 2 |
专题九解析几何第二十五讲直线与圆十年高考数学(理科)真题题型分类汇编

专题九分析几何第二十五讲直线与圆2019年ì1.(2019 北京理 3)已知直线l 的参数方程为 x=1+3t (t 为参数),则点(1,0) í?y=2+4t到直线l的距离是(A )1(B )2(C )4(D )65 5 552.(2019 江苏10)在平面直角坐标系xOy 中,P 是曲线y x 4(x0)上的一个动点,x则点P 到直线x+y=0的距离的最小值是 .3(2019江苏18)如图,一个湖的界限是圆心为 O 的圆,湖的一侧有一条直线型公路 l ,湖 上有桥AB (AB 是圆O 的直径).规划在公路 l 上选两个点P 、Q ,并修筑两段直线型道路 PB 、QA .规划要求:线段 PB 、QA 上的全部点到点 O 的距离均不小于圆 O 的半径.已知....点A 、B 到直线l 的距离分别为AC 和BD (C 、D 为垂足),测得AB=10,AC=6,BD=12(单位:百米).(1)若道路PB 与桥AB 垂直,求道路PB 的长;(2)在规划要求下, P 和Q 中可否有一个点选在D 处?并说明原因;(3)在规划要求下,若道路PB 和QA 的长度均为 d (单位:百米) .求当d 最小时,P 、Q两点间的距离.4.(2019浙江12)已知圆C 的圆心坐标是(0,m),半径长是r.若直线2x y 3 0与圆C 相切于点A(2,1),则m=_____,r=______.2010-2018年2010-2018年一、选择题1.(2018全国卷Ⅲ)直线x y20分别与x轴,y轴交于A,B两点,点P在圆(x2)2y22上,则ABP面积的取值范围是A .[2,6]..[2,32]D.[22,32] B[4,8]Cx12t,2.(2018天津)已知圆x2y22x 0的圆心为C,直线2(t为参数)与该圆y32t2订交于A,B两点,则△ABC的面积为.3.(2018北京)在平面直角坐标系中,记d为点P(cos ,sin)到直线x my20的距离,当,m变化时,d的最大值为A.1B.2C.3D.44.(2017新课标Ⅲ)已知椭圆C:x2y21(ab0)的左、右极点分别为A1,A2,a2b2且以线段A1A2为直径的圆与直线bx ay2ab 0相切,则C的离心率为6B.321A.3C.D.3335.(2017新课标Ⅲ)在矩形ABCD中,AB1,AD 2,动点P在以点C为圆心且与BD相切的圆上.若AP AB AD,则的最大值为A.3B.22C.5D.26.(2015山东)一条光芒从点(2,3)射出,经y轴反射后与圆(x3)2(y2)21相切,则反射光芒所在直线的斜率为53B.325443A.或或C.或D.或352345347.(2015广东)平行于直线2x y10且与圆x2y25相切的直线的方程是A.2xy50或2xy50B.2xy50或2xy50 C.2xy50或2xy50D.2xy50或2xy508.(2015新课标2)过三点A(1,3),B(4,2),C(1,7)的圆交于y轴于M、N两点,则MN=A.26B.8C.46D.109.(2015重庆)已知直线l:x ay10(a R)是圆C:x2y24x2y10的对称轴,过点A(4,a)作圆C的一条切线,切点为B,则AB=A.2B.42C.6D.21010.(2014新课标2)设点M(x,1),若在圆O:x 22=1上存在点N,使得OMN°y45,则x的取值范围是A.1,1B.11C.2,2D.2,2 2,22 211.(2014福建)已知直线l过圆x2y24的圆心,且与直线x y10垂直,则3l的方程是A.xy20B.xy20C.xy30D.xy3012.(2014北京)已知圆C:x32y421和两点A m,0,B m,0m0,若圆C上存在点P,使得APB 90,则m的最大值为A.7B.6C.5D.413.(2014湖南)若圆C1:x2y21与圆C2:x2y26x8y m0外切,则m A.21B.19C.9D.11( 3,1)2 y 2 1有公共点,则直线l 的倾斜角的 14.(2014安徽)过点P 的直线l 与圆x取值范围是A .(, ]B .(,]C . ,]D . ,] 0 6 0 [0 [03 3 615.(2014浙江)已知圆x 2y 2 2x 2y a0 截直线x y 2 0所得弦的长度为 4,则实数a 的值是A .-2B .-4C .-6D .-8 16.(2014四川)设m R ,过定点A 的动直线xmy 0 和过定点B 的动直线mx y m 30 交于点P(x,y),则|PA| |PB|的取值范围是A . [ 5,2 5] .[ 10,25] C .[ 10,4 5] D . [25,4 5]B 17 2014 江西)在平面直角坐标系中, A,B 分别是x 轴和y 轴上的动点,若以 AB 为直径.( 的圆C 与直线2x y 40相切,则圆C 面积的最小值为A . 4B . 3C . (625) 5 5 4D .418.(2013山东)过点(3,1)作圆 x 2 y 21的两条切线,切点分别为 A ,B ,则直线1 AB 的方程为A .2x y 3 0B .C .4x y 3 0D .2x y 304x y 3019.(2013重庆)已知圆C 1:x 2y3 2C 2:x2 29,M,N2 1,圆 3 y4 分别是圆C 1,C 2上的动点,P 为x 轴上的动点,则PM PN 的最小值为A .524 B. 171 C .622 D .1720.(2013安徽)直线x2y 5 50被圆x 2y 2 2x4y0截得的弦长为 A .1 B .2 C .4D .4621.(2013新课标2)已知点A 1,0 ;B1,0 ;C 0,1 ,直线y axb(a0) 将△ABC切割为面积相等的两部分,则 b 的取值范围是A .(0,1)B .12 , 1 C .1 2 , 1 D .1,1 2 2 2 33 222.(2013陕西)已知点M(a,b)在圆O:x 2y 2 1外,则直线ax by 1与圆O 的地点关系是A .相切B .订交C .相离D .不确立23.(2013天津)已知过点P(2,2)的直线与圆(x2 2相切,且与直线axy10 1) y5 垂直,则a A . 1 B .1C .2D .12224.(2013广东)垂直于直线y x1且与圆x 2y 21相切于第一象限的直线方程是A .xy 20B .xy10C .xy10D .xy20 25.(2013新课标 2)设抛物线C:y 24x 的焦点为F ,直线l 过F 且与C 交于A ,B 两 点.若|AF| 3|BF|,则 l 的方程为A .yx 1或yx1B .C .y3(x 1)或y3(x1)D .y 3(x1)或y 3(x1)3 3 y2(x1)或y2(x1)2 226.(2012浙江)设aR ,则“a 1”是“直线l 1:ax2y10与直线l 2:x(a1)y4 0平行”的 A .充足不用要条件 B .必需不充足条件 C .充足必需条件 D .既不充足也不用要条件27.(2012天津)设m,nR ,若直线(m1)x+(n1)y 2=0与圆(x1)2+(y 1)2=1相 切,则m+n 的取值范围是 A .[13,1+ 3]B .(,13] [1+ 3,+ )C .[22 2,2+2 2]D .(,2 2 2] [2+2 2,+ )28.(2012湖北)过点P(1,1)的直线,将圆形地区(x,y)|x2y2, 4分为两部分,使得这两部分的面积之差最大,则该直线的方程为A.xy 2 0B.y1 0C.xy 0D.x3y 4029.(2012天津)在平面直角坐标系xOy中,直线3x4y50与圆x2y24订交于A,B两点,则弦AB的长等于A.33B.23C.D.30.(2011北京)已知点A(0,2),B(2,0).若点C在函数y=x的图像上,则使得ABC的面积为2的点C的个数为A.4B.3C.2D.131.(2011江西)若曲线C1:x2y22x 0与曲线C2:y(y mxm)0有四个不一样的交点,则实数m的取值范围是33A.(,3333 C.[,33)B.(3(0,3,0))33]D.(,3)(3,+) 3332.(2010福建)以抛物线y24x的焦点为圆心,且过坐标原点的圆的方程为A.x2+y2+2x=0B.x2+y2+x=0C.x2+y2x=0D.x2+y22x=033.(2010广东)若圆心在x轴上、半径为5的圆O位于y轴左边,且与直线x2y0相切,则圆O的方程是A.(x5)2y25B .C.(x5)2y25D.(x5)2y25(x 5)2 y25二、填空题34.(2018江苏)在平面直角坐标系xOy中,A为直线l:y 2x上在第一象限内的点,B(5,0),以AB为直径的圆C与直线l交于另一点D.若ABCD 0,则点A 的横坐标为.35.(2017江苏)在平面直角坐标系xOy 中,A(,,点P在圆O:x2y250 12,0)B(0,6)上,若PA PB≤20,则点P的横坐标的取值范围是.36.(2015湖北)如图,圆C与x轴相切于点T(1,0),与y轴正半轴交于两点A,B(B在A的上方),且AB2.(Ⅰ)圆C的标准方程为;..(Ⅱ)过点A任作一条直线与圆O:x2y21订交于M,N两点,以下三个结论:NA MA NB MA2NB MA22.①;②NA MB ;③MBNB MB NA此中正确结论的序号是.(写出全部正确结论的序号)37.(2014江苏)在平面直角坐标系 xOy中,直线x 2y 3 0被圆(x 2)2 (y 1)24截得的弦长为.382014重庆)已知直线ax y20与圆心为C的圆x12y a24订交于A,B(.两点,且ABC为等边三角形,则实数a_________.39.(2014湖北)直线l1:y x a和l2:y xb将单位圆C:x2y21分红长度相等的四段弧,则a2b2________.40.(2014山东)圆心在直线x2y0上的圆C与y轴的正半轴相切,圆C截x轴所得弦的长为23,则圆C的标准方程为.41.(2014陕西)若圆C 的半径为1,其圆心与点(1,0)对于直线yx对称,则圆C的标准方程为____.42.(2014重庆)已知直线xy a0与圆心为C的圆x2y22x4y40订交于A,B两点,且ACBC,则实数a的值为_________.43.(2014湖北)已知圆O:x2y21和点A(2,0),若定点B(b,0)(b2)和常数知足:对圆O上随意一点M,都有|MB||MA|,则(Ⅰ)b;(Ⅱ).44.(2013浙江)直线y2x 3被圆x2y26x8y0所截得的弦长等于__________.45.(2013湖北)已知圆O :x2y25,直线l:xcos ysin1(0π).设圆O上2到直线l的距离等于1的点的个数为k,则k.46.(2012北京)直线y x被圆x2(y2)24截得的弦长为.472011浙江)若直线x2y50与直线2x my60相互垂直,则实数m=__..(48.(2011辽宁)已知圆C经过A(5,1),B(1,3)两点,圆心在x轴上,则C的方程为__.49.(2010新课标)圆心在原点上与直线x y20相切的圆的方程为.50.(2010新课标)过点A(4,1)的圆C与直线x y 0相切于点B(2,1),则圆C 的方程为.三、解答题51(2016年全国I)设圆x2y22x150的圆心为A,直线l过点B(1,0)且与x轴不重.合,l交圆A于C,D两点,过B作AC的平行线交AD于点E.(I)证明EA EB为定值,并写出点E的轨迹方程;(II)设点E的轨迹为曲线C1,直线l交C1于M,N两点,过B且与l垂直的直线与圆A交于P,Q两点,求四边形MPNQ面积的取值范围.52.(2014江苏)如图,为了保护河上古桥OA,规划建一座新桥BC,同时建立一个圆形保护区.规划要求:新桥BC 与河岸AB 垂直;保护区的界限为圆心M在线段OA上并与BC相切的圆.且古桥两头O和A到该圆上随意一点的距离均许多于80m.经丈量,点A位于点O正北方向60m处,点C位于点O正东方向170m处(OC为河岸),tan BCO4.3(I)求新桥BC的长;II)当OM多长时,圆形保护区的面积最大?53.(2013江苏)如图,在平面直角坐标系xOy中,点A0,3,直线l:y 2x4.设圆C的半径为1,圆心在l上.ylAxO(I)若圆心C也在直线yx 1上,过点A作圆C的切线,求切线的方程;(II)若圆C上存在点M,使MA2MO,求圆心C的横坐标a的取值范围.54(2013新课标2)在平面直角坐标系xOy中,已知圆P在x轴上截得线段长为22,在y.轴上截得线段长为23.(I)求圆心P的轨迹方程;(II)若P点到直线y x的距离为2,求圆P的方程.255.(2011新课标)在平面直角坐标系xoy中,曲线yx26x1与坐标轴的交点都在圆C上.(I)求圆C的方程;(II)若圆C与直线xy a 0交于A,B两点,且OAOB,求a的值.56.(2010北京)已知椭圆C的左、右焦点坐标分别是(2,0),( 2,0),离心率是6,3专题九解析几何第二十五讲直线与圆十年高考数学(理科)真题题型分类汇编直线y t椭圆C交与不一样的两点M,N,以线段MN为直径作圆P,圆心为P.I)求椭圆C的方程;II)若圆P与x轴相切,求圆心P的坐标;(Ⅲ)设Q(x,y)是圆P上的动点,当t变化时,求y的最大值.。
十年高考真题分类汇编(2010-2019) 数学 专题01 集合

十年高考真题分类汇编(2010—2019)数学专题01 集合1.(2019•全国1•理T1)已知集合M={x|-4<x<2},N={x|x2-x-6<0},则M∩N=( )A.{x|-4<x<3}B.{x|-4<x<-2}C.{x|-2<x<2}D.{x|2<x<3}【答案】C【解析】由题意得N={x|-2<x<3},则M∩N={x|-2<x<2},故选C.2.(2019•全国1•文T2)已知集合U={1,2,3,4,5,6,7},A={2,3,4,5},B={2,3,6,7},则B∩∁U A=( )A.{1,6}B.{1,7}C.{6,7}D.{1,6,7}【答案】C【解析】由已知得∁U A={1,6,7},∴B∩∁U A={6,7}.故选C.3.(2019•全国2•理T1)设集合A={x|x2-5x+6>0},B={x|x-1<0},则A∩B=( )A.(-∞,1)B.(-2,1)C.(-3,-1)D.(3,+∞)【答案】A【解析】由题意,得A={x|x<2,或x>3},B={x|x<1},所以A∩B={x|x<1},故选A.4.(2019•全国2•文T1)已知集合A={x|x>-1},B={x|x<2},则A∩B=( )A.(-1,+∞)B.(-∞,2)C.(-1,2)D.⌀【答案】C【解析】由题意,得A∩B=(-1,2),故选C.5.(2019•全国3•T1)已知集合A={-1,0,1,2},B={x|x2≤1},则A∩B=( )A.{-1,0,1}B.{0,1}C.{-1,1}D.{0,1,2}【答案】A【解析】A={-1,0,1,2},B={x|-1≤x≤1},则A∩B={-1,0,1}.故选A.6.(2019•北京•文T1)已知集合A={x|-1<x<2},B={x|x>1},则A∪B=( )A.(-1,1)B.(1,2)C.(-1,+∞)D.(1,+∞)【答案】C【解析】∵A={x|-1<x<2},B={x|x>1},∴A∪B=(-1,+∞),故选C.7.(2019•天津•T1)设集合A={-1,1,2,3,5},B={2,3,4},C={x∈R|1≤x<3},则(A∩C)∪B=( )A.{2}B.{2,3}C.{-1,2,3}D.{1,2,3,4}【答案】D【解析】A∩C={1,2},(A∩C)∪B={1,2,3,4},故选D.8.(2019•浙江•T1)已知全集U={-1,0,1,2,3},集合A={0,1,2},B={-1,0,1},则(∁U A)∩B=( )A.{-1}B.{0,1}C.{-1,2,3}D.{-1,0,1,3}【答案】A【解析】∁U A={-1,3},则(∁U A)∩B={-1}.9.(2018•全国1•理T2)已知集合A={x|x2-x-2>0},则∁R A=( )A.{x|-1<x<2}B.{x|-1≤x≤2}C.{x|x<-1}∪{x|x>2}D.{x|x≤-1}∪{x|x≥2}【答案】B【解析】A={x|x<-1或x>2},所以∁R A={x|-1≤x≤2}.10.(2018•全国1•文T1)已知集合A={0,2},B={-2,-1,0,1,2},则A∩B=( )A.{0,2}B.{1,2}C.{0}D.{-2,-1,0,1,2}【答案】A【解析】由交集定义知A∩B={0,2}.11.(2018•全国2•文T2,)已知集合A={1,3,5,7},B={2,3,4,5},则A∩B=( )A.{3}B.{5}C.{3,5}D.{1,2,3,4,5,7}【答案】C【解析】集合A、B的公共元素为3,5,故A∩B={3,5}.12.(2018•全国3•T1)已知集合A={x|x-1≥0},B={0,1,2},则A∩B=( )A.{0}B.{1}C.{1,2}D.{0,1,2}【答案】C【解析】由题意得A={x|x≥1},B={0,1,2},∴A∩B={1,2}.13.(2018•北京•T1)已知集合A={x||x|<2},B={-2,0,1,2},则A∩B=( )A.{0,1}B.{-1,0,1}C.{-2,0,1,2}D.{-1,0,1,2}【答案】A【解析】∵A={x|-2<x<2},B={-2,0,1,2},∴A∩B={0,1}.14.(2018•天津•理T1)设全集为R,集合A={x|0<x<2},B={x|x≥1},则A∩(∁R B)=( )A.{x|0<x≤1}B.{x|0<x<1}C.{x|1≤x<2}D.{x|0<x<2}【答案】B【解析】∁R B={x|x<1},A∩(∁R B)={x|0<x<1}.故选B.15.(2018•天津•文T1)设集合A={1,2,3,4},B={-1,0,2,3},C={x∈R|-1≤x<2},则(A∪B)∩C=( )A.{-1,1}B.{0,1}C.{-1,0,1}D.{2,3,4}【答案】C【解析】A∪B={-1,0,1,2,3,4}.又C={x∈R|-1≤x<2},∴(A∪B)∩C={-1,0,1}.16.(2018•浙江•T1)已知全集U={1,2,3,4,5},A={1,3},则∁U A=( )A.⌀B.{1,3}C.{2,4,5}D.{1,2,3,4,5}【答案】C【解析】∵A={1,3},U={1,2,3,4,5},∴∁U A={2,4,5},故选C.17.(2018•全国2•理T2,)已知集合A={(x,y)|x2+y2≤3,x∈Z,y∈Z},则A中元素的个数为( )A.9B.8C.5D.4【答案】A【解析】满足条件的元素有(-1,-1),(-1,0),(-1,1),(0,1),(0,0),(0,-1),(1,-1),(1,0),(1,1),共9个。
十年真题(2010_2019)高考数学真题分类汇编专题10平面解析几何选择填空题文(含解析)

专题10平面解析几何选择填空题历年考题细目表历年高考真题汇编1.【2019年新课标1文科10】双曲线C:1(a>0,b>0)的一条渐近线的倾斜角为130°,则C的离心率为()A.2sin40°B.2cos40°C.D.【解答】解:双曲线C:1(a>0,b>0)的渐近线方程为y,由双曲线的一条渐近线的倾斜角为130°,得,则,∴,得,∴e.故选:D.2.【2019年新课标1文科12】已知椭圆C的焦点为F1(﹣1,0),F2(1,0),过F2的直线与C交于A,B 两点.若|AF2|=2|F2B|,|AB|=|BF1|,则C的方程为()A.y2=1 B. 1C. 1 D. 1【解答】解:∵|AF2|=2|BF2|,∴|AB|=3|BF2|,又|AB|=|BF1|,∴|BF1|=3|BF2|,又|BF1|+|BF2|=2a,∴|BF2|,∴|AF2|=a,|BF1|a,在Rt△AF2O中,cos∠AF2O,在△BF1F2中,由余弦定理可得cos∠BF2F1,根据cos∠AF2O+cos∠BF2F1=0,可得0,解得a2=3,∴a.b2=a2﹣c2=3﹣1=2.所以椭圆C的方程为:1.故选:B.3.【2018年新课标1文科04】已知椭圆C:1的一个焦点为(2,0),则C的离心率为()A.B.C.D.【解答】解:椭圆C:1的一个焦点为(2,0),可得a2﹣4=4,解得a=2,∵c=2,∴e.故选:C.4.【2017年新课标1文科05】已知F是双曲线C:x21的右焦点,P是C上一点,且PF与x轴垂直,点A的坐标是(1,3),则△APF的面积为()A.B.C.D.【解答】解:由双曲线C:x21的右焦点F(2,0),PF与x轴垂直,设(2,y),y>0,则y=3,则P(2,3),∴AP⊥PF,则丨AP丨=1,丨PF丨=3,∴△APF的面积S丨AP丨×丨PF丨,同理当y<0时,则△APF的面积S,故选:D.5.【2017年新课标1文科12】设A,B是椭圆C:1长轴的两个端点,若C上存在点M满足∠AMB =120°,则m的取值范围是()A.(0,1]∪[9,+∞)B.(0,]∪[9,+∞)C.(0,1]∪[4,+∞)D.(0,]∪[4,+∞)【解答】解:假设椭圆的焦点在x轴上,则0<m<3时,设椭圆的方程为:(a>b>0),设A(﹣a,0),B(a,0),M(x,y),y>0,则a2﹣x2,∠MAB=α,∠MBA=β,∠AMB=γ,tanα,tanβ,则tanγ=tan[π﹣(α+β)]=﹣tan(α+β),∴tanγ,当y最大时,即y=b时,∠AMB取最大值,∴M位于短轴的端点时,∠AMB取最大值,要使椭圆C上存在点M满足∠AMB=120°,∠AMB≥120°,∠AMO≥60°,tan∠AMO tan60°,解得:0<m≤1;当椭圆的焦点在y轴上时,m>3,当M位于短轴的端点时,∠AMB取最大值,要使椭圆C上存在点M满足∠AMB=120°,∠AMB≥120°,∠AMO≥60°,tan∠AMO tan60°,解得:m≥9,∴m的取值范围是(0,1]∪[9,+∞)故选A.故选:A.6.【2016年新课标1文科05】直线l经过椭圆的一个顶点和一个焦点,若椭圆中心到l的距离为其短轴长的,则该椭圆的离心率为()A.B.C.D.【解答】解:设椭圆的方程为:,直线l经过椭圆的一个顶点和一个焦点,则直线方程为:,椭圆中心到l的距离为其短轴长的,可得:,4=b2(),∴,3,∴e.故选:B.7.【2015年新课标1文科05】已知椭圆E的中心在坐标原点,离心率为,E的右焦点与抛物线C:y2=8x 的焦点重合,A,B是C的准线与E的两个交点,则|AB|=()A.3 B.6 C.9 D.12【解答】解:椭圆E的中心在坐标原点,离心率为,E的右焦点(c,0)与抛物线C:y2=8x的焦点(2,0)重合,可得c=2,a=4,b2=12,椭圆的标准方程为:,抛物线的准线方程为:x=﹣2,由,解得y=±3,所以A(﹣2,3),B(﹣2,﹣3).|AB|=6.故选:B.8.【2014年新课标1文科04】已知双曲线1(a>0)的离心率为2,则实数a=()A.2 B.C.D.1【解答】解:由题意,e2,解得,a=1.故选:D.9.【2014年新课标1文科10】已知抛物线C:y2=x的焦点为F,A(x0,y0)是C上一点,AF=|x0|,则x0=()A.1 B.2 C.4 D.8【解答】解:抛物线C:y2=x的焦点为F,∵A(x0,y0)是C上一点,AF=|x0|,x0>0.∴x0,解得x0=1.故选:A.10.【2013年新课标1文科04】已知双曲线C:(a>0,b>0)的离心率为,则C的渐近线方程为()A.y B.y C.y=±x D.y【解答】解:由双曲线C:(a>0,b>0),则离心率e,即4b2=a2,故渐近线方程为y=±x x,故选:D.11.【2013年新课标1文科08】O为坐标原点,F为抛物线C:y2=4x的焦点,P为C上一点,若|PF|=4,则△POF的面积为()A.2 B.2C.2D.4【解答】解:∵抛物线C的方程为y2=4x∴2p=4,可得,得焦点F()设P(m,n)根据抛物线的定义,得|PF|=m4,即m4,解得m=3∵点P在抛物线C上,得n2=4324∴n∵|OF|∴△POF的面积为S|OF|×|n|2故选:C.12.【2012年新课标1文科04】设F1、F2是椭圆E:1(a>b>0)的左、右焦点,P为直线x 上一点,△F2PF1是底角为30°的等腰三角形,则E的离心率为()A.B.C.D.【解答】解:∵△F2PF1是底角为30°的等腰三角形,∴|PF2|=|F2F1|∵P为直线x上一点∴∴故选:C.13.【2012年新课标1文科10】等轴双曲线C的中心在原点,焦点在x轴上,C与抛物线y2=16x的准线交于点A和点B,|AB|=4,则C的实轴长为()A.B.C.4 D.8【解答】解:设等轴双曲线C:x2﹣y2=a2(a>0),y2=16x的准线l:x=﹣4,∵C与抛物线y2=16x的准线l:x=﹣4交于A,B两点,∴A(﹣4,2),B(﹣4,﹣2),将A点坐标代入双曲线方程得4,∴a=2,2a=4.故选:C.14.【2011年新课标1文科09】已知直线l过抛物线C的焦点,且与C的对称轴垂直.l与C交于A,B两点,|AB|=12,P为C的准线上一点,则△ABP的面积为()A.18 B.24 C.36 D.48【解答】解:设抛物线的解析式为y2=2px(p>0),则焦点为F(,0),对称轴为x轴,准线为x∵直线l经过抛物线的焦点,A、B是l与C的交点,又∵AB⊥x轴∴|AB|=2p=12∴p=6又∵点P在准线上∴DP=(||)=p=6∴S△ABP(DP•AB)6×12=36故选:C.15.【2011年新课标1文科04】椭圆1的离心率为()A.B.C.D.【解答】解:根据椭圆的方程1,可得a=4,b=2,则c2;则椭圆的离心率为e,故选:D.16.【2010年新课标1文科05】中心在原点,焦点在x轴上的双曲线的一条渐近线经过点(4,2),则它的离心率为()A.B.C.D.【解答】解:∵渐近线的方程是y=±x,∴2•4,,a=2b,c a,e,即它的离心率为.故选:D.17.【2018年新课标1文科15】直线y=x+1与圆x2+y2+2y﹣3=0交于A,B两点,则|AB|=.【解答】解:圆x2+y2+2y﹣3=0的圆心(0,﹣1),半径为:2,圆心到直线的距离为:,所以|AB|=22.故答案为:2.18.【2016年新课标1文科15】设直线y=x+2a与圆C:x2+y2﹣2ay﹣2=0相交于A,B两点,若|AB|=2,则圆C的面积为.【解答】解:圆C:x2+y2﹣2ay﹣2=0的圆心坐标为(0,a),半径为,∵直线y=x+2a与圆C:x2+y2﹣2ay﹣2=0相交于A,B两点,且|AB|=2,∴圆心(0,a)到直线y=x+2a的距离d,即3=a2+2,解得:a2=2,故圆的半径r=2.故圆的面积S=4π,故答案为:4π19.【2015年新课标1文科16】已知F是双曲线C:x21的右焦点,P是C的左支上一点,A(0,6).当△APF周长最小时,该三角形的面积为.【解答】解:由题意,设F′是左焦点,则△APF周长=|AF|+|AP|+|PF|=|AF|+|AP|+|PF′|+2≥|AF|+|AF′|+2(A,P,F′三点共线时,取等号),直线AF′的方程为与x21联立可得y2+6y﹣96=0,∴P的纵坐标为2,∴△APF周长最小时,该三角形的面积为12.故答案为:12.20.【2010年新课标1文科13】圆心在原点上与直线x+y﹣2=0相切的圆的方程为.【解答】解:圆心到直线的距离:r,所求圆的方程为x2+y2=2.故答案为:x2+y2=221.【2019年新课标1文科21】已知点A,B关于坐标原点O对称,|AB|=4,⊙M过点A,B且与直线x+2=0相切.(1)若A在直线x+y=0上,求⊙M的半径;(2)是否存在定点P,使得当A运动时,|MA|﹣|MP|为定值?并说明理由.【解答】解:∵⊙M故点A,B且A在直线x+y=0上,∴点M在线段AB的中垂线x﹣y=0上,设⊙M的方程为:(x﹣a)2+(y﹣a)2=R2(R>0),则圆心M(a,a)到直线x+y=0的距离d,又|AB|=4,∴在Rt△OMB中,d2+(|AB|)2=R2,即①又∵⊙M与x=﹣2相切,∴|a+2|=R②由①②解得或,∴⊙M的半径为2或6;(2)∵线段为⊙M的一条弦,∴圆心M在线段AB的中垂线上,设点M的坐标为(x,y),则|OM|2+|OA|2=|MA|2,∵⊙M与直线x+2=0相切,∴|MA|=|x+2|,∴|x+2|2=|OM|2+|OA|2=x2+y2+4,∴y2=4x,∴M的轨迹是以F(1,0)为焦点x=﹣1为准线的抛物线,∴|MA|﹣|MP|=|x+2|﹣|MP|=|x+1|﹣|MP|+1=|MF|﹣|MP|+1,∴当|MA|﹣|MP|为定值时,则点P与点F重合,即P的坐标为(1,0),∴存在定点P(1,0)使得当A运动时,|MA|﹣|MP|为定值.考题分析与复习建议本专题考查的知识点为:直线方程、圆的方程,直线与圆、圆与圆的位置关系,椭圆、双曲线、抛物线及其性质,直线与圆锥曲线,曲线与方程等.历年考题主要以选择填空题型出现,重点考查的知识点为:直线与圆、圆与圆的位置关系,椭圆、双曲线、抛物线及其性质,直线与圆锥曲线等,预测明年本考点题目会比较稳定,备考方向以知识点直线与圆、圆与圆的位置关系,椭圆、双曲线、抛物线及其性质,直线与圆锥曲线等为重点较佳.最新高考模拟试题1.已知双曲线的右焦点为F,直线l经过点F且与双曲线的一条渐近线垂直,直线l与双曲线的右支交于不同两点A,B,若3AF FB=,则该双曲线的离心率为()A B C D【答案】A【解析】由题意得直线l的方程为bx y ca=+,不妨取1a=,则x by c=+,且221b c=-.将x by c =+代入2221y x b-=,得.设()11,A x y ,()22,B x y ,则,.由3AF FB =,得123y y =-,所以,得,解得214b =,所以,故该双曲线的离心率为c e a ==,故选A 。
十年高考真题分类汇编(2010-2019) 数学 专题01 集合

A.{1,6}B.{1,7}C.{6,7}D.{1,6,7}
【答案】C
【解析】由已知得∁UA={1,6,7},∴B∩∁UA={6,7}.故选C.
3.(2019•全国2•理T1)设集合A={x|x2-5x+6>0},B={x|x-1<0},则A∩B=()
【答案】C
【解析】由题意,得A∩B=(-1,2),故选C.
5.(2019•全国3•T1)已知集合A={-1,0,1,2},B={x|x2≤1},则A∩B=()
A.{-1,0,1}B.{0,1}C.{-1,1}D.{0,1,2}
【答案】A
【解析】A={-1,0,1,2},B={x|-1≤x≤1},则A∩B={-1,0,1}.故选A.
A.{x|0<x≤1}B.{x|0<x<1}C.{x|1≤x<2}D.{x|0<x<2}
【答案】B
【解析】∁RB={x|x<1},A∩(∁RB)={x|0<x<1}.故选B.
15.(2018•天津•文T1)设集合A={1,2,3,4},B={-1,0,2,3},C={x∈R|-1≤x<2},则(A∪B)∩C=()
13.(2018•北京•T1)已知集合A={x||x|<2},B={-2,0,1,2},则A∩B=()
A.{0,1}B.{-1,0,1}
C.{-2,0,1,2}D.{-1,0,1,2}
【答案】A
【解析】∵A={x|-2<x<2},B={-2,0,1,2},∴A∩B={0,1}.
十年真题(2010-2019)高考数学(文)分类汇编专题09 立体几何(新课标Ⅰ卷)(解析版)
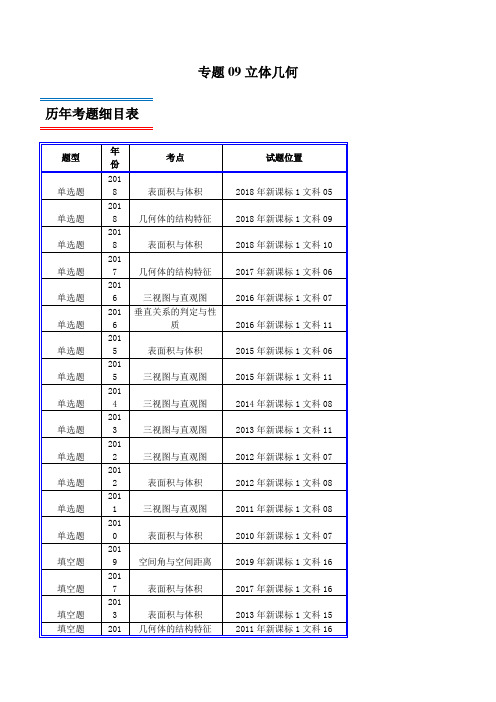
专题09立体几何历年考题细目表1填空题2010 三视图与直观图2010年新课标1文科15解答题2019 空间角与空间距离2019年新课标1文科19解答题2018 表面积与体积2018年新课标1文科18解答题2017 表面积与体积2017年新课标1文科18解答题2016 表面积与体积2016年新课标1文科18解答题2015 表面积与体积2015年新课标1文科18解答题2014 表面积与体积2014年新课标1文科19解答题2013 表面积与体积2013年新课标1文科19解答题2012 表面积与体积2012年新课标1文科19解答题2011 表面积与体积2011年新课标1文科18解答题2010 表面积与体积2010年新课标1文科18历年高考真题汇编1.【2018年新课标1文科05】已知圆柱的上、下底面的中心分别为O1,O2,过直线O1O2的平面截该圆柱所得的截面是面积为8的正方形,则该圆柱的表面积为()A.12πB.12πC.8πD.10π【解答】解:设圆柱的底面直径为2R,则高为2R,圆柱的上、下底面的中心分别为O1,O2,过直线O1O2的平面截该圆柱所得的截面是面积为8的正方形,可得:4R2=8,解得R,则该圆柱的表面积为:12π.故选:B.2.【2018年新课标1文科09】某圆柱的高为2,底面周长为16,其三视图如图.圆柱表面上的点M在正视图上的对应点为A,圆柱表面上的点N在左视图上的对应点为B,则在此圆柱侧面上,从M到N的路径中,最短路径的长度为()A.2B.2C.3 D.2【解答】解:由题意可知几何体是圆柱,底面周长16,高为:2,直观图以及侧面展开图如图:圆柱表面上的点N在左视图上的对应点为B,则在此圆柱侧面上,从M到N的路径中,最短路径的长度:2.故选:B.3.【2018年新课标1文科10】在长方体ABCD﹣A1B1C1D1中,AB=BC=2,AC1与平面BB1C1C所成的角为30°,则该长方体的体积为()A.8 B.6C.8D.8【解答】解:长方体ABCD﹣A1B1C1D1中,AB=BC=2,AC1与平面BB1C1C所成的角为30°,即∠AC1B=30°,可得BC12.可得BB12.所以该长方体的体积为:28.故选:C.4.【2017年新课标1文科06】如图,在下列四个正方体中,A,B为正方体的两个顶点,M,N,Q为所在棱的中点,则在这四个正方体中,直线AB与平面MNQ不平行的是()A.B.C.D.【解答】解:对于选项B,由于AB∥MQ,结合线面平行判定定理可知B不满足题意;对于选项C,由于AB∥MQ,结合线面平行判定定理可知C不满足题意;对于选项D,由于AB∥NQ,结合线面平行判定定理可知D不满足题意;所以选项A满足题意,故选:A.5.【2016年新课标1文科07】如图,某几何体的三视图是三个半径相等的圆及每个圆中两条相互垂直的半径.若该几何体的体积是,则它的表面积是()A.17πB.18πC.20πD.28π【解答】解:由题意可知三视图复原的几何体是一个球去掉后的几何体,如图:可得:,R=2.它的表面积是:4π•2217π.故选:A.6.【2016年新课标1文科11】平面α过正方体ABCD﹣A1B1C1D1的顶点A,α∥平面CB1D1,α∩平面ABCD =m,α∩平面ABB1A1=n,则m、n所成角的正弦值为()A.B.C.D.【解答】解:如图:α∥平面CB1D1,α∩平面ABCD=m,α∩平面ABA1B1=n,可知:n∥CD1,m∥B1D1,∵△CB1D1是正三角形.m、n所成角就是∠CD1B1=60°.则m、n所成角的正弦值为:.故选:A.7.【2015年新课标1文科06】《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有委米依垣内角,下周八尺,高五尺.问:积及为米几何?”其意思为:“在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆底部的弧长为8尺,米堆的高为5尺,问米堆的体积和堆放的米各为多少?”已知1斛米的体积约为1.62立方尺,圆周率约为3,估算出堆放的米约有()A.14斛B.22斛C.36斛D.66斛【解答】解:设圆锥的底面半径为r,则r=8,解得r,故米堆的体积为π×()2×5,∵1斛米的体积约为1.62立方,∴ 1.62≈22,故选:B.8.【2015年新课标1文科11】圆柱被一个平面截去一部分后与半球(半径为r)组成一个几何体,该几何体三视图中的正视图和俯视图如图所示.若该几何体的表面积为16+20π,则r=()A.1 B.2 C.4 D.8【解答】解:由几何体三视图中的正视图和俯视图可知,截圆柱的平面过圆柱的轴线,该几何体是一个半球拼接半个圆柱,∴其表面积为:4πr2πr22r×2πr+2r×2rπr2=5πr2+4r2,又∵该几何体的表面积为16+20π,∴5πr2+4r2=16+20π,解得r=2,故选:B.9.【2014年新课标1文科08】如图,网格纸的各小格都是正方形,粗实线画出的是一个几何体的三视图,则这个几何体是()A.三棱锥B.三棱柱C.四棱锥D.四棱柱【解答】解:根据网格纸的各小格都是正方形,粗实线画出的是一个几何体的三视图,可知几何体如图:几何体是三棱柱.故选:B.10.【2013年新课标1文科11】某几何体的三视图如图所示,则该几何体的体积为()A.16+8πB.8+8πC.16+16πD.8+16π【解答】解:三视图复原的几何体是一个长方体与半个圆柱的组合体,如图,其中长方体长、宽、高分别是:4,2,2,半个圆柱的底面半径为2,母线长为4.∴长方体的体积=4×2×2=16,半个圆柱的体积22×π×4=8π所以这个几何体的体积是16+8π;故选:A.11.【2012年新课标1文科07】如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则此几何体的体积为()A.6 B.9 C.12 D.18【解答】解:该几何体是三棱锥,底面是俯视图,三棱锥的高为3;底面三角形斜边长为6,高为3的等腰直角三角形,此几何体的体积为V6×3×3=9.故选:B.12.【2012年新课标1文科08】平面α截球O的球面所得圆的半径为1,球心O到平面α的距离为,则此球的体积为()A.πB.4πC.4πD.6π【解答】解:因为平面α截球O的球面所得圆的半径为1,球心O到平面α的距离为,所以球的半径为:.所以球的体积为:4π.故选:B.13.【2011年新课标1文科08】在一个几何体的三视图中,正视图和俯视图如图所示,则相应的侧视图可以为()A.B.C.D.【解答】解:由俯视图和正视图可以得到几何体是一个简单的组合体,是由一个三棱锥和被轴截面截开的半个圆锥组成,∴侧视图是一个中间有分界线的三角形,故选:D.14.【2010年新课标1文科07】设长方体的长、宽、高分别为2a、a、a,其顶点都在一个球面上,则该球的表面积为()A.3πa2B.6πa2C.12πa2D.24πa2【解答】解:根据题意球的半径R满足(2R)2=6a2,所以S球=4πR2=6πa2.故选:B.15.【2019年新课标1文科16】已知∠ACB=90°,P为平面ABC外一点,PC=2,点P到∠ACB两边AC,BC的距离均为,那么P到平面ABC的距离为.【解答】解:∠ACB=90°,P为平面ABC外一点,PC=2,点P到∠ACB两边AC,BC的距离均为,过点P作PD⊥AC,交AC于D,作PE⊥BC,交BC于E,过P作PO⊥平面ABC,交平面ABC于O,连结OD,OC,则PD=PE,∴CD=CE=OD=OE1,∴PO.∴P到平面ABC的距离为.故答案为:.16.【2017年新课标1文科16】已知三棱锥S﹣ABC的所有顶点都在球O的球面上,SC是球O的直径.若平面SCA⊥平面SCB,SA=AC,SB=BC,三棱锥S﹣ABC的体积为9,则球O的表面积为.【解答】解:三棱锥S﹣ABC的所有顶点都在球O的球面上,SC是球O的直径,若平面SCA⊥平面SCB,SA=AC,SB=BC,三棱锥S﹣ABC的体积为9,可知三角形SBC与三角形SAC都是等腰直角三角形,设球的半径为r,可得,解得r=3.球O的表面积为:4πr2=36π.故答案为:36π.17.【2013年新课标1文科15】已知H是球O的直径AB上一点,AH:HB=1:2,AB⊥平面α,H为垂足,α截球O所得截面的面积为π,则球O的表面积为.【解答】解:设球的半径为R,∵AH:HB=1:2,∴平面α与球心的距离为R,∵α截球O所得截面的面积为π,∴d R时,r=1,故由R2=r2+d2得R2=12+(R)2,∴R2∴球的表面积S=4πR2.故答案为:.18.【2011年新课标1文科16】已知两个圆锥有公共底面,且两个圆锥的顶点和底面的圆周都在同一个球面上,若圆锥底面面积是这个球面面积的,则这两个圆锥中,体积较小者的高与体积较大者的高的比值为.【解答】解:不妨设球的半径为:4;球的表面积为:64π,圆锥的底面积为:12π,圆锥的底面半径为:2;由几何体的特征知球心到圆锥底面的距离,求的半径以及圆锥底面的半径三者可以构成一个直角三角形由此可以求得球心到圆锥底面的距离是,所以圆锥体积较小者的高为:4﹣2=2,同理可得圆锥体积较大者的高为:4+2=6;所以这两个圆锥中,体积较小者的高与体积较大者的高的比值为:.故答案为:19.【2010年新课标1文科15】一个几何体的正视图为一个三角形,则这个几何体可能是下列几何体中的(填入所有可能的几何体前的编号)①三棱锥②四棱锥③三棱柱④四棱柱⑤圆锥⑥圆柱.【解答】解:一个几何体的正视图为一个三角形,显然①②⑤正确;③是三棱柱放倒时也正确;④⑥不论怎样放置正视图都不会是三角形;故答案为:①②③⑤20.【2019年新课标1文科19】如图,直四棱柱ABCD﹣A1B1C1D1的底面是菱形,AA1=4,AB=2,∠BAD =60°,E,M,N分别是BC,BB1,A1D的中点.(1)证明:MN∥平面C1DE;(2)求点C到平面C1DE的距离.【解答】解法一:证明:(1)连结B1C,ME,∵M,E分别是BB1,BC的中点,∴ME∥B1C,又N为A1D的中点,∴ND A1D,由题设知A 1B1DC,∴B1C A1D,∴ME ND,∴四边形MNDE是平行四边形,MN∥ED,又MN⊄平面C1DE,∴MN∥平面C1DE.解:(2)过C作C1E的垂线,垂足为H,由已知可得DE⊥BC,DE⊥C1C,∴DE⊥平面C1CE,故DE⊥CH,∴CH⊥平面C1DE,故CH的长即为C到时平面C1DE的距离,由已知可得CE=1,CC1=4,∴C1E,故CH,∴点C到平面C1DE的距离为.解法二:证明:(1)∵直四棱柱ABCD﹣A1B1C1D1的底面是菱形,AA1=4,AB=2,∠BAD=60°,E,M,N分别是BC,BB1,A1D的中点.∴DD1⊥平面ABCD,DE⊥AD,以D为原点,DA为轴,DE为y轴,DD1为轴,建立空间直角坐标系,M(1,,2),N(1,0,2),D(0,0,0),E(0,,0),C1(﹣1,,4),(0,,0),(﹣1,),(0,),设平面C1DE的法向量(,y,),则,取=1,得(4,0,1),∵•0,MN⊄平面C1DE,∴MN∥平面C1DE.解:(2)C(﹣1,,0),(﹣1,,0),平面C1DE的法向量(4,0,1),∴点C到平面C1DE的距离:d.21.【2018年新课标1文科18】如图,在平行四边形ABCM中,AB=AC=3,∠ACM=90°,以AC为折痕将△ACM折起,使点M到达点D的位置,且AB⊥DA.(1)证明:平面ACD⊥平面ABC;(2)Q为线段AD上一点,P为线段BC上一点,且BP=DQ DA,求三棱锥Q﹣ABP的体积.【解答】解:(1)证明:∵在平行四边形ABCM中,∠ACM=90°,∴AB⊥AC,又AB⊥DA.且AD∩AC=A,∴AB⊥面ADC,∵AB⊂面ABC,∴平面ACD⊥平面ABC;(2)∵AB=AC=3,∠ACM=90°,∴AD=AM=3,∴BP=DQ DA=2,由(1)得DC⊥AB,又DC⊥CA,∴DC⊥面ABC,∴三棱锥Q﹣ABP的体积V1.22.【2017年新课标1文科18】如图,在四棱锥P﹣ABCD中,AB∥CD,且∠BAP=∠CDP=90°.(1)证明:平面P AB⊥平面P AD;(2)若P A=PD=AB=DC,∠APD=90°,且四棱锥P﹣ABCD的体积为,求该四棱锥的侧面积.【解答】证明:(1)∵在四棱锥P﹣ABCD中,∠BAP=∠CDP=90°,∴AB⊥P A,CD⊥PD,又AB∥CD,∴AB⊥PD,∵P A∩PD=P,∴AB⊥平面P AD,∵AB⊂平面P AB,∴平面P AB⊥平面P AD.解:(2)设P A=PD=AB=DC=a,取AD中点O,连结PO,∵P A=PD=AB=DC,∠APD=90°,平面P AB⊥平面P AD,∴PO⊥底面ABCD,且AD,PO,∵四棱锥P﹣ABCD的体积为,由AB⊥平面P AD,得AB⊥AD,∴V P﹣ABCD,解得a=2,∴P A=PD=AB=DC=2,AD=BC=2,PO,∴PB=PC2,∴该四棱锥的侧面积:S侧=S△P AD+S△P AB+S△PDC+S△PBC=6+2.23.【2016年新课标1文科18】如图,已知正三棱锥P﹣ABC的侧面是直角三角形,P A=6,顶点P在平面ABC内的正投影为点D,D在平面P AB内的正投影为点E,连接PE并延长交AB于点G.(Ⅰ)证明:G是AB的中点;(Ⅱ)在图中作出点E在平面P AC内的正投影F(说明作法及理由),并求四面体PDEF的体积.【解答】解:(Ⅰ)证明:∵P﹣ABC为正三棱锥,且D为顶点P在平面ABC内的正投影,∴PD⊥平面ABC,则PD⊥AB,又E为D在平面P AB内的正投影,∴DE⊥面P AB,则DE⊥AB,∵PD∩DE=D,∴AB⊥平面PDE,连接PE并延长交AB于点G,则AB⊥PG,又P A=PB,∴G是AB的中点;(Ⅱ)在平面P AB内,过点E作PB的平行线交P A于点F,F即为E在平面P AC内的正投影.∵正三棱锥P﹣ABC的侧面是直角三角形,∴PB⊥P A,PB⊥PC,又EF∥PB,所以EF⊥P A,EF⊥PC,因此EF⊥平面P AC,即点F为E在平面P AC内的正投影.连结CG,因为P在平面ABC内的正投影为D,所以D是正三角形ABC的中心.由(Ⅰ)知,G是AB的中点,所以D在CG上,故CD CG.由题设可得PC⊥平面P AB,DE⊥平面P AB,所以DE∥PC,因此PE PG,DE PC.由已知,正三棱锥的侧面是直角三角形且P A=6,可得DE=2,PG=3,PE=2.在等腰直角三角形EFP中,可得EF=PF=2.所以四面体PDEF的体积V DE×S△PEF22×2.24.【2015年新课标1文科18】如图,四边形ABCD为菱形,G为AC与BD的交点,BE⊥平面ABCD.(Ⅰ)证明:平面AEC⊥平面BED;(Ⅱ)若∠ABC=120°,AE⊥EC,三棱锥E﹣ACD的体积为,求该三棱锥的侧面积.【解答】证明:(Ⅰ)∵四边形ABCD为菱形,∴AC⊥BD,∵BE⊥平面ABCD,∴AC⊥BE,则AC⊥平面BED,∵AC⊂平面AEC,∴平面AEC⊥平面BED;解:(Ⅱ)设AB=,在菱形ABCD中,由∠ABC=120°,得AG=GC,GB=GD,∵BE⊥平面ABCD,∴BE⊥BG,则△EBG为直角三角形,∴EG AC=AG,则BE,∵三棱锥E﹣ACD的体积V,解得=2,即AB=2,∵∠ABC=120°,∴AC2=AB2+BC2﹣2AB•BC cos ABC=4+4﹣212,即AC,在三个直角三角形EBA,EBD,EBC中,斜边AE=EC=ED,∵AE⊥EC,∴△EAC为等腰三角形,则AE2+EC2=AC2=12,即2AE2=12,∴AE2=6,则AE,∴从而得AE=EC=ED,∴△EAC的面积S3,在等腰三角形EAD中,过E作EF⊥AD于F,则AE,AF,则EF,∴△EAD的面积和△ECD的面积均为S,故该三棱锥的侧面积为3+2.25.【2014年新课标1文科19】如图,三棱柱ABC﹣A1B1C1中,侧面BB1C1C为菱形,B1C的中点为O,且AO⊥平面BB1C1C.(1)证明:B1C⊥AB;(2)若AC⊥AB1,∠CBB1=60°,BC=1,求三棱柱ABC﹣A1B1C1的高.【解答】(1)证明:连接BC1,则O为B1C与BC1的交点,∵侧面BB1C1C为菱形,∴BC1⊥B1C,∵AO⊥平面BB1C1C,∴AO⊥B1C,∵AO∩BC1=O,∴B1C⊥平面ABO,∵AB⊂平面ABO,∴B1C⊥AB;(2)解:作OD⊥BC,垂足为D,连接AD,作OH⊥AD,垂足为H,∵BC⊥AO,BC⊥OD,AO∩OD=O,∴BC⊥平面AOD,∴OH⊥BC,∵OH⊥AD,BC∩AD=D,∴OH⊥平面ABC,∵∠CBB1=60°,∴△CBB1为等边三角形,∵BC=1,∴OD,∵AC⊥AB1,∴OA B1C,由OH•AD=OD•OA,可得AD,∴OH,∵O为B1C的中点,∴B1到平面ABC的距离为,∴三棱柱ABC﹣A1B1C1的高.26.【2013年新课标1文科19】如图,三棱柱ABC﹣A1B1C1中,CA=CB,AB=AA1,∠BAA1=60°(Ⅰ)证明:AB⊥A1C;(Ⅱ)若AB=CB=2,A1C,求三棱柱ABC﹣A1B1C1的体积.【解答】(Ⅰ)证明:如图,取AB的中点O,连结OC,OA1,A1B.因为CA=CB,所以OC⊥AB.由于AB=AA1,,故△AA1B为等边三角形,所以OA1⊥AB.因为OC∩OA1=O,所以AB⊥平面OA1C.又A1C⊂平面OA1C,故AB⊥A1C;(Ⅱ)解:由题设知△ABC与△AA1B都是边长为2的等边三角形,所以.又,则,故OA1⊥OC.因为OC∩AB=O,所以OA1⊥平面ABC,OA1为三棱柱ABC﹣A1B1C1的高.又△ABC的面积,故三棱柱ABC﹣A1B1C1的体积.27.【2012年新课标1文科19】如图,三棱柱ABC﹣A1B1C1中,侧棱垂直底面,∠ACB=90°,AC=BC AA1,D是棱AA1的中点.(Ⅰ)证明:平面BDC1⊥平面BDC(Ⅱ)平面BDC1分此棱柱为两部分,求这两部分体积的比.【解答】证明:(1)由题意知BC⊥CC1,BC⊥AC,CC1∩AC=C,∴BC⊥平面ACC1A1,又DC1⊂平面ACC1A1,∴DC1⊥BC.由题设知∠A1DC1=∠ADC=45°,∴∠CDC1=90°,即DC1⊥DC,又DC∩BC=C,∴DC1⊥平面BDC,又DC1⊂平面BDC1,∴平面BDC1⊥平面BDC;(2)设棱锥B﹣DACC1的体积为V1,AC=1,由题意得V11×1,又三棱柱ABC﹣A1B1C1的体积V=1,∴(V﹣V1):V1=1:1,∴平面BDC1分此棱柱两部分体积的比为1:1.28.【2011年新课标1文科18】如图,四棱锥P﹣ABCD中,底面ABCD为平行四边形.∠DAB=60°,AB =2AD,PD⊥底面ABCD.(Ⅰ)证明:P A⊥BD(Ⅱ)设PD=AD=1,求棱锥D﹣PBC的高.【解答】解:(Ⅰ)证明:因为∠DAB=60°,AB=2AD,由余弦定理得BD,从而BD2+AD2=AB2,故BD⊥AD又PD⊥底面ABCD,可得BD⊥PD所以BD⊥平面P AD.故P A⊥BD.(II)解:作DE⊥PB于E,已知PD⊥底面ABCD,则PD⊥BC,由(I)知,BD⊥AD,又BC∥AD,∴BC⊥BD.故BC⊥平面PBD,BC⊥DE,则DE⊥平面PBC.由题设知PD=1,则BD,PB=2.根据DE•PB=PD•BD,得DE,即棱锥D﹣PBC的高为.29.【2010年新课标1文科18】如图,已知四棱锥P﹣ABCD的底面为等腰梯形,AB∥CD,AC⊥BD,垂足为H,PH是四棱锥的高.(Ⅰ)证明:平面P AC⊥平面PBD;(Ⅱ)若AB,∠APB=∠ADB=60°,求四棱锥P﹣ABCD的体积.【解答】解:(1)因为PH是四棱锥P﹣ABCD的高.所以AC⊥PH,又AC⊥BD,PH,BD都在平PHD内,且PH∩BD=H.所以AC⊥平面PBD.故平面P AC⊥平面PBD(2)因为ABCD为等腰梯形,AB∥CD,AC⊥BD,AB.所以HA=HB.因为∠APB=∠ADB=60°所以P A=PB,HD=HC=1.可得PH.等腰梯形ABCD的面积为S ACBD=2所以四棱锥的体积为V(2).考题分析与复习建议本专题考查的知识点为:空间几何体的结构、三视图和直观图,空间几何体的表面积与体积,空间点、直线、平面之间的位置关系,直线、平面平行、垂直的判定与性质等.历年考题主要以选择填空或解答题题型出现,重点考查的知识点为:三视图和直观图,空间几何体的表面积与体积,直线、平面平行、垂直的判定与性质等.预测明年本考点题目会比较稳定,备考方向以知识点三视图和直观图,空间几何体的表面积与体积,直线、平面平行、垂直的判定与性质等为重点较佳. 最新高考模拟试题1.在正方体1111ABCD A B C D -中, 1AD 与BD 所成的角为( )A .45?oB .90oC .60oD .120o【答案】C【解析】如图,连结BC 1、BD 和DC 1,在正方体ABCD-A 1B 1C 1D 1中,由AB=D 1C 1,AB ∥D 1C 1,可知AD 1∥BC 1,所以∠DBC 1就是异面直线AD 1与BD 所成角,在正方体ABCD-A 1B 1C 1D 1中,BC 1、BD 和DC 1是其三个面上的对角线,它们相等.所以△DBC 1是正三角形,∠DBC 1=60°故异面直线AD 1与BD 所成角的大小为60°.故选:C .2.在正方体1111ABCD A B C D -中,用空间中与该正方体所有棱成角都相等的平面α去截正方体,在截面边数最多时的所有多边形中,多边形截面的面积为S ,周长为l ,则( )A .S 为定值,l 不为定值B .S 不为定值,l 为定值C .S 与l 均为定值D .S 与l 均不为定值【答案】C【解析】正方体的所有棱中,实际上是3组平行的棱,每条棱所在直线与平面α所成的角都相等,如图:与面1A BD 平行的面且截面是六边形时满足条件,不失一般性设正方体边长为1,即六边形EFGHMN ,其中,,,,,E F G H M N 分别为其所在棱的中点, 由正方体的性质可得22EF = ∴六边形的周长l 为定值32 ∴六边形的面积为23233 (6⨯= 由正方体的对称性可得其余位置时也为正六边形,周长与面积不变,故S 与l 均为定值,故选C.3.在四面体P ABC -中,ABC ∆为等边三角形,边长为3,3PA =,4PB =,5PC =,则四面体P ABC -的体积为( )A .3B .3C 11D 10 【答案】C【解析】如图,延长CA 至D ,使得3AD =,连接,DB PD ,因为3AD AB ==,故ADB ∆为等腰三角形,又180120DAB CAB ∠=︒-∠=︒,故()1180120302ADB ∠=︒-︒=︒, 所以90ADB DCB ∠+∠=︒即90DBC ∠=︒,故CB DB ⊥,因为4,5,3PB PC BC ===,所以222PC PB BC =+,所以CB PB ⊥,因DB PB B =I ,DB ⊂平面PBD ,PB ⊂平面PBD ,所以CB ⊥平面PBD , 所以13PBD P CBD C PBD V V CB S ∆--==⨯⨯三棱锥三棱锥,因A 为DC 的中点,所以1113262PBD PBD P ABC P CBD V V S S ∆∆--==⨯⨯=三棱锥三棱锥, 因为3DA AC AP ===,故PDC ∆为直角三角形,所以22362511PD CD PC =-=-=,又333DB AD ==,而4PB =,故222DB PD PB =+即PBD ∆为直角三角形,所以14112112PBD S ∆=⨯⨯=,所以11P ABC V -=三棱锥,故选C.4.若,a b 是不同的直线,,αβ是不同的平面,则下列命题中正确的是( )A .若,,ab a b αβ⊥‖‖,则αβ⊥ B .若,,ab a b αβ‖‖‖,则αβ‖ C .若,,a b ab αβ⊥⊥‖,则αβ‖ D .若,,ab a b αβ⊥⊥‖,则αβ‖ 【答案】C【解析】A 中,若,,ab a b αβ⊥‖‖,平面,αβ可能垂直也可能平行或斜交,不正确; B 中,若,,ab a b αβ‖‖‖,平面,αβ可能平行也可能相交,不正确; C 中,若,a b αβ⊥⊥,则,a b 分别是平面,αβ的法线,a b ‖必有αβ‖,正确; D 中,若,,ab a b αβ⊥⊥‖,平面,αβ可能平行也可能相交,不正确.故选C. 5.某几何体的三视图如图所示,则该几何体的外接球的体积是( )A .2πB .3π C .3πD .43π【答案】B【解析】解:根据几何体的三视图,该几何体是由一个正方体切去一个正方体的一角得到的.故:该几何体的外接球为正方体的外接球,所以:球的半径2221113r ++==, 则:34333V ππ⎛⎫=⋅⋅= ⎪ ⎪⎝⎭. 故选:B .6.如图,正方体1111ABCD A B C D -中,E 为棱1BB 的中点,用过点A 、E 、1C 的平面截去该正方体的下半部分,则剩余几何体的正视图(也称主视图)是( )A .B .C .D .【答案】A【解析】解:正方体1111ABCD A B C D 中,过点1,,A E C 的平面截去该正方体的上半部分后,剩余部分的直观图如图:则该几何体的正视图为图中粗线部分.故选:A .7.下列说法错误的是( )A .垂直于同一个平面的两条直线平行B .若两个平面垂直,则其中一个平面内垂直于这两个平面交线的直线与另一个平面垂直C .一个平面内的两条相交直线均与另一个平面平行,则这两个平面平行D .一条直线与一个平面内的无数条直线垂直,则这条直线和这个平面垂直【答案】D【解析】由线面垂直的性质定理知,垂直于同一个平面的两条直线平行,A 正确;由面面垂直的性质定理知,若两个平面垂直,则其中一个平面内垂直于这两个平面交线的直线与另一个平面垂直,B 正确;由面面平行的判定定理知,一个平面内的两条相交直线均与另一个平面平行,则这两个平面平行,C 正确; 当一条直线与平面内无数条相互平行的直线垂直时,该直线与平面不一定垂直,D 错误,故选D. 8.《九章算术》中,将四个面都为直角三角形的四面体称之为“鳖臑”.在如图所示的四棱锥P ABCD -中,PD ⊥平面ABCD ,底面ABCD 是正方形,且PD CD =,点E ,F 分别为PC ,PD 的中点,则图中的鳖臑有( )A .2个B .3个C .4个D .5个【答案】C【解析】 由题意,因为PD ⊥底面ABCD ,所以PD DC ^,PD BC ⊥,又四边形ABCD 为正方形,所以BC CD ⊥,所以BC ⊥平面PCD ,BC PC ⊥,所以四面体PDBC 是一个鳖臑,因为DE ⊂平面PCD ,所以BC DE ⊥,因为PD CD =,点E 是PC 的中点,所以DE PC ⊥,因为PC BC C =I ,所以DE ⊥平面PBC ,可知四面体EBCD 的四个面都是直角三角形,即四面体EBCD 是一个鳖臑,同理可得,四面体PABD 和FABD 都是鳖臑,故选C.9.在三棱锥P ABC -中,平面PAB ⊥平面ABC ,ABC △是边长为6的等边三角形,PAB △是以AB 为斜边的等腰直角三角形,则该三棱锥外接球的表面积为_______.【答案】48π【解析】如图,在等边三角形ABC 中,取AB 的中点F ,设其中心为O ,由6AB =, 得2233AO BO CO CF ====, PAB ∆Q 是以AB 为斜边的等腰角三角形,PF AB ∴⊥,又因为平面PAB ⊥平面ABC ,PF ∴⊥平面 ABC ,PF OF ∴⊥,2223OP OF PF =+=则O 为棱锥P ABC -的外接球球心, 外接球半径23R OC == 该三棱锥外接球的表面积为(24348ππ⨯=, 故答案为48π.10.若将一个圆锥的侧面沿一条母线剪开,其展开图是半径为3,圆心角为23π的扇形,则该圆锥的体积为_______. 【答案】23 【解析】因为展开图是半径为3,圆心角为23π的扇形,所以圆锥的母线3l =,圆锥的底面的周长为2323ππ⨯=,因此底面的半径1r =,根据勾股定理,可知圆锥的高2222h l r =-= 所以圆锥的体积为212212233π⋅⨯=. 11.设m ,n 是两条不同的直线,α,β是两个不同的平面,下列正确命题序号是_____.(1)若m αP ,n α∥,则m n ∥(2)若m α⊥,m n ⊥则n α∥(3)若m α⊥,n β⊥且m n ⊥,则αβ⊥;(4)若m β⊂,αβP ,则m αP【答案】(3)(4)【解析】若m n αα,∥∥,则m 与n 可能平行,相交或异面,故(1)错误;若m m n α⊥⊥,则n α∥或n α⊂,故(2)错误;若m n αβ⊥⊥,且m n ⊥,则αβ⊥,故(3)正确;若m βαβ⊂P ,,由面面平行的性质可得m αP ,故(4)正确;故答案为:(3)(4)12.长方体1111ABCD A B C D -的底面ABCD 是边长为1的正方形,若在侧棱1AA 上存在点E ,使得190C EB ∠=︒,则侧棱1AA 的长的最小值为_______.【答案】2【解析】设侧棱AA 1的长为,A 1E =t ,则AE =﹣t ,∵长方体ABCD ﹣A 1B 1C 1D 1的底面是边长为1的正方形,∠C 1EB =90°,∴22211C E BE BC +=,∴2+t 2+1+(﹣t )2=1+2,整理,得:t 2﹣t+1=0,∵在侧棱AA 1上至少存在一点E ,使得∠C 1EB =90°,∴△=(﹣)2﹣4≥0,解得≥2.∴侧棱AA 1的长的最小值为2.故答案为2.13.如图,在Rt ABC ∆中,1AB BC ==,D 和E 分别是边BC 和AC 上一点,DE BC ⊥,将CDE ∆沿DE 折起到点P 位置,则该四棱锥P ABDE -体积的最大值为_______.【答案】3 【解析】 在Rt ABC ∆中,由已知,1AB BC ==,DE BC ⊥,所以设()01CD DE x x ==<<,四边形ABDE 的面积为()()()21111122=S x x x +-=-, 当CDE ∆⊥平面ABDE 时,四棱锥P ABDE -体积最大,此时PD ABDE ⊥平面,且PD CD x ==,故四棱锥P ABDE -体积为()31136=V S PD x x =⋅- , ()21136V x '=-,30,x ⎛⎫∈ ⎪ ⎪⎝⎭ 时,0V '> ;3332x ⎛⎫∈ ⎪ ⎪⎝⎭,时,0V '<, 所以,当33x =时,max 327V =. 故答案为3 14.三棱锥P ABC -的4个顶点在半径为2的球面上,PA ⊥平面ABC ,V ABC 是边长为3的正三角形,则点A 到平面PBC 的距离为______.【答案】65【解析】△ABC 是边长为3的正三角形,可得外接圆的半径2r a sin60==︒2,即r =1. ∵PA ⊥平面ABC ,PA =h ,球心到底面的距离d 等于三棱锥的高PA 的一半即h 2, 那么球的半径R 22h r 2()=+=2,解得h=2,又534PBC S ∆= 由P ABC A PBC V V --= 知'13153××3?2=?3434d ,得'65d = 故点A 到平面PBC 的距离为65 故答案为65. 15.如图,该几何体由底面半径相同的圆柱与圆锥两部分组成,且圆柱的高与底面半径相等.若圆柱与圆锥的侧面积相等,则圆锥与圆柱的高之比为_______.3【解析】设圆柱和圆锥的底面半径为R ,则圆柱的高1h =R ,圆锥的母线长为L ,因为圆柱与圆锥的侧面积相等, 所以,1222R R R L ππ⨯=⨯⨯,解得:L =2R ,得圆锥的高为2h 3,所以,圆锥与圆柱的高之比为33R R=. 故答案为:3 16.直三棱柱111ABC A B C -中,190,2BC A A A ︒∠==,设其外接球的球心为O ,已知三棱锥O ABC -的体积为1,则球O 表面积的最小值为__________. 【答案】16π.【解析】如图,在Rt ABC ∆中,设,AB c BC a ==,则22AC a c =+.分别取11,AC A C 的中点12,O O ,则12,O O 分别为111Rt A B C ∆和Rt ABC ∆外接圆的圆心,连12,O O ,取12O O 的中点O ,则O 为三棱柱外接球的球心.连OA ,则OA 为外接球的半径,设半径为R .∵三棱锥O ABC -的体积为1,即1()1132O ABC ac V -=⨯⨯=, ∴6ac =.在2Rt OO C ∆中,可得2222222212()()112224O O AC a c a c R ++=+=+=+, ∴222244(1)4(1)1644a c ac S R ππππ+==+≥+=球表,当且仅当a c =时等号成立, ∴O 球表面积的最小值为16π.故答案为:16π.17.在三棱锥P ABC -中,ABC ∆是边长为4的等边三角形,23PA PB ==25PC =(1)求证:平面PAB ⊥平面ABC ;(2)若点M ,N 分别为棱BC ,PC 的中点,求三棱锥N AMC -的体积V .【答案】(1)见证明;(2) 26=V 【解析】 (1)取AB 中点H ,连结PH ,HC .∵23PA PB ==,4AB =,∴PH AB ⊥,22PH =∵等边ABC ∆的边长为4∴23HC =,又25PC =∴22220PH HC PC +==∴90PHC ∠=o ,即PH HC ⊥又∵HC AB H =I ,AB Ì平面ABC ,CH ⊂平面ABC∴PH ⊥平面ABC ,又PH ⊂平面PAB∴平面PAB ⊥平面ABC(2)∵点M ,N 分别为棱BC ,PC 的中点 ∴点N 到平面ABC 的距离为122PH 且21134=2322AMC ABC S S ∆∆==∴三棱锥N AMC -的体积126=223=3V ⨯⨯ 18.如图所示,三棱柱111ABC A B C -中,90BCA ∠=°,1AC ⊥平面1A BC .(1)证明:平面ABC ⊥平面11ACC A ;(2)若2BC AC ==,11A A A C =,求点1B 到平面1A BC 的距离.【答案】(1)见解析;(23【解析】(1)证明:1AC ⊥Q 平面1A BC ,1AC BC ∴⊥.90BCA ∠︒Q =,BC AC ∴⊥,BC ∴⊥平面11ACC A .又BC ⊂平面ABC ,平面ABC ⊥平面11ACC A .(2)解:取AC 的中点D ,连接1A D .11A A A C =Q ,1A D AC ∴⊥.又平面ABC ⊥平面11ACC A ,且交线为AC ,则1A D ⊥平面ABC .1AC ⊥Q 平面1A BC ,11AC AC ∴⊥,四边形11ACC A 为菱形,1AA AC ∴=. 又11A A A C =,1A AC ∴V 是边长为2正三角形,13A D ∴=1111223232ABC A B C V -∴=⨯⨯=. 111,AA BB AA ⊄Q P 面11BB C C ,1BB ⊂面11BB C C1AA ∴P 面11BB C C1111A B BC A B BC B ABC V V V ---∴==11112333ABC A B C V -==设点1B 到平面1A BC 的距离为h .则11113B A BC A BC V h S -∆=⋅. 1AC BC ⊥Q ,12A C AC BC ===11122A BC S BC AC ∆∴=⋅=,3h ∴=. 所以点1B 到平面1A BC 的距离为3.19.在边长为3的正方形ABCD 中,点E ,F 分别在边AB ,BC 上(如左图),且=BE BF ,将AED V ,DCF V 分别沿DE ,DF 折起,使A ,C 两点重合于点A ¢(如右图).(1)求证:A D EF '⊥;(2)当13BF BC =时,求点A ¢到平面DEF 的距离. 【答案】(1)见解析;(237 【解析】(1)由ABCD 是正方形及折叠方式,得:A E A D '⊥',A F A D '⊥',A E A F A '⋂''Q =,A D ∴'⊥平面A EF ',-1? { 2?x y ==平面A EF ',A D EF ∴'⊥.(2)113BE BF BC ===Q 2,2,3A E A F EF A D '''∴====, EF 72A S '∆∴=,13DE DF ∴==,52DEF S ∴=V 设点A ¢到平面DEF 的距离为d ,A DEF D A EF V V '--'Q =,1133DEF A EF d S A D S ''∴⨯⨯=⨯⨯V V ,解得375d =. 点A ¢到平面DEF 的距离为37. 20.如图,四棱锥S ABCD -中,SD ⊥平面ABCD ,//AB CD ,AD CD ⊥,SD CD =,AB AD =,2CD AD =,M 是BC 中点,N 是SA 上的点.(1)求证://MN 平面SDC ;(2)求A 点到平面MDN 的距离.【答案】(1)见证明;(2)127d =【解析】(1)取AD 中点为E ,连结ME ,NE ,则//ME DC ,因为ME ⊄平面SDC ,所以//ME 平面SDC ,同理//NE 平面SDC .所以平面//MNE 平面SDC ,从而因此//MN 平面SDC .(2)因为CD AD ⊥,所以ME AD ⊥.因为SD ⊥平面ABCD ,所以SD CD ⊥,ME SD ⊥.所以ME ⊥平面SAD .设2DA =,则3ME =,2NE =,2213MN NE ME +=,10MD =,5ND =.在MDN ∆中,由余弦定理2cos MDN ∠=, 从而2sin 10MDN ∠=,所以MDN ∆面积为72. 又ADM ∆面积为12332⨯⨯=. 设A 点到平面MDN 的距离为d ,由A MDN N AMD V V --=得732d NE =, 因为2NE =,所以A 点到平面MDN 的距离127d =. 21.如图,在四棱锥P ABCD -中,PA ⊥平面ABCD ,3PA =//AB CD ,AB AD ⊥,1AD DC ==,2AB =,E 为侧棱PA 上一点. (Ⅰ)若13PE PA =,求证:PC //平面EBD ; (Ⅱ)求证:平面EBC ⊥平面PAC ;(Ⅲ)在侧棱PD 上是否存在点F ,使得AF ⊥平面PCD ?若存在,求出线段PF 的长;若不存在,请说明理由.【答案】(Ⅰ)详见解析;(Ⅱ)详见解析;(Ⅲ)存在,线段PF 长32. 【解析】(Ⅰ)设AC BD G ⋂=,连结EG ,由已知AB//CD ,DC 1=,AB 2=,得AG AB 2GC DC==. 由1PE PA 3=,得AE 2EP=. 在ΔPAC 中,由AE AG EP GC=,得EG //PC . 因为EG ⊂平面EBD ,PC ⊄平面EBD ,所以PC //平面EBD .(Ⅱ)因为PA ⊥平面ABCD ,BC ⊂平面ABCD ,所以BC PA ⊥.由已知得AC 2=BC 2=,AB 2=,所以222AC BC AB +=.所以BC AC ⊥.又PA AC A ⋂=,所以BC ⊥平面PAC .因为BC ⊂平面EBC ,所以平面EBC ⊥平面PAC .(Ⅲ)在平面PAD 内作AF PD ⊥于点F ,由DC PA ⊥,DC AD ⊥,PA AD A ⋂=,得DC ⊥平面PAD .因为AF ⊂平面PAD ,所以CD AF ⊥.又PD CD D ⋂=,所以AF ⊥平面PCD . 由PA 3=,AD 1=,PA AD ⊥,得3PF 2=. 22.已知三棱柱ABC A B C '''-的底面ABC 是等边三角形,侧面AA C C ''⊥底面ABC ,D 是棱BB '的中点.(1)求证:平面DA C '⊥平面ACC A '';(2)求平面DA C '将该三棱柱分成上下两部分的体积比.【答案】(1)见证明;(2)1:1【解析】(1)取,AC A C ''的中点,O F ,连接OF 与C A '交于点E ,连接DE ,,OB B F ',则E 为OF 的中点,OF AA BB ''P P , 且OF AA BB ''==,所以BB FO '是平行四边形.又D 是棱BB '的中点,所以DE OB P .侧面AA C C ''⊥底面ABC ,且OB AC ⊥ ,所以OB ⊥平面ACC A '' . 所以DE ⊥平面ACC A '',又DE Ì平面DA C ',所以平面DA C '⊥平面ACC A ''.(2)连接A B ', 设三棱柱ABC A B C '''-的体积为V .故四棱锥A BCC B -'''的体积1233A BCCB V V V V '''-=-= 又D 是棱BB '的中点,BCD ∆的面积是BCC B ''面积的14 , 故四棱锥A B C CD '''-的体积33214432A B C CD A BCC B V V V V ''''''--==⨯= 故平面DA C '将该三棱柱分成上下两部分的体积比为11.。
十年高考真题分类汇编(2010-2019) 数学 专题18 坐标系与参数方程 无答案原卷版

十年高考真题分类汇编(2010—2019)数学专题18坐标系与参数方程1.(2018·北京·理T10)在极坐标系中,直线ρcos θ+ρsin θ=a(a>0)与圆ρ=2cos θ相切,则a=___________.2.(2019·全国1·理T22文T22)在直角坐标系xOy中,曲线C的参数方程为 (t为参数).以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为2ρcos θ+ρsin θ+11=0.(1)求C和l的直角坐标方程;(2)求C上的点到l距离的最小值.3.(2019·全国2·理T22文T22)[选修4—4:坐标系与参数方程]在极坐标系中,O为极点,点M(ρ0,θ0)(ρ0>0)在曲线C:ρ=4sin θ上,直线l过点A(4,0)且与OM垂直,垂足为P.(1)当θ0=时,求ρ0及l的极坐标方程;(2)当M在C上运动且P在线段OM上时,求P点轨迹的极坐标方程.4.(2019·全国3·理T22文T22)[选修4—4:坐标系与参数方程]如图,在极坐标系Ox中,A(2,0),B,C,D(2,π),弧所在圆的圆心分别是(1,0),,(1,π),曲线M1是弧,曲线M2是弧,曲线M3是弧.(1)分别写出M1,M2,M3的极坐标方程;(2)曲线M由M1,M2,M3构成,若点P在M上,且|OP|=5.(2018·全国1·文T理22)[选修4—4:坐标系与参数方程]在直角坐标系xOy中,曲线C1的方程为y=k|x|+2.以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ2+2ρcos θ-3=0.(1)求C2的直角坐标方程;(2)若C1与C2有且仅有三个公共点,求C1的方程.6.(2018·全国2·理T22文T22)[选修4—4:坐标系与参数方程]在直角坐标系xOy中,曲线C的参数方程为(θ为参数),直线l的参数方程为(t 为参数).(1)求C和l的直角坐标方程;(2)若曲线C截直线l所得线段的中点坐标为(1,2),求l的斜率.7.(2018·全国3·文T理22)[选修4—4:坐标系与参数方程]在平面直角坐标系xOy中,☉O的参数方程为(θ为参数),过点(0,-)且倾斜角为α的直线l与☉O交于A,B两点.(1)求α的取值范围;(2)求AB中点P的轨迹的参数方程.8.(2017·全国1·理T22文T22)[选修4—4:坐标系与参数方程]在直角坐标系xOy中,曲线C的参数方程为(θ为参数),直线l的参数方程为(t为参数).(1)若a=-1,求C与l的交点坐标;(2)若C上的点到l距离的最大值为,求a.9.(2017·全国2·理T22文T22)[选修4—4:坐标系与参数方程]在直角坐标系xOy中,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C1的极坐标方程为ρcos θ=4.(1)M为曲线C1上的动点,点P在线段OM上,且满足|OM|·|OP|=16,求点P的轨迹C2的直角坐标方程;(2)设点A的极坐标为,点B在曲线C2上,求△OAB面积的最大值.10.(2017·全国3·理T22文T22)[选修4—4:坐标系与参数方程]在直角坐标系xOy中,直线l1的参数方程为(t为参数),直线l2的参数方程为(m为参数).设l1与l2的交点为P,当k变化时,P的轨迹为曲线C.(1)写出C的普通方程;(2)以坐标原点为极点,x轴正半轴为极轴建立极坐标系,设l3:ρ(cos θ+sin θ)- =0,M为l3与C的交点,求M的极径.11.(2017·江苏·T21)在平面直角坐标系xOy中,已知直线l的参数方程为(t为参数),曲线C的参数方程为(s为参数).设P为曲线C上的动点,求点P到直线l的距离的最小值.12.(2016·全国1·理T23文T23)在直角坐标系xOy中,曲线C1的参数方程为 (t为参数,a>0).在以坐标原点为极点,x轴正半轴为极轴的极坐标系中,曲线C2:ρ=4cos θ.(1)说明C1是哪一种曲线,并将C1的方程化为极坐标方程;(2)直线C3的极坐标方程为θ=α0,其中α0满足tan α0=2,若曲线C1与C2的公共点都在C3上,求a.13.(2016·全国2·理T23文T23)在直角坐标系xOy中,圆C的方程为(x+6)2+y2=25.(1)以坐标原点为极点,x轴正半轴为极轴建立极坐标系,求C的极坐标方程;(2)直线l的参数方程是(t为参数),l与C交于A,B两点,|AB|=,求l的斜率.14.(2016·全国3·理T23文T23)在直角坐标系xOy中,曲线C1的参数方程为(α为参数).以坐标原点为极点,以x轴的正半轴为极轴,建立极坐标系,曲线C2的极坐标方程为ρsin=2.(1)写出C1的普通方程和C2的直角坐标方程;(2)设点P在C1上,点Q在C2上,求|PQ|的最小值及此时P的直角坐标.15.(2015·全国1·理T23文T23)在直角坐标系xOy中,直线C1:x=-2,圆C2:(x-1)2+(y-2)2=1,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系.(1)求C1,C2的极坐标方程;(2)若直线C3的极坐标方程为θ=(ρ∈R),设C2与C3的交点为M,N,求△C2MN的面积.16.(2015·全国2·理T23文T23)在直角坐标系xOy中,曲线C1:(t为参数,t≠0),其中0≤α<π.在以O为极点,x轴正半轴为极轴的极坐标系中,曲线C2:ρ=2sin θ,C3:ρ=2cos θ.(1)求C2与C3交点的直角坐标;(2)若C1与C2相交于点A,C1与C3相交于点B,求|AB|的最大值.17.(2015·陕西·理T23文T23)在直角坐标系xOy中,直线l的参数方程为(t为参数),以原点为极点,x轴正半轴为极轴建立极坐标系,☉C的极坐标方程为ρ=2sin θ.(1)写出☉C的直角坐标方程;(2)P为直线l上一动点,当P到圆心C的距离最小时,求P的直角坐标.18.(2015·湖南·理T16文T16)已知直线l:(t为参数).以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρ=2cos θ.(1)将曲线C的极坐标方程化为直角坐标方程;(2)设点M的直角坐标为(5, ),直线l与曲线C的交点为A,B,求|MA|·|MB|的值.19.(2014·全国1·理T23文T23)已知曲线C:=1,直线l:(t为参数).(1)写出曲线C的参数方程,直线l的普通方程;(2)过曲线C上任意一点P作与l夹角为30°的直线,交l于点A,求|PA|的最大值与最小值.20.(2014·全国2·理T23文T23)在直角坐标系xOy中,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,半圆C的极坐标方程为ρ=2cos θ,θ∈.(1)求C的参数方程;(2)设点D在C上,C在D处的切线与直线l:y=x+2垂直,根据(1)中你得到的参数方程,确定D的坐标.21.(2013·全国2·理T23文T23)已知动点P,Q都在曲线 C:(t为参数)上,对应参数分别为t=α与t=2α(0<α<2π),M为PQ的中点.(1)求M的轨迹的参数方程;(2)将M到坐标原点的距离d表示为α的函数,并判断M的轨迹是否过坐标原点.22.(2013·全国1·理T23文T23)已知曲线C1的参数方程为(t为参数),以坐标原点为极点,x 轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=2sin θ.(1)把C1的参数方程化为极坐标方程;(2)求C1与C2交点的极坐标(ρ≥0,0≤θ<2π).23.(2013·江苏·T21)在平面直角坐标系xOy中,直线l的参数方程为(t为参数),曲线C的参数方程为(θ为参数).试求直线l和曲线C的普通方程,并求出它们的公共点的坐标.24.(2012·全国·理T23文T23)已知曲线C1的参数方程是(φ为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程是ρ=2.正方形ABCD的顶点都在C2上,且A,B,C,D依逆时针次序排列,点A的极坐标为.(1)求点A,B,C,D的直角坐标;(2)设P为C1上任意一点,求|PA|2+|PB|2+|PC|2+|PD|2的取值范围.25.(2011·全国·理T23文T23)在直角坐标系xOy中,曲线C1的参数方程为(α为参数).M是C1上的动点,P点满足=2,P点的轨迹为曲线C2.(1)求C2的方程;(2)在以O为极点,x轴的正半轴为极轴的极坐标系中,射线θ=与C1的异于极点的交点为A,与C2的异于极点的交点为B,求|AB|.26.(2010·全国·理T23文T23)已知直线C1:(t为参数),圆C2:(θ为参数).(1)当α=时,求C1与C2的交点坐标;(2)过坐标原点O作C1的垂线,垂足为A,P为OA的中点.当α变化时,求P点轨迹的参数方程,并指出它是什么曲线.。
十年真题(2010-2019)高考数学(文)分类汇编专题10 平面解析几何选择填空题(新课标Ⅰ卷)(解析版)

领军高考十年真题(2010-2019)数学学科深度思考(新课标1卷文科版)专题10平面解析几何选择填空题历年考题细目表8填空题2016 圆的方程2016年新课标1文科15填空题2015 双曲线2015年新课标1文科16填空题2010 圆的方程2010年新课标1文科13解答题2019 双曲线2019年新课标1文科21历年高考真题汇编1.【2019年新课标1文科10】双曲线C:1(a>0,b>0)的一条渐近线的倾斜角为130°,则C的离心率为()A.2sin40°B.2cos40°C.D.【解答】解:双曲线C:1(a>0,b>0)的渐近线方程为y,由双曲线的一条渐近线的倾斜角为130°,得,则,∴,得,∴e.故选:D.2.【2019年新课标1文科12】已知椭圆C的焦点为F1(﹣1,0),F2(1,0),过F2的直线与C交于A,B两点.若|AF2|=2|F2B|,|AB|=|BF1|,则C的方程为()A.y2=1 B. 1C. 1 D. 1【解答】解:∵|AF2|=2|BF2|,∴|AB|=3|BF2|,又|AB|=|BF1|,∴|BF1|=3|BF2|,又|BF1|+|BF2|=2a,∴|BF2|,∴|AF2|=a,|BF1|a,在Rt△AF2O中,cos∠AF2O,在△BF1F2中,由余弦定理可得cos∠BF2F1,根据cos∠AF2O+cos∠BF2F1=0,可得0,解得a2=3,∴a.b2=a2﹣c2=3﹣1=2.所以椭圆C的方程为:1.故选:B.3.【2018年新课标1文科04】已知椭圆C:1的一个焦点为(2,0),则C的离心率为()A.B.C.D.【解答】解:椭圆C:1的一个焦点为(2,0),可得a2﹣4=4,解得a=2,∵c=2,∴e.故选:C.4.【2017年新课标1文科05】已知F是双曲线C:21的右焦点,P是C上一点,且PF与轴垂直,点A的坐标是(1,3),则△APF的面积为()A.B.C.D.【解答】解:由双曲线C:21的右焦点F(2,0),PF与轴垂直,设(2,y),y>0,则y=3,则P(2,3),∴AP⊥PF,则丨AP丨=1,丨PF丨=3,∴△APF的面积S丨AP丨×丨PF丨,同理当y<0时,则△APF的面积S,故选:D.5.【2017年新课标1文科12】设A,B是椭圆C:1长轴的两个端点,若C上存在点M满足∠AMB=120°,则m的取值范围是()A.(0,1]∪[9,+∞)B.(0,]∪[9,+∞)C.(0,1]∪[4,+∞)D.(0,]∪[4,+∞)【解答】解:假设椭圆的焦点在轴上,则0<m<3时,设椭圆的方程为:(a>b>0),设A(﹣a,0),B(a,0),M(,y),y>0,则a2﹣2,∠MAB=α,∠MBA=β,∠AMB=γ,tanα,tanβ,则tanγ=tan[π﹣(α+β)]=﹣tan(α+β),∴tanγ,当y最大时,即y=b时,∠AMB取最大值,∴M位于短轴的端点时,∠AMB取最大值,要使椭圆C上存在点M满足∠AMB=120°,∠AMB≥120°,∠AMO≥60°,tan∠AMO tan60°,解得:0<m≤1;当椭圆的焦点在y轴上时,m>3,当M位于短轴的端点时,∠AMB取最大值,要使椭圆C上存在点M满足∠AMB=120°,∠AMB≥120°,∠AMO≥60°,tan∠AMO tan60°,解得:m≥9,∴m的取值范围是(0,1]∪[9,+∞)故选A.故选:A.6.【2016年新课标1文科05】直线l经过椭圆的一个顶点和一个焦点,若椭圆中心到l的距离为其短轴长的,则该椭圆的离心率为()A.B.C.D.【解答】解:设椭圆的方程为:,直线l经过椭圆的一个顶点和一个焦点,则直线方程为:,椭圆中心到l的距离为其短轴长的,可得:,4=b2(),∴,3,∴e.故选:B.7.【2015年新课标1文科05】已知椭圆E的中心在坐标原点,离心率为,E的右焦点与抛物线C:y2=8的焦点重合,A,B是C的准线与E的两个交点,则|AB|=()A.3 B.6 C.9 D.12【解答】解:椭圆E的中心在坐标原点,离心率为,E的右焦点(c,0)与抛物线C:y2=8的焦点(2,0)重合,可得c=2,a=4,b2=12,椭圆的标准方程为:,抛物线的准线方程为:=﹣2,由,解得y=±3,所以A(﹣2,3),B(﹣2,﹣3).|AB|=6.故选:B.8.【2014年新课标1文科04】已知双曲线1(a>0)的离心率为2,则实数a=()A.2 B.C.D.1【解答】解:由题意,e2,解得,a=1.故选:D.9.【2014年新课标1文科10】已知抛物线C:y2=的焦点为F,A(0,y0)是C上一点,AF=|0|,则0=()A.1 B.2 C.4 D.8【解答】解:抛物线C:y2=的焦点为F,∵A(0,y0)是C上一点,AF=|0|,0>0.∴0,解得0=1.故选:A.10.【2013年新课标1文科04】已知双曲线C:(a>0,b>0)的离心率为,则C的渐近线方程为()A.y B.y C.y=±D.y【解答】解:由双曲线C:(a>0,b>0),则离心率e,即4b2=a2,故渐近线方程为y=±,故选:D.11.【2013年新课标1文科08】O为坐标原点,F为抛物线C:y2=4的焦点,P为C上一点,若|PF|=4,则△POF的面积为()A.2 B.2C.2D.4【解答】解:∵抛物线C的方程为y2=4∴2p=4,可得,得焦点F()设P(m,n)根据抛物线的定义,得|PF|=m4,即m4,解得m=3∵点P在抛物线C上,得n2=4324∴n∵|OF|∴△POF的面积为S|OF|×|n|2故选:C.12.【2012年新课标1文科04】设F1、F2是椭圆E:1(a>b>0)的左、右焦点,P为直线上一点,△F2PF1是底角为30°的等腰三角形,则E的离心率为()A.B.C.D.【解答】解:∵△F2PF1是底角为30°的等腰三角形,∴|PF2|=|F2F1|∵P为直线上一点∴∴故选:C.13.【2012年新课标1文科10】等轴双曲线C的中心在原点,焦点在轴上,C与抛物线y2=16的准线交于点A和点B,|AB|=4,则C的实轴长为()A.B.C.4 D.8【解答】解:设等轴双曲线C:2﹣y2=a2(a>0),y2=16的准线l:=﹣4,∵C与抛物线y2=16的准线l:=﹣4交于A,B两点,∴A(﹣4,2),B(﹣4,﹣2),将A点坐标代入双曲线方程得4,∴a=2,2a=4.故选:C.14.【2011年新课标1文科09】已知直线l过抛物线C的焦点,且与C的对称轴垂直.l与C交于A,B两点,|AB|=12,P为C的准线上一点,则△ABP的面积为()A.18 B.24 C.36 D.48【解答】解:设抛物线的解析式为y2=2p(p>0),则焦点为F(,0),对称轴为轴,准线为∵直线l经过抛物线的焦点,A、B是l与C的交点,又∵AB⊥轴∴|AB|=2p=12∴p=6又∵点P在准线上∴DP=(||)=p=6∴S△ABP(DP•AB)6×12=36故选:C.15.【2011年新课标1文科04】椭圆1的离心率为()A.B.C.D.【解答】解:根据椭圆的方程1,可得a=4,b=2,则c2;则椭圆的离心率为e,故选:D.16.【2010年新课标1文科05】中心在原点,焦点在轴上的双曲线的一条渐近线经过点(4,2),则它的离心率为()A.B.C.D.【解答】解:∵渐近线的方程是y=±,∴2•4,,a=2b,c a,e,即它的离心率为.故选:D.17.【2018年新课标1文科15】直线y=+1与圆2+y2+2y﹣3=0交于A,B两点,则|AB|=.【解答】解:圆2+y2+2y﹣3=0的圆心(0,﹣1),半径为:2,圆心到直线的距离为:,所以|AB|=22.故答案为:2.18.【2016年新课标1文科15】设直线y=+2a与圆C:2+y2﹣2ay﹣2=0相交于A,B两点,若|AB|=2,则圆C的面积为.【解答】解:圆C:2+y2﹣2ay﹣2=0的圆心坐标为(0,a),半径为,∵直线y=+2a与圆C:2+y2﹣2ay﹣2=0相交于A,B两点,且|AB|=2,∴圆心(0,a)到直线y=+2a的距离d,即3=a2+2,解得:a2=2,故圆的半径r=2.故圆的面积S=4π,故答案为:4π19.【2015年新课标1文科16】已知F是双曲线C:21的右焦点,P是C的左支上一点,A(0,6).当△APF周长最小时,该三角形的面积为.【解答】解:由题意,设F′是左焦点,则△APF周长=|AF|+|AP|+|PF|=|AF|+|AP|+|PF′|+2≥|AF|+|AF′|+2(A,P,F′三点共线时,取等号),直线AF′的方程为与21联立可得y2+6y﹣96=0,∴P的纵坐标为2,∴△APF周长最小时,该三角形的面积为12.故答案为:12.20.【2010年新课标1文科13】圆心在原点上与直线+y﹣2=0相切的圆的方程为.【解答】解:圆心到直线的距离:r,所求圆的方程为2+y2=2.故答案为:2+y2=221.【2019年新课标1文科21】已知点A,B关于坐标原点O对称,|AB|=4,⊙M过点A,B且与直线+2=0相切.(1)若A在直线+y=0上,求⊙M的半径;(2)是否存在定点P,使得当A运动时,|MA|﹣|MP|为定值?并说明理由.【解答】解:∵⊙M故点A,B且A在直线+y=0上,∴点M在线段AB的中垂线﹣y=0上,设⊙M的方程为:(﹣a)2+(y﹣a)2=R2(R>0),则圆心M(a,a)到直线+y=0的距离d,又|AB|=4,∴在Rt△OMB中,d2+(|AB|)2=R2,即①又∵⊙M与=﹣2相切,∴|a+2|=R②由①②解得或,∴⊙M的半径为2或6;(2)∵线段为⊙M的一条弦,∴圆心M在线段AB的中垂线上,设点M的坐标为(,y),则|OM|2+|OA|2=|MA|2,∵⊙M与直线+2=0相切,∴|MA|=|+2|,∴|+2|2=|OM|2+|OA|2=2+y2+4,∴y2=4,∴M的轨迹是以F(1,0)为焦点=﹣1为准线的抛物线,∴|MA|﹣|MP|=|+2|﹣|MP|=|+1|﹣|MP|+1=|MF|﹣|MP|+1,∴当|MA|﹣|MP|为定值时,则点P与点F重合,即P的坐标为(1,0),∴存在定点P(1,0)使得当A运动时,|MA|﹣|MP|为定值.考题分析与复习建议本专题考查的知识点为:直线方程、圆的方程,直线与圆、圆与圆的位置关系,椭圆、双曲线、抛物线及其性质,直线与圆锥曲线,曲线与方程等.历年考题主要以选择填空题型出现,重点考查的知识点为:直线与圆、圆与圆的位置关系,椭圆、双曲线、抛物线及其性质,直线与圆锥曲线等,预测明年本考点题目会比较稳定,备考方向以知识点直线与圆、圆与圆的位置关系,椭圆、双曲线、抛物线及其性质,直线与圆锥曲线等为重点较佳.最新高考模拟试题1.已知双曲线22221(0,0)x y a b a b-=>>的右焦点为F ,直线l 经过点F 且与双曲线的一条渐近线垂直,直线l 与双曲线的右支交于不同两点A ,B ,若3AF FB =u u u r u u u r ,则该双曲线的离心率为( )ABCD【答案】A【解析】由题意得直线l 的方程为b x y c a =+,不妨取1a =,则x by c =+,且221b c =-. 将x by c =+代入2221y x b -=,得()4234120b y b cy b -++=. 设()11,A x y ,()22,B x y ,则312421b c y y b +=--,41241b y y b =-. 由3AF FB u u u r u u u r =,得123y y =-,所以324422422131bc y b by b ⎧-=-⎪⎪-⎨⎪-=⎪-⎩,得22431b c b =-,解得214b =,所以c ===2c e a ==,故选A 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
APB=90°,则 m 的最大值为( )
A.7
B.6
C.5
D.4
16.(2014·四川·文 T9)设 m∈R,过定点 A 的动直线 x+my=0 和过定点 B 的动直线 mx-y-m+3=0 交于点 P(x,y),
则|PA|+|PB|的取值范围是( ) A.[√5,2√5] B.[√10,2√5] C.[√10,4√5] D.[2√5,4√5]
ABP 面积的取值范围是( )
A.[2,6]
B.[4,8]
C.[√2,3√2] D.[2√2,3√2]
4.(2016·山东·文
T7)已知圆
22
M:x +y -2ay=0(a>0)截直线
x+y=0
所得线段的长度是
2√2.则圆
M
与圆
2
2
N:(x-1) +(y-1) =1 的位置关系是( )
A.内切
B.相交 C.外切
2
2
2
2
2
17.(2013·重庆·理 T7)已知圆 C1:(x-2) +(y-3) =1,圆 C2:(x-3) +(y-4) =9,M,N 分别是圆 C1,C2 上的动点,P
为 x 轴上的动点,则|PM|+|PN|的最小值为( )
A.5√2-4
B.√17-1
C.6-2√2
D.√17
18.(2013·湖南·理 T8)在等腰直角三角形 ABC 中,AB=AC=4,点 P 为边 AB 上异于 A,B 的一点,光线从点 P 出
2
2
B.(x+1) +(y+1) =1
2
2
C.(x+1) +(y+1) =2
2
2
D.(x-1) +(y-1) =2
22
9.(2015·广东·理 T5)平行于直线 2x+y+1=0 且与圆 x +y =5 相切的直线的方程是( )
1
A.2x+y+5=0 或 2x+y-5=0 B.2x+y+√5=0 或 2x+y-√5=0
十年(2010—2019)数学高考真题分类汇编
直线与圆
一、选择题
2
2
1.(2019·全国 2·理 T11 文 T12)设 F 为双曲线 C: 2 − 2=1(a>0,b>0)的右焦点,O 为坐标原点,以 OF 为直径
222
的圆与圆 x +y =a 交于 P,Q 两点.若|PQ|=|OF|,则 C 的离心率为( )
()
A.[-1,1] C.[-√2, √2]
11
B. - 2 , 2
√2 √2
D. - 2 , 2
22
13.(2014·浙江·文 T5)已知圆 x +y +2x-2y+a=0 截直线 x+y+2=0 所得弦的长度为 4,则实数 a 的值是( )
A.-2 B.-4 C.-6 D.-8
14.(2014·安徽·文
距离的最小值是 .
=2+2 2.(2019·天津·理 T12)设 a∈R,直线 ax-y+2=0 和圆 = 1 + 2
,! (θ 为参数)相切,则 a 的值为____.
3.(2019·浙江·T12)已知圆 C 的圆心坐标是(0,m),半径长是 r.若直线 2x-y+3=0 与圆 C 相切于点 A(-2,-1),
C.2x-y+5=0 或 2x-y-5=0
D.2x-y+√5=0 或 2x-y-√5=0
2
2
10.(2015·山东·理 T9)一条光线从点(-2,-3)射出,经 y 轴反射后与圆(x+3) +(y-2) =1 相切,则反射光线所
在直线的斜率为( )
53
A.-3或-5
32
B.-2或-3
54
C.-4或-5
D.相离
22
5.(2016·全国 2·理 T4 文 T6)圆 x +y -2x-8y+13=0 的圆心到直线 ax+y-1=0 的距离为 1,则 a=( )
4
A.-3
3
B.-4
C.√3
D.2
6.(2015·全国 2·理 T7)过三点 A(1,3),B(4,2),C(1,-7)的圆交 y 轴于 M,N 两点,则|MN|=( )
43
D.-3或-4
22
11.(2015·重庆·理 T8)已知直线 l:x+ay-1=0(a∈R)是圆 C:x +y -4x-2y+1=0 的对称轴.过点 A(-4,a)作圆 C
的一条切线,切点为 B,则|AB|=( )
A.2
B.4√2
C.6
D.2√10
22
12.(2014·全国 2·文 T12)设点 M(x0,1),若在圆 O:x +y =1 上存在点 N,使得∠OMN=45°,则 x0 的取值范围是
A.√2
B.√3
C.2
D.√5
2.(2018·北京·理 T7)在平面直角坐标系中,记 d 为点 P(cos θ,sin θ)到直线 x-my-2=0 的距离.当 θ,m
变化时,d 的最大值为( )
A.1 B.2 C.3 D.4
22
3.(2018·全国 3·理 T6 文 T8)直线 x+y+2=0 分别与 x 轴、y 轴交于 A,B 两点,点 P 在圆(x-2) +y =2 上,则△
A.2√6
B.8
C.4√6 D.10
7.(2015·全国 2·文 T7)已知三点 A(1,0),B(0,√3),C(2,√3),则△ABC 外接圆的圆心到原点的距离为( )
5
√21
2√5
4
A.3
B. 3
C. 3
D.3
8.(2015·北京·文 T2)圆心为(1,1)且过原点的圆的方程是( )
2
2
A.(x-1) +(y-1) =1
T6)过点
P(-√3,-1)的直线
l
与圆
22
x +y =1
有公共点,则直线
l
的倾斜角的取值范围是
()
A. 0, 6
B. 0, 3
C. 0, 6
D. 0, 3
2
2
15.(2014·北京·文 T7)已知圆 C:(x-3) +(y-4) =1 和两点 A(-m,0),B(m,0)(m>0).若圆 C 上存在点 P,使得∠
发,经 BC,CA 反射后又回到点 P.若光线 QR 经过△ABC 的重心,则 AP 等于( )
8
4
A.2
B.1
C.3
D.3
19.(2012·浙江·理 T3)设 a∈R,则“a=1”是“直线 l1:ax+2y-1=0 与直线 l2:x+(a+1)y+4=0 平行”的( )
A.充分不必要条件
B.必要不充分条件
C.充分必要条件
D.既不充分也不必要条件
20.(2010·安徽·文 T4)过点(1,0)且与直线 x-2y-2=0 平行的直线方程是( )
A.x-2y-1=0 B.x-2y+1=0
C.2x+y-2=0 D.x+2y-1=0
二、填空题
4
1.(2019·江苏·T10)在平面直角坐标系 xOy 中,P 是曲线 y=x+x(x>0)上的一个动点,则点 P 到直线 x+y=0 的
