共边定理和共角定理
共边共角相似三角形在圆中的应用

共边共角相似三角形在圆中的应用一、基本概念:1.定义:如图,△ABC与△ACD有一条公共边AC和一个公共角∠ A,这样的两个三角形叫做共边共角三角形.这样的两个三角形若又有一个角对应相等,则两个三角形相似,那么这样的两个三角形称为共边共角相似三角形.2.性质定理:共边共角的两个相似三角形的公共边是夹公共角的另一条对应边的比例中项.如图1,在△ABC中,∠ACD=∠B,则△ACD∽△ABC,那么可得:AC2= AD·AB .特别地,当△ABC是直角三角形,且CD⊥AB时(如图2),AC2 =AD·AB,即为射影定理.二、应用举例:例1.如图3,P为⊙O外一点,PA、PB分别切⊙O于A、B 两点,OP与AB相交于M,C是上一点. 求证:∠OPC=∠OCM .分析:若∠OPC=∠OCM,又∠O=∠O,所以必有△OCM∽△OPC,显然,这一结论只有通过“两边对应成比例,夹角相等”来实现.为此,应当设法证明= ,即OC2= OM·OP.这由OA2= OM·OP, OA= OP 即得.评析:图中△OCM与△OPC 为共边共角相似三角形.例2. 已知⊙C的半径为R,⊙O 过点C,且与⊙C相交于A、B 两点. D为⊙O上一点,弦AB、CD 相交于点E. 求证:CE·CD为定值分析:如图4,由于CE是线段CD的一部分,可构造以C为公共顶点的共边共角三角形.由于⊙C的半径已知为R,所以,只要能与R建立联系,即可得证. 为此,连结AC、AD 由∠ACE是公共角,及∠CAE =∠D,即得△ACE ∽△DCA,从而,CE·CD = R2为定值.评析:图中,△ACE与△D CA 是共边共角相似三角形.例3. 在圆内接四边形ABCD中,BC= CD= 4cm, AC交BD于E,AE=6 cm, 设BE=xcm ,DE = ycm , x、y 均为整数,求x、y 的值解:如图5, 由相交弦定理: x·y = AE·CE = 6CE ,图5故要求x、y的值,必须先求CE的长. 注意到∠3 =∠1,联想到△CBE与△CAB是共边共角的相似三角形,可得:BC2 = CE·CA∴ 42= CE·(CE + 6),可得CE=2 或CE=-8(舍去),从而,x·y = 6×2 =12 ,∴x=3, y =4 或x=4, y=3 .评析:△CBE与△CAB是共边共角相似三角形例4.已知AC、AB是⊙O 的弦, AB>AC.⑴如图6, 能否在AB 上确定一点E,使AC2 = AE·AB, 为什么?⑵如图7, 在条件⑴的结论下延长EC到P, 连结PB.如果PB=PE, 试判断PB和⊙O 的位置关系, 并说明理由.⑶在条件⑵的情况下, 如果E 是PD的中点, 那么C是PE的中点吗?为什么?分析:⑴观察图6,联想共边共角相似三角形的特征,那么只要AB上的点满足:∠ACE=∠B即可.为此连结并延长CE交⊙O于点C ' (如图6),所以只要=.故,满足题目要求的点E是存在的.作法:在优弧上取=.连CC’ ,交AB于点E,即可. 且AC2 = AE·AB.这里,△ACE与△ACB是共边共角相似三角形⑵由⑴及PB =PE 可得∠3 =∠A,过B⊙O的直径,那么可证PB是⊙O的切线( 如图7);⑶连结BD,即可证明△PBC与△PBD是共边共角的相似三角形,那么PB2 = PC·PD,又PD=2PE, PE=PB, 可得C是PE的中点 .评析:⑴中,△ACE与△ACB是共边共角相似三角形;⑶中,△PBC与△PBD是共边共角相似三角形.参考习题1. 如图8,已知⊙O的内接四边形ABCD,D 是的中点,BC、AD的延长线相交于点E,DH切⊙O于D,交EB于点H.⑴求证:DH平分∠CDE;⑵在图中的已知线段中找出两条线段,使它们的积等于DE2,并加以证明.2.已知如图9,在△ABC中, AB=AC, 过点A(图8)的直线与△ABC的外接圆O交于D, 与BC 的延长线交于点F, DE是BD的延长线,连接CD.求证: ⑴ DF平分∠EDC; ⑵ AB2=AD·AF;⑶ AF2-AB2=AF·DF.3.如图10,PA切⊙O于A ,割线PBC交⊙O于B、C两点,D为PC的中点, AD的延长线交⊙O 于E,又BE2 =DE·AE,求证:⑴PA =PD; ⑵ 2PB2 = AD ·DE [ 提示: 由切割线定理证PA =2PB ,∴ B是PD的中点]4.如图11,ΔABC内接于⊙O,AB = AC,直线XY切⊙O于点C,弦BD∥XY,AC、BD相交于点E,(1)求证:ΔABE≌ΔACD;(2)若AB = 6cm,BC = 4 cm,求AE的长.5 .如图12,PA为⊙O的切线,从PA的中点B做割线BCD,交圆于点C、D,连结PC、PD 分别交圆于点E、F. 求证:∠APD = ∠EFD.6.已知如图13,A 是⊙O上一点,割线PC交⊙O于B、C两点,PD是PB和PC 的比例中项,PA=PD,连结AD并延长交⊙O于E,求证:BE= CE.(图9)(图10)(图11)(图12)(图13)。
共边定理

SoPAB QM
A~
D
B
图2
、、、Q / 户、 :、
B _ 刀E_ _ 一 _ _ 图 伟,
、
一、 材
学 过 相 似 三角 形 的读 者很 快 就会 发
现 △PDM- △口EM , 因而有_PQDE_PQM那
汉 、、、Q ﹄ 、、1
么,没有学过相似三角形的读者能否明白 J之二 里
F G S AAGQ 2
EF=(1 土BG FG=主 BG
3
I1
2 祷‘二61 BG.BE:
11 /
33
E F F G = 1 1: 16 :6 .
例 5 如 图 10 ,过 △ABC 的顶点 B 的两条直 线 BG ,BH 与 BC 边 上 的 中 线 AD 交 于 E ,F ,且
6
F\ G
图9
夕 F
f3y+4=x 2. 设绳子有二尺 ,环绕大树一周需要Y尺,则有方程组
,
l4y - 3 =x .
习题 7.5
1. 设租住三人 间x间 ,两人间Y间 ,则有方程组 3x+2y=50 ,
25xx3+35yx 2= 15 10 .
2. 设甲、乙的速度分别为二m/ s ,y m/ s,则有方程组 30(x+y )=400 ,
不 改 ,照搬 就 可 以 了.
证明 : 在直线 AB 上取一点 N ,使得 MN=AB ,则 △PMN 与 △口MN 共
高(分别以 PM,QM 为底 ) ,则有 S OPAR
P 1l 夕
S }QAB
QM
从本质上讲 ,共边定理是 “等底等高的三角形
面积相等 ”这一性 质 的推论 .它 的用途 相 当广泛 ,下
初中平面几何四个重要定理

初中平⾯⼏何四个重要定理初中数学知识重点整理-平⾯⼏何四个重要定理四个重要定理:梅涅劳斯(Menelaus)定理(梅⽒线)△ABC的三边BC、CA、AB或其延长线上有点P、Q、R,则P、Q、R共线的充要条件是。
塞⽡(Ceva)定理(塞⽡点)△ABC的三边BC、CA、AB上有点P、Q、R,则AP、BQ、CR共点的充要条件是。
托勒密(Ptolemy)定理四边形的两对边乘积之和等于其对⾓线乘积的充要条件是该四边形内接于⼀圆。
西姆松(Simson)定理(西姆松线)从⼀点向三⾓形的三边所引垂线的垂⾜共线的充要条件是该点落在三⾓形的外接圆上。
例题:1.设AD是△ABC的边BC上的中线,直线CF交AD于F。
求证:。
【分析】CEF截△ABD→(梅⽒定理)【评注】也可以添加辅助线证明:过A、B、D之⼀作CF的平⾏线。
2.过△ABC的重⼼G的直线分别交AB、AC于E、F,交CB于D。
求证:。
【分析】连结并延长AG交BC于M,则M为BC的中点。
DEG截△ABM→(梅⽒定理)DGF截△ACM→(梅⽒定理)∴===1【评注】梅⽒定理3. D、E、F分别在△ABC的BC、CA、AB边上,,AD、BE、CF交成△LMN。
求S△LMN。
【分析】【评注】梅⽒定理4.以△ABC各边为底边向外作相似的等腰△BCE、△CAF、△ABG。
求证:AE、BF、CG相交于⼀点。
【分析】【评注】塞⽡定理5.已知△ABC中,∠B=2∠C。
求证:AC2=AB2+AB·BC。
【分析】过A作BC的平⾏线交△ABC的外接圆于D,连结BD。
则CD=DA=AB,AC=BD。
由托勒密定理,AC·BD=AD·BC+CD·AB。
【评注】托勒密定理6.已知正七边形A 1A2A3A4A5A6A7。
求证:。
(第21届全苏数学竞赛)【分析】【评注】托勒密定理7.△ABC的BC边上的⾼AD的延长线交外接圆于P,作PE⊥AB于E,延长ED交AC延长线于F。
高中数学平面几何拓展-数学竞赛知识
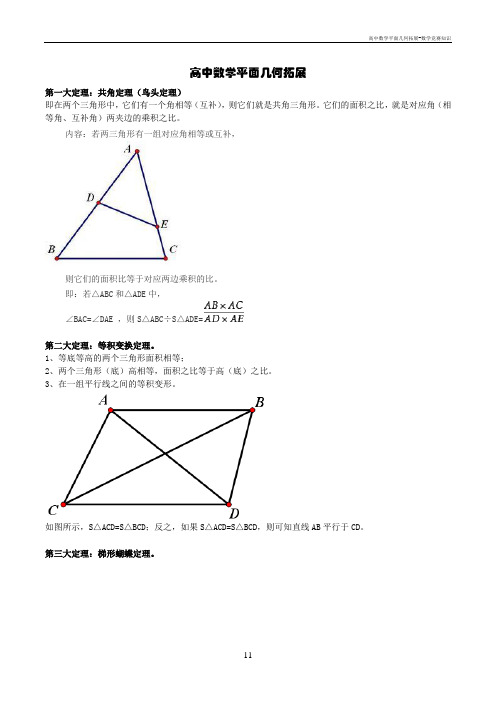
高中数学平面几何拓展第一大定理:共角定理(鸟头定理)即在两个三角形中,它们有一个角相等(互补),则它们就是共角三角形。
它们的面积之比,就是对应角(相等角、互补角)两夹边的乘积之比。
内容:若两三角形有一组对应角相等或互补,则它们的面积比等于对应两边乘积的比。
即:若△ABC和△ADE中,∠BAC=∠DAE ,则S△ABC÷S△ADE=第二大定理:等积变换定理。
1、等底等高的两个三角形面积相等;2、两个三角形(底)高相等,面积之比等于高(底)之比。
3、在一组平行线之间的等积变形。
如图所示,S△ACD=S△BCD;反之,如果S△ACD=S△BCD,则可知直线AB平行于CD。
第三大定理:梯形蝴蝶定理。
任意四边形中,同样也有蝴蝶定理。
上述的梯形蝴蝶定理,就是因为AD‖EC得来的第四大定理:相似三角形定理。
1、相似三角形:形状相同,大小不相等的两个三角形相似;2、寻找相似模型的大前提是平行线:平行于三角形一边的直线和其他两边或两边延长线相交,所构成的三角形与原三角形相似。
3、相似三角形性质:1.相似三角形的一切对应线段(对应高、对应边)的比等于相似比;②相似三角形周长的比等于相似比;③相似三角形面积的比等于相似比的平方。
相似模型大致分为金字塔模型、沙漏模型这两大类,注意这两大类中都含有BC平行DE这样的一对平行线!图形:第五大定理:燕尾定理。
性质:△ABG:S△ACG=S△BGE:S△CGE=BE:CE△BGA:S△BGC=S△GAF:S△GCF=AF:CF△AGC:S△BGC=S△AGD:S△BGD=AD:BD这就是燕尾模型。
其他几何定理:塞瓦定理塞瓦定理是指在△ABC内任取一点O,延长AO、BO、CO分别交对边于D、E、F,则(BD/DC)×(CE/EA)×(AF/FB)=1。
梅涅劳斯定理当直线交三边所在直线于点时,使用梅涅劳斯定理可以进行直线形中线段长度比例的计算,其逆定理还可以用来解决三点共线、三线共点等问题的判定方法,是平面几何学以及射影几何学中的一项基本定理,具有重要的作用。
共角定理

共角定理
共角定理内容:若两三角形有一组对应角相等或互补,则它们的面积比等于对应两边乘积的比。
别称鸟头模型、鸟头定理
定理内容:若两三角形有一组对应角相等或互补,
则它们的面积比等于对应两边乘积的比。
即:若△ABC和△ADE中,
∠BAC=∠DAE ,则S△ABC÷S△ADE=
推导过程
方法一:证明:
由三角形面积公式S=×a×b×sinC可推导出S△ABC=1/2*AB*AC*sinA
S△ADE=1/2*AD*AE*sinA
∴S△ABC:S△ADE=AB×AC:AD×AE
证毕。
方法二:
看到面积可作垂直做铺垫。
如右图,
分别过B、D点作AC垂线DF、BG交AC于点F、G。
则DF∥BG。
∴∠ADF=∠ABG
∵S△ABC:S△ADE=AC×BG:AE×DF
∠ADF=∠ABG
∴AD:DF=AB:BG
∴AD:AB=DF:BG
∴S△ABC:S△ADE=AB×AC:AD×AE。
THANKS !!!
致力为企业和个人提供合同协议,策划案计划书,学习课件等等
打造全网一站式需求
欢迎您的下载,资料仅供参考。
小学奥数专题训练平面几何五种面积模型(等积_鸟头_蝶形_相似_共边)

另解:从整体上来看,四边形 EFGO 的面积 三角形 AFC 面积 三角
形 BFD 面积 白色部分的面积,而三角形 AFC 面积 三角形 BFD 面积为
长方形面积的一半,即60,白色部分的面积等于长方形面积减去阴
影部分的面积,即120 70 50 ,所以四边形的面积为 60 50 10 .
21 28
SADG
7
, , SAED 28 SADG
于是:
21 28
SADG
15 27
SCBF
65
;
7 28 SADG
12 27 SCBF
38
;
可得 SADG 40 .故三角形 ADG 的面积是40.
【例 6】 如图在 △ ABC 中, D, E 分别是 AB, AC 上的点,且 AD : AB 2 : 5 , AE : AC 4 : 7 , S△ ADE 16 平方厘米,求 △ ABC 的面积.
二等分,另一组对边三等分,分别与 P 点连接,求阴影部分面积.
A
D
A (P)
D
A
D
P
P
B
C
B
C
B
C
【解析】(法1)特殊点法.由于 P 是正方形内部任意一点,可采用特殊点 法,假设 P 点与 A 点重合,则阴影部分变为如上中图所示,图中的两
11
个阴影三角形的面积分别占正方形面积的 4 和 6 ,所以阴影部分的面
小学奥数平面几何五种模型(等积,鸟头,蝶形,相似,共边)
目标:熟练掌握五大面积模型等积,鸟头,蝶形,相似(含金字塔模型和
沙漏模型),共边(含燕尾模型和风筝模型), 掌握五大面积模型的各种
变形
知识点拨
一、等积模型 ①等底等高的两个三角形面积相等;
三角形共角定理
三角形共角定理三角形共角定理是指在一个三角形中,三个内角的和等于180度。
这个定理是几何学中的基本定理之一,它说明了三角形的内角之间存在着一种特定的关系,无论三角形的形状如何。
首先,我们来看一个有趣的观察:无论是正三角形、等腰三角形还是一般的任意三角形,它们的内角和都等于180度。
这种现象被称为三角形共角定理。
那么,为什么三角形的内角和恒等于180度呢?要解答这个问题,我们需要从几何学的基本概念出发。
首先,我们先来看一个简单的等腰三角形。
等腰三角形的两条边长度相等,两个相邻的内角也相等。
在等腰三角形中,我们可以通过绘制一条高线,将三角形分割成两个相等的直角三角形。
而直角三角形的内角和是180度,所以等腰三角形的内角和也等于180度。
接下来,我们来看一下正三角形。
正三角形的三个边长度相等,三个内角也相等。
我们可以利用等腰三角形的性质来证明正三角形的内角和等于180度。
我们可以将正三角形分割成三个等腰三角形,每个等腰三角形的内角和都是180度。
所以正三角形的内角和也等于180度。
那么,对于一般的任意三角形来说,我们能够得出什么结论呢?我们可以利用等腰三角形和正三角形的性质,来推导一般三角形的共角定理。
设任意三角形的三个内角分别为A、B、C,边长分别为a、b、c。
我们可以将任意三角形分割成两个三角形:一个由角A和边a构成,另一个由角B和角C以及边b、c构成。
根据等腰三角形的性质,我们可以得出这两个三角形中的等腰三角形,它们的内角和都是180度。
所以,我们可以得到以下等式:∠A + ∠BAC = 180度∠B + ∠BCA + ∠C = 180度将这两个等式相加,得到:∠A + ∠BAC + ∠B + ∠BCA + ∠C = 360度然后,我们再次利用等腰三角形的性质,将等腰三角形拆解成两个直角三角形。
直角三角形的内角和为180度,所以可以得到:∠BAC + ∠BCA = 180度将这个等式代入上面的等式中,得到:∠A + ∠B + ∠C = 180度从而证明了任意三角形的内角和等于180度。
25、 共角定理
华数知识点点击破
陈拓老师讲义
呢?一般有平行线出现的时候,有双垂直出现的时候,看下面几个相似三角形,都是上面几个模型的特殊 情况产生的. A A A B D B ADDB,AEEC DE / /BC E D C B E E C C D
AD AE DE DB EC BC
AB AE BE CD ED EC
1 36 . 62
F
A I 4 1 E 2 O 1 9 3 G1 C
D
B
2
H
【评注】如果两个三角形有两组角对应相等,那么这两个三角形就相似,面积的比等于相似比的平 方.相似三角形是共角三角形的特殊情况,因为共角只需一组角对应相等或互补,而相似需要两组角对应 相等. H D G
2)如图,四边形 ABCD 的面积是 36 平方厘米,点 E、F、G、H 分别在 AB、BC、 CD、DA 上,AE2EB,AH2HD,CG2GD,CF2FB.那么四边形 EFGH 的面积 E 是_________. 【分析】 “阴影面积有点难,咱就把它放一边.空白面积都求完,阴影面积自 B 出现. ”连结 BD,由 AE2EB,AH2HD,得到 EH//BD,△AEH 与△ABD 相似.同 理△CGF 与△CDB 相似,可以使用鸟头模型或相似.
5 5 7
1
F E
A 5 B I 1 J C 5 7 D
A
A
先求四个正方形的面积,它们的和为 12525272100. 1 再求四边形 ABCD 的面积.如图 2,连结 BD, S ABD 5 5 12.5 ,BD 52 52 50 ,又知 BC1, 2
1 CD7,则 BC 2 CD 2 12 72 50 BD 2 ,勾股定理逆运用,得到BCD90° ,所以 SBCD 1 7 3.5 , 2
共边比例定理
共边比例定理
(实用版)
目录
1.共边定理的概念
2.共边定理的证明
3.共边定理的应用
4.结论
正文
一、共边定理的概念
共边定理是指在两个相交线段组成的两个三角形中,如果这两个三角形有一个公共边,那么这两个三角形的面积之比等于这个公共边的长度与它到另一个公共顶点的距离之比。
这个定理在解决一些几何问题时非常有用,尤其是在求解一些比例问题时。
二、共边定理的证明
为了证明共边定理,我们可以将问题分为四种情况进行讨论:
1.当两个三角形的高相等时,两个三角形的面积之比就等于它们的底边长度之比。
2.当两个三角形的底边相等时,两个三角形的面积之比就等于它们的高之比。
3.当两个三角形的高和底边都不相等时,我们可以通过相似三角形的性质来证明两个三角形的面积之比等于它们的高和底边长度之比。
4.当两个三角形的高和底边都不相等,且它们的顶点也不在同一条直线上时,我们同样可以通过相似三角形的性质来证明两个三角形的面积之比等于它们的高和底边长度之比。
三、共边定理的应用
共边定理在实际应用中非常广泛,它可以用来求解一些比例问题,例如在求解三角形的面积比例时,我们可以通过共边定理来求解。
另外,共边定理还可以用来证明一些几何问题,例如证明两个三角形的面积之和等于另一个三角形的面积等。
四、结论
共边定理是几何学中的一个基本定理,它对于解决一些比例问题和几何问题非常有用。
共边三角形定理的证明及应用
共边三角形定理的证明及应用
共边三角形定理是一种广泛的几何定理,它可以提供重要的指导,以便快速准确地推断某些几何特性。
共边三角形定理可以用数学语言来描述:当三条直线相交时,任一直线上的两条内角的和等于另外一直线上的那一内角的度数。
这个定理的证明是将这一性质抽象成一种普遍类型的三角形:三角形ABC,其中AB和BC是它的共边(这也就是定理的名字提示:共边三角形定理)。
证明这个定理需要使用平行线定理:如果线段AB平行线段CD,则一边平行一边垂直的角相等。
可以证明:如果AB平行CD,那么∠A=∠C,∠ B=∠D。
这就意味着三角形ABC 和三角形ADC具有同样的三边,因此它们有相同的两个内角,例如∠A=∠C和
∠B=∠D,所以这可以用来证明共边三角形定理。
这个定理还有很多实用的应用,比如在工程设计中分析和计算不同几何形状的尺寸大小和形状。
在三角形上应用这个定理可以计算出未知边长,从而准确计算出每个角的度数。
这可以节省大量的时间和精力,使工程绘图获得更大的准确性。
另外,它还可以用来解决棘手的几何问题。
比如,当某些边增加时,需要计算出某个三角形中某个角的度数,可以使用这个定理,在增加的一边的时候,轻松准确地得出角的度数。
总之,共边三角形定理是一种实用的几何定理,它可以用来证明和计算许多几何变换,而不需要耗费大量精力。
结论:共边三角形定理是一种广泛而有价值的几何学定理,它可以用来证明和计算几何变换,以及解决复杂几何问题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
共边定理和共角定理
共边定理(SSS定理):
三角形三条边RM,RS,SM所对应的角(依次称为α角、β角、γ角),若满足以下等式:RM/RS=α角/β角=SM/RS=α角/γ角,则这三条边
所构成的是相等三角形。
共边定理又称为SSS定理,其来源于古希腊几何大师欧几里得的几何论文《几何》(Element)。
欧几里得提出的这一定理指出,若一个三角形的三条边的比值相等,则这
个三角形是等边三角形。
从解决问题的角度来看,欧几里得SSS定理可以帮助人们确定给
定三角形是否为等边三角形;从物理原理的角度来看,SSS定理可以帮助用户理解和抽象
三角形的概念;从数学应用的角度来看,欧几里得的SSS定理可以帮助人解决几何相关的
大多数问题。
HL定理,又称为共角定理,是由古希腊几何大师黑格尔提出的结论。
黑格尔利用直角三角形的特性推出的定理,认为若三角形的边满足某种比例关系,则它们的角也满足一定
比例关系,以此定理可以判断一个三角形是否是等腰三角形。
黑格尔的HL定理也可以用
来解决三角形面积和外接圆相关的问题,从而获得更多的几何理论。
同时,它也给出了比
例关系在几何学中的应用,是这个应用最经典的例子。
