汽车半悬挂系统建模与分析(现代控制理论大作业)(DOC)
某型轨道车辆悬挂系统动力学建模与优化设计

某型轨道车辆悬挂系统动力学建模与优化设计随着城市轨道交通的不断发展,轨道车辆已经成为人们出行的主要方式之一。
而在轨道车辆的设计中,悬挂系统的作用尤为重要。
悬挂系统不仅能够保护乘客的安全,还能够提高车辆的运行效率。
因此,对悬挂系统的动力学建模与优化设计成为轨道车辆设计中的重要课题。
一、动力学建模悬挂系统是轨道车辆中最为复杂的系统之一。
它由车体、车轮、弹簧、减震器等组成,能够有效地减小车体与轮轨之间的震动。
在进行动力学建模时,需要考虑到这些组成部分之间的相互作用。
1.车体运动方程车体的运动方程是悬挂系统动力学建模的基础,它是控制车体运动的核心。
车体的运动方程可以分为纵向运动和横向运动两个方面。
在纵向运动中,车体受到曲径半径变化和斜坡高度变化的影响。
在横向运动中,车体受到曲线曲率和横向加速度的影响。
2.车轮运动方程车轮的运动方程也是悬挂系统动力学建模中的重要组成部分。
车轮的运动受到车体和轮轨之间的摩擦力,以及摩擦力方向的变化等因素的影响。
对车轮的运动方程的建立能够更加准确地反映车辆的行驶状态。
3.弹簧和减震器运动方程弹簧和减震器是悬挂系统中的核心部件,对于车辆的悬挂效果具有至关重要的影响。
在建立弹簧和减震器的运动方程时,需要考虑到它们吸收和释放能量的过程,以及它们与车体、车轮之间的相互作用。
二、优化设计悬挂系统的优化设计是悬挂系统动力学建模的重要应用之一。
通过对悬挂系统的结构和材料等参数进行优化,可以达到减小车辆震动、提高车辆安全性和乘坐舒适性、降低车辆维护成本等目的。
1.结构优化结构优化是悬挂系统优化设计的核心,它能够通过对悬挂系统的结构进行合理化设计,达到减小车辆震动、降低车辆噪音、提高车辆安全性、降低车辆维护成本等目的。
在进行结构优化时,需要考虑到悬挂系统的材料、强度、刚度和减震器的特性等因素。
2.材料优化材料优化是悬挂系统优化设计的重要组成部分,它能够通过优化悬挂系统的材料选择,达到减小车辆震动、提高车辆安全性和乘坐舒适性、延长车辆使用寿命等目的。
基于2自由度模型的汽车半主动悬挂系统设计方案

鉴于二自由度模型的汽车半主动悬挂系统设计作者:侯书毅指导老师:宋宇(安徽农业大学工学院 04级机械设计制造及其自动化合肥 230036)纲要:汽车悬架系统性能的好坏直接影响汽车的乘坐舒坦性和操控安全性。
传统的被动悬架因为其参数固定不变,而悬架性能不够理想;主动悬架虽性能较好,但是需要耗费过多的能源,都没有被宽泛应用,近来几年来半主动悬架因其不需要过多的能源,且其性能也靠近于主动悬架,所以半主动悬架的发展远景有待看好。
关于汽车半主动悬架系统的建模,分别以阶跃函数和白噪声为输入并进行PID 控制,利用matlab语言强盛的算法能力对其编制仿真控制软件,并在simulink 环境下对汽车1/4半主动悬架模型进行计算机仿真,仿真结果表示,此算法设计的PID控制器有优异的性能指标。
要点词:PID;控制器;Matlab;半主动悬架1 前言汽车自19世纪末出生到现在100余年时期,汽车工业从无到有,以惊人的速度发展,写下了人类近代文明的重要篇章。
汽车是数目最多、最普及、活动范围最宽泛、运输量最大的重要的现代化陆地交通工具。
能够断言,没有哪一种机械产品像汽车那样对人类社会产生这样宽泛而深远的影响。
跟着制造工艺的不停发展,汽车的外形愈来愈流线化,速度也在不停上涨。
但是人们对汽车的要求其实不仅限于这些,人们对汽车的乘坐舒坦性提出了更高的要求。
汽车的悬架设计的利害直接影响到汽车行驶的平顺性、驾驶的舒坦性、行驶的安全性等,此中,舒坦性是轿车最重要的使用性能之一。
舒坦性与车身的固有振动特征有关,而车身的固有振动特征又与悬架的特征有关。
所以,汽车悬架是保证乘坐舒坦性的重要零件。
同时,汽车悬架做为车架(或车身)与车轴(或车轮)之间作连结的传力机件,又是保证汽车行驶安全的重要零件。
所以,汽车悬架常常列为重要零件编入轿车的技术规格表,作为权衡轿车质量的指标之一。
从控制力学角度将过去的惯例悬架称为被动悬架,被动悬架性能渐渐知足不了人们的需要,跟着科学的发展以及社会的进步,近来在汽车工业相续出现性能更为优胜的主动悬架和半主动悬架,此中主动悬架耗能较大,而半主动悬架又以低能耗和结构简单,将会被看好,并且已经遇到了许多汽车生产厂家以及汽车设计师们的喜爱。
悬架建模教学设计方案

一、教学目标1. 理解悬架系统在汽车中的作用和重要性。
2. 掌握悬架系统的基本组成部分和结构。
3. 学会使用专业软件进行悬架系统的建模和仿真。
4. 培养学生解决实际工程问题的能力和创新思维。
二、教学内容1. 悬架系统概述- 悬架系统的定义和作用- 悬架系统的基本组成部分(弹簧、减震器、控制臂等) - 悬架系统的分类(独立悬架、非独立悬架等)2. 悬架系统建模原理- 建模软件介绍(如ANSYS、MATLAB等)- 建模流程和方法- 建模中的关键参数设置3. 悬架系统仿真分析- 仿真软件操作- 仿真参数设置- 仿真结果分析4. 悬架系统优化设计- 优化设计的基本概念和方法- 优化设计在悬架系统中的应用- 优化设计实例分析三、教学方法- 系统讲解悬架系统的基本概念、原理和建模方法。
2. 案例分析法- 通过实际案例,引导学生分析悬架系统在实际应用中的问题,并学习如何通过建模和仿真解决这些问题。
3. 讨论法- 组织学生就悬架系统建模中的难点和重点进行讨论,培养学生的合作意识和解决问题的能力。
4. 实践操作法- 在软件操作平台上进行实际操作,让学生亲手搭建悬架模型,并进行仿真分析。
四、教学过程1. 准备阶段- 教师准备教学课件、软件操作指南、相关案例资料等。
- 学生预习教材,了解悬架系统的基本知识。
2. 讲解阶段- 教师讲解悬架系统的基本概念、原理和建模方法。
- 结合案例,分析悬架系统在实际应用中的问题。
3. 实践阶段- 学生在教师的指导下,使用专业软件进行悬架系统的建模。
- 学生进行仿真分析,观察和分析仿真结果。
4. 讨论阶段- 学生就建模过程中遇到的问题进行讨论,教师进行解答和指导。
- 学生分享自己的建模心得和仿真结果。
- 教师总结本次课程的重点和难点。
- 学生提交建模报告,教师进行点评和反馈。
五、教学评价1. 学生对悬架系统知识的掌握程度。
2. 学生在建模过程中的操作熟练程度和创新能力。
3. 学生提交的建模报告的质量和仿真结果的分析深度。
基于Simulink的车辆半主动悬架建模仿真及控制器设计

0引言车辆的安全性、操作稳定性及乘坐舒适性是车辆在行驶过程中非常重要的性能指标,而悬架系统作为车辆的重要部分,对其有重要的影响。
随着汽车技术的发展,车辆主动悬架慢慢地取代了被动悬架,而对于悬架控制器方面的设计也层出不穷。
常用的主动悬架的控制方法有自适应控制、模糊控制、神经网络智能控制及最优控制等,而最优控制作为现代控制理论的核心,理论基础最为完善。
通过线性最优控制算法,综合考虑悬架系统的各因素,设计一个半主动悬架最优控制策略,与被动悬架进行对比研究,从而起到对系统性能的改善。
1系统模型的建立结合研究对象建立如图1所示1/4车辆简化模型。
以牛顿运动定律为基础建立运动方程,如下:(1)同时建立滤波高斯白噪声路面的输入数学模型,如下:(2)式中,x g -路面的垂向位移(m );f 0-下截止频率(Hz );G 0-路面不平度系数(m 3/cycle );ω-期望值为零的高斯白噪声;u-前进速度(m/s )。
由式(1)和式(2)将方程写成相应矩阵形式,可得系统的空间状态方程:(3)(4)式中为系统的状态矢量,其中x ̇b 为簧载质量速度;x b 为簧载质量位移;x ̇w 为非簧载质量速度;x w 为非簧载质量位移;x g 为路面位移;U 为作动器控制力输入矩阵;W为白噪声输入矩阵。
2控制器设计对于车辆悬架设计来说,主要性能指标有轮胎动位移(轮胎接地性);悬架动行程(影响车身布置及结构设计);车身垂向振动加速度(乘坐舒适性)。
由此利用最优控制理论可设计控制器性能指标的表达式如下:(5)式中q 1-轮胎动位移的加权系数,q 2-悬架动行程的加权系数,q 3-车身垂向振动加速度的加权系数,T-时域。
从表达式中可以看出三个加权系数的选取决定了悬架性能的好坏,如果悬架系统目标为提高乘坐舒适性,则可选择车身垂向振动加速度较大的权值;若悬架系统目标为提高车辆的操作稳定性,则可选择轮胎动位移较大的权值。
因此在本研究中选取车身垂向振动加速度的加权系数q 3=1。
半主动、主动悬架滑模控制综述

基于滑模控制的汽车主动、半主动悬架控制方法的研究现状(关键词:sliding mode control, active\semi-active suspension)1、滑模控制(Sliding Mode Control)简介滑模控制是变结构控制系统的一种控制策略。
滑模控制以实现简单,且对外界干扰和系统匹配不确定性有着完全的鲁棒性和自适应性。
滑模控制变结构策略与常规的控制根本区别在于控制的不连续性,即一种是系统“结构”随时间变化的开关特性下沿规定的状态轨迹作小幅度、高频率的上下运动,即所谓的“滑模动态”或“滑模”运动。
这种滑模动态是可设计的,且与系统的参数及扰动无关。
这样,处于滑模运动的系统就有很好的鲁棒性。
2、滑模控制的优缺点滑模控制主要具有以下主要优点[1-2]:(1)一旦系统相应点达到切换面后,系统运行方式指决定于切换面的方程,与系统原来的参数无关。
及时系统的参数有较大的变化,只要切换面是可达的,则都可以实现滑模变结构控制。
(2)可以实现对任一连续变化的输入信号的跟踪。
(3)对外界干扰有较强的鲁棒性。
(4)滑模变结构控制响应快。
(5)滑模变结构控制算法简单,易于工程实现。
虽然滑模结构有诸多优点,但也存在一些不足之处,主要如下[1-2][3]:(1)为实现滑模控制要取得系统的全部状态变量,这在许多情况下是很困难的,尤其对于高阶系统,要取得高阶微分实际上是做不到的。
(2)在实际滑模变结构的控制系统中,由于开关器件的时滞及惯性等因素的影响,系统的状态到达滑模面后,不是保持在滑模面上作滑动运动,而是在滑模面附近作来回穿越运动,甚至产生极限环振荡,这种现象就是滑模变结构控制系统所固有的“抖振”现象。
(3)滑模控制还存在需知不确定参数上下界等问题。
3、基于滑模控制的其它控制策略由于常规的滑模控制具有上述缺点,为克服上述缺点,出现了其它控制模式与滑模控制的有效结合,极大提高了控制效能,例如模糊滑模控制(Fuzzy Sliding Mode control),自适应模糊滑模控制(Adaptive Fuzzy Sliding Mode control),基于模糊神经网络的滑模控制(SMC based on fuzzy neutral networks)等控制策略[4]。
汽车悬架半主动控制响应分析
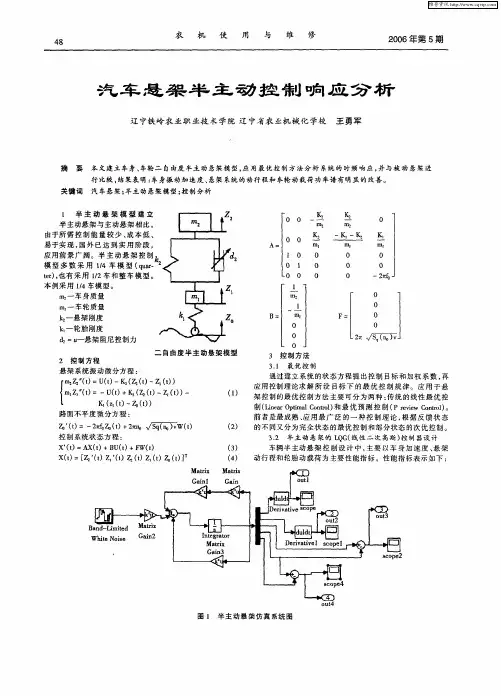
B=
1
1 1 '1 1
F=
0 0
0 O O
2 = 一 _
3 控 制 方 法 3 1 最 优 控 制 .
() 7
40 0
U t = 一K () X
锄
萋
0
Fe uny ') rqe l ̄z ; l
F qe c(z m un y") 1 l
图 3 半主 动悬 架 车 身 、 轮 加速 度 、 架 动 行 程 、 胎 动 载 荷 功 率 谱 车 悬 轮
图 4 被 动 悬 架 仿 真 系 统 图
x t =[ ()z t ( 。t () () t () t () t] )z
() 4
车辆半 主动悬架 控制 设计 中, 主要 以车 身加速 度、 架 悬 动行 程和 轮 胎 动 载 荷 为 主要 性 能 指 标 。性 能 指 标 表 示 如 下 :
图 1 半 主 动 悬 架 仿 真 系统 图
行比较 , 结果表 明: 车身振动加速度 、 悬架 系统的动行程和车轮动 载荷功 率谱 有明显 的改善 。
关 键 词 汽 车 悬 架 ; 半主 动 悬 架 模 型 ; 带 分析 控 】
l 半 主 动 悬 架 模 型 建 立 半 主 动悬 架 与 主 动悬 架 相 比 ,
o o
一
{ ll t=一 ( + t一 。t) mZ ( ) u t K ( ) z( 一 ) ( )
L K ( () Z ( ) 。z t ~ ot ) 路 面 不平 度 微 分 方 程 :
() 1
第五章汽车电子控制悬架系统讲课文档
第三十二页,共38页。
32
• 车高控制执行机构主要由空气阀、空气压缩机和设置在悬架之 上的主气室组成。
• 车高控制主要是利用空气弹簧中主气室空气量的多少来进行调节。
车身高度控制原理如图2-17所示。
第二十四页,共38页。
24
第二十五页,共38页。
25
2.4 执行机构
• 空主气气弹室簧被压缩的空气量发生变 化,即可改变空气弹簧的刚度 •。空气弹簧主要由主气室、副 气室、弹性刚度执行机构、
• 执行器带动阻尼调节杆转动可改
阻尼转换执行机构和液压减
变活塞上阻尼孔的大小,从而改
变减振振器器等的组阻成尼,系如数图。2-12所
• 车身高度传感器常用的有片簧开关式、霍尔式和光 电式传感器。
第十七页,共38页。
17
• 光电式车身高度传感器一般安装在车身与车桥之间 (图2-5),其结构及工作原理如图2-6所示(与转向 盘转角传感器类似)。
图2-5 光电式车身高度传感器的安装位置
第十八页,共38页。
18
加速度传感器
• 当车轮打滑时,不能以转向角和汽车车速正确判断车 身侧向力的大小。
第五章汽车电子控制悬架系统
第一页,共38页。
优选第五章汽车电子控制悬架 系统
第二页,共38页。
相关知识
2.1 概述 2.2 传感器及开关 2.3 电子控制单元(ECU) 2.4 执行机构 2.5 LS400电子控制悬架系统
3
第三页,共38页。
2.1 概述
• 传统的悬架系统一般具有固定的弹簧刚度和减振器阻尼, 不能同时满足汽车行驶平顺性和操纵稳定性的要求.
车辆悬挂系统的非线性特性分析与控制
车辆悬挂系统的非线性特性分析与控制车辆悬挂系统是车辆运动学和动力学性能的重要组成部分。
传统的线性控制方法针对车辆悬挂系统往往难以满足实际的控制需求,因为悬挂系统具有显著的非线性特性。
因此,本文将对车辆悬挂系统的非线性特性进行分析,并提出相应的控制方法。
一、非线性特性的表现形式车辆悬挂系统的非线性特性主要表现在以下几个方面:1. 阻尼特性的非线性:车辆悬挂系统的阻尼特性随着行程变化呈非线性变化。
在小行程范围内,阻尼力随位移的增加呈线性变化;但在大位移范围内,阻尼力的增加速度减缓,呈非线性变化。
2. 弹簧刚度的非线性:车辆悬挂系统的弹簧刚度也随行程的变化而变化。
在小行程范围内,弹簧刚度随位移的增加基本保持不变;但在大行程范围内,弹簧刚度随位移的增加逐渐减小,呈非线性变化。
3. 悬挂系统的干摩擦力:车辆悬挂系统中存在着干摩擦力,其大小与悬挂行程的方向变化有关。
干摩擦力会导致悬挂系统的非对称性和非线性特性,进而影响车辆的稳定性和悬挂系统的控制效果。
二、非线性特性的影响车辆悬挂系统的非线性特性对车辆的运动稳定性和乘坐舒适性都具有重要影响。
1. 运动稳定性:非线性特性可能引起悬挂系统在行驶过程中出现跳动、抖动等现象,进而影响车辆的稳定性和行驶安全性。
2. 乘坐舒适性:非线性特性使得悬挂系统难以在不同行程范围内提供恰当的减震效果,从而影响乘坐的舒适性和悬挂系统的振动控制效果。
三、非线性特性的控制方法针对车辆悬挂系统的非线性特性,可以采用以下几种控制方法:1. 非线性控制器设计:基于非线性特性的具体表现形式,设计适应于车辆悬挂系统的非线性控制器。
可以采用神经网络、滑模控制等方法来提高悬挂系统的控制性能。
2. 自适应控制:通过在线辨识悬挂系统的非线性特性参数,并实时调整控制策略,使得控制器具有较强的适应性和鲁棒性。
3. 模糊控制:利用模糊逻辑来处理悬挂系统中存在的不确定性,设计模糊控制器来实现对非线性特性的控制。
轮式车辆半主动悬挂系统动态特性研究
轮式车辆半主动悬挂系统动态特性研究本文简要介绍目前轮式车辆常用的三种悬挂,对比三种悬挂的系统特性,分析半主动悬挂的优点。
以半主动悬挂为研究对象,利用最优控制方法建立,建立轮式车辆半主动悬挂的整车模型,推导半主动悬挂整车模型的状态方程,并利用非经典模态分析法对轮式车辆半主动悬挂进行了推导得到矩阵方程,为后续研究打下基础。
标签:半主动悬挂;整车模型;状态方程1 前言悬挂系统起着弹性连接车架与轮胎、减缓和衰减不同道路情况颠簸而引起的冲击振动,确保车辆行驶平稳与驾驶人员的舒适性。
性能良好的悬挂应满足车辆高速机动性、高通过性和高乘员舒适性[1]。
被动悬挂系统:主要由弹簧和减振器组成,减振器的阻尼力随着振动速度的增大而增大,振動频率增加,等效刚度增大,对高频衰减能力降低,不能随着路面情况的变化进行调节,结构简单,减振效果一般。
主动悬挂系统:悬挂系统中加入有源可控元件—作动器,按照控制规律产生合适的悬挂力,抑制振动,它由执行机构和决策机构构成闭合控制系统,结构复杂,减振效果优异。
半主动悬挂系统:使阻尼器按照路线和车辆实际情况调整阻尼的大小,做到无极调节,避免了主动悬挂中高成本的作动器和复杂的能量控制系统,结构相对简单,减振效果好。
半主动悬挂相对于被动悬挂在减震效果上有明显的优势,在达到接近主动悬挂性能的同时,又具备结构简单、成本低廉、能耗较低等特点,具有良好的工程应用前景,已成为车辆工程领域的研究热点。
彭志召对半主动悬挂的频域控制算法进行了研究[2],陈兵对履带车辆的半主动悬挂的仿真进行了分析等。
本文将以半主动悬挂为研究对象,利用最优控制方法建立半主动悬挂整车模型,通过非经典线性系统模型分析法对整车状态方程进行研究和分析。
2 模型建立目前对半主动悬挂系统的研究多采用四分之一车体或者半车模型,虽然能够分析,但是和实际工况的响应有着一定的出入,为符合实际运行情况下轮式车辆悬挂的减振效果,考虑车体质心振动和各个车轮轮心自由度的相关性。
普通级轿车前悬架(麦弗逊式)设计毕业论文.doc
摘要悬架是现代汽车上的重要总成之一,它把车架(或车身)与车轴(或轮胎)弹性地连接起来。
它的主要作用是传递作用在车轮和车身之间的一切力和力矩,比如支撑力、制动力和驱动力等,并且缓和由不平路面传给车身的冲击载荷、衰减由此引起的振动、保证乘员的舒适性、减小货物和车辆本身的动载荷。
本文完成的是东方之子轿车前悬架设计,重点从东方之子轿车前悬架的选型、减振器的计算及选型、弹性元件形式的选择计算及选型和横向稳定杆的设计计算。
首先,我把形式不同的悬架的优缺点进行了比较,然后定下东方之子轿车前悬架的形式—麦弗逊式悬架,最后围绕麦弗逊式悬架的部件进行设计。
先是弹簧的设计计算,再是减振器的计算选型,最后是横向稳定杆的设计。
关键词:悬架;麦弗逊式;设计AbstractSuspension is an important element of one of the modern automobile, it flexibly to link the chassis (orbody) and axle (or tires) . Its main role is the role of transmission in the bodybetween the wheels and all the power and moment, such as support of, system dynamics anddriving force, and easing the road to the whole body impact load, decay resulting vibration,ensure the comfort of the crew, cargo and vehicles reduce their moving load.The main stress is front suspension design,Training emphasis from the former car models,and models Absorber calculations, flexible choice of components and models and forms ofstabilizer bar design data.First of all, I have a different form of a suspension of the advantages and disadvantagescompared to the previous suspension of the car and then set form Eastar on suspension.Then design around Eastar suspension components. First, the spring-loaded design terms,to be absorber calculation models, a horizontal stabilizer bar final calculation. stabilizer bar.Keyword : Suspension, Macpherson ,Design目录摘要 (I)Abstract (II)1绪论 (1)1.1课题背景和意义 (1)1.2 悬架的发展历史和现状 (2)1.3 悬架的发展趋势 (4)1.4课题主要内容和研究目的 (5)2悬架结构方案分析 (6)2.1 悬架总成分析 (6)2.2独立悬架优缺点分析 (7)2.3独立悬架特点与分类 (8)2.3.1双横臂式悬架结构及特性分析 (8)2.3.2单横臂式悬架结构及特性分析 (9)2.3.3单纵臂式悬架结构及特性分析 (10)2.3.4单斜臂式悬架结构及特性分析 (11)2.3.5麦弗逊式悬架结构及特性分析 (12)2.1.6扭转梁式悬架结构及特性分析 (13)3麦弗逊式独立悬架设计 (14)3.1麦弗逊式独立悬架设计概述 (14)3.3麦弗逊悬架的结构分析 (15)3.4悬架的弹性特性设计 (16)3.5 悬架挠度fc 的设计 (17)3.5.1悬架静挠度 fc 的设计 (17)3.5.2悬架动挠度fd设计 (18)3.6悬架弹性元件设计 (18)3.6.1螺旋弹簧分析 (18)3.6.2螺旋弹簧的材料及许用应力选择 (19)3.6.3 弹簧参数的计算选择 (20)3.6.4计算空载刚度 (20)3.6.5计算满载刚度 (20)3.6.6按满载计算弹簧钢丝直径 (21)3.6.7螺旋弹簧校核 (21)3.6.8小结 (22)3.7导向机构设计 (23)3.7.1导向机构的设计要求 (23)3.7.2导向机构的布置参数 (24)3.7.3导向机构的受力分析 (27)3.7.4横臂轴线布置方式的选择 (27)3.7.5横摆臂参数对车轮定位参数的影响 (28)3.7.6 导向机构建模 (29)3.8 减振器的设计 (30)3.8.1减振器的简单分类 (30)3.8.2双向筒式液力减振器工作原理 (30)3.8.3相对阻力系数ψ (31)3.8.4减振器阻尼系数δ的确定 (32)3.8.5减振器工作缸直径D的确定 (33)3.8.6小结 (33)3.9横向稳定器 (34)3.10 悬架结构元件 (35)4 前轮定位参数 (37)4.1主销后倾角 (37)4.2主销内倾角 (39)4.3 前轮外倾角 (40)4.4前轮前束 (41)5 麦弗逊悬架其他零件基于CATIA的建模 (43)5.1车轮的建模 (43)5.2车轮轴承建模 (44)5.3转向节建模 (44)5.4 减振器与转向节连接件建模 (45)5.5 车架和横向稳定器联合建模 (45)5.6 麦弗逊悬架建模装配图 (46)6 基于adams的悬架仿真分析 (47)6.1主销内倾角仿真分析 (47)6.2 主销后倾角分析 (47)6.3前轮外倾角分析 (48)6.4 车轮跳动量分析 (49)6.5 前轮前束分析 (49)6.6定位参数与车轮跳动量联合分析 (50)6.7小结 (51)结束语 (52)致谢.................................................................................................错误!未定义书签。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
XX大学 现代控制理论 ——汽车半主动悬架系统的建模与分析
姓名:XXX 学号:XXXX 专业:XXXX 一. 课题背景 汽车的振动控制是汽车设计的一个重要研究内容,涉及到汽车的平顺性和操纵稳定性。悬架系统是汽车振动系统的一个重要子系统,其振动传递特性对汽车性能有很大影响。因此设计性能良好的悬架系统以减少路面激励的振动传递,从而提高汽车的平顺性和操纵稳定性是汽车振动控制研究的重要课题。 悬架系统是汽车车身与轮胎间的弹簧和避震器组成整个支撑系统,用于支撑车身,改善乘坐舒适度。而半主动悬架是悬架弹性元件的刚度和减振器的阻尼系数之一可以根据需要进行调节控制的悬架。 目前,半主动悬架研究主要集中在调节减振器的阻尼系数方面,即将阻尼可调减振器作为执行机构,通过传感器检测到汽车行驶状况和道路条件的变化以及车身的加速度,由ECU根据控制策略发出脉冲控制信号实现对减振器阻尼系数的有级可调和无级可调。
二. 系统建模与分析
1.1 半主动悬架系统的力学模型 以二自由度 1/4半主动悬架模型为例,并对系统作如下假设: (1) 悬挂质量与非悬挂质量均为刚体; (2) 悬架系统具有线性刚度和阻尼; (3) 悬架在工作过程中不与缓冲块碰撞; (4) 轮胎具有线性刚度,且在汽车行驶过程中始终与地面接触。 综上,我们将该系统等效为两个质量块M,m;两个弹簧系统Ks,Kt;一个可调阻尼器(包含一个常规阻尼器Cs和一个变化阻尼力F),如图1所示。 图1 系统力学模型 1.2 半主动悬架系统的数学模型
由减振器的简化模型得:NS
FCVF
对m进行分析:211201122()tss
dzdzdzmKzzKzzCFdtdtdt
即:1011212()tssmzKzzKzzCzzF
对M进行分析:2212122()ss
dzdzdzMKzzCFdtdtdt
即:21212ssMzKzzCzzF 选取状态变量:1102213142
xzzxzzxzxz,,,
输入变量:uF 输出变量:1122
yxyx,
综上可得,系统状态空间表达式为:110322143
31234
4234
1
1tsss
sss
xzzxxzzxxKKCCxxxxxFmmmmmKCCxxxxFMMMM
整理得:00100
00110110tssssssKKCCmmmmmKCCMMMM
xxu
10000100
yx
三. 数值化分析 选取系统参数为:M=391 kg,m=50.7 kg,Ks=60KN/m,Kt=362 KN/m,Cs取1 KN·s/m。
状态空间表达式变为:001000011071401183.4319.7219.72-0.020-153.452.56-2.560.0026xxu 10000100
yx
四. 能控性与能观性分析 00100001101000,,71401183.4319.7219.72-0.0201000-153.452.56-2.560.0026
Abc
4.1 能控性分析 能控性矩阵:23(,,,)MbAbAbAb
通过matlab计算得:Rank(M)=4,满秩,故系统可控。 4.2 能观性分析
能观性矩阵:23,,,TNCCACACA 通过matlab计算得:Rank(N)=4,满秩,故系统可观。 五. 稳定性分析 存在唯一平衡点x=0,对矩阵A进行特征值计算:
通过MATLAB计算,我们得到特征值为:-10.2018+90.5683i,-10.2018-90.5683i,-0.9382+11.4463i,-0.9382-11.4463i。由于矩阵A的特征值均有负实部,所以系统是大范围渐近稳定的。
六. 状态观测器设计 因为系统完全能观,所以可以设计状态观测器。 6.1 全维观测器 将系统极点配置为:-1,-2,-3,-4. MATLAB程序: >>A=[0,0,1,0;0,0,-1,1;-7140,1183.43,-19.72,19.72;0,-153.45,2.56,-2.56]; b=[0;0;-0.02;0.0026]; c=[1,0,0,0;0,1,0,0]; opt=[-1,-2,-3,-4]; G=(place(A,c',opt))’;
输出结果为:7877.00131.08140.09822.03395.101621.13873.789405.1G 所以,全维观测器方程为: 001001.940578.3873001101.162110.3395ˆˆˆ()71401183.4319.7219.72-0.020.98220.81400-153.452.56-2.560.00260.01310.7877yy
xxu+
6.2 降维观测器 由于rank(c)=2,n=4,所以将系统极点配置为-1,-2.
构造变换阵作线性变换,设10010001000010001,1000100001000100TT
。
则,119.719.771401183.42.62.60153.410001100ATAT
,
10.020.00260010,000010BTBCCT
。
MATLAB程序: >>opt2=[-1,-2]; T=[0,0,1,0;0,0,0,1;1,0,0,0;0,1,0,0; ]; Tni=inv(T); A_2=Tni*A*T; B_2=Tni*B; C_2=C*T; A_11=A_2(1:2,1:2); A_21=A_2(3:4,1:2); G2=(place(A_11',A_21',opt2))';
输出结果为:56.0272.1912G。
所以,降维观测器方程为:11
0.980.0271401183.40.02ˆˆ0.042.040153.40.0026119.72ˆˆ20.56wxyuxwy
七. 最优控制
对于半主动悬架系统,最优控制器的设计目的就是寻找最优控制F ,使实现控制所需的能量为最小:dtxxqxqJ024222211,其中,1q,2q分别为轮胎动变形加权系数,悬架动挠度加权系数,为车身加速度加权系数。 将目标性能泛函改写成二次型性能指标形式:dtRuuQxxJTT0)(,
这里,0000000000000021qqQ,为半正定常数矩阵;21MR,为正定常数矩阵。 所以,最优控制存在,且唯一:)()(1tPxBRtuT 式中,P为44维正定常数矩阵,满足黎卡提矩阵代数方程: 01QPBPBRPAPATT
采用试探法取三组不同权系数1q、2q,运用MATLAB进行计算分析:(1)q1=3.35e5,q2=40.5e5;(2)q1=3.35e8,q2=40.5e8;(3)q1=3.35e9,q2=40.5e9; Matlab程序: %最优控制 clc;clear; M=391; A=[0,0,1,0;0,0,-1,1;-7140,1183.43,-19.72,19.72;0,-153.45,2.56,-2.56]; B=[0;0;-0.02;0.0026]; C=[1,0,0,0;0,1,0,0]; D=0; R=1/M^2; %求不同Q、R下的状态反馈阵K Q1=3.35e5;Q2=40.5e5; Q=[Q1,0,0,0;0,Q2,0,0;0,0,0,0;0,0,0,0]; [K P e]=lqr(A,B,Q,R) Ac=(A-B*K);Bc=B; Cc=C;Dc=D; T=0:0.05:5; U=0.2*ones(size(T)); [Y,X1]=lsim(Ac,Bc,Cc,Dc,U,T); Q1=3.35e8;Q2=40.5e8; Q=[Q1,0,0,0;0,Q2,0,0;0,0,0,0;0,0,0,0]; [K P e]=lqr(A,B,Q,R) Ac=(A-B*K);Bc=B; Cc=C;Dc=D; T=0:0.05:5; U=0.2*ones(size(T)); [Y,X2]=lsim(Ac,Bc,Cc,Dc,U,T);
