动量传输习题参考答案
化工传递过程基础(第三版)习题答案详解_部分1

+ aA
dM dθ
=0
(1) (2)
又由全组分质量衡算:
得: 上式积分:
w2
− w1
+
dM dθ
=0
dM dθ
= w1
− w2
= 100 − 60 = 40kg/min
M = 40θ + 2000kg
(3) (4) (5)
设搅拌良好,任何瞬时 θ,
aA2 = aA
(6)
将式(3)~式(6)及已知数据代入式(2),得:
θ2 0
=
−
1 100
[ln(100aA
−
0.2)] |
0.01 0.1
ln 40θ2 + 2000 = −0.4ln 100 × 0.01 − 0.2
2000
100 × 0.1 − 0.2
ln 40θ2 + 2000 = ln(9.8)0.4 = ln 2.724
2000
0.8
40θ2 + 2000 = 2.724 2000
说明
本习题解系普通高等教育“十一五”国家级规划教材《化工传递过程基础》(第三版) 中所附习题的解答,共 205 题。各题均有较详尽的解题步骤,供本课程同仁教学辅导参考。
参加解题工作的有天津大学化工学院陈涛(第一、十二章)、张国亮(第二~五章)、张 凤宝(第六~八章)、贾绍义(第九~十一章),由陈涛、张国亮对全书进行统编和整理。
lg p′ = lg133.3 + 6.926 − 1284 T − 54
lg p′ = 9.051 − 1284 T − 54
1-3 黏性流体在圆管内做一维稳态流动,设 r 表示径向、y 表示由管壁指向中心的方向。 已知温度 t 和组分 A 的质量浓度 ρA 的梯度与流速 ux 的梯度方向相同,试用“通量=-扩散系
动量定理习题参考答案及解答
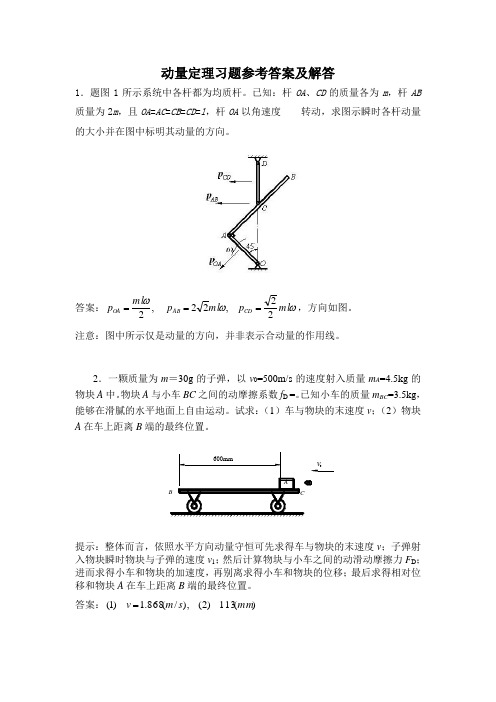
动量定理习题参考答案及解答1.题图1所示系统中各杆都为均质杆。
已知:杆OA 、CD 的质量各为m ,杆AB 质量为2m ,且OA =AC =CB =CD =l ,杆OA 以角速度转动,求图示瞬时各杆动量的大小并在图中标明其动量的方向。
答案:ωωωml p ml p ml p CD AB OA 22,22 ,2===,方向如图。
注意:图中所示仅是动量的方向,并非表示合动量的作用线。
2.一颗质量为m =30g 的子弹,以v 0=500m/s 的速度射入质量m A =4.5kg 的A B600mmACv答案:)(113)2(),/(868.1)1(mm s m v =3.如题图3所示,均质杆AB ,长l ,直立在滑腻水平面上。
求它从铅直位置无初速地倒下时,端点A 相对图示坐标系的轨迹。
提示:水平方向质心守恒。
答案: 2224l y x =+4.质量为m 1的棱柱体A ,其顶部铰接一质量为m 2、边长为a 和b 的棱柱体B ,初始静止,如下图。
忽略棱柱A 与水平面的摩擦,假设作用在B 上的力偶使其绕O 轴转动90o (由图示的实线位置转至虚线位置),试求棱柱体A 移动的距离。
设A 与B 的各边平行。
提示:水平方向质心守恒。
答案:棱柱体A 移动的距离 )(2)(212m m b a m x ++= (向左)5.如图所示水平面上放一均质三棱柱A,在其斜面上又放一均质三棱柱B。
两三棱柱的横截面均为直角三角形。
三棱柱A的质量m A为三棱柱B质量m B的3倍,其尺寸如题图5所示。
设遍地摩擦不计,初始时系统静止。
求三棱柱B滑落地面之前,三棱柱A运动的加速度及地面的支持力。
BAa解:先取整体进行受力与加速度分析,见左以下图,有raaa+=AB依照质心运动定理,(2))sin4()(sin:(1)cos4)(cos:NNθθθθrBABrBArAABrBagmFFgmmamyaaammamx-=⇒-+==⇒=+-再以三棱柱B为研究对象(见右上图),将质心运动定理在a r方向投影得)3(sincossin)cos(θθθθgaagmaamArBArB+=⇒=-联立解方程式(1)、(2)和(3)得θθθθθθ222sin312,sin3sin4,sin3cossin+=+=+=gmFgaga BNrA6.图示凸轮导板机构,半径为r 的偏心轮的偏心距OC =e ,偏心轮绕水平轴以匀速度ω转动,导板的质量为m 。
大学物理《力学4·动量》复习题及答案

( )选坐标系如图:有动量守恒定律 1
x方向:mu 5m v2 cosq
y方向: mv1 5mv2 sinq 0
解(1)、 )式得: (2 v2 u / 5 cosq(1) Nhomakorabea( 2)
B
y
u
u u / 5 1 sin2q 4
q
v2
x
A
v1 3u / 4
v1
(2).A球碰前后动能变化:
9.体重相同的甲乙两人,分别用双手握住 跨过无摩擦滑轮的绳子两端,当他们由同 一高度向上爬时,相对于绳子,甲的速度 是乙的两倍,则到达顶点情况是
(A)甲先到达。 (B)乙先到达。 (C)同时到达。 (D)谁先到达不能确定。
[ ]
• 动量选择题答案:CCCDADACC
10.质量为 M=2.0 kg 的物体(不考虑体 积),用一根长 l =1.0 m 为的细绳悬挂在天 花板上,今有一质量为 m=20 g 的子弹以 v0=600 m/s 的水平速度射穿物体,刚射出物 体时子弹的速度大小 v0 = 30 m/s, 设穿透 时间极短,求:
14. 光滑斜面与水平面的夹角为,轻质弹簧 上端固定,今在弹簧的另一端轻轻地挂上质 量为 M=1.0kg 的木块,则木块沿斜面向下 滑动。当木块向下滑 x =30 cm 时,恰好有 一质量 m = 0.01 kg 的子弹,沿水平方向以 速度 v = 200 m/s 射中木块并陷在其中,设 弹簧的倔强系数 k=25 N/m 为,求子弹打入 木块后它们的共同速度。 k M m 解:( )木块下滑中,以 1 x 木块、弹簧、 地球为系统。
v2 M v1 mv cos / M m
0.89(m/s)
方向向上。
物理动量定理题20套(带答案)及解析

物理动量定理题20套(带答案)及解析一、高考物理精讲专题动量定理1. 2022年将在我国举办第二十四届冬奥会, 跳台滑雪是其中最具观赏性的项目之一. 某滑道示意图如下, 长直助滑道AB 与弯曲滑道BC 平滑衔接, 滑道BC 高h=10 m, C 是半径R=20 m 圆弧的最低点, 质量m=60 kg 的运动员从A 处由静止开始匀加速下滑, 加速度a=4.5 m/s2, 到达B 点时速度vB=30 m/s. 取重力加速度g=10 m/s2.(1)求长直助滑道AB 的长度L ;(2)求运动员在AB 段所受合外力的冲量的I 大小;(3)若不计BC 段的阻力, 画出运动员经过C 点时的受力图, 并求其所受支持力FN 的大小.【答案】(1)100m (2)1800N s ⋅(3)3 900 N【解析】(1)已知AB 段的初末速度, 则利用运动学公式可以求解斜面的长度, 即2202v v aL -=可解得:2201002v v L m a-== (2)根据动量定理可知合外力的冲量等于动量的该变量所以01800B I mv N s =-=⋅(3)小球在最低点的受力如图所示由牛顿第二定律可得:从B 运动到C 由动能定理可知:221122C B mgh mv mv =- 解得;3900N N =故本题答案是: (1) (2) (3)点睛:本题考查了动能定理和圆周运动, 会利用动能定理求解最低点的速度, 并利用牛顿第二定律求解最低点受到的支持力大小.2. 图甲为光滑金属导轨制成的斜面, 导轨的间距为 , 左侧斜面的倾角 , 右侧斜面的中间用阻值为 的电阻连接。
在左侧斜面区域存在垂直斜面向下的匀强磁场, 磁感应强度大小为 , 右侧斜面轨道及其右侧区域中存在竖直向上的匀强磁场, 磁感应强度为 。
在斜面的顶端e 、f 两点分别用等长的轻质柔软细导线连接导体棒ab, 另一导体棒cd 置于左侧斜面轨道上, 与导轨垂直且接触良好, ab 棒和cd 棒的质量均为 , ab 棒的电阻为 , cd 棒的电阻为 。
冲量和动量练习题及答案

冲量和动量练习题及答案精诚——动量冲量动量和冲量是物理学中重要的概念,下面是对它们的相关问题的解答。
1.关于动量,正确的说法是:A。
物体的质量越大,动量越大。
B。
物体的质量和速度相同,动量相同。
C。
物体速度的变化会导致动量的变化。
D。
物体运动状态的变化会导致动量的变化。
2.对于合力F在时间t内对某物体冲量I=-2N·s的作用,正确的说法是:A。
F的方向与冲量的方向相反。
B。
F的方向与冲量的方向相同。
C。
物体的动量一定会减少。
D。
F的方向与选取的冲量的正方向相反。
3.关于冲量和动量,正确的说法是:A。
冲量是反映力作用时间累积效果的物理量。
B。
动量是描述物体运动状态的物理量。
C。
冲量是过程量,动量是状态量。
D。
冲量的方向和动量的方向一致。
4.正确的说法是:A。
物体动量的改变,可能是速度大小的改变。
B。
物体动量的改变,可能是速度方向的改变。
C。
物体运动状态的改变,会导致动量的变化。
D。
物体速度方向的改变,会导致动量的变化。
5.质量为m的物体放在光滑水平地面上,在与水平方向成θ角的恒定推力F作用下,由静止开始运动,在时间t内推力的冲量和重力的冲量大小分别为:A。
Ft;0B。
FtcosθC。
Ft;mgtD。
Ftcosθ;mgt6.如果物体在任何相等的时间内受到的冲量都相同,那么这个物体的运动可能是:A。
匀变速直线运动。
B。
匀速圆周运动。
C。
匀变速曲线运动。
D。
匀变速运动。
7.质量为5kg的小球从距地面高为20m处水平抛出,初速度为10m/s,从抛出到落地过程中,重力的冲量是:A。
60N·sB。
80N·sC。
100N·sD。
120N·s8.关于物体受到的冲量,正确的说法是:A。
物体上升阶段和下落阶段受到的重力冲量方向相反。
B。
物体上升阶段和下落阶段受到的空气阻力冲量方向相反。
C。
物体在下落阶段受到的重力冲量大于上升阶段受到的重力冲量。
D。
物体从抛出到返回抛出点,所受各力冲量的总和方向向下。
(完整版)动量定理精选习题+答案

三、计算题(本大题共 10 小题,共 100.0 分)
M 在水平轨道上向右移动了 0.54 m
11. 如图所示,质量为 5kg 的木板 B 静止于光滑水平面上,物块 A 质量为 5kg,停在 B 的左端 .质量为 1kg
的小球用长为 0.45??的轻绳悬挂在固定点 O 上,将轻绳拉直至水平位置后, 由静止释放小球, 小球在最
m 的静
止木块发生碰撞,碰撞的时间极短 .在此碰撞过程中,下列哪个或哪些说法是可
能发生的? ( )
A. 在此过程中小车、木块、摆球的速度都发生变化,分别变为
??1、 ??2 、 ?3?,满足 (?? + ??0 )??= ???1? +
???2? + ??0 ??3
B. 在此碰撞过程中, 小球的速度不变, 小车和木块的速度分别为 ?1?和 ?2?,满足 (?? + ??0)??= ???1?+ ???2?
4
B. 5 ??0
1
C. 5 ??0
1
D. 25 ??0
2. 如图所示,小车静止在光滑水平面上, AB 是小车内半圆弧轨道的水平直径,现 将一小球从距 A 点正上方 h 高处由静止释放,小球由 A 点沿切线方向经半圆轨 道后从 B 点冲出,在空中能上升的最大高度为 0.8? ,不计空气阻力 .下列说法正 确的是 ( )
1
大学物理动量与角动量练习题与答案
第三章 动量与角动量一、选择题[ A ] 1.(基础训练2)一质量为m 0的斜面原来静止于水平光滑平面上,将一质量为m 的木块轻轻放于斜面上,如图3-11.如果此后木块能静止于斜面上,则斜面将(A) 保持静止. (B) 向右加速运动.(C) 向右匀速运动. (D) 向左加速运动.提示:假设斜面以V 向右运动。
由水平方向动量守恒得0(cos )0m V m V v θ+-= ,而0v =,得0V =[C ]2.(基础训练3)如图3-12所示,圆锥摆的摆球质量为m ,速率为v ,圆半径为R ,当摆球在轨道上运动半周时,摆球所受重力冲量的大小为(A) 2m v . (B) 22)/()2(v v R mg m π+(C) v /Rmg π.(D) 0.提示:2T mg I G ⨯= , vRT π2=[ B ]3. (自测提高2)质量为20 g 的子弹,以400 m/s 的速率沿图3-15入一原来静止的质量为980 g 的摆球中,摆线长度不可伸缩.子弹射入后开始与摆球一起运动的速率为 (A) 2 m/s . (B) 4 m/s . (C) 7 m/s . (D) 8 m/s .提示:对摆线顶部所在点角动量守恒。
2sin 30()mv l M m lV ︒=+;其中m 为子弹质量,M 为摆球质量,l 为 摆线长度。
[D ]4.(自测提高4)用一根细线吊一重物,重物质量为5 kg ,重物下面再系一根同样的细线,细线只能经受70 N 的拉力.现在突然向下拉一下下面的线.设力最大值为50 N ,则(A)下面的线先断. (B)上面的线先断. (C)两根线一起断. (D)两根线都不断.提示:下面的细线能承受的拉力大于所施加的最大力,所以下面的细线不断。
对重物用动量定理:0'''=--⎰⎰⎰++dt T mgdt dt T t t t t t 下上't 为下拉力作用时间,由于't t >>,因此,上面的细线也不断。
高中物理动量定理解题技巧分析及练习题(含答案)及解析
高中物理动量定理解题技巧剖析及练习题( 含答案 ) 及分析一、高考物理精讲专题动量定理1.如下图,粗拙的水平面连结一个竖直平面内的半圆形圆滑轨道,其半径为R=0.1 m,半圆形轨道的底端搁置一个质量为m=0.1 kg 的小球 B,水平面上有一个质量为M=0.3 kg 的小球 A 以初速度 v0 =4.0 m/ s 开始向着木块 B 滑动,经过时间t=0.80 s 与 B 发生弹性碰撞.设两小球均能够看作质点,它们的碰撞时间极短,且已知木块 A 与桌面间的动摩擦因数μ=0.25,求:(1)两小球碰前 A 的速度;(2)球碰撞后 B,C 的速度大小;(3)小球 B 运动到最高点 C 时对轨道的压力;【答案】( 1) 2m/s( 2)v A=1m/s , v B= 3m/ s( 3) 4N,方向竖直向上【分析】【剖析】【详解】(1)选向右为正,碰前对小球 A 的运动由动量定理可得:–μMg t = M v –M v 0解得: v= 2m/s(2)对 A、 B 两球构成系统碰撞前后动量守恒,动能守恒:Mv Mv A mv B1 Mv21Mv A21mv B2222解得: v A= 1m/ s v B= 3m/ s(3)因为轨道圆滑, B 球在轨道由最低点运动到 C 点过程中机械能守恒:1mv B21mv C2mg2R22在最高点 C 对小球 B 受力剖析,由牛顿第二定律有:mg F N m v C2R解得: F N= 4N由牛顿第三定律知,F N '= F N= 4N小球对轨道的压力的大小为3N,方向竖直向上.2.蹦床运动是运动员在一张绷紧的弹性网上蹦跳、翻腾并做各样空中动作的运动项目。
一个质量为 60kg 的运动员,从离水平网面 3.2m 高处自由着落,着网后沿竖直方向蹦回离水平网面 5.0m 高处。
已知运动员与网接触的时间为 1.2s,若把这段时间内网对运动员的作用力看作恒力来办理,求此力的大小和方向。
高二物理动量练习题(含答案)
A B 左v B 右 v A 高二物理限时训练一出题:张强智 审题:唐一峰一、单选(36分)1.下列说法中不正确的是 ( )A .物体的速度大小改变时,物体的动量一定改变B .物体的速度方向改变时,其动量不一定改变C .物体的动量不变,其速度一定不变D .运动物体在任一时刻的动量方向,一定是该时刻的速度方向2.如图所示,运动员挥拍将质量为m 的网球击出.如果网球被拍子击出前、后瞬间速度的大小分别为v 1、v 2,v 1与v 2方向相反,且v 2>v 1.忽略网球的重力,则此过程中拍子对网球作用力的冲量( )A .大小为m (v 2-v 1),方向与v 1方向相同B .大小为m (v 2+v 1),方向与v 1方向相同C .大小为m (v 2-v 1),方向与v 2方向相同D .大小为m (v 2+v 1),方向与v 2方向相同3.质量为1kg 的物体在距离地面5m 高处,由静止开始自由落下,正落在以5m/s 速度沿光滑水平面匀速行驶的装有砂子的小车中,车与砂的总质量为4kg ,当物体与小车相对静止后,小车的速度为A .4m/sB .5m/sC .6m/sD .3m/s4.人从高处跳到低处时,为了安全,一般都是让脚尖先着地,这是为了A .减小冲量B .减小动量的变化量C .增长和地面的冲击时间,从而减小冲力D .增大人对地的压强,起到安全作用5.如图所示,在光滑水平面上质量分别为m A =2 kg 、m B =4 kg ,速率分别为v A =5 m/s 、v B =2 m/s 的A 、B 两小球沿同一直线相向运动( )A .它们碰撞前的总动量是18 kg · m/s,方向水平向右B .它们碰撞后的总动量是18 kg · m/s,方向水平向左C .它们碰撞前的总动量是2 kg · m/s,方向水平向右D .它们碰撞后的总动量是2 kg · m/s,方向水平向左6、质量为1kg 的A 球以3m/s 的速度与质量为2kg 静止的B 球发生碰撞,碰后两球以1m/s 的速度一起运动。
传输原理课后答案
非稳定流动:流场中运动参数不仅随时间发生改变,又与位置改变而发生改变的流动。
什么是迹线?什么是流线?
答:迹线就是在流场中同一运动质点在不同时刻的运动轨迹线;流线就是不同质点在同一时刻的运动方向线。
P62 3-2沿程阻力和局部阻力的物理本质是什么?
10-6外径d=150mm的蒸汽管道要求散量不大于465J/(m·s),试确定用珍珠岩磷酸盐制品〔λ=0.052+0.29×10·-3tW/(m·℃)〕作保温材料包扎层的最小厚度。设蒸汽管外表温度为400℃,保温层外壳250℃。
解:λ=0.052+0.29×10-3tW/(m·℃)
=0.052+0.29×10-3×(400+250)/2
(2)内、外直径分别为d1和d2的同心圆环套管.
解:
(1)由当量直径的公式de=4A/s
A-导管或设备的流通截面积,
S-被流体所浸润的导管或设备的周长
因为正六边形的横截面是由6个正三角形组成,S六边形=6*S三角形=6*a* a*1/2=
3* *
正六边形横截面管道周长S=6a,de=(4*3* * )/6a= a.
(2)S同心圆= = ( - )/4
同心圆周长=
同心圆环管道的当量直径de= ( - )/4]/
= +
第四章边界层理论
1、什么叫边界层厚度?
答:流速相当于主流区速度的0.99处到固定体壁面间的距离叫边界层厚度
1.简述拉瓦尔喷管的原理。
答:拉瓦尔喷管的前半部是一段由大变小向中间收缩的管道。收缩到一定程度之后又由小变大向外扩张。这种管路可使气流的速度因喷管截面积的变化而变化,使气流从亚音速到音速,直至加速到跨音速。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第四章习题参考答案(仅限参考)
1. 错、错、错 2.a 3.c
4.解:根据平面不可压缩流体连续性的性质:
(1)0xzVVxz;流场连续
(2)101xzVVxz;流场不连续
(3)21xzVVxxz;流场不连续
5. 解:同题4,
(1)cos()cos()xyVAyxyxVAxxyy;0)cos()(xyxyAyVxVyx,流场不连续
(2)xyVAxyVAyy;0yVxVyx 流场连续
6. 解:以水龙头中心线0-0为基准位,无位能变化,对2-2点打开前后应用伯努
利方程:
'2
+0+0+02pvpggg
解得'220.98/vppms
流量
23313.142.3710/4Qdvms
7. 解:根据流体静力学知识得到以下关系式:
12
2pghpghgh
水
根据p1=p2时 h=0,有:
4πh24
dπ22D
h
得:222dhhD,代入可解得:
12
2
2
0.12pphmdgggD
水
8. 解:选取圆柱坐标系,假设流动是沿z轴方向进行,且为充分发展的层流流
动。根据已知条件可知,流动是轴对称,θ方向可不考虑,仅z方向有流动。由
连续性方程、稳定流动,忽略质量力,则有:
222
2222
111zzzzzzzzrzzPFtrrzzrrrrz
0r
;0zzz;22220zzz;0t;
化简得:
11()zPrrrrz
;
vx只是半径r的函数,p为z方向的函数,即得
dzdpudrdvrdrdr
z
11
进行第一次积分,并将边界条件r=0处,代入,算得积分常数C1=0;再进行第
二次积分,并将r=R处,υz=0代入,算得出C2=dzdpuR42最后得到:
2
222
1()[1()]44zdPRdPr
RrdzdzR
式中r为管截面上速度为υz处到管中心的距离,R为圆管半径。显然其速度分
布呈抛物线形。下面很容易推导出υz与υzmax的关系为:
2
max[1()]zz
r
R
9.解:取截面2的位置为位能为0,考虑到出口水压与入口水压同为一个大气压,
用相对压强计算,则截面1和截面2处的压强都为0。取截面1和截面2建立能
量方程
22
12
2
00022vvgh
由于水槽的直径比虹吸管的直径大很多,那么就可以近似设v1等于0。
代入可得2228.86/vghms
流量 223322223.1423.146.2610/44ddQvghms
同理列截面2与截面3处的伯努利方程:(以2处为0基点)
2
2
33
2
12
()0022pvvghh
根据质量守恒:3处和2处的速度满足:
323222
4π4
π
vdvd, 得232.215/4vvms
代入得:
22
21
312
()22024.32vvphhgPag
负号表示C处的压强低于一个大气压,处于真空状态。正是由于这一真空,才
可将水箱中的水吸起。
用绝对压强表示:p=p大气+p3=101325-22024.3=79300.7 Pa.
第五章习题参考答案(仅限参考)
1.a 2.b 3.d 4.c 5.d
6.
解:
2
2mvLpd
假设雷诺数小于2300,有6464Remλvd,代入上式得:
22
2
6464222mmmmvvLv
LL
pdvddd
226
4220.150.965101.84/64644109201000mdpvmsL
检验假设
41.840.15Re6902300410mvd
,符合假设
22
3
3.140.151.840.03ms44mmdQAvv
7.
解: 首先判断流动状态
22
440.030.425ms3.140.3mQvd
40.4250.3Re106323001.210mvd
,
属于层流
64
0.06
Re
λ
沿程损失
2
2
300.4250.060.0620.329.81mfvL
hmdg
8.
解:
计算流速
22
440.051.02ms3.140.25mQvd
55
6101053.210007.125.002.1Re
dv
m
按光滑管区考虑
查莫迪图得
015.0
沿程水头损失mgvdLhmf32.081.9202.125.0100015.022
9.
解: 220.329442601.4ms3.140.05mQvd
2
2mvpLhgdg
22
226168.6100.036.2960.2910001.40.05mpLvd
10
解:227001.132.930.026.6420.1529.81miivLhmdg
11.
解:采用欧根公式计算
m
m
m
m
vddvLp23322175.11150/
计算Δp
取1,代入题中各数据计算得
Pap6.12386.351887305.025.023.10012.039.039.0175.1305.039.00012.039.0125.01078.1150233225
12.
解:2212000044606025ms3.14mQvdd
解得d=1.3m
65
5251.3Re2.0710101.5710mvd
0.0005
0.0003851.3d
;查莫迪图得016.0
弯曲半径R1=2.6的弯管局部阻力系数由21dR,查表得ζ1=0.15
弯曲半径R2=2.6的弯管局部阻力系数由12dR,查表得ζ2=0.3
mgvdLhm7.2688.92255.223.0415.053.1120016.02)245(2221
Pahgp32397.2688.923.1
555
1055.232391001325.110569.1pppp
Mi
大气
13.
解:221750044606011.9ms3.140.72mQvd
5
411.90.72Re5.46100.15710mvd
(1)0.20.000278720d;查莫迪图得
0.0147λ
2
2
28.611.90.01474.2120.7229.81mfvL
hmdg
(2)20.00278720d;查莫迪图得
0.0265λ
2
2
28.611.90.03657.6020.7229.81mfvL
hmdg
