(完整版)圆的基本性质练习题一
小学五年级圆练习题

小学五年级圆练习题圆是平面上所有与给定点(圆心)距离相等的点的集合。
这个距离称为半径。
下面是一些适合小学五年级学生的圆练习题:1. 圆的基本性质- 问题:什么是圆心,半径,直径?圆心和半径有什么关系?- 答案:圆心是圆的中心点,半径是从圆心到圆上任意一点的距离,直径是穿过圆心的最长弦,长度是半径的两倍。
2. 圆的周长- 问题:已知圆的半径是3厘米,求这个圆的周长。
- 答案:圆的周长公式是 \( C = 2\pi r \),其中 \( r \) 是半径。
将半径3厘米代入公式,得 \( C = 2 \times 3.14 \times 3 = 18.84 \) 厘米。
3. 圆的面积- 问题:如果圆的半径是4厘米,那么它的面积是多少?- 答案:圆的面积公式是 \( A = \pi r^2 \)。
将半径4厘米代入公式,得 \( A = 3.14 \times 4^2 = 50.24 \) 平方厘米。
4. 圆与正方形的比较- 问题:如果一个圆的直径和正方形的边长相等,都是10厘米,哪个图形的面积更大?- 答案:圆的面积是 \( 3.14 \times (10/2)^2 = 78.5 \) 平方厘米,正方形的面积是 \( 10 \times 10 = 100 \) 平方厘米。
所以正方形的面积更大。
5. 圆的切线- 问题:什么是圆的切线?圆的切线有哪些特点?- 答案:圆的切线是一条刚好接触到圆的直线,且只接触一点。
切线在接触点处的切线与半径垂直。
6. 圆的弧和扇形- 问题:什么是弧?什么是扇形?- 答案:弧是圆上任意两点之间的曲线部分。
扇形是圆心角和它所对的弧以及两条半径所围成的图形。
7. 圆的对称性- 问题:圆有哪些对称性?- 答案:圆是轴对称图形,任何经过圆心的直线都是它的对称轴。
8. 圆的周长和面积的比较- 问题:如果两个圆的周长相等,它们的面积也相等吗?- 答案:是的,如果两个圆的周长相等,根据周长公式 \( C =2\pi r \),它们的半径也相等,因此它们的面积也相等。
圆的基本性质习题课.doc

图22、如图2,已知半径OD与弦AB互相垂直,垂足为点C,若AB=8cm, CD=3cm,的半径为o3、如图3,将半径为2cm的圆形纸片折叠后,圆弧恰好经过圆心O,则折痕AB的长为则圆ocm.1、如图1, OO的直径AB=12, CD是。
O的弦,CD_LAB,垂足为P,旦BP: AP=1:5, 则CD的长为______________________4、如图4, AB是OO的弦,AB长为8, P是。
O上一个动点(不与A、B重合),过点O 作OCLAP于点C, OD1PB于点D,则CD的长为5、。
0的半径为10cm,两平行弦AC,BD的长分别为12cm, 16cm,则两弦间的距离是()A. 2cmB. 14cmC. 6cm 或8cmD. 2cm 或14cm6、。
的直径为10,弦AB的长为6, M是弦AB±的一动点,则线段的OM的长的取值范围是()A. 3WOMW5B. 4WOMW5C. 3<OM<5D. 4<OM<57、在OO中,弦CD与直径AB相交于点E, K ZAEC =30° , AE=lcm, BE=5cm,那么弦CD的弦心距OF=cm,弦CD的长为cm。
例1、如图,半径为2的圆内有两条互相垂直的弦AB和CD,AB、CD交于E,OE=1,^.AB^CD2的值。
变式练习、如图,弓玄CD1AB于P, AB=8, CD=8,例2、如图,。
0的半径为10cm, G是直径AB上一点,弦CD经过点G,CD=16cm, AE1CD 于E, BF1CD 于F,求AE-BF 的值。
第2题图变式练习:如图:AB是的直径,CD是弦,过A、B两点作CD的垂线,垂足分别为E、F, 若AB=10, AE=3, BF=5,求ECHOIC1、如图,。
中,砂为直径,弦CD交AB于P,丘0顷,试猜想赤与虱之间的关系,并证明你的猜想.2、己知:如图,<30中,AB是直径,CO_LAB, D是CO的中点,DE〃AB,求证:CE =2 AE四.练习检测,自我反思.1、如图所示,D、E分别是孤AB、孤AC的中点,DE交AB于M、交AC于N.求证AM=AN.4、已如图5;的半径为5, AB. BE为方程x2-8kx+12k2=0的两个根,CD为。
精品 九年级数学上册 圆的基本性质讲义+同步练习题

圆的基本性质知识点圆的定义几何定义:线段OA,绕O点旋转一周得到的图形,叫做圆。
其中,O为圆心,OA为半径。
集合定义:到定点等于定长的所有点的集合。
其中,定点为圆心,定长为半径。
圆的书写格式:圆的对称性(1)圆是轴对称图形,它的对称轴是直径所在的直线。
(2)圆是中心对称图形,它的对称中心是圆心。
(3)圆是旋转对称图形。
与圆有关的线段半径:圆上一点与圆心的连线段。
确定一个圆的要素是圆心和半径。
弦:连结圆上任意两点的线段叫做弦。
直径:经过圆心的弦叫做直径。
弦心距:圆心到弦的垂线段的长。
弧:圆上任意两点间的部分叫做圆弧,简称弧。
劣弧:小于半圆周的圆弧叫做劣弧。
表示方法:优弧:大于半圆周的圆弧叫做优弧。
表示方法:在同圆或等圆中,能够互相重合的弧叫做等弧。
注意:同弧或等弧对应的弦相等。
垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧。
注意:定理中的“垂直于弦的直径”可以是直径,也可以是半径,深圳可以是过圆心的直线或线段;该定理也可以理解为:若一条直线具有两条性质:①过圆心;②垂直于一条弦,则此直线具有另外三条性质:①平分此弦;②平分此弦所对的优弧;③平分此弦所对的劣弧.推论1:(1)平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧。
(2)弦的垂直平分线经过圆心,并且平分弦所对的两条弧。
(3)平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧。
推论2:圆的两条平行弦所夹的弧相等。
在下列五个条件中:①CD是直径;②CD⊥AB;③AM=BM;④AC=BC;⑤AD=BD.只要具备其中两个条件,就可推出其余三个结论.注意:(1)在圆中,与已知弦(非直径)相等的弦共有条;共端点且相等的弦共有条。
(2)在圆中,与已知弦(非直径)平行的弦共有条;平行且相等的弦共有条。
例1.如图:OA、OB为⊙O的半径,C、D分别为OA、OB的中点,求证:AD=BC.例2.如图,已知AB是⊙O的直径,弦CD⊥AB,垂足是E,如果AB=10cm,CD=8cm,求AE的长。
中考数学复习之圆的基本性质,考点过关与基础练习题

32.圆的有关性质➢ 知识过关1. 圆有相关概念(1)圆:在一个平面内,线段OA 绕它固定的一个端点O 旋转_____,另一个端点A 所于形成的图形叫做圆,圆心为O ,半径为r 的圆可以看成是所有到定点O 的距离等于____r 的点的集合.(2)弧、弦、等圆、等弧①弧:圆上任意_____的部分叫做弧,大于半圆的弧叫做优弧,小于半圆的弧叫做劣弧; ①弦:连接圆上任意两点的____叫做弦,经过_____的弦叫做直径. ①等圆:能够_____的两个圆叫做等圆;①等弧:在_____或等圆中,能够互相重合的弧叫做等弧. 2. 垂径定理及其推论 (1) 对称性:①圆是中心对称图形,其对称中心是圆心 ①圆是轴对称图形,其对称轴是_______. (2) 垂径定理及其推论①垂径定理:垂直于弦的直径______这条弦,并且平分这条弦所对的______; ①推论:平分弦(非直径)的直径______于弦,并且平分这条弦所对的两条弧.➢ 考点分类考点1 圆心角、弧、弦之间的关系例1如图所示,圆O 通过五边形OABCD 的四个顶点,若D AB=150°,A=65°,D=60°,则的度数为( )A.25°B.40°C.50°D.55°考点2垂径定理及简单应用例2如图所示,水平放置的圆柱形排水管道的截面直径是1m,其中水面的宽AB 为0.8m,则排水管内水的深度为_______m.考点3垂径定理与其他知识的综合运用例3如图,线段AB 是⊙O 的直径,弦CD ⊥AB 于点H ,点M 是弧CBD 上任意一点,AH =2,CH =4.(1)求⊙O 的半径r 的长度; (2)求sin ∠CMD ;(3)直线BM 交直线CD 于点E ,直线MH 交⊙O 于点N ,连接BN 交CE 于点F ,求HE •HF 的值.➢ 真题演练1.如图,AB 是⊙O 的弦,半径OC ⊥AB 于点D ,连接AO 并延长,交⊙O 于点E ,连接BE ,DE .若DE =3DO ,AB =4√5,则△ODE 的面积为( )A .4B .3√2C .2√5D .2√62.如图,⊙O 的半径为5,弦AB 的长为8,M 是弦AB 上的一个动点,则线段OM 的长的最小值为( )A .3B .4C .6D .83.在正方形网格中,以格点O 为圆心画圆,使该圆经过格点A ,B ,并在点A ,B 的右侧圆弧上取一点C ,连接AC ,BC ,则sin C 的值为( )A .√32B .12C .1D .√224.如图,半径为5的⊙A 与y 轴交于点B (0,2)、C (0,10),则点A 的横坐标为( )A .﹣3B .3C .4D .65.如图,在⊙O 中,直径AB =10,CD ⊥AB 于点E ,CD =8.点F 是弧BC 上动点,且与点B 、C 不重合,P 是直径AB 上的动点,设m =PC +PF ,则m 的取值范围是( )A .8<m ≤4√5B .4√5<m ≤10C .8<m ≤10D .6<m <106.在⊙O 中内接四边形ABCD ,其中A ,C 为定点,AC =8,B 在⊙O 上运动,BD ⊥AC ,过O 作AD 的垂线,垂足为E ,若⊙O 的直径为10,则OE 的最大值接近于( )A .52B .5√23C .4D .57.如图,点A ,B ,C 都在⊙O 上,B 是AC ̂的中点,∠OBC =50°,则∠AOB 等于 °.8.如图,将半径为rcm 的⊙O 折叠,弧AB 恰好经过与AB 垂直的半径OC 的中点D ,已知弦AB 的长为4√15cm ,则r = cm .9.如图,AB是⊙O的直径,∠BOD=120°,C为弧BD的中点,AC交OD于点E,DE =1,则AE的长为.10.如图,AB为⊙O的直径,AE为⊙O的弦,C为优弧ABÊ的中点,CD⊥AB,垂足为D.若AE=8,DB=2,则⊙O的半径为.11.如图,⊙O中,直径CD⊥弦AB于E,AM⊥BC于M,交CD于N,连接AD.(1)求证:AD=AN;(2)若AB=8,ON=1,求⊙O的半径.➢课后练习1.如图,在⊙O中,直径CD垂直弦AB于点E,且OE=DE.点P为BĈ上一点(点P不与点B,C重合),连接AP,BP,CP,AC,BC.过点C作CF⊥BP于点F.给出下列结论:①△ABC是等边三角形;②在点P从B→C的运动过程中,CFAP−BP的值始终等于√32.则下列说法正确的是()A.①,②都对B.①对,②错C.①错,②对D.①,②都错2.如图,在半径为5的⊙O 内有两条互相垂直的弦AB 和CD ,AB =8,CD =8,垂足为E .则tan ∠OEA 的值是( )A .1B .√63C .√156D .2√1593.如图,四边形ABCD 内接于半径为5的⊙O ,AB =BC =BE ,AB ⊥BE ,则AD 的长为( )A .5B .5√2C .5√3D .104.如图,点A ,B ,C 在⊙O 上,∠AOC =90°,AB =√2,BC =1,则⊙O 的半径为( )A .√3B .√52C .√102D .√2+125.下列说法正确的是( )A .同弧或等弧所对的圆心角相等B .所对圆心角相等的弧是等弧C .弧长相等的弧一定是等弧D .平分弦的直径必垂直于弦6.如图,A ,B 为圆O 上的点,且D 为弧AB 的中点,∠ACB =120°,DE ⊥BC 于E ,若AC =√3DE ,则BE CE的值为( )A .3B .2C .√33+1D .√3+17.如图所示,在⊙O 中,BC 是弦,AD 过圆心O ,AD ⊥BC ,E 是⊙O 上一点,F 是AE 延长线上一点,EF =AE .若AD =9,BC =6,设线段CF 长度的最小值和最大值分别为m 、n ,则mn =( )A .100B .90C .80D .708.如图,A ,B 是⊙O 上的点,∠AOB =120°,C 是AB̂的中点,若⊙O 的半径为5,则四边形ACBO 的面积为( )A .25B .25√3C .25√34D .25√329.如图,AB 是⊙O 的直径,点C 是半圆上的一个三等分点,点D 是AĈ的中点,点P 是直径AB 上一点,若⊙O 的半径为2,则PC +PD 的最小值是 .10.如图,一下水管道横截面为圆形,直径为260cm ,下雨前水面宽为100cm ,一场大雨过后,水面宽为240cm ,则水位上升 cm .11.如图,在⊙O 中,点C 在弦AB 上,连接OB ,OC .若OB =5,AC =1,BC =5,则线段OC 的长为 .12.如图,以G(0,3)为圆心,半径为6的圆与x轴交于A,B两点,与y轴交于C,D 两点,点E为⊙G上一动点,CF⊥AE于F,点E在⊙G的运动过程中,线段FG的长度的最大值为.13.如图,⊙O的半径OD⊥弦AB于点C,连接AO并延长交⊙O于点E,连接EC.若AB =8,OC=3,则EC的长为.14.如图,射线PE平分∠CPD,O为射线PE上一点,以O为圆心作⊙O,与PD边交于点A、点B,连接OA,且OA∥PC.(1)求证:AP=AO.(2)若⊙O的半径为10,tan∠OPB=12,求弦AB的长.15.如图,在⊙O中,直径AB与弦CD相交于点E,OF⊥CD,垂足为F.设已知BE=5,AE=12OE,OF=1,求CD的长.➢冲击A+在Rt①ABC中,①BAC=90°,(1)如图1,D、E分别在BC、BA的延长线上,①ADE=2①CAD,求证:DA=DE;(2)如图2,在(1)的条件下,点F在BD上,①AFB=①EFD,求证:①FAD=①FED(3)如图3,若AB=AC,过点C作CN||AB,连接AN,在AN上取一点G,使GA=AC,连接BG交AC于点H,连接CG,试探究CN、CH、GN之间满足的数量关系式,并给出证明;。
《圆的基本性质》奥数复习题

《圆的基本性质》复习题姓名 学号一、填空题1.如果圆中一条弦长与半径相等,那么此弦所对的圆周角的度数为 .2.在Rt ΔABC 中,AB =6,BC =8,则这个三角形的外接圆直径是3.在等边三角形ABC 外有一点D ,满足AD=AC ,则∠BDC= 。
4.在四边形ABCD 中,AB=BC=AC=AD ,AH ⊥CD 于H ,CP ⊥BC 交AH 于P ,若AP=l ,则BD=5.如图,点A 、B 、Q 、D 、C 在圆上,BQ 与QD 分别是42°和38°, 则∠P+∠Q= . 6.(1998年全国初中数学竞赛试题)已知圆环内直径为a cm ,外直径为b cm ,将50个这样的圆环一个接一个环套地连成一条锁链,那么这条锁链拉直后的长度为 cm 。
7.如图,扇形MON 中,∠MON=90°,过线段MN 的中点A 作AB ∥ON ,交MN 于B ,∠BON= 8.(2008年蚌埠二中自主招生考试数学素质测试题)已知⊙O 的半径1=OA ,弦AB 、AC 的长分别是2、3,则BAC ∠的度数是 。
9.(2006年“TRULY 信利杯”全国初中数学竞赛初赛试题)半径为2的⊙O 中,弦AB 与弦CD 垂直相交于点P ,连结OP ,若OP =1,则AB ²+CD ²的值为 。
10.如图,在△ABC 中,∠A= 70°,⊙O 截△ABC 的三边所截得的弦长都相等,则∠BOC= .11.如图,△ABC 内接于直径为d 的圆.设BC=a ,AC=b ,那么△ABC 的高 CD= .12.(北京市竞赛题)如图所示,正方形ABCD 的中心为O ,面积为1989 cm ²,P 为正方形内一点,且∠OPB=45°,PA :PB=5:14,则PB 的长为 。
13.如图,在直径为20cm 的半圆0上P 、Q 两点,PC ⊥ AB 于C,QD ⊥AB 于D,QE ⊥ PO 于 E,AC=4cm ,则DE= cm.14.已知P 是正方形ABCD 内的一点,O 为正方形的中心,AP⊥BP ,OP=,PA=6,则正方形ABCD 的边长为 。
圆的基本性质-测试题
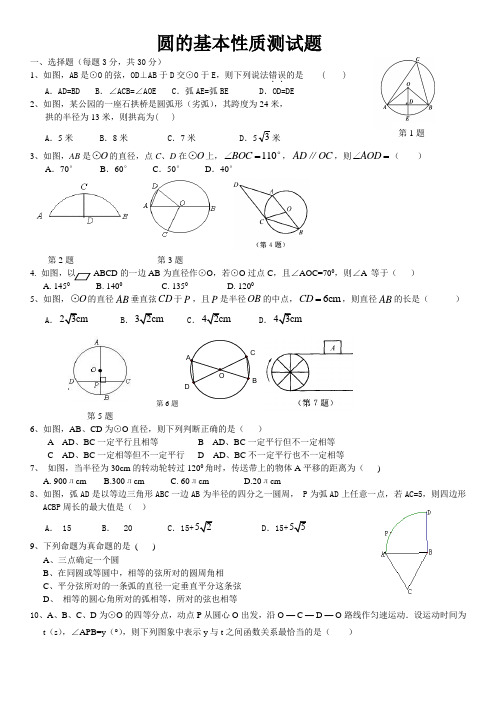
CBOAD圆的基本性质测试题一、选择题(每题3分,共30分)1、如图,AB 是⊙O 的弦,OD ⊥AB 于D 交⊙O 于E ,则下列说法错误..的是 ( ) A .AD=BD B .∠ACB=∠AOE C .弧AE=弧BE D .OD=DE2、如图,某公园的一座石拱桥是圆弧形(劣弧),其跨度为24米,拱的半径为13米,则拱高为( )A .5米B .8米C .7米D .53米3、如图,AB 是O ⊙的直径,点C 、D 在O ⊙上,110BOC ∠=°,AD OC ∥,则AOD ∠=( )A .70°B .60°C .50°D .40°第2题 第3题4. 如图,以 ABCD 的一边AB 为直径作⊙O ,若⊙O 过点C ,且∠AOC=700,则∠A 等于( ) A. 1450 B. 1400 C. 1350 D. 12005、如图,O ⊙的直径AB 垂直弦CD 于P ,且P 是半径OB 的中点,6cm CD =,则直径AB 的长是( )A .23cmB .32cmC .42cmD .43cm第5题6、如图,AB 、CD 为⊙O 直径,则下列判断正确的是( )A AD 、BC 一定平行且相等B AD 、BC 一定平行但不一定相等 C AD 、BC 一定相等但不一定平行 D AD 、BC 不一定平行也不一定相等7、 如图,当半径为30cm 的转动轮转过1200角时,传送带上的物体A 平移的距离为( ) A. 900лcm B.300лcm C. 60лcm D.20лcm8、如图,弧AD 是以等边三角形ABC 一边AB 为半径的四分之一圆周, P 为弧AD 上任意一点,若AC=5,则四边形ACBP 周长的最大值是( )A . 15B . 20C .15+52D .15+55 9、下列命题为真命题的是 ()A 、三点确定一个圆B 、在同圆或等圆中,相等的弦所对的圆周角相C 、平分弦所对的一条弧的直径一定垂直平分这条弦D 、 相等的圆心角所对的弧相等,所对的弦也相等10、A 、B 、C 、D 为⊙O 的四等分点,动点P 从圆心O 出发,沿O — C — D — O 路线作匀速运动.设运动时间为t (s ),∠APB=y (°),则下列图象中表示y 与t 之间函数关系最恰当的是( )第6题第1题OAC B第16题 第14题图ECDAB二、填空题(每题4分,共32分)11、已知⊙O 的周长为6π,当PO 时,点P 在⊙O 上。
圆的基本性质练习
第二十四章圆的基本性质练习班级_____________ 学号__________ 姓名_________ 成绩评定________一、看准了再选1..如图,⊙O中,ABDC是圆内接四边形,∠BOC=110°,则∠BDC的度数是()A.110°B.70°C.55°D.125°2.如图,⊙O的直径CD过弦EF的中点G且EF⊥CD,若∠EOD=40°,则∠DCF等于() A.80° B. 50° C.40° D. 20°3.直线a上有一点到圆心O的距离等于⊙O的半径,则直线a与⊙O的位置关系是()A、相离B、相切C、相切或相交D、相交4.在⊙O中,弦AB垂直并且平分一条半径,则劣弧AB的度数等于()A.30°B.120°C.150°D.60°5.如图,⊙O的半径OA=3,以点A为圆心,OA的长为半径画弧交⊙O于B,C•则BC=(). A.B..326..如图所示,∠1,∠2,∠3的大小关系是().A.∠1>∠2>∠3 B.∠3>∠1>∠2 C.∠2>∠1>∠3 D.∠3>∠2>∠1 7..如图,已知∠BAC=45°,一动点O在射线AB上运动(点O•与点A不重合),设OA=x,如果半径为1的圆O与射线AC有公共点,那么x的取值范围是()OCFGDEA.0<x.1<xC.1≤xD.8.如图,AB、AC与⊙O相切于点B、C,∠A=50°,点P是圆上异于B、C的一动点,则∠BPC的度数是()A.65° B.115° C.65°或115° D.130°或50°9如图,PA、PB分别切⊙O于A、B,AC是⊙O的直径,连结AB、BC、OP,则与∠PAB相等的角有()个。
2018中考复习-圆的基本性质练习题.docx
1、(2017黄冈)已知:如图,在00中,OA 丄BC.ZAOB = 70°,则Z/EC 的度数为( )••• ZADC -ZA0B=35°故选:B.2、(2017毕节)如图,AB 是O0的直径,CD 是O0的眩,ZACD 二30° ,则ZBAD 为(V ZACD=30° ,A ZABD=30° ,VAB 为直径,AZADB=90° ,AZBAD=90° - ZABD 二60。
.故选C.A. 30° B. 35° C. 45° D. 70°解:TOA 丄BC•••BC 二ACT ZA0B=70°A解:连接BD,60° D. 70°3、如图,0为原点,点A 的坐标为(3, 0),点B 的坐标为(0, 4) , 0D 过A 、B. 0三点,如图,连接AB,V ZA0B=90° ,・・・AB 为圆的直径,由圆周角定理,得ZC=ZAB0,在RtAAB0中,023, 0B=4,由勾股定理,得AB 二5,OB 4•I cosC 二 cos ZAB0 二 - =— .AB 5故选D.4、(2016南宁)如图,点A, B, C, P 在上,CD 丄0A, CE 丄0B,垂足分別为D, E, ZDCE 二40° , 则ZP 的度数为( )A. 140°B. 70°C. 60°D. 40°解:TCD 丄0A, CE 丄0B,垂足分别为 D, E, ZDCE 二40° ,・・・ZD0E 二 180° ・40° 二 140° ,A ZP=izD0E=70° ・故选 B.点C 为念) 上一点(不与0、A 两点重合), 则cosC 的值为(5、(2017泸州)如图,AB是。
0的直径,弦CD丄AB于点E,若AB=8, AE=1,则弦CD的长是()A. V7B. 2>/7C. 6D. 8【答案】B.【解析】试题分析:已知AE=1,可得024, 0E=3,连结0C,在RtAOCE中,根据勾股定理可得CE 二历;又因CD丄AB、根据垂径定理可得CD=2CE=2护,故选B.6、(2017青岛)如图,AB是<30的直径,C, D, E在00上,若ZAED = 20°,则ZBCD的度数为()A. 100°110° C. 115°D、120°【答案】B【解析】试题分析:如下图,连接AD, ADVZAED=20°.\ZABD=ZAED=20°VAB是的直径・•・ ZADB=90°AZ BAD=70 °・・・ZBCD二110°7、(2017南京)过三点A (2, 2) , B (6, 2) , C (4, 5)的圆的圆心坐标为()已知 A (2, 2) , B (6, 2) , C (4,・・・AB 的垂直平分线是x 二晋二4,设直线BC 的解析式为y 二kx+b,把B (6, 2) , C (4, 5)代入上式得y=--|x+ll, 9设BC 的垂直平分线为y-|x+m,7把线段BC 的屮点坐标(5,言)代入得m・••过A 、B 、C 三点的圆的圆心坐标为(4,里).6故选A.8、(2017贵港)如图,A, B, C, D 是00上的四个点,B 是葢的中点,M •是半径0D 上任意 一点.若ZBDC 二40。
圆的基本性质经典题库
第三章圆的基本性质第一节圆第1课时[基础训练]1.下列结论正确的是( )A.弦是直径B.弧是半圆C.半圆是弧D.过圆心的线段是直径2.两圆的圆心都是O,半径分别是r1, r2( r l < r2 ) , 若r l <OP<r2、则点P在( )A.大圆外B.小圆内C.大圆内,小圆外D.无法确定3.若OP的半径为13,圆心P的坐标为(5, 12 ), 则平面直角坐标系的原点O与OP的位置关系是( )A.在⊙P内B.在⊙P内上C.在⊙P外D.无法确定4.已知⊙O的半径长6cm,P为线段O A的中点,若点P在⊙O上,则OA的长是( )A.等于6cm B.等于12cm C.小于6cm D.大于12cm5.圆上各点到圆心的距离都等于 , 到圆心距离等于半径的点都在 .6.在Rt△ABC中,∠C=900, CD⊥AB, AB=2, BC=3,若以C为圆心,以2为半径作⊙C,则点A在⊙C ,点B 在⊙C ,点D在⊙C .7.一个点到定圆上最近点的距离为4,最远点的距离为9,则此圆的半径是__________.8.如图,AB, CD为⊙O的两条直径,E, F分别为OA, OB的中点,求证:四边形CEDF是平行四边形.[综合提高]1. ⊙0的半径为13cm,圆心O到直线l的距离d=OD=5cm.在直线l上有三点P,Q,R,且PD = 12cm, QD<12cm, RD>12cm,则点P在,点Q在,点R在 .2.在以AB=5cm为直径的圆上,到直线AB的距离为2.5cm的点有( )A.无数个 B.1个 C. 2个 D. 4个3. AB为⊙0的直径,C为⊙O上一点,过C作CD⊥AB于点D,延长CD至E,使DE=CD,那么点E的位置( )A.在⊙0 内B.在⊙0上C.在⊙0外D.不能确定4. 在⊙0中,半径为6,圆心O在坐标原点上,点P的坐标为(3,5),则点P与⊙0的位置关系是( )A.点P在⊙0内B.点P在⊙0上C.点P在⊙0外D.不能确定5.如图,点A,D,G,M在半圆上,四边形ABOC, DEOF,HMNO均为矩形,BC=a,EF=b, NH=C,则下列各式中正确的是( )A.a>b>cB.a=b=cC.c>a>bD.b>c>a6.在平面直角坐标系内,以原点O为圆心、5为半径作O,已).试知A、B、C三点的坐标分别为A(3,4),B(-3,-3),C(4,10判断A、B、C三点与O的位置关系.7.⊙0的半径为2,点P到圆心的距离OP=m, 且m使关于二的方程2x2-22x+m-1=0有实根,试确定点P的位置.[拓展延伸]如图,点P的坐标为(4,0), p的半径为5,且p与x轴交于点A,B,与y轴交于点 C,D, 试求出点A , B,C,D的坐标.第2课时[基础训练]1.判断正误.(1)三点确定一个圆. ( )(2)已知圆心和半径可以确定一个圆. ( )(3)已知圆心和圆上一点可以确定一个圆. ( )(4) 已知半径和圆上一点可以确定一个圆. ( )(5)已知半径和圆上两点可以确定一个圆. ( )2.下列说法正确的是( )A.一个点可以确定一条直线 B.两个点可以确定两条直线C.三个点可以确定一个圆 D.不在同一直线上的三点确定一个圆3.直角三角形两直角边长分别为3和l,那么它的外接圆的直径是( )A.1B.2C.3D.44.下列命题中,正确的是()A.三角形的外心是三角形的三条高线的交点B.等腰三角形的外心一定在它的内部C.任何一个三角形有且仅有一个外接圆D.任何一个四边形都有一个外接圆5. 下图是一个圆形轮子的一部分,请你用直尺和圆规把它补完整.[综合提高]1._______ 三角形的外心在它的内部,_______三角形的外心在它的外部;直角三角形的外心在______________.2.如果以平行四边形的对角线的交点为圆心,以它和一边中点的距离为半径画圆,若这个四边形四条边的中点都在这个圆上,那么这个四边形是 ( )A .矩形B .正方形C .等腰梯形D .菱形3. 下列命题正确的个数有( )① 矩形的四个顶点在同一个圆上; ② 梯形的四个顶点在同一个圆上; ③ 菱形的四边中点在同一个圆上; ④ 平行四边形的四边中点在同一个圆上.A. 1个B. 2个C. 3个D. 4个4.在Rt △ABC 中,AB=6 , BC=8,那么这个三角形的外接圆直径是( )A. 5B.10C.5 或 4D. 10或85.已知等腰三角形ABC 中,AB=AC ,O 是ABC ∆的外接圆,若 O 的半径是4,120BOC ∠=,求AB 的长.6.如图所示,平原上有三个村庄A 、B 、C ,现计划打一口水井p ,使水井到三个村庄的距离相等。
圆的基本性质经典题库
第三章圆的基本性质第一节圆第1课时[基础训练]1.下列结论正确的是( )A.弦是直径 B.弧是半圆 C.半圆是弧 D.过圆心的线段是直径2.两圆的圆心都是O,半径分别是r1, r2 ( r l < r2 ) , 若r l <OP<r2、则点P在( )A.大圆外 B.小圆内 C.大圆内,小圆外 D.无法确定3.若OP的半径为13,圆心P的坐标为(5, 12 ), 则平面直角坐标系的原点O与OP的位置关系是( )A.在⊙P内 B.在⊙P内上 C.在⊙P外 D.无法确定4. 已知⊙O的半径长6cm,P为线段O A的中点,若点P在⊙O上,则OA的长是( )A.等于6cm B.等于12cm C.小于6cm D .大于12cm5.圆上各点到圆心的距离都等于 , 到圆心距离等于半径的点都在 .6.在Rt△ABC中,∠C=900, CD⊥AB, AB=2, BC=3,若以C为圆心,以2为半径作⊙C,则点A在⊙C ,点 B 在⊙C ,点D在⊙C .7.一个点到定圆上最近点的距离为4,最远点的距离为9,则此圆的半径是__________.8.如图,AB, CD为⊙O的两条直径,E, F 分别为OA, OB的中点,求证:四边形CEDF是平行四边形.[综合提高]1. ⊙0的半径为13cm,圆心O到直线l的距离d=OD=5cm.在直线l上有三点P,Q,R,且PD = 12cm , QD<12cm, RD>12cm,则点P在,点Q在,点R在 .2.在以AB=5cm为直径的圆上,到直线AB的距离为2.5cm的点有( )A.无数个个 C. 2个 D. 4个3. AB为⊙0的直径,C为⊙O上一点,过C作CD⊥AB于点D,延长CD至E,使DE=CD,那么点E的位置( )A.在⊙0 内 B.在⊙0上 C.在⊙0外 D.不能确定4. 在⊙0中,半径为6,圆心O在坐标原点上,点P的坐标为(3,5),则点P与⊙0的位置关系是( )A.点P在⊙0内 B.点P在⊙0上 C.点P在⊙0外 D.不能确定5.如图,点A,D,G,M在半圆上,四边形ABOC, DEOF,HMNO均为矩形,BC=a,EF=b, NH=C,则下列各式中正确的是( )>b>c =b=c >a>b >c>a6.在平面直角坐标系内,以原点O为圆心、5为半径作O,已知A、B、C).试判断A、B、三点的坐标分别为A(3,4),B(-3,-3),C(4,10C三点与O的位置关系.7.⊙0的半径为2,点P到圆心的距离OP=m, 且m使关于二的方程2x2-22x+m-1=0有实根,试确定点P的位置.[拓展延伸]如图,点P的坐标为(4,0), p的半径为5,且p与x轴交于点A,B,与y轴交于点 C,D, 试求出点A , B,C,D的坐标.第2课时[基础训练]1.判断正误.(1)三点确定一个圆. ( )(2)已知圆心和半径可以确定一个圆. ( )(3)已知圆心和圆上一点可以确定一个圆. ( )(4) 已知半径和圆上一点可以确定一个圆. ( )(5)已知半径和圆上两点可以确定一个圆. ( )2.下列说法正确的是( )A.一个点可以确定一条直线 B.两个点可以确定两条直线C.三个点可以确定一个圆 D.不在同一直线上的三点确定一个圆3. 直角三角形两直角边长分别为3和l,那么它的外接圆的直径是( ).2 C4. 下列命题中,正确的是()A.三角形的外心是三角形的三条高线的交点B.等腰三角形的外心一定在它的内部C.任何一个三角形有且仅有一个外接圆D.任何一个四边形都有一个外接圆5. 下图是一个圆形轮子的一部分,请你用直尺和圆规把它补完整.[综合提高]三角形的外心在它的内部,_______三角形的外心在它的外部;直角三角形的外心在______________.2.如果以平行四边形的对角线的交点为圆心,以它和一边中点的距离为半径画圆,若这个四边形四条边的中点都在这个圆上,那么这个四边形是 ( ) A .矩形 B .正方形 C .等腰梯形 D .菱形3. 下列命题正确的个数有( )① 矩形的四个顶点在同一个圆上; ② 梯形的四个顶点在同一个圆上; ③ 菱形的四边中点在同一个圆上; ④ 平行四边形的四边中点在同一个圆上. A. 1个 B. 2个 C. 3个 D. 4个 4.在Rt △ABC 中,AB=6 , BC=8,那么这个三角形的外接圆直径是( ) A. 5 .10 C 或 4 D. 10或8 5.已知等腰三角形ABC 中,AB=AC ,O 是ABC ∆的外接圆,若 O 的半径是4,120BOC ∠=,求AB 的长.6.如图所示,平原上有三个村庄A 、B 、C ,现计划打一口水井p ,使水井到三个村庄的距离相等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
圆的基本性质练习
一、看准了再选
1..如图,⊙O 中,ABDC 是圆内接四边形,∠BOC=110°,则∠BDC 的度数是( ) A.110° B.70° C.55° D.125°
2.如图,⊙O 的直径CD 过弦EF 的中点G 且EF ⊥CD ,若∠EOD=40°,则∠DCF 等于( ) A.80° B. 50° C.40° D. 20°
3.直线a上有一点到圆心O 的距离等于⊙O 的半径,则直线a与⊙O 的位置关系是( ) A、相离 B、相切 C、相切或相交 D、相交
4.在⊙O 中,弦AB 垂直并且平分一条半径,则劣弧AB 的度数等于( ) A.30° B.120° C.150° D.60°
5.如图,⊙O 的半径OA=3,以点A 为圆心,OA 的长为半径画弧交⊙O 于B ,C•则BC=( ). A .32 B .33 C .
3
2
3 D .
33
2
6..如图所示,∠1,∠2,∠3的大小关系是( ).
A .∠1>∠2>∠3
B .∠3>∠1>∠2
C .∠2>∠1>∠3
D .∠3>∠2>∠1 7..如图,已知∠BAC=45°,一动点O 在射线AB 上运动(点O•与点A 不重合),设OA=x ,如果半径为1的圆O 与射线AC 有公共点,那么x 的取值范围是( ) A .0<x ≤2 B .1<x ≤2 C .1≤x ≤2 D .x>2
8.如图,AB 、AC 与⊙O 相切于点B 、C ,∠A=50°,点P 是圆上异于B 、C 的一动点,则∠
BPC 的度数是( )
O
C
F
G
D E
A
P
B
C O
A .65°
B .115°
C .65°或115°
D .130°或50°
9如图,PA 、PB 分别切⊙O 于A 、B ,AC 是⊙O 的直径,连结AB 、BC 、OP ,则与∠PAB 相等
的角有( )个。
A 、1
B 、2
C 、3
D 、4
10.边长分别为3,4,5的三角形的内切圆半径与外接圆的半径之比为( ). A .1:5 B .2:5 C .3:5 D .4:5
11.如图所示,圆弧形桥拱的跨度AB=12m ,拱高CD=4m ,则拱桥的直径为( ).
A .6.5m
B .9m
C .13m
D .15m 二.想好了再规范的写画
12.如图所示,线段AD 过圆心O 交⊙O 于D ,C 两点,∠EOD=78°,AE 交⊙O 于B ,• 且AB=OC ,求∠A 的度数.
O
E
D
C B
A
13.如图AB 是⊙O 的直径,AC 是弦,OD ⊥AB 于O ,交AC 于D ,OD=2,∠A=30°,求CD 。
14.如图,已知在Rt △ABC 中,AC=12,BC=9,D 是AB 上一点,以O 为圆心,BD 为直径的⊙O 切AC 于E ,求AD 的长。
15.如图所示,AB 是⊙O 的直径,AB=AC ,D ,E 在⊙O 上,说明BD=DE
C
E
B
· B
A C D O
圆的基本性质练习
一、想好了再填
1.6cm 长的一条弦所对的圆周角为90°,则此圆的直径为 ___________ 。
2.已知I 是△ABC 的内心,且∠BIC=130°,则∠A=_______. 3.已知:△ABC 中,∠C=90°,AC=5cm ,AB=13cm ,以B 为圆心,以12cm 长为半径作⊙B ,则C 点在⊙B_____________.
4.如图,△ABC 为⊙O 的内接三角形,O 为圆心,OD ⊥AB ,•垂足为D ,OE ⊥AC ,垂足为E ,若DE=3,则BC=________.
5.如图,在直径为10m 的圆柱形油槽内装入一些油后,油面宽AB=8m ,•那么油的最大深度是_________. 6.如图,△ABC 内接于⊙O ,∠BAC =120°,AB =AC ,BD 为 ⊙O 的直径,AD =6,则BC
= 。
7.如图所示,∠APB=60°,半径为a 的⊙O 切PB 于P 点,若将⊙O 在PB 上向右滚动,则当滚动到⊙O 与PA 也相切时,圆心O 移动的水平距离是_________.
8.如图,在以O 为圆心的两个同心圆中,大圆的弦AB 是小圆的切线,点P 为切点,已知AB=8,大圆半径为5,则小圆半径为_______.
9.如图,已知A ,B ,C ,D ,E 均在⊙O 上,且AC 为⊙O 的直径,则∠A+•∠B+•∠C=________. 10.若Rt △ABC 的内切圆半径为1,斜边长是6,则此三角形的周长为________. 22.如图,PA 、PB 、DE 分别切⊙O 于A 、B 、C ,若⊙O 的半径为6cm ,PO=10cm ,则△PDE 的周长为___________
11.)已知,如图:AB 为⊙O 的直径,AB =AC ,BC 交⊙O 于点D ,AC 交⊙O 于点E ,∠BAC =450。
给出以下五个结论:①∠EBC =22.50,;②BD =DC ;③AE =2EC ;④劣
A B
D C O
E
弧是劣弧的2倍;⑤AE =BC 。
其中正确结论的序号是 。
三、解答题:
12.如图,AB 是⊙O 的直径,CO ⊥AB 于O ,连CB 交⊙O 于D ,过D 作⊙O 的切线EF 交CO
于E ,求证:CE=DE
13.如图,AD 是△ABC 的外接圆的⊙O 的直径,AD=10㎝,∠DAC=∠ABC ,求AC 的长。
14.如图所示,某地有一座圆弧形的拱桥,桥下的水平宽度为7.2m ,•拱顶高出水面2.4m ,现有一艘宽为3m ,船舱顶部为长方形,并高出水面2m 的货船要经过这里,此货船能顺利通过这座拱桥吗?用你所学的数学知识说明理由.
15.如图所示,AB ,AC 是⊙O 的弦,AD ⊥BC 于D ,交⊙O 于F ,AE 与⊙O 的直径,试问两
弦BE 与CF 的大小有何关系,说明理由.
B
A C
O
D C
O
B
E
D
F。
