广州大学2013-2014(1)概率统计(A)
南京理工大学 2013概率与统计(A)试题
(1)常数 ;
(2)随机变量X的分布函数 ;
(3) .
(注: )
3、(10分)设随机变量X的概率密度为 求 的概率密度函数。
4、(15分)设二维连续型随机变量( )的概率密度函数为
求(1)常数 ;
(2)随机变量X,Y的边缘概率密度函数 , ;
(3)
第1页共1页
第页共页
南京理工大学课程考试试卷(学生考试用)
课程名称:概率与统计(A)学分:3教学大纲编号:11022601
试卷编号:考试方式:笔试,闭卷满分分值:100考试时间:120分钟
组卷日期:2013年1月2日组卷教师(签字):审定人(签字):
5、(15分)已知二维随机变量 ,且 ,记 ,求 与 的相关系数 。
6、(10分)在次品率为 的一大批产品中,任意抽取300件产品,利用德莫佛一拉普照拉斯定理近似计算抽取的产品中次品数在40与60之绝域
Z检验
t检验
检验
1、(10分)试卷中有一道选择题,共有4个答案可供选择,其中只有1个答案是正确的.任一考生如果会解这道题,则一定能选出正确答案;如果他不会解这道题,则任选一个答案。设考生会解这道题的概率是0.8,求:
(1)考生选出正确答案的概率;
(2)已知某考生所选答案是正确的,则他确实会解这道题的概率。
(注: =0.939)
7、(15分)设随机变量 与 相互独立且分别服从正态分布 与 ,其中 是未知参数且 ,设 ,
(1)求 的概率密度 ;
(2)设 为来自总体 的简单随机样本,求 的最大似然估计量 ;
2013-2014-北邮概率论研究生概率论-答案

北京邮电大学2013——2014学年第1学期《概率论与随机过程试题》期末考试试题答案考试注意事项:学生必须将答题内容(包括填空题)做在试题答题纸上,做在试卷纸上一律无效。
在答题纸上写上你的班号和选课单上的学号,班内序号!一、 填空题:(每空3分,共30分)1.给定集合A ⊂Ω,则定义在Ω上的包含A 的最小σ-代数是 .{,,,}A A ΩΦ2.若12A ,A 是Ω上的两个非空集合类,i ν是i A (1,2)i =上的测度,若满足:(1) ;(2)112,()()A A A νν∀∈=有A ,则称2ν是1ν在2A 上的扩张。
12⊂A A3.某集代数包含了所有的左开右闭区间(实数集上的). 该集代数上有一个测度P ,对于任意可测集(,]a b ,其中a b <,均有()(,]P a b b a =-.将该测度扩张到某σ-代数上记为μ.对单点集{}1,{}()1μ= . 04.设概率测度空间(),,F P Ω,,,A F B F AB ∈∈=Φ,()()11,23P A P B ==,两个简单函数()()()2A A f ωχωχω=+,()()()2B B g ωχωχω=+,则[]E f = ,[]E fg = .37,235. 设X 为定义某概率空间上的随机变量,若X 的分布函数为()F x ,则数学期望EX 的L-S 积分形式为 .()xdF x +∞-∞⎰6. 设三维随机变量(,,)X Y Z 服从正态分布(,)N a B ,其中()1,2,3a =,211121112B ⎛⎫ ⎪= ⎪ ⎪⎝⎭,则[[|]]E E X YZ =17.设随机过程{(),}t t X -∞<<+∞为平稳二阶矩过程,且均方连续.设该过程的均值函数为1μ=,相关函数(,)2t sR s t e --=,均方积分220()X t dt π⎰记为随机变量ξ. 则()E ξ= .π8.设()N t 为泊松过程,则条件概率((2)2|(3)3)P N N === .499. 设()W t 为参数为2σ的维纳过程,(0)0W =,则()cov (1),(2)W W = .2σ二.(8分)设A 是λ系,证明A 是单调类;若A 也是π系,证明A 是σ-代数。
0270统计学一级学科硕士研究生培养方案(2013)

统计学硕士研究生培养方案(2013级研究生开始使用)一、专业学科、学制、学习方式一级学科名称:统计学(代码: 0270 )二级学科名称:金融统计与风险管理(代码: 027001 )二级学科名称:经济统计(代码: 027002 )二级学科名称:应用统计(代码: 027003 )二级学科名称:管理统计与决策(代码: 027004 )二级学科名称:数量金融与保险精算(代码: 027005 )学制:三年学习方式:全日制二、本学科情况介绍1、本学科建设时间较长,师资力量雄厚,科研实力强。
我校统计学学科作为应用数学的一个分支,建立于1958年,1994年经广州市人民政府批准成立了广州市系统工程研究所,以社会、经济、科教、环境等领域中的复杂大系统为研究对象,开展一系列统计分析研究工作。
1997年开始招收硕士生,2009年开始招收博士生。
2011年我校统计学被批准为一级学科博士和硕士授予权。
本学科现有教授11人,副教授8人,其中博士18人,博士生导师7人。
先后主持国家自然科学基金、国家社科基金、国家统计局以及国家软科学基金等30余项,省部级项目30项,合计获得科研经费1000多万元,获省部级以上科研奖励3项。
出版学术专著9部,教材12部。
在《Biometrika》《Statistica Sinica》、《中国科学》、《统计研究》、《金融研究》等重要刊物上发表了一系列重要论文。
2、主要研究方向稳定,特色鲜明,学科带头人影响大。
学科带头人长期从事数理统计、经济统计理论与方法、管理统计与决策分析的研究,取得了一批重要成果,在国内外有重要影响。
如,本学科在时间序列分析领域已成为国内主要研究中心之一,在国际上具有重大影响的第八届泛华统计国际学术会议就是2010年在我校召开的。
3、学术交流频繁,学术地位高。
五年来,本学科组织了国际国内学术会议10次,与美国、加拿大、英国、德国、香港等海外10多所高校与研究所开展了频繁的国际交流与合作,先后有20多人次参加国际会议并做大会报告。
统计学班大二2013-2014第一学期课表
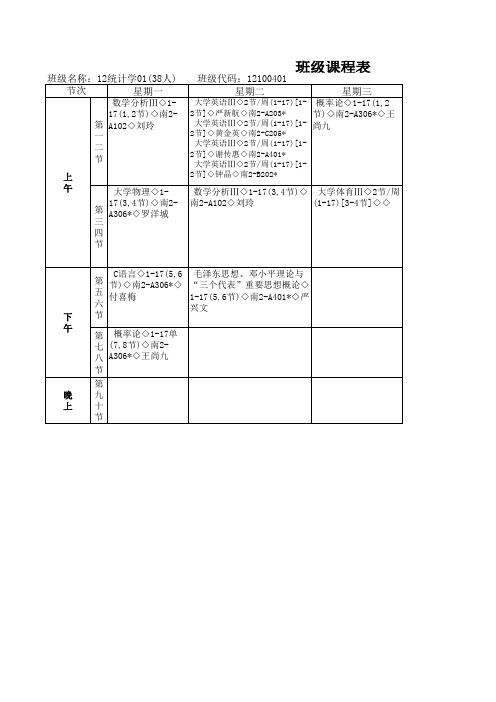
班级名称:12统计学01(38人) 节次 星期一
数学分析Ⅲ◇117(1,2节)◇南2第 A102◇刘玲 一 二 节 上 午
班级代码:12100401 星期二
星期三
大学英语Ⅲ◇2节/周(1-17)[1- 概率论◇1-17(1,2 2节]◇严新航◇南2-A203* 节)◇南2-A306*◇王 大学英语Ⅲ◇2节/周(1-17)[1- 尚九 2节]◇黄金英◇南2-C205* 大学英语Ⅲ◇2节/周(1-17)[12节]◇谢传惠◇南2-A401* 大学英语Ⅲ◇2节/周(1-17)[12节]◇钟晶◇南2-B202*
毛泽东思想、邓小平 理论与“三个代表”重 要思想概论◇1-17(5,6 节)◇南2-A401*◇严兴 文
C语言◇(A教学班)◇617(5,6节)◇科技-A205◇付 喜梅 C语言◇1-5(5,6节)◇南2A104*◇付喜梅
心理学◇1-17(7,8节) 数学分析Ⅲ◇1-17(7,8节) ◇南2-A104*◇穆湘兰 ◇南2-A102◇刘玲
大学物理◇117(3,4节)◇南2第 A306*◇罗洋城 三 四 节
数学分析Ⅲ◇1-17(3,4节)◇ 大学体育Ⅲ◇2节/周 南2-A102◇刘玲 (1-17)[3-4节]◇◇
下 午
C语言◇1-17(5个代表”重要思想概论◇ 五 付喜梅 1-17(5,6节)◇南2-A401*◇严 六 兴文 节 第 概率论◇1-17单 七 (7,8节)◇南2八 A306*◇王尚九 节 第 九 十 节
晚 上
表
星期四
大学物理◇1-17(1,2 节)◇南2-A306*◇罗洋 城
2013-2014学年第1学期 星期五
大学英语Ⅲ◇2节/周(1-17)[3大学物理实验◇14节]◇钟晶◇南2-B202* 15(3,4节)◇信息-2楼 ◇陈慧清/陈莹梅/李芝 大学英语Ⅲ◇2节/周(1-17)[3梅/彭瑞明/许海娟/张 4节]◇严新航◇南2-A203* 大学英语Ⅲ◇2节/周(1-17)[3德钱 4节]◇黄金英◇南2-C205* 大学英语Ⅲ◇2节/周(1-17)[34节]◇谢传惠◇南2-A401*
概率统计01概率【解析版】

第十一章 概率和统计第一节 概率1.【广东省惠州市2013届高三第一次模拟考试(理)】设随机变量ξ服从正态分布(3,4)N ,若(23)(2)P a P a ξξ<-=>+,则a =( )A .3B .53 C .5 D .733.【广东省湛江市2014届高三菩提高考调研考试(理)】已知离散型随机变量X 的分布列为:X 1 2 3 Pa b0.1且() 1.5E X =,则a b -= . 【答案】0.3. 【解析】试题分析:由概率的性质知0.110.9a b a b ++=⇒+=,由数学期望的定义知()1230.1 1.52 1.2E X a b a b =⨯+⨯+⨯=⇒+=,解得0.6a =,0.3b =,0.60.30.3a b ∴-=-=.考点:1.概率的基本性质;2.数学期望的定义4. 【广东省汕头四中2014届高三第一次月考(理)】从如图所示的正方形OABC 区域内任取一个点(,)M x y ,则点M 取自阴影部分的概率为( )A.12 B.13 C.14 D.165. 【广东省佛山市南海区2014届高三8月质检(理)】如右下图所示,EFGH 是以O 为圆心,半径为1的圆的内接正方形,将一粒豆子随机地扔到该圆内,用A 表示事件“豆子落在正方形EFGH 内”,B 表示事件“豆子落在扇形OHE (阴影部分)内”,则(|)P B A = .6.【广东省广州市越秀区2014届高三上学期摸底考试(理)】在区间[0,2]上随机取一个数a ,在区间[0,4]上随机取一个数b ,则关于x 的方程22x ax b ++0=有实根的概率是 .7.【广东省东莞市2013届高三模拟考试一(理)】某学生在参加政、史、地三门课程的学业水平考试中,取得A 等级的概率分别为54、53、52,且三门课程的成绩是否取得A 等级相互独立.记ξ为该生取得A 等级的课程数,其分布列如表所示,则数学期望ξE 的值为______________. 【答案】59 【解析】 试题分析:42313312237555555555125a =⨯⨯+⨯⨯+⨯⨯=,624581125125125b a =---=,所以6375824901231251251251255E ξ=⨯+⨯+⨯+⨯=.考点:1.独立性事件的概率计算;2.随机变量概率分布列的性质;3.数学期望的定义.8.【广东省汕头四中2014届高三第一次月考(理)】乒乓球单打比赛在甲、乙两名运动员间进行,ξ1 2 3P6125ab24125比赛采用7局4胜制(即先胜4局者获胜,比赛结束),假设两人在每一局比赛中获胜的可能性相同.(1)求甲以4比1获胜的概率;(2)求乙获胜且比赛局数多于5局的概率;(3)求比赛局数的分布列.9.【广东省惠州市2013届高三第一次模拟考试(理)】在某校高三学生的数学校本课程选课过程中,规定每位同学只能选一个科目.已知某班第一小组与第二小组各有六位同学选择科目甲或科目乙,情况如下表:科目甲科目乙总计第一小组 1 5 6 第二小组 2 4 6 总计 3 9 12 现从第一小组、第二小组中各任选2人分析选课情况.(1)求选出的4 人均选科目乙的概率;(2)设ξ为选出的4个人中选科目甲的人数,求ξ的分布列和数学期望.考点:1.独立事件的概率;2.离散型随机变量的期望和分布列.10.【广东省珠海市2014届高三9月摸底考试(理)】某大学一个专业团队为某专业大学生研究了多款学习软件,其中有A、B、C三种软件投入使用,经一学年使用后,团队调查了这个专业大一四个班的使用情况,从各班抽取的样本人数如下表班级一二三四人数 3 2 3 4(1)从这12人中随机抽取2人,求这2人恰好来自同一班级的概率.(2)从这12名学生中,指定甲、乙、丙三人为代表,已知他们下午自习时间每人选择A、B两个软件学习的概率每个都是16,且他们选择A、B、C任一款软件都是相互独立的.设这三名学生中下午自习时间选软件C的人数为ξ,求ξ的分布列和数学期望.【答案】(1)1366;(2)ξ的分布列如下ξ0123P1272949827ξ的期望是124801232279927Eξ=⨯+⨯+⨯+⨯=.ξ的期望是124801232279927Eξ=⨯+⨯+⨯+⨯=.考点:1.古典概型;2.排列组合;3.随机变量的分布列及其数学期望.11.【广东省广州市越秀区2014届高三上学期摸底考试(理)】某超市为了解顾客的购物量及结算时间等信息,安排一名员工随机收集了在该超市购物的50位顾客的相关数据,如下表所示:一次购物量n (件) 1≤n ≤3 4≤n ≤6 7≤n ≤9 10≤n ≤12 n ≥13 顾客数(人)x 20 10 5 y结算时间(分钟/人) 0.511.522.5已知这50位顾客中一次购物量少于10件的顾客占80%. (1)确定x 与y 的值;(2)若将频率视为概率,求顾客一次购物的结算时间X 的分布列与数学期望;(3)在(2)的条件下,若某顾客到达收银台时前面恰有2位顾客需结算,且各顾客的结算相互独立,求该顾客结算前的等候时间不超过...2分钟的概率.(3)记“该顾客结算前的等候时间不超过2分钟”为事件A ,该顾客前面第i 位顾客的结算时间为(1,2)i X i ,由于各顾客的结算相互独立,且12,X X 的分布列都与X 的分布列相同,所以121212()(0.5(0.5)(0.5(1)(0.5( 1.5)P A P X P X P X P X P X P X ==⋅=+=⋅=+=⋅=))) 121212(1(0.5)(1(1)( 1.5(0.5)P X P X P X P X P X P X +=⋅=+=⋅=+=⋅=))) 0.20.20.20.40.20.20.40.20.40.40.20.20.44=⨯+⨯+⨯+⨯+⨯+⨯= 为所求.考点:1.离散型随机变量及其分布列;2.独立事件的概率12. 【广东省珠海一中等六校2014届高三第一次联考(理)】甲乙丙三人商量周末去玩,甲提议去市中心逛街,乙提议去城郊觅秋,丙表示随意.最终,商定以抛硬币的方式决定结果.规则是:由丙抛掷硬币若干次,若正面朝上则甲得一分乙得零分,反面朝上则乙得一分甲得零分,先得4分者获胜,三人均执行胜者的提议.记所需抛币次数为ξ. (1)求ξ=6的概率; (2)求ξ的分布列和期望. 【答案】(1)()5616P ξ==;(2)详见解析.()323511156222216P C ξ⎛⎫⎛⎫==⨯⨯⨯⨯= ⎪ ⎪⎝⎭⎝⎭,()3336111572122216P C ξ⎛⎫⎛⎫==⋅⋅-⋅= ⎪ ⎪⎝⎭⎝⎭,故随机变量ξ分布列如下表所示:ξ 4 5 6 7P 1814516516……………………10分∴115593456784161616Eξ=⨯+⨯+⨯+⨯=………………………12分考点:1.超几何分布;2.离散型随机变量的分布列与数学期望13.【广东省湛江市2014届高三普通高考调研考试(理)】某种品牌的啤酒开展促销活动,期间销售的啤酒瓶盖内印有“再来一瓶”或“谢谢购买”字样,购买一瓶若其瓶盖内印有“再来一瓶”字样即为中奖,中奖概率为16,甲、乙、丙三位同学每人购买了一瓶该饮料.(1)求三位同学都没有中奖的概率;(2)求三位同学中至少有两位没有中奖的概率.()321512366627P ⎛⎫⎛⎫=+⨯⨯= ⎪ ⎪⎝⎭⎝⎭“至多一人不中奖”, 所以,“至少有两位没有中奖”的概率为 ()225112727P A B C A B C A B C A B C -⋅⋅+⋅⋅+⋅⋅+⋅⋅=-=. 考点:1.独立事件的概率;2.对立事件 14. 【广东省中山市高三级2013-2014学年第一学期期末统一考试】如图,一不规则区域内,有一边长为1米的正方形,向区域内随机地撒1000颗黄豆,数得落在正方形区域内(含边界)的黄豆数为 375 颗,以此实验数1000据为依据可以估计出该不规则图形的面积为 平方米.(用分数作答)15. 【广东省广州市2014届高三年级调研测试】如图3,设D 是图中边长为4的正方形区域,E 是D 内函数2y x =图象下方的点构成的区域.在D 内随机取一点,则该点落在E 中的概率为 .【答案】13. 【解析】 试题分析:图中阴影部分的面积22322211633S x dx x --'===⎰,而正方形区域的面积为Ox y 2 4-24416S =⨯=,故该点落在E 中的概率16113163S P S '==⨯=. 考点:1.定积分;2.几何概型 16. 【广东省华附、省实、广雅、深中2014届高三上学期期末联考】盒子中装有四张大小形状均相同的卡片,卡片上分别标有数i,i,2,2,--其中i 是虚数单位.称“从盒中随机抽取一张,记下卡片上的数后并放回”为一次试验(设每次试验的结果互不影响).(1)求事件A “在一次试验中,得到的数为虚数”的概率()P A 与事件B “在四次试验中,至少有两次得到虚数” 的概率()P B ;(2)在两次试验中,记两次得到的数分别为,a b ,求随机变量a b ξ=⋅的分布列与数学期望.E ξ所以1119()124.4244E =ξ⨯+⨯+⨯= 考点:1.随机事件、对立事件、独立重复事件的概率;2.随机变量的分布列和期望值.17. 【广东省梅州市2014届高三3月质检】如图,设D 是图中边长为2的正方形区域.,E 是函数3y x =的图像与x 轴及1x =±围成的阴影区域,项D 中随机投一点,则该点落入E 中的概率为( ) A .116B .18C .14D .1218.【广东省韶关市2014届高三调研考试】已知实数[0,10]x ,执行如图所示的程序框图,则输出的x不小于47的概率为.【答案】1 2【解析】试题分析:由几何概型得到输出的x不小于47的概率为P==考点:程序框图几何概型19.【广东省揭阳市2014届高三3月第一次模拟考试】从[]0,10中任取一个数x ,从[]0,6中任取一个数y ,则使534x y -+-≤的概率为 .20.【2014年广东省广州市普通高中毕业班综合测试一】甲、乙、丙三人参加某次招聘会,假设甲能被聘用的概率是25,甲、丙两人同时不能被聘用的概率是625,乙、丙两人同时能被聘用的概率为310,且三人各自能否被聘用相互独立. (1)求乙、丙两人各自被聘用的概率;(2)设ξ为甲、乙、丙三人中能被聘用的人数与不能被聘用的人数之差的绝对值,求ξ的分布列与均值(数学期望).213213191152552525⎛⎫⎛⎫+⨯-⨯+⨯⨯-= ⎪ ⎪⎝⎭⎝⎭, ()2132136311152552525P ξ⎛⎫⎛⎫⎛⎫==-⨯-⨯-+⨯⨯= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭, 因此随机变量ξ的分布列如下表所示 ξ1 3 P 1925 625所以随机变量ξ的均值(即数学期望)1963713252525E ξ=⨯+⨯=. 考点:1.独立事件概率的计算;2.离散型随机变量的概率分布列与数学期望21. 【广东省揭阳市2014届高三3月第一次模拟考试】图(5)是某市2月1日至14日的空气质量指数趋势图,空气质量指数(AQI )小于100表示空气质量优良,空气质量指数大于200表示空气重度污染,某人随机选择2月1日至2月12日中的某一天到达该市,并停留3天.(1)求此人到达当日空气质量重度污染的概率;(2)设ξ是此人停留期间空气重度污染的天数,求ξ的分布列与数学期望.(2)由题意可知,ξ的所有可能取值为0、1、2、3且()()()()()489489310124P P A A A P A P A P A ξ===++==, ()()()()211211212126P P A A P A P A ξ===+==, ()()()()112112213126P P A A P A P A ξ===+==,()()()()111511023146612P P P P ξξξξ==-=-=-==---=, (或()()3567105112P P A A A A A ξ===). 所以ξ的分布列为 ξ0 1 2 3 P 14 51216 16故ξ的期望151150123412664E ξ=⨯+⨯+⨯+⨯=. 考点:1.古典概型;2.离散型随机变量的分布列与数学期望.。
【推荐】2013-2019高考理科数学分类汇编-第13章 概率与统计

第十三章 概率与统计第1节 概率及其计算题型140 古典概型1.(2013广东理17)某车间共有12名工人,随机抽取6名,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数.(1) 根据茎叶图计算样本均值;(2) 日加工零件个数大于样本均值的工人为优秀工人.根据茎叶图推断该车间12名工人中有几名优秀工人;(3) 从该车间12名工人中,任取2人,求恰有1名优秀工人的概率.2. (2013全国新课标卷理14)从n 个正整数12n ,,,中任意取出两个不同的数,若取出的两数之和等于5的概率为114,则n = . 3.(2013江苏7)现在某类病毒记作n m Y X ,其中正整数m ,n (7m ,9n )可以任意选取,则n m ,都取到奇数的概率为 . 4. (2013安徽理21)某高校数学系计划在周六和周日各举行一次主题不同的心里测试活动,分别由李老师和 张老师负责.已知该系共有n 位学生,每次活动均需要该系k 位学生参加(n 和k 都是固定的正整数).假设李老师和张老师分别将各自活动通知的信息独立、随机的发给该系k 位学生,且所发信息都能收到.记该系收到李老师或张老师所发活动通知信息的学生人数为X . (1)求该系学生甲收到李老师或张老师所发活动通知信息的概率; (2)求使()P X m =取得最大值的整数m .5.(2014 江西理 12)10件产品中有7件正品,3件次品,从中任取4件,则恰好取到1件次品的概率是 .6.(2014 江苏理 4 )从1,2,3,6这4个数中一次随机地取2个数,则所取2个数的乘积为6的概率是 .7.(2014 广东理 11)从0,1,2,3,4,5,6,7,8,9中任取七个不同的数,则这七个数的中位数是6的概率为 .8.(2014 新课标1理5)4位同学各自在周六、周日两天中任选一天参加公益活动,则周六、周日都有同学参加公益活动的概率( ).A.18 B.38 C. 58 D. 789.(2014 陕西理 6)从正方形四个顶点及其中心这5个点中,任取2个点,则这2个点的距离不小于该正方形边长的概率为( ).A.15 B. 25 C. 35 D. 4510.(2014 新课标1理5)4位同学各自在周六、周日两天中任选一天参加公益活动,则周六、周日都有同学参加公益活动的概率( ).A.18 B.38 C. 58 D. 7811.(2014 陕西理 6)从正方形四个顶点及其中心这5个点中,任取2个点,则这2个点的距离不小于该正方形边长的概率为( ).A.15 B. 25 C. 35 D. 4512.(2015广东理科4)袋中共有15个除了颜色外完全相同的球,其中有10个白球,5个红球.从袋中任取2个球,所取的2个球中恰有1个白球,1个红球的概率为( ). A .521 B .1021 C .1121D .1 12.解析 从袋中任取2个球共有215C 105=种,其中恰好1个白球1个红球共有11105C C 50=种,所以恰好1个白球1个红球的概率为501010521=.故选B . 13. (2015北京理科16) A ,B 两组各由7位病人,他们服用某种药物后的康复时间(单位:天)记录如下:A 组:10,11,12,13,14,15,16B 组:12,13,15,16,17,14,a假设所有病人的康复时间互相独立,从A ,B 两组随机各选1人,A 组选出的人记为甲,B 组选出的人记为乙.(1)求甲的康复时间不少于14天的概率;(2)如果25a =,求甲的康复事件比乙的康复时间长的概率; (3)当a 为何值时,A ,B 两组病人康复时间的方差相等?(结论不要求证明)13. 解析 (1)设甲的康复事件为ξ,则()3147P ξ= , 即甲的康复时间不少于14天的概率为37.(2)设乙的康复事件为η,集合{}10,11,12,13,14,15,16A =,{}12,13,14,15,16,17,25B =,则选取病人的基本事件空间为(){},,A B ξηξη∈∈,共49个基本事件,其中符合题意的基本事件为:()13,12,()14,12,()14,13,()15,12,()15,13,()15,14,()16,12,()16,13,()16,14, ()16,15,共10个.从而()1049P ξη>=.(3)可以看出A 组7个连续的正整数,B 组为12至17共6个连续的正整数和a ,从而11a =或18时,两组离散程度相同,即方差相等.14.(2016江苏7)将一颗质地均匀的骰子(一种各个面上分别标有个点的正方体玩具)先后抛掷次,则出现向上的点数之和小于的概率是 . 14.解析 将先后两次点数记为,则基本事件共有(个), 其中点数之和大于等于有,共种,则点数之和小于共有种,所以概率为. 15.(2016上海理14)如图所示,在平面直角坐标系中,为正八边形的中心,,任取不同的两点,点满足,则点落在第一象限的概率是 .15. 解析 由题意,若要使得点落在第一象限,则只需使在第三象限,可考虑变动,当时,不存在;当时,符合要求,同理顺次画图即可.1,2,3,4,5,621056(),x y 6636⨯=10()()()()()()4,6,5,5,5,6,6,4,6,5,6,661030305366=xOy O 128A A A ()11,0A ,i j AA P i j OP OA OA ++=0P 528()i j OP OA OA =-+ P i j OA OA +i 1,2,3i=4i =7j =(((所有的满足条件的的数组为,共组, 故所求概率为.故填. 16.(2017山东理18(1))在心理学研究中,常采用对比试验的方法评价不同心理暗示对人的影响,具体方法如下:将参加试验的志愿者随机分成两组,一组接受甲种心理暗示,另一组接受乙种心理暗示,通过对比这两组志愿者接受心理暗示后的结果来评价两种心理暗示的作用,现有6名男志愿者1A ,2A ,3A ,4A ,5A ,6A 和4名女志愿者1B ,2B ,3B ,4B ,从中随机抽取5人接受甲种心理暗示,另5人接受乙种心理暗示.(1)求接受甲种心理暗示的志愿者中包含1A 但不包含1B 的概率.16.解析 (1)记接受甲种心理暗示的志愿者中包含1A 但不包含1B 的事件为M ,则48510C 5().C 18P M ==17.(2018全国2卷理科8)我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先的成果.哥德巴赫猜想是“每个大于2的偶数可以表示为两个素数的和”,如30723=+.在不超过30的素数中,随机选取两个不同的数,其和等于30的概率是( ). A .112B .114C .115D .11817.解析 不超过30的素数有2、3、5、7、11、13、17、19、23、29,共10个,随机选取两数有210C 45=(种)情况,其中两数相加和为30的有7和23,11和19,13和17,共3种情况,根据古典概型得314515P ==.故选C. 18.(2018上海9)有编号互不相同的五个砝码,其中5克、3克、1克砝码各一个,2克砝码两个,从中随机选取三个,则这三个砝码的总质量为9克的概率是______.(结果用最简分数表示)18. 解析 从五个砝码中选取三个共有35C 10=(种)情况,其中三个砝码总质量为9克的有:522++,共531++,共两种情况,根据古典概型得21105P ==. 19.(2018北京理17)电影公司随机收集了电影的有关数据,经分类整理得到下表:电影类型 第一类第二类第三类第四类第五类第六类(),i j ()()()()()4,7,5,6,5,7,5,8,6,75285528C =528电影部数 140 50 300 200 800 510 好评率0.4 0.2 0.15 0.25 0.2 0.1好评率是指:一类电影中获得好评的部数与该类电影的部数的比值. 假设所有电影是否获得好评相互独立.(1)从电影公司收集的电影中随机选取1部,求这部电影是获得好评的第四类电影的概率; (2)从第四类电影和第五类电影中各随机选取1部,估计恰有1部获得好评的概率; (3)假设每类电影得到人们喜欢的概率与表格中该类电影的好评率相等.用“1k ξ=”表示第k 类电影得到人们喜欢,“0k ξ=”表示第k 类电影没有得到人们喜欢(1,2,3,4,5,6k =).写出方差123456,,,,,D D D D D D ξξξξξξ的大小关系.19.解析(1)由题意知,样本中电影的总部数是140503002008005102000+++++=, 第四类电影中获得好评的电影部数是2000.2550⨯=. 故所求概率为500.0252000=. (2)设事件A 为“从第四类电影中随机选出的电影获得好评”, 事件B 为“从第五类电影中随机选出的电影获得好评”.故所求概率为()()()()()()()()()11P AB AB P AB P A P A P B P A P B B +=+=-+-. 由题意知:()P A 估计为0.25,()P B 估计为0.2. 故所求概率估计为0.250.80.750.20.35⨯+⨯=. (3)由题意可知,定义随机变量如下:0,1k k k ξ⎧=⎨⎩第类电影没有得到人们喜欢,第类电影得到人们喜欢,则k ξ显然服从两点分布,则六类电影的分布列及方差计算如下. 第一类电影:1ξ1 0 P0.40.6()110.400.60.4E ξ=⨯+⨯=,()()()22110.40.400.40.60.24D ξ=-⨯+-⨯=第二类电影:2ξ1 0 P0.20.8()210.200.80.2E ξ=⨯+⨯=,()()()22210.20.200.20.80.16D ξ=-⨯+-⨯=.第三类电影:3ξ1 0 P0.150.85()310.1500.850.15E ξ=⨯+⨯=,()()()22310.150.1500.150.850.1275D ξ=-⨯+-⨯=第四类电影:4ξ1 0 P0.250.75()410.2500.750.25E ξ=⨯+⨯=,()()()22110.250.2500.250.750.1875D ξ=-⨯+-⨯=.第五类电影:5ξ1 0 P0.20.8()510.200.80.2E ξ=⨯+⨯=,()()()22510.20.200.20.80.16D ξ=-⨯+-⨯=.第六类电影:5ξ1 0 P0.10.9()610.100.90.1E ξ=⨯+⨯=,()()()22610.10.100.10.90.09D ξ=-⨯+-⨯=.综上所述,142536D D D D D D ξξξξξξ>>=>>.20.(2018天津理16)已知某单位甲、乙、丙三个部门的员工人数分别为24,16,16. 现采用分层抽样的方法从中抽取7人,进行睡眠时间的调查. (I )应从甲、乙、丙三个部门的员工中分别抽取多少人?(II )若抽出的7人中有4人睡眠不足,3人睡眠充足,现从这7人中随机抽取3人做进一步的身体检查.(i )用X 表示抽取的3人中睡眠不足的员工人数,求随机变量X 的分布列与数学期望; (ii )设A 为事件“抽取的3人中,既有睡眠充足的员工,也有睡眠不足的员工”,求事件A 发生的概率.20.命题意图 本小题主要考查分层抽样、离散型随机变量的分布列与数学期望、互斥事件的概率加法公式等基础知识.考查运用概率知识解决简单实际问题的能力.解析(Ⅰ)由已知,甲、乙、丙三个部门的员工人数之比为322∶∶,由于采用分层抽样的方法从中抽取7人,因此应从甲、乙、丙三个部门的员工中分别抽取3人,2人,2人. (Ⅱ)(i )随机变量X 的所有可能取值为0,1,2,3. 3433701C 23C C k kP X k k -=⋅==()(,,,).所以,随机变量X 的分布列为随机变量X 的数学期望11218412()0123353535357E X =⨯+⨯+⨯+⨯=. (ii )设事件B 为“抽取的3人中,睡眠充足的员工有1人,睡眠不足的员工有2人”;事件C 为“抽取的3人中,睡眠充足的员工有2人,睡眠不足的员工有1人”,则A B C = ,且B 与C 互斥,由(i )知,()()()()()(62)(17))2(1P B P X P C P X P A P B C P X P X =======+== ,,故.所以,事件A 发生的概率为67. 2019年21.(2019全国I 理6)我国古代典籍《周易》用“卦”描述万物的变化.每一“重卦”由从下到上排列的6个爻组成,爻分为阳爻“——”和阴爻“— —”,如图就是一重卦.在所有重卦中随机取一重卦,则该重卦恰有3个阳爻的概率是A .516B .1132C .2132D .111621.解析 在所有重卦中随机取一重卦,基本事件总数6264n ==,该重卦恰有3个阳爻包含的基本个数3363C C 20m ==,则该重卦恰有3个阳爻的概率2064m p n ===22.(2019江苏6)从3名男同学和2名女同学中任选2名同学参加志愿者服务,则选出的2名同学中至少有1名女同学的概率是 .22. 解析 从3名男同学和2名女同学中任选2名同学参加志愿者服务,基本事件总数25C 10n ==,选出的2名同学中至少有1名女同学包含的基本事件个数112322C C C 7m =+=,所以选出的2名同学中至少有1名女同学的概率是710m P n ==.23.(2019天津理16)设甲、乙两位同学上学期间,每天7:30之前到校的概率均为23.假定甲、乙两位同学到校情况互不影响,且任一同学每天到校情况相互独立.(Ⅰ)用X 表示甲同学上学期间的三天中7:30之前到校的天数,求随机变量X 的分布列和数学期望;(Ⅱ)设M 为事件“上学期间的三天中,甲同学在7:30之前到校的天数比乙同学在7:30之前到校的天数恰好多2”,求事件M 发生的概率.23.解析(Ⅰ)因为甲同学上学期间的三天中到校情况相互独立,且每天7:30之前到校的概率均为23,故2~3,3X B ⎛⎫ ⎪⎝⎭,从而3321(),0,1,2,333k kk P X k C k -⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭.所以,随机变量X 的分布列为随机变量X 的数学期望()323E X =⨯=. (Ⅱ)设乙同学上学期间的三天中7:30之前到校的天数为Y ,则2~3,3Y B ⎛⎫⎪⎝⎭,且{3,1}{2,0}M X Y X Y ===== .由题意知事件{3,1}X Y ==与{2,0}X Y ==互斥,且事件{}3X =与{}1Y =,事件{}2X =与{}0Y =均相互独立,从而由(Ⅰ)知()({3,1}{2,0})(3,1)(2,0)P M P X Y X Y P X Y P X Y ========+==824120(3)(1)(2)(0)279927243P X P Y P X P Y ===+===⨯+⨯=.题型141 几何概型1.(2013四川理9)节日 家前的树上挂了两串彩灯,这两串彩灯的第一次闪亮相互独立,若接通电后的4秒内任一时刻等可能发生,然后每串彩灯在内4秒为间隔闪亮,那么这两串彩灯同时通电后,它们第一次闪亮的时刻相差不超过2秒的概率是( ). A.14 B.12 C.34 D.782. (2013陕西理5)如图,在矩形区域ABCD 的AC ,两点处各有一个通信基站,假设其信号覆盖范围分别是扇形区域ADE 和扇形区域CBF (该矩形区域内无其他信号来源,基站工作正常).若在该矩形区域内随机地选一地点,则该地点无信号的概率是( ).A. π14-B. π12-C. π22-D. π43. (2013福建理11)利用计算机产生0~1之间的均匀随机数a ,则事件“310a ->”发生的概率为_________.4.(2013山东理14) 在区间[]3,3-上随机取一个数x ,使得121x x +-- 成立的概率为__________.5.(2014 辽宁理 14)正方形的四个顶点()1,1A --,()1,1B -,()1,1C ,()1,1D -,分别在抛物线2y x =-和2y x =上,如图所示,若将一个质点随机投入正方形ABCD中,则质点落在阴影区域的概率是.6.(2014 福建理 14)如图所示,在边长为e (e 为自然对数的底数)的正方形中随机撒一粒黄豆,则它落到阴影部分的概率为 .7.(2015陕西理科11)设复数()1i z x y =-+(,)x y ∈R ,若1z ,则y x 的概率为( ). A .3142π+B .1142π-C .112π-D .112π+ 7. 解析 由||1z ()22111x y ⇒-+ .所以y x 表示如图所示的阴影部分,所以2211π1111142π142πS P S ⨯-⨯⨯===-⨯阴总.故选B. 命题意图 考查复数的基本概念与知识,并与几何概型相结合,具备一定的新颖性.8.(2015湖北理科7)在区间[0,1]上随机取两个数,x y ,记1p 为事件“12x y + ”的概率,1-11-12p 为事件“1||2x y -”的概率,3p 为事件“12xy ”的概率,则( ). A .123p p p << B .231p p p << C .312p p p <<D .321p p p <<8. 解析 123,,p p p 依次为如图所示的三个图形的面积,观察知,选B. 也可作如下的计算: 由图(1)得11117=12228p -⨯⨯=; 由图(2)得21113=122224p -⨯⨯⨯=; 由图(3)得111312211111ln2=1d ln 222222p x x x ⨯+=+|=+⎰. 三个值比较得231p p p <<,故选B.命题意图 考查不等式表示的平面区域、几何概型及定积分的计算.9.(2016全国乙理4)某公司的班车在7:00,8:00,8:30发车,学.小明在7:50至8:30之间到达发车站乘坐班车,且到达发车站的时刻是随机的,则他等车时间不超过10分钟的概率是( ). A. B. C. D. 9. B 解析 如图所示,画出时间轴.小明到达的时间会随机的落在图中线段中,而当他的到达时间落在线段或时,才能保证他等车的时间不超过分钟. 根据几何概型,所求概率.故选B. 10.(2016山东理14)在上随机地取一个数,则事件”直线与圆相交”发生的概率为 .图2图3图112x-y =12x+y =1213122334BD C A 7:408:108:208:307:30AB A C DB 1010101402P +==[1,1] k y kx =22(5)9x y -+=10.解析 首先的取值空间的长度为2,由直线与圆相交,所 以,解得,所以得事件发生时的取值空间为,其长度为,利用几何概型可知,所求概率为 . 11.(2016全国甲理10)从区间随机抽取2n 个数,,…,,,,…,,构成n 个数对,,…,,其中两数的平方和小于1的数对共有m 个,则用随机模拟的方法得到的圆周率的近似值为( ). A. B. C. D. 11. C 解析 由题意得:在如图所示方格中,而平方和小于1的点均在如图所示的阴影中,由几何概型概率计算公式知,所以.故选C .12.(2017江苏07)记函数()f x =的定义域为D .在区间[]4,5-上随机取一个数x ,则x D ∈的概率是 . 12.解析 由题意260x x +- ,故[]2,3D =-,所以()()325549P --==--.故填59.13.(2017全国1卷理科2)如图所示,正方形ABCD 内的图形来自中国古代的太极图,正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称. 在正方形内随机取一点,则此点取自黑色部分的概率是( ). A.14 B. π8 C. 12 D. π434k kx y =22(5)9x y -+=3<3344k - k 33,44⎡⎤-⎢⎥⎣⎦2343=223[]0,11x 2x n x 1y 2y n y ()11,x y ()22,x y (),n n x y π4n m 2n m 4m n 2m n()()12i i x y i n =⋅⋅⋅,,,,π41m n=4πmn=13. 解析 设正方形的边长为2,则圆的半径为1,则正方形的面积为224⨯=,圆的面积为2π1π⨯=,图中黑色部分的面积为π2,则此点取自黑色部分的概率为ππ248=.故选B.14.(2018全国I 卷理科10)下图来自古希腊数学家希波克拉底所研究的几何图形,此图由三个半圆构成,三个半圆的直径分别为直角三角形ABC 的斜边BC ,直角边AB ,AC ,ABC △的三边所围成的区域记为Ⅰ,黑色部分记为Ⅱ,其余部分记为Ⅲ,在整个图形中随机取一点,此点取自Ⅰ,Ⅱ,Ⅲ的概率分别记为1p ,2p ,3p ,则 A .12p p =B .13p p =C .23p p =D .123p p p =+14.解析 概率为几何概型,总区域面积一定,只需比较Ⅰ,Ⅱ,Ⅲ区域面积即可.设直角三角形ABC 的三个角A ,B ,C 所对的边长分别为a ,b ,c ,则区域Ⅰ的面积为112S ab =, 区域Ⅱ的面积为222211111111πππ22222222S c b ab a ab ⎛⎫⎛⎫⎛⎫=++-= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,区域Ⅲ的面积为22231111111πππ2222282S c b ab a ab ⎛⎫⎛⎫=+-=- ⎪ ⎪⎝⎭⎝⎭.显然12p p =.故选A.15.(2018江苏6)某兴趣小组有2名男生和3名女生,现从中任选2名学生去参加活动,则恰好选中2名女生的概率为 ▲ .15. 解析 2325C 3C 10P ==.AB CD第2节 随机变量及其分布题型142 条件概率及相互独立事件同时发生的概率1.(2014 新课标2理5)某地区空气质量监测资料表明,一天的空气质量为优良的概率是0.75,连续两天为优良的概率是0.6,已知某天的空气质量为优良,则随后一天的空气质量为优良的概率是( ).A.0.8B.0.75C.0.6D.0.452.(2015全国Ⅰ理科4)投篮测试中,每人投3次,至少投中2次才能通过测试,已知某同学每次投篮投中的概率为0.6,且各次投篮是否投中相互独立,则该同学通过测试的概率为( ).A .0.648B .0.432C .0.36D .0.3122. 解析 根据独立重复试验公式得,该同学通过测试的概率为2233=C 0.60.40.6P ⨯⨯+=0.648.故选A .3.(2015江苏5)袋中有形状、大小都相同的4只球,其中1只白球,1只红球,2只黄球,从中一次随机摸出2只球,则这2只球颜色不同的概率为 . 3. 解析 解法一:1只白球设为a ,1只红球设为b ,2只黄球设为c ,d , 则摸球的所有情况为(),a b ,(),a c ,(),a d ,(),b c ,(),b d ,(),c d ,共6件,满足题意的事件为(),a b ,(),a c ,(),a d ,(),b c ,(),b d ,共5件,故概率为56P =. 解法二(理科做法):从反面考查,反面情况为摸出的2只球颜色相同,故2224C 51C 6P =-=. 4.(2015陕西理科19)设某校新、老校区之间开车单程所需时间为T ,T 只与道路畅通状况有关,对其容量为100的样本进行统计,结果如下:T(分钟)25 30 35 40 频数(次)20304010(1)求T 的分布列与数学期望ET ;(2)刘教授驾车从老校区出发,前往新校区做一个50分钟的讲座,结束后立即返回老校区,求刘教授从离开老校区到返回老校区共用时间不超过120分钟的概率. 4. 解析 (1)以频率估计概率得T 的分布列为:T25 30 35 40P0.2 0.3 0.4 0.1所以250.2300.3350.4400.132ET =⨯+⨯+⨯+⨯=(分钟).(2)设12,T T 分别表示往返所需时间,设A =从离开老校区到返回老校区共用时间不超过120分钟,则:()()1212()(25)40(30)40P A P T P T P T P T ==+=+ ()()1212(35)35(40)30P T P T P T P T =+==0.210.310.40.90.10.50.91⨯+⨯+⨯+⨯=.5.(2015湖北理科20)某厂用鲜牛奶在某台设备上生产,A B 两种奶制品.生产1吨A 产品需鲜牛奶2吨,使用设备1小时,获利1000元;生产1吨B 产品需鲜牛奶1.5吨,使用设备1.5小时,获利1200元.要求每天B 产品的产量不超过A 产品产量的2倍,设备每天生产,A B 两种产品时间之和不超过12小时. 假定每天可获取的鲜牛奶数量W (单位:吨)是一个随机变量,其分布列为W1215 18 P0.30.50.2该厂每天根据获取的鲜牛奶数量安排生产,使其获利最大,因此每天的最大获利Z (单位:元)是一个随机变量. (1)求Z 的分布列和均值;(2) 若每天可获取的鲜牛奶数量相互独立,求3天中至少有1天的最大获利超过10000元的概率.5. 解析 (1)设每天,A B 两种产品的生产数量分别为,x y ,相应的获利为z , 则有2 1.5,1.512, 20,0, 0.x y W x y x y x y +⎧⎪+⎪⎨-⎪⎪⎩ (1)目标函数为10001200z x y =+.当12W =时,(1)表示的平面区域如图1,三个顶点分别为(0, 0), (2.4, 4.8), (6, 0)A B C . 将10001200z x y =+变形为561200z y x =-+,当 2.4, 4.8x y ==时,直线l :561200zy x =-+在y 轴上的截距最大,最大获利max 2.41000 4.812008160Z z ==⨯+⨯=.当15W =时,(1)表示的平面区域如图2,三个顶点分别为(0, 0), (3, 6), (7.5, 0)A B C . 将10001200z x y =+变形为561200zy x =-+,当3, 6x y ==时,直线l :561200zy x =-+在y 轴上的截距最大,最大获利max 310006120010200Z z ==⨯+⨯=. 当18W =时,(1)表示的平面区域如图3,四个顶点分别为(0, 0), (3, 6), (6, 4), (9, 0)A B C D . 将10001200z x y =+变形为 561200z y x =-+,当6,4x y ==时,直线l :561200zy x =-+在y 轴上的截距最大,最大获利max 610004120010800Z z ==⨯+⨯=. 故最大获利Z 的分布列为:Z 8160 10200 10800 P0.30.50.2因此,()81600.3102000.5108000.29708.E Z =⨯+⨯+⨯=(2)由(1)知,一天最大获利超过10000元的概率1(10000)0.50.20.7p P Z =>=+=, 由二项分布,3天中至少有1天最大获利超过10000元的概率为:()3311110.30.973P p =--=-=.命题意图 考查线性规划,分布列、均值与二项分布.6.(2107天津理16(2))从甲地到乙地要经过3个十字路口,设各路口信号灯工作相互独立,且在各路口遇到红灯的概率分别为111,,234.图3()图2()图1()D 9,0(A 0,0()B 3,6(C 6,4(A 0,0()C 7.5,0(C (A 0,0()O O(2)若有2辆车独立地从甲地到乙地,求这2辆车共遇到1个红灯的概率.6.解析 (2)设Y 表示第一辆车遇到红灯的个数,Z 表示第二辆车遇到红灯的个数,则所求事件的概率为(1)(0,1)(1,0)P Y Z P Y Z P Y Z +====+===(0)(1)(1)(0)P Y P Z P Y P Z ==+==1111111142424448=⨯+⨯=. 所以这2辆车共遇到1个红灯的概率为1148. 2019年7.(2019全国I 理15)甲、乙两队进行篮球决赛,采取七场四胜制(当一队赢得四场胜利 时,该队获胜,决赛结束).根据前期比赛成绩,甲队的主客场安排依次为“主主客客主客 主”.设甲队主场取胜的概率为0.6,客场取胜的概率为0.5,且各场比赛结果相互独立,则 甲队以4∶1获胜的概率是____________.7.解析 由题意可得,一共比赛了5场,且第5场甲获胜,前4场甲队胜3场,输1场,有2种情况:①甲队主场输1场,其概率为:122122C 0.60.4C 0.50.12P =⨯⨯⨯⨯=, ②甲队客场输1场,其概率为:221222C 0.6C 0.50.50.18P =⨯⨯⨯⨯=由于第5场必定是甲队胜,所以()2120.60.18P P P =+⨯=则甲队以4:1获胜的概率为0.18.8.(2019全国II 理18)11分制乒乓球比赛,每赢一球得1分,当某局打成10:10平后,每球交换发球权,先多得2分的一方获胜,该局比赛结束.甲、乙两位同学进行单打比赛,假设甲发球时甲得分的概率为0.5,乙发球时甲得分的概率为0.4,各球的结果相互独立.在某局双方10:10平后,甲先发球,两人又打了X 个球该局比赛结束.(1)求P (X =2);(2)求事件“X =4且甲获胜”的概率.8.解析(1)X =2就是10:10平后,两人又打了2个球该局比赛结束,则这2个球均由甲得分, 或者均由乙得分.因此P (X =2)=0.5×0.4+(1–0.5)×(1–04)=05.(2)X =4且甲获胜,就是10:10平后,两人又打了4个球该局比赛结束,且这4个球的得分情况为:前两球是甲、乙各得1分,后两球均为甲得分. 因此所求概率为[0.5×(1–0.4)+(1–0.5)×0.4]×0.5×0.4=0.1.题型143 离散型随机变量的分布列及其数学期望与方差1.(2013湖北理9)如图,将一个各面都凃了油漆的正方体,切割为125个同样大小的小正方体,经过搅拌后,从中随机取一个小正方体,记它的油漆面数为X ,则X 的均值()E X =( ).A .125126 B .56C .125168D .572.(2013广东理4则X A .32 B .2 C .52D .33.(2013江西理18)小波以游戏方式决定参加学校合唱团还是参加学校排球队.游戏规则为:以O 为起点,再从12345678,,,,,,,A A A A A A A A (如图)这8个点中任取两点分别为终点得到两个向量,记这两个向量的数量积为X .若0X =就参加学校合唱团,否则就参加学校排球队. (1) 求小波参加学校合唱团的概率;(2) 求X 的分布列和数学期望.4.(2013湖南理18)某人在如图4所示的直角边长为4米的三角形地块的每个格点(指纵、横的交叉点记忆三角形的顶点)处都种了一株相同品种的作物.根据历年的种植经验,一株该种作物的年收获量Y (单位:kg )与它的“相近”作物株数X 之间的关系如下表所示:X 1 23 4 Y51 484542这里,两株作物“相近”是指它们之间的直线距离不超过1米.(1)从三角形地块的内部和边界上分别随机选取一株作物,求它们恰好“相近”的概率;(2)从所种作物中随机选取一株,求它的年收获量的分布列与数学期望.5. (2013重庆理18)某商场举行的“三色球”购物摸奖活动规定:在一次摸奖中,摸奖者先从装有3个红球与4个白球的袋中任意摸出3个球,再从装有1个蓝球与2个白球的袋中任意摸出1个球,根据摸出4个球中红球与蓝球的个数,设一、二、三等奖如下:奖级 摸出红、蓝球个数获奖金额一等奖 3红1蓝 200元 二等奖 3红0蓝50元 三等奖2红1蓝 10元其余情况无奖且每次摸奖最多只能获得一个奖级. (1)求一次摸奖恰好摸到1个红球的概率;(2)求摸奖者在一次摸奖中获奖金额X 的分布列与期望()E X . 6. (2013全国新课标卷理19)经销商经销某种农产品,在一个销售季度内,每售出1t 该产品获利润500元,未售出的产品,每1t 亏损300元.根据历史资料,得到销售季度内市场需求量的频率分布直方图,如图所示.经销商为下一个销售季度购进了130t 该农产品.以x (单位:t ,100150x ≤≤)表示市场需求量,T 表示下一个销售季度内经销该农产品的利润.(1)将T 表示为x 的函数;(2)根据直方图估计利润T 不少于57000元的概率;(3)在直方图的需求量分组中,以各组的区间中点值代表该组的各个值,需求量落入该区间的频率作为需求量取该区间中点值的概率(例如:若[100,110)x ∈,则取105x =,且105x =的概率等于需求量落入[100,110)的T 的数学期望.7. (2013天津理16)一个盒子里装有7张卡片,其中有红色卡片4张,编号分别为1, 2, 3, 4;白色卡片3张,编号分别为2,3,4.从盒子中任取4张卡片 (假设取到任何一张卡片的可能性相同).(1) 求取出的4张卡片中, 含有编号为3的卡片的概率;(2) 再取出的4张卡片中, 红色卡片编号的最大值设为X , 求随机变量X 的分布列和数学期望.8.(2013山东理19)甲、乙两支排球队进行比赛,约定先胜3局者获得比赛的胜利,比赛随即结束,除第五局甲队获胜的概率是12外,其余每局比赛甲队获胜的概率都是23,假设各局比赛结果相互独立.(1)分别求甲队以3:0,3:1,3:2胜利的概率;(2)若比赛结果为3:0或3:1,则胜利方得3分、对方得0分;若比赛结果为3:2,则胜利方得2分;对方得1分;求乙队得分X 的分布列及数学期望.10. (2013福建理16)某联欢晚会举行抽奖活动,举办方设置了甲、乙两种抽奖方案,方案甲的中奖率为32,中奖可以获得2分;方案乙的中奖率为52,中奖可以获得3分;未中奖则不得分.每人有且只有一次抽奖机会,每次抽奖中奖与否互不影响,晚会结束后凭分数兑换奖品. (1)若小明选择方案甲抽奖,小红选择方案乙抽奖,记他们的累计得分为X ,求3≤X 的概率;(2)若小明、小红两人都选择方案甲或都选择方案乙进行抽奖,问:他们选择何种方案抽奖,累 计得分的数学期望较大?11.(2013四川理18)某算法的程序框图如图所示,其中输入的变量x 在1,2,3,,24⋅⋅⋅这24个整数中等可能随机产生.(1)分别求出按程序框图正确编程运行时输出y 的值为i 的概率(1,2,3)i P i =;(2)甲、乙两同学依据自己对程序框图的理解,各自编写程序重复运行n 次后,统计记录了输出y 的值为(1,2,3)i i =的频数.以下是甲、乙所作频数统计表的部分数据.甲的频数统计表(部分)乙的频数统计表(部分)当2100n =时,根据表中的数据,分别写出甲、乙所编程序各自输出y 的值为(1,2,3)i i =的频率(用分数表示),并判断两位同学中哪一位所编写程序符合算法要求的可能性较大;(3)按程序框图正确编写的程序运行3次,求输出y 的值为2的次数ξ的分布列及数学期望.12. (2013陕西理19)在一场娱乐晚会上,有5位民间歌手(1至5号)登台演唱,由现场数百名观众投票选出最受欢迎歌手. 各位观众须彼此独立地在选票上选3名歌手,其中观众甲是1号歌手的歌迷,他必选1号,不选2号,另在3至5号中随机选2名. 观众乙和丙对5位歌手的演唱没运行 次数n输出y 的值 为1的频数输出y 的值 为2的频数输出y 的值 为3的频数3014610…………2100 1027 376 697运行 次数n输出y 的值为1的频数 输出y 的值为2的频数 输出y 的值为3的频数3012117…………2100 1051 696 353。
统计学13-14A
成都理工大学2013—2014学年《统计学》(第一套)练习题和答案一、选择题(在备选答案中只有一个是正确的,选择一个正确答案填入下方表格内题号对应的位置,不选、错选、多选均不得分不答题或者答错题既不得分,也不倒扣分.每题1分,共10分) 1、一所大学从全校学生中随机抽取300人作为样本进行调查,其中80%的人回答他们的月生活费支出在500元以上。
这里的300人是( )。
A 。
总体B 。
样本C 。
变量D 。
统计量2、指出下面的数据哪一个属于分类数据( ).A.某种产品的销售价格(元):21,26,19,22,28B.某汽车生产企业各季度的产量(万辆):25,27,30,26C.产品的质量等级:一等品,二等品,三等品D.上网的方式:有线宽带,无线宽带3、为了解大学生的上网时间,从全校所有学生宿舍中随机抽取50个宿舍,然后对抽中宿舍中的每个学生进行调查,这种抽样调查方法是( )。
A 。
分层抽样 B.简单随机抽样 C.系统抽样 D 。
整群抽样4、在对数值型数据进行分组后,统计各组频数时,通常要求一个组的变量值满足( )。
A. B. B. D 。
5、大学生中每周的上网时间的偏态系数为0。
3,这表明学生每周上网时间的分布是得分().A。
对称的 B.左偏的C。
右偏的 D.严重左偏的6、某地区每个人的年收入是右偏的,均值为5000元,标准差为1200元.随机抽取900人并记录他们的年收入,则样本均值的分布为()。
A。
近似正态分布,均值为5000元,标准差为40元B。
近似正态分布,均值为5000元,标准差为1200元C。
右偏分布,均值为5000,标准差为40D. 左偏分布,均值为5000元,标准差为1200元7、某电池生产商声称,它们生产的5号电池的平均使用时间为85小时。
质检部门抽取20节电池的随机样本,在的显著性水平下,检验结果是未能拒绝原假设,这意味着().A.该企业生产的5号电池的平均使用时间是85小时B.该企业生产的5号电池的平均使用时间不是85小时C.没有证据证明该企业生产的5号电池的平均使用时间是85小时D.没有证据证明该企业生产的5号电池的平均使用时间不是85小时8、在一元回归模型中,反映的是( )。
广州大学2017-2018(1)概率论与数理统计A卷
广州大学 2017- 2018 学年第 一 学期考试卷课 程:概率论与数理统计(48学时) 考 试 形 式:闭卷考试授予学士学位。
一、选择题(每小题3分,总计15分) 1.三人各投一次球,设i A 表示“第i 人投中”(1,2,3)i =,则事件123A A A 表示( ). (A )三人都投中; (B )至少有一人投中; (C )至多有两人投中;(D )三人都没投中.2.设随机事件,A B 满足0()1P A <<,()0P B >,且(/)(/)P B A P B A =,则必有( ). (A) (/)(/)P A B P A B =; (B) (/)(/)P A B P A B ≠; (C) (/)(/)P A B P B A =; (D) ()()()P AB P A P B =.3.设2~(5,3)X N ,且常数c 满足{}{}P X c P X c >=≤,则c =( ). (A) 0; (B) 1; (C) 3; (D) 5.4. 设X 和Y 为两个随机变量,则能说明X 和Y 独立的是( ).(A) (,)()()X Y F x y F x F y = ; (B) ()()()E XY E X E Y =; (C) ()()()E X Y E X E Y +=+; (D) ()()()D X Y D X D Y +=+. 5.设二维随机变量(,)X Y 的联合概率分布为已知随机事件{0}Y =与{1}X Y +=相互独立,则( ).(A) 0.3,0.2a b ==; (B) 0.4,0.1a b ==;(C) 0.2,0.3a b ==; (D) 0.1,0.4a b ==.二、填空题(每空3分,总计15分)1.设()0.28, P B =(/)0.6, (/)0.75P B A P A B ==,那么()P A B ⋃= . 2.将一颗骰子连续掷三次,则恰好有两次出现“6”点的概率为 .3.从数1,2,3中任取一个数记为X ,再从1,,X 中任取一个数记为Y ,则{2}P Y == .4.设随机变量~(,)U a b ξ,且4, 3E D ξξ==, 则{05}P ξ<≤= . 5.设连续型随机变量X 的分布函数为50, 0,(),0,xx F x a e x -≤⎧=⎨->⎩ 则{1}P X >= .三、(本题满分8分)袋中标有不同号码的红、黑、黄球各2个,现随机从袋中有放回地抽取3次,每次取1个,求下列事件的概率: (1) A={三次未抽到红球}; (2) B={颜色不全相同}. 四、(本题满分8分)已知甲、乙两箱装有同种产品,甲箱装有10只,其中有6只一等品;乙箱装有6只,其中有3只一等品,今从两箱中任取一箱,然后从该箱中不放回地取两次,每次取一只,求:(1) 第一次取到的是一等品的概率;(2) 在第一次取到一等品的条件下,第二次取到的也是一等品的概率.求:(1) (2) 21Y X =-的分布律. 六、(本题满分10分)设某种电子产品的使用寿命X 的概率密度为3()3, ,(,)0, ,x e x f x x ββββ--⎧>=⎨≤⎩ 其中0β>为未知参数,又设12,,,n x x x 是来自X 的一组样本观察值,求参数β的最大似然估计值.设随机变量X 的概率密度为;01;();12;0;x x f x a x x 其它.<≤⎧⎪=-<≤⎨⎪⎩求:(1)常数a 的值;(2)关于t 的方程22(1)50t X t X ++-+=有实根的概率; (3)()E X .设二维随机变量(,)X Y的联合分布律如下:求:(1){}>;P X Y(2)X,Y的边缘分布律;(3)Z X Y=+的概率分布.某学校召开家长座谈会,前来参加家长会的家长人数是一个随机变量,已知一个学生无家长、有1个家长来参加会议的概率分别为0.2,0.8。
2005―2014广东省数学高考(理科)概率统计模块试题(含.
2005年8.先后抛掷两枚均匀的正方体骰子(它们的六个面分别标有点数1、2、3、4、5、6,骰子朝上的面的点数分别为X 、Y ,则1log 2=Y X 的概率为(A .61B .365 C .121 D .21 8C 18.(本小题满分12分箱中装有大小相同的黄、白两种颜色的乒乓球,黄、白乒乓球的数量比为s:t.现从箱中每次任意取出一个球,若取出的是黄球则结束,若取出的是白球,则将其放回箱中,并继续从箱中任意取出一个球,但取球的次数最多不超过n 次,以ξ表示取球结束时已取到白球的次数.(Ⅰ求ξ的分布列; (Ⅱ求ξ的数学期望.18.解:(Iξ的可能取值为:0,1,2,…,n ξ的分布列为ξ12…n-1npt s s+ 2(t s st + 32(t s st +…11(--+n n t s stnnt s t (+(II ξ的数学希望为nnn n t s t n t s st n t s st t s st t s s E ((1(...(2(1011322+⨯++⨯-+++⨯++⨯++⨯=--ξ…(1 111113322((1((2(...(2(++---+++-++-+++++=+n n n n n n t s nt t s st n t s st n t s st t s st E t s t ξ…(2 (1 -(2得nnn n n n t s nt t s t n t s s t s t E((1((11+++--+-=--ξ2006年16、(本小题满分12分某运动员射击一次所得环数X 的分布列如下:X 0-6 7 8910Y 00.2 0.3 0.3 0.2现进行两次射击,以该运动员两次射击中最高环数作为他的成绩,记为ξ. (Ⅰ求该运动员两次都命中7环的概率; (Ⅱ求ξ分布列;(Ⅲ求ξ的数学希望.16解:(Ⅰ求该运动员两次都命中7环的概率为04.02.02.07(=⨯=P ; (Ⅱ ξ的可能取值为7、8、9、1004.07(==ξP 21.03.03.02.028(2=+⨯⨯==ξP39.03.03.03.023.02.029(2=+⨯⨯+⨯⨯==ξP36.02.02.03.022.03.022.02.0210(2=+⨯⨯+⨯⨯+⨯⨯==ξPξ分布列为ξ78910P0.04 0.21 0.39 0.36(Ⅲ ξ的数学希望为07.936.01039.0921.0804.07=⨯+⨯+⨯+⨯=ξE .2007年9.甲、乙两个袋中装有红、白两种颜色的小球,这些小球除颜色外完全相同,其中甲袋装有4个红球,2个白球,乙袋装有1个红球,5个白球.现分别从甲、乙两袋中各随机取出一个球,则取出的两球是红球的概率为 .(答案用分数表示 9.411(((669P AB P A P B ==⋅= 17.(12分下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x (吨与相应的生产能耗y (吨标准煤的几组对照数据.x 3 4 5 6 y2.5344.5(1请画出上表数据的散点图;(2请根据上表提供的数据,用最小二乘法求出y 关于x 的线性回归方程ˆˆy bxa =+; (3已知该厂技改前100吨甲产品的生产能耗为90吨标准煤.试根据(2求出的线性回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤? (参考数值:3 2.543546 4.566.5⨯+⨯+⨯+⨯= 17.(1(略(297,22x y ==,4166.5i i i x y ==∑,42186i i x ==∑,414221466.5630.786814i ii i i x y x yb x x==--===--∑∑0.35a y bx =-=,故现线性回归方程为0.70.35y x =+(3当100x =时,70.35y =,9070.3519.65-=,故预测生产100吨甲产品的生产能耗比技改前降低19.65吨标准煤。
数学类考研院校排名
14 北京理工大学 A 28 电子科技大学 AB+等(63个):湖南师范大学、重庆大学、华中师范大学、东华大学、河北师范大学、桂林电子科技大学、辽宁大学、内蒙古大学、哈尔滨工程大学、南京师范大学、华南师范大学、华东理工大学、陕西师范大学、西北师范大学、广东工业大学、安徽师范大学、徐州师范大学、东北大学、北京交通大学、辽宁师范大学、上海师范大学、西南交通大学、山东科技大学、武汉理工大学、暨南大学、南京航空航天大学、郑州大学、大连海事大学、江苏大学、合肥工业大学、上海理工大学、浙江工业大学、宁波大学、四川师范大学、浙江师范大学、河海大学、北京科技大学、安徽大学、福建师范大学、中国矿业大学、广西大学、南昌大学、北方工业大学、西安建筑科技大学、河南师范大学、温州大学、成都理工大学、扬州大学、武汉科技大学、长江大学、南京信息工程大学、北京工业大学、兰州理工大学、湖南科技大学、南京财经大学、西安理工大学、青岛大学、南京农业大学、河北工业大学、五邑大学、太原理工大学、渤海大学、江南大学B等(62个):山东师范大学、山西大学、中北大学、哈尔滨理工大学、深圳大学、广西师范大学、云南师范大学、长春工业大学、大连大学、安庆师范学院、湖北大学、汕头大学、烟台大学、黑龙江大学、河北大学、河南大学、杭州电子科技大学、西南大学、长沙理工大学、信阳师范学院、北京邮电大学、西安科技大学、兰州交通大学、南京邮电大学、西北农林科技大学、中国海洋大学、江西师范大学、集美大学、重庆师范大学、中国人民大学、上海财经大学、南京理工大学、中国计量学院、聊城大学、宁夏大学、海南师范大学、西华师范大学、辽宁工程技术大学、中国传媒大学、中国农业大学、漳州师范学院、中国地质大学、青岛科技大学、辽宁工学院、西华大学、贵州大学、安徽理工大学、哈尔滨师范大学、天津工业大学、三峡大学、华北水利水电学院、华北电力大学、重庆工学院、天津工程师范学院、山东理工大学、湖北师范学院、北京化工大学、中国石油大学、青岛理工大学、河北科技大学、华东交通大学、广西师范学院C等(42个):名单略关键词:考研应用数学院校排名概率论与数理统计考研院校排名来源: 2011-01-18 14:30:37 编辑:sunrain 浏览次数:3849 网友评论0 条转播至:我很喜欢这篇文章!收藏到网摘:高等学校概率统计课的教材,内容包括概率论的基本概念、随机变量及其概率分布、数字特征、大数定律与中心极限定理、统计量及其概率分布、参数估计和假设检验、回归分析、方差分析以及用Excel进行概率统计计算。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第 1 页 共 4 页《概率论与数理统计》A卷
院、系领导
审批并签名
A 卷
广州大学2013-2014学年第一学期考试卷
课 程:概率论与数理统计(48学时) 考 试 形 式:闭卷考试
学院:____________ 专业班级:__________ 学号:____________ 姓名:___________
题 次 一 二 三 四 五 六 七 八 九 总 分 评卷人
分 数 15 15 8 8 10 14 10 10 10 100
得 分
一、选择题(每小题3分,总计15分)
1.设随机变量X的分布律为()2kcPXk,(0,1,2,3,4k),则c( ).
(A) 12; (B) 1615; (C) 1; (D) 1631.
2.设,AB是二随机事件,如果等式( )成立,则称,AB为相互独立的随机事
件.
(A) ()0PAB; (B) ()1PAB; (C) ()()PABPA; (D) ()0PAB.
3.设()0.4PA,()0.5PB,且()0.7PAB,则(|)PAB( ).
(A) 0.8; (B) 0.6; (C) 0.4; (D) 0.2.
4.若随机变量的期望E存在,则[()]EEE( ).
(A) 0; (B) ; (C) E; (D) 2()E.
5. 设连续型随机变量X的概率密度为)(xf, 则( ).
(A) 1)(0xf; (B) 1)(limxfx;
(C) 1)(dxxf; (D) )()(}{afbfbXaP.
二、填空题(每小题3分,总计15分)
1.将两封信随机地投入四个邮筒中,则未向前面两个邮筒投信的概率为 .
2.每次试验中A出现的概率为p,在三次试验中A出现至少一次的概率是26/27,
则p .
3.随机变量X的分布律为15}{kkXP,5,,1k,则}31{XP .
4.设)6,1(~UX,则(21)EX .
第 2 页 共 4 页《概率论与数理统计》A卷
5.设~(21,4)XN,125,,XX为X的一个样本,则样本均值X的方差为 .
三、(本题满分8分)
将标号为1, 2, 3, 4的四个球随意地排成一行,求下列各事件的概率:
(1)各球自左至右或自右至左恰好排成1, 2, 3, 4的顺序;
(2)第1号球排在最右边或最左边.
四、(本题满分8分)
设某批产品中,甲,乙,丙三厂生产的产品分别占45%,35%,20%,各厂的产
品的次品率分别为4%,2%,5%,现从中任取一件,求取到的是次品的概率.
五、(本题满分10分)
设随机变量X的分布函数为
0,1,9/19,12,()15/19,23,1,3.xxFxxx
(1)求X的概率分布律;(2)求(21)EX.
第 3 页 共 4 页《概率论与数理统计》A卷
六、(本题满分14分)
设连续型随机变量X的概率密度为
1,01()20,Axxfx其它
(1)求常数A;(2)求数学期望()EX;(3)求方差()DX.
七、(本题满分为10分)
设),(YX的分布律如下
X
Y
1 2 3
1 1/6 1/9 1/18
2 1/3
问,为何值时,X与Y相互独立?并求Y的边缘分布律.
第 4 页 共 4 页《概率论与数理统计》A卷
八、(本题满分10分)
一保险公司有10000人投保,每人每年付12元保险费,已知一年内投保人死亡率
为0.006, 如死亡,公司付给死者家属1000元,求:保险公司年利润不少于60000
元的概率.
九、(本题满分10分)
设总体X服从0-1分布(1,)bp,12,,,nxxx是来自总体X的一组样本观察值,求参
数p的最大似然估计值.
