2013年高考数学试题分类汇编:10排列、组合及二项式定理(理)
2013届高三数学二轮复习课件专题8第4讲排列、组合与二项式定理(理)

• [评析] 区分某一问题是排列还是组合问 题,关键看选出的元素与顺序是否有关, 若交换某两个元素的位置对结果产生影响, 则是排列问题;若交换任意两个元素的位 置对结果没有影响,则是组合问题,也就 是说排列问题与选取元素的顺序有关,组 合问题与选取元素的顺序有关.
• 某台小型晚会由6个节目组成,演出顺序 有如下要求:节目甲必须排在前两位,节 目乙不能排在第一位,节目丙必须排在最 后一位,该台晚会节目演出顺序的编排方 案共有( )
• (1)若只需一人参加,有多少种不同选法?
• (2)若需老师、男生、女生各一人参加,有 多少种不同选法?
• (3)若需一名老师、一名学生参加,有多少 种不同选法?
• [分析] 根据“分类互斥”、“分步互依” 合理地选用计数原理.
• [解析] (1)有三类选人的办法:3名老师中 选一人,有3种方法;8名男生中选一人, 有8种方法;5名女生中选一人,有5种方 法.
• 1.本部分内容在高考中所占分数大约在 3%—6%之间.
• 2.本部分考查的内容主要是:分类与分 步计数原理,排列与组合及二项式定理的 有关内容.
• 3.命题规律:此部分在命题时,题目类 型一般为选择或填空题,高考对本部分内 容的考查特点是侧重基础,多数高考试题 的难度与课本中习题难度相当,但在高考 试卷中分值所占比例超过占总课时的比 例.在解答题时,将可能出现与其它知识 点(函数、不等式、几何等)相结合的综合
• (3)应用题
• ①解排列组合问题应遵循的原则:先特殊 后一般,先选后排,先分类后分步.
• ②常用策略:(a)相邻问题捆绑法;(b)不 相邻问题插空法;(c)多排问题单排法;(d) 定序问题倍缩法;(e)多元问题分类法;(f) 有序分配问题分步法;(g)交叉问题集合法; (h)至少或至多问题间接法;(i)选排问题先 取后排法;(j)局部与整体问题排除法;(k) 复杂问题转化法.
2013届高考数学排列组合.doc
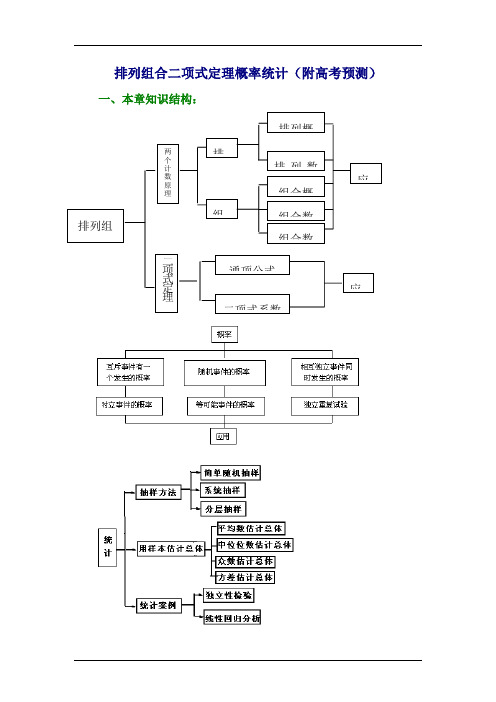
排列组合二项式定理概率统计(附高考预测)一、本章知识结构:二、重点知识回顾 1.排列与组合⑪ 分类计数原理与分步计数原理是关于计数的两个基本原理,两者的区别在于分步计数原理和分步有关,分类计数原理与分类有关.⑫ 排列与组合主要研究从一些不同元素中,任取部分或全部元素进行排列或组合,求共有多少种方法的问题.区别排列问题与组合问题要看是否与顺序有关,与顺序有关的属于排列问题,与顺序无关的属于组合问题.⑬ 排列与组合的主要公式 ①排列数公式:)1()1()!(!+-⋅⋅⋅-=-=m n n n m n n A m n (m ≤n) A n n =n! =n(n ―1)(n ―2) ·…·2·1. ②组合数公式:12)1()1()1()!(!!⨯⨯⋅⋅⋅⨯-⨯+-⋅⋅⋅-=-=m m m n n n m n m n C m n (m ≤n).③组合数性质:①m n n m n C C -=(m ≤n). ②n n n n n n C C C C 2210=+⋅⋅⋅+++③1314202-=⋅⋅⋅++=⋅⋅⋅++n n n n n n C C C C C2.二项式定理 ⑪ 二项式定理(a +b)n =C 0n a n +C 1n a n -1b+…+C r n a n -r b r +…+C n n b n ,其中各项系数就是组合数C r n ,展开式共有n+1项,第r+1项是T r+1 =C r n a n -r b r .⑫ 二项展开式的通项公式二项展开式的第r+1项T r+1=C r n a n -r b r (r=0,1,…n)叫做二项展开式的通项公式。
⑬ 二项式系数的性质①在二项式展开式中,与首末两端“等距离”的两个二项式系数相等,即C r n = C rn n - (r=0,1,2,…,n).②若n 是偶数,则中间项(第12+n 项)的二项公式系数最大,其值为C 2n n;若n 是奇数,则中间两项(第21+n 项和第23+n 项)的二项式系数相等,并且最大,其值为C21-n n= C21+n n.③所有二项式系数和等于2n ,即C 0n +C 1n +C 2n +…+C nn =2n .④奇数项的二项式系数和等于偶数项的二项式系数和,即C 0n +C 2n +…=C 1n +C 3n+…=2n ―1. 3.概率(1)事件与基本事件::S S S ⎧⎪⎧⎨⎨⎪⎩⎩随机事件在条件下,可能发生也可能不发生的事件事件不可能事件:在条件下,一定不会发生的事件确定事件必然事件:在条件下,一定会发生的事件基本事件:试验中不能再分的最简单的“单位”随机事件;一次试验等可能的产生一个基本事件;任意两个基本事件都是互斥的;试验中的任意事件都可以用基本事件或其和的形式来表示.(2)频率与概率:随机事件的频率是指此事件发生的次数与试验总次数的比值.频率往往在概率附近摆动,且随着试验次数的不断增加而变化,摆动幅度会越来越小.随机事件的概率是一个常数,不随具体的实验次数的变化而变化. (3)互斥事件与对立事件:(4)古典概型与几何概型:古典概型:具有“等可能发生的有限个基本事件”的概率模型. 几何概型:每个事件发生的概率只与构成事件区域的长度(面积或体积)成比例.两种概型中每个基本事件出现的可能性都是相等的,但古典概型问题中所有可能出现的基本事件只有有限个,而几何概型问题中所有可能出现的基本事件有无限个.(5)古典概型与几何概型的概率计算公式: 古典概型的概率计算公式:()A P A =包含的基本事件的个数基本事件的总数.几何概型的概率计算公式:()A P A =构成事件的区域长度(面积或体积)试验全部结果构成的区域长度(面积或体积).两种概型概率的求法都是“求比例”,但具体公式中的分子、分母不同.(6)概率基本性质与公式①事件A 的概率()P A 的范围为:0()1P A ≤≤.②互斥事件A 与B 的概率加法公式:()()()P A B P A P B =+ . ③对立事件A 与B 的概率加法公式:()()1P A P B +=.(7) 如果事件A 在一次试验中发生的概率是p ,则它在n 次独立重复试验中恰好发生k 次的概率是p n (k) = C k np k (1―p)n ―k . 实际上,它就是二项式[(1―p)+p]n 的展开式的第k+1项. (8)独立重复试验与二项分布①.一般地,在相同条件下重复做的n 次试验称为n 次独立重复试验.注意这里强调了三点:(1)相同条件;(2)多次重复;(3)各次之间相互独立;②.二项分布的概念:一般地,在n 次独立重复试验中,设事件A 发生的次数为X ,在每次试验中事件A 发生的概率为p ,那么在n 次独立重复试验中,事件A 恰好发生k 次的概率为()(1)(012)k kn k n P X k C p p k n -==-= ,,,,,.此时称随机变量X服从二项分布,记作~()X B n p ,,并称p 为成功概率.4、统计(1)三种抽样方法 ①简单随机抽样简单随机抽样是一种最简单、最基本的抽样方法.抽样中选取个体的方法有两种:放回和不放回.我们在抽样调查中用的是不放回抽取.简单随机抽样的特点:被抽取样本的总体个数有限.从总体中逐个进行抽取,使抽样便于在实践中操作.它是不放回抽取,这使其具有广泛应用性.每一次抽样时,每个个体等可能的被抽到,保证了抽样方法的公平性.实施抽样的方法:抽签法:方法简单,易于理解.随机数表法:要理解好随机数表,即表中每个位置上等可能出现0,1,2,…,9这十个数字的数表.随机数表中各个位置上出现各个数字的等可能性,决定了利用随机数表进行抽样时抽取到总体中各个个体序号的等可能性. ②系统抽样系统抽样适用于总体中的个体数较多的情况.系统抽样与简单随机抽样之间存在着密切联系,即在将总体中的个体均分后的每一段中进行抽样时,采用的是简单随机抽样. 系统抽样的操作步骤:第一步,利用随机的方式将总体中的个体编号;第二步,将总体的编号分段,要确定分段间隔k ,当N n(N为总体中的个体数,n 为样本容量)是整数时,N k n=;当N n不是整数时,通过从总体中剔除一些个体使剩下的个体个数N能被n 整除,这时N k n'=;第三步,在第一段用简单随机抽样确定起始个体编号l ,再按事先确定的规则抽取样本.通常是将l 加上间隔k 得到第2个编号()l k +,将()l k +加上k ,得到第3个编号(2)l k +,这样继续下去,直到获取整个样本. ③分层抽样当总体由明显差别的几部分组成时,为了使抽样更好地反映总体情况,将总体中各个个体按某种特征分成若干个互不重叠的部分,每一部分叫层;在各层中按层在总体中所占比例进行简单随机抽样. 分层抽样的过程可分为四步:第一步,确定样本容量与总体个数的比;第二步,计算出各层需抽取的个体数;第三步,采用简单随机抽样或系统抽样在各层中抽取个体;第四步,将各层中抽取的个体合在一起,就是所要抽取的样本. (2)用样本估计总体样本分布反映了样本在各个范围内取值的概率,我们常常使用频率分布直方图来表示相应样本的频率分布,有时也利用茎叶图来描述其分布,然后用样本的频率分布去估计总体分布,总体一定时,样本容量越大,这种估计也就越精确.①用样本频率分布估计总体频率分布时,通常要对给定一组数据进行列表、作图处理.作频率分布表与频率分布直方图时要注意方法步骤.画样本频率分布直方图的步骤:求全距→决定组距与组数→分组→列频率分布表→画频率分布直方图.②茎叶图刻画数据有两个优点:一是所有的信息都可以从图中得到;二是茎叶图便于记录和表示,但数据位数较多时不够方便.③平均数反映了样本数据的平均水平,而标准差反映了样本数据相对平均数的波动程度,其计算公式为s=.有时也用标准差的平方———方差来代替标准差,两者实质上是一样的.(3)两个变量之间的关系变量与变量之间的关系,除了确定性的函数关系外,还存在大量因变量的取值带有一定随机性的相关关系.在本章中,我们学习了一元线性相关关系,通过建立回归直线方程就可以根据其部分观测值,获得对这两个变量之间的整体关系的了解.分析两个变量的相关关系时,我们可根据样本数据散点图确定两个变量之间是否存在相关关系,还可利用最小二乘估计求出回归直线方程.通常我们使用散点图,首先把样本数据表示的点在直角坐标系中作出,形成散点图.然后从散点图上,我们可以分析出两个变量是否存在相关关系:如果这些点大致分布在通过散点图中心的一条直线附近,那么就说这两个变量之间具有线性相关关系,这条直线叫做回归直线,其对应的方程叫做回归直线方程.在本节要经常与数据打交道,计算量大,因此同学们要学会应用科学计算器.(4)求回归直线方程的步骤:第一步:先把数据制成表,从表中计算出211nni i i i i x y x y x ==∑∑,,,;第二步:计算回归系数的a ,b ,公式为1112211()()()n n ni i i i i i i n ni i i i n x y x y b n x x a y bx =====⎧-⎪⎪=⎪⎨-⎪⎪=-⎪⎩∑∑∑∑∑,;第三步:写出回归直线方程 y bx a =+.(4)独立性检验①22⨯列联表:列出的两个分类变量X 和Y ,它们的取值分别为12{,}x x 和12{,}y y 的样本频数表称为22⨯列联表1构造随机变量22()()()())n ad bc K a b c d a c b d -=++++(其中n a b c d =+++)得到2K 的观察值k 常与以下几个临界值加以比较:如果 2.706k >,就有0090的把握因为两分类变量X 和Y 是有关系;如果 3.841k>就有0095的把握因为两分类变量X和Y是有关系;如果 6.635k>就有0099的把握因为两分类变量X和Y是有关系;如果低于 2.706k≤,就认为没有充分的证据说明变量X和Y是有关系.②三维柱形图:如果列联表1的三维柱形图如下图由各小柱形表示的频数可见,对角线上的频数的积的差的绝对值-较大,说明两分类变量X和Y是有关的,否则的话是无关的.||ad bc图重点:一方面考察对角线频数之差,更重要的一方面是提供了构造随机变量进行独立性检验的思路方法。
北京市各地市2013年高考数学 最新联考试题分类汇编(11)排列组合.pdf

北京市各地市2013年高考数学 最新联考试题分类汇编(11)排列组合
一、选择题:
6. (北京市海淀区2013年4月高三第二学期期中练习理)一个盒子里有3个分别标有号码为1,2,3的小球,每次取出一个,记下它的标号后再放回盒子中,共取3次,则取得小球标号最大值是3的取法有
A.12种
B. 15种
C. 17种
D.19种
【答案】D
(6)(北京市昌平区2013年1月高三期末考试理)在高三(1)班进行的演讲比赛中,共有5位选手参加,其中3位女生,2位男生.如果2位男生不能连续出场,且女生甲不能排在第一个,那么出场顺序的排法种数为
A. 24
B. 36
C. 48
D.60
二、填空题:
11. (北京市房山区2013年4月高三第一次模拟理)在航天员进行的一项太空实验中,要先后实施个程序,其中程序A只能在第一或最后一步实施,程序B和C在实施时必须相邻,则实验顺序的编排方法共有 种.(用数字作答)
【答案】
三、解答题:
(20)(北京市朝阳区2013年4月高三第一次综合练习理)(本小题满分13分)
设是数的任意一个全排列,定义,其中.
(Ⅰ)若,求的值;
(Ⅱ)求的最大值;
(Ⅲ)求使达到最大值的所有排列的个数.
(20)(本小题满分13分)
最大值的所有排列的个数为,由轮换性知,使达到最大值的所有排列的个数为. ……………………………13分。
2013年高考数学成功方案系列课件第十章第二节排列与组合(理)
法二:“至少有1名女运动员”的反面为“全是男运动员”
可用间接法求解.
从10人中任选5人有C
5 10
种选法,其中全是男运动员的选法
有C56种.
所以“至少有1名女运动员”的选法为C510-C65=246(种).
(3)法一:可分类求解: “只有男队长”的选法为 C48; “只有女队长”的选法为 C48; “男、女队长都入选”的选法为 C38; 所以共有 2C48+C38=196(种)选法. 法二:间接法: 从 10 人中任选 5 人有 C150种选法. 其中不选队长的方法有 C85种. 所以“至少有 1 名队长”的选法为 C510-C58=196(种).
[做一题] [例2] 男运动员6名,女运动员4名,其中男女队长各1人, 选派5人外出比赛,在下列情形中各有多少种选派方法? (1)男运动员3名,女运动员2名; (2)至少有1名女运动员; (3)队长中至少有1人参加; (4)既要有队长,又要有女运动员.
[自主解答] (1)第一步:选3名男运动员,有C63种选法. 第二步:选2名女运动员,有C42种选法. 共有C36·C24=120(种)选法. (2)法一:至少有1名女运动员包括以下几种情况: 1女4男,2女3男,3女2男,4女1男. 由分类加法计数原理可得总选法数为 C14C46+C24C36+C43C62+C44C16=246(种).
(4)先从除去该男生该女生的6人中选3人有C
3 6
种,再安排该
男生有C
1 3
种,选出的3人全排有A
3 3
种,共C
3 6
·C
1 3
·A
3 3
=
360(种).
[悟一法] 排列、组合的综合问题,一般是将符合要求的元素 取出(组合)或进行分组,再对取出的元素或分好的组进行 排列.其中分组时,要注意“平均分组”与“不平均分组” 的差异及分类的标准.
高考数学试题分类汇编---- 排列组合二项式定理

高考数学试题分类汇编---- 排列组合二项式定理一. 选择题:1.(全国一3)512x ⎛⎫+ ⎪⎝⎭的展开式中2x 的系数为( C ) A .10 B .5 C .52 D .12.(全国一12)将1,2,3填入33⨯的方格中,要求每行、每列都没有重复数字,下面是一种填法,则不同的填写方法共有( B ) A .6种 B .12种 C .24种 D .48种3.(全国二9)44)1()1(x x +-的展开式中x 的系数是( A )A .4-B .3-C .3D .44.(安徽卷7)设88018(1),x a a x a x +=+++则0,18,,a a a 中奇数的个数为( A ) A .2 B .3 C .4 D .55.(安徽卷12)12名同学合影,站成前排4人后排8人,现摄影师要从后排8人中抽2人调整到前排,若其他人的相对顺序不变,则不同调整方法的总数是 ( C )A . 2686C AB . 2283C A C .2286C AD .2285C A6.(福建卷9)某班级要从4名男士、2名女生中选派4人参加某次社区服务,如果要求至少有1名女生,那么不同的选派方案种数为AA.14B.24C.28D.487.(湖北卷9)从5名男生和5名女生中选3人组队参加某集体项目的比赛,其中至少有一名女生入选的组队方案数为BA.100B.110C.120D.1808.(湖南卷8)某市拟从4个重点项目和6个一般项目中各选2个项目作为本年度启动的项目,则重点项目A 和一般项目B 至少有一个被选中的不同选法种数是( C )A .15B .45C .60D .759.(江西卷8)10101(1)(1)x x++展开式中的常数项为 D A .1 B .1210()C C .120C D .1020C10.(辽宁卷7)4张卡片上分别写有数字1,2,3,4,从这4张卡片中随机抽取2张,则取出的2张卡片上的数字之和为奇数的概率为( C )A .13B .12C .23D .3411.(辽宁卷10)一生产过程有4道工序,每道工序需要安排一人照看.现从甲、乙、丙等6名工人中安排4人分别照看一道工序,第一道工序只能从甲、乙两工人中安排1人,第四道工序只能从甲、丙两工人中安排1人,则不同的安排方案共有( B )A .24种B .36种C .48种D .72种12.(浙江卷6)在)5)(4)(3)(2)(1(-----x x x x x 的展开式中,含4x 的项的系数是(A )-15 (B )85 (C )-120 (D )27413.(重庆卷10)若(x +12x)n 的展开式中前三项的系数成等差数,则展开式中x 4项的系数为B(A)6 (B)7 (C)8 (D)9 二. 填空题:1.(全国二14)从10名男同学,6名女同学中选3名参加体能测试,则选到的3名同学中既有男同学又有女同学的不同选法共有 种(用数字作答)4202.(北京卷12)5231x x ⎛⎫+ ⎪⎝⎭的展开式中常数项为 ;各项系数之和为 .(用数字作答)10, 323.(福建卷13)(x +1x)9展开式中x 2的系数是 .(用数字作答)84 4.(湖南卷13)记n x x )12(+的展开式中第m 项的系数为m b ,若432b b =,则n =__________.55.(辽宁卷15)6321(1)x x x ⎛⎫++ ⎪⎝⎭展开式中的常数项为 .356.(陕西卷14)72(1)x -的展开式中21x的系数为 84 .(用数字作答) 7.(陕西卷16)某地奥运火炬接力传递路线共分6段,传递活动分别由6名火炬手完成.如果第一棒火炬手只能从甲、乙、丙三人中产生,最后一棒火炬手只能从甲、乙两人中产生,则不同的传递方案共有 96 种.(用数字作答).8.(四川卷13)()()34121x x +-展开式中x 的系数为______2_________。
2013高考数学压轴题突破训练——排列、组合、二项式定理与概率统计(含详解)要点

高考数学压轴题突破训练排列、组合、二项式定理与概率统计(含详解)1. 袋里装有30个球,每个球上都记有1到30的一个号码, 设号码为n 的球的重量为344342nn (克). 这些球以等可能性(不受重量, 号码的影响)从袋里取出.w.w.w.k.s.5.u.c.o.m(Ⅰ)如果任意取出1球, 求其号码是3的倍数的概率. (Ⅱ)如果任意取出1球, 求重量不大于号其码的概率; (Ⅲ)如果同时任意取出2球, 试求它们重量相同的概率.2. 从10个元件中(其中4个相同的甲品牌元件和6个相同的乙品牌元件)随机选出3个参加某种性能测试. 每个甲品牌元件能通过测试的概率均为54,每个乙品牌元件能通过测试的概率均为53.试求:(I )选出的3个元件中,至少有一个甲品牌元件的概率;(II )若选出的三个元件均为乙品牌元件,现对它们进行性能测试,求至少有两个乙品牌元件同时通过测试的概率.3. 设在12个同类型的零件中有2个次品,抽取3次进行检验,每次任取一个,并且取出不在放回,若以和分别表示取出次品和正品的个数。
(1)求的分布列,期望及方差;(2)求的分布列,期望及方差;4. 某大型商场一个结算窗口,每天排队结算的人数及相应概率如下:排队人数0—5 6—10 11—15 16—20 21—2525以上概率0.1 a 0.25 0.25 0.2 0.05(1)每天不超过20人排队结算的概率是多少?(2)一周7天中,若有三天以上(含三天)出现超过15人排队结算的概率大于0.75,商场就需要增加结算窗口,请问,该商场是否需要增加结算窗口?5. 某售货员负责在甲、乙、丙三个柜面上售货.如果在某一小时内各柜面不需要售货员照顾的概率分别为0.9,0.8,0.7.假定各个柜面是否需要照顾相互之间没有影响,求在这个小时内:(1)只有丙柜面需要售货员照顾的概率;(2)三个柜面最多有一个需要售货员照顾的概率;(3)三个柜面至少有一个需要售货员照顾的概率.6. 某同学上楼梯的习惯每步走1阶或2阶,现有一个11阶的楼梯,该同学从第1阶到第11阶用7步走完。
专题13 排列组合与二项式定理-十年(2012-2021)高考数学真题分项详解(全国通用)(解析版)
专题13 排列组合与二项式定理【2021年】1.(2021年全国高考乙卷数学(理)试题)将5名北京冬奥会志愿者分配到花样滑冰、短道速滑、冰球和冰壶4个项目进行培训,每名志愿者只分配到1个项目,每个项目至少分配1名志愿者,则不同的分配方案共有( ) A .60种 B .120种 C .240种 D .480种【答案】C【分析】根据题意,有一个项目中分配2名志愿者,其余各项目中分配1名志愿者,可以先从5名志愿者中任选2人,组成一个小组,有25C 种选法;然后连同其余三人,看成四个元素,四个项目看成四个不同的位置,四个不同的元素在四个不同的位置的排列方法数有4!种,根据乘法原理,完成这件事,共有254!240C ⨯=种不同的分配方案,故选:C.2.(2021年全国高考甲卷数学(理)试题)将4个1和2个0随机排成一行,则2个0不相邻的概率为( ) A .13B .25C .23D .45【答案】C【分析】将4个1和2个0随机排成一行,可利用插空法,4个1产生5个空,若2个0相邻,则有155C =种排法,若2个0不相邻,则有2510C =种排法,所以2个0不相邻的概率为1025103=+. 故选:C.【2012年——2020年】1.(2020年全国统一高考数学试卷(理科)(新课标Ⅰ))25()()x x y xy ++的展开式中x 3y 3的系数为( )A .5B .10C .15D .20【答案】C【分析】5()x y +展开式的通项公式为515r r rr T C x y -+=(r N ∈且5r ≤)所以2y x x ⎛⎫+ ⎪⎝⎭的各项与5()x y +展开式的通项的乘积可表示为:56155r rrr rrr xT xC xy C xy --+==和22542155r r rr r r r T C x y xC y y y x x --++==在615r rr r xT C xy -+=中,令3r =,可得:33345xT C x y =,该项中33x y 的系数为10,在42152r r r r T C x xy y -++=中,令1r =,可得:521332T C y x x y =,该项中33x y 的系数为5所以33x y 的系数为10515+= 故选:C2.(2019年全国统一高考数学试卷(理科)(新课标Ⅰ))我国古代典籍《周易》用“卦”描述万物的变化.每一“重卦”由从下到上排列的6个爻组成,爻分为阳爻“——”和阴爻“— —”,如图就是一重卦.在所有重卦中随机取一重卦,则该重卦恰有3个阳爻的概率是A .516B .1132C .2132D .1116【答案】A【分析】由题知,每一爻有2种情况,一重卦的6爻有62情况,其中6爻中恰有3个阳爻情况有36C ,所以该重卦恰有3个阳爻的概率为3662C =516,故选A .3.(2019年全国统一高考数学试卷(理科)(新课标Ⅰ))(1+2x 2 )(1+x )4的展开式中x 3的系数为 A .12 B .16 C .20 D .24【答案】A【分析】由题意得x 3的系数为314424812C C +=+=,故选A .4.(2018年全国普通高等学校招生统一考试理数(全国卷II ))我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先的成果.哥德巴赫猜想是“每个大于2的偶数可以表示为两个素数的和”,如30723=+.在不超过30的素数中,随机选取两个不同的数,其和等于30的概率是 A .112B .114C .115D .118【答案】C【详解】:不超过30的素数有2,3,5,7,11,13,17,19,23,29,共10个,随机选取两个不同的数,共有21045C =种方法,因为7+23=11+19=13+17=30,所以随机选取两个不同的数,其和等于30的有3种方法,故概率为31=4515,选C. 5.(2018年全国卷Ⅰ理数高考试题)522x x ⎛⎫+ ⎪⎝⎭的展开式中4x 的系数为 A .10 B .20 C .40 D .80【答案】C【详解】::由题可得()5210315522rrrr r r r T C x C x x --+⎛⎫== ⋅⋅⎪⎝⎭⋅⋅ 令103r 4-=,则r 2=所以22552240r r C C ⋅⋅==故选C.6.(2017年全国普通高等学校招生统一考试理科数学(新课标1卷))(2017新课标全国卷Ⅰ理科)621(1)(1)x x++展开式中2x 的系数为 A .15 B .20 C .30 D .35【答案】C 【解析】因为6662211(1)(1)1(1)(1)x x x x x++=⋅++⋅+,则6(1)x +展开式中含2x 的项为22261C 15x x ⋅=,621(1)x x ⋅+展开式中含2x 的项为442621C 15x x x⋅=,故2x 的系数为151530+=,选C. 7.(2017年全国普通高等学校招生统一考试理科数学(新课标2卷))安排3名志愿者完成4项工作,每人至少完成1项,每项工作由1人完成,则不同的安排方式共有( ) A .12种B .18种C .24种D .36种【答案】D【详解】4项工作分成3组,可得:24C=6,安排3名志愿者完成4项工作,每人至少完成1项,每项工作由1人完成, 可得:36363A ⨯=种.故选D.8.(2015年全国普通高等学校招生统一考试理科数学(新课标Ⅰ))()52x x y ++的展开式中,52x y 的系数为 A .10 B .20 C .30 D .60【答案】C【解析】在25()x x y ++的5个因式中,2个取因式中2x 剩余的3个因式中1个取x ,其余因式取y,故52x y 的系数为212532C C C =30,故选 C.9.(2013年全国普通高等学校招生统一考试理科数学(新课标1卷))设m 为正整数,(x +y)2m 展开式的二项式系数的最大值为a ,(x +y)2m +1展开式的二项式系数的最大值为b ,若13a=7b ,则m =A .5B .6C .7D .8【答案】B【详解】:由题意可知221,m m m m C a C b +==,137a b =,221137m m m m C C +∴=,即()()()2!21!137!!!1!m m m m m m +=⋅⋅+,211371m m +∴=⋅+,解得6m =.故B 正确.10.(2013年全国普通高等学校招生统一考试理科数学(新课标2))已知(1+ax )·(1+x )5的展开式中x 2的系数为5,则a = A .-4 B .-3 C .-2 D .-1【答案】D 【详解】由题意知:21555C aC +=,解得1a =-,故选D.11.(2012年全国普通高等学校招生统一考试理科数学(课标卷))将2名教师,4名学生分成2个小组,分别安排到甲、乙两地参加社会实践活动,每个小组由1名教师和2名学生组成,不同的安排方案共有 A .12种 B .10种 C .9种 D .8种【答案】A【详解】:第一步,为甲地选一名老师,有122C =种选法;第二步,为甲地选两个学生,有246C =种选法;第三步,为乙地选1名教师和2名学生,有1种选法,故不同的安排方案共有26112⨯⨯=种,故选A .12.(2012年全国普通高等学校招生统一考试理科数学(大纲卷))将字母a,a,b,b,c,c,排成三行两列,要求每行的字母互不相同,每列的字母也互不相同,则不同的排列方法共有 A .12种 B .18种 C .24种 D .36种【答案】A【解析】:先排第一列,由于每列的字母互不相同,因此共有3×2×1种不同的方法;再排第二列,其中第二列第一行的字母共有2种不同的排法,第二列第二、三行的字母只有1种排法,因此共有3×2×1×2=12(种)不同的方法.二、填空题13.(2020年全国统一高考数学试卷(理科)(新课标Ⅰ))4名同学到3个小区参加垃圾分类宣传活动,每名同学只去1个小区,每个小区至少安排1名同学,则不同的安排方法共有__________种. 【答案】36【分析】4名同学到3个小区参加垃圾分类宣传活动,每名同学只去1个小区,每个小区至少安排1名同学∴先取2名同学看作一组,选法有:246C = 现在可看成是3组同学分配到3个小区,分法有:336A =根据分步乘法原理,可得不同的安排方法6636⨯=种 故答案为:36.14.(2020年全国统一高考数学试卷(理科)(新课标Ⅰ))262()x x+的展开式中常数项是__________(用数字作答). 【答案】240【分析】622x x ⎛⎫+ ⎪⎝⎭ 其二项式展开通项:()62612rrrr C xx T -+⎛⎫⋅⋅ ⎪⎝⎭= 1226(2)r r r r x C x --⋅=⋅1236(2)r r r C x -=⋅当1230r -=,解得4r =∴622x x ⎛⎫+ ⎪⎝⎭的展开式中常数项是:664422161516240C C ⋅=⋅=⨯=.故答案为:240.15.(2018年全国普通高等学校招生统一考试理科数学(新课标I 卷))从2位女生,4位男生中选3人参加科技比赛,且至少有1位女生入选,则不同的选法共有_____________种.(用数字填写答案) 【答案】16【分析】根据题意,没有女生入选有344C =种选法,从6名学生中任意选3人有3620C =种选法,故至少有1位女生入选,则不同的选法共有20416-=种,故答案是16.16.(2017年全国普通高等学校招生统一考试理科数学)5(2x 的展开式中,x 3的系数是_________.(用数字填写答案) 【答案】10【详解】:5(2x 的展开式的通项为555255(2)2rr r r r r C x C x---=(0r =,1,2,…,5),令532r -=得4r =,所以3x 的系数是452C 10=.17.(2016年全国普通高等学校招生统一考试理科数学(全国2卷))有三张卡片,分别写有1和2,1和3,2和3.甲,乙,丙三人各取走一张卡片,甲看了乙的卡片后说:“我与乙的卡片上相同的数字不是2”,乙看了丙的卡片后说:“我与丙的卡片上相同的数字不是1”,丙说:“我的卡片上的数字之和不是5”,则甲的卡片上的数字是________. 【答案】1和3.【详解】根据丙的说法知,丙的卡片上写着1和2,或1和3;(1)若丙的卡片上写着1和2,根据乙的说法知,乙的卡片上写着2和3; 所以甲的说法知,甲的卡片上写着1和3;(2)若丙的卡片上写着1和3,根据乙的说法知,乙的卡片上写着2和3; 又加说:“我与乙的卡片上相同的数字不是2”; 所以甲的卡片上写的数字不是1和2,这与已知矛盾; 所以甲的卡片上的数字是1和3.18.(2015年全国普通高等学校招生统一考试理科数学(新课标Ⅰ))4()(1)a x x ++的展开式中,若x 的奇数次幂的项的系数之和为32,则a =________. 【答案】3【解析】:由已知得4234(1)1464x x x x x +=++++,故4()(1)a x x ++的展开式中x 的奇数次幂项分别为4ax ,34ax ,x ,36x ,5x ,其系数之和为441+6+1=32a a ++,解得3a =.19.(2014年全国普通高等学校招生统一考试理科数学(新课标Ⅰ))()()8x y x y -+的展开式中27x y 的系数为________.(用数字填写答案) 【答案】20-【详解】:由题意,8()x y +展开式通项为818k k k k T C x y -+=,08k ≤≤.当7k =时,777888T C xy xy ==;当6k =时,626267828T C x y x y ==,故()()8x y x y -+的展开式中27x y 项为726278()2820x xy y x y x y ⋅+-⋅=-,系数为20-.20.(2014年全国普通高等学校招生统一考试理科数学(全国Ⅰ卷))()10x a +的展开式中,7x 的系数为15,则a=________.(用数字填写答案) 【答案】12【详解】因为10110r r rr T C x a -+=,所以令107r -=,解得3r =,所以373410T C x a ==157x ,解得12a =.。
2013年、2012年、2011年高考题分类汇编之计数原理和二项式定理
答案:B 11.(2013 年重庆卷,理 13)从 3 名骨科、 4 名脑外科和 5 名内科医生中选派 5 人组成一个抗震救灾医疗小组, 则骨科、脑外科和内科医生都至少有 1 人的选派方法种数是 (用数字作答). 解析:选派骨科、脑外科、内科医生的人数依次为 3,1,1;2,2,1;2,1,2;1,3,1;1,2,2;1,1,3.
第十一章
第一节
计数原理
排列与组合
高考试题
考点一 两个计数原理
1.(2013 年福建卷,理 5)满足 a,b∈{-1,0,1,2},且关于 x 的方程 ax +2x+b=0 有实数解的有序数对(a,b)的 个数为( (A)14 ) (B)13 (C)12 (D)10
2 2
解析:若 a=0,则 b 可以为-1,0,1,2,此时(a,b)的取值有 4 个;若 a≠0,方程 ax +2x+b=0 有实数解,需Δ=4-4ab ≥0,所以 ab≤1,此时(a,b)的取值为(-1,-1),(-1,0),(-1,1),(-1,2),(1,-1),(1,0),(1,1),(2,-1),(2,0), 共 9 个. ∴(a,b)的个数为 4+9=13.故选 B. 答案:B 2.(2012 年大纲全国卷,理 11)将字母 a,a,b,b,c,c 排成三行两列,要求每行的字母互不相同,每列的字母也 互不相同,则不同的排列方法共有( ) (A)12 种 (B)18 种 (C)24 种 (D)36 种 解析:利用分步计数原理,先填最左上角的数,有 3 种,再填最右上角的数,有 2 种,再填写第二行第一列的数, 有 2 种,一共有 3×2×2=12 种. 答案:A 3.(2012 年北京卷,理 6)从 0,2 中选一个数字,从 1,3,5 中选两个数字,组成无重复数字的三位数,其中奇数 的个数为( (A)24 ) (B)18 (C)12 (D)6
2013年全国高考理科数学分类汇编
2013年全国高考理科数学分类汇编一、集合与简易逻辑辽宁2013(2)已知集合{}{}4|0log 1,|2A x x B x x AB =<<=≤=,则A .()01,B .(]02,C .()1,2D .(]12, 辽宁2013(4)下面是关于公差0d >的等差数列()n a 的四个命题:{}1:n p a 数列是递增数列;{}2:n p na 数列是递增数列; 3:n a p n ⎧⎫⎨⎬⎩⎭数列是递增数列; {}4:3n p a nd +数列是递增数列;其中的真命题为(A )12,p p (B )34,p p (C )23,p p (D )14,p p 江西2013.1.已知集合M={1,2,zi},i ,为虚数单位,N={3,4},则复数z=A.-2iB.2iC.-4iD.4i 全国1.1、已知集合A={x |x 2-2x >0},B={x |-5<x <5},则 ( )A 、A∩B=∅B 、A ∪B=RC 、B ⊆AD 、A ⊆B全国2.1.已知集合{}{}3,2,1,0,1,,4)1(|2-=∈<-=N R x x x M ,则=⋂N M ( )A {}2,1,0B {}2,1,0,1-C {}3,2,0,1-D {}3,2,1,0北京2013.1.已知集合A={-1,0,1},B={x |-1≤x <1},则A∩B= ( ) A.{0} B.{-1,0} C.{0,1} D.{-1,0,1}四川1.设集合{|20}A x x =+=,集合2{|40}B x x =-=,则AB =( )(A ){2}- (B ){2} (C ){2,2}- (D )∅ 重庆(1)已知集合{1,2,3,4}U =,集合={1,2}A ,={2,3}B ,则()UA B =(A ){1,3,4} (B ){3,4} (C ){3} (D ){4} 天津卷(1) 已知集合A = {x ∈R | |x |≤2}, A = {x ∈R | x ≤1}, 则A B ⋂= (A) (,2]-∞ (B) [1,2] (C) [-2,2](D) [-2,1]2013安微(1)设集合{}{}{}1,2,3,4,5,|,,,A B M x x a b a A b B ====+∈∈则M 中元素的个数为(A )3 (B )4 (C )5 (D )6 山东(2)设集合A={0,1,2},则集合B={x-y|x ∈A, y ∈A }中元素的个数是()A. 1B. 3C. 5D.9重庆(2)命题“对任意x R ∈,都有20x ≥”的否定为(A )对任意x R ∈,使得20x < (B )不存在x R ∈,使得20x <(C )存在0x R ∈,都有200x ≥ (D )存在0x R ∈,都有200x <2013广东1.设集合M={x ∣x 2+2x=0,x ∈R},N={x ∣x 2-2x=0,x ∈R},则M ∪N= A. {0} B. {0,2} C. {-2,0} D {-2,0,2} 北京2013.3.“φ=π”是“曲线y=sin(2x +φ)过坐标原点的” A.充分而不必要条件 B.必要而不充分条件 C.充分必要条件 D.既不充分也不必要条件四川4.设x Z ∈,集合A 是奇数集,集合B 是偶数集.若命题:,2p x A x B ∀∈∈,则( ) (A ):,2p x A x B ⌝∃∈∉ (B ):,2p x A x B ⌝∀∉∉ (C ):,2p x A x B ⌝∃∉∈ (D ):,2p x A x B ⌝∃∈∈2013广东8.设整数n≥4,集合X={1,2,3……,n }。
(浙江版)高考数学分项汇编专题11排列组合、二项式定理(含解析)理
第十一章 排列组合、二项式定理一.基础题组1. 【2014年.浙江卷.理5】在46)1()1(y x ++的展开式中,记nm y x 项的系数为),(n m f ,则=+++)3,0(2,1()1,2()0,3(f f f f ) ( ) A.45 B.60 C.120 D. 210【答案】:C2. 【2014年.浙江卷.理14】在8张奖券中有一、二、三等奖各1张,其余5张无奖.将这8张奖券分配给4个人,每人2张,不同的获奖情况有_____种(用数字作答).【答案】:60【解析】:3. 【2013年.浙江卷.理11】设二项式53x x ⎛- ⎪⎝⎭的展开式中常数项为A ,则A =__________. 【答案】:-104. 【2013年.浙江卷.理14】将A ,B ,C ,D ,E ,F 六个字母排成一排,且A ,B 均在C 的同侧,则不同的排法共有__________种(用数字作答).【答案】:480【解析】:如图六个位置.若C 放在第一个位置,则满足条件的排法共有55A 种情况;若C 放在第2个位置,则从3,4,5,6共4个位置中选2个位置排A ,B ,再在余下的3个位置排D ,E ,F ,5. 【2012年.浙江卷.理6】若从1,2,3,…,9这9个整数中同时取4个不同的数,其和为偶数,则不同的取法共有( )A .60种B .63种C .65种D .66种【答案】D6. 【2012年.浙江卷.理14】若将函数f (x )=x 5表示为f (x )=a 0+a 1(1+x )+a 2(1+x )2+…+a 5(1+x )5,其中a 0,a 1,a 2,…,a 5为实数,则a 3=__________.【答案】107. 【2011年.浙江卷.理13】若二项式)0(6>⎪⎪⎭⎫ ⎝⎛-a x a x 的展开式中x 3的系数为A , 常数项为B ,若4B A =,则a 的值是 .【答案】 28. 【2009年.浙江卷.理4】在二项式251()x x -的展开式中,含4x 的项的系数是( )A .10-B .10C .5-D .5答案:B 【解析】对于()251031551()()1r r r r r r r T C x C x x--+=-=-,对于1034,2r r -=∴=,则4x 的项的系数是225(1)10C -=9. 【2009年.浙江卷.理16】甲、乙、丙3人站到共有7级的台阶上,若每级台阶最多站2人,同一级台阶上的人不区分站的位置,则不同的站法种数是 (用数字作答).【答案】:33610. 【2008年.浙江卷.理4】在)5)(4)(3)(2)(1(-----x x x x x 的展开式中,含4x 的项的系数是(A )-15 (B )85 (C )-120 (D )274【答案】A11. 【2006年.浙江卷.理8】若多项式210910019109(1)(1)(1),x x a a x a x a x +=+++++++=则a (A)9 (B)10 (C)-9 (D)-10【答案】D【解析】因为 ()()2102101111x x x x +=+-++-⎡⎤⎡⎤⎣⎦⎣⎦,所以()1910110a C =⨯-=- ,故选D.12. 【2005年.浙江卷.理5】在(1-x )5+(1-x )6+(1-x )7+(1-x )8的展开式中,含x 3的项的系数是( )(A) 74 (B) 121 (C) -74 (D) -121【答案】D二.能力题组1. 【2008年.浙江卷.理16】用1,2,3,4,5,6组成六位数(没有重复数字),要求任何相邻两个数字的奇偶性不同,且1和2相邻,这样的六位数的个数是 (用数字作答)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2013年高考理科数学试题分类汇编:10排列、组合及二项式定理
一、选择题
错误!未指定书签。 .(2013年普通高等学校招生统一考试新课标Ⅱ卷数学(理)(纯WORD
版含答案))已知5)1)(1(xax的展开式中2x的系数为5,则a ( )
A.4 B.3 C.2 D.1
【答案】D
错误!未指定书签。 .(2013年普通高等学校招生统一考试山东数学(理)试题(含答案))
用0,1,,9十个数字,可以组成有重复数字的三位数的个数为 ( )
A.243 B.252 C.261 D.279
【答案】B
错误!未指定书签。 .(2013年高考新课标1(理))设m为正整数,2()mxy展开式的二
项式系数的最大值为a,21()mxy展开式的二项式系数的最大值为b,若137ab,
则m ( )
A.5 B.6 C.7 D.8
【答案】B
错误!未指定书签。 .(2013年普通高等学校招生统一考试大纲版数学(理)WORD版含答
案(已校对))8411+xy的展开式中22xy的系数是 ( )
A.56 B.84 C.112 D.168
【答案】D
错误!未指定书签。 .(2013年普通高等学校招生统一考试福建数学(理)试题(纯WORD
版))满足,1,0,1,2ab,且关于x的方程220axxb有实数解的有序数对
(,)ab
的个数为 ( )
A.14 B.13 C.12 D.10
【答案】B
错误!未指定书签。 .(2013年上海市春季高考数学试卷(含答案))10(1)x的二项展开式
中的一项是 ( )
A.45x B.290x C.3120x D.4252x
【答案】C
错误!未指定书签。 .(2013年普通高等学校招生统一考试辽宁数学(理)试题(WORD版))
使得13nxnNnxx的展开式中含有常数项的最小的为 ( )
A.4 B.5 C.6 D.7
【答案】B
错误!未指定书签。 .(2013年高考四川卷(理))从1,3,5,7,9这五个数中,每次取出两个
不同的数分别为,ab,共可得到lglgab的不同值的个数是 ( )
A.9 B.10 C.18 D.20
【答案】C
错误!未指定书签。 .(2013年高考陕西卷(理))设函数61,00.,(),xxfxxxx , 则
当x>0时, [()]ffx表达式的展开式中常数项为 ( )
A.-20 B.20 C.-15 D.15
【答案】A
错误!未指定书签。.(2013年高考江西卷(理))(x2-32x)5展开式中的常数项为 ( )
A.80 B.-80 C.40 D.-40
【答案】C
二、填空题
错误!未指定书签。.(2013年上海市春季高考数学试卷(含答案))36的所有正约数之和可
按如下方法得到:因为2236=23,所以36的所有正约数之和为
22222222
(133)(22323)(22323)(122)133)91(
参照上述方法,可求得2000的所有正约数之和为________________________
【答案】4836
错误!未指定书签。.(2013年高考四川卷(理))二项式5()xy的展开式中,含23xy的项
的系数是_________.(用数字作答)
【答案】10
错误!未指定书签。.(2013年上海市春季高考数学试卷(含答案))从4名男同学和6名女
同学中随机选取3人参加某社团活动,选出的3人中男女同学都有的概率为________(结
果用数值表示).
【答案】45
错误!未指定书签。.(2013年普通高等学校招生统一考试浙江数学(理)试题(纯WORD版))
将FEDCBA,,,,,六个字母排成一排,且BA,均在C的同侧,则不同的排法共有
________种(用数字作答)
【答案】480
错误!未指定书签。.(2013年普通高等学校招生统一考试重庆数学(理)试题(含答案))
从3名骨科.4名脑外科和5名内科医生中选派5人组成一个抗震救灾医疗小组,则骨科.
脑外科和内科医生都至少有1人的选派方法种数是___________(用数字作答)
【答案】590
错误!未指定书签。.(2013年普通高等学校招生统一考试天津数学(理)试题(含答案))
6
1
xx
的二项展开式中的常数项为______.
【答案】15
错误!未指定书签。.(2013年普通高等学校招生统一考试浙江数学(理)试题(纯WORD版))
设二项式53)1(xx的展开式中常数项为A,则A________.
【答案】10
错误!未指定书签。.(2013年高考上海卷(理))设常数aR,若52axx的二项展开式
中7x项的系数为10,则______a
【答案】2a
错误!未指定书签。.(2013年高考北京卷(理))将序号分别为1,2,3,4,5的5张参观券全
部分给4人,每人至少1张,如果分给同一人的2张参观券连号,那么不同的分法种数是
_________.
【答案】96
错误!未指定书签。.(2013年普通高等学校招生统一考试安徽数学(理)试题(纯WORD版))
若83axx的展开式中4x的系数为7,则实数a______.
【答案】21
错误!未指定书签。.(2013年普通高等学校招生统一考试大纲版数学(理)WORD版含答案
(已校对))6个人排成一行,其中甲、乙两人不相邻的不同排法共有____________
种.(用数字作答).
【答案】480
