三视图 北师大版 必修2 含答案 2017_2018学年高中数学课下能力提升
(北师大版)数学必修二课时作业:1.3三视图(含答案)

温馨提示:此套题为Word版,请按住Ctrl,滑动鼠标滚轴,调节合适的观看比例,答案解析附后。
关闭Word文档返回原板块。
课时提升作业(三)三视图一、选择题(每小题3分,共18分)1.(2018·江西高考)一几何体的直观图如图,下列给出的四个俯视图中正确的是( )【解析】选B.因为俯视图是几何体在下底面上的投影,所以选B.2.(2018·福州高一检测)一个几何体的三视图形状都相同,大小均相等,则该几何体不可以是( )A.球B.三棱锥C.正方体D.圆柱【解析】选D.圆柱的三视图分别是矩形,矩形,圆,不可能三个视图都一样,球的三视图都是圆,三棱锥的三视图都是三角形,正方体的三视图都是正方形.3.(2018·广州高一检测)如图,△A′B′C′为正三角形,与底面不平行,且CC′>BB′>AA′,则多面体的主视图为( )【解析】选D.因为△A′B′C′为正三角形,面A′B′BA向前,所以主视图不可能是A,B,C,只能是D.4.一个几何体由几个相同的小正方体组合而成,它的主视图、左视图、俯视图如图所示,则这个几何体包含的小正方体的个数是( )A.7B.6C.5D.4【解析】选C.由三视图知小正方体底层4个,上层1个,共5个.【变式训练】该几何体的三视图如图所示,则搭成该几何体需要的小正方体的块数是( )A.8B.7C.6D.5【解析】选C.由主视图和左视图,知该几何体由两层小正方体拼接成,由俯视图可知,最下层有5个小正方体,由主、左视图知上层仅有一个小正方体,则共有6个小正方体.5.(2018·四川高考)一个几何体的三视图如图所示,则该几何体的直观图可以是( )【解析】选D.根据几何体的三视图中正视图与侧视图一致,并且俯视图是两个圆,可知只有选项D适合,故选D.6.(2018·北京高一检测)一个长方体去掉一个长方体,所得几何体的主视图与左视图分别如图所示.则该几何体的俯视图为( )【解题指南】从主视图和左视图上分析,去掉长方体的位置所在的方位,然后判断俯视图的正确图形.【解析】选C.由主视图可知去掉的长方体在正视线的方向,从左视图可以看出去掉的长方体在原长方体的左侧,可知俯视图为C.二、填空题(每小题4分,共12分)7.下图中三视图表示的几何体是________.【解析】由主视图和左视图知为柱体,又底面为四边形,所以此几何体为四棱柱.答案:四棱柱8.如图所示,图①②③是图④表示的几何体的三视图,其中图①是____________,图②是____________,图③是____________(填写视图名称).【解析】由三视图可知,①为主视图,②为左视图,③为俯视图.答案:主视图左视图俯视图9.(2018·南昌高一检测)一个三棱柱的左视图和俯视图如图:则该三棱柱主视图的面积为________.【解析】由题知主视图如图,其高与左视图中三角形的高相等,由俯视图的高为2,知左视图的底边为2,故左视图为正三角形,而主视图的长为1,高为,则主视图的面积为1×=.答案:三、解答题(每小题10分,共20分)10.画出如图所示物体的三视图.【解析】此物体的三视图如图所示:11.(2018·洛阳高一检测)如图所示是一个半圆柱OO1与三棱柱ABC A1B1C1的组合体,其中,圆柱OO1的轴截面ACC1A1是边长为4的正方形,△ABC为等腰直角三角形,AB⊥BC,试画出此组合体的三视图.【解析】由题意可知几何体的主视图与左视图都是中间有一条线段的矩形,俯视图由半圆与等腰三角形组成,如图:一、选择题(每小题4分,共16分)1.(2018·阜阳高一检测)如图是长和宽分别相等的两个矩形,给定下列三个 A.3B.2C.1D.0【解析】选A.对于①可以为放倒的直三棱柱;②可以为长方体;③可以为放倒的圆柱.2.(2018·泸州高一检测)将一个正方体沿其棱的中点截去两个三棱锥后所得几何体如图所示,则其俯视图为( )【解题指南】根据正方体的几何特征,分析几何体俯视图外轮廓的形状及截面截正方体表面所得的棱能否看到,进而得到答案.【解析】选C.将一个正方体沿其棱的中点截去两个三棱锥后所得几何体的俯视图满足:外轮廓是一个正方形,左上角能看到上底面被截所成的棱,为实线,右下角看不到下底面被截所成的棱,为虚线,故选C.3.如图,直三棱柱的所有棱长均为2,主视图和俯视图如图所示,则其左视图的面积为( )A.2B.2C.4D.4【解题指南】先确定出左视图的形状,再求面积.【解析】选B.左视图是长为2,宽为底面三角形的高,即为的矩形.所以S=2×=2.4.(2018·湖南高考)一块石材表示的几何体的三视图如图所示,将该石材切削、打磨,加工成球,则能得到的最大球的半径等于( )A.1B.2C.3D.4【解题指南】先由三视图画出直观图,判断这个几何体是底面是边长为6,8,10的直角三角形,高为12的躺下的直三棱柱,底面的内切圆的半径就是做成的最大球的半径.【解析】选B.由三视图画出直观图如图,判断这个几何体是底面是边长为6,8,10的直角三角形,高为12的躺下的直三棱柱,直角三角形的内切圆的半径为r==2,这就是做成的最大球的半径.二、填空题(每小题5分,共10分)5.(2018·淮北高一检测)正方形ABCD的边长为3cm,以直线AB为轴,将正方形旋转一周,所得几何体的主视图的周长是__________cm.【解析】正方形旋转一周,所得几何体是圆柱,主视图是矩形,矩形的长为6cm,宽是3cm,因此,所得几何体的主视图的周长为2×(6+3)=18(cm).答案:186.用n个体积为1的正方体搭成一个几何体,其主视图、左视图都是如图所示的图形,则n的最大值与n的最小值之差是________.【解析】由主视图、左视图可知,正方体个数最少时,底层有3个小正方体,上面有2个,共5个;个数最多时,底层有9个小正方体,上面有2个,共11个.故n的最大值与最小值之差是6.答案:6三、解答题(每小题12分,共24分)7.如图是根据某一种型号的滚筒洗衣机抽象出来的几何体,数据如图所示(单位:cm).试画出它的三视图.【解析】这个几何体是由一个长方体挖去一个圆柱体构成的,三视图如图所示.【拓展延伸】画三视图的诀窍由三视图的作图原则可知:(1)主视图和俯视图共同反映了物体左右方向的尺寸.(2)主视图和左视图共同反映了物体上下方向的尺寸.(3)俯视图和左视图共同反映了物体前后方向的尺寸.因此画一个物体的三视图不仅要确定其形状,而且要确定三视图之间的线段大小关系.画三视图时一般遵循从下层向上层,从左边到右边的原则.【变式训练】如图,BC⊥CD,且CD⊥MN,ABCD绕AD所在直线MN旋转,在旋转前,点A可以在DM上选定.当点A选在射线DM上的不同位置时,形成的几何体大小、形状不同,分别画出它的三视图并比较异同.【解析】(1)当点A在图(a)中射线DM的位置时,绕MN旋转一周所得几何体为底面半径为CD的圆柱和圆锥叠加而成,其三视图如图(a).(2)当点A在图(b)中射线DM的位置时,即点A是B到MN作垂线的垂足时旋转后的几何体为圆柱,其三视图如图(b).(3)当点A在图(c)中所示位置时,其旋转所得几何体为圆柱中挖去同底的圆锥,其三视图如图(c).(4)当点A位于点D时,如图(d)中,旋转体为圆柱中挖去同底等高的圆锥,其三视图如图(d).8.如图是由小立方块组成的几何体的俯视图,小正方形中的数字表示该位置的小立方块的个数,请画出它的主视图和左视图.【解题指南】从俯视图可以看出,其主视图应该是3列,每列的立方块的个数分别是4,4,3;左视图应该是4列,每列的立方块的个数分别是3,3,4,3,由此可以想象该几何体的形状,得到其主视图和左视图.【解析】该几何体的主视图和左视图如图:【变式训练】某座楼由相同的若干个房间组成,该楼的三视图如图所示,其中图中每一个小矩形表示一个房间.该楼有几层?最多有多少个房间?画出房间最多时此楼的大致形状.【解析】由主视图和左视图可知,该楼共3层,由俯视图可知该楼一层共5个房间,结合主视图和左视图可知二楼最多有四个房间,三楼一个房间,故最多有10个房间,此时楼的大致形状如图所示.关闭Word文档返回原板块。
北师大版高中数学必修二 三视图

多面体的三视图
正六棱柱
思考
几何体的三视图是不是唯一的?
结论: 不一定,角度不一样可能 三视图就不一样!
三、三视图的作图步骤
1.确定视图方向 2.画出能反映物体真实形状的一个视图
3.运用长对正、高平齐、宽相等的原 则画出其它视图
4.检查,加深
我相信你一定能 画出这个复杂几 何体的三视图!
三视图的形成及其投影规则 (1)
三视图的形成及其投影规则 (2)
二、三视图的作图规则
主—俯:长对正 主—左:高平齐 主 左—俯:宽相等 视
图 左视图
俯视图
错误三视图——长未对正
错误三视图——高不平齐
错误三视图——宽不相等
旋转体的三视图
俯
左 圆台
请思考:把圆台倒过来三视图如何画?
旋转体的三视图
横看成岭侧成峰,远近高低各不同。 不识庐山真面目,只缘身在此山中。
——苏轼
横看成岭侧成峰,远近高低各不同。 不识庐山真面目,只缘身在此山中。
——苏轼
中心投影
• 把光由一点向外散射形成的投影,叫做中心投影 – 投影线交于一点
– 随着物体距离光源(屏幕)的远近,形成的投影 大小不同,相似图形
平行投影
• 把在一束平行光线照射下形成的投影,叫平行投影 – 投影线平行
中心投影法 投影法
平行投影法
投影法分类
正投影 斜投影
一、三视图相关概念 视图
正投影
从左面看 主视图
你能总结出三
视图的概念吗
从上面看
主视图 左视图
正面
高
长
宽
宽 俯视图
三视图概念:
将空间图形分别从正面,左 面和上面向三个两两垂直的 平面作正投影,然后把这三 个投影按一定的布局放在一 个平面内,这样构成的图形 叫做空间图形的三视图.
北师大版高中数学必修2《三视图》参考课件

主视图
左视图
俯视图
老师提示:画三视图要认真准确 Nhomakorabea主视图
左视图
俯视图
球的三视图
老师提示:画三视图要认真准确
主视图
左视图
俯视图
圆台
四棱柱
例1. 如图所示的长方体的长、宽、高分别为 5cm、4cm、3cm,画出这个长方体的三视图。
讨论:①这个长方体的三视图分别是什么形状的?
水平投射面
侧立投射面
直立投射面
主视图(正视图):光线自物体的 前面向后投射所得的投影
俯视图:自上向下
左视图:自左向右
用三种视图刻画空间物体的结构
三视图
2、三视图表达的意义
左视图:宽和高
三视图能反应物体真实的形状和长、宽、高。
俯视图:长和宽
主视图:长和高
三视图的对应规律
俯视图和左视图
主视图和俯视图
棱锥的三视图
棱台的三视图
画下列几何体的三视图
六棱柱
画出下图的俯视图
俯视图
蒙古包
下图是一个蒙古包的照片. 请画出这个几何体的三种视图.
主视图
左视图
俯视图
画下例几何体的三视图
主视图
左视图
画出下列几何体的三视图
主视图
左视图
俯视图
“三视图” 知多少
画一个物体的三视图时,主视图,左视图,俯视图所画的位置如图所示,且要符合如下原则:
“长对正、高平齐、宽相等”主视图和俯视图一样长;主视图和左视图一样高;俯视图和左视图一样宽“主俯一样长,主左一样高,俯左一样宽”
1、练习:课本P16练习的1、2题及课本P18A组的1、2、3题2、作业:课本P20的4、5、题
北师大版高中数学必修二§3 三视图

§3 三视图【课时目标】1.初步认识简单几何体的三视图.2.会画出空间几何体的三视图并会由空间几何体的三视图画出空间几何体.1.空间几何体的三视图是指__________、__________、__________.2.三视图的排列规则是__________放在主视图的下方,长度与主视图一样,__________放在主视图的右面,高度与主视图一样,宽度与俯视图的宽度一样.3.三视图的主视图、俯视图、左视图分别是从________、__________、________观察同一个几何体,画出空间几何体的图形.一、选择题1.下列说法正确的是( )A.任何几何体的三视图都与其摆放的位置有关B.任何几何体的三视图都与其摆放的位置无关C.有的几何体的三视图与其摆放的位置无关D.正方体的三视图一定是三个全等的正方形2.如图所示的一个几何体,哪一个是该几何体的俯视图( )3.如图所示,下列几何体各自的三视图中,有且仅有两个视图相同的是( )A.①②B.①③C.①④D.②④4.一个长方体去掉一个小长方体,所得几何体的主视图与左视图分别如图所示,则该几何体的俯视图为( )5.实物图如图所示.无论怎样摆放物体,如图所示中不可能为其主视图的是( ) 6.一个长方体去掉一角的直观图如图所示,关于它的三视图,下列画法正确的是( )二、填空题7.根据如图所示俯视图,找出对应的物体.(1)对应________;(2)对应________;(3)对应________;(4)对应________;(5)对应________.8.若一个三棱柱的三视图如图所示,则这个三棱柱的高(两底面之间的距离)和底面边长分别是________和________.9.用小正方体搭成一个几何体,如图是它的主视图和左视图,搭成这个几何体的小正方体的个数最多为________个.三、解答题10.在下面图形中,图(b)是图(a)中实物画出的主视图和俯视图,你认为正确吗?如果不正确,请找出错误并改正,然后画出左视图(尺寸不作严格要求).11.如图是截去一角的长方体,画出它的三视图.能力提升12.如图,螺栓是棱柱和圆柱的组合体,画出它的三视图.13.用小立方体搭成一个几何体,使它的主视图和俯视图如图所示,搭建这样的几何体,最多要几个小立方体?最少要几个小立方体?在绘制三视图时,要注意以下三点:1.若两相邻物体的表面相交,表面的交线是它们的原分界线,在三视图中,分界线和可见轮廓都用实线画出,不可见轮廓用虚线画出.2.一个物体的三视图的排列规则是:俯视图放在主视图的下面,长度和主视图一样.左视图放在主视图的右面,高度和主视图一样,宽度和俯视图一样,简记为“长对正,高平齐,宽相等”.3.在画物体的三视图时应注意观察角度,角度不同,往往画出的三视图不同.§3 三视图答案知识梳理1.主视图左视图俯视图2.俯视图左视图3.正前方正上方左侧作业设计1.C[球的三视图与其摆放位置无关.]2.C3.D[在各自的三视图中,①正方体的三个视图都相同;②圆锥有两个视图相同;③三棱台的三个视图都不同;④正四棱锥有两个视图相同.]4.C[由三视图中的正、左视图得到几何体的直观图如图所示,所以该几何体的俯视图为C.]5.D[A图可看做该物体槽向前时的主视图,B图可看做槽向下时的主视图,C图可看做槽向后时的主视图.]6.A7.(1)D(2)A(3)E(4)C(5)B8.2 4解析三棱柱的高同左视图的高,左视图的宽度恰为底面正三角形的高,故底边长为4.9.710.解图(a)是由两个长方体组合而成的,主视图正确,俯视图错误,俯视图应该画出不可见轮廓线(用虚线表示),左视图轮廓是一个矩形,有一条可视的交线(用实线表示),正确画法如图所示.11.解该图形的三视图如图所示.12.解该物体是由一个正六棱柱和一个圆柱组合而成的,主视图反映正六棱柱的三个侧面和圆柱侧面,左视图反映正六棱柱的两个侧面和圆柱侧面,俯视图反映该物体投影后是一个正六边形和一个圆(中心重合).它的三视图如图所示.13.解由于主视图中每列的层数即是俯视图中该列的最大数字,因此,用的立方块数最多的情况是每个方框都用该列的最大数字,即如图①所示,此种情况共用小立方块17块.而搭建这样的几何体用方块数最少的情况是每列只要有一个最大的数字,其他方框内的数字可减少到最少的1,即如图②所示,这样的摆法只需小立方块11块.。
【数学】三视图(北师大版必修2)(2)

解 决问题
学 以 致 用
(2)形成演示
(3)形成演示
(4)形成演示
(2)形成演示
(3)形成演示
(3)形成演示
小结
拓展Biblioteka • 1、三视图 • 主视图——从正面看到的图 • 左视图——从左面看到的图 • 俯视图——从上面看到的图 • 2、位置:主视图 左视图
• 俯视图 大小:长对正,高平齐,宽相等
探索5
下面物体的三视图有无错误?如果有,
请指出并改正.
正视图
左视图
正视
图6.1
俯视图 图6.2
探索6 学生分组画出下列各组合体的三视图 并探讨简单组合体的三视图的画法
图(1)
图(2)
图(3)
画简单组合体的三视图要注意:
(1)明确物体的主视、俯视、左视方向,对同一物体,若放置的位置不同,则所画 的三视图就有可能不同; (2)要分清楚简单组合体是由哪些简单几何体组合成的,要注意它们的组合方式, 特别是它们的交线
设计师:赫佐格和德梅隆
2、中国中央电视台总部大楼
设计师:史蒂文.霍尔
问题一:要很好的描绘 这幢房子,需要从哪些 方向去看?
问题二:如果要建造房 子,你是工程师, 需要 给施工员提供哪几种的 图纸?
三视图法:从正面、上面和侧面(左面)三个不同的方向 看一个物体,然后描绘三张所看到的图,即三视图。
正视图
左视图
俯视图
正视图
左视图
俯视图
探索2 如图是一个倒置的四棱柱的两种摆放,
试分别画出其三视图,并比较它们的异同.
图4.1 主视
图5.1
主视
主视图
左视图
图4.2
图4.1
主视
北师大高中数学必修二课后作业4 三视图 含解析
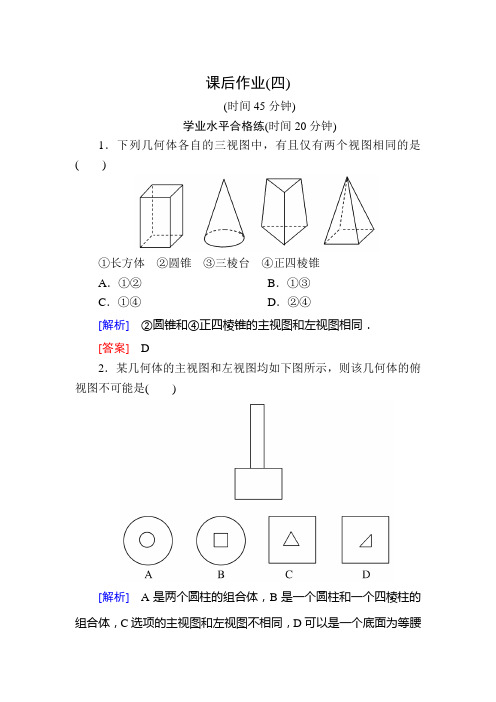
课后作业(四)(时间45分钟)学业水平合格练(时间20分钟)1.下列几何体各自的三视图中,有且仅有两个视图相同的是()①长方体②圆锥③三棱台④正四棱锥A.①②B.①③C.①④D.②④[解析]②圆锥和④正四棱锥的主视图和左视图相同.[答案] D2.某几何体的主视图和左视图均如下图所示,则该几何体的俯视图不可能是()[解析]A是两个圆柱的组合体,B是一个圆柱和一个四棱柱的组合体,C选项的主视图和左视图不相同,D可以是一个底面为等腰直角三角形的直三棱柱与一个四棱柱的组合体.[答案] C3.如图所示的三视图表示的几何体可能是()A.圆台B.四棱台C.四棱锥D.三棱台[解析]由三视图可知,该几何体是四棱台.[答案] B4.某空间几何体的主视图是三角形,则该几何体不可能是()A.圆柱B.圆锥C.四面体D.三棱柱[解析]圆柱的主视图不可能是三角形.[答案] A5.若一个几何体的三视图如下图所示,则这个几何体是()A.三棱锥B.四棱锥C.三棱柱D.四棱柱[解析]由俯视图可知底面为四边形,由主视图和左视图知侧面为三角形,故几何体为四棱锥.[答案] B6.水平放置的下列几何体,主视图是长方形的是________(填序号).[解析]①③④的主视图为长方形,②的主视图为等腰三角形.[答案]①③④7.一物体及其主视图如图:则它的左视图与俯视图分别是图形中的________.[解析]左视图是矩形中间有条实线,应选③;俯视图为矩形中间有两条实线,且为上下方向,应选②.[答案]③②8.如图所示,在正方体ABCD-A1B1C1D1中,点P是上底面A1B1C1D1内一动点,则三棱锥P-ABC的主视图与左视图的面积的比值为________.[解析]三棱锥P-ABC的主视图与左视图为等底等高的三角形,故它们的面积相等,面积比值为1.[答案] 19.如图,四棱锥的底面是正方形,顶点在底面上的射影是底面正方形的中心,试画出其三视图.[解]所给四棱锥的三视图如下图.10.如图所示的螺栓是由棱柱和圆柱构成的组合体,试画出它的三视图.[解]三视图如图所示.应试能力等级练(时间25分钟)11.如果用□表示1个立方体,用表示2个立方体叠加,用表示3个立方体叠加,那么图中由7个立方体叠成的几何体,从正前方观察,可画出的平面图形是()[解析]从正前方观察,有两层,下边一层有3个立方体,且中间为3个立方体叠加;第二层中间有一个立方体,且有2个立方体叠加,故选B.[答案] B12.如图所示为一个简单几何体的三视图,则其对应的几何体是()[解析]对于A,该几何体的三视图恰好与已知图形相符,故A 符合题意;对于B,该几何体的主视图的矩形中,对角线应该是虚线,故不符合题意;对于C,该几何体的主视图的矩形中,对角线应该是从左上到右下的方向,故不符合题意;对于D,该几何体的左视图的矩形中,对角线应该是虚线,故不符合题意.故选A.[答案] A13.已知某组合体的主视图与左视图相同(其中AB=AC,四边形BCDE为矩形),则该组合体的俯视图可以是图中的________.(把你认为所有正确图象的序号都填上)[解析]由主视图和左视图可知几何体为锥体和柱体的组合体.(1)若几何体为圆柱与圆锥的组合体,则俯视图为③;(2)若几何体为棱柱与圆锥的组合体,则俯视图为④;(3)若几何体为棱柱与棱锥的组合体,则俯视图为①;(4)若几何体为圆柱与棱锥的组合体,则俯视图为②.[答案]①②③④14.如图是一个棱柱的三视图,根据三视图的作图原则,则x=________,y=________.[解析] 棱柱的底面是一个直角三角形,根据“长对正、高对平、宽相等”的原则可知两直角边分别为x +y -2(或8)和x -y +5(或3y ),则⎩⎨⎧ x +y -2=8,x -y +5=3y即⎩⎨⎧ x +y =10,x -4y =-5解得⎩⎨⎧ x =7,y =3.[答案] 7 3 15.如图,该几何体是由一个长方体木块锯成的.(1)判断该几何体是否为棱柱;(2)画出它的三视图.[解] (1)是棱柱.因为该几何体的前、后两个面互相平行,其余各面都是矩形,而且相邻矩形的公共边都互相平行.(2)该几何体的三视图如图.。
北师大版必修2高中数学1.3《三视图》随堂练习
"【世纪金榜】高中数学 1.3三视图课时提能演练北师大版必修2 "(30分钟 50分)一、选择题(每小题4分,共16分)1.(2018·江西高考)将长方体截去一个四棱锥,得到的几何体如下图所示,则该几何体的左视图为( )2.(2018·湖南高考)某几何体的正视图和侧视图均如图所示,则该几何体的俯视图不可能是( )3.(2018·山东高考)如图是长和宽分别相等的两个矩形.给定下列三个命题:①存在三棱柱,其正(主)视图、俯视图如图;②存在四棱柱,其正(主)视图、俯视图如图;③存在圆柱,其正(主)视图、俯视图如图,其中真命题的个数是( )(A)3 (B)2(C)1 (D)04.(2018·浙江高考)若某几何体的三视图如图所示,则这个几何体的直观图可以是( )二、填空题(每小题4分,共8分)5.(2018·深圳高一检测)一个几何体的主视图为一个三角形,则这个几何体可能是下列几何体中的_________.(填入所有可能的几何体前的编号)①三棱锥②四棱锥③三棱柱④四棱柱⑤圆锥⑥圆柱6.(易错题)一个正三棱柱的侧棱长和底面边长均等于它的三视图中的俯视图如图所示,左视图是一个矩形,则该矩形的面积为_________.三、解答题(每小题8分,共16分)7.画出下面物体的三视图.8.下面是几何体的三视图,请画出该几何体的实物草图.【挑战能力】(10分)如图是由小立方块组成的几何体的俯视图,小正方形中的数字表示该位置的小立方块的个数,请画出它的主视图和左视图.答案解析1.【解析】选D.被截去的四棱锥的三条可见侧棱中,有两条为正方体的面对角线,它们在右侧面上的投影与右侧面(正方形)的两条边重合,另一条为正方体的体对角线,它在右侧面上的投影与右侧面的对角线重合,对照各图及对角线方向,D正确.2.【解题指南】从俯视图观察可知,正视图和侧视图不同的是D,正视图应有虚线.【解析】选D.由“正视图俯视图等长,侧视图俯视图等宽”,知该几何体正视图与侧视图相同,而D项中正视图与侧视图不同,可知选D.3.【解析】选A.①可以是放倒的三棱柱,故①正确.存在正四棱柱,其三视图均为矩形,满足条件,故②正确.对于任意的圆柱,其三视图有两个为矩形,一个是以底面半径为半径的圆,满足条件,故③正确.故选A.4.【解题指南】结合三视图利用排除法求解.【解析】选B.由主视图可排除A,C,由左视图可判断该几何体的直观图是B.5.【解析】三棱锥、四棱锥和圆锥的主视图都是三角形,当三棱柱的一个侧面平行于水平面、底面对着观测者时其主视图是三角形,四棱柱、圆柱无论怎样放置,其主视图都不可能是三角形.答案:①②③⑤6.【解析】由俯视图知该正三棱柱的直观图如图所示,其中M,N分别是边AB,A1B1的中点,矩形MNC1C为左视图.∵△ABC为正三角形且M为边AB的中点,==⨯=∴CM AB6,22∴矩形MNC1C的面积为6×,即左视图的面积为答案:【误区警示】解答本题易把侧面AA1C1C当作该几何体的左视图而致错.7.【解析】三视图如图所示:【方法技巧】画三视图的诀窍由三视图的作图原则可知:(1)主视图和俯视图共同反映了物体左右方向的尺寸;(2)主视图和左视图共同反映了物体上下方向的尺寸;(3)俯视图和左视图共同反映了物体前后方向的尺寸.因此画一个物体的三视图不仅要确定其形状,而且要确定三视图之间的线段大小关系.画三视图时一般遵循从下层向上层,从左边到右边的原则.8.【解析】由三视图得实物草图如下图所示.【挑战能力】【解题指南】从俯视图可以看出,其主视图应该是3列,每列的立方块的个数分别是4,4,3;左视图应该是4列,每列的立方块的个数分别是3,3,4,3,由此可以想象该几何体的形状,得到其主视图和左视图.【解析】该几何体的正视图和左视图如图:。
数学北师大版高中必修2立体几何---三视图
(A)
(B)
(C)
(D)
正(主)视图
俯(左)视图
(2)如图,已知三棱锥的底面是直角三角形,直角边长分别为3和4,过直角顶 点的侧棱长为4,且垂直于底面,该三棱锥的主视图是( ) z 3
4 4 A. 3 B.
4
4
5
4 x 3 4 y
4 O
C.
D.
(3)将正三棱柱截去三个角(如图1所示 A,B,C 分别是 △GHI 三边的中点)得到几 何体如图2,则该几何体按图2所示方向的侧视图(或称左视图)为( )
6 3 6
(单位:cm)
(6)一空间几何体的三视图如图所示,则该几何体的体积为( 2 3 2 3 A.2π+2 3 B.4π+2 3 C.2π+ D.4π+
3 3
2 2
)
2
2 正(主)视图
2 侧(左)视图
俯视图
4、直观图与三视图综合运用
(1)某高速公路收费站入口处的安全标识墩如图1所示.墩的上半部分是正四棱 锥 P EFGH ,下半部分是长方体 ABCD EFGH .图2、图3分别是该标识墩的 正(主)视图和俯视图. (Ⅰ)请画出该安全标识墩的侧(左)视图; (Ⅱ)求该安全标识墩的体积; (Ⅲ)证明:直线 BD 平面 PEG . (
1 主视图 1
左视图
2
(3)如图,网格纸的小正方形的边长是1,在其上用粗线画出了某多面体的三视 图,则这个多面体最长的一条棱的长为______. (4)图4中的三个直角三角形是一个体积为20cm 的几何体的 三视图,则 h . h cm
5 正视图 6
侧视图
1
1
俯视图
3
(单位:cm) 俯视图
北师大版必修2高中数学1.3《三视图》ppt课件
6.(2011·镇江模拟)用单位立方块搭一个几何体,使它的 主视图和俯视图如图所示,则它的体积的最小值为_____, 最大值为__________.
【解题提示】解答本题可先由俯视图确定“基座”再分 析各列有几层,找出单位立方块个数的最小值和最大值. 【解析】综合分析俯视图和主视图可知单位立方块最少的 情况如图(1)(不唯一),共10个. 单位立方块最多的情况如 图(2),共16个.
3.如图是一个几何体的三视图,由图可以判断此几何体是 __________.
【解析】由三视图可知此几何体是正六棱台. 答案:正六棱台
4.主视图为一个三角形的几何体可以是__________.(写出 三种) 【解析】由几何体的三视图可知,主视图为三角形的几何 体可以是三棱锥、圆锥、四棱锥等. 答案:三棱锥、圆锥、四棱锥(不唯一)
【挑战能力】 (10分)如图(1)是由8个小正方体构成的大正方体,如图(2) 是由7个小正方体构成的组合体. (1)试画出这两个几何体的三视图. (2)你能想到还有哪些组合体(由6个小正方体构成)的三视 图与以上两个几何体的三视图相同吗?
【解析】(1)这两个几何体的三视图相同,三视图如下:
(2)与以上两个几何体的三视图相同的几何体还有(不唯一):
二、填空题(每题4分,共8分) 5.(2011·杭州高一检测)一个几何体的三视图如图所示, 其中主视图和左视图是腰长为6的两个全等的等腰直角三角 形,用__________个这样的几何体可以拼成一个棱长为6的 正方体.
【解析】如图所示,该几何体是一个 四棱锥,记作四棱锥P—ABCD,由图 可见,用3个这样的几何体可以拼成 一个棱长为6的正方体. 答案:3
④ 紧跟老师的推导过程抓住老师的思路。老师在课堂上讲解某一结论时,一般有一个推导过程,如数学问题的来龙去脉、物理概念的抽象归纳、语 文课的分析等。感悟和理解推导过程是一个投入思维、感悟方法的过程,这有助于理解记忆结论,也有助于提高分析问题和运用知识的能力。
2017-2018学年北师大版高中数学必修二课时作业检测模块提升卷(A)Word版含答案
化工企业述职报告1500字10篇精选栏目推选:“化工企业述职报告”。
光阴不待人,匆匆不回头。
对于职场人来说,撰写述职报告并不陌生,述职报告一定要树立一个明确的鲜明的主题。
如何让自己的岗位的述职报告看起来条理清晰呢?编辑经过搜集和处理,为你提供化工企业述职报告,供大家参考借鉴,希望可以帮助到有需要的朋友。
化工企业述职报告【篇1】20xx年x月xx日,这是一个不一样的日子,从此我正式进入xx 集团xx化工厂聚合干燥分厂,开始了自己真正意义上成为一个产业工人的日子。
这里对于刚出校门初涉世事的我来说,一切都是那么好奇、新鲜。
如今半年转瞬离去,我已经成为这里的正式员工,为生产的正常运行出着自己的绵薄之力。
下面对这半年的工作进行一下总结,并计划一下明年的工作。
一、学习方面这里和学校是完全不同的,学生时代,我们可以一知半解,这里绝对不行。
学校的学习是以应付考试为主要目的的,你可以不太懂,但必须要记住,因为你要把它填在试卷上才能得到分数。
而这里,你必须达到百分之一百的理解,任何一个操作有问题,都是关乎生产,关乎安全甚至关乎生命的大事,不可有半点差错。
学员的学习期为三个月,这期间我学到了很多。
在师傅的带领和指导下,我认识了很多新事物,这包括理论知识,工艺流程以及设备的用途和工作原理,弥补了在学校时一知半解的知识。
最重要的是交给了我很多学校学不到的知识——实际操作,这是我走的收获。
我认识了各种不同的阀门,了解了不同类型的离心泵,知道了水环式压缩机的工作原理,认识了现场和远传压力表,液位计,温度计。
了解了压缩岗位的重点设备和巡检注意事项,这些都是弥足珍贵的。
安全是关乎自己和他人生命和财产的,安全知识就像一剂汤药,有病治病,无病防身,这是最重要的。
我学会了三不伤害,设备检修禁令,动火操作禁令,个人安全防护设备的使用方法等。
同时我也明白了一个道理——“山外有山、人外有人”,所以不能满足于现状,应该时刻鞭策自己努力奋进,不断学习新的知识,才不会故步自封。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
课下能力提升(四)三视图
一、选择题
1.已知某空间几何体的三视图如图所示,则此几何体为( )
A.圆台 B.四棱锥
C.四棱柱 D.四棱台
2.(湖南高考)已知正方体的棱长为1,其俯视图是一个面积为1的正方形,侧视图是
一个面积为2的矩形,则该正方体的正视图的面积等于( )
A.32 B.1
C.2+12 D.2
3.三棱柱ABCA1B1C1,如下图所示,以BCC1B1的前面为正前方画出的三视图,正确的是
( )
4.(福建高考)一个几何体的三视图形状都相同、大小均相等,那么这个几何体不可以
是( )
A.球 B.三棱锥
C.正方体 D.圆柱
5.一个几何体的三视图如图所示,其中主视图中△ABC是边长为2的正三角形,俯视
图为正六边形,那么该几何体的左视图的面积为( )
A.32 B.23 C.12 D.6
二、填空题
6.如图所示,为一个简单几何体的三视图,它的上部是一个________,下部是一个
________.
7.用小正方体搭成一个几何体,如图是它的主视图和左视图,搭成这个几何体的小正
方体的个数最多为________个.
8.如图(1),E、F分别为正方体的面ADD1A1和面BCC1B1的中心,则四边形BED1F在该正
方体的面上的射影可能是图(2)中的________(要求:把可能的图的序号都填上).
三、解答题
9.如图所示,图②是图①中实物的主视图和俯视图,你认为正确吗?如果不正确,请
找出错误并改正,然后画出它的左视图.
10.某建筑由若干个面积相同的房间组成,其三视图如下,其中每一个小矩形表示一个
房间.
(1)该楼有几层?共有多少个房间?
(2)画出此楼的大致形状.
答 案
1. 解析:选D 由主视图和左视图可以判断一定为棱台或圆台,又由俯视图可知其一
定为棱台且为四棱台.
2. 解析:选D 由已知,正方体的正视图与侧视图都是长为2,宽为1的矩形,所以
正视图的面积等于侧视图的面积,为2.
3. 解析:选A 正面是BCC1B1的矩形,故主视图为矩形,左侧为△ABC,所以左视图为
三角形,俯视图为两个有一条公共边的矩形,公共边为CC1在面ABB1A1内的投影.
4. 解析:选D 球的三视图是三个相同的圆;当三棱锥为正三棱锥时其三视图可能是
三个全等的三角形;正方体的三视图可能是三个相同的正方形;不论圆柱如何放置,其三视
图形状都不会完全相同.
5. 解析:选A 由主视图、左视图、俯视图之间的关系可以判断该几何体是一个底面
为正六边形的正六棱锥.
∵主视图中△ABC是边长为2的正三角形,此三角形的高为3,∴左视图的高为3.
俯视图中正六边形的边长为1,其小正三角形的高为32,∴左视图的底为32×2=3,
∴左视图的面积为12×3×3=32.
6. 解析:由三视图可知该几何体图示为
所以,其上部是一个圆锥,下部是一个圆柱.
答案:圆锥 圆柱
7. 解析:其俯视图如图所示时为小正方体个数最多情况(其中小正方形内的数字表示小
正方体的个数)共需7个小正方体.
1 2 1
1 1 1
答案:7
8. 解析:根据平行投影的理论,从正方体的上下、前后、左右三个角度分别投影,从
上往下投影,选择②,从前往后投影,选择②,从左往右投影,选择③.
答案:②③
9. 解:图①是由两个长方体组合而成的,主视图正确,俯视图错误.俯视图应该画出
不可见轮廓(用虚线表示),左视图轮廓是一个矩形,有一条可视的交线(用实线表示),正确
画法如图所示.
10. 解:(1)由主视图和左视图可知,该楼共3层,由俯视图可知,该楼一楼有5个房
间,结合主视图与左视图,易知二楼和三楼分别有4个,1个房间,故共10个房间.
(2)此楼的大致形状如图:
