角的比较课件PPT
合集下载
沪科版七年级数学上册角的比较与补(余)角【教案+课件】

∠AOB是∠AOC与∠COB的差,
记作∠AOB=∠AOC-∠COB.
O
A
类似地,∠AOC-∠AOB=∠COB.
探究新知
例1 如图④,求解下列问题: (1)比较∠ AOC与∠BOC,∠BOD与∠COD的大小; (2)将∠AOC写成两个角的和与两个角的差的情势.
A B C
O
图④
D
解:(1)由图④可以看出: ∠AOC>∠BOC(OB在∠AOC 内) ∠BOD>∠COD(OC在∠BOD内) (2)∠AOC=∠AOB+∠BOC, ∠AOC=∠AOD—∠DOC.
探究新知
(2)叠合法:
叠合∠DEF与∠ABC,把∠DEF移动,使它的顶点E移到和∠ABC的顶点B重合,
一边ED和BA重合,另一边EF和BC落在BA的同旁.
如图①,如果EF和BC重合,那么∠DEF=∠ABC.
C(F)
B(E) 图①
A(D)
探究新知
(2)叠合法:
如图②,如果EF落在∠ABC的内部,那么∠DEF<∠ABC;
探究新知
例2 如图⑥,∠1=∠3,∠1与∠2互补,∠3与∠4互补,那么∠2与∠4有什 么关系?
图⑥ 解:因为∠1与∠2互补,所以∠2=180°-∠1. 因为∠3与∠4互补,所以∠4=180°-∠3. 又因为∠1=∠3,所以∠2=∠4.究新知
问题:余角有无上面补角类似的性质?如果有,你能说明道理吗?
课堂总结
问题:通过这节课的学习,你有哪些收获?
1. 角的大小的比较方法:(1)度量法;(2)叠合法.
2. 角平分线的定义及性质: 在角的内部,以角的顶点为端点的一条射线把这个角分成两个相等的角,这 条射线叫做这个角的平分线. 若OC是∠AOB的平分线,则∠AOC=∠COB=1∠AOB,∠AOB=2∠AOC=
《角的比较》参考课件1

观察与思考:
① 使用叠合法比较角的大小必须注意哪些细节? ②角的大小与两边画出部分的长短是否相关?
【例
1】
根据下图,求解下列问题:
(1)比较∠AOB、∠AOC、∠AOD、∠AOE的大小,并指出 其中 的锐角、直角、钝角、平角. (2)写出∠AOB、∠AOC、∠BOC、 ∠AOE中某些角之间的两个等量 关系. (3)借助三角尺估测 图中各角的度数. C O D E A B
一个含150角的方法很多。请你画出其中两种不
同构成的示意图,并在图上作出必要的标注,
不写作法。
想一想:
用一副三角板可以画出哪些不同度数的角?
4.4 角的比较
想一想:
► 如何比较两条线段的长短? ► 如何比较两个角的大小呢?
A O B
A
O
B c
c
c
o
D
o
D
D
o
与比较线段的长短类似,如果直接观察难以判断,我们可以 用两种方法对角进行比较: 一种方法是用量角器量出它们的度数,在进行比较; 另一种方法是将两个角的定点及一条边重合,另一边放在重 合的同侧就可比较大小。
在方格纸上有三个角,试确定每个角的大小及各角之
间的等量关系.(直接作在课本上)
闯一闯:
(1) 如图,∠AOC和∠BOD都是直角。
①估测∠COB的度数;
②若∠DOC=28°,说出∠AOB的度数。
D A B O C
试一试:
一副三角板由一个等腰直角三角形和一个含
300角的直角三角形组成。利用这副三角板构成
角平分线
A B
C O D
∠AOE =2∠AOC =2∠COE 1 ∠AOC =∠COE = ∠AOE 2
七年级上册 数学 课件 4.5 角的比较与补角
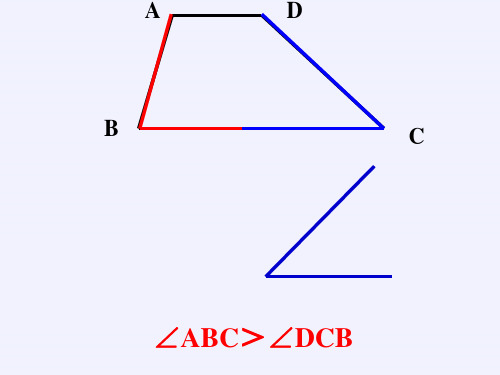
请准备一张纸(最好是透明的),在上面作任意 角∠AOB,把这个角对折,使角的两边OA与OB 重合,然后把这张纸展开、铺平,画出折痕OC。 ∠AOC与∠BOC之间有怎样的大小关系?
B
C
O A
一条射线把一个角分成两个相等的角, 则这条射线叫这个角的角平分线。
∵∠1=∠3 (或∠2= 2∠1 , ∠2= 2∠3)
3、读数—读出角∠的A另B一C边>所∠对D的E度F 数
700 B
D
300
C
E
F
二. 叠合法 1. 将两个角的顶点及一边重合
2. 两个角的另一边落在重合一边的同侧
3.由两个角的另一边的位置确定两个角
的大小 E
A
C
DO
B
∠ECD>∠AOB
A
E
C
D
O
B
∠ECD<∠AOB
E
A
C
DO
B
∠ECD=∠AOB
问题:(1)在放大镜下,一个角的度数
如图,OB是∠AOC的平分线,
C
OE是∠COD的平分线,
若∠AOC=50°, ∠COD=80°,
B 那么∠BOE是多少度?
A 解:因为OB是AOC的平分线,
所以BOC = 1 AOC=25. 2
因为OE是COD的平分线,
所以COE= 1 COD=40. 2
所以BOE =BOC COE=65.
感悟与收获
解:
ห้องสมุดไป่ตู้
A
(1) ∠AOC= ∠AOB+ ∠BOC
B
(2) ∠BOD= ∠AOD- ∠AOB
C
O
D
⑶如果∠AOB=∠COD,那么 ∠AOC=∠BOD吗?
B
C
O A
一条射线把一个角分成两个相等的角, 则这条射线叫这个角的角平分线。
∵∠1=∠3 (或∠2= 2∠1 , ∠2= 2∠3)
3、读数—读出角∠的A另B一C边>所∠对D的E度F 数
700 B
D
300
C
E
F
二. 叠合法 1. 将两个角的顶点及一边重合
2. 两个角的另一边落在重合一边的同侧
3.由两个角的另一边的位置确定两个角
的大小 E
A
C
DO
B
∠ECD>∠AOB
A
E
C
D
O
B
∠ECD<∠AOB
E
A
C
DO
B
∠ECD=∠AOB
问题:(1)在放大镜下,一个角的度数
如图,OB是∠AOC的平分线,
C
OE是∠COD的平分线,
若∠AOC=50°, ∠COD=80°,
B 那么∠BOE是多少度?
A 解:因为OB是AOC的平分线,
所以BOC = 1 AOC=25. 2
因为OE是COD的平分线,
所以COE= 1 COD=40. 2
所以BOE =BOC COE=65.
感悟与收获
解:
ห้องสมุดไป่ตู้
A
(1) ∠AOC= ∠AOB+ ∠BOC
B
(2) ∠BOD= ∠AOD- ∠AOB
C
O
D
⑶如果∠AOB=∠COD,那么 ∠AOC=∠BOD吗?
青岛版数学七年级下册第八章《角的大小比较》课件

1 / 2 BOD = 1 / 3 AOD
A E
B
D
C
AD是 BAC的平分线
BAD = CAD ( 角平分线的意义 ) ABC = 2 ABE BE 平分 ABC ( 角平分线的意义 )
1.角的大小比较方法(叠合、度量)。 2.角的和差关系。 3.角的平分线的性质。
已知O为直线AB上一点,OE平分∠AOC,OF平分 ∠COB,求∠EOF的大小?
二.角的和差
已知两个角 1和 2( 1 > 2 ), 把它们的顶点和一边重合。
B
C
1
2
O
A
O
B
C B
顶
2
点
1
与
O
A
一
( AOC为 1 和 2 的和
边
记作 AOC = 1 + 2 )
重
合
B
21
C
O
A
( AOC为 1与 2 的差
记作 AOC = 1 – 2 )
1.看图填空
C
D
( 1 ) DAB = DAC+ CAB
C F
B
A
E
D
•1、使教育过程成为一种艺术的事业。 •2、教师之为教,不在全盘授予,而在相机诱导。2021/10/262021/10/262021/10/2610/26/2021 5:40:48 PM •3、一年之计,莫如树谷;十年之计,莫如树木;终身之计,莫如树人4、智力教育就是要扩大人的求知范围 •5、教育是一个逐步发现自己无知的过程。 •6、要经常培养开阔的胸襟,要经常培养知识上诚实的习惯,而且要经常学习向自己的思想负责任。2021年10月 2021/10/262021/10/262021/10/2610/26/2021
北师大版七年级数学上册《基本平面图形——角的比较》教学PPT课件(4篇)

角的大小的比较方法: (1)如果已知角是锐角、直角、钝角、平角、周角几类中不同 类的角,就可以直接由它们之间的关系比较出它们的大小; (2)可以通过量角器进行量度来比较角的大小; (3)可以根据各角在同一图中的位置关系比较角的大小.
角的平分线
活动:大家在练习本上画一个角,然后把角的两边 对折,展开以后你会发现折痕把角分成了两个角, 这两个角有什么关系呢,它们又和原来的角有着怎 样的等量关系?
4.4 角的比较
知识回顾 比较两条线段的长短的方法? 1、度量法:用刻度尺测量线段的长度的方法。 2、叠合法:将其中一条线段移到另一条线段 上作比较。
猜想:比较两个角的大小方法?
获取新知
问题:有一天学生张虎和王鹏各带了一把折扇(如图),下面是他们的 一段对话:
张:我的折扇大一些,所以我的折扇的角也大一些.
2
2
2
(2)结合(1)的结论可求出∠DOE的度数,从而求出∠BOE的度数
解:(1)因为OC平分∠AOD,
1 所以∠DOC= 2 ∠AOD.
因为OE平分∠BOD,
1
所以∠DOE= 2∠BOD.
所以∠COE=∠DOC+∠DOE=
1
(∠AOD+∠BOD)
= 1 ∠AOB= 1 ×130°=65°.
2
2
2
2. 已知,如图,∠AOB = 130°,∠AOD = 30°,∠BOC = 70° ,问:OC 是∠AOB 的平 分线吗?OD 是∠AOC 的平分线吗?
解: OC不是∠AOB 的平分线 OD是∠AOC 的平分线 B
C D
A O
3. 如图,直线 m 外有一定点 O,A 是 m 上的 一个动点,当点 A 从左向右运动时,观察∠α 和 ∠β 是如何变化的,∠α 和 ∠β 之间有关系吗?
4.3.2角的比较与运算 课件人教版七年级数学上册

典型例题 例2 把一个周角7等分,每一份是多少度的角(精确到分)?
解:360º÷7=51º+3º÷7 =51º+180′÷7 ≈ 51º26′.
答:每份约是51º26′.
创设情境 探究新知 应用新知 巩固新知 课堂小结 布置作业
随堂练习
练习1 按图填空: (1)∠AOB+∠BOC=_∠__A__O_C____; (2)∠AOC+∠COD=_∠__A_O__D____; (3)∠BOD-∠COD=_∠__B_O__C____; (4)∠AOD-__∠__B_O_D____=∠AOB.
探究 怎么用符号语言表示角平分线呢?
C
O
B
A
∵OB平分∠AOC,
∴∠AOB =∠BOC = 1 ∠AOC
2
(或者∠AOC =2 ∠AOB = 2∠COB ).
创设情境 探究新知 应用新知 巩固新知 课堂小结 布置作业
探究 类似角平分线,如图射线OB、OC是∠AOD的三等分线.
D
α α α
O
C B
A
创设情境 探究新知 应用新知 巩固新知 课堂小结 布置作业
随堂练习
练习2 如图,OP是∠AOB的平分线,则下列说法错误的是( C )
A.∠AOB=2∠AOP
C.∠AOB= 1 ∠BOP 2
B.∠AOP= 1 ∠AOB 2
D.∠AOP=∠BOP
创设情境
探究新知
角
的
应用新知
比
较
巩固新知
与 运
算
课堂小结
创设情境 探究新知 应用新知 巩固新知 课堂小结 布置作业
典型例题 例1 如图,O是直线AB上一点,∠AOC=53º17′,求∠BOC的度数.
角的比较与补(余)角课件沪科版数学七年级上册
三、概念剖析
想一想
(1)已知∠1与∠2,∠3都互为补角.那么∠2和∠3的大小有什么关系?
解:因为∠1与∠2和∠3都互为补角, 那么 ∠2=180º-∠1,∠3=180º-∠1, 所以∠2=∠3.
三、概念剖析
(2)已知∠1与∠2互补,∠3与∠4互补.若∠1=∠3,那么∠2和∠4 相等 吗?为什么?
∴∠COD=∠AOD=
1 2
∠AOC
∠COE=∠BOE=
1 2
∠BOC
∴∠COD+∠COE=∠DOE=90° ∴∠DOB的补角:∠AOD、∠COD.
而∠AOB=180°
∠BOE的余角:∠AOD、∠COD;
【当堂检测】
1. 关于下图的说法正确的是( C ) A. ∠AOC是∠DOC的补角 B. ∠COB是∠AOD的余角 C. ∠AOC是∠BOC的补角 D. ∠DOC是∠AOD的余角
五、课堂总结
1.角的大小比较方法:①度量法;②叠合法。 2.角的平分线:从一个角的顶点出发,把这个角分成相等的两个角的射 线,叫这个角的平分线,角平分线必须是一条射线.
3.余角和补角 (1)如果两个角的和等于180°,那么我们就称这两个角互为补角,简称互补. (2)如果两个角的和等于90°,那么我们就称这两个角互为余角,简称互余.
∴∠1=90°﹣50°=40°,
∵∠2的补角是150°,
∴∠2=180°﹣150°=30°,
∴∠1>∠2.
四、典型例题
例题3:一个角比它的余角大25°,那么这个角的补角的度数是?
【分析】不明确这个角的具体度数,我们可以假定一个值,然后根据补角、余角的 定义表示出它的补角、余角就能快速解题了。
解:设这个角为a, 则x=90°-x+25°, 解得:x=57.5°, 这个角的补角=180°-57.5° =122.5°.
人教版初中数学七年级上册教学课件 第四章 几何图形初步 角 角的比较与运算
课堂小结
比较 度量法;叠合法. 角 运算 度与度、分与分、秒与秒分别相加、减.分秒 相加时逢60要进位,相减时借1作60.
课后作业
1.从课后习题中选取; 2.完成练习册本课时的习题。
分析:∠AOB是 平角, ∠BOC=∠AOB-∠AOC .
解:由题意可知,∠AOB是平角, ∠AOB=∠AOC+∠BOC,
所以∠BOC= ∠AOB-∠AOC =180°- 53°17′ =126°43′.
例2 把一个周角7等分,每一份是多少度的 角(精确到分)?
解:360°÷7=51°+3°÷7 =51°+180′÷7 ≈51°26′.
【课本P136 练习 第1题】
2. 估计图中∠1与∠2的大小关系,并用适当的方法 检验.
【课本P136 练习 第2题】
3. 如图,把一个蛋糕等分成8份,每份 中的角是多少度?如果要使每份中的角 是15°,这个蛋糕应等分成多少份?
【课本P136 练习 第3题】
4. 如图,О是直线AB上一点,OC是∠AOB的平分线, ∠COD=31°28‘,求∠AOD的度数.
D C
E
A
O
B
2. 如果EC落在∠BOD的内部,那么∠AEC小 于∠BOD,记作∠AEC<∠BOD.
C D
E
AO
B
3. 如果EC落在∠BOD的外部,那么∠AEC大于 ∠BOD,记作∠AEC>∠BOD.
思考 图中共有几个角?它们之间有什么关 系?
图中共有 3 个角.
∠AOC是∠AOB与∠BOC的 和 .记作∠AOC= ∠AOB+∠BOC ;∠AOB是∠AOC与∠BOC的 差 ,记作:∠AOB=∠AOC-∠BOC ;类似地, ∠BOC= ∠AOC-∠AOB .
《角的度量》PPT优秀课件
再见
中心对顶点, 零线对一边, 它边看度数, 内外要分辨。
选一选:看量角器上的刻度,读出每个角的度数。
① ①50° ②130°
选一选:看量角器上的刻度,读出每个角的度数。
③ ①65° ②135° ③55°
练习巩固
体会量角的用处
飞船的发射角度一般是42.4度,有利于 返回和应急救生;在帆船行驶中,迎风的风 向角大约在30至80度,可使船保持较快的速 度。
为什么同一个刻度,一个表示30°,另一个却表示150°?
量出角的度数
2
量出角的度数
2
量出角的度数
75°
量出角的度数
135°
量角的步骤
1.把量角器的中心与角的 (顶点)重合,0°刻 度线与角的一条边 (重合 )。 2.角的另一条边所对的量角器上的刻度,就是 这个角的( 度数 )。
量角歌
135°
角的计量单位
1度,记作1°
估一估,这个角 的大小是几度?
每一份所对的角的大小是1°。
量角器
二、合作研究量角器探究新知
外圈刻度
内圈刻度
中心点
0 0
0°刻度线
0°刻度线
读出角的度数
1°
二、探究读新出知角的度数
2°
二、探究读新出知角的度数
5°
二、探究读新出知角的度数
10°
二、探究读新出知角的度数
部编版数学四年级上册
角的度量
比一比哪个角比较大?
1
2
180°
90°80°70°60° 50° 40° 30° 20°
10°
360°
这个角的大 小就是1度。
270°
在古代美索不达米亚地区,他们通过天文观察并结合 当时的历法发现,用360个太阳一个挨着一个紧紧排列, 恰好就是一圈。按照这样的观察结果,人们把圆平均分成 360份,其中的一份所对的角的大小就是1度。
8.2角与角的大小比较_PPT课件
角的分类
钝角 平角 周角
提示:直角可以用Rt∠表示,画图时常在直角
的顶点处加上“ ”来表示这个角是直角.
∟
根据右图解下列问题
(1)找出图中的直角、锐角和钝角A (2)比较∠AOB、∠AOC ∠AOD、∠AOE的大小 解:(2)由右图可以看出:
B C E D
O
∠ AOB < ∠ AOC < ∠ AOD < ∠ AOE
DEF 1 2. 记作:
图1
图2
练习: 已知如下图, 1 ,画 2 ,使 2 1 1 .
例题 (1)根据图形填空:
①∠DBA=∠DBC+ ∠ABC ;
D
C P
30°
②∠DBC=∠DBP- ∠PBC =∠DBA- ∠ABC ;
90°
(2)变式
B
A
Ⅰ:如图若∠ABC=90º ,∠CBD=30º ,你能求出哪些角的度数? Ⅱ:若在Ⅰ的条件下再添上条件BP平分∠ABD,你还能求出 哪些角的度数?
55°
D
62.5°
A
C
利用一副三角板,你能画 出哪些度数的角?
0 1 2 3 4 5
0
1
2
3
4
5
利用一副三角板,我们能 画出哪些度数的角?
180 º
150 º
135 º
120 º
105 º
75 º
60 º
15º ,30º ,45º ,60º ,75º ,90º , 105º ,120º ,135º ,150º , 165º 15 º 等
(1)若 AOC 50 ,则 BOC ______ ;
(2) AOC 50 , COE 80 ,则 BOD ____ .
