七年级数学上册合并同类项专项训练32
专题24合并同类项-2021-2022学年七年级数学上(解析版)【人教版】

2021-2022学年七年级数学上册尖子生同步培优题典【人教版】专题2.4合并同类项姓名:__________________ 班级:______________ 得分:_________________注意事项:本试卷满分100分,试题共24题,选择10道、填空8道、解答6道.答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置.一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.1.(2020秋•白银期末)下列单项式中,与a3b是同类项的是()A.ab B.2ab3C.﹣4a3b D.3a3b3【分析】根据同类项的定义求解即可,所含字母相同,并且相同字母的指数也相同,这样的项叫做同类项.【解析】A、ab与a3b所含字母相同,但相同字母的指数不尽相同,所以不是同类项,故本选项不合题意;B、2ab3与a3b所含字母相同,但相同字母的指数不相同,所以不是同类项,故本选项不合题意;C、﹣4a3b与a3b所含所含字母相同,并且相同字母的指数也相同,是同类项,故本选项符合题意;D、3a3b3与a3b所含字母相同,但相同字母的指数不尽相同,所以不是同类项,故本选项不合题意.故选:C.2.(2019秋•通州区期末)下列各单项式中,与xy2是同类项的是()A.x2y B.x2y2 C.x2yz D.9xy2【分析】根据同类项的定义,所含字母相同且相同字母的指数也相同的项是同类项,同类项与字母的顺序无关,与系数无关.【解析】与xy2是同类项的是9xy2.故选:D.3.(2020秋•福田区校级期末)若﹣3a2b x与﹣3a y b是同类项,则y x的值是()A.1B.2C.3D.4【分析】根据同类项的概念求出x、y的值,再代入所求式子计算即可.【解析】∵﹣3a2b x与﹣3a y b是同类项,∴x=1,y=2,∴y x=21=2.故选:B .4.(2020秋•铁西区期末)计算5x 2﹣3x 2的结果是( )A .2B .2x 2C .2xD .4x 2【分析】利用合并同类项法则,直接计算即可.【解析】5x 2﹣3x 2=(5﹣3)x 2=2x 2.故选:B .5.(2021春•道外区期末)下列计算正确的是( )A .5x +2y =7xyB .3x 2y ﹣4yx 2=﹣x 2yC .x 2+x 5=x 7D .3x ﹣2x =1 【分析】根据合并同类项的法则判断各选项即可.【解析】A 选项,5x 和2y 不是同类项,不能合并,故该选项计算错误;B 选项,原式=3x 2y ﹣4x 2y =﹣x 2y ,故该选项计算正确;C 选项,x 2和x 5不是同类项,不能合并,故该选项计算错误;D 选项,3x ﹣2x =x ,故该选项计算错误;故选:B .6.(2020秋•渑池县期末)已知x 3﹣m ﹣n y 2与2xy 2是同类项,则m ,n 可以是( ) A .1,0 B .﹣1,3C .﹣2,1D .﹣3,1 【分析】由同类项的定义(所含字母相同,相同字母的指数相同)可得:3﹣m ﹣n =1,进一步可得m 和n 的值.【解析】∵x 3﹣m ﹣n y 2与2xy 2是同类项,∴3﹣m ﹣n =1,∴m +n =2,∴m ,n 可以是﹣1,3,故选:B .7.(2019秋•满城区期末)下列结论不正确的是( )A .π2不是单项式B .﹣3ab 2和b 2a 是同类项C .式子a 4﹣2a 2b 2+b 3是整式D .单项式−3xy 4的系数是−34【分析】根据单项式和多项式的有关概念求解可得.【解析】A 、π2是单项式,原说法不正确,故这个选项符合题意; B 、﹣3ab 2和b 2a 是同类项,原说法正确,故这个选项不符合题意;C 、式子a 4﹣2a 2b 2+b 3是整式,原说法正确,故这个选项不符合题意;D 、单项式−3xy 4的系数是−34,原说法正确,故这个选项不符合题意; 故选:A .8.(2019秋•新洲区期末)如果单项式x 2y m +2与x n y 的和仍然是一个单项式,则m 、n 的值是( )A .m =2,n =2B .m =﹣1,n =2C .m =﹣2,n =2D .m =2,n =﹣1 【分析】本题考查同类项的定义,单项式x 2y m +2与x n y 的和仍然是一个单项式,意思是x 2y m +2与x n y 是同类项,根据同类项中相同字母的指数相同得出.【解析】由同类项的定义,可知2=n ,m +2=1,解得m =﹣1,n =2.故选:B .9.(2020秋•渝中区期末)若多项式x 2﹣2kx ﹣x +7化简后不含x 的一次项,则k 的值为( )A .0B .﹣2C .12D .−12【分析】合并同类项,使x 的系数为0,从而求得k 的值.【解析】x 2﹣2kx ﹣x +7=x 2﹣(2k +1)x +7,∵多项式x 2﹣2kx ﹣x +7化简后不含x 的一次项,∴2k +1=0,解得:k =−12.故选:D .10.(2020秋•龙华区期末)若﹣2xy m +x n y 4=﹣x n y 4,那么m +n 的值是( )A .4B .5C .6D .不能确定 【分析】由﹣2xy m +x n y 4=﹣x n y 4,可得﹣2xy m 与x n y 4是同类项,根据所含字母相同,并且相同字母的指数也相同,这样的项叫做同类项.据此求得m 、n 的值,代入计算可得.【解析】∵﹣2xy m +x n y 4=﹣x n y 4,∴﹣2xy m 与x n y 4是同类项,∴m =4,n =1,∴m +n =4+1=5.故选:B .二、填空题(本大题共8小题,每小题3分,共24分)请把答案直接填写在横线上11.(2021•天津)计算4a +2a ﹣a 的结果等于 5a .【分析】合并同类项的法则:把同类项的系数相加,所得结果作为系数,字母和字母的指数不变.据此计算即可.【解析】4a +2a ﹣a =(4+2﹣1)a =5a .故答案为:5a .12.(2020秋•清涧县期末)若﹣x 3y 3n 与x m ﹣1y 9是同类项,则m +n = 7 . 【分析】根据同类项的定义求解即可,所含字母相同,并且相同字母的指数也相同,这样的项叫做同类项.【解析】由题意得:m ﹣1=3,3n =9,∴m =4,n =3,∴m +n =4+3=7,故答案为:7.13.(2021•深圳模拟)单项式13x m+1y 6与﹣2x 2y 3m﹣n 是同类项,则m +n = ﹣2 .【分析】根据同类项的定义(所含字母相同,相同字母的指数相同)列出方程m +1=2,3m ﹣n =6,求出n ,m 的值,再代入代数式计算即可.【解析】∵单项式13x m+1y 6与﹣2x 2y 3m﹣n 是同类项,∴{m +1=23m −n =6, 解得{m =1n =−3, ∴m +n =1﹣3=﹣2,故答案为:﹣2.14.(2021•岳阳一模)若7a x b 2与﹣3a 3b y 的和为单项式,则x y = 9 .【分析】直接利用已知得出x,y的值,进而得出答案.【解析】∵7a x b2与﹣3a3b y的和为单项式,∴x=3,y=2,∴x y=32=9.故答案为:9.15.(2020秋•永吉县期末)若﹣x a y﹣2x2y c=bx2y总成立,则abc的值为﹣6.【分析】合并同类项是指同类项的系数的相加,并把得到的结果作为新的系数,要保持同类项的字母和字母的指数不变.【解析】因为﹣x a y﹣2x2y c=bx2y总成立,所以a=2,b=﹣1﹣2=﹣3,c=1,所以abc=2×(﹣3)×1=﹣6.故答案为:﹣6.16.(2020秋•浦东新区校级月考)若xy≠0,那么当a=﹣5,b=3,c=2时,5x3y2+ax b y c=0.【分析】根据单项式的和是单项式,可得同类项,根据同类项的意义,可得答案.【解析】由题意,得a=﹣5,b=3,c=2,故答案为:﹣5;3;2.17.(2021•滨海新区一模)计算﹣6ab+ab+8ab的结果等于3ab.【分析】合并同类项是指同类项的系数相加,并把得到的结果作为新系数,要保持同类项的字母和字母的指数不变,据此计算即可.【解析】原式=(﹣6+1+8)ab=3ab,故答案为:3ab.18.(2020秋•巧家县期末)若多项式x2﹣4kxy+5y2﹣xy+9不含有xy项,则k=−14.【分析】将多项式整理后,使xy的系数为0,从而求得k的值.【解析】原式=x2﹣(4k+1)xy+5y2+9,∵合并后不含有xy的项,∴4k+1=0,解得:k=−1 4.故答案是:−14.三、解答题(本大题共6小题,共46分.解答时应写出文字说明、证明过程或演算步骤)19.(2019秋•普陀区校级月考)速算题(合并同类项):(1)﹣4a +9b =(2)﹣4b ﹣8b =(3)﹣8x +2x =(4)﹣0.1x 2+5x 2=(5)23y +y = (6)−45b −2b =【分析】先找出同类项,再合并即可.【解析】(1)﹣4a +9b =9b ﹣4a ;(2)﹣4b ﹣8b =﹣12b ;(3)﹣8x +2x =﹣6x ;(4)﹣0.1x 2+5x 2=4.9x 2;(5)23y +y =5y 3; (6)−45b −2b =−14b 5. 20.(2020秋•东莞市校级期中)化简:(1)﹣3x 2y +3xy 2﹣2xy 2+2x 2y ;(2)2a 2﹣5a +a 2+6+4a ﹣3a 2.【分析】合并同类项时,把同类项的系数相加作为结果的系数,字母和字母的指数不变,据此计算即可.【解析】(1)﹣3x 2y +3xy 2﹣2xy 2+2x 2y=(﹣3x 2y +2x 2y )+(3xy 2﹣2xy 2)=﹣x 2y +xy 2;(2)2a 2﹣5a +a 2+6+4a ﹣3a 2=(2a 2+a 2﹣3a 2)+(4a ﹣5a )+6=﹣a +6.21.(2019秋•松江区期中)若3x m +2n y 8与﹣2x 2y 3m +4n 是同类项,试求m ﹣n 的值.【分析】根据同类项的定义得到{m +2n =23m +4n =8,解方程组得{m =4n =−1,然后把它们代入m ﹣n 中进行计算即可.【解析】由题意得,{m +2n =23m +4n =8, 解得{m =4n =−1, 则m ﹣n =4﹣(﹣1)=5.22.(2019秋•双清区期末)(1)关于x ,y 的多项式4x 2y m +2+xy 2+(n ﹣2)x 2y 3+xy ﹣4是七次四项式,求m 和n 的值;(2)关于x ,y 的多项式(5a ﹣2)x 3+(10a +b )x 2y ﹣x +2y +7不含三次项,求5a +b 的值.【分析】(1)根据多项式的有关定义得到2+m +2=7,n ﹣2=0,然后解方程即可;(2)根据多项式的有关定义得到5a ﹣2=0且10a +b =0,所以5a =2,b =﹣4,然后利用整体代入的方法计算5a +b .【解析】(1)根据题意得2+m +2=7,n ﹣2=0,解得m =3,n =2;(2)根据题意得5a ﹣2=0且10a +b =0,所以5a =2,b =﹣4,所以5a +b =2﹣4=﹣2.23.(2020秋•吉安期中)阅读材料:我们知道,4x ﹣2x +x =(4﹣2+1)x =3x ,类似地,我们把(a +b )看成一个整体,则4(a +b )﹣2(a +b )+(a +b )=(4﹣2+1)(a +b )=3(a +b ).“整体思想”是中学教学解题中的一种重要的思想方法,它在多项式的化简与求值中应用极为广泛,尝试应用:(1)把(a ﹣b )2看成一个整体,求出3(a ﹣b )2+6(a ﹣b )2﹣2(a ﹣b )2的结果.(2)已知x 2﹣2y =4,求3x 2﹣6y ﹣21的值.【分析】(1)根据合并同类项法则、运用整体思想计算;(2)根据添括号法则把原式变形,把x 2﹣2y =4代入计算,得到答案.【解析】(1)3(a ﹣b )2+6(a ﹣b )2﹣2(a ﹣b )2=(3+6﹣2)(a ﹣b )2=7(a ﹣b )2;(2)∵x 2﹣2y =4,∴原式=3(x 2﹣2y )﹣21=12﹣21=﹣9.24.(2020秋•滨湖区期中)规定符号(a,b)表示a,b两个数中较小的一个,规定符号[a,b]表示两个数中较大的一个.例如(3,1)=1,[3,1]=3.(1)计算:(−2,3)+[−23,−34];(2)若(m,m﹣2)+3[﹣m,﹣m﹣1]=﹣5,求m的值.【分析】(1)根据定义得出(﹣2,3),[−23,−34]表示的数,再根据有理数的加法法则计算即可;(2)根据定义可得关于m的一元一次方程,再解方程即可求出m的值.【解析】(1)由题意可知:(−2,3)+[−23,−34]=﹣2+(−2 3)=−223;(2)根据题意得:m﹣2+3×(﹣m)=﹣5,解得m=3 2.。
北师大版七年级数学上册第三章 3.4.1合并同类项 同步测试题

北师大版七年级数学上册第三章 3.4.1合并同类项 同步测试题一、选择题1.下列各式中,与3x 2y 3是同类项的是( )A .2x 5B .3x 3y2C .-12x 2y 3D .-13y 52.下列各组中的两项,不是同类项的是( ) A .a 2b 与-3ab 2B .-x 2y 与2yx 2C .2πr 与π2rD .35与533.如果3ab 2m -1与9ab m +1是同类项,那么m 等于( )A .2B .1C .-1D .04.合并同类项-4a 2b +3a 2b =(-4+3)a 2b =-a 2b 时,依据的运算律是( ) A .加法交换律B .乘法交换律C .乘法对加法的分配律D .乘法结合律5.计算3x 2-x 2的结果是( ) A .2B .2x 2C .2xD .4x 26.下列各组中的两个单项式能合并的是( ) A .4和4xB .3x 2y 3和-y 2x 3C .2ab 2和100ab 2cD .m 和m27.把多项式2x 2-5x +x +4-2x 2合并同类项后,所得多项式是( ) A .二次二项式B .二次三项式C .一次二项式D .三次二项式8.下列运算正确的是( ) A .3a +2a =5a2B .3a +3b =3abC .2a 2bc -a 2bc =a 2bcD .a 5-a 2=a 39.若单项式am -1b 2与12a 2b n 的和仍是单项式,则n m的值是( )A .3B .6C .8D .910.如果多项式x 2-7ab +b 2+kab -1中不含ab 项,那么k 的值为( ) A .0 B .7 C .1 D .不能确定二、填空题11.计算:(1)a -3a =______;(2)(南通中考)3a 2b -a 2b =______. 12.已知3x 5y 2和-2x 3m y n是同类项,则6m -3n 的值为______. 13.如图,阴影部分的面积为______.14.三个连续的整数中,n 是最大的一个,这三个数的和为______. 三、解答题 15.合并同类项: (1)2x -3y +5x -8y -2;(2)23m -1-56m +1+12m ;(3)6x -10x 2+12x 2-5x.(4)x 2y -3xy 2+2yx 2-y 2x.16.先合并同类项,再求值.(1)3a 2-5a +2-6a 2+6a -3,其中a =-1;(2)3a +abc -13c 2-3a +13c 2,其中a =-16,b =2,c =-3;(3)-xyz -4yz -6xz +3xyz +5xz +4yz ,其中x =-2,y =-10,z =-5.17.为了绿化校园,学校决定修建一块长方形草坪,长30 m ,宽20 m ,并在草坪上修建如图所示的等宽的十字路,小路宽为x m. (1)用含x 的代数式表示小路的面积; (2)当x =3时,求小路的面积.18.如果单项式5mx a y与-5nx2a-3y是关于x,y的单项式,且它们是同类项.(1)求(7a-22)2 020的值;(2)若5mx a y-5nx2a-3y=0,且xy≠0,求(5m-5n)2 019的值.19.有这样一道题:“当a=0.35,b=-0.28时,求多项式7a3-6a3b+3a2b+3a3+6a3b-3a2b-10a3的值.”小明说:本题中a=0.35,b=-0.28是多余的条件;小强马上反对说:这不可能,多项式中每一项都含有a和b,不给出a,b的值怎么能求出多项式的值呢?你同意哪名同学的观点?请说明理由.参考答案 一、选择题1.下列各式中,与3x 2y 3是同类项的是(C)A .2x 5B .3x 3y2C .-12x 2y 3D .-13y 52.下列各组中的两项,不是同类项的是(A) A .a 2b 与-3ab 2B .-x 2y 与2yx 2C .2πr 与π2rD .35与533.如果3ab 2m -1与9ab m +1是同类项,那么m 等于(A)A .2B .1C .-1D .04.合并同类项-4a 2b +3a 2b =(-4+3)a 2b =-a 2b 时,依据的运算律是(C) A .加法交换律B .乘法交换律C .乘法对加法的分配律D .乘法结合律5.计算3x 2-x 2的结果是(B) A .2B .2x 2C .2xD .4x 26.下列各组中的两个单项式能合并的是(D)A .4和4xB .3x 2y 3和-y 2x 3C .2ab 2和100ab 2cD .m 和m27.把多项式2x 2-5x +x +4-2x 2合并同类项后,所得多项式是(C) A .二次二项式B .二次三项式C .一次二项式D .三次二项式8.下列运算正确的是(C) A .3a +2a =5a2B .3a +3b =3abC .2a 2bc -a 2bc =a 2bcD .a 5-a 2=a 39.若单项式am -1b 2与12a 2b n 的和仍是单项式,则n m的值是(C)A .3B .6C .8D .910.如果多项式x 2-7ab +b 2+kab -1中不含ab 项,那么k 的值为(B) A .0 B .7 C .1 D .不能确定二、填空题11.计算:(1)a -3a =-2a ;(2)(南通中考)3a 2b -a 2b =2a 2b . 12.已知3x 5y 2和-2x 3m y n是同类项,则6m -3n 的值为4. 13.如图,阴影部分的面积为112x .14.三个连续的整数中,n 是最大的一个,这三个数的和为3n -3. 三、解答题15.合并同类项: (1)2x -3y +5x -8y -2; 解:原式=7x -11y -2.(2)23m -1-56m +1+12m ; 解:原式=13m.(3)6x -10x 2+12x 2-5x. 解:原式=2x 2+x.(4)x 2y -3xy 2+2yx 2-y 2x. 解:原式=3x 2y -4xy 2.16.先合并同类项,再求值.(1)3a 2-5a +2-6a 2+6a -3,其中a =-1; 解:原式=-3a 2+a -1.当a =-1时,原式=-3-1-1=-5.(2)3a +abc -13c 2-3a +13c 2,其中a =-16,b =2,c =-3;解:原式=abc.当a =-16,b =2,c =-3时,原式=-16×2×(-3)=1.(3)-xyz -4yz -6xz +3xyz +5xz +4yz ,其中x =-2,y =-10,z =-5. 解:原式=(-1+3)xyz +(4-4)yz +(5-6)xz =2xyz -xz.当x =-2,y =-10,z =-5时,原式=2×(-2)×(-10)×(-5)-(-2)×(-5) =-200-10 =-210.17.为了绿化校园,学校决定修建一块长方形草坪,长30 m ,宽20 m ,并在草坪上修建如图所示的等宽的十字路,小路宽为x m. (1)用含x 的代数式表示小路的面积; (2)当x =3时,求小路的面积.解:(1)小路的面积为30x +20x -x 2=(50x -x 2)m 2. (2)当x =3时,50x -x 2=50×3-32=141. 答:当x =3时,小路的面积为141 m 2.18.如果单项式5mx a y与-5nx2a-3y是关于x,y的单项式,且它们是同类项.(1)求(7a-22)2 020的值;(2)若5mx a y-5nx2a-3y=0,且xy≠0,求(5m-5n)2 019的值.解:(1)由题意,得a=2a-3,解得a=3.所以(7a-22)2020=(7×3-22)2 020=(-1)2020=1.(2)由题意,得5m-5n=0,所以(5m-5n)2 019=02 019=0.19.有这样一道题:“当a=0.35,b=-0.28时,求多项式7a3-6a3b+3a2b+3a3+6a3b-3a2b-10a3的值.”小明说:本题中a=0.35,b=-0.28是多余的条件;小强马上反对说:这不可能,多项式中每一项都含有a和b,不给出a,b的值怎么能求出多项式的值呢?你同意哪名同学的观点?请说明理由.解:我同意小明的观点.理由如下:因为7a3-6a3b+3a2b+3a3+6a3b-3a2b-10a3=(7+3-10)a3+(-6+6)a3b+(3-3)a2b=0,所以a=0.35,b=-0.28是多余的条件,故小明的观点正确.。
七年级数学上册合并同类项基础过关测试题试卷
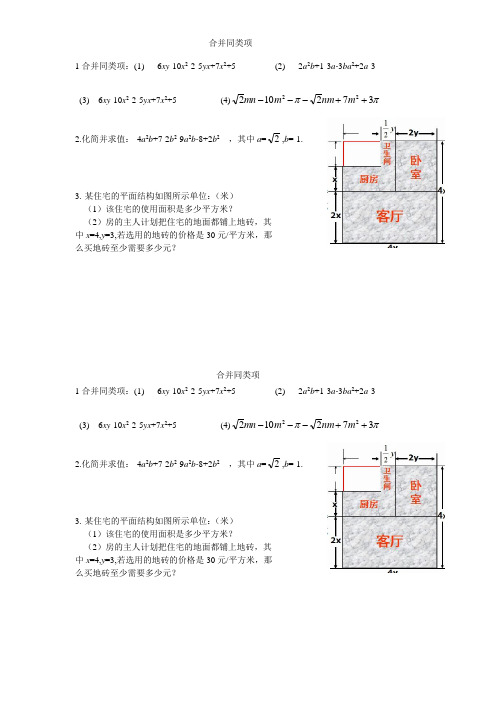
1合并同类项:(1) 6xy -10x 2-2-5yx +7x 2+5 (2) 2a 2b +1-3a-3ba 2+2a -3(3) 6xy -10x 2-2-5yx +7x 2+5 (4)ππ37210222++---m nm m mn2.化简并求值:-4a 2b +7-2b 2-9a 2b-8+2b 2 ,其中a =2,b =-1.3. 某住宅的平面结构如图所示单位:(米)(1)该住宅的使用面积是多少平方米?(2)房的主人计划把住宅的地面都铺上地砖,其中x =4,y =3,若选用的地砖的价格是30元/平方米,那么买地砖至少需要多少元?1合并同类项:(1) 6xy -10x 2-2-5yx +7x 2+5 (2) 2a 2b +1-3a-3ba 2+2a -3(3) 6xy -10x 2-2-5yx +7x 2+5 (4)ππ37210222++---m nm m mn2.化简并求值:-4a 2b +7-2b 2-9a 2b-8+2b 2 ,其中a =2,b =-1.3. 某住宅的平面结构如图所示单位:(米)(1)该住宅的使用面积是多少平方米?(2)房的主人计划把住宅的地面都铺上地砖,其中x =4,y =3,若选用的地砖的价格是30元/平方米,那么买地砖至少需要多少元?合并同类项合并同类项4.拓展提升(1)若代数式xy 2与-3x m -1y 2n 的和是-2xy 2,则2m +n 的值是( ) A.1 B.3 C.4 D.5(2)将代数式25xy 2+2522xy y x -合并同类项,结果是( ) A.21x 2y B.21x 2y +5xy 2 C.211x 2y D.-21x 2y +x 2y +5xy 2 (3)已知︱m +1︱+︱2-n ︱=0,则31x m + n y 与-3xy 3m +2n 同类项(“是”或“不是”).(4)要使关于x,y 的多项式mx 3+3nxy 2+2x 3-xy 2+y 不含二次项,求2m +3n 的值(5)把(a +b )看作一个因式,合并同类项4(a +b )2+2(a +b )-7(a +b )+3(a +b )25.拓展提升(1)若代数式xy 2与-3x m -1y 2n 的和是-2xy 2,则2m +n 的值是( ) A.1 B.3 C.4 D.5(2)将代数式25xy 2+2522xy y x -合并同类项,结果是( ) A.21x 2y B.21x 2y +5xy 2 C.211x 2y D.-21x 2y +x 2y +5xy 2 (3)已知︱m +1︱+︱2-n ︱=0,则31x m + n y 与-3xy 3m +2n 同类项(“是”或“不是”).(5)要使关于x,y 的多项式mx 3+3nxy 2+2x 3-xy 2+y 不含二次项,求2m +3n 的值(5)把(a +b )看作一个因式,合并同类项4(a +b )2+2(a +b )-7(a +b )+3(a +b )2。
七年级数学合并同类项

[单选]下述客运专线预制梁模板安装质量要求说法错误的是()A、使用前,应对模板进行清理、打磨,均匀涂刷脱模剂B、模板表面平整度应≤2mm/m,四支座预埋板位臵高差≤2mmC、为了保证支座预埋板的平整度,底模不可设臵反拱 [单选]在计算应收账款周转天数时,应收账款平均余额()。A.应当扣除坏账准备B.按期初应收账款金额计算C.不应当扣除坏账准备D.按期末应收账款金额计算 [名词解释]芽的晚熟性 [单选,A型题]患者女性,25岁,阵发性心悸6年。平时心电图显示为预激综合征,心电图如图3-16-4所示,旁路可初步定位在()。A.右侧壁B.左侧壁C.左后壁D.右后壁E.右后间隔 [单选]下列选项中哪项不是小肠运动的基本形式?()A、钟摆运动B、集团蠕动C、蠕动和逆蠕动D、分节运动 [单选]当事人在签订合同的过程中约定,双方在履行合同过程中发生的争议,提交北京的仲裁委员会仲裁。下列说法中正确的是:()A.该约定意思表示明确,有效B.纠纷发生后,当事人可以选择位于北京的任何一家仲裁机构申请仲裁,但当事人对仲裁机构不能达成一致的,仲裁协议无效C.由于 [单选]曲线积分(3dx+dy)/(|x|+|y|),其中L为由点(1,0)经(0,1)至(-1,0)的折线,则其值是:()A.-4B.-2C.0D.-6 [单选]拟定沿岸航线,确定航线离岸距离时应考虑下列哪项因素()。Ⅰ.经济航速;Ⅱ.船员技术水平;Ⅲ.船舶操纵性能;Ⅳ.测定船位的难易;Ⅴ.能见度的好坏。A.Ⅱ~ⅤB.Ⅰ~ⅢC.Ⅰ,Ⅱ,Ⅳ,ⅤD.Ⅰ,Ⅱ,Ⅲ,Ⅴ [单选]交接班时间为下班时间前()分钟到达岗位。A.15B.20C.30D.10 [单选]纳税人已在工商行政管理机关办理变更登记的,应当自工商行政管理机关变更登记之日起(),申报办理变更税务登记。A.30日内B.15日内C.45日内D.60日内 [单选]惰性气体含量增加,H2、N2在混合气中的分压()。A.增大B.降低C.不变 [不定项选择]装置引蒸气时所要进行的操作有:()。A、排凝B、暖管C、检查保温D、检查流程 [单选]旷葡萄糖苷酶抑制剂常见不良反应是()A.低血糖症B.腹胀和腹泻C.下肢浮肿D.乳酸性酸中毒E.充血性心力衰竭 [单选]“管理的艺术在于驾驭信息”的含义是()。A、管理者要善于掌握信息,提高信息的时效性B、管理者要善于转换信息,实现信息的价值C、管理者要善于对信息分类,掌握战略级信息,完成企业战略目标D、管理者要善于将企业内部的物质流转换成信息流 [判断题]银行卡按发卡对象分可分为贵宾卡和普通卡。A.正确B.错误 [单选,A2型题,A1/A2型题]高温作业工人在供给饮料和补充营养时,下列不合理的是()。A.饮料应含适当的盐分B.饮水方式以少量多次为宜C.水分和盐分应与出汗量相当D.膳食总热量应比普通工人低E.蛋白质占总热量比例比普通工人高 [单选]微波中继通信中继方式中,适于上下话路的方式是().A.直接中继B.外差中继C.基带中继 [单选,A2型题,A1/A2型题]1979年,国际疼痛协会将疼痛重新定义为()A.是用疼痛来描述的一种不愉快的感觉和情绪B.是由于真正潜在组织损伤而引起的一种不愉快的感觉和情绪C.是指维持较长时间,一般大于3个月,常在损伤愈合后中止D.为最近产生并能持续较短的疼痛,常与明确的损伤和疾 [单选]患者,男性,18岁,发热8天,每天午后开始发热,体温达39.5℃,次日晨可降至37.9℃。该患者的热型是()A.稽留热B.弛张热C.间歇热D.回归热E.马鞍热 [单选,A1型题]实施监测的方法包括()A.记录与报告B.审计C.现场考察D.定量与定性调查E.以上均正确 [单选,A1型题]参与促进乳腺发育及泌乳功能的激素,错误的是()A.雌激素B.甲状旁腺素C.胎盘催乳素D.皮质醇E.胰岛素 [单选]大脑中动脉深穿支闭塞的最常见表现是()A.四肢瘫痪,双侧面瘫,不能言语,不能进食,只有眼球上下运动B.眼球震颤,同侧Homner征,交叉性感觉障碍,同侧小脑性共济失调C.对侧偏瘫,无感觉障碍及偏盲,优势侧伴失语D.对侧偏瘫,偏身感觉障碍,同向偏盲E.对侧偏瘫,深感觉障碍 [单选]发热恶寒,汗出,口渴,心烦,头痛如劈,舌红苔黄,脉滑数,属于:().A.卫分证B.卫气同病C.气分证D.卫营同病 [判断题]金属氧化物避雷器运行电压下当阻性电流增加1倍时,应加强监督。A.正确B.错误 [填空题]客运经营者、货运经营者强行招揽旅客、货物的,由县级以上道路运输管理机构(),处1000元以上3000元以下的罚款;情节严重的,由原许可机关吊销《道路运输经营许可证》。 [单选]车辆类别代号5说明该车属于()汽车。A.载货B.自卸C.专用D.载客 [单选,A1型题]26岁初产妇,因宫缩乏力致第二产程延长行产钳助娩,产后阴道流血量约800ml,诊为宫缩乏力所致,其主要临床表现应为()A.胎盘娩出后阵发性出血量多B.胎盘未娩出时出血不止C.胎儿娩出后立即出血不止D.胎盘剥离延缓而出血E.胎盘娩出后出血无血块 [单选,A1型题]临床证见皮肤瘙痒,且漫无定处,彼此起伏,可引起该症状的主要致病因素是()A.暑邪B.寒邪C.燥邪D.风邪E.湿邪 [单选]世界消除对妇女暴力日是哪月哪日?()A、11月25日B、10月25日C、9月25日D、8月25日 [填空题]能溶解其它物质的液体称为()。被溶解的物质叫()。所形成的均匀状态的液体叫做()。 [单选,A2型题,A1/A2型题]缺铁性贫血时红细胞实验室检查应是()A.MCV<100fl,MCHC35%B.MCV<80fl,MCHC32%C.MCV80~100fl,MCHC35%D.MCV80~100fl,MCHC32%E.MCV<80fl,MCHC35% [单选]()是按照相互之间的从属关系来划分的。A.从合同B.有名合同C.默示合同D.书面合同 [单选,A1型题]下列有关认知训练的表述正确的是()A.治疗师使用模仿、角色扮演帮助患者演示未来生活B.治疗师帮助患者在情景中学会应对策略C.认知训练能够改变患者的自动思维D.通过认知训练治疗师能够发现患者的歪曲认知E.通过认知训练使患者掌握更合理的思维和行为方式 [问答题,简答题]简述最大离散熵定理。对于一个有m个符号的离散信源,其最大熵是多少? [单选]莱姆病患者关节液中可检测到细胞因子是()。A.IL-1B.HLA-DR3C.IL-2D.HLA-DR2E.HLA-DR4 [单选]按1980年的美元记价,设GD表示GDP平减指数。则1990年的实际GDP等于1990年名义GDP()。A.乘以(GD80/GD90);B.乘以(GD90/GD80);C.除以1980年的GD;D.除以1990年GD和1980年GD的差额。 [单选]是否做到(),是人员招聘成败的关键。A.公开招聘B.择优录用C.公平公正D.效率优先 [判断题]半抗原不具有反应原性,但具有免疫原性。()A.正确B.错误 [单选]离心式给水泵随着锅炉压力的升高,泵的()。A.轴功率增大B.轴功率下降C.流量增大D.B和C [填空题]氨合成催化剂的毒物主要有()、()、()。
冀教版数学七年级上册第四章4.2合并同类项同步测试(含答案)

4.2 合并同类项一.选择题1.下列合并同类项正确的是( )A .437a a +=B .222358m n mn mn +=C .3343m m -=D .22265x x x -+= 2.计算a ·a 5 - (2a 3)2 的结果为( )A .a 6-2a 5B .-a 6C .a 6-4a 5D .-3a 6 3.下列计算正确的是( )A .()325b b =B .()2362a ba b -=- C .325a b a +=D .()32628a a = 4.下列算式中,正确的是( )A .770xy yx -=B .33523x x -+=-C .347x y xy +=D .22440x y xy -= 5.若322m a b 与238n a b -的和仍是一个单项式,则m 与n 的值分别是( ) A .1,2 B .2,1 C .1,1 D .4,3 6.给出下列合并同类项的运算:①55541a a -=;②336x y xy +=;③0ax ax -+=;④347a a a +=;⑤2221233m n nm m n -+=-;⑥22223xy x y xy +=.其正确的有( ) A .2个 B .3个C .4个D .5个 7.下列各组中的两项不是同类项的是( )A .与B .与C .与D .与 8.下列各式运算正确的是( )A .B .C .D . 9.在①23x y -与22xy ,②4xy 与-5yx ,③3xy 与-yxz ,④32与23中,是同类项的组数是( )A .1组B .2组C .3组D .4组 10.当整式21072x a b +.和116x y a b--是同类项时,则y 值是( ) A .4 B .3 C .2 D .111.若,则m 与n 的值为( ) A ., B ., C ., D ., 12.下面关于同类项的说法,正确的是( )A .所含字母相同B .所含字母相同,且字母的指数相等C .所含字母完全相同的项D .所含字母相同,且相同字母的指数分别相同13.下列说法正确的是( )A .单项式233x y π-的系数是-3;B .多项式2231a bc ab -+的次数是3;C .23和32是同类项;D .合并同类项2a +3b =5ab .14.若多项式x 2﹣2kxy ﹣y 2+xy ﹣8化简后不含x 、y 的乘积项,则k 的值为( ) A .0 B .12 C .﹣12 D .1315.已知2a 6b 2和13a 3m b n 是同类项,则代数式9m 2-mn -36的值为( ) A .-1B .-2C .-3D .-4二.填空题 16.若32mx y 与23n x y 是同类项,则m n -=________. 17.如果两个单项式7m x y -与33nx y -的和是一个单项式,那么m =_________,n =________.18.370.1250.2548x x -+-合并同类项后是________. 19.下列各组单项式中:①237m n 与2332m n -;②32-与23;③24a b 与2ba ;④2x 与2x ,不是同类项的是________(填序号).20.当k=________时,多项式21383x kxy xy -++中不含xy 项. 21.在多项式2246532a a a a -+-+-中,同类项分别___________________.三.解答题22.合并同类项:(1)2232231x x x x -+-+-+;(2)222213134222x y xy xy x y xy xy -++--; 23.如果2a mx y 与235a nxy --是关于x ,y 的单项式,且它们是同类项. (1)求2018(413)a -的值; (2)若23250a a mx y nx y -+=,且0xy ≠,求()201825m n +的值.24.若36x y ax y ++-合并同类项后不含x 项,则a 的值为多少?25.已知223m n +=,1mn =-,求多项式22225371275m mn n mn m n --+-+的值.26.已知单项式33m x y 与1312n x y --的差是单项式. (1)试求m 、n 的值;(2)求这两个单项式的和.参考答案1-5.DDDAD6-10.ACDBA11-15.BDCBD16.1-17.3 118.x-119.④ 20.1921.24a 与2a -,6a -,与3a ,5与-222.(1)21x -(2)22322x y xy xy --23.(1)1(2)024.-325.-1526.(1)3m =,4n =;(2) 3352x y .。
合并同类项- 2022-2023学年七年级上册数学同步培优题库(浙教版)(解析卷)

专题4.5 合并同类项模块一:知识清单同类项:所含字母相同,并且相同字母的指数也相同的项(即仅系数不同或系数也相同的项)。
例:5abc 2:与3abc 2 3abc 与3abc 。
判断同类项需要同时满足2个条件:①所含字母相同;②相同字母的指数相同 合并同类项:将多项式中的同类项合并成一项叫做合并同类项; 同类项合并的计算方法:系数对应向加减,字母及指数不变。
去(添)括号法则1)括号前是“+”,去括号后,括号内的符号不变 2)括号前是“-”,去括号后,括号内的符号全部要变号。
3)括号前有系数的,去括号后,括号内所有因素都要乘此系数。
注意:去多重括号,可以先去大括号,在去中括号,后去小括号;也可以先从最内层开始,先去小括号,在去中括号,最后去大括号。
可依据简易程度,选择合适顺序。
模块二:同步培优题库全卷共24题 测试时间:80分钟 试卷满分:100分一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.1.(2022·河北·平泉市教育局教研室七年级期末)与14ab -是同类项的为( )A .2abcB .22abC .abD .12【答案】C【分析】根据同类项的定义进行判断即可.【详解】A.14ab -与2abc 不是同类项,故A 错误,不符合题意;B.14ab -与22ab 不是同类项,故B 错误,不符合题意;C.14ab -与ab 是同类项,故C 正确,符合题意;D.14ab -与12不是同类项,故D 错误,不符合题意.故选:C .【点睛】本题主要考查了同类项的定义,熟记同类项的定义,含有的字母相同,相同字母的指数也相同的单项式叫做同类项.2.(2022·内蒙古赤峰·一模)下列代数式中,互为同类项的是( )A .22a b -与23abB .2218x y 与2292x y +C .()n a b +与()3a b +D .2xy -与2y x【答案】D【分析】根据同类项的定义逐项进行判断即可.【详解】A.22a b -与23ab 相同字母的指数不同,因此不是同类项,故A 错误; B.2292x y +是多项式,所以2218x y 与2292x y +不是同类项,故B 错误;C.()n a b +与3()a b +是多项式,且含有的字母也不同,因此它们不是同类项,故C 错误;D.−xy 2与y 2x 含有的字母相同,相同字母的指数也相同,因此它们是同类项,故D 正确.故选:D . 【点睛】本题主要考查了同类项的定义,熟练掌握同类项的定义,含有字母相同,相同字母的指数也相同的单项式为同类项,是解题的关键.3.(2022·河南洛阳市·七年级期末)在下列单项式中:①26x ;②23xy ; ③20.37y x -; ④214y -;⑤213x y ;⑥332⨯,说法正确的是( ) A .②③⑤是同类项 B .②与③是同类项 C .②与⑤是同类项 D .①④⑥是同类项 【答案】B【分析】根据同类项的定义(所含字母相同,相同字母的指数相同),即可判断. 【详解】解:A 、②③是同类项,⑤与②③不是同类项,故不符合题意; B 、②与③是同类项,故符合题意;C 、②和⑤所含字母相同,但相同字母的指数不相同,不是同类项,故不符合题意;D 、①④⑥所含字母不同,不是同类项.故不符合题意;故选:B .【点睛】本题考查了同类项的判定,掌握同类项的定义,所含字母相同,且相同字母的指数相等,是判断同类项的关键.4.(2022·湖南长沙·七年级期末)下列各题中去括号正确的是( ) A .()531531x x -+=-- B .1242414x x ⎛⎫-+=-+ ⎪⎝⎭C .1241244x x ⎛⎫-+=-- ⎪⎝⎭D .()()22312433x y x y ---=---【答案】C【分析】根据去括号法则即可求出答案.【详解】解:A .()531533x x -+=--,故A 不符合题意. B .1242414x x ⎛⎫-+=-- ⎪⎝⎭,故B 不符合题意.C .1241244x x ⎛⎫-+=-- ⎪⎝⎭,故C 符合题意.D .()()22312433x y x y ---=--+,故D 不符合题意.故选∶C .【点睛】本题考查去括号,解题的关键是正确运用去括号法则,本题属于基础题型.5.(2022·山西临汾·七年级期末)不改变代数式22a a b c +-+的值,下列添括号错误的是( ) A .2(2)a a b c +-+ B .2(2)a a b c --+- C .2(2)a a b c --+D .22()a a b c ++-+【答案】C【分析】将各选项代数式去括号,再与已知代数式比较即可.【详解】解:A 、a 2+(2a -b +c )=a 2+2a -b +c ,正确,此选项不符合题意; B 、a 2-(-2a +b -c )=a 2+2a -b +c ,正确,此选项不符合题意; C 、a 2-(2a -b +c )=a 2-2a +b -c ,错误,此选项符合题意;D 、 a 2+2a +(-b +c )=a 2+2a -b +c ,正确,此选项不符合题意;故选:C .【点睛】本题主要考查整式的加减,将各选项去括号,与题干整式比较是否一致是解题的关键. 6.(2022·湖北武汉·七年级期末)计算:68ab ab ab -++=( ) A .ab B .3abC .4abD .6ab【答案】B【分析】利用合并同类项即可得解. 【详解】原式=(-6+1+8)ab =3ab ,故选:B .【点睛】本题考查了使用合并同类项对代数式进行化简计算的知识,掌握同类项的概念是解答本题的关键.7.(2022·甘肃武威·模拟预测)下列运算正确的是( ) A .2ab +3ba =5ab B .2a a a +=C .5ab -2a =3bD .22770a b ab -=【答案】A【分析】利用合并同类项的方法进行判定即可.【详解】解:A 、2ab +3ba =5ab ,正确;B 、a +a =2a ,错误; C 、5ab 与-2a 不是同类项,不能合并,错误;D 、7a 2b 与−7ab 2不是同类项,不能合并,错误;故选择A .【点睛】本题考查合并同类项,掌握同类项的定义和合并同类项法则是解决问题的关键.8.(2022·浙江·七年级期末)把多项式2237256x x x x x -+--+-合并同类项后所得的结果是( ). A .二次三项式 B .二次二项式C .一次二项式D .单项式【答案】B【分析】先进行合并同类项,再判断多项式的次数与项数即可. 【解析】2237256x x x x x -+--+-221x =--.221x --最高次为2,项数为2,即为二次二项式.故选B .【点睛】本题考查了多项式的次数与项数,合并同类项,掌握多项式的系数与次数是解题的关键. 9.(2022·云南·七年级期末)若23x a b -与y a b -是同类项,则x y 的值是( ) A .1 B .2C .3D .4【答案】B【分析】利用同类项的特点得出2y =,1x =,代入x y 即可示解. 【详解】解:∵23x a b -与y a b -是同类项, ∴2y =,1x =,∴122x y ==.故选:B .【点睛】本题考查同类项,掌握同类项的定义是解题的关键.10.(2021·江苏南通·七年级期中)多项式x 2-3kxy -3y 2+6xy 不含xy 项,则k 的值为( ) A .0 B .-2C .2D .任意有理数【答案】C【分析】首先根据题意合并同类项为x 2+(6-3k )xy -3y 2,由题意可得出6-3k =0,解方程即可求出k 的值. 【详解】解:x 2-3kxy -3y 2+6xy = x 2+(6-3k )xy -3y 2, ∵多项式不含xy 项,∴6-3k =0,解得:k =2.故选:C .【点睛】此题考查了合并同类项,以及对多项式中项的概念的理解,解题的关键是根据题意得出xy 项的系数为0.二、填空题(本大题共8小题,每小题3分,共24分.不需写出解答过程,请把答案直接填写在横线上)11.(2022·天津·二模)计算222324a a a -+的结果等于______. 【答案】25a【分析】直接根据合并同类项法则进行计算即可.【详解】解:222324a a a -+=2(324)a -+=25a .故答案为:25a .【点睛】本题主要考查了合并同类项,熟练掌握运算法则是解答本题的关键.12.(2022·河北邢台·八年级阶段练习)在等号右边的横线上填空:2m ﹣n +1=2m ﹣( );3x +2y +1=3x ﹣( ).【答案】 ()1n - ()21y -- 【分析】根据加括号法则求解即可.【详解】解:2m ﹣n +1=2m ﹣()1n -,3x +2y +1=3x ﹣()21y --, 故答案为:()1n -;()21y --.【点睛】此题考查了有理数加减运算的加括号,解题的关键是熟练掌握加括号法则.13. (2022·绵阳市七年级期末)a ﹣b ﹣c +d =a ﹣b ﹣( )=a +( )=a ﹣( ). 【分析】根据添括号法则即可求解.【解答】解:a ﹣b ﹣c +d =a ﹣b ﹣(c ﹣d )=a +(﹣b ﹣c +d )=a ﹣(b +c ﹣d ). 故答案是:c ﹣d ,﹣b ﹣c +d ,b +c ﹣d .14.(2022·江苏七年级期中)关于x 的多项式222514x mx nx x x -++--+,它的值与x 的取值无关,则m n +=________. 【答案】3【分析】先合并同类项,再根据关于x 的多项式222514x mx nx x x -++--+的值与x 的取值无关,得出n -2=0,m -1=0,再求出m 和n 的值,代入计算即可.【详解】解:222514x mx nx x x -++--+=()()2211n x m x -+--∵多项式222514x mx nx x x -++--+的值与x 的取值无关, ∴n -2=0,m -1=0,∴m =1,n =2,∴m +n =3,故答案为:3【点睛】此题考查了整式的加减,关键是根据多项式的值与x 的取值无关,得出关于m ,n 的方程.15.(2022·辽宁锦州市·七年级期中)写出32xyz 的一个同类项:_____________.【答案】35xyz -(答案不唯一)【分析】根据同类项的定义分析,即可得到答案.【详解】32xyz 的一个同类项为:35xyz -故答案为:35xyz -(答案不唯一).【点睛】本题考查了同类项的知识,解题的关键是熟练掌握同类项的定义,从而完成求解. 16.(2022·湖南七年级期末)若多项式322321x x x -++与多项式3236x mx x +-相加后不含二次项,则m 的值为_______. 【答案】3.【分析】先进行整式相加,结果不含二次项说明二次项系数为0,据此列方程即可.【详解】解:3232322321(36)5(3)41x x x x mx x x m x x -++++-=+--+,结果不含二次项,则30m -=,解得,3m =,故答案为:3.【点睛】本题考查了多项式不含某项和整式加减以及一元一次方程的解法,解题关键是熟练运用整式加减进行计算,根据系数为0列方程. 17.(2022·浙江·七年级期中)已知abc >0,||b b=﹣1,|c |=c ,化简|a +b |﹣|a ﹣c |﹣|b ﹣c |=__. 【答案】﹣2c【分析】先根据已知条件确定a ,b ,c 的符号,再化简绝对值即可. 【解析】∵abc >0,1bb=-,c =c ,∴a <0,b <0,c >0, ∴a +b <0,a ﹣c <0,b ﹣c <0,∴a b +﹣a c -﹣b c -=﹣a ﹣b +a ﹣c +b ﹣c =﹣2c .故答案为:﹣2c .【点睛】本题考查绝对值化简,合并同类项法则,解题关键是根据已知条件判断绝对值内的式子的正负性.18.(2022·湖南永州·二模)如果233x y 与12m n x y +-的和仍是单项式,则()2n m -的值为______. 【答案】16【分析】根据题意可知233x y 与12m n x y +-是同类项,从而求出m 和n ,然后代入计算即可. 【详解】解:∵233x y 与12m n x y +-的和仍是单项式, ∴233x y 与12m n x y +-是同类项.∴m +1=2,n -2=3,∴m =1,n =5, ∴()22416n m -==,故答案为:16.【点睛】此题考查了合并同类项及单项式,掌握含有相同字母,相同字母的指数相同的单项式叫同类项是解决此题关键.三、解答题(本大题共6小题,共46分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤)19.(2022·全国·七年级)先去括号,再合并同类项:(1)6a 2﹣2ab ﹣2(3a 2-12ab ); (2)2(2a ﹣b )﹣[4b ﹣(﹣2a +b )]; (3)9a 3﹣[﹣6a 2+2(a 3-23a 2)]; (4)﹣[t ﹣(t 2﹣t ﹣3)﹣2]+(2t 2﹣3t +1). 【答案】(1)﹣ab (2)2a ﹣5b (3)7a 3+223a 2(4)3t 2﹣3t 【分析】(1)先去括号,再合并同类项即可; (2)先去小括号,再去中括号,然后合并同类项即可; (3)先去小括号,再去中括号,然后合并同类项即可; (4)先去小括号,再去中括号,然后合并同类项即可.(1)解:6a 2﹣2ab ﹣2(3a 2-12ab )=6a 2﹣2ab ﹣6a 2+ab =﹣ab ;(2)解:2(2a ﹣b )﹣[4b ﹣(﹣2a +b )] =4a ﹣2b ﹣4b ﹣2a +b =2a ﹣5b ;(3)解:9a 3﹣[﹣6a 2+2(a 3-23a 2)]=9a 3+6a 2﹣2a 3+43a 2=7a 3+223a 2; (4)解:2t ﹣[t ﹣(t 2﹣t ﹣3)﹣2]+(2t 2﹣3t +1) =2t ﹣t +t 2﹣t ﹣3+2+2t 2﹣3t +1 =3t 2﹣3t .【点睛】本题考查整式的加法,熟练掌握合并同类项法则与去括号法则是解题的关键. 20.(2022·新疆·乌鲁木齐八一中学七年级期中)计算(1)()()33223410310a b b a b b -+-+;(2)22135322x x x x ⎡⎤⎛⎫---+ ⎪⎢⎥⎝⎭⎣⎦.【答案】(1)32243a b a b -;(2)2932x x --【分析】直接去括号,合并同类项即可,注意去括号的法则:括号前是“+”号,去括号和它前面的“+”号后,原括号里的各项符号都不改变;括号前是“-”号,去括号和它前面的“-”号后,原括号里的各项符号都要改变.【详解】(1)()()33223410310a b b a b b -+-+33223410310a b b a b b =--+32243a b a b =-(2)22135322x x x x ⎡⎤⎛⎫---+ ⎪⎢⎥⎝⎭⎣⎦22135322x x x x =--++() 2293322x x x =-++()2293322x x x =---2932x x =--【点睛】本题考查代数式的化简,关键在熟练掌握去括号的法则,去括号是易错点. 21.(2022·山东泰安·期末)化简下列各式(1)22235a ab a ab ++-- (2)()22221232x y x x y x ⎛⎫ -⎪⎭-⎝+(3)2(27)3(25)a b b a --- (4)()2323123313313322m n m m n m -++---⎛⎫ ⎪⎝⎭【答案】(1)243a ab -++(2)222x y x -+(3)1920a b -(4)-1 【分析】(1)直接进行同类项的合并即可. (2)先去括号,然后进行同类项的合并. (3)先去括号,然后进行同类项的合并. (4)先去括号,然后进行同类项的合并. (1)原式=22252343a a ab ab a ab -+-+=-++ (2)原式=222222232x y x x y x x y x +-+-+= (3)原式=4146151920a b b a a b --+=-(4)原式=232312313m n m m n m ---++=--【点睛】本题考查整式的加减,解决此类题目的关键是熟记去括号法则,熟练运用合并同类项的法则. 22.(2022·广东江门·七年级期末)已知213a b x y -与23x y -是同类项. (1)请直接写出:a =______,b =______;(2)在(1)的条件下,求()()2222523425a b ab b a +--+的值.【答案】(1)1,−2(2)32【分析】(1)两个单项式为同类项,则字母相同,对应字母的指数也相同,据此可求得a 、b 的值; (2)先去括号再合并同类项,最后代入求值. (1)解:∵213a b x y -与23x y -是同类项, ∴2a =2,1−b =3, ∴a =1,b =−2; 故答案为:1,−2;(2)解:()()2222523425a b ab b a +--+=5a 2+6b 2-8ab -2b 2-5a 2 =4b 2-8ab ,当a =1,b =−2时,原式=4×(−2) 2-8×1×(−2)=16-(-16)=32.【点睛】本题考查整式的化简求值,同类项,解题的关键是掌握同类项的定义,整式的加减运算法则. 23.(2021·陕西咸阳·七年级期中)已知多项式22622452x mxy y xy x化简后的结果中不含xy项.(1)求m 的值;(2)求代数式32322125m m mm mm 的值.【答案】(1)2m =;(2)14-.【分析】(1)先合并已知多项式中的同类项,然后根据合并后的式子中不含xy 项即可求出m 的值; (2)由(1)得m =2,先化简合并同类项,然后代入m 的值计算即可. 【详解】解:(1)22622452x mxyy xyx, 22=6+42252x m xy y x由题意中不含xy 项,可得4-2m =0, ∴m =2; (2)32322125m m mm mm=3226m m .当m =2时,原式=322226 =14-.【点睛】本题考查了整式的加减,正确理解题意、熟练掌握合并同类项的法则是解题的关键. 24.(2021·吉林吉林市·九年级一模)某同学化简()()32a b a b +--时出现了错误,解答过程如下: 原式3322a b a b =+--(第一步) a b =+(第二步)(1)该同学解答过程从第______步开始出错,错误原因是__________________; (2)写出此题正确的解答过程.【答案】(1)一,去括号法则用错;(2)5a b +,解答过程见解析. 【分析】(1)根据去括号法则观察系数与符号本题变化即可确定答案; (2)正确去括号,在合并同类项即可.【详解】(1)由于第一步中2b 没变号,∴错误出现在第一步,去括号时没有准确变号, 故答案为:一,去括号法则用错;(2)原式3322a b a b =+-+,5a b =+.【点睛】本题考查利用乘法对加法分配律去括号问题,掌握去括号的方法与注意事项是解题关键.。
人教版七年级上册数学3.2 解一元一次方程(一)——合并同类项与移项课件
分析: 设这个班有x名学生. 这批书共有(3x+20)本.
盈不足问题
这批书共有(4x-25)本.
表示同一个量的两个不同的式子相等.
(即:这批书的总数是一个定值)
3x+20=4x-25
请运用等式的性质解下列方程:
(1) 4x-15 = 9; 解:两边都加15,得
4x-15+15 = 9 +15 合并同类项,得
解得
x=33,
所以 x+3=36,x+6=39.
故这三张卡片上面的数分别是33,36,39.
亲爱的读者: 1、盛 生年 活不重 相来 信, 眼一泪日 ,难 眼再 泪晨 并。 不及 代时 表宜 软自 弱勉 。,20岁.7.月12不7.待12人.2。02。00290:.071.10297:0.112:4.250J2u0l-0290:0091:091:01:45Jul-2009:01 亲爱的读者: 2、千世里上之没行有,绝始望于的足处下境。,只20有20对年处7月境1绝2日望星的期人日。二〇二〇年七月十二日2020年7月12日星期日 春去春又回,新桃换旧符。在那桃花盛开的地方,在 3、少成年功易都学永老远难不成会,言一弃寸,光放阴弃不者可永轻远。不。会成09功:01。7.12.202009:017.12.202009:0109:01:457.12.202009:017.12.2020
这醉人芬芳的季节,愿你生活像春天一样阳光,心情像桃 76、人生生命贵太相过知短,暂何,用今金天与放钱弃。了明20天.7.不12一20定.7能.1得22到0.。7.192时。12分092时0年1分7月121-2J日ul星-20期7日.12二.2〇02二0〇年七月十二日 花一样美丽,感谢你的阅读。 87、勇放气眼通前往方天,堂只,要怯我懦们通继往续地,狱收。获的09季:01节0就9:0在1前:45方7.。122.02.072.102S2u0n.d7a.1y2, 2J0u.l7y.12,。22002200年7月12日星期日二〇二〇年七月十
人教版数学七年级上册3.2 解一元一次方程(一)——合并同类项与移项 课件(共17张PPT)
B
知识点二 合并同类项
把方程两边的____同__类__项______分别合并,从而把方程转化 为_____a_x_=__b_____的形式,然后再转化为x=c的形式(其中 a,b,c是常数).
2. 解方程-7x+4x=9的步骤: (1)__合__并__同__类__项__,__得__-__3_x_=__9_______; (2)__系__数__化__为__1_,__得__x_=__-__3_________.
【例3】解下列方程: (1)3x+2x+x=24; 解:合并同类项,得6x=24. 系数化为1,得x=4.
(2)-3x+6x=18. 解:合并同类项,得3x=18. 系数化为1,得x=6.
思路点拨:先合并同类 项,再将系数化为1即 可.
解:合并同类项,得-x=-3. 系数化为1,得x=3.
【例4】有一列数,按一定的规律排列成-2,4,-8,16 ,…,其中某三个相邻的数的和为-384,求这三个数各为 多少.
第三章Байду номын сангаас一元一次方程
第27课时 解一元一次方程(一)——合并同类项
目录
01 本课目标 02 课堂导练
本课目标
1. 运用合并同类项解形如 ax+bx+cx=p的方程. 2. 经历运用方程解决实际问题的过程,体会方程是刻画现 实世界的有效数学模型.
知识点一 未知数系数化为1
把形如ax=b的方程,利用等式的性质,两边同时 ____除__以__a______,从而把方程转化为x=c的形式(其中a,b ,c是常数).
谢谢
课堂导练
解:系数化为1,得x=2. 思路点拨:利用将未知数系数化为1的方法解答即可.
解:系数化为1,得x=-3.
D
七年级数学上册合并同类项练习题精编333
七年级数学上册合并同类项练习题精编 -5n+(6n+8) 3n-(5n-7p)-(7p-n)
6(4m-7)+7m 5+(5y-4)+(2y+4) 5(-ab+9a)+(4a-4b) 20(abc-7a)-9(7a-7abc) 3(xy-6z)+(-xy-7z) -9(pq+pr)+(9pq-pr) 8m+(6m-4) m-(7m+5c)+(9c+m) 七年级数学上册合并同类项练习题精编 8(3m+2)-4m 2+(7m+2)+(2m-8)
8(-ab-5a)-(9a+7b) 4(abc-7a)-2(7a-2abc) 4(xy-6z)+(-xy+3z) -9(pq-pr)-(3pq+pr) 9x+(5x+6) 4x-(7x+4s)+(8s-7x) 9(6a+8)-9a 1-(4n-6)+(3n+10) 七年级数学上册合并同类项练习题精编 2(-ab-3a)+(4a-2b) 6(abc-7a)-9(6a+3abc)
3(xy+9z)-(-xy+2z) -9(pq+pr)-(5pq+pr) 7n+(3n-9) n+(3n-6d)-(9d+8n) 3(5b-2)-4b 2-(3y-10)-(6y-1) 9(ab+8a)+(6a+7b) 3(abc+6a)-2(9a+8abc) 七年级数学上册合并同类项练习题精编 7(xy+2z)+(-xy-2z) -5(pq+pr)+(9pq+pr)
-5a+(3a+4) 4a-(6a+7d)+(6d+a) 4(8s-3)-8s 7+(2y+7)+(6y+9) 7(ab+9a)+(3a+3b) 12(abc+9a)+3(4a-5abc) 9(xy+3z)-(-xy-3z) -3(pq+pr)+(3pq+pr) 七年级数学上册合并同类项练习题精编 -4x+(6x+6) 7x+(8x-6s)-(5s-4x)
-6(9s+8)+2s 5+(9a+9)-(9a+6) 9(ab-8a)-(2a+2b) 11(abc+9a)+4(4a-7abc) 5(xy+4z)-(-xy-4z) -3(pq+pr)-(7pq-pr) -9b+(5b-1) b-(8b-2s)+(5s-9b) 七年级数学上册合并同类项练习题精编 9(3a-5)-8a 9-(8a+7)+(9a+1)
新苏科版七年级数学上册:3.4.2《合并同类项》导学案
3.4.2 合并同类项
姓名学号_________ 班级_________
一、【学习目标】1会合并同类项:
2知道合并同类项的所依据的运算律。
二、【学习重难点】会合并同类项:
三、【自主学习】
1、自学课本P81到P82,完成练一练。
2、若3x m y4和5xy n是同类项,则m= , n= .
3、任意写出3x3y的2个同类项
4、求代数式6x+2x2-3x+x2+1的值,其中x=-5
四、【合作探究】
1、自学例2,回忆一下合并同类项的方法。
2、小组讨论书上“做一做”,想一想哪种方法更简便。
3、总结:求代数式的值时,如果代数式中含有同类项,通常先合并同类项再进行计算。
4、练习:
求代数式的值
提醒:合并同类项是计算的第一步,同时应注意:(1)判断那些项是同类项;
(2)连同项的符号变更项的位置;
(3)避免漏项。
五、【达标巩固】
求下列代数式的值:。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
七年级数学上册合并同类项专项训练 -6n-(7n-6) n-(9n-2c)+(7c-n)
-8(8s-2)+9s 9+(5y+1)-(7y+5) 6(-ab+5a)+(8a+2b) 4(abc+7a)+3(2a-9abc) 8(xy-8z)+(-xy-8z) -3(pq+pr)+(7pq-pr) -3x+(5x+5) x+(4x+5s)-(5s+6x) 4(8t-2)-3t 6+(5n-8)-(4n-1) 七年级数学上册合并同类项专项训练 5(ab-9a)+(4a+6b) 20(abc+9a)+3(8a-8abc)
8(xy-9z)-(-xy+6z) -9(pq-pr)+(9pq+pr) 6y-(5y-6) 8y-(7y-3p)-(8p-7y) 2(4s+2)+4s 3-(4a-8)-(2a+2) 6(ab-4a)+(3a-8b) 6(abc+3a)+7(9a-7abc) 2(xy-7z)-(-xy-9z) -6(pq+pr)+(3pq+pr) 七年级数学上册合并同类项专项训练 2b-(6b-5) b+(8b+6c)-(6c+4b)
6(3t-3)+7t 7-(4y+4)-(7y+7) 3(ab+3a)-(5a-6b) 13(abc+2a)+4(8a+5abc) 3(xy-6z)-(-xy-8z) -2(pq+pr)+(3pq+pr) -9a+(6a-4) 8a+(8a+3p)+(8p+4a) -2(6s-1)-6s 1+(9x+4)+(7x-7) 七年级数学上册合并同类项专项训练 8(ab+3a)-(4a+4b) 2(abc+8a)+5(9a-7abc)
3(xy+9z)+(-xy-9z) -8(pq+pr)-(2pq+pr) 8n-(2n+5) n+(6n-7c)-(5c-n) 8(2b+6)-7b 7-(6m-3)-(7m-8) 9(ab-5a)-(7a+8b) 9(abc-2a)+5(7a+8abc) 2(xy+2z)-(-xy+5z) -8(pq-pr)-(4pq-pr) 七年级数学上册合并同类项专项训练 2a-(3a-9) 2a+(9a+8d)-(4d+5a)
8(3t+4)-8t 5+(9x+1)-(5x+8) 9(ab+9a)+(9a+6b) 14(abc-8a)+4(4a-6abc) 5(xy+5z)-(-xy-5z) -4(pq-pr)+(9pq+pr) 9y+(9y-7) y-(4y-6q)+(5q+5y) -5(6n-6)+4n 2-(2m+5)-(2m+9) 七年级数学上册合并同类项专项训练 4(-ab+9a)+(3a-6b) 16(abc+4a)-6(7a+5abc)
5(xy-8z)+(-xy-7z) -8(pq+pr)-(7pq+pr) 3x-(3x+6) 3x+(9x-8d)-(9d-6x) -7(7a+7)+2a 9+(8y+10)+(5y-5) 9(-ab+3a)-(3a+2b) 19(abc+5a)-7(7a-7abc) 9(xy-3z)+(-xy+5z) -3(pq+pr)+(9pq-pr) 七年级数学上册合并同类项专项训练 2n+(7n-4) 7n-(9n+6q)+(4q-n)
-8(5b-10)-6b 4+(9a-8)-(3a-7) 3(ab-3a)-(8a+3b) 13(abc+7a)+8(6a+6abc) 6(xy+7z)+(-xy+6z) -6(pq-pr)-(3pq-pr) -9a+(7a-5) 7a+(2a-3p)+(7p+5a) 2(9t-7)-8t 5-(2y-10)-(7y-7) 七年级数学上册合并同类项专项训练 5(ab+2a)+(8a+8b) 9(abc+3a)-4(6a+6abc)
5(xy+5z)-(-xy-5z) -9(pq-pr)-(7pq-pr) 5x+(8x+1) 6x+(4x-4c)+(8c+x) 8(9n+10)-3n 6-(7y+10)-(2y-6) 9(-ab+3a)+(9a-7b) 18(abc-3a)+3(9a-8abc) 5(xy-7z)+(-xy-2z) -3(pq+pr)+(4pq-pr) 七年级数学上册合并同类项专项训练 8m+(9m-6) m+(2m+9s)+(5s-5m)
-2(2m+3)+9m 3-(9n+3)+(6n+6) 3(-ab+4a)-(6a-2b) 12(abc-6a)+3(5a+6abc) 3(xy-6z)-(-xy-2z) -6(pq+pr)-(6pq+pr) -7m+(7m-2) m-(3m-9p)-(8p-m) -3(7s+6)+4s 7-(7y-5)+(5y+8) 七年级数学上册合并同类项专项训练 3(-ab-6a)+(5a+3b) 19(abc-7a)-7(5a-4abc)
3(xy+3z)+(-xy+6z) -2(pq-pr)-(9pq+pr) -7y+(8y+8) y-(3y+4c)-(4c-y) 8(2n-2)+8n 2-(5n-5)+(2n-3) 9(-ab-7a)+(2a+4b) 4(abc-6a)+9(6a-6abc) 4(xy+2z)+(-xy-3z) -3(pq-pr)-(8pq+pr) 七年级数学上册合并同类项专项训练 3n+(3n+3) n+(8n-3z)-(6z+n)
4(9a-8)-3a 3+(9n+3)-(4n-2) 3(ab+5a)+(9a-3b) 17(abc+9a)-6(8a-5abc) 5(xy+6z)-(-xy-2z) -9(pq-pr)+(9pq+pr) 4x+(5x+3) 5x-(9x+9z)+(9z-x) 4(8t-7)+5t 10-(4x-4)+(9x-8) 七年级数学上册合并同类项专项训练 5(ab+5a)+(6a-8b) 17(abc+8a)-5(9a-8abc)
5(xy-7z)-(-xy+3z) -8(pq-pr)+(8pq+pr) -9b+(7b+2) b+(6b+9s)-(4s+4b) 3(8b+9)-3b 6+(7a-8)-(9a-1) 2(ab-7a)+(4a-8b) 12(abc-6a)+9(3a-9abc) 7(xy-5z)+(-xy+7z) -9(pq-pr)-(2pq-pr) 七年级数学上册合并同类项专项训练 -6m-(6m+7) 5m+(8m-6c)-(9c+m)
-7(3s-2)-6s 1-(8m+2)-(9m+2) 7(-ab-8a)-(2a+3b) 16(abc+3a)+4(5a-8abc) 9(xy-6z)-(-xy-5z) -7(pq-pr)-(9pq-pr) 4y-(3y-7) y+(2y+6p)+(7p-y) -5(3b-2)-3b 1+(3a-4)+(4a+5) 七年级数学上册合并同类项专项训练 5(ab+8a)+(5a+8b) 13(abc+7a)-2(6a+6abc)
6(xy+9z)-(-xy-8z) -9(pq+pr)-(6pq+pr) -6y+(7y-8) 8y-(5y+3q)+(8q+y) -5(3s+1)-4s 4+(4a-9)-(2a+3) 4(ab+8a)-(9a-9b) 2(abc-8a)+2(9a+8abc) 2(xy-6z)+(-xy-7z) -5(pq-pr)+(5pq-pr) 七年级数学上册合并同类项专项训练 -9b+(5b+4) 3b-(4b+7c)+(4c+2b)
-2(8m+2)+8m 1-(4a+8)-(9a-2) 8(ab+9a)+(6a-5b) 18(abc-7a)+3(2a-8abc) 5(xy-8z)-(-xy-8z) -5(pq-pr)-(8pq+pr) 6x-(6x-2) 6x+(5x+3p)-(7p+x) 5(7a-5)-9a 2-(5a-7)-(9a+4) 七年级数学上册合并同类项专项训练 9(-ab+5a)+(7a+4b) 11(abc-4a)+7(3a-4abc)
3(xy-6z)+(-xy+6z) -3(pq-pr)+(6pq+pr) -2n-(5n-8) 2n-(5n-8d)+(6d+6n) -6(4s+6)-3s 4-(8b-3)+(6b+1) 8(-ab+2a)-(2a+6b) 14(abc+7a)-3(8a+6abc) 3(xy-7z)+(-xy+5z) -9(pq+pr)+(9pq-pr) 七年级数学上册合并同类项专项训练 -3y+(2y+3) 2y+(6y+9p)+(7p+y)
2(7s+7)+2s 6+(5x+1)+(9x-6) 5(ab-5a)-(3a-5b) 8(abc+4a)-6(7a-8abc) 7(xy-7z)+(-xy-4z) -3(pq-pr)-(9pq+pr) 2n-(4n-7) n-(2n-8z)-(6z-6n) 3(9s+1)+3s 2-(6b-3)-(3b-5) 七年级数学上册合并同类项专项训练 4(-ab-5a)-(3a+5b) 16(abc-5a)+4(2a-3abc)
3(xy-5z)+(-xy+4z) -2(pq-pr)-(9pq+pr) 8m+(3m+6) 5m-(3m-6s)+(7s+m) -3(7a+3)+2a 3+(4x-4)+(5x-2) 6(ab+6a)+(4a+3b) 17(abc+8a)+4(2a-5abc) 7(xy-8z)+(-xy+5z) -3(pq+pr)+(6pq+pr)
