《数学史》朱家生版课后题目参考答案第一章
高等数学课后习题答案--第一章
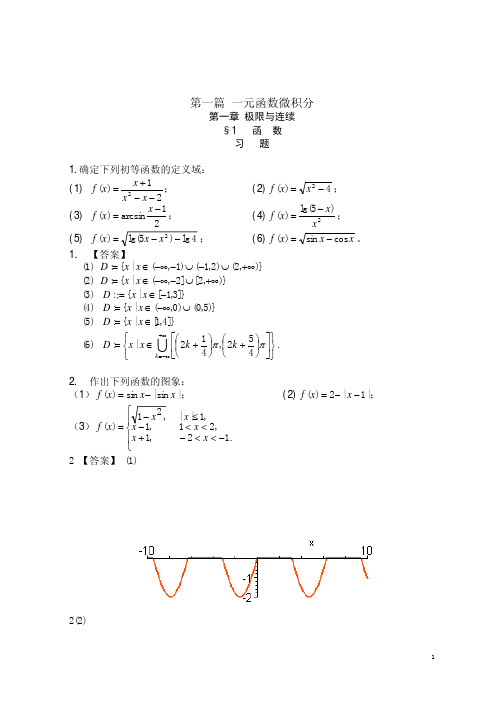
《高等数学》习题参考资料第一篇 一元函数微积分第一章 极限与连续§1 函 数习 题1.确定下列初等函数的定义域:(1) 21)(2−−+=x x x x f ;(2)4)(2−=x x f ;(3) 21arcsin )(−=x x f ;(4)2)5lg()(x x x f −=;(5) 4lg )5lg()(2−−=x x x f ;(6)x x x f cos sin )(−=。
1. 【答案】(1) )},2()2,1()1,(|{:+∞∪−∪−−∞∈=x x D (2) )},2[]2,(|{:+∞∪−−∞∈=x x D (3) ]}3,1[|{:;−∈=x x D (4) )}5,0()0,(|{:∪−∞∈=x x D (5) ]}4,1[|{:∈=x x D (6)+ +∈=+∞−∞=U k k k x x D ππ452,412|:.2. 作出下列函数的图象:(1)|sin |sin )(x x x f −=;(2)|1|2)(−−=x x f ;(3)+−−=,1,1,21)(x x x x f .12,21,1||−<<−<<≤x x x 2 【答案】 (1)2(2)2 (3)3.判断下列函数的奇偶性:(1)x x x f ++−=11)(;(2)xxx f x x +−+−=11lg110110)(;(3)x x a a x f x x sin )(++=−;(4))1lg()(2x x x f ++=。
3. 【答案】 (1) 偶函数; (2) 偶函数; (3) 偶函数; (4) 奇函数 .4.证明:两个奇函数的乘积是偶函数;一个奇函数与一个偶函数的乘积是奇函数。
4. 【答案】 设)(x f ,)(x h 是奇函数, )(x g 是偶函数,)()()(x h x f x f =,)()()(x g x f x G =, 于是)()()(x h x f x F −−=−))())(((x h x f −−=)()()(x F x h x f ==, 因此)(x F 是偶函数.)()()(x g x f x G −−=−)()(x g x f −=)(x G −=, 因此)(x G 是奇函数.5.设函数f 满足:D (f )关于原点对称,且()xc x bf x af =+1)(,其中a ,b ,c 都是常数,||||b a ≠,试证明f 是奇函数。
高等数学第一章课后习题答案

高等数学(本)第一章 函数与极限1. 设 ⎪⎩⎪⎨⎧≥<=3||,03|||,sin |)(ππϕx x x x , 求).2(446ϕπϕπϕπϕ、、、⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛6sin )6(ππϕ=21=224sin )4(==ππϕ ()0222)4sin()4(==-=-ϕππϕ2. 设()x f 的定义域为[]1,0,问:⑴()2x f ; ⑵()x f sin ; ⑶()()0>+a a x f ; ⑷()()a x f a x f -++ ()0>a 的定义域是什么?(1)][;,-的定义域为所以知-11)(,111022x f x x ≤≤≤≤[]ππππ)12(,2)(sin ),()12(21sin 0)2(+∈+≤≤≤≤k k x f Z k k x k x 的定义域为所以知由][a a a x f ax a a x -+-≤≤≤+≤1,)(110)3(-的定义域为所以知-由][φ时,定义域为当时,定义域为当从而得-知由211,210111010)4(>-≤<⎩⎨⎧+≤≤-≤≤⎩⎨⎧≤-≤≤+≤a a a a a x a ax a a x a x班级 姓名 学号3. 设()⎪⎩⎪⎨⎧>-=<=111011x x x x f ,()x e x g =,求()[]x g f 和()[]x f g ,并做出这两个函数的图形。
⎪⎪⎩⎪⎪⎨⎧>=<==⎪⎩⎪⎨⎧>-=<=⎪⎩⎪⎨⎧>-=<=-1,1,11,)]([.)20,10,00,1)]([1)(,11)(,01)(,1)]([.)11)(x e x x e e x f g x x x x g f x g x g x g x g f x f 从而得4. 设数列{}n x 有界, 又,0lim =∞→n n y 证明: .0lim =∞→n n n y x{}结论成立。
现代数学引论第一章部分习题参考答案

现代数学引论第一章部分习题参考答案第4页(2)证明:1lim n k n n k nx A A +∞+∞→∞==∈=k k nA +∞= 是一个单调递增的集合序列,而根据定义,limn n A →∞是这些集合的并集,即1k n k nA +∞+∞== ,那么肯定存在一个足够大的0N 使得k k NA +∞= 中包含了x ,即0kk N x A +∞=∈上式中,对于任意的0nN ≥,都有0k n k N A A +∞=⊆因此只要取0N N =,即有,对于所有n N>,0k n k N xA A +∞=∈⊆证毕。
第10页证明:因为iA 是可列集,因此可以将iA 中的元素一一列出如下:1A :111213,,,...a a a2A :212223,,,...a a a 3A :313233,,,...a a a如下图所示,对上述元素按照对角线顺序从左上到右下扫描在此基础上定义一个映射:使得某集合元素ij a 映射到扫描的顺序值n (1,2,3,4...n=) 那么i i IA ∈ 中的元素与自然数n 之间构成了一一对应的关系,所以是可列集。
第12页【说明:(10 or 1 for all i 2ii ii a a +∞==∑)表示的是一个二进制的小数,记为1232(0.......)k a a a a ,该小数的每一位相应的权值为:1232,2,2,...,2,...k----每一位ka 都可以取0或者1,所有可能的组合对应[0,1]之间所有的实数。
提示中定义的映射,对应到的是一个集合{,1}n n n N a ∈= ,表示的是数1232(0.......)k aa a a 中所有取值为1的位k a 对于的下标k例如2(0.0101)对应到集合{2,4} 】 证明: 定义映射对所有1[0,1]0 or 1 for all i 2i i ii a x a +∞=⎧⎫∈==⎨⎬⎩⎭∑ 1()(){,1}2in ii a f x f n n N a +∞===∈=∑那么x 和以自然数为元素构成的集合{,1}n n n N a ∈=形成了一一对应的关系。
初一上册数学第一章习题及答案讲解

第1章《有理数》易错题集(05):1.4 有理数的乘除法© 2011 菁优网选择题1、(2010•菏泽)负实数a的倒数是()A、﹣aB、C、﹣D、a2、如果m是有理数,下列命题正确的是()①|m|是正数;②|m|是非负数;③|m|≥m;④m的倒数是.A、①和②B、②和④C、②和③D、②、③和④3、﹣的负倒数是()A、﹣B、2001C、﹣2001D、4、两个互为相反数的有理数相乘,积为()A、正数B、负数C、零D、负数或零5、绝对值不大于4的整数的积是()A、16B、0C、576D、﹣16、五个有理数的积为负数,则五个数中负数的个数是()A、1B、3C、5D、1或3或57、现有四种说法:①几个有理数相乘,当负因数有奇数个时,积为负;②几个有理数相乘,积为负时,负因数有奇数个;③当x<0时,|x|=﹣x;④当|x|=﹣x时,x<0.其中正确的说法是()A、②③B、③④C、②③④D、①②③④8、某校期末统一考试中,A班满分人数占2%,B班满分人数占4%,那么满分人数()A、A班多于B班B、A班与B班一样多C、A班少于B班D、不能比较9、5个非零实数相乘,结果为负.则负因数的个数为()A、1个B、3个C、5个D、1个或3个或5个10、下列说法中错误的是()A、零不能做除数B、零没有倒数C、零没有相反数D、零除以任何非零数都得零11、若ab<0,则的值()A、是正数B、是负数C、是非正数D、是非负数12、某种药品的说明书上,贴有如图所示的标签,一次服用这种药品的剂量范围是()A、15mg~30mgB、20mg~30mgC、15mg~40mgD、20mg~40mg13、下列算式中,与相等的是()A、B、5C、5D、514、下列等式中不成立的是()A、﹣B、=C、÷1.2÷D、15、两个不为零的有理数的和等于0,那么它们的商为()A、0B、﹣1C、1D、不能确定16、甲小时做16个零件,乙小时做18个零件,那么()A、甲的工作效率高B、乙的工作效率高C、两人工作效率一样高D、无法比较17、若两个有理数的商是正数,和为负数,则这两个数()A、一正一负B、都是正数C、都是负数D、不能确定填空题18、(2007•云南)的倒数是_________.19、﹣0.5的相反数是_________,倒数是_________,绝对值是_________.20、倒数是它本身的数是_________,相反数是它本身的数是_________.21、﹣1的负倒数是_________;﹣(﹣3)的相反数是_________.22、﹣2的倒数是_________;小于的最大整数是_________.23、﹣2的倒数是_________,相反数大于﹣2且不大于3的整数是_________.24、﹣4×125×(﹣25)×(﹣8)=_________.25、商场在促销活动中,将标价为200元的商品,在打八折的基础上再打八折销售,则该商品的售价是_________元.26、比﹣3大,但不大于2的所有整数的和为_________,积为_________.27、已知四个数:2,﹣3,﹣4,5,任取其中两个数相乘,所得积的最大值是_________.28、科学家最新研究表明,吸烟会导致人的寿命减少,按天计算,平均每天吸一包烟可以导致寿命减少2小时20分,如果一个人一个月有n天每天吸一包烟,则这个月他的寿命减少了_________天.29、(2009•泉州)计算:(﹣4)÷2=_________.30、12和15的最大公因数是_________.答案与评分标准选择题1、(2010•菏泽)负实数a的倒数是()A、﹣aB、C、﹣D、a考点:倒数。
第一章作业参考答案

1.证明:(1)若a|b,c|d,则ac|bd(2)若a|b 1,a|b 2,…,a|b k ,则对任意整数c 1,c 2,…,c k ,有a|(b 1c 1+b 2c 2+…b k c k ).证:1)a|b 可知存在整数m 使得b=ma , c|d 可知存在整数n 使得d=nc得bd=acmn 即ac|bd 。
2) a|b 1,a|b 2,由性质1-1(3)可得a|(b 1c 1+ b 2c 2),其中c 1和c 2为任意整数。
递归可证得a|(b 1c 1+b 2c 2+…b k c k )。
2.若3|a,5|a 且7|a,则105|a.证明: 3|a ∴存在整数m 使得a=3m5|a 即 5|3m,又∵ 5|5m∴ 5|(2*3m-5m)即5|m∴ 5*3|m*3 即 15|3m 即 15|a同理, 15|a ∴存在整数n 使得a=15n ,7|a 即7|15n,又∵7|7n∴ 7|(15-7*2)n 即7|n∴ 7*15|15n 即105|a3.设p 是正整数n 的最小素因数,证明,若n>p>n 1/3,则n/p 是素数。
证明:反证法。
假设n/p 不是素数,则必是合数,则有:n/p=p 1*p 2*…*p k (其中k ≥2, p 1,p 2,…,p k 为素数,且都≥p ,且都为n 的因数) p 为最小素因数, ∴p 1,p 2,…,p k 都≥p∴n/p= p 1*p 2*…*p k ≥p 1*p 2≥p 2 ∴n ≥p 3,即p ≤n 1/3与题设矛盾,所以n 一定是素数,得证。
4.设n ≠1,证明:(n-1)2|(n k -1)的充要条件是(n-1)|k.证: n k -1≡((n-1)+1) k -1≡ 011221(1)(1)...(1)(1)k k k k k k k k C n C n C n C n ----+-++-+- ≡ k(n-1)mod(n-1)2充分条件:若(n-1)|k ,则(n-1)2|k(n-1),上式= 0mod(n-1)2,所以(n-1)2|(n k -1)必要条件:Q (n-1)2|(n k -1) ∴ (n-1)2|k(n-1) ∴ (n-1)|k7.证明:形如6k-1的素数有无穷多个。
数学史习题及答案

第六讲思考题解析几何产生的时代背景是什么解析几何的实际背景更多的是来自对变量数学的需求。
文艺复兴后的欧洲进入了一个生产迅速发展,思想普遍活跃的时代。
机械的广泛使用,促使人们对机械性能进行研究,这需要运动学知识和相应的数学理论;建筑的兴盛、河道和堤坝的修建又提出了有关固体力学和流体力学的问题,这些问题的合理解决需要正确的数学计算;航海事业的发展向天文学,实际上也是向数学提出了如何精确测定经纬度、计算各种不同形状船体的面积、体积以及确定重心的方法,望远镜与显微镜的发明,提出了研究凹凸透镜的曲面形状问题。
在数学上就需要研究求曲线的切线问题。
所有这些都难以仅用初等几何或仅用初等代数在常量数学的范围内解决,于是,人们就试图创设变量数学。
作为代数与几何相结合的产物――解析几何,也就在这种背景下问世了。
解析几何的实际背景更多的是来自对变量数学的需求。
从16世纪开始,欧洲资本主义逐渐发展起来,进入了一个生产迅速发展,思想普遍活跃的时代。
生产实践积累了大量的新经验,并提出了大量的新问题。
可是,对于机械、建筑、水利、航海、造船、显微镜和火器制造等领域的许多数学问题,已有的常量数学已无能为力,人们迫切地寻求解决变量问题的新数学方法。
第七讲思考题谈谈您对于“读读欧拉,他是我们大家的老师”(拉普拉斯语)的看法莱昂哈德·欧拉(Leonhard Euler ,1707年4月5日~1783年9月18日)是瑞士数学家和物理学家。
他被一些数学史学者称为历史上最伟大的两位数学家之一(另一位是卡尔·弗里德里克·高斯)。
欧拉是第一个使用“函数”一词来描述包含各种参数的表达式的人,例如:y = F(x) (函数的定义由莱布尼兹在1694年给出)。
他是把微积分应用于物理学的先驱者之一。
他的全部创造在整个物理学和许多工程领域里都有着广泛的应用。
欧拉的数学和科学成果简直多得令人难以相信。
他写了三十二部足本著作,其中有几部不止一卷,还写下了许许多多富有创造性的数学和科学论文。
高等数学第一章课后习题答案

高等数学(本)第一章 函数与极限1. 设 ⎪⎩⎪⎨⎧≥<=3||,03|||,sin |)(ππϕx x x x , 求).2(446ϕπϕπϕπϕ、、、⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛6sin )6(ππϕ=21=224sin )4(==ππϕ ()0222)4sin()4(==-=-ϕππϕ2. 设()x f 的定义域为[]1,0,问:⑴()2x f ; ⑵()x f sin ; ⑶()()0>+a a x f ; ⑷()()a x f a x f -++ ()0>a 的定义域是什么?(1)][;,-的定义域为所以知-11)(,111022x f x x ≤≤≤≤[]ππππ)12(,2)(sin ),()12(21sin 0)2(+∈+≤≤≤≤k k x f Z k k x k x 的定义域为所以知由][a a a x f ax a a x -+-≤≤≤+≤1,)(110)3(-的定义域为所以知-由][φ时,定义域为当时,定义域为当从而得-知由211,210111010)4(>-≤<⎩⎨⎧+≤≤-≤≤⎩⎨⎧≤-≤≤+≤a a a a a x a ax a a x a x班级 姓名 学号3. 设()⎪⎩⎪⎨⎧>-=<=111011x x x x f ,()x e x g =,求()[]x g f 和()[]x f g ,并做出这两个函数的图形。
⎪⎪⎩⎪⎪⎨⎧>=<==⎪⎩⎪⎨⎧>-=<=⎪⎩⎪⎨⎧>-=<=-1,1,11,)]([.)20,10,00,1)]([1)(,11)(,01)(,1)]([.)11)(x e x x e e x f g x x x x g f x g x g x g x g f x f 从而得4. 设数列{}n x 有界, 又,0lim =∞→n n y 证明: .0lim =∞→n n n y x{}结论成立。
1.-第一章课后习题及标准答案

第一章1.(Q1) What is the difference between a host and an end system? List the types of endsystems. Is a Web server an end system?Answer: There is no difference. Throughout this text, the words “host” and “end system” are used interchangeably. End systems include PCs, workstations, Web servers, mail servers, Internet-connected PDAs, WebTVs, etc.2.(Q2) The word protocol is often used to describe diplomatic relations. Give an example of adiplomatic protocol.Answer: Suppose Alice, an ambassador of country A wants to invite Bob, an ambassador of country B, over for dinner. Alice doesn’t simply just call Bob on the phone and say, come to our dinner table now”. Instead, she calls Bob and suggests a date and time. Bob may respond by saying he’s not available that particular date, but he is available another date. Alice and Bob continue to send “messages” back and forth until they agree on a date and time. Bob then shows up at the embassy on the agreed date, hopefully not more than 15 minutes before or after the agreed time. Diplomatic protocols also allow for either Alice or Bob to politely cancel the engagement if they have reasonable excuses.3.(Q3) What is a client program? What is a server program? Does a server program requestand receive services from a client program?Answer: A networking program usually has two programs, each running on a different host, communicating with each other. The program that initiates the communication is the client.Typically, the client program requests and receives services from the server program.4.(Q4) List six access technologies. Classify each one as residential access, company access, ormobile access.Answer:1. Dial-up modem over telephone line: residential; 2. DSL over telephone line: residential or small office; 3. Cable to HFC: residential; 4. 100 Mbps switched Etherent: company; 5. Wireless LAN: mobile; 6. Cellular mobile access (for example, 3G/4G): mobile5.(Q5) List the available residential access technologies in your city. For each type of access,provide the advertised downstream rate, upstream rate, and monthly price.Answer: Current possibilities include: dial-up (up to 56kbps); DSL (up to 1 Mbps upstream, up to 8 Mbps downstream); cable modem (up to 30Mbps downstream, 2 Mbps upstream.6.(Q7) What are some of the physical media that Ethernet can run over?Answer: Ethernet most commonly runs over twisted-pair copper wire and “thin” coaxial cable. It also can run over fibers optic links and thick coaxial cable.7.(Q8) Dial-up modems, HFC, and DSL are all used for residential access. For each of theseaccess technologies, provide a range of transmission rates and comment on whether the transmission rate is shared or dedicated.Answer:Dial up modems: up to 56 Kbps, bandwidth is dedicated; ISDN: up to 128 kbps, bandwidth is dedicated; ADSL: downstream channel is .5-8 Mbps, upstream channel is up to1 Mbps, bandwidth is dedicated; HFC, downstream channel is 10-30 Mbps and upstreamchannel is usually less than a few Mbps, bandwidth is shared.8.(Q13) Why is it said that packet switching employs statistical multiplexing? Contraststatistical multiplexing with the multiplexing that takes place in TDM.Answer: In a packet switched network, the packets from different sources flowing on a link do not follow any fixed, pre-defined pattern. In TDM circuit switching, each host gets the same slot in a revolving TDM frame.9.(Q14) Suppose users share a 2Mbps link. Also suppose each user requires 1Mbps whentransmitting, but each user transmits only 20 percent of the time. (See the discussion of statistical multiplexing in Section 1.3.)a.When circuit switching is used, how many users can be supported?b.For the remainder of this problem, suppose packet switching is used. Why will there beessentially no queuing delay before the link if two or fewer users transmit at the same time? Why will there be a queuing delay if three users transmit at the same time?c.Find the probability that a given user is transmitting.d.Suppose now there are three users. Find the probability that at any given time, allthree users are transmitting simultaneously. Find the fraction of time during which the queue grows.Answer:a. 2 users can be supported because each user requires half of the link bandwidth.b.Since each user requires 1Mbps when transmitting, if two or fewer users transmitsimultaneously, a maximum of 2Mbps will be required. Since the available bandwidth of the shared link is 2Mbps, there will be no queuing delay before the link. Whereas, if three users transmit simultaneously, the bandwidth required will be 3Mbps which is more than the available bandwidth of the shared link. In this case, there will be queuing delay before the link.c.Probability that a given user is transmitting = 0.2d.Probability that all three users are transmitting simultaneously=(33)p3(1−p)0=0.23=0.008. Since the queue grows when all the users are transmitting, the fraction oftime during which the queue grows (which is equal to the probability that all three users are transmitting simultaneously) is 0.008.10.(Q16) Consider sending a packet from a source host to a destination host over a fixed route.List the delay components in the end-to-end delay. Which of these delays are constant and which are variable?Answer:The delay components are processing delays, transmission delays, propagation delays, and queuing delays. All of these delays are fixed, except for the queuing delays, which are variable.11.(Q19) Suppose Host A wants to send a large file to Host B. The path from Host A to Host Bhas three links, of rates R1 = 250 kbps, R2 = 500 kbps, and R3 = 1 Mbps.a.Assuming no other traffic in the network, what is the throughput for the file transfer.b.Suppose the file is 2 million bytes. Roughly, how long will it take to transfer the file toHost B?c.Repeat (a) and (b), but now with R2 reduced to 200 kbps.Answer:a.250 kbpsb.64 secondsc.200 kbps; 80 seconds12.(P2) Consider the circuit-switched network in Figure 1.8. Recall that there are n circuits oneach link.a.What is the maximum number of simultaneous connections that can be in progress atany one time in this network?b.Suppose that all connections are between the switch in the upper-left-hand cornerand the switch in the lower-right-hand corner. What is the maximum number ofsimultaneous connections that can be in progress?Answer:a.We can n connections between each of the four pairs of adjacent switches. This gives amaximum of 4n connections.b.We can n connections passing through the switch in the upper-right-hand corner andanother n connections passing through the switch in the lower-left-hand corner, giving a total of 2n connections.13.(P4) Review the car-caravan analogy in Section 1.4. Assume a propagation speed of 50km/hour.a.Suppose the caravan travels 150 km, beginning in front of one tollbooth, passingthrough a second tollbooth, and finishing just before a third tollbooth. What is theend-to-end delay?b.Repeat (a), now assuming that there are five cars in the caravan instead of ten.Answer: Tollbooths are 150 km apart, and the cars propagate at 50 km/hr, A tollbooth services a car at a rate of one car every 12 seconds.a.There are ten cars. It takes 120 seconds, or two minutes, for the first tollbooth to servicethe 10 cars. Each of these cars has a propagation delay of 180 minutes before arriving at the second tollbooth. Thus, all the cars are lined up before the second tollbooth after 182 minutes. The whole process repeats itself for traveling between the second and third tollbooths. Thus the total delay is 364 minutes.b.Delay between tollbooths is 5*12 seconds plus 180 minutes, i.e., 181minutes. The totaldelay is twice this amount, i.e., 362 minutes.14.(P5) This elementary problem begins to explore propagation delay and transmission delay,two central concepts in data networking. Consider two hosts, A and B, connected by a single link of rate R bps. Suppose that the two hosts are separated by m meters, and suppose the propagation speed along the link is s meters/sec. Host A is to send a packet of size L bits to Host B.a.Express the propagation delay, d prop , in terms of m and s.b.Determine the transmission time of the packet, d trans , in terms of L and R.c.Ignoring processing and queuing delays, obtain an expression for the end-to-enddelay.d.Suppose Host A begins to transmit the packet at time t = 0. At time t = d trans , whereis the last bit of the packet?e.Suppose d prop is greater than d trans . At time t = d trans , where is the first bit of thepacket?f.Suppose d prop is less than d trans . At time t = d trans , where is the first bit of thepacket?g.Suppose s = 2.5*108, L = 100bits, and R = 28kbps. Find the distance m so that d propequals d trans .Answer:a. d prop = m/s seconds.b. d trans = L/R seconds.c. d end-to-end = (m/s + L/R) seconds.d.The bit is just leaving Host A.e.The first bit is in the link and has not reached Host B.f.The first bit has reached Host B.g.Wantm=LRS=10028∗103(2.5∗108)=893 km.15.(P6) In this problem we consider sending real-time voice from Host A to Host B over apacket-switched network (VoIP). Host A converts analog voice to a digital 64 kbps bit stream on the fly. Host A then groups the bits into 56-Byte packets. There is one linkbetween Host A and B; its transmission rate is 500 kbps and its propagation delay is 2 msec.As soon as Host A gathers a packet, it sends it to Host B. As soon as Host B receives an entire packet, it converts the packet’s bits to an analog signal. How much time elapses from the time a bit is created (from the original analog signal at Host A) until the bit is decoded (as part of the analog signal at Host B)?Answer: Consider the first bit in a packet. Before this bit can be transmitted, all of the bits in the packet must be generated. This requires56∗8sec=7 msec64∗103The time required to transmit the packet is56∗8sec=896 μsec500∗103Propagation delay = 2 msec.The delay until decoding is7msec + 896μsec + 2msec = 9.896 msecA similar analysis shows that all bits experience a delay of 9.896 msec.16.(P9) Consider a packet of length L which begins at end system A, travels over one link to apacket switch, and travels from the packet switch over a second link to a destination end system. Let d i, s i, and R i denote the length, propagation speed, and the transmission rate of link i, for i= 1, 2. The packet switch delays each packet by d proc. Assuming no queuing delays, in terms of d i, s i, R i, (i= 1, 2), and L, what is the total end-to-end delay for the packet? Suppose now the packet Length is 1,000 bytes, the propagation speed on both links is 2.5 * 108m/s, the transmission rates of both links is 1 Mbps, the packet switch processing delay is 2 msec, the length of the first link is 6,000 km, and the length of the last link is 3,000 km. For these values, what is the end-to-end delay?Answer: The first end system requires L/R1to transmit the packet onto the first link; the packet propagates over the first link in d1/s1; the packet switch adds a processing delay ofd proc; after receiving the entire packet, the packet switch requires L/R2to transmit the packetonto the second link; the packet propagates over the second link in d2/s2. Adding these five delays givesd end-end = L/R1 + L/R2 + d1/s1 + d2/s2 + d procTo answer the second question, we simply plug the values into the equation to get 8 + 8 +24 + 12 + 2 = 54 msec.17.(P10) In the above problem, suppose R1 = R2 = R and d proc= 0. Further suppose the packetswitch does not store-and-forward packets but instead immediately transmits each bit it receivers before waiting for the packet to arrive. What is the end-to-end delay?Answer: Because bits are immediately transmitted, the packet switch does not introduce any delay; in particular, it does not introduce a transmission delay. Thus,d end-end = L/R + d1/s1 + d2/s2For the values in Problem 9, we get 8 + 24 + 12 = 44 msec.18.(P11) Suppose N packets arrive simultaneously to a link at which no packets are currentlybeing transmitted or queued. Each packet is of length L and the link has transmission rate R.What is the average queuing delay for the N packets?Answer:The queuing delay is 0 for the first transmitted packet, L/R for the second transmitted packet, and generally, (n-1)L/R for the nth transmitted packet. Thus, the average delay for the N packets is(L/R + 2L/R + ....... + (N-1)L/R)/N = L/RN(1 + 2 + ..... + (N-1)) = LN(N-1)/(2RN) = (N-1)L/(2R)Note that here we used the well-known fact that1 +2 + ....... + N = N(N+1)/219.(P14) Consider the queuing delay in a router buffer. Let I denote traffic intensity; that is, I =La/R. Suppose that the queuing delay takes the form IL/R (1-I) for I<1.a.Provide a formula for the total delay, that is, the queuing delay plus the transmissiondelay.b.Plot the total delay as a function of L/R.Answer:a.The transmission delay is L / R . The total delay isILR(1−I)+LR=L/R1−Ib.Let x = L / R.Total delay=x 1−αx20.(P16) Perform a Traceroute between source and destination on the same continent at threedifferent hours of the day.a.Find the average and standard deviation of the round-trip delays at each of the threehours.b.Find the number of routers in the path at each of the three hours. Did the pathschange during any of the hours?c.Try to identify the number of ISP networks that the Traceroute packets pass throughfrom source to destination. Routers with similar names and/or similar IP addresses should be considered as part of the same ISP. In your experiments, do the largest delays occur at the peering interfaces between adjacent ISPs?d.Repeat the above for a source and destination on different continents. Compare theintra-continent and inter-continent results.Answer: Experiments.21.(P18) Suppose two hosts, A and B, are separated by 10,000 kilometers and are connectedby a direct link of R = 2 Mbps. Suppose the propagation speed over the link is 2.5•108 meters/sec.a.Calculate the bandwidth-delay product, R •d prop.b.Consider sending a file of 400,000 bits from Host A to Host B. Suppose the file is sentcontinuously as one large message. What is the maximum number of bits that will be in the link at any given time?c.Provide an interpretation of the bandwidth-delay product.d.What is the width (in meters) of a bit in the link? Is it longer than a football field?e.Derive a general expression for the width of a bit in terms of the propagation speed s,the transmission rate R, and the length of the link m.Answer:a.d prop = 107 / 2.5•108 = 0.04 sec; so R •d prop = 80,000bitsb.80,000bitsc.The bandwidth-delay product of a link is the maximum number of bits that can be in thelink.d. 1 bit is 125 meters long, which is longer than a football fielde.m / (R •d prop ) = m / (R * m / s) = s/R22.(P20) Consider problem P18 but now with a link of R = 1 Gbps.a.Calculate the bandwidth-delay product, R·d prop .b.Consider sending a file of 400,000 bits from Host A to Host B. Suppose the file is sentcontinuously as one big message. What is the maximum number of bits that will be inthe link at any given time?c.What is the width (in meters) of a bit in the link?Answer:a.40,000,000 bits.b.400,000 bits.c.0.25 meters.23.(P21) Refer again to problem P18.a.How long does it take to send the file, assuming it is sent continuously?b.Suppose now the file is broken up into 10 packet is acknowledged by the receiver andthe transmission time of an acknowledgment packet is negligible. Finally, assumethat the sender cannot send a packet until the preceding one is acknowledged. Howlong does it take to send the file?pare the results from (a) and (b).Answer:a. d trans + d prop = 200 msec + 40 msec = 240 msecb.10 * (t trans + 2 t prop ) = 10 * (20 msec + 80 msec) = 1.0 sec。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
多练出技巧 巧思出硕果 1.数学的起源于世界古老文明产生的关系 11数本(1)班 郭奇 2011041047 “数学”这个词在我们的生活中可谓是无处不在,他作为人类思维的表达形式,反映了人们的积极进取的意志、缜密周详的推理及对完美境界的追求。“数学”与我们身边的其他学科也有着密切联系。例如在天文学方面、医学方面、经济学方面等等。大到天文地理,小到生活琐事,数学的魅力可谓是发挥的淋漓尽致。 然而关于数学的起源,却有着一个古老而神奇的传说。相传在非常非常遥远的古代,有一天在黄河的波涛中突然跳出一匹“龙马”来,马背上驮着一幅图,图上画着许多神秘的数学符号,后来,从波澜不惊的河水中又爬出一只“神龟”来,龟背上也驮着一卷书,书中则阐述了数的排列方法。马背上的图叫“河图”,乌龟背上的书叫做“洛书”,当“河图洛书”出现后,数学也就诞生了。 当然,这个也只不过是个传说罢了。数学作为最古老的一门学科,他的起源可以上溯到一万多年以前。但是,公元1000年以前的资料留存下来的极少,迄今所知,只有在古代埃及和巴比伦发现了比较系统的数学文献。 远在一万五千年以前,人类就可以相当逼真的描绘出人和动物的形象,这是萌发图形意识的最早证据。后来就开始逐渐对圆形和直线型的追求,从而成为数学图形的最早的原型。在日常的生活实践中又逐渐产生了记数的意识和系统。人类摸索过许多种记数的方法,例如用石块记数,结绳记数等,最后逐步发展到现在我们所用的数字。图多练出技巧 巧思出硕果 形意识和记数意识发展到一定阶段,又产生了度量的意识。 从人类社会的发展史来看,人们对数学本质特征的认识也在不断变化和深化着。欧几里得说过“数学的根源在于普通的常识,最显著的例子是非负整数。”他的算术来自于普通常识中的非负整数。而且直到十九世纪中叶,对于数的科学探索还停留在普通的常识。因此,十九世纪以前,人们普遍认为数学是一门自然学科,经验学科,因为那时的数学与现实之间的联系非常密切。随着数学研究的不断深入,从十九世纪中叶以后,数学是一门演绎科学的观点逐渐占据主导地位。这种观点在布尔巴基学派的研究中得到发展,他们认为数学是研究结构的科学,一切数学都建立在代数结构、序结构和拓扑结构这三种母结之上。 与这种观点相对应,从古希腊的柏拉图开始,许多人认为数学是研究模式的学问。数学家怀特海在《数学与善》一书中说到:“数学的本质特征就是,在从模式化的个体作抽象的过程中对模式进行研究,数学对于理解模式和分析模式之间的关系,是最强有力的技术。”1931年,歌德尔的不完全性定理的的证明,宣告了公理化逻辑演绎系统中存在的缺憾。人们此时又想到了数学是经验科学的观点。著名数学家冯·诺依曼就认为,数学兼有演绎科学和经验科学两种特性。波利亚则认为:“数学有两个侧面,他是欧几里得式的严谨的科学,但他也是别的什么东西。” 然而,人们对数学还有些其他的理解。有人认为“数学是一种文化体系”,“数学是一种语言”数学活动是社会性的。他是在人类文明多练出技巧 巧思出硕果 发展的历史进程中,人类认识自然,适应和改造自然,完善自我与社会的一种高度智慧的结晶。数学对人类的思维方式产生了关键性的影响。也有人认为,数学是一门艺术,“和把数学看做一门学科相比,我更喜欢把他看做是一门艺术”数学家在理性世界指导下所表现出的经久的创造性活动,具有和艺术家的相似之处,这是真实的而并非臆造的。 而我渐渐认为,数学是贯穿于我们生活中的必需品。我们的生活无处不用到数学,他不单单是艺术、是语言等。而是很多种事物的结合体,更多的是在生活中帮助我们的一种工具。 对于中国数学的起源来说,最早可以追溯到上古时期。在殷墟出土的甲骨文卜辞中有很多记数的文字。从一到十、百、千、万,出现的最大的数字是三万。可见,中国数学的起源也是相当之早的。 在古代,算筹是一种计算工具,这种计算方法叫筹算。筹算产生的年代已不可考,但可以肯定得是,在春秋时期筹算已经是很普遍的计算方法了。直到十五世纪元朝末年才逐渐为珠算所代替。中国古代数学就是在筹算的基础上取得其辉煌成就的。在几何学方面,早在夏禹治水时已使用了规、距、准、绳等作图和测量工具,并早已发现了勾股定理。然而,战国时期的百家争鸣,也促进了数学的发展,尤其是对于正名和一些命题的争论直接与数学有关。一些学派还总结和概括出与数学有关的许多抽象概念。 秦汉是封建社会的上升时期,经济和文化均得到迅速发展。中国古代数学体系正是形成于这个时期,它的主要标志是算术已成为一个多练出技巧 巧思出硕果 专门的学科,以及以《九章算术》为代表的数学著作的出现。 《九章算术》是战国、秦、汉封建社会创立并巩固时期数学发展的总结,就其数学成就来说,堪称是世界数学名著。就其特点来说,它形成了一个以筹算为中心、与古希腊数学完全不同的独立体系。《九章算术》有几个显著的特点:采用按类分章的数学问题集的形式;算式都是从筹算记数法发展起来的;以算术、代数为主,很少涉及图形性质;重视应用,缺乏理论阐述等。这些特点是同当时社会条件与学术思想密切相关的。秦汉时期,一切科学技术都要为当时确立和巩固封建制度,以及发展社会生产服务,强调数学的应用性。最后成书于东汉初年的《九章算术》,排除了战国时期在百家争鸣中出现的名家和墨家重视名词定义与逻辑的讨论,偏重于与当时生产、生活密切相结合的数学问题及其解法,这与当时社会的发展情况是完全一致的。 《九章算术》在隋唐时期曾传到朝鲜、日本,并成为这些国家当时的数学教科书。它的一些成就如十进位值制、今有术、盈不足术等还传到印度和阿拉伯,并通过印度、阿拉伯传到欧洲,促进了世界数学的发展。 16世纪末以后,西方初等数学陆续传入中国,使中国数学研究出现一个中西融合贯通的局面;鸦片战争以后,近代数学开始传入中国,中国数学便转入一个以学习西方数学为主的时期;到19世纪末20世纪初,近代数学研究才真正开始。 1840年鸦片战争以后,西方近代数学开始传入中国。首先是英人在上海设立墨海书馆,介绍西方数学。第二次鸦片战争后,曾国藩、多练出技巧 巧思出硕果 李鸿章等官僚集团开展“洋务运动”,也主张介绍和学习西方数学,组织翻译了一批近代数学著作。 由于输入的近代数学需要一个消化吸收的过程,加上清末统治者十分腐败,在太平天国运动的冲击下,在帝国主义列强的掠夺下,焦头烂额,无暇顾及数学研究。直到1919年五四运动以后,中国近代数学的研究才真正开始。 看了数学的起源和发展,我不得不说,数学的确是最古老的一门学科了。在现实生活中,我们也常常和数学打着交道。从小父母就教我们认一、二、三、四。上学期间也一直不间断的学习着数学。起初我只觉得学习数学就是为了考试,为了做题。直到上了大学,我才发现,原来数学并不简简单单是做题考试那么简单,我们要学习的并不是如何利用数学解题,而是要理解数学的含义,把他和生活联系在一起,并且运用到生活中去。 2、进行调查研究,探讨古埃及和巴比伦人哪些古老的数学知识在我们的生活(包括学习、工作等)中还具有现实意义。 答:在公元前5000年到公元前4000年间,古巴比伦人就已开始使用年、月、日的天文历法,他们的年历是从春分开始的,一年有12月,每月有30天。所谓“星期”也就是指星的日期,我们现在的“星期制”就是在古巴比伦时代所创立的。从古巴比伦和古埃及的数学,可以看出,它们的内容都与那个地区的社会和生活的需要密切相关。古巴比伦人对天文学的研究比较感兴趣,因此,相对而言,他们的以60进位记数法为基础的算术与代数较为领先。 古埃及人偏重多练出技巧 巧思出硕果 于测量与建筑施工,因而他们的几何成果比较突出 3.古埃及和古巴比伦人是如何利用归纳思想发现和得到数学结论的,并进一步探讨这种古老的思想方法对于我们今天的数学研究的现实意义。
11数本(1)班 郭奇 2011041047 数学知识伴随着人类文明的产生而起源,并率先在几个文明古国开始了漫长的原始积累过程,人类的祖先为我们留下了珍贵的、可供研究的原始资料,最著名的古埃及象形文字纸草书和巴比伦楔形文字泥板书,较为集中地反映了古埃及数学和巴比的水平,它们被视为人类早期数学知识积累的代表。 古埃及纸草书,是用尼罗河流域沼泽地水生植物的茎皮压制、粘连成纸草卷,用天然涂料液书写而成的。有两份纸草书直接书写着数学内容。一份叫做“莫斯科纸草”,大约出自公元前1850年左右,它包括25个数学问题。这份纸草书于1893年被俄国人戈兰尼采夫买得,也称之为“戈兰尼采夫纸草”,现藏莫斯科美术博物馆。另一份叫做“莱因特纸草”,大约成书于公元前1650年左右,开头写有:“获知一切奥秘的指南”的字样,接着是作者阿默士从更早的文献中抄下来的85个数学问题。这份纸草书于1858年被格兰人莱因特购得,后为博物馆收藏。这两份草书是我们研究古埃及数学的重要资料,其内容丰富,记述了古埃及的记数法、整数四则运算、单位分数的独特用法、多练出技巧 巧思出硕果 试位法、求几何图形的面积、体积问题,以及数学在生产、生活初中中的应用问题。 古巴比伦泥板书,是用截面呈三角形的利器作笔,在将干未干的胶泥板上刻写而成的,由于字体为楔形笔划,故称之为楔形文字泥板,从19世纪前期至今,相继出土了这种泥板有50万块之多。它们分别属于公元前2100年苏美尔文化末期,公元前1790年至公元前1600年间汉莫拉比时代和公元前600年至公元300年间新巴比伦帝国及随后的波斯、塞流西得时代。其中,大约有300至400块是数学泥板,数学泥板中又以数表居多,据信这些数学表是用来运算和解题的。这些古老的泥板,现在散藏于世界各地许多博物馆,并且被一一编号,成为我们研究巴比伦数学最可靠的资料。巴比伦数学从整体上讲比古埃及数学高明,古巴比伦人采用60进位制记数法,并计算出倒数表、平方表、立方表、平方根表和立方根表,其中2的平方根近似为1.414213...。巴比伦的代数有相当水平,他们用语言文字叙述方程问题及其解法,常用特殊的“长”、“宽”、“面积”等字眼表示未知量,除求解二次、三次方程的问题之外,也有一些数论性质的问题。巴比伦的几何似乎没有古埃及的几何那么重要,只是收罗了一些计算简单图形的面积、体积的法则,也许他们只是在解决实际问题时才搞点几何。 此外,巴比伦数学中有很明显的商业、农业和天文的应用背景。我们可以说,在人类早期数学知识积累过程中,由于计数物件的需要,产生了自然数,随着记数法的产生和发展,逐渐形成了运算,导致算
