建模第三次作业
经济数学建模作业及答案

2、如果连续复利时,以什么利率才能使本金在8年内变成3倍?1、在每半年复利一次的情况下,以8%的利率,需要经过多长时间才能使现值增到2.5倍?3、连续收益流量每年按80万元持续5年,若以年利率5%贴现,其现值应是多少?T=11.68年r=13.73%55%00S 80353.92t e dt -==⎰8003S S re =4、某汽车使用寿命为10年,若购买此车需35000元,若租用此车每年租金为7200元,若资金的年利率为14%,按连续复利计算,问买车与租车哪一种方式合算。
计算租车资金流量总值的现值,然后与购买费相比。
租车租金流量总值的现值为所以买车比租车合算。
002.5S S +=2T0.08(1)2101014141172003875635000i i i i i S e e -%-%==≈>=∑∑5、一商家销售某种商品的价格满足关系x p 2.07-=(万元/吨),x 为销售量(单位:吨);商品的成本函数是C =3x +1(万元)。
(1) 若每销售一吨商品,政府要征税t (万元),求该商家获最大利润时商品的销售量;(2) t 为何值时,政府税收总额最大。
6、已知某企业生产的商品的需求弹性为1.2,如果该企业准备明年将价格降低15%,问这种商品的销量预期会增长多少?总收益会增长多少?2'5(2) 10 0 22T tx t t T t ==-=⇒=R18%,3%R Q Q∆∆==令2(70.2)31(4)0.21Px C Tx x x tx t x x --=----=---'''5()0,()0102L x L x x t=<⇒=-(1)利润L(x)=7、某消费者打算购买两种商品q 1和q 2,他的预算约束是240元,两种商品的单价分别是10元和2元,其效用函数为U=q 1q 2,消费者的最优商品组合是什么?一元钱的边际效用是多少?8、效用函数U (q 1,q 2) 应满足的条件是以下的A,B 之一:A. U (q 1,q 2) =c 所确定的函数q 2=q 2(q 1)单调减、下凸;0,0,0,0,0.B 21222221221>∂∂∂<∂∂<∂∂>∂∂>∂∂q q Uq U q U q U q U AB ⇒证明:对U (q ,q 2) =c 两端求q 1的一阶导和二阶导12102240q q +=1212MU MU P P =1212,60q q ==解建立方程组得解出一元钱边际效用为610、在确定性存贮模型中,在费用中增加购买货物本身的费用,确定不允许缺货的最优订货周期和订货批量。
数学建模作业及答案

数学建模作业姓名:叶勃学号:班级:024121一:层次分析法1、 分别用和法、根法、特征根法编程求判断矩阵1261/2141/61/41A ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦11/2433217551/41/711/21/31/31/52111/31/5311A ⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦的特征根和特征向量(1)冪法求该矩阵的特征根和特征向量 程序为:#include<iostream> #include<math.h> using namespace std;#define n 3 //三阶矩阵#define N 20 #define err 0.0001 //幂法求特征值特征向量 void main(){cout<<"**********幂法求矩阵最大特征值及特征向量***********"<<endl; int i,j,k;double A[n][n],X[n],u,y[n],max;cout<<"请输入矩阵:\n"; for(i=0;i<n;i++) for(j=0;j<n;j++)cin>>A[i][j]; //输入矩阵 cout<<"请输入初始向量:\n"; for(i=0;i<n;i++)cin>>X[i]; //输入初始向量 k=1; u=0;while(1){ max=X[0]; for(i=0;i<n;i++) {if(max<X[i]) max=X[i]; //选择最大值 }for(i=0;i<n;i++)y[i]=X[i]/max; for(i=0;i<n;i++)X[i]=0;for(j=0;j<n;j++)X[i]+=A[i][j]*y[j]; //矩阵相乘}if(fabs(max-u)<err){cout<<"A的特征值是 :"<<endl; cout<<max<<endl; cout<<"A的特征向量为:"<<endl; for(i=0;i<n;i++) cout<<X[i]/(X[0]+X[1]+X[2])<<" ";cout<<endl;break;}else{if(k<N) {k=k+1;u=max;} else {cout<<"运行错误\n";break;}}} }程序结果为:(2)和法求矩阵最大特征值及特征向量程序为:#include<stdio.h>#include<iostream>#include<math.h> using namespace std;#define n 3 //三阶矩阵#define N 20void main(){int i,j,k;double A[n][n],w[n],M[n],u[n],W[n][n],max;cout<<"********和法求矩阵的特征根及特征向量*******"<<endl;cout<<"请输入矩阵:\n";for(i=0;i<n;i++)for(j=0;j<n;j++)cin>>A[i][j]; //输入矩阵 //计算每一列的元素和M[0]=0;M[1]=0;M[2]=0;for(i=0;i<n;i++)for(j=0;j<n;j++){M[i]+=A[j][i];}//将每一列向量归一化for(i=0;i<n;i++)for(j=0;j<n;j++){W[j][i]=A[j][i]/M[i];}//输出按列归一化之后的矩阵Wcout<<"按列归一化后的矩阵为:"<<endl;for(i=0;i<n;i++)for(j=0;j<n;j++){cout<<W[i][j]<<" ";if(j==2)cout<<endl;} //求特征向量w[0]=0;w[1]=0;w[2]=0;for(i=0;i<n;i++)for(j=0;j<n;j++){w[i]+=W[i][j];}cout<<"特征向量为:"<<endl; for(i=0;i<n;i++){u[i]=w[i]/(w[0]+w[1]+w[2]);cout<<u[i]<<" "<<endl;}//求最大特征值max=0;for(i=0;i<n;i++){w[i] = 0;for(j=0;j<n;j++){w[i] += A[i][j]*u[j];}}for(i = 0;i < n;i++){max += w[i]/u[i];}cout<<"最大特征根为:"<<endl;cout<<max/n<<endl; }运行结果为:(3)根法求矩阵最大特征值及特征向量:程序为:#include<stdio.h>#include<iostream>#include<math.h>using namespace std;#define n 3 //三阶矩阵#define N 20void main(){int i,j;double A[n][n],w[n],M[n],u[n],W[n][n],max;cout<<"********根法求矩阵的特征根及特征向量*******"<<endl; cout<<"请输入矩阵:\n";for(i=0;i<n;i++)for(j=0;j<n;j++)cin>>A[i][j]; //输入矩阵//计算每一列的元素和M[0]=0;M[1]=0;M[2]=0;for(i=0;i<n;i++)for(j=0;j<n;j++){M[i]+=A[j][i];}//将每一列向量归一化for(i=0;i<n;i++)for(j=0;j<n;j++){W[j][i]=A[j][i]/M[i];}//输出按列归一化之后的矩阵Wcout<<"按列归一化后的矩阵为:"<<endl;for(i=0;i<n;i++)for(j=0;j<n;j++){cout<<W[i][j]<<" ";if(j==2)cout<<endl;}//求特征向量//w[0]=A[0][0];w[1]=A[0][1];w[2]=A[0][2];w[0]=1;w[1]=1;w[2]=1;for(i=0;i<n;i++){for(j=0;j<n;j++){w[i]=w[i]*W[i][j];}w[i]=pow(w[i], 1.0/3);}cout<<"特征向量为:"<<endl;for(i=0;i<n;i++){u[i]=w[i]/(w[0]+w[1]+w[2]);cout<<u[i]<<" "<<endl;}//求最大特征值max=0;for(i=0;i<n;i++){w[i] = 0;for(j=0;j<n;j++){w[i] += A[i][j]*u[j];}}for(i = 0;i < n;i++){max += w[i]/u[i];}cout<<"最大特征值为:"<<endl; cout<<max/n;}运行结果为:2、编程验证n阶随机性一致性指标RI:运行结果:3、考虑景色、费用、居住、饮食、旅途五项准则,从桂林、黄山、北戴河三个旅游景点选择最佳的旅游地。
3D one 作业及答案
姓名:学校:模型作业提交昵称及学校为:一、选择题(每题4分)1.检查草图轮廓是否封闭在建模过程中是非常重要的,如图所示的射箭草图图形,可以使用( A )命令让系统自动检测出开放端位置并显示出来。
A.显示曲线连通性B.偏移曲线C.修剪/延伸曲线D.单击修剪2.如图所示,要把作为树冠的顶部圆锥体向下移动5mm,可以在基本编辑工具栏中找到( A )命令,将其向下移动。
A.移动B.DE移动C.对齐移动D.缩放3.通过下列哪个命令,可以由左图的草图图形快速得到右图的草图图形?( C )A. 修剪/延伸曲线B. 通过点绘制曲线C. 偏移曲线D. 草图绘制4.下面左图的球体里面有一个“乐”字草图,但是在着色模式下看不到、也选不到它,选择( A )命令,可以将右图转变成左图的效果。
A.线框模式B.着色模式C.显示模式D.显示几何体5.对实体进行抽壳时,开放面选择的个数是( D )。
A.只能选择1个B.最多选择2个C.最多选择3个D.按需选择合适个数6.在3D One中“阵列”命令有三种方式,下列哪种方式没有?( C )A. 线性阵列B. 圆形阵列C.球形阵列D. 在曲线上阵列7. 在“铅笔形笔筒的制作”中,画出六棱柱、圆锥后,最后生成铅笔形笔筒的方法是:( C )A. 用组合编辑命令中的“加”运算,最后再抽壳B. 用组合编辑命令中的“减”运算,最后再抽壳C. 用组合编辑命令中的“交”运算,最后再抽壳D. 用镜像命令中的圆形阵列8.二维草图转换成三维实体,除了“拉伸”这种方法之外,还可以用多种方法生成,下列哪个命令不能将草图生成三维实体?( D )A. 用旋转命令B. 用扫掠命令C. 用放样命令D. 用抽壳命令9. 把绘制的二维轮廓草图通过拉伸命令转换成三维实体,绘制的草图轮廓需要满足以下哪个条件?( A )A.轮廓封闭B.轮廓开放C.轮廓交叉D.轮廓叠加10.:哨子是大家熟悉的工具,如果自己设计一个哨子,能吹响吗?判断以下关于哨子能否吹响的说法中不正确的是( A )。
数学建模作业

题目:
某厂按合同规定须于当年每个季度末分别提供10,15,25,20台同一规格的 柴油机。
已知该厂各季度的生产能力及生产每台柴油机的成本如下表所示,如果生产出的柴油机当季不交货,每台积压一个季度需储存、维护等费用0.15万元,建立一个数学模型(不要求求解),要求在完成合同的情况下,使该厂全年生产
解: 设ij x 为第i 季度生产的用于第j 季度交货的柴油机的台数,则由题意 :
=+++=++=+=20
251510
44342414332313221211x x x x x x x x x x
又由生产能力的要求,有
<+++<++<+<25
35301413121124232234334410x x x x x x x x x x
再设ij c 表示第i 季度生产的用于第j 季度交货的每台柴油机的实际成本,其值如下表:
设i a 表示第j 季度的生产能力,j b 表示第i 季度的合同供应量,则建立本问题模型:
∑∑===414
1
i j ij ij x c z min
4
14
1≥=∑≤∑==ij j i ij
i j ij x b x a x t s .
.。
数学建模作业
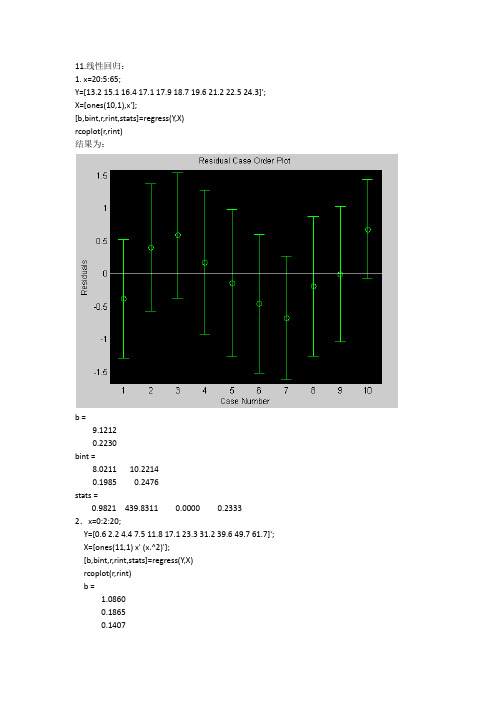
11.线性回归:1. x=20:5:65;Y=[13.2 15.1 16.4 17.1 17.9 18.7 19.6 21.2 22.5 24.3]'; X=[ones(10,1),x'];[b,bint,r,rint,stats]=regress(Y,X)rcoplot(r,rint)结果为:b =9.12120.2230bint =8.0211 10.22140.1985 0.2476stats =0.9821 439.8311 0.0000 0.23332.x=0:2:20;Y=[0.6 2.2 4.4 7.5 11.8 17.1 23.3 31.2 39.6 49.7 61.7]'; X=[ones(11,1) x' (x.^2)'];[b,bint,r,rint,stats]=regress(Y,X)rcoplot(r,rint)b =1.08600.18650.14070.3850 1.78700.0234 0.34960.1328 0.1485stats =1.0e+004 *0.0001 1.3288 0.0000 0.000010.数据的统计描述与分析1. x=[93 75 83 93 91 85 84 82 77 76 77 95 94 89 91 88 86 83 96 81 79 97 78 75 67 69 68 84 83 81 75 66 85 70 94 84 83 82 80 78 74 73 76 70 86 76 90 89 71 66 86 73 80 94 79 78 77 63 53 55]; save qq x在m文件中输入load qqm=mean(x)t=range(x)s=std(x)v=var(x)s=skewness(x)k=kurtosis(x)可得到结果为:m =80.100044s =9.7106v =94.2949s =-0.4682k =3.1529再输入:load qqhist(x,10)可得到结果如下:在matlab的命令窗口中数额load qqnormplot(x)可得到如下如下图:由图可知道:大部分的点都落在线的两侧,由此可知道这些数据是满足正态分布的。
数学建模作业

数学建模1.一电路由三个电阻123,,R R R 并联,再与电阻4R 串联而成,记k R 上电流为k I ,电压为k V ,在下列情况下确定k R 使电路总功率最小(k =1,2,3,4):(1)1234,6,8,210;k I I I V ===≤≤(2)1234,6,8,2 6.k V V V I ===≤≤c=[16 36 64 324];解:(1)A=[ ];b=[ ];Aeq=[ ];beq=[ ];vlb=[1/2;1/3;1/4;1/9];vub=[5/2;5/3;5/4;5/9];[x,favl]=linprog(c,A,b,Aeq,beq,vlb,vub)x =0.50000.33330.25000.1111favl =72.0000 (2)c=[16 36 64 324];A=[ ];b=[ ];Aeq=[ ];beq=[ ];vlb=[2/3;1;4/3;3];vub=[2;3;4;9];[x,favl]=linprog(c,A,b,Aeq,beq,vlb,vub)x =0.66671.00001.33333.0000favl = 1.1040e+0033.要设计和发射一个带有X 射线望远镜和其他科学仪器的气球。
对于性能的粗糙的度量方法是以气球所能到达的高度和所携仪器的重量来表达,很清楚,高度本身是气球体积的一个函数。
根据过去的经验作出的结论,是求极大满意性能函数()22,1000.3800.2P f V W V V W W ==-+-,此处V 是体积,W 是仪器重量。
承包项目的预算限额为1040美元,与体积有关V 的费用是2V ,和设备有关的费用是4W ,为了保证在高度方面的性能与科学设备方面的性能之间合理平衡,设计者要满足约束条件80100W V ≥。
找出由体积和设备重量来表达的最优设计,并求解。
.建立模型: 22max 1000.3800.22520.540f V V W W V W s t V W =-+-+<=⎧⎨-<=⎩.法一:用MATLAB 求解H=[0.3;0.2];c=[-100;-80];A=[2 4;100 -80];b=[1040;0];Aeq=[ ];beq=[ ];vlb=[0;0];vub=[ ];[x,-z]=quadprog(H,c,A,b,Aeq,beq,vlb,vub) 运用K-T 条件求解:12()(0.6100,0.480)Tf x x x ∇=--12112211221212()(2,4),()(5,4)0.6100250.480440(24)0(54)0,0T Tg x g x x x x x x x μμμμμμ∇=∇=--⎛⎫⎛⎫⎛⎫⎛⎫--= ⎪ ⎪ ⎪ ⎪--⎝⎭⎝⎭⎝⎭⎝⎭+=-=>=解得12120,0,500/3,200x x μμ====,f=16333.3法二:用线性化方法求解:给定初始可行点1(150,185)T X =步长限制stepsize: 1algorithm: 'medium-scale: SQP , Quasi-Newton, line-search'firstorderopt: 10.0000cgiterations: []message: [1x130 char]5.钢管下料问题 某钢管零售商从钢管厂进货,将钢管按照顾客的要求切割出售。
数学建模作业43508
数学建模作业1、在甲乙双方的一场战争中,部分甲方部队被乙方部队包围长达4个月,乙方封锁了所有水陆交通通道,因此被包围的甲方只能依靠空中交通维持补给,运送4个月的供给依此分别需要2次、3次、3次、4次飞行,每次飞行编队由50架飞机组成,每架飞机都需要3名飞行员,每架飞机每月只能飞行一次,每名飞行员每月也只能飞行一次,每次执行完运输飞行任务后的返回途中有20%的飞机被乙方部队击落,导致机上的飞行员也牺牲或失踪。
在第一个月开始时,甲方拥有110架飞机和330名熟练的飞行员,每个月开始时,甲方可以招聘新飞行员和购买新飞机,新飞机必须经过一个月的检查磨合后才可以投入使用,新飞行员也必须在熟练飞行员的指导下经过一个月的训练才能成为熟练飞行员而投入飞行(作为教练的熟练飞行员本月不能参与飞行任务),每名熟练飞行员作为教练每月指导20名飞行员(包括自己在内)进行训练,每名飞行员在完成本月的飞行任务后必须有一个月的带薪休假,然后返回待命可再次投入飞行,已知各项费用平均单价如下表所示(单位:千元)。
第一个月第二个月第三个月第四个月新飞机价格200 195 190 185闲置的熟练飞行员报酬7 6.9 6.8 6.710 9.9 9.8 9.7教练及飞行员报酬和训练费用执行飞行任务的飞行员报9 8.9 9.8 9.7酬休假期的飞行员报酬 5 4.9 4.8 4.7(1)为甲方安排一个总费用最小的飞行计划。
(2)如果每名熟练飞行员作为教练每月指导不超过20名飞行员(包括自己在内)进行训练,相应的模型和安排将会发生怎样的改变?解:(1)设每月初购买飞机数量为d1,d2,d3,d4架,每月闲置飞机数量为y1,y2,y3,y4架,每月教练与新飞行员总数量为a1,a2,a3,a4人,每月闲置熟练飞行员的数量为b1,b2,b3,b4人。
由于每月执行任务的飞行员和休假期的飞行员的数量是固定的,即这部分的花费是固定的,所以在优化目标中可以不必考虑。
计算机导论作业第三次
计算机导论作业第3次1、关于计算系统与程序,下列说法正确的是_____。
(A)只有用计算机语言编写出来的代码才是程序,其他都不能称其为程序;(B)构造计算系统是不需要程序的,程序对构造计算系统没有什么帮助;(C)任何系统都需要程序,只是这个程序是由人来执行还是由机器自动执行,可以由机器自动执行程序的系统被称为计算系统;(D)程序是用户表达的随使用者目的不同而千变万化的复杂动作,不是使用者实现的而是需要计算系统事先完成的。
2、关于程序,下列说法不正确的是_____。
(A)“程序”是由人编写的、以告知计算系统实现人所期望的复杂动作;(B)“程序”可以由系统自动解释执行,也可以由人解释由系统执行;(C)普通人是很难理解“程序”的,其也和“程序”无关;(D)“程序”几乎和每个人都有关系,如自动售票系统、自动取款机等。
3、关于程序,下列说法不正确的是_____。
(A)程序的基本特征是复合、抽象与构造;(B)复合就是对简单元素的各种组合,即将一个(些)元素代入到另一个(些)元素中;(C)抽象是对各种元素的组合进行命名,并将该名字用于更复杂的组合构造中;(D)程序就是通过组合、抽象、再组合等构造出来的;(E)上述说法有不正确的。
4、关于“递归”,下列说法不正确的是_____。
(A)“递归”源自于数学上的递推式和数学归纳法。
(B)“递归”与递推式一样,都是自递推基础计算起,由前项(第n-1项)计算后项(第n项),直至最终结果的获得。
(C)“递归”是自后项(即第n项)向前项(第n-1项)代入,直到递归基础获取结果,再从前项计算后项获取结果,直至最终结果的获得;(D)“递归”是由前n-1项计算第n项的一种方法。
5、关于“程序”和“递归”的关系,下列说法不正确的是_____。
(A) “程序”是计算系统体现千变万化功能的一种重要手段:计算系统仅需要实现简单元素以及一个程序执行机构即可;(B) 本质上章,“程序”就是对简单元素的组合(或称复合);此外,“程序”需要有能力对一些常见的组合A进行命名,并利用该名字参与更为复杂的组合B的构造中,此即为“抽象”;在执行时(或称计算时),再将该组合A替换组合B中的该名字,实现计算并获取结果;(C) “程序”的基本特征是复合、抽象与构造。
数学建模全部作业
一、图论(组合优化)和排列论实验解:设cij表示i年开始到j-1年结束购车的总消费,则有:C12=2.5+0.3-2.0=0.8,C13=2.5+0.3+0.5-1.6=1.7,C14=2.5+0.3+0.5+0.8-1.3=2 .8,C15=2.5+0.3+0.5+0.8+1.2-1.1=4.2,C23=2.6+0.3-2.0=0.9,C24=2.6+0.3+0. 5-1.6=1.8,C25=2.6+0.3+0.5+0.8-1.3=2.9,C34=2.8+0.3-2.0=1.1,C35=2.8+0.3 +0.5-1.6=2,C45=3.1+0.3-2.0=1.4;建模如下:sets:nodes/1..5/;arcs(nodes, nodes)|&1 #lt# &2: c, x;endsetsdata:c = 0.8 1.7 2.8 4.20.9 1.8 2.91.12.01.4;enddatan = @size(nodes);min = @sum(arcs: c * x);@for(nodes(i)| i #ne# 1 #and# i #ne# n:@sum(arcs(i,j): x(i,j)) = @sum(arcs(j,i): x(j,i)));@sum(arcs(i,j)| i #eq# 1 : x(i,j)) = 1;LINGO运行如下:Global optimal solution found.Objective value: 3.700000Total solver iterations: 0Variable Value Reduced CostX( 1, 2) 1.000000 0.000000X( 2, 5) 1.000000 0.000000由计算结果分析可得,其最短路径为1->2->5,最小花费为3.7万元。
即:该单位应该在第一年购买新设备,年末卖掉设备;第二年初更换新设备,一直用到第四年年末,再卖出。
《数学建模》作业
要求1、选题要求,学号是1号的选A组第1题,2号选A组第2题,以此类推,15号选A组第15题,16号回头选A组第1题。
如果对上面的题目把握不大或不敢兴趣的,可以在B组题目中任选一题。
2、答卷论文内容包括:摘要(100——300字,含研究的问题、建模的方法及模型、模型解法和主要结果),问题分析与假设,符号说明,问题分析,模型建立,计算方法设计和实现(框图及计算机输出的计算结果),结果的分析和检验,优缺点和改进方向等。
用软件求解的,请在附件中附上算法程序。
3、论文(答卷)用白色A4纸,上下左右各留出2.5厘米的页边距。
4、第一页为封面(自己下载),写上学号、姓名、第二页为论文标题和摘要,从第三页开始是论文正文。
论文从第二页开始编写页码,页码必须位于每页页脚中部,用阿拉伯数字从“1”开始连续编号。
5、论文题目用3号黑体字、一级标题用4号黑体字,并居中。
论文中其他汉字一律采用小4号宋体字,行距用单倍行距。
6、引用别人的成果或其他公开的资料(包括网上查到的资料) 必须按照规定的参考文献的表述方式在正文引用处和参考文献中均明确列出。
正文引用处用方括号标示参考文献的编号,如[1][3]等;引用书籍还必须指出页码。
参考文献按正文中的引用次序列出,其中书籍的表述方式为:[编号] 作者.书名[M].出版地:出版社,出版年参考文献中期刊杂志论文的表述方式为:[编号] 作者.论文名[J].杂志名,卷期号:起止页码,出版年参考文献中网上资源的表述方式为:[编号] 作者.资源标题.网址,访问时间(年月日)。
论文提交:2015年5月(本学期第11周)论文打印装订成册上交注:2015年5月(本学期第11,12周)答辩大作业题目A组1、生产计划高校现有一笔资金100万元,现有4个投资项目可供投资。
项目A:从第一年到底四年年初需要投资,并于次年年末回收本利115%。
项目B:从第三年年初需要投资,并于第5年末才回收本利135%,但是规定最大投资总额不超过40万元。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2、如果连续复利时,以什么利率才能使本金在8年内变成3倍? 3、连续收益流量每年按80万元持续5年,若以年利率5%贴现,其 现值应是多少?
4、一位居民想买一栋别墅,现价为300万元,如以分期付款方式
购买,每年需付21万,20年付清。银行存款利率为4%,如何付款 才合算? 5、推导期初产生资金的离散型资金流的终值和现值公式 6、 设某10年期面值为1000元的国债,利率为5%,国债投资者每年在 付息日都会收到50元利息,并在第1算投资者的终值和现值。
7、 购买设备A,花费80000元,设备使用年限5年,现金流依次为 [-80000,25000,15000,30000,10000,20000], 1)、如果对于企业来说投资的必要收益率为8%,计算净现值(NPV); 2)、计算内部收益率(IRR)。
