2013─2018新课标理科数学函数与导数解答题

合集下载

2018年高考真题汇编(函数与导数)

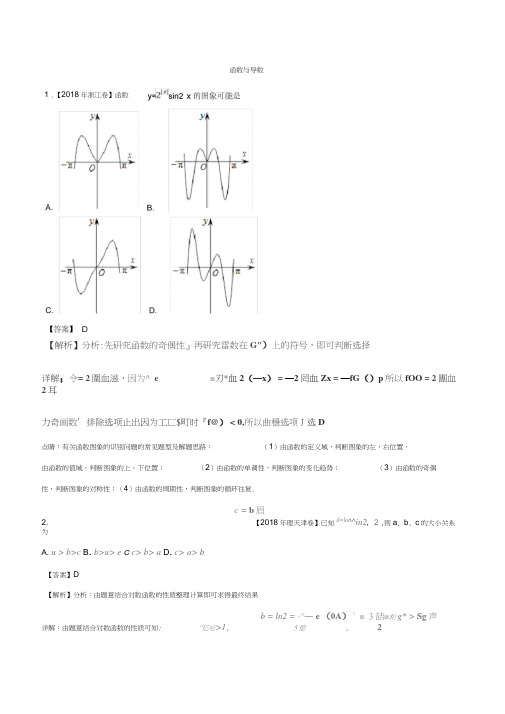
函数与导数1 .【2018年浙江卷】函数【解析】分析:先研究函数的奇偶性』再研究雷数在G"）上的符号，即可判断选择详解；令= 2圍血滋，因为^ e =刃*血2（—x） = —2罔血Zx = —fG（）p所以fOO = 2團血2耳力奇画数’排除选项止出因为工匸$町时『f@） < 0,所以曲穩选项J选D点睛：有关函数图象的识别问题的常见题型及解题思路：（1）由函数的定义域，判断图象的左、右位置，由函数的值域，判断图象的上、下位置；（2）由函数的单调性，判断图象的变化趋势；（3）由函数的奇偶性，判断图象的对称性；（4）由函数的周期性，判断图象的循环往复.c = b眉2. 【2018年理天津卷】已知il=lo^^in2, 2 ,则a, b, c的大小关系为A. u > b>cB.b>u> e C c> b> a D.c> a> b【答案】D【解析】分析：由题意结合对数函数的性质整理计算即可求得最终结果b = ln2 = -^―e （0A）c= 3詰=和g* > Sg声详解：由题意结合对数函数的性质可知: "忆吆>1, 5慾, 2据此可得：•本题选择D选项.点睛：对于指数幕的大小的比较，我们通常都是运用指数函数的单调性，但很多时候，因幕的底数或指数不相同，不能直接利用函数的单调性进行比较•这就必须掌握一些特殊方法•在进行指数幕的大小比较时，若底数不同，则首先考虑将其转化成同底数，然后再根据指数函数的单调性进行判断•对于不同底而同指数的指数幕的大小的比较，利用图象法求解，既快捷，又准确.龙兰0*3. 【2018年理新课标I卷】已知函数I曲乩北〉心饥巧二“/) + +a .若g (x)存在2个零点，则a的取值范围是A. [ - 1, 0)B. [0 , +R)C. [ - 1 , +R)D. [1 , +R)【答案】C【解析】分析；首先根据存在2个零点，得到方程f CO十""哨两个亀将其转化为金〉二-覽-口有两个解，即直线y =-第-诣曲^二fCO有两个交点”根据題中所给的函数解析式，画出函数f何的團像(将町4掉A再画出直绳=-补并将其上下移动』从图中可臥发现走丄时/龊7=-電-口与曲线y=f^＞有两个玄点'从而求得结果.详解：画出函数的图像，7■-了在y轴右侧的去掉，再画出直线卜:讨，之后上下移动，可以发现当直线过点A时，直线与函数图像有两个交点，并且向下可以无限移动，都可以保证直线与函数的图像有两个交点，即方程■有两个解，也就是函数有两个零点，此时满足，即• ，故选C.点睛：该题考查的是有关已知函数零点个数求有关参数的取值范围问题，在求解的过程中，解题的思路是将函数零点个数问题转化为方程解的个数问题，将式子移项变形，转化为两条曲线交点的问题，画出函数的图像以及相应的直线，在直线移动的过程中，利用数形结合思想，求得相应的结果4. 【2018年理新课标I卷】设函数兀心--，若$叩为奇函数，则曲线：在点’ 处的切线方程为A.卜「阙B. H" - '■ - -IC."划D.【答案】D【解析】分析；利用奇函数偶此项系数为零求得"X进而得到的解析式，再对“）求导得出桩戋的斜率©进而求得切线方程.详解；因豹画数雇苛函数J 解得"二4所以』⑴二卯1,门>）二阪y 所臥厂◎二九代町二g所汰曲线y二厲刃在点（啦处的切线方程为y-m））二比建简可得y二知故选D点睛：该题考查的是有关曲线卜在某个点凤煮強；；|处的切线方程的问题，在求解的过程中，首先需要确定函数解析式，此时利用到结论多项式函数中，奇函数不存在偶次项，偶函数不存在奇次项，从而求得相应的参数值，之后利用求导公式求得帀，借助于导数的几何意义，结合直线方程的点斜式求得结果•5. 【2018年全国卷川理】设“=』0目仇2°収，方=衍的帖，贝UA. N + bunbcOB.C. u + bcOca/iD. kb<OCQ +市【答案】B1 i I 11【解析】分析：求出-= io^^ 2t-=lo^.32,得到- +二的范围，进而可得结果。

2018年高考理科数学全国卷二导数压轴题解析

2018年高考理科数学全国卷二导数压轴题解析已知函数2()x f x e ax =-.（1）若1a =，证明：当0x ≥时，()1f x ≥. （2）若()f x 在(0,)+∞只有一个零点，求a . 题目分析：本题主要通过函数的性质证明不等式以及判断函数零点的问题考察学生对于函数单调性以及零点存在定理性的应用，综合考察学生化归与分类讨论的数学思想，题目设置相对较易，利于选拔不同能力层次的学生。

第1小问，通过对函数以及其导函数的单调性以及值域判断即可求解。

官方标准答案中通过()()x g x e f x -=的变形化成2()x ax bx c e C -+++的形式，这种形式的函数求导之后仍为2()x ax bx c e -++这种形式的函数，指数函数的系数为代数函数，非常容易求解零点，并且这种变形并不影响函数零点的变化。

这种变形思想值得引起注意，对以后导数命题有着很大的指引作用。

但是，这种变形对大多数高考考生而言很难想到。

因此，以下求解针对函数()f x 本身以及其导函数的单调性和零点问题进行讨论，始终贯穿最基本的导函数正负号与原函数单调性的关系以及零点存在性定理这些高中阶段的知识点，力求完整的解答该类题目。

题目解答：（1）若1a =，2()x f x e x =-，()2x f x e x '=-，()2x f x e ''=-.当[0,ln 2)x ∈时，()0f x ''<，()f x '单调递减；当(ln 2,)x ∈+∞时，()0f x ''>，()f x '单调递增；所以()(ln 2)22ln 20f x f ''≥=->，从而()f x 在[0,)+∞单调递增；所以()(0)1f x f ≥=，得证. （2）当0a ≤时，()0f x >恒成立，无零点，不合题意.当0a >时，()2x f x e ax '=-，()2x f x e a ''=-.当[0,ln 2)x a ∈时，()0f x ''<，()f x '单调递减；当(ln 2,)x a ∈+∞时，()0f x ''>，()f x '单调递增；所以()(ln 2)2(1ln 2)f x f a a a ''≥=-.当02ea <≤时，()0f x '≥，从而()f x 在[0,)+∞单调递增，()(0)1f x f ≥=，在(0,)+∞无零点，不合题意.当2ea >时，易证2ln 2a a >. (0)10f '=>，(ln 2)0f a '<，由（1）可知，22(2)=(2)10a f a e a '->>.由零点存在性定理可知必然存在一点1(0,ln 2)x a ∈使得1()0f x '=，2(ln 22)x a a ∈，使得2()0f x '=；所以当1(0,)x x ∈时，()0f x '>，()f x 单调递增，12(,)x x x ∈，()0f x '<，()f x 单调递减，2(,)x x ∈+∞，()0f x '>，()f x 单调递增，即当2x x =时()f x 取得极小值2222()x f x e ax =-由2()0f x '=得222x e a x = 从而222222()(2)2x x e f x e ax x =-=-当22x =时，即24e a =时，极小值2()0f x =恰好成立，此时在()f x 在(0,)+∞只有一个零点2x =，满足题意.当224e e a <<时，即212x <<时（易证2xe x在(1,)+∞单调递增），极小值2()0f x >，此时在(0,)+∞无零点，不合题意.x当24e a >时，即22x >时，(0)10f =>，2()0f x <， 32(3)(3)0a f a e a a =-> （易证313x e x >恒成立），由零点存在性定理可知()f x 在区间2(0,)x 和2(,3)x a 各有一根，不合题意.综上所述，24e a =.。

2018年全国各地高考数学试题及解答分类大全(导数及其应用)

2
（2）方法一：由（1）得 f x ax2 a 1 x 1 ex ax 1 x 1 ex ．
若
a
1 ，则当
x
1 a
,1
时，
f
x
0
；当
x
1,
时，
f
x
0
．
所以 f x 在 x 1处取得极小值．
若 a 1，则当 x 0,1 时， ax 1 x 1 0 ， f x 0 ．所以 1 不是 f x 的极小值点．综上可知， a 的取值范围是 1, ．
第 4页（共 12页）
4．（2018 浙江）已知函数 f(x)= x −lnx．（Ⅰ）若 f(x)在 x=x1，x2(x1≠x2)处导数相等，证明：f(x1)+f(x2)>8−8ln2；（Ⅱ）若 a≤3−4ln2，证明：对于任意 k>0，直线 y=kx+a 与曲线 y=f(x)有唯一公共点．
2
2
所以 2 不是 f x 的极小值点．
综上可知，
a
的取值范围是
1 2
,
．
3．（2018 江苏）记 f (x), g(x) 分别为函数 f (x), g(x) 的导函数．若存在 x0 R ，满足 f (x0 ) g(x0 ) 且 f (x0 ) g(x0 ) ，则称 x0 为函数 f (x) 与 g(x) 的一个“S 点”．
4．.答案：（1）略；（2）略.
解答：（1）
f
( x)
1 2x
1 x
，不妨设
f
( x1 )
f
(x2 )
t ，即 x1, x2 是方程
1 2x
1 x
t 的两
根，即
x1 ,

2010-2018年全国新课标卷(ⅠⅡⅢ卷)理科数学试题分类汇编——03、导数及其应用

2010-2018年全国新课标卷（ⅠⅡⅢ卷）理科数学试题分类汇编03、导数及其应用一、选择题与填空题.【2010年新课标卷，3】曲线2xy x =+在点()1,1--处的切线方程为（）（A ）21y x =+ （B ）21y x =- （C ）23y x =-- （D ）22y x =--【答案】A 【解析】''122,|2(2)x y k y x =-=∴==+，切线方程为[](1)2(1)y x --=--，即21y x =+. 【2011年新课标卷，9】由曲线y ，直线2y x =-及y 轴所围成的图形的面积为( ) （A ）103 （B ）4 （C ）163（D ）6【答案】C【解析】用定积分求解432420021162)(2)|323s x dx x x x =+=-+=⎰，选C【2012年新课标卷，12】设点P 在曲线12xy e =上，点Q 在曲线ln(2)y x =上，则||PQ 的最小值为（） A ．1ln 2-B ln 2)-C ．1ln 2+D ln 2)+【答案】B【解析】函数12xy e =与函数ln(2)y x =互为反函数，图象关于y x =对称函数12x y e =上的点1(,)2x P x e 到直线y x =的距离为d=设函数m i n m i 112()()1()1l n 222x x g x e x g x e g x d '=-⇒=-⇒=-⇒=由图象关于y x =对称得：PQ 最小值为m i n 2(1l n 2)d -, 【2013年新课标Ⅰ卷，16】若函数f (x )＝(1－x 2)(x 2＋ax ＋b )的图像关于直线x ＝－2对称，则f (x )的最大值为__________．【答案】16【解析】∵函数f (x )的图像关于直线x ＝－2对称，∴f (x )满足f (0)＝f (－4)，f (－1)＝f (－3)，即15164,0893,b a b a b =-(-+)⎧⎨=-(-+)⎩解得8,15.a b =⎧⎨=⎩∴f (x )＝－x 4－8x 3－14x 2＋8x ＋15. 由f ′(x )＝－4x 3－24x2－28x ＋8＝0，得x 1＝－2x 2＝－2，x 3＝－2易知，f (x )在(－∞，－2上为增函数，在(－22)上为减函数，在(－2，－2上为增函数，在(－2∞)上为减函数．∴f (－2＝[1－(－2－2][(－22＋8(－2＋15]＝(－8－－＝80－64＝16.f (－2)＝[1－(－2)2][(－2)2＋8×(－2)＋15]＝－3(4－16＋15)＝－9.f (－2＝[1－(－22][(－22＋8(－2＋15]＝(－8＋＋＝80－64＝16. 故f (x )的最大值为16.【2013年新课标Ⅱ卷，10】已知函数32()f x x ax bx c =+++，下列结论中错误的是（）A.00,()0x f x ∃∈=RB.函数()y f x =的图像是中心对称图形C.若0x 是()f x 的极小值点，则()f x 在区间0(,)x -∞单调递减D.若0x 是()f x 的极值点，则0()0f x '= 【答案】C【解析】∵f ´(x )=3x 2+2ax +b ，∴y ＝f (x )的图像大致如右图所示，若x 0是f (x )的极小值点，则则在(－∞，x 0)上不单调，故C 不正确．【2014年新课标Ⅰ卷，11】已知函数()f x =3231ax x -+，若()f x 存在唯一的零点0x ，且0x ＞0，则a 的取值范围为（）A .（2，+∞）B .（-∞，-2）C .（1，+∞）D .（-∞，-1）【答案】B【解析1】由已知0a ≠，2()36f x ax x '=-，令()0f x '=，得0x =或2x a=，当0a >时，()22,0,()0;0,,()0;,,()0x f x x f x x f x a a ⎛⎫⎛⎫'''∈-∞>∈<∈+∞> ⎪ ⎪⎝⎭⎝⎭；且(0)10f =>，()f x 有小于零的零点，不符合题意．当0a <时，()22,,()0;,0,()0;0,,()0x f x x f x x f x a a ⎛⎫⎛⎫'''∈-∞<∈>∈+∞< ⎪ ⎪⎝⎭⎝⎭要使()f x 有唯一的零点0x 且0x ＞0，只需2()0f a>，即24a >，2a <-．选B 【解析2】由已知0a ≠，()f x =3231ax x -+有唯一的正零点，等价于3113a x x =- 有唯一的正零根，令1t x=，则问题又等价于33a t t =-+有唯一的正零根，即y a =与33y t t =-+有唯一的交点且交点在在y 轴右侧记3()3f t t t =-+，2()33f t t '=-+，由()0f t '=，1t =±，()(),1,()0;1,1,()0;t f t t f t ''∈-∞-<∈->，()1,,()0t f t '∈+∞<，要使33a t t =-+有唯一的正零根，只需(1)2a f <-=-，选B【2014年新课标Ⅱ卷，8】设曲线y =ax -ln(x +1)在点(0,0)处的切线方程为y =2x ，则a =（）A ．0B ．1C ．2D ．3【答案】D 【解析】∵1'1y a x =-+，且在点(0,0)处的切线的斜率为2，∴01'|201x y a ==-=+，即3a =.【2014年新课标Ⅱ卷，12】设函数()x f x mπ=，若存在()f x 的极值点0x 满足22200[()]x f x m +<，则m 的取值范围是（）A ．(,6)(6,+)-∞-∞UB ．(,4)(4,+)-∞-∞UC ．(,2)(2,+)-∞-∞UD ．(,1)(4,+)-∞-∞U 【答案】C【解析】∵()xf x mπ'=，令()0xf x m π'==得1(),2x m k k Z =+∈， ∴01(),2x m k k Z =+∈，即01|||||()|22m x m k =+≥，mxx f πsin 3)(= 的极值为3±，∴3)]([20=x f ，，34)]([22020+≥+∴m x f x 22200[()]x f x m +<， 2234∴m m <+，即：24m >，故：2m <-或2m >.【2015年新课标Ⅰ卷，12】设函数()f x =(21)x e x ax a --+,其中1a <，若存在唯一的整数0x ，使得0()0f x <，则a 的取值范围是（）A ．3,12e ⎡⎫-⎪⎢⎣⎭ B ． 33,2e 4⎡⎫-⎪⎢⎣⎭ C ． 33,2e 4⎡⎫⎪⎢⎣⎭ D ． 3,12e ⎡⎫⎪⎢⎣⎭【答案】D【解析】设()g x =(21)x e x -，y ax a =-，由题知存在唯一的整数0x ，使得0()g x 在直线y ax a =-的下方.因为()(21)x g x e x '=+，所以当12x <-时，()g x '＜0，当12x >-时，()g x '＞0，所以当12x =-时，min [()]g x =122e --，当0x =时，(0)1g =-，(1)30g e =>，直线y ax a =-恒过（1,0）斜率且a ，故(0)1a g ->=-，且1(1)3g e a a --=-≥--，解得32e≤a ＜1，故选D ．. 作为选择题，该题也可先找到满足0()0f x <的整数0x ，由0x 的唯一性列不等式组求解.由(0)10f a =-+<得00x =.又0x 是唯一使()0f x <的整数，所以(1)0(1)0f f -≥⎧⎨≥⎩，解得32a e ≥，又1a <，且34a =时符合题意.故选D ．. 【2015年新课标Ⅱ卷，12】设函数()f x '是奇函数()()f x x R ∈的导函数，(1)0f -=，当x >0时，()()0xf x f x '-<，则使得f (x ) >0成立的x 的取值范围是（） A ．(,1)(0,1)-∞-UB ．(1,0)(1,)-+∞UC ．(,1)(1,0)-∞--UD ．(0,1)(1,)+∞U【答案】A【解析】记函数()()f x g x x =，则2()()()x f x f x g x x '-'=，因为当x >0时，xf ´(x )-f (x )<0，故当x >0时，g ´ (x )<0，所以g (x )在(0, +∞)单调递减；又因为函数f (x )(x ∈R )是奇函数，故函数g (x )是偶函数，所以g (x )在(-∞, 0)单调递增，且g (-1)=g (1)=0．当0<x <1时，g (x )>0，则f (x )>0；当x <-1时，g (x )<0，则f (x )>0，综上所述，使得f (x )>0成立的x 的取值范围是(-∞, -1)∪(0, 1)，故选A ．【2016年新课标Ⅱ卷，16】若直线y = kx +b 是曲线y = ln x +2的切线，也是曲线y = ln(x +1)的切线，则b = . 【答案】1ln2-【解析】ln 2y x =+的切线为：111ln 1y x x x =⋅++（设切点横坐标为1x ），()ln 1y x =+的切线为：()22221ln 111x y x x x x =++-++，∴()122122111ln 1ln 11x x x x x x ⎧=⎪+⎪⎨⎪+=+-⎪+⎩，解得112x = 212x =-，∴1l n 11l n 2b x =+=-．【2016年新课标Ⅲ卷，15】已知()f x 为偶函数，当0x <时，()ln()3f x x x =-+，则曲线()y f x =在点(1,3)-处的切线方程是_______________．【答案】21y x =--【解析】当0x >时，0x -<，则()ln 3f x x x -=-．又因为()f x 为偶函数，所以()()ln 3f x f x x x =-=-，所以1()3f x x '=-，则切线斜率为(1)2f '=-，所以切线方程为32(1)y x +=--，即21y x =--．【2017年新课标Ⅰ卷，16】如图，圆形纸片的圆心为O ，半径为5 cm ，该纸片上的等边三角形ABC 的中心为O ．D 、E 、F 为圆O 上的点，△DBC ，△ECA ，△FAB 分别是以BC ，CA ，AB 为底边的等腰三角形．沿虚线剪开后，分别以BC ， CA ，AB 为折痕折起△DBC ，△ECA ，△FAB ，使得D ，E ，F 重合，得到三棱锥．当△ABC 的边长变化时，所得三棱锥体积（单位：cm 3）的最大值为_______．【答案】【解析】由题，连接OD ，交BC 与点G ，由题，OD BC ⊥，OG =，即OG 的长度与BC 的长度或成正比，设OG x =，则BC =，5DG x =-，三棱锥的高h =2132ABC S x =⋅=△，则213ABC V S h =⋅=△令()452510f x x x =-，5(0,)2x ∈，()3410050f x x x '=-，令()0f x '>，即4320x x -<，2x <，则()()280f x f =≤，则45V ，∴体积最大值为3．【2017年新课标Ⅱ卷，11】若2x =-是函数21`()(1)x f x x ax e -=+-的极值点，则()f x 的极小值为（）A.1-B.32e -- C.35e - D.1【2018年新课标Ⅰ卷，16】已知函数()2sin sin2f x x x =+，则()f x 的最小值是______．【答案】2-【解析】易知()f x 的最小正周期为2T π=，则问题转化求()f x 在[]0,2π的最小值.()2sin sin 2f x x x =+'2()2cos 2cos22cos 2(2cos 1)f x x x x x ∴=+=+-22(2cos cos 1)2(cos 1)(2cos 1)x x x x =+-=+-令cos (11)t x t =-≤≤，则'()2(1)(21)f x t t =+- 令'()0f x =，得112t t =-=或 ∴当112t -≤<时，'()0f x ≤，()f x 单调递减；当112t <≤时，'()0f x >，()f x 单调递增. ∴当12t =时，()f x 取得最小值，此时15cos 233x x x ππ=⇒==或又2()2sin sin 333f πππ=+=5510()2sin sin 333f πππ=+=min ()f x ∴= 【2018年新课标Ⅱ卷，13】曲线2ln(1)y x =+在点(0,0)处的切线方程为__________．【答案】2y x =【解析】21y x '=+Q ，2201k ∴==+，2y x ∴=．【2018年新课标Ⅲ卷，14】曲线()1e x y ax =+在点()01，处的切线的斜率为2-，则a =______．【答案】3-【解析】(1)x x y ae ax e =+，则(0)12f a '=+=-，所以3a =-.二、解答题.【2010年新课标卷，21】设函数f(x)=21x e x ax ---. （Ⅰ)若a=0,求f(x)的单调区间;（Ⅱ）若当x≥0时f(x)≥0，求a 的取值范围.解：（I ）0a =时，()1x f x e x =--，'()1x f x e =-当(,0)x ∈-∞时，'()0f x <，当(0,)x ∈+∞时，'()0f x > 故()f x 在(,0)-∞上单调递减，在(0,)+∞单调递增（II ）'()12x f x e ax =--由（I ）可知1xe x ≥+，当且仅当0x =时等号成立，故 '()2(12)f x x ax a x ≥-=-∴当120a -≥，即12a ≤时，'()0(0)f x x ≥≥， (0)0f =∴当0x ≥时，()0f x ≥由1(0)xe x x >+≠可得1(0)xe x x ->-≠则当12a >时，'()12(1)(1)(2)x x x x xf x e a e e e e a --<-+-=-- ∴当(0,ln 2)x a ∈时，'()0f x <，而(0)0f = ∴当(0,ln 2)x a ∈时，()0f x <综上得a 的取值范围为1(,]2-∞【2011年新课标卷，21】已知函数ln ()1a x bf x x x=++，曲线()y f x =在点(1,(1))f 处的切线方程为230x y +-=．（Ⅰ）求a 、b 的值；（Ⅱ）如果当0x >，且1x ≠时，ln ()1x kf x x x>+-，求k 的取值范围．解：（I ）()()221ln 1x a x b x f x x x +⎛⎫- ⎪⎝⎭'=-+ 由于直线230x y +-=的斜率为12-，且过点()1,1，故()()11112f f =⎧⎪⎨'=-⎪⎩，即1122b a b =⎧⎪⎨-=-⎪⎩，解得1a =，1b =.（II ）由（I ）知()ln 11x f x x x =++，所以()()()2211ln 12ln 11k x x k f x x x x x x ⎛⎫--⎛⎫ ⎪-+=+ ⎪ ⎪--⎝⎭⎝⎭考虑函数()()()()2112ln 0k x h x x x x--=+>，则()()()22112k x xh x x -++'=（i ）设0k ≤，由()()()22211k x x h x x +--'=知，当1x ≠时，()0h x '<. 而()10h =，故当()0,1x ∈时，()0h x <，可得()2101h x x >-；当()1,x ∈+∞时，()0h x <，可得()2101h x x >- 从而当0x >，且1x ≠时，()ln 01x k f x x x ⎛⎫-+> ⎪-⎝⎭，即()ln 1x k f x x x ⎛⎫>+ ⎪-⎝⎭.（ii ）设01k <<，由于当11,1x k ⎛⎫∈ ⎪-⎝⎭时，()()21120k x x -++>，故()0h x '>，而()10h =，故当11,1x k ⎛⎫∈ ⎪-⎝⎭时，()0h x >，可得()2101h x x <-，与题设矛盾. （iii ）设1k ≥，此时()0h x '>，而()10h =，故当()1,x ∈+∞时，()0h x >，得()2101h x x <-，与题设矛盾. 综合得，k 的取值范围为(],0-∞.【2012年新课标卷，21】已知函数)(x f 满足2121)0()1(')(x x f e f x f x +-=-．（1）求)(x f 的解析式及单调区间；（2）若b ax x x f ++≥221)(，求b a )1(+的最大值．解：（1）因为2121)0()1(')(x x f e f x f x +-=-，所以1'()'(1)(0)x f x f e f x -=-+，所以1(0)'(1)'(1)'(1)(0)1f f ef f f ⎧=⋅⎪⎨⎪=-+⎩，解得(0)1f =，'(1)f e =．所以)(x f 的解析式为21()2xf x e x x =-+，由此得'()1x f x e x =-+．而'()1x f x e x =-+是R 上的增函数，且'(0)0f =，因此，当(0,)x ∈+∞时，'()'(0)0f x f >=，)(x f 在(0,)+∞上是增函数；当(,0)x ∈-∞时，'()'(0)0f x f <=，)(x f 在(,0)-∞上是减函数．综上所述，函数)(x f 的增区间为(0,)+∞，减区间为(,0)-∞．（2）由已知条件得(1)x e a x b -+≥． ①（i ）若10a +<，则对任意常数b ，当0x <，且11bx a -<+，可得(1)x e a x b -+<，因此①式不成立．（ii ）若10a +=，则(1)0a b +=．（iii ）若10a +>，设()(1)x g x e a x =-+，则'()(1)x g x e a =-+．当(,ln(1))x a ∈-∞+，'()0g x <；当(ln(1),)x a ∈++∞，'()0g x > 从而()g x 在(,ln(1))a -∞+单调递减，在(ln(1),)a ++∞单调递增．所以b ax x x f ++≥221)(等价于1(1)ln(1)b a a a ≤+-++． ② 因此22(1)(1)(1)ln(1)a b a a a +≤+-++．设22()(1)(1)ln(1)h a a a a =+-++，则'()(1)(12ln(1))h a a a =+-+．所以()h a 在12(1,1)e --单调递增，在12(1,)e -+∞单调递减，故()h a 在121a e =-在处取得最大值，从而()2e h a ≤，即(1)2e a b +≤．当121a e =-，122e b =时，②式成立，故b ax x x f ++≥221)(．综合得，b a )1(+的最大值为2e．【2013年新课标Ⅰ卷，21】设函数f (x )＝x 2＋ax ＋b ，g (x )＝e x (cx ＋d )．若曲线y ＝f (x )和曲线y ＝g (x )都过点P (0,2)，且在点P 处有相同的切线y ＝4x ＋2.(1)求a ，b ，c ，d 的值；(2)若x ≥－2时，f (x )≤kg (x )，求k 的取值范围．解：(1)由已知得f (0)＝2，g (0)＝2，f ′(0)＝4，g ′(0)＝4.而f ′(x )＝2x ＋a ，g ′(x )＝e x (cx ＋d ＋c )，故b ＝2，d ＝2，a ＝4，d ＋c ＝4.从而a ＝4，b ＝2，c ＝2，d ＝2.(2)由(1)知，f (x )＝x 2＋4x ＋2，g (x )＝2e x (x ＋1)．设函数F (x )＝kg (x )－f (x )＝2k e x (x ＋1)－x 2－4x －2，则F ′(x )＝2k e x (x ＋2)－2x －4＝2(x ＋2)(k e x －1)．由题设可得F (0)≥0，即k ≥1.令F ′(x )＝0得x 1＝－ln k ，x 2＝－2.①若1≤k ＜e 2，则－2＜x 1≤0.从而当x ∈(－2，x 1)时，F ′(x )＜0；当x ∈(x 1，＋∞)时，F ′(x )＞0.即F (x )在(－2，x 1)单调递减，在(x 1，＋∞)单调递增．故F (x )在[－2，＋∞)的最小值为F (x 1)．而F (x 1)＝2x 1＋2－21x －4x 1－2＝－x 1(x 1＋2)≥0.故当x ≥－2时，F (x )≥0，即f (x )≤kg (x )恒成立．②若k ＝e 2，则F ′(x )＝2e 2(x ＋2)(e x －e －2)．从而当x ＞－2时，F ′(x )＞0，即F (x )在(－2，＋∞)单调递增．而F (－2)＝0，故当x ≥－2时，F (x )≥0，即f (x )≤kg (x )恒成立．③若k ＞e 2，则F (－2)＝－2k e －2＋2＝－2e －2(k －e 2)＜0. 从而当x ≥－2时，f (x )≤kg (x )不可能恒成立．综上，k 的取值范围是[1，e 2]．【2013年新课标Ⅱ卷，21】已知函数()ln()x f x e x m =-+. （Ⅰ）设0x =是()f x 的极值点，求m ，并讨论()f x 的单调性；（Ⅱ）当2m ≤时，证明()0f x >. 解：（Ⅰ）f ′(x )＝1xe x m-+. 由x ＝0是f (x )的极值点得f ′(0)＝0，所以m ＝1. 于是f (x )＝e x -ln(x +1)，定义域为(-1，+∞)，f ′(x )＝11x e x -+.函数f ′(x )＝11xe x -+在(-1，+∞)单调递增，且f ′(0)＝0.因此当x ∈(-1,0)时，f ′(x )＜0；当x ∈(0，＋∞)时，f ′(x )＞0.所以f (x )在(-1,0)单调递减，在(0，＋∞)单调递增．（Ⅱ）当m ≤2，x ∈(-m ，+∞)时，ln(x +m )≤ln(x +2)，故只需证明当m =2时，f (x )＞0.当m =2时，函数f ′(x )=12xe x -+在(-2，+∞)单调递增．又f ′(-1)＜0，f ′(0)＞0，故f ′(x )=0在(-2，+∞)有唯一实根x 0，且x 0∈(-1,0)．当x ∈(-2，x 0)时，f ′(x )＜0；当x ∈(x 0，+∞)时，f ′(x )＞0，从而当x =x 0时，f (x )取得最小值．由f ′(x 0)=0得0xe =012x +，ln(x 0+2)=-x 0，故f (x ) ≥ f (x 0)=012x ++x 0=20012x x (+)+＞0. 综上，当m ≤2时，f (x )＞0.【2014年新课标Ⅰ卷，21】设函数1(0ln x xbe f x ae x x-=+，曲线()y f x =在点（1，(1)f 处的切线为(1)2y e x =-+. （Ⅰ）求,a b ；（Ⅱ）证明：()1f x >.解：(Ⅰ) 函数()f x 的定义域为()0,+∞，112()ln xx x x a b b f x ae x e e e x x x--'=+-+ 由题意可得(1)2,(1)f f e '==，故1,2a b == ……………6分（Ⅱ）由(Ⅰ)知，12()ln x xe f x e x x-=+，从而()1f x >等价于2ln xx x xe e ->-设函数()ln g x x x =，则()ln g x x x '=+，所以当10,x e ⎛⎫∈ ⎪⎝⎭时，()0g x '<，当1,x e ⎛⎫∈+∞ ⎪⎝⎭时，()0g x '>，故()g x 在10,e ⎛⎫ ⎪⎝⎭单调递减，在1,e ⎛⎫+∞ ⎪⎝⎭单调递增，从而()g x 在()0,+∞的最小值为11()g ee =-.设函数2()xh x xe e-=-，则()()1x h x e x -'=-，所以当()0,1x ∈时，()0h x '>，当()1,x ∈+∞时，()0h x '<，故()h x 在()0,1单调递增，在()1,+∞单调递减，从而()h x ()g x 在()0,+∞的最小值1(1)h e=-.综上：当0x >时，()()g x h x >，即()1f x >. ……………12分【2014年新课标Ⅱ卷，21】已知函数()2x x f x e e x -=--. （Ⅰ）讨论()f x 的单调性；（Ⅱ）设()(2)4()g x f x bf x =-，当0x >时，()0g x >，求b 的最大值；（Ⅲ）已知1.4142 1.4143<<，估计ln2的近似值（精确到0.001）.解：（Ⅰ）1()2()2=220.x x x x x x f x e e x x R f x e e e e --'=--∈∴=+-+-≥=，， ∴当且仅当x =0时等号成立，所以函数()f x 在R 上单调递增．（Ⅱ）22()(2)4()44(2),x x x x g x f x bf x e e x b e e x --=-=-----∴当x >0时，2244(2)0,x x x x e e x b e e x ------->22()2[2()(42)]x x x x g x e e b e e b --'∴=+-++-2(2)[(22)]x x x x e e e e b --=+-+--，2x x e e -+≥，2(2)0x x e e -∴+-≥，(1) 当2b ≤时，()0g x '≥，当且仅当x =0时等号成立. 所以此时g (x )在R 上单调递增，而g (0)=0，所以对任意x >0，有g (x )>0.(2) 当2b >时，若x 满足222x x e e b -<+<-时，即0ln(1x b <<-时，()0g x '<，而g (0)=0，因此当0ln(1x b <<-时，g (x )<0.综上可知，当2b ≤时，才对任意的x >0，有g (x )>0，因此b 的最大值为2.（Ⅲ）由(Ⅱ)知，32(21)ln 22g b =-+-，当b =2时，3(ln 6ln 202g =->，3ln 20.692812>>；当14b =+时，ln(1b -=，32)ln 202g =--<，ln 20.6934<<，所以ln2的近似值为0.693. 【2015年新课标Ⅰ卷，21】已知函数31()4f x x ax =++，()ln g x x =-. （Ⅰ）当a 为何值时，x 轴为曲线()y f x =的切线；（Ⅱ）用min{,}m n 表示,m n 中的最小值，设函数min{),()(}()h x f x g x =（0x >），讨论()h x 零点的个数.解：（Ⅰ）2()3f x x a '=+，若x 轴为曲线()y f x =的切线，则切点0(,0)x 满足00()0,()0f x f x '==，也就是2030x a +=且300104x ax ++=，解得012x =，34a =-，因此，当34a =-时，x 轴为曲线()y f x =的切线；（Ⅱ）当1x >时，()ln 0g x x =-<，函数()()()(min{}),h x f x g x g x ≤=没有零点；当1x =时，若54a ≥-，则5(1)04f a =+≥，min{,(1)(1)(1)}(1)0h fg g ===，故1x =是()h x 的零点；当01x <<时，()ln 0g x x =->，以下讨论()y f x =在区间(0,1)上的零点的个数.对于2()3f x x a '=+，因为2033x <<，所以令()0f x '=可得23a x =-，那么（i ）当3a ≤-或0a ≥时，()f x '没有零点（()0f x '<或()0f x '>），()y f x =在区间(0,1)上是单调函数，且15(0),(1)44f f a ==+，所以当3a ≤-时，()y f x =在区间(0,1)上有一个零点；当0a ≥时，()y f x =在区间(0,1)上没有零点；（ii ）当30a -<<时，()0f x '<（0x <<）且()0f x '>（1x <<），所以x =14f =.显然，若0f >，即304a -<<时，()y f x =在区间(0,1)上没有零点；若0f =，即34a =-时，()y f x =在区间(0,1)上有1个零点；若0f <，即334a -<<-时，因为15(0),(1)44f f a ==+，所以若5344a -<<-，()y f x =在区间(0,1)上有2个零点；若534a -<≤-，()y f x =在区间(0,1)上有1个零点.综上，当34a >-或54a <-时，()h x 有1个零点；当34a =-或54a =-时，()h x 有2个零点；当5344a -<<-时，()h x 有3个零点.【2015年新课标Ⅱ卷，21】设函数2()mx f x e x mx =+-.（Ⅰ）证明：f (x )在（-∞，0）单调递减，在（0，+∞）单调递增；（Ⅱ）若对于任意x 1,，x 2∈[-1，1]，都有｜f (x 1)- f (x 2)｜≤ e -1，求m 的取值范围．解：（Ⅰ）()(1)2mx f x m e x '=-+，若0m ≥，则当(,0)x ∈-∞时，10,()0mx e f x '-≤<；当(0,)x ∈+∞时，10mxe-≥，()0f x '>. 若0m <，则当(,0)x ∈-∞时，10,()0mx e f x '-><；当(0,)x ∈+∞时，10mx e -<，()0f x '>，所以，()f x 在(,0)-∞单调递减，在(0,)+∞单调递增.（Ⅱ）由（Ⅰ）知，对任意的m ，()f x 在[-1，0]单调递减，在[0,1]单调递增，故()f x 在0x =处取得最小值，所以对于任意12,[1,1]x x ∈-，12|()()|1f x f x e -≤-的充要条件是(1)(0)1(1)(0)1f f e f f e -≤-⎧⎨--≤-⎩，即11mm e m e e m e -⎧-≤-⎪⎨+≤-⎪⎩①. 设函数()1t g t e t e =--+，则()1t g t e '=-，当0t <时，()0g t '<；当0t >时，()0g t '>，故()g t 在(,0)-∞单调递减，在(0,)+∞单调递增.又(1)0g =，1(1)20g e e --=+-<，故当[1,1]t ∈-时，()0g t ≤.当[1,1]m ∈-时，()0,()0g m g m ≤-≤，即①式成立；当1m >时，由()g t 的单调性，()0g m >，即1me m e ->-；当1m <-时，()0g m ->，即1me m e -+>-，综上，m 的取值范围是[-1,1].【2016年新课标Ⅰ卷，12】已知函数2)1()2()(-+-=x a e x x f x 有两个零点．（Ⅰ）求a 的取值范围；（Ⅱ）设21,x x 是)(x f 的两个零点，证明：221<+x x ．解：（1）由已知得，'()(1)2(1)(1)(2)xxf x x e a x x e a =-+-=-+①当0a =时，则()(2)x f x x e =-，()f x 只有一个零点，不合题意． ②当0a >时，则当(,1)x ∈-∞时，'()0f x <；当(1,)x ∈+∞时，'()0f x >．()f x ∴在(,1)-∞上单调递减，在(1,)+∞上单调递增．又(1)f e =-，且当x →-∞时，()f x →+∞；当x →+∞时，()f x →+∞.故()f x 存在两个零点，符合题意．③当0a <时，由'()0f x =得 1x =或ln(2)x a =-． <1>若02ea -≤<，则ln(2)1a -≤，故当(1,)x ∈+∞时，'()0f x >，因此()f x 在(1,)+∞上单调递增．又当1x ≤时，()0f x <，所以()f x 不存在两个零点，不合题意． <2>若2e a <-，则ln(2)1a ->，故当(1,ln(2))x a ∈-时，'()0f x <；当(ln(2),)x a ∈-+∞时，'()0f x >．因此()f x 在(1,ln(2))a -上单调递减，在(ln(2),)a -+∞上单调递增．又当1x ≤时，()0f x <，所以()f x 不存在两个零点，不合题意．综上所述，a 的取值范围为(0,)+∞．（2）由（1）知，函数()f x 在(,1)-∞上单调递减，在(1,)+∞上单调递增. 设12x x <，则121x x <<.令22()()(2)(2)(1)(22)(21)xxF x f x f x x e a x x e a x =--=-+------- (22)(1)x x e x =-> 则'()2(22)20(1)xxxF x e x e xe x =+-=>>∴函数()F x 在(1,)+∞上单调递增.()(1)0F x F ∴>=，即()(2)(1)f x f x x >->21x > 122()()(2)f x f x f x ∴=>- 又121,21x x <-<，且函数()f x 在(,1)-∞单调递减122x x ∴<-，即122x x +<.【2016年新课标Ⅱ卷，21】（Ⅰ）讨论函数2()2xx f x e x -=+ 的单调性，并证明当x >0时，(2)20x x e x -++>；（Ⅱ）证明：当[0,1)a ∈时，函数2()=(0)x e ax ag x x x-->有最小值.设g (x )的最小值为()h a ，求函数()h a 的值域.证明：⑴()()()22224e e 222xxx x f x x x x ⎛⎫-' ⎪=+= ⎪+++⎝⎭，∵当x ∈()()22,-∞--+∞，时，()0f x '>，∴()f x 在()()22,-∞--+∞，和上单调递增，∴0x >时，()2e 0=12xx f x ->-+，∴()2e 20x x x -++>. ⑵ ()()()24e2e xxa x x ax a g x x ----'=()4e 2e 2xxx x ax a x -++=32(2)(e )2xx x a x x -+⋅++=，[)01a ∈，，由(1)知，当0x >时，()2e 2xx f x x -=⋅+的值域为()1-+∞，，只有一解．使得2e 2tt a t -⋅=-+，(]02t ∈，，当(0,)x t ∈时，()0g x '<，()g x 单调减；当(,)x t ∈+∞时()0g x '>，()g x 单调增，()()()222e 1e e 1e 22tt t t t t a t t h a t t t -++⋅-++===+，记()e 2t k t t =+，在(]0,2t ∈时，()()()2e 102tt k t t +'=>+，∴()k t 单调递增，∴()()21e 24h a k t ⎛⎤=∈ ⎥⎝⎦，．【2016年新课标Ⅲ卷，21】设函数()cos 2(1)(cos 1)f x a x a x =+-+，其中0a >，记|()|f x 的最大值为A ．（Ⅰ）求()f x '；（Ⅱ）求A ；（Ⅲ）证明|()|2f x A '≤．解：（Ⅰ）'()2sin 2(1)sin f x a x a x =---．（Ⅱ）当1a ≥时，'|()||sin 2(1)(cos 1)|f x a x a x =+-+2(1)a a ≤+-32a =-(0)f =因此，32A a =-． ………4分当01a <<时，将()f x 变形为2()2cos (1)cos 1f x a x a x =+--．令2()2(1)1g t at a t =+--，则A 是|()|g t 在[1,1]-上的最大值，(1)g a -=，(1)32g a =-，且当14at a -=时，()g t 取得极小值，极小值为221(1)61()1488a a a a g a a a --++=--=-．令1114a a --<<，解得13a <-（舍去），15a >．（ⅰ）当105a <≤时，()g t 在(1,1)-内无极值点，|(1)|g a -=，|(1)|23g a =-，|(1)||(1)|g g -<，所以23A a =-．（Ⅲ）由（Ⅰ）得'|()||2sin 2(1)sin |2|1|f x a x a x a a =---≤+-. 当105a <≤时，'|()|1242(23)2f x a a a A ≤+≤-<-=.当115a <<时，131884a A a =++≥，所以'|()|12f x a A ≤+<.当1a ≥时，'|()|31642f x a a A ≤-≤-=，所以'|()|2f x A ≤. 【2017年新课标Ⅰ卷，21】已知函数()()22xx f x ae a e x =+--．（1）讨论()f x 的单调性；（2）若()f x 有两个零点，求a 的取值范围．解：（1）()f x 的定义域为(,)-∞+∞，2()2e(2)e 1(e 1)(2e 1)xx x x f x a a a '=+--=-+，（ⅰ）若0a ≤，则()0f x '<，所以()f x 在(,)-∞+∞单调递减. （ⅱ）若0a >，则由()0f x '=得ln x a =-.当(,ln )x a ∈-∞-时，()0f x '<；当(ln ,)x a ∈-+∞时，()0f x '>，所以()f x 在(,ln )a -∞-单调递减，在(ln ,)a -+∞单调递增.（2）令()0f x =，则22x x xe x a e e +=+．再令0xt e =>，则22ln t t a t t +=+，而()f x 有两个零点，则22ln t t a t t +=+有两解，即直线y a =与曲线22ln t t y t t+=+有两个交点；令()22ln (0)t t g t t t t +=>+，则()()()()()2222211ln 2ln t t t t t g t t t t t +--+'==++，令()1ln h t t t =--，则()110h t t'=--<，注意到()10h =，所以()g t 在()0,1上单调递增，在()1,+∞上单调递减，即()()max 11g t g ==；而0lim (),lim ()0t t g t g t →→+∞→-∞→，所以当()0,1t ∈时，()(),1g t ∈-∞；当()0,1t ∈时，()()0,1g t ∈，所以，当22ln t ta t t+=+有两解时，a 的取值范围为()0,1．【2017年新课标Ⅱ卷，21】已知函数2()ln ,f x ax ax x x =--且()0f x ≥.（1）求a ；（2）证明：()f x 存在唯一的极大值点0x ，且220()2e f x --<<. 解：(1)由题知：()()ln f x x ax a x =--()0x >，且()0f x ≥ ，所以()1ln 0a x x --≥，即当()0,1x ∈时，ln 1x a x ≤-；当()1,x ∈+∞时，ln 1xa x ≥-；当1x =时，()1ln 0a x x --≥成立.令()1ln g x x x =--，()11'1x g x x x-=-=，当()0,1x ∈时，()'0g x <，()g x 递减，()()10g x g <=，所以：1ln x x ->，即：ln 11xx >-，所以1a ≤；当()1,x ∈+∞时，()'0g x >，()g x 递增，()()10g x g >=，所以：1ln x x ->，即：ln 11xx <-. 所以，1a ≥. 综上，1a =.（2）由(1)知：()()1ln f x x x x =--，()'22ln f x x x =--，设()22ln x x x ϕ=--，则()1'2x x ϕ=-.当10,2x ⎛⎫∈ ⎪⎝⎭时，()'0x ϕ<；当1,2x ⎛⎫∈+∞ ⎪⎝⎭时，()'0x ϕ>. 所以()x ϕ在10,2⎛⎫ ⎪⎝⎭递减，在1,2⎛⎫+∞ ⎪⎝⎭递增.又()20e ϕ->，102ϕ⎛⎫< ⎪⎝⎭，()10ϕ=，所以()x ϕ在10,2⎛⎫ ⎪⎝⎭有唯一零点0x ，在1,2⎛⎫+∞ ⎪⎝⎭有唯一零点1，且当()00,x x ∈时，()0x ϕ>；当()0,1x x ∈时，()0x ϕ<；当()1,x ∈+∞时，()0x ϕ>.又()()'f x x ϕ=，所以0x x =是()f x 的唯一极大值点. 由()0'0f x =得()00ln 21x x =-，故()()0001f x x x =-. 由()00,1x ∈得()014f x <.因为0x x =是()f x 在()0,1的唯一极大值点，由()10,1e -∈，()10f e-≠得()()120f x f e e -->=所以220()2e f x --<<.【2017年新课标Ⅲ卷，21】已知函数()1ln f x x a x =--．（1）若()0f x ≥，求a 的值；（2）设m 为整数，且对于任意正整数n ，2111(1)(1)(1)222nm ++鬃?<，求m 的最小值．解：⑴ ()1ln f x x a x =--，0x >则()1a x af x x x-'=-=，且(1)0f =当0a ≤时，()0f x '>，()f x 在()0+∞，上单调增，所以01x <<时，()0f x <，不满足题意；当0a >时，当0x a <<时，()0f x '<，则()f x 在(0,)a 上单调递减；当x a >时，()0f x '>，则()f x 在(,)a +∞上单调递增．①若1a <，()f x 在(,1)a 上单调递增∴当(,1)x a ∈时()(1)0f x f <=矛盾 ②若1a >，()f x 在(1,)a 上单调递减∴当(1,)x a ∈时()(1)0f x f <=矛盾 ③若1a =，()f x 在(0,1)上单调递减，在(1,)+∞上单调递增∴()(1)0f x f =≥满足题意综上所述1a =．⑵ 当1a =时()1ln 0f x x x =--≥即ln 1x x -≤则有ln(1)x x +≤当且仅当0x =时等号成立∴11ln(1)22k k +<，*k ∈N一方面：221111111ln(1)ln(1)...ln(1) (112222222)n n n ++++++<+++=-<，即2111(1)(1)...(1)e 222n +++<．另一方面：223111111135(1)(1)...(1)(1)(1)(1)222222264n +++>+++=>当3n ≥时，2111(1)(1)...(1)(2,e)222n +++∈∵*m ∈N ，2111(1)(1)...(1)222n m +++<，∴m 的最小值为3．【2018年新课标Ⅰ卷，21】已知函数1()ln f x x a x x=-+．（1）讨论()f x 的单调性；（2）若()f x 存在两个极值点12,x x ，证明：()()12122f x f x a x x -<--．解：（1）()f x 的定义域为(0,)+∞，22211()1a x ax f x x x x -+'=--+=-.（i ）若2a ≤，则()0f x '≤，当且仅当2a =，1x =时()0f x '=，所以()f x 在(0,)+∞单调递减.（ii ）若2a >，令()0f x '=得，x =x =当)x ∈+∞U 时，()0f x '<；当x ∈时，()0f x '>.所以()f x 在(0,),(,)22a a +∞单调递减，在(22a a +单调递增.（2）由（1）知，()f x 存在两个极值点当且仅当2a >.由于()f x 的两个极值点12,x x 满足210x ax -+=，所以121x x =，不妨设12x x <，则21x >.由于12121221212121222()()ln ln ln ln 2ln 11221f x f x x x x x x a a a x x x x x x x x x x ----=--+=-+=-+----，所以1212()()2f x f x a x x -<--等价于22212ln 0x x x -+<.设函数1()2ln g x x x x=-+，由（1）知，()g x 在(0,)+∞单调递减，又(1)0g =，从而当(1,)x ∈+∞时，()0g x <.所以22212ln 0x x x -+<，即1212()()2f x f x a x x -<--. 【2018年新课标Ⅱ卷，21】已知函数2()e x f x ax =-．（1）若1a =，证明：当0x ≥时，()1f x ≥；（2）若()f x 在(0,)+∞只有一个零点，求a ．解：（1）当1a =时，()1f x ≥等价于()21e 10xx -+-≤，设函数()()21e 1x g x x -=+-，则()()()2221e 1e x xg'x x x x --=--+=--，当1x ≠时，()0g'x <，所以()g x 在()0,+∞单调递减，而()00g =，故当0x ≥时，()0g x ≤，即()1f x ≥．（2）设函数()21e xh x ax -=-，()f x 在()0,+∞只有一个零点当且仅当()h x 在()0,+∞只有一个零点．当0a ≤时，()0h x >，()h x 没有零点；当0a >时，()()2e xh x ax x -'=-．当()0,2x ∈时，()0h'x <；当()2,x ∈+∞时，()0h'x >．()h x ∴在()0,2单调递减，在()2,+∞单调递增．故()2421eah =-是()h x 在[)0,+∞的最小值． ①若()20h >，即2e 4a <，()h x 在()0,+∞没有零点；②若()20h =，即2e 4a =，()h x 在()0,+∞只有一个零点；③若()20h <，即2e 4a >，由于()01h =，所以()h x 在()0,2有一个零点，由（1）知，当0x >时，2e x x >，所以()()()33324421616161411110e 2ea a a a a h a a a =-=->-=->．故()h x 在()2,4a 有一个零点，因此()h x 在()0,+∞有两个零点．综上，()f x 在()0,+∞只有一个零点时，2e 4a =．【2018年新课标Ⅲ卷，21】已知函数()()()22ln 12f x x ax x x =+++-．（1）若0a =，证明：当10x -<<时，()0f x <；当0x >时，()0f x >；（2）若0x =是()f x 的极大值点，求a ．解：（1）若0a =时，()(2)ln(1)2(1)f x x x x x =++->-，∴1()ln(1)(2)21f x x x x '=+++-+1ln(1)11x x =++-+. 令1()ln(1)11h x x x =++-+， ∴2211()1(1)(1)xh x x x x '=-=+++. ∴当0x >时，()0h x '>，()h x 在(0,)+∞上单调递增，当10x -<<时，()0h x '<，()h x 在(1,0)-上单调递减. ∴min ()(0)ln1110h x h ==+-=， ∴()0f x '≥恒成立，∴()f x 在(1,)-+∞上单调递增，又(0)2ln100f =-=，∴当10x -<<时，()0f x <；当0x >时，()0f x >.（2）21()(21)ln(1)11ax f x ax x x +'=+++-+，22212(1)1()2ln(1)01(1)ax ax x ax f x a x x x ++--''=+++≤++， 222(1)ln(1)(21)(1)210a x x ax x ax ax +++++++-≤， 222(1)ln(1)340a x x ax ax x +++++≤， 22[2(1)ln(1)34]a x x x x x ++++≤-. 设22()2(1)ln(1)34h x x x x x =++++，∴()4(1)ln(1)2(1)64h x x x x x '=++++++，(0)60h '=>，(0)0h =， ∴在0x =邻域内，0x >时，()0h x >，0x <时，()0h x <.0x >时，222(1)ln(1)34xa x x x x-≤++++，由洛必达法则得16a ≤-， 0x <时，222(1)ln(1)34xa x x x x-≥++++，由洛必达法则得16a ≥-，综上所述，16a =-.。

2018年高考理科数学全国卷三导数压轴题解析

2018年高考理科数学全国卷三导数压轴题解析已知函数2()(2)ln(1)2f x x ax x x =+++-（1）若0a =，证明：当10x -<<时，()0f x <；当0x >时，()0f x >；（2）若0x =是()f x 的极大值点，求a .考点分析综合历年试题来看，全国卷理科数学题目中，全国卷三的题目相对容易。

但在2018年全国卷三的考察中，很多考生反应其中的导数压轴题并不是非常容易上手。

第1小问，主要通过函数的单调性证明不等式，第2小问以函数极值点的判断为切入点，综合考察复杂含参变量函数的单调性以及零点问题，对思维能力（化归思想与分类讨论）的要求较高。

具体而言，第1问，给定参数a 的值，证明函数值与0这一特殊值的大小关系，结合函数以及其导函数的单调性，比较容易证明，这也是大多数考生拿到题目的第一思维方式，比较常规。

如果能结合给定函数中20x +>这一隐藏特点，把ln(1)x +前面的系数化为1，判断ln(1)x +与2/(2)x x +之间的大小关系，仅通过一次求导即可把超越函数化为求解零点比较容易的代数函数，解法更加容易，思维比较巧妙。

总体来讲，题目设置比较灵活，不同能力层次的学生皆可上手。

理解什么是函数的极值点是解决第2问的关键。

极值点与导数为0点之间有什么关系：对于任意函数，在极值点，导函数一定等于0么（存在不存在）？导函数等于0的点一定是函数的极值点么？因此，任何不结合函数的单调性而去空谈函数极值点的行为都是莽撞与武断的。

在本题目中，0x =是()f x 的极大值点的充要条件是存在10δ<和20δ>使得对于任意1(,0)x δ∈都满足()(0)=0f x f <( 或者()f x 单调递增)，对于任意2(0,)x δ∈都满足()(0)=0f x f <( 或者()f x 单调递减)，因此解答本题的关键是讨论函数()f x 在0x =附近的单调性或者判断()f x 与(0)f 的大小关系。

2018高考理科数学试卷分类汇编14：导数与积分(修改)

2018年全国高考理科数学试卷分类汇编14：导数与积分一、选择题1 ．<2018年高考湖北卷<理））已知a 为常数,函数()()ln f x x x ax =-有两个极值点1212,()x x x x <,则< ）b5E2RGbCAP A ．121()0,()2f x f x >>-B ．121()0,()2f x f x <<- C ．121()0,()2f x f x ><-D ．121()0,()2f x f x <>-【答案】D2 ．<2018年普通高等学校招生统一考试新课标Ⅱ卷数学<理）<纯WORD 版含答案））已知函数32()f x x ax bx c =+++,下列结论中错误的是< ）p1EanqFDPw A ．0x ∃∈R,0()0f x =B ．函数()y f x =的图像是中心对称图形 C ．若0x 是()f x 的极小值点,则()f x 在区间0(,)x -∞上单调递减 D ．若0x 是()f x 的极值点,则0'()0f x = 【答案】C3 ．<2018年高考江西卷<理））若22221231111,,,x S x dx S dx S e dx x===⎰⎰⎰则123S S S 的大小关系为< ）DXDiTa9E3d A ．123S S S <<B ．213S S S << C ．231S S S <<D ．321S S S << 【答案】B4 ．<2018年普通高等学校招生统一考试辽宁数学<理）试卷<WORD 版））设函数()()()()()222,2,0,8x e e f x x f x xf x f x f x x '+==>满足则时，< ）RTCrpUDGiT A ．有极大值,无极小值B ．有极小值,无极大值C ．既有极大值又有极小值D ．既无极大值也无极小值【答案】D5 ．<2018年普通高等学校招生统一考试福建数学<理）试卷<纯WORD 版））设函数()f x 的定义域为R,00(0)x x ≠是()f x 的极大值点,以下结论一定正确的是< ）5PCzVD7HxA A ．0,()()x R f x f x ∀∈≤B ．0x -是()f x -的极小值点C ．0x -是()f x -的极小值点D ．0x -是()f x --的极小值点【答案】D6 ．<2018年高考北京卷<理））直线l 过抛物线C: x2=4y 的焦点且与y 轴垂直,则l 与C 所围成的图形的面积等于< ）jLBHrnAILgA ．43B ．2C ．83D 【答案】C7 ．<2018年普通高等学校招生统一考试浙江数学<理）试卷<纯WORD 版））已知e 为自然对数的底数,设函数)2,1()1)(1()(=--=k x e x f k x ,则< ）xHAQX74J0X A ．当1=k 时,)(x f 在1=x 处取得极小值B ．当1=k 时,)(x f 在1=x 处取得极大值C ．当2=k 时,)(x f 在1=x 处取得极小值D ．当2=k 时,)(x f 在1=x 处取得极大值【答案】C 二、填空题8 ．<2018年高考江西卷<理））设函数()f x 在(0,)+∞内可导,且()x x f e x e =+,则(1)x f =______________LDAYtRyKfE 【答案】2 9 ．<2018年高考湖南卷<理））若209,Tx dx T =⎰则常数的值为_________.Zzz6ZB2Ltk 【答案】310．<2018年普通高等学校招生统一考试广东省数学<理）卷<纯WORD 版））若曲线ln y kx x =+在点()1,k 处的切线平行于x 轴,则k =______.dvzfvkwMI1【答案】1- 三、解答题11．<2018年普通高等学校招生统一考试新课标Ⅱ卷数学<理）<纯WORD 版含答案））已知函数)ln()(m x e x f x +-=.rqyn14ZNXI (Ⅰ>设0x =是()f x 的极值点,求m ,并讨论()f x 的单调性; (Ⅱ>当2m ≤时,证明()0f x >. 【答案】12．<2018年普通高等学校招生统一考试辽宁数学<理）试卷<WORD 版））已知函数()()()[]321,12cos .0,12e xx f x x g x ax x x x -=+=+++∈当时，EmxvxOtOco (I>求证:()11-;1x f x x≤≤+ (II>若()()f x g x ≥恒成立,求实数a 取值范围.请考生在第22、23、24三题中任选一题做答,如果多做,则按所做的第一题计分.作答时用2B 铅笔在答题卡上把所选题目对应题号下方的方框涂黑.SixE2yXPq5【答案】13．<2018年普通高等学校招生全国统一招生考试江苏卷<数学）<已校对纯WORD 版含附加题））本小题满分16分.6ewMyirQFL 设函数ax x x f -=ln )(,ax e x g x -=)(,其中a 为实数.(1>若)(x f 在),1(+∞上是单调减函数,且)(x g 在),1(+∞上有最小值,求a 的取值范围;(2>若)(x g 在),1(+∞-上是单调增函数,试求)(x f 的零点个数,并证明你的结论.卷Ⅱ 附加题部分答案word 版[选做题]第21题,本题包括A 、B 、C 、D 四小题,请选定其中两题,并在相应的答题区域内作答,若多做,则按作答的前两题评分.解答时应写出文字说明、证明过程或演算步骤.kavU42VRUs【答案】解:(1>由01)('≤-=a xx f 即a x≤1对),1(+∞∈x 恒成立,∴max 1⎥⎦⎤⎢⎣⎡≥x a而由),1(+∞∈x 知x1<1 ∴1≥a 由a e x g x -=)('令0)('=x g 则a x ln = 当x <a ln 时)('x g <0,当x >a ln 时)('x g >0, ∵)(x g 在),1(+∞上有最小值 ∴a ln >1 ∴a >e综上所述:a 的取值范围为),(+∞e(2>证明:∵)(x g 在),1(+∞-上是单调增函数 ∴0)('≥-=a e x g x 即x e a ≤对),1(+∞-∈x 恒成立, ∴[]min x e a ≤而当),1(+∞-∈x 时,x e >e1 ∴ea 1≤ 分三种情况:(Ⅰ>当0=a 时, x x f 1)('=>0 ∴f(x>在),0(+∞∈x 上为单调增函数 ∵0)1(=f ∴f(x>存在唯一零点(Ⅱ>当a <0时,a x x f -=1)('>0 ∴f(x>在),0(+∞∈x 上为单调增函数 ∵)1()(a a a e a ae a e f -=-=<0且a f -=)1(>0 ∴f(x>存在唯一零点(Ⅲ>当0<ea 1≤时,a xx f -=1)(',令0)('=x f 得ax 1=∵当0<x <a 1时,x a x a x f )1()('--=>0;x >a1时,x a x a x f )1()('--=<0 ∴a x 1=为最大值点,最大值为1ln 11ln )1(--=-=a aa a a f①当01ln =--a 时,01ln =--a ,e a 1=,)(x f 有唯一零点e ax ==1②当1ln --a >0时,0<ea 1≤,)(x f 有两个零点实际上,对于0<ea 1≤,由于e a e a e ef --=-=111ln )1(<0,1ln 11ln )1(--=-=a aa a a f >0 且函数在⎪⎭⎫ ⎝⎛a e 1,1上的图像不间断 ∴函数)(x f 在⎪⎭⎫⎝⎛a e 1,1上有存在零点另外,当⎪⎭⎫ ⎝⎛∈a x 1,0,a xx f -=1)('>0,故)(x f 在⎪⎭⎫ ⎝⎛a 1,0上单调增,∴)(x f 在⎪⎭⎫ ⎝⎛a 1,0只有一个零点下面考虑)(x f 在⎪⎭⎫ ⎝⎛+∞,1a的情况,先证)(ln ln )(1111121------=-=-=--a a a a a eaa aee a ae eef <0为此我们要证明:当x >e 时,x e >2x ,设2)(x e x h x -= ,则x e x h x 2)('-=,再设x e x l x 2)(-=∴2)('-=x e x l当x >1时,2)('-=x e x l >e -2>0,x e x l x 2)(-=在()+∞,1上是单调增函数故当x >2时,x e x h x 2)('-=>4)2(2'-=e h >0从而2)(x e x h x -=在()+∞,2上是单调增函数,进而当x >e 时,2)(x e x h x -=>2)(e e e h e -=>0 即当x >e 时,x e >2x ,当0<a <e1时,即1-a >e 时,)(ln ln )(1111121------=-=-=--a a a a a e a a ae e a ae e e f <0 又1ln 11ln )1(--=-=a aa a a f >0 且函数)(x f 在[]1,1--a e a 上的图像不间断, ∴函数)(x f 在()1,1--ae a上有存在零点,又当x >a1时,x a x a x f )1()('--=<0故)(x f 在()+∞-,1a 上是单调减函数∴函数)(x f 在()+∞-,1a 只有一个零点综合(Ⅰ>(Ⅱ>(Ⅲ>知:当0≤a 时,)(x f 的零点个数为1;当0<a <e1时,)(x f 的零点个数为214．<2018年普通高等学校招生统一考试广东省数学<理）卷<纯WORD 版））设函数()()21x f x x e kx =--(其中k ∈R >.y6v3ALoS89(Ⅰ> 当1k =时,求函数()f x 的单调区间;(Ⅱ> 当1,12k ⎛⎤∈ ⎥⎝⎦时,求函数()f x 在[]0,k 上的最大值M .【答案】(Ⅰ> 当1k =时,()()21x f x x e x =--,()()()1222x x x x f x e x e x xe x x e '=+--=-=-令()0f x '=,得10x =,2ln 2x =当x 变化时,()(),f x f x '的变化如下表:x (),0-∞0 ()0,ln 2ln 2()ln 2,+∞()f x ' +-+()f x极大值极小值右表可知,函数()f x 的递减区间为()0,ln 2,递增区间为(),0-∞,()ln 2,+∞. (Ⅱ> ()()()1222x x x x f x e x e kx xe kx x e k '=+--=-=-,令()0f x '=,得10x =,()2ln 2x k =,令()()ln 2g k k k =-,则()1110k g k kk -'=-=>,所以()g k 在1,12⎛⎤⎥⎝⎦上递增, 所以()ln 21ln 2ln 0g k e ≤-=-<,从而()ln 2k k <,所以()[]ln 20,k k ∈ 所以当()()0,ln 2x k ∈时,()0f x '<;当()()ln 2,x k ∈+∞时,()0f x '>; 所以()(){}(){}3max 0,max 1,1k M f f k k e k ==---令()()311k h k k e k =--+,则()()3k h k k e k '=-,令()3k k e k ϕ=-,则()330k k e e ϕ'=-<-<所以()k ϕ在1,12⎛⎤ ⎥⎝⎦上递减,而()()1313022e ϕϕ⎛⎫⎫⋅=--< ⎪⎪⎝⎭⎭所以存在01,12x ⎛⎤∈ ⎥⎝⎦使得()00x ϕ=,且当01,2k x ⎛⎫∈⎪⎝⎭时,()0k ϕ>,当()0,1k x ∈时,()0k ϕ<,所以()k ϕ在01,2x ⎛⎫⎪⎝⎭上单调递增,在()0,1x 上单调递减.因为17028h ⎛⎫=+> ⎪⎝⎭,()10h =,所以()0h k ≥在1,12⎛⎤⎥⎝⎦上恒成立,当且仅当1k =时取得“=”.综上,函数()f x 在[]0,k 上的最大值()31k M k e k =--.15．<2018年高考江西卷<理））已知函数1()=(1-2-)2f x a x ,a 为常数且>0a .M2ub6vSTnP (1> 证明:函数()f x 的图像关于直线1=2x 对称;(2>若0x 满足00(())=f f x x ,但00()f x x ≠,则称0x 为函数()f x 的二阶周期点,如果()f x 有两个二阶周期点12,,x x 试确定a 的取值范围; (3>对于(2>中的12,x x 和a , 设x3为函数f(f(x>>的最大值点,A(x1,f(f(x1>>>,B(x2,f(f(x2>>>,C(x3,0>,记△ABC 的面积为S(a>,讨论S(a>的单调性.0YujCfmUCw 【答案】(1>证明:因为11()(12),()(12)22f x a x f x a x +=--=-,有11()()22f x f x +=-, 所以函数()f x 的图像关于直线12x =对称.(2>解:当102a <<时,有224,(())4(1),a x f f x a x ⎧⎪=⎨-⎪⎩1,21.2x x ≤> 所以(())f f x x =只有一个解0x =,又(0)0f =,故0不是二阶周期点.当12a =时,有,(())1,x f f x x ⎧=⎨-⎩1,21.2x x ≤> 所以(())f f x x =有解集1|2x x ⎧⎫≤⎨⎬⎩⎭,又当12x ≤时,()f x x =,故1|2x x ⎧⎫≤⎨⎬⎩⎭中的所有点都不是二阶周期点.当12a >时,有222221,44,11,24,42(())1412(12)4,,2444,41.4x aa x x a a x a f f x a a a a x x a a a x a x a≤⎧⎪<≤-⎪=⎨--+⎪<≤⎪-⎩-> 所以(())f f x x =有四个解2222240,,,141214a a a a a a +++,又22(0)0,()1212a af f a a ==++, 22222244(),()14141414a a a af f a a a a ≠≠++++,故只有22224,1414a a a a ++是()f x 的二阶周期点.综上所述,所求a 的取值范围为12a >.(3>由(2>得2122224,1414a a x x a a==++, 因为3x 为函数(())f f x 的最大值点,所以314x a =或3414a x a-=. 当314x a =时,221()4(14)a S a a -=+.求导得:'()S a =所以当1(2a ∈时,()S a 单调递增,当)a ∈+∞时()S a 单调递减;当3414a x a -=时,22861()4(14)a a S a a -+=+,求导得:2221243'()2(14)a a S a a +-=+,因12a >,从而有2221243'()02(14)a a S a a +-=>+, 所以当1(,)2a ∈+∞时()S a 单调递增.16．<2018年普通高等学校招生统一考试重庆数学<理）试卷<含答案））设()()256ln f x a x x =-+,其中a R ∈,曲线()y f x =在点()()1,1f 处的切线与y 轴相交于点()0,6.eUts8ZQVRd (1>确定a 的值; (2>求函数()f x 的单调区间与极值. 【答案】(3)26ln 3f =+17．<2018年高考四川卷<理））已知函数22,0()ln ,0x x a x f x x x ⎧++<=⎨>⎩,其中a 是实数.设11(,())A x f x ,22(,())B x f x 为该函数图象上的两点,且12x x <.sQsAEJkW5T (Ⅰ>指出函数()f x 的单调区间;(Ⅱ>若函数()f x 的图象在点,A B 处的切线互相垂直,且20x <,求21x x -的最小值;(Ⅲ>若函数()f x 的图象在点,A B 处的切线重合,求a 的取值范围. 【答案】解:()I 函数()f x 的单调递减区间为(),1-∞-,单调递增区间为[)1,0-,()0,+∞()II 由导数的几何意义可知,点A 处的切线斜率为()1f x ',点B 处的切线斜率为()2f x ',故当点A 处的切线与点B 处的切垂直时,有()()121f x f x ''=-.GMsIasNXkA 当0x <时,对函数()f x 求导,得()22f x x '=+. 因为120x x <<,所以()()1222221x x ++=-, 所以()()12220,220x x +<+>.因此()()21121222212x x x x -=-+++≥=⎡⎤⎣⎦ 当且仅当()122x -+=()222x +=1,即123122x x =-=且时等号成立.所以函数()f x 的图象在点,A B 处的切线互相垂直时,21x x -的最小值为1()III 当120x x <<或210x x >>时,()()12f x f x ''≠,故120x x <<.当10x <时,函数()f x 的图象在点()()11,x f x 处的切线方程为()()()21111222y x x a x x x -++=+-,即()21122y x x x a =+-+当20x >时,函数()f x 的图象在点()()22,x f x 处的切线方程为()2221ln y x x x x -=-,即221ln 1y x x x =∙+-.两切线重合的充要条件是1222112 2 ln 1 x x x x a ⎧=+⎪⎨⎪-=-+⎩①② 由①及120x x <<知,110x -<<. 由①②得,()2211111ln1ln 22122a x x x x =+-=-+-+. 设()()21111ln 221(10)h x x x x =-+--<<, 则()1111201h x x x '=-<+. 所以()()1110h x x -<<是减函数. 则()()10ln 21h x h >=--, 所以ln 21a >--.又当1(1,0)x ∈-且趋近于1-时,()1h x 无限增大,所以a 的取值范围是()ln 21,--+∞.故当函数()f x 的图像在点,A B 处的切线重合时,a 的取值范围是()ln 21,--+∞ 18．<2018年高考湖南卷<理））已知0a >,函数()2x af x x a-=+.TIrRGchYzg (I>记[]()0,4f x a 在区间上的最大值为g(),求a g()的表达式;(II>是否存在a ,使函数()y f x =在区间()0,4内的图像上存在两点,在该两点处的切线相互垂直?若存在,求a 的取值范围;若不存在,请说明理由.7EqZcWLZNX 【答案】解:⎪⎪⎩⎪⎪⎨⎧<<-++=++-≥-<+=+-=>时，是单调递减的。

备战2018年高考理科数学解答题核心考点答题模板与模拟训练专题6 函数与导数

1 2 blnx （ a, b R ）, g x x . x
(1)若 a ห้องสมุดไป่ตู้ 1 ,曲线 y f x 在点 1, f 1 处的切线与 y 轴垂直,求 b 的值；

备战 2018 年高考理科数学解答题核心考点答题模板与模拟训练
(2)若 b 2 ,试探究函数 f x 与 g x 的图象在其公共点处是否存在公切线.若存在,研究 a 值的个数；若不存在,请说明理由. 【解析】（1）当 a 1 时, f x x 依题意得 f' 1 2 b 0 ,∴ b 2 .
令 g' x 0 解得 0 x 1 所以 g x 在 , 0 , 1, 单调递减,在 0,1 单调递增
g x 极大值 g 1 1, g x 极小值 g 0 3 ,
所以若有三个交点,则 t 3, 1 , 所以当 t 3, 1 时,过点 P 1, t 存在 3 条直线与曲线 y f x 相切. 【解题技巧】 (1)已知切点 A(x0,f(x0))求斜率 k,即求该点处的导数值：k＝f′(x0)． (2)已知斜率 k,求切点 A(x1,f(x1)),即解方程 f′(x1)＝k. (3)若求过点 P(x0,y0)的切线方程,可设切点为(x1,y1),由
y0＝f（x0），第三步,如果已知点(x1,y1)不在曲线上,则设出切点(x0,y0),解方程组y1－y0 得切点(x0,y0),进＝f′（x0）， x1－x0
而确定切线方程；第四步,反思回顾,查看有无忽略特殊情况. 【满分答案】设切点坐标为 x0 , y0 ,切线斜率为 k ,则有：
备战 2018 年高考理科数学解答题核心考点答题模板与模拟训练

2018年高考(理科)数学专题训练卷：函数与导数

函数与导数一、选择题（12*5=60分）1．等于（）A. B. C. 1 D. 2【答案】B【解析】，选B.2．下列函数中，既是偶函数，又在单调递增的函数是（）A. B. C. D.【答案】C3．【2018届北京市西城区44中高三上12月月考】集合，，那么“”是“”的（）．A. 充分而不必要条件B. 必要而不充分条件C. 充要条件D. 既不充分也不必要条件【答案】A【解析】∵集合，，∴，∴“” 是“”的充分而不必要条件．选．4．设是定义在上的奇函数，当时，，则A. B. C. D.【答案】C5．【2018届福建省德化一中、永安一中、漳平一中高三上学期三校联考】定义运算,则函数的图象是下图中A. B. C. D.【答案】D【解析】由题意可得,则答案为D.6．【2018届全国名校第三次大联考】已知为自然对数的底数，则曲线在点处的切线方程为（）A. B. C. D.【答案】C【解析】因为，所以，曲线在点处的切线斜率，切线方程为，化简得，故选C.7．【2018届山东省淄博市部分学校高三12月摸底】已知函数的图象如图所示，则其导函数的图象可能为A. B. C. D.【答案】D8．已知函数为上的单调函数，则实数的取值范围是（）A. B. C. D.【答案】A9．设实数满足：，则的大小关系为（）A. c<a<bB. c<b< aC. a <c<bD. b<c< a【答案】A【解析】由题意得，所以.选A.10．【2018届湖北省稳派教育高三上第二次联考】函数的图象在点处的切线方程是，则（）A. 7B. 4C. 0D. －4【答案】A11．已知定义在上的函数,满足①;②(其中是的导函数, 是自然对数的底数),则的取值范围为A. B. C. D.【答案】A【解析】构造函数,则,所以函数上是增函数,所以,即,则;令,则, 函数上是减函数,所以,即,则.综上, ,故答案为A.12．设函数是定义为R的偶函数，且对任意的，都有且当时，，若在区间内关于的方程恰好有3个不同的实数根，则的取值范围是（）学科！网A. B. C. D.【答案】D【解析】∵对于任意的x∈R,都有f(x−2)=f(2+x),∴函数f(x)是一个周期函数，且T=4.又∵当x∈[−2,0]时,f(x)= −1,且函数f(x)是定义在R上的偶函数，若在区间(−2,6]内关于x的方程恰有3个不同的实数解，则函数y=f(x)与y=在区间(−2,6]上有三个不同的交点，如下图所示：又f(−2)=f(2)=3，则对于函数y=，由题意可得，当x=2时的函数值小于3，当x=6时的函数值大于3，即<3,且>3,由此解得：<a<2，故答案为：(,2).二、填空题（4*5=20分）13.【2018届北京市第四中学高三上期中】若函数则等于__________。

2018年全国统一高考数学试卷(理科)(新课标ⅱ)(含解析版)

2018年全国统一高考数学试卷（理科）（新课标Ⅱ）一、选择题：本题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．（5分）=（）A．i B．C．D．2．（5分）已知集合A={（x，y）|x2+y2≤3，x∈Z，y∈Z}，则A中元素的个数为（）A．9B．8C．5D．43．（5分）函数f（x）=的图象大致为（）A．B．C．D．4．（5分）已知向量，满足||=1，=﹣1，则•（2）=（）A．4B．3C．2D．05．（5分）双曲线=1（a＞0，b＞0）的离心率为，则其渐近线方程为（）A．y=±x B．y=±x C．y=±x D．y=±x6．（5分）在△ABC中，cos=，BC=1，AC=5，则AB=（）A．4B．C．D．27．（5分）为计算S=1﹣+﹣+…+﹣，设计了如图的程序框图，则在空白框中应填入（）A．i=i+1B．i=i+2C．i=i+3D．i=i+48．（5分）我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先的成果．哥德巴赫猜想是“每个大于2的偶数可以表示为两个素数的和”，如30=7+23．在不超过30的素数中，随机选取两个不同的数，其和等于30的概率是（）A．B．C．D．9．（5分）在长方体ABCD﹣A1B1C1D1中，AB=BC=1，AA1=，则异面直线AD1与DB1所成角的余弦值为（）A．B．CD．10．（5分）若f（x）=cosx﹣sinx在[﹣a，a]是减函数，则a的最大值是（）A．B．C．D．π11．（5分）已知f（x）是定义域为（﹣∞，+∞）的奇函数，满足f（1﹣x）=f（1+x），若f（1）=2，则f（1）+f（2）+f（3）+…+f（50）=（）A．﹣50B．0C．2D．5012．（5分）已知F1，F2是椭圆C：=1（a＞b＞0）的左、右焦点，A是C的左顶点，点P在过A 且斜率为的直线上，△PF1F2为等腰三角形，∠F1F2P=120°，则C的离心率为（）A．B．C．D．二、填空题：本题共4小题，每小题5分，共20分。

2018年高考数学理科考点过关习题第二章函数导数及其应用12和答案

考点测试12 函数与方程一、基础小题1．若函数f(x)＝ax＋1在区间(－1,1)上存在一个零点，则实数a的取值范围是( )A．(1，＋∞)B．(－∞，1)C．(－∞，－1)∪(1，＋∞)D．(－1,1)答案 C解析由题意知，f(－1)f(1)<0，即(1－a)(1＋a)<0，解得a<－1或a>1.2．下列函数图象与x轴均有公共点，其中能用二分法求零点的是( )答案 C解析能用二分法求零点的函数必须在给定区间上连续不断，并且有f (a )·f (b )<0.A 、B 中不存在f (x )<0，D 中函数不连续．故选C.3．二次函数f (x )＝ax 2＋bx ＋c ，若f (1)>0，f (2)<0，则f (x )在(1,2)上零点的个数为( )A ．至多有一个B ．有一个或两个C ．有且仅有一个D ．一个也没有答案 C解析 ∵f (1)>0，f (2)<0，∴f (x )在(1,2)上必有零点，又∵函数为二次函数，∴有且只有一个零点．4．已知函数f (x )＝⎝ ⎛⎭⎪⎫12x －x 13，那么在下列区间中含有函数f (x )零点的是( )A ．⎝ ⎛⎭⎪⎫0，13B ．⎝ ⎛⎭⎪⎫13，12 C ．⎝ ⎛⎭⎪⎫12，1D ．(1,2)答案 B解析 f (0)＝1>0，f ⎝ ⎛⎭⎪⎫13＝⎝ ⎛⎭⎪⎫12 13 －⎝ ⎛⎭⎪⎫13 13 >0，f ⎝ ⎛⎭⎪⎫12＝⎝ ⎛⎭⎪⎫12 12 －⎝ ⎛⎭⎪⎫1213<0，∵f ⎝ ⎛⎭⎪⎫13·f ⎝ ⎛⎭⎪⎫12<0，且函数f (x )的图象为连续曲线，∴函数f (x )在⎝ ⎛⎭⎪⎫13，12内有零点．5．函数 f (x )＝⎩⎨⎧x 2＋2x －3，x ≤0，－2＋ln x ，x >0的零点个数为( ) A ．0 B ．1 C ．2 D ．3答案 C解析由⎩⎨⎧x ≤0，x 2＋2x －3＝0，得x ＝－3.又⎩⎨⎧x >0，－2＋ln x ＝0，得x ＝e 2.∴f (x )的零点个数为2.故选C.6．已知a 是函数f (x )＝2x －log 12 x 的零点，若0<x 0<a ，则f (x 0)的值满足( )A ．f (x 0)＝0B ．f (x 0)<0C ．f (x 0)>0D ．f (x 0)的符号不确定答案 B 解析分别作出y ＝2x 与y ＝log 12 x 的图象如图，当0<x 0<a 时，y ＝2x 的图象在y＝log 12x 图象的下方，所以f (x 0)<0.7．若a <b <c ，则函数f (x )＝(x －a )·(x －b )＋(x －b )(x －c )＋(x －c )(x －a )的两个零点分别位于区间( )A ．(a ，b )和(b ，c )内B ．(－∞，a )和(a ，b )内C ．(b ，c )和(c ，＋∞)内D ．(－∞，a )和(c ，＋∞)内答案 A解析易知f (a )＝(a －b )(a －c )，f (b )＝(b －c )(b －a )，f (c )＝(c －a )(c －b )．又a <b <c ，则f (a )>0，f (b )<0，f (c )>0，又该函数是二次函数，且图象开口向上，可知两个零点分别在(a ，b )和(b ，c )内．8．已知函数f (x )与g (x )的图象均在R 上不间断，由下表知方程f (x )＝g (x )的实数解所在的区间是( )C．(1,2) D．(2,3)答案 B解析设h(x)＝f(x)－g(x)，则h(－1)＝－0.147，h(0)＝－0.44，h(1)＝0.542，所以h(0)·h(1)<0，h(x)的零点在(0,1)内，即f(x)＝g(x)的实数解所在的区间为(0,1)．9．函数f(x)＝e x＋ln x，g(x)＝e－x＋ln x，h(x)＝e－x－ln x的零点分别是a，b，c，则( )A．a<b<c B．c<b<aC．c<a<b D．b<a<c答案 A解析由f(x)＝e x＋ln x＝0，得e x＝－ln x，但x>0，e x>1，故－ln x>1，即ln x<－1，所以0<a<1e；由g(x)＝e－x＋ln x＝0，得e－x＝－ln x，但x>0,0<e－x<1，故0<－ln x<1，即－1<ln x<0，所以1e<b<1；由h(x)＝e－x－ln x＝0，得e－x＝ln x，但x>0,0<e－x<1，故0<ln x<1，所以1<c<e.综上可知a<b<c，正确选项为A.10．已知f(x)＝2－x－ln (x3＋1)，实数a，b，c满足f(a)f(b)f(c)<0，且0<a<b<c，若实数x0是函数f(x)的一个零点，那么下列不等式中，不可能成立的是( )A．x0<a B．x0>bC．x0<c D．x0>c答案 D解析由已知f(x)＝2－x－ln (x3＋1)在(0，＋∞)上为减函数，且f(x0)＝0，f(a)f(b)f(c)<0可分为以下两种情形：①f(a)，f(b)，f(c)均小于0，如图所示，此时x0<a<b<c.②f (a )>0，f (b )>0，f (c )<0，如图所示，此时a <b <x 0<c ，综上，不可能成立的是x 0>c ，故选D.11．已知函数f (x )＝ln x －⎝ ⎛⎭⎪⎫12x －2的零点为x 0，则x 0所在的区间是( )A ．(0,1)B ．(1,2)C ．(2,3)D ．(3,4)答案 C解析 ∵f (x )＝ln x －⎝ ⎛⎭⎪⎫12x －2在(0，＋∞)是增函数，又f (1)＝ln 1－⎝ ⎛⎭⎪⎫12－1＝ln 1－2<0，f (2)＝ln 2－⎝ ⎛⎭⎪⎫120<0，f (3)＝ln 3－⎝ ⎛⎭⎪⎫121>0，∴x 0∈(2,3)，故选C.12．函数f (x )＝⎩⎨⎧|x 2＋2x －1|，x ≤0，2x －1＋a ，x >0有两个不同的零点，则实数a 的取值范围为________．答案 ⎝⎛⎭⎪⎫－∞，－12解析由于当x ≤0，f (x )＝|x 2＋2x －1|时图象与x 轴只有1个交点，即只有1个零点，故由题意只需方程2x －1＋a ＝0有1个正根即可，变形为2x ＝－2a ，结合图形只需－2a >1⇒a <－12即可．二、高考小题13．下列函数中，既是偶函数又存在零点的是( ) A ．y ＝cos x B ．y ＝sin x C ．y ＝ln x D ．y ＝x 2＋1答案 A解析 y ＝cos x 是偶函数，且存在零点；y ＝sin x 是奇函数；y ＝ln x 既不是奇函数也不是偶函数；y ＝x 2＋1是偶函数，但不存在零点．故选A.14．已知函数f (x ) ＝⎩⎨⎧x 2＋a －x ＋3a ，x <0，log ax ＋＋1，x ≥0(a >0，且a ≠1)在R 上单调递减，且关于x 的方程|f (x )|＝2－x 恰有两个不相等的实数解，则a 的取值范围是( )A ．⎝⎛⎦⎥⎤0，23B ．⎣⎢⎡⎦⎥⎤23，34 C ．⎣⎢⎡⎦⎥⎤13，23∪⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫34D ．⎣⎢⎡⎭⎪⎫13，23∪⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫34 答案 C解析要使函数f (x )在R 上单调递减，只需⎩⎪⎨⎪⎧3－4a 2≥0，0<a <1，3a ≥1，解之得13≤a ≤34，因为方程|f (x )|＝2－x 恰有两个不相等的实数解，所以直线y ＝2－x 与函数y ＝|f (x )|的图象有两个交点，如图所示．易知y ＝|f (x )|的图象与x 轴的交点的横坐标为1a －1，又13≤1a －1≤2，故由图可知，直线y ＝2－x 与y ＝|f (x )|的图象在x >0时有一个交点；当直线y ＝2－x 与y ＝x 2＋(4a －3)x ＋3a (x <0)的图象相切时，设切点为(x 0，y 0)，则⎩⎨⎧2－x 0＝x 20＋a －x 0＋3a ，－1＝2x 0＋a －，整理可得4a 2－7a ＋3＝0，解得a ＝1(舍)或a＝34.而当3a ≤2，即a ≤23时，直线y ＝2－x 与y ＝|f (x )|的图象在y 轴左侧有一个交点，综合可得a ∈⎣⎢⎡⎦⎥⎤13，23∪⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫34.15．已知函数f (x )＝⎩⎨⎧|x |，x ≤m ，x 2－2mx ＋4m ，x >m ，其中m >0.若存在实数b ，使得关于x 的方程f (x )＝b 有三个不同的根，则m 的取值范围是________．答案 (3，＋∞)解析 f (x )的大致图象如图所示，若存在b ∈R ，使得方程f (x )＝b 有三个不同的根，只需4m －m 2<m ，又m >0，所以m >3.16．设函数f (x )＝⎩⎨⎧2x－a ，x <1，x －ax －2a ，x ≥1.①若a ＝1，则f (x )的最小值为________；②若f (x )恰有2个零点，则实数a 的取值范围是________．答案 ①－1 ②⎣⎢⎡⎭⎪⎫12，1∪已知函数f (x )＝⎩⎨⎧x 3，x ≤a ，x 2，x >a .若存在实数b ，使函数g (x )＝f (x )－b 有两个零点，则a 的取值范围是________．答案 (－∞，0)∪(1，＋∞)解析当a <0时，若x ∈(a ，＋∞)，则f (x )＝x 2，当b ∈(0，a 2)时，函数g (x )＝f (x )－b 有两个零点，分别是x 1＝－b ，x 2＝b .当0≤a ≤1时，f (x )的图象如图所示，易知函数g (x )＝f (x )－b 最多有一个零点．当a >1时，f (x )的图象如图所示，当b ∈(a 2，a 3]时，函数g (x )＝f (x )－b 有两个零点，分别是x 1＝3b ，x 2＝b . 综上，a ∈(－∞，0)∪(1，＋∞)．18．函数f(x)＝4cos2x2cos⎝⎛⎭⎪⎫π2－x－2sin x－|ln (x＋1)|的零点个数为________．答案 2解析f(x)＝2(1＋cos x)sin x－2sin x－|ln (x＋1)|＝sin2x－|ln (x＋1)|，x>－1，函数f(x)的零点个数即为函数y＝sin2x与y＝|ln (x＋1)|(x>－1)的图象的交点个数．分别作出两个函数的图象，如图，可知有两个交点，则f(x)有两个零点．三、模拟小题19．若f(x)是奇函数，且x0是y＝f(x)＋e x的一个零点，则－x0一定是下列哪个函数的零点( )A．y＝f(－x)e x－1 B．y＝f(x)e－x＋1C．y＝e x f(x)－1 D．y＝e x f(x)＋1答案 C解析由已知可得f(x0)＝－e x0，则e－x0f(x0)＝－1，e－x0f(－x0)＝1，故－x一定是y＝e x f(x)－1的零点．20．若函数y＝f(x)在区间上的图象是连续的，则下列说法正确的是( ) A．若f(a)f(b)>0，则不存在实数c∈(a，b)使得f(c)＝0B．若f(a)f(b)>0，则有可能存在实数c∈(a，b)使得f(c)＝0C．若f(a)f(b)<0，则有可能不存在实数c∈(a，b)使得f(c)＝0D．若f(a)f(b)<0，则有且只有一个实数c∈(a，b)使得f(c)＝0答案 B解析由函数零点存在性定理可知，选B.21．已知f (x )是定义在R 上的奇函数，且当x ∈(0，＋∞)时，f (x )＝2016x＋log 2016x ，则函数f (x )的零点个数是( )A ．1B ．2C ．3D ．4答案 C 解析作出函数y ＝2016x 和y ＝－log 2016x 的图象如图所示，可知函数f (x )＝2016x＋log 2016x 在x ∈(0，＋∞)上存在一个零点，又f (x )是定义在R 上的奇函数，∴f (x )在x ∈(－∞，0)上只有一个零点，又f (0)＝0，∴函数f (x )的零点个数是3，故选C.22．设函数f (x )＝⎩⎨⎧2x，x ≤0，log 2x ，x >0，若关于x 的方程2－af (x )＝0恰有三个不同的实数解，则实数a 的取值范围为( )A ．(0,1]B ．(0,1)C ．2－af (x )＝0的解为f (x )＝0或f (x )＝a ，而函数f (x )的图象如图所示，由图象可知，方程f (x )＝0只有一解x ＝1，而原方程有三解，所以方程f (x )＝a 有两个不为1的相异的解，即0<a ≤1.23．函数f (x )的定义域为，图象如图1所示；函数g (x )的定义域为，图象如图2所示，方程f (g (x ))＝0有m 个实数根，方程g (f (x ))＝0有n 个实数根，则m ＋n ＝( )A．14 B．12C．10 D．8答案 A解析由题图1可知，若f(g(x))＝0，则g(x)＝－1或g(x)＝0或g(x)＝1，由题图2可知，g(x)＝－1时，x＝－1或x＝1；g(x)＝0对应的x值有3个；g(x)＝1时，x＝2或x＝－2，故m＝7.若g(f(x))＝0，则f(x)＝－1.5或f(x)＝1.5或f(x)＝0，由题图1知，f(x)＝1.5与f(x)＝－1.5对应的x值各有2个，f(x)＝0时，x＝－1或x＝1或x＝0，故n＝7，故m＋n＝14.故选A.24．已知函数y＝f(x)的图象是连续的曲线，且对应值如表：答案 3解析依题意知f(2)>0，f(3)<0，f(4)>0，f(5)<0，根据零点存在性定理可知，f(x)在区间(2,3)，(3,4)，(4,5)内均至少含有一个零点，故函数y＝f(x)在区间上的零点至少有3个．一、高考大题本考点在近三年高考中未涉及此题型．二、模拟大题1．若关于x 的方程(lg ax )·(lg ax 2)＝4的所有解都大于1，求实数a 的取值范围．解原方程可化为(lg a ＋lg x )·(lg a ＋2lg x )＝4，即2(lg x )2＋3(lg a )·(lg x )＋(lg a )2－4＝0，令lg x ＝t >0，则有2t 2＋3(lg a )·t ＋(lg a )2－4＝0的解都是正数，设f (t )＝2t 2＋3(lg a )·t ＋(lg a )2－4，则⎩⎪⎨⎪⎧Δ＝a2－a2－4]≥0，－3lg a4>0，f ＝a2－4>0，解得lg a <－2，∴0<a <1100，∴实数a 的取值范围是⎝⎛⎭⎪⎫0，1100. 2．已知函数f (x )＝－x 2－2x ，g (x )＝⎩⎨⎧x ＋14x ，x >0，x ＋1，x ≤0.(1)求g 的值；(2)若方程g －a ＝0有4个实数根，求实数a 的取值范围．解 (1)利用解析式直接求解得g ＝g (－3)＝－3＋1＝－2.(2)令f (x )＝t ，则原方程化为g (t )＝a ，易知方程f (x )＝t 在t ∈(－∞，1)内有2个不同的解，则原方程有4个解等价于函数y ＝g (t )(t <1)与y ＝a 的图象有2个不同的交点，作出函数y ＝g (t )(t <1)的图象，由图象可知，当1≤a <54时，函数y ＝g (t )(t <1)与y ＝a 有2个不同的交点，即所求a 的取值范围是⎣⎢⎡⎭⎪⎫1，54.3．已知关于x 的二次方程x 2＋2mx ＋2m ＋1＝0.(1)若方程有两根，其中一根在区间(－1,0)内，另一根在区间(1,2)内，求m 的范围；(2)若方程两根均在区间(0,1)内，求m 的范围．解 (1)由条件，抛物线f (x )＝x 2＋2mx ＋2m ＋1与x 轴的交点分别在区间(－1,0)和(1,2)内，如图1所示，得⎩⎨⎧f ＝2m ＋1<0，f －＝2>0，f＝4m ＋2<0，f＝6m ＋5>0⇒⎩⎪⎨⎪⎧m <－12，m ∈R ，m <－12，m >－56.即－56<m <－12.(2)抛物线与x 轴交点均落在区间(0,1)内，如图2所示，列不等式组⎩⎨⎧f ＝2m ＋1>0，f ＝4m ＋2>0，Δ＝4m 2－m ＋，0<－m <1⇒⎩⎪⎨⎪⎧m >－12，m >－12，m ≥1＋2或m ≤1－2，－1<m <0，即－12<m ≤1－ 2.4．已知函数f (x )＝－x 2＋2e x ＋m －1，g (x )＝x ＋e 2x(x >0)．(1)若y ＝g (x )－m 有零点，求m 的取值范围；(2)确定m 的取值范围，使得g (x )－f (x )＝0有两个相异实根．解 (1)解法一：∵g (x )＝x ＋e 2x≥2e 2＝2e ，等号成立的条件是x ＝e ，故g (x )的值域是[2e ，＋∞)，因而只需m ≥2e，则y ＝g (x )－m 就有零点．解法二：由g ′(x )＝1－e 2x2＝x ＋x －x 2，可作出g (x )＝x ＋e 2x(x >0)的大致图象(如图1)．可知若使y ＝g (x )－m 有零点，则只需m ≥2e.(2)若g (x )－f (x )＝0有两个相异的实根，即g (x )与f (x )的图象有两个不同的交点，作出g (x )＝x ＋e 2x(x >0)的大致图象(如图2)．∵f (x )＝－x 2＋2e x ＋m －1 ＝－(x －e)2＋m －1＋e 2，∴其图象的对称轴为x ＝e ，开口向下，最大值为m －1＋e 2.故当m －1＋e 2>2e ，即m >－e 2＋2e ＋1时，g (x )与f (x )有两个交点，即g (x )－f (x )＝0有两个相异实根．∴m的取值范围是(－e2＋2e＋1，＋∞)．。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

⇒ ≥ ⇒f(x)≥0，“=”成立的条件是：x1=x2即0=1-m且x+ 1 =x+m1
即m=1且m=2（矛盾）
所以f(x)>0
2014年全国高考理科数学2卷：
21.（本小题满分12分）
已知函数 =
（Ⅰ）讨论的单调性；
（Ⅱ）设，当时， ,求的最大值；
（Ⅲ）已知，估计ln2的近似值（精确到0.001）
2015年全国高考理科数学2卷：
21．（本题满分12分）
设函数．
(Ⅰ)证明：在单调递减，在单调递增；
（Ⅱ）若对于任意，都有，求的取值范围．
点评：恒成立，等价于．
2016年全国高考理科数学3卷：
（21）（本小题满分12分）
设函数f（x）=acos2x+（a-1）（cosx+1），其中a＞0，记的最大值为A.
（Ⅰ）求；（Ⅱ）求A；（Ⅲ）证明 ≤2A
（21）（本小题满分12分）
解：（Ⅰ）．
（Ⅱ）当时，
因此，．………4分
当时，将变形为．
令，则是在上的最大值，，，且当时，取得极小值，极小值为．
令，解得（舍去），．
（ⅰ）当时，在内无极值点，，，，所以．
（ⅱ）当时，由，知．
又，所以．
综上，． ………9分
（Ⅲ）由（Ⅰ）得 .
当时， .
当时，，所以 .
当时，，所以 .
2017年全国高考理科数学3卷：
21．（12分）已知函数
(Ⅰ)若，求a的值;
（Ⅱ）设m为整数，且对于任意正整数n， ﹤m，求m的最小值．
解:(Ⅰ)
当时，，在（0，+∞）上是增函数。又f(1)=0，所以0<x<1时， <0,不合题意；
=0,因此当0<X ln(b-1+ )时，g(x)<0
综上，b的最大值为2
（3）由（2）知，g(ln )= -2 b+2(2b-1)ln2
当b=2时，g(ln )= -4 +6ln2>0,ln2> >0.6928
当b= +1时，ln(b-1+ )=ln
g(ln )= -2 +(3 +2)ln2<0
ln2< <0.693
只需证明 ≥x+ 1，且 ≤x+m1
再指出“=”不能成立即可.
设g(x) = (x+1)，g'(x)= 1
x1= 0是g(x)的极小值点，也是最小值点，即
g(x)≥g(0) = 0⇒ ≥x+ 1
设h(x) = (x+m1)
h'(x)= 1
x2= 1m是h(x)的极大值点，也是最大值点，即
h(x)≤h(1m) = 0⇒ ≤x+m1(当m≤2时，x+ 1≥x+m1)
21、已知函数
（1）若a=0,证明：当-1<x<0时，当x>0时， ;
（2）若x=0是f(x)的极大值点，求a．
参考答案
2013年全国高考理科数学2卷：
21.（本小题满分12分）
已知函数
（Ι）设x= 0是f(x)的极值点，求m，并讨论f(x)的单调性；
（Ⅱ）当m≤2时，证明f(x)>0 .
解:（Ⅰ）f'(x)=
（21）解
（Ⅰ） ≥0，等号仅当x=0时成立，所以f（x）在（—∞，+∞）单调递增
（Ⅱ) =f(2x)-4bf(x)= -4b( )+(8b-4)x
（1）当b 2时, ,等号仅当x=0时成立，所以g(x)在(- ,+ )单调递增，而，所以对任意x>0,g(x)>0;
（2）当b>2时，若x满足，2< <2b-2即0<x<ln(b-1+ )时 ,而
（2）若x=0是f(x)的极大值点，求a．
解:（1）若时，，
∴
令，
∴ .
∴当时，，在上单调递增，
当时，，在上单调递减.
∴ ，
∴ 恒成立，
∴ 在上单调递增，
又，
∴当时，；当时， .
（2），
，
，
，
.
设，
∴ ，，，
∴在邻域内，时，，时， .
时，，由洛必达法则得，
设函数f（x）=acos2x+（a-1）（cosx+1），其中a＞0，记的最大值为A.
（Ⅰ）求；（Ⅱ）求A；（Ⅲ）证明 ≤2A
（21）（本小题满分12分）
2017年全国高考理科数学3卷：
21．（12分）已知函数
(Ⅰ)若，求a的值;
（Ⅱ）设m为整数，且对于任意正整数n， ﹤m，求m的最小值．
2018年全国高考理科数学3卷：
2013─2018新课标理科数学函数与导数解答题
2013年全国高考理科数学2卷：
21.（本小题满分12分）
已知函数
（Ι）设x= 0是f(x)的极值点，求m，并讨论f(x)的单调性；
（Ⅱ）当m≤2时，证明f(x)>0 .
2014年全国高考理科数学2卷：
21.（本小题满分12分）
已知函数 =
（Ⅰ）讨论的单调性；
x= 0是f(x)的极值点⇒f'(0)= 0⇒m= 1.
此时，f'(x)= 在(1,+∞)上是增函数，又知f'(0)= 0，
所以x∈(1,0)时,f'(x)< 0；x∈(0,+∞)时,f'(x)> 0.
所以f(x)在(1,0)上是减函数，在(0,+∞)上是增函数.
（Ⅱ）如图所示，当m≤2时，x+ 1≥x+m1
当时，在上递减， y在
∴ ，即
因此时，满足 .
综上所述．
（Ⅱ）由（1）知当时即
则有，当且仅当时等号成立
∴ ，
一方面：，
即．
另一方面：
当时，
∵ ，，
∴ 的最小值为．
2018年全国高考理科数学3卷：
21、已知函数
（1）若a=0,证明：当-1<x<0时，当x>0时， ;
时，，由洛必达法则得，
综上所述，
（Ⅱ）设，当时， ,求的最大值；
（Ⅲ）已知，估计ln2的近似值（精确到0.001）
2015年全国高考理科数学2卷：
21．（本题满分12分）
设函数．
(Ⅰ)证明：在单调递减，在单调递增；
（Ⅱ）若对于任意，都有，求的取值范围．
2016年全国高考理科数学3卷：
（21）（本小题满分12分）