理想流体模型 定常流动 伯努利方程
伯努利方程讲解

关于伯努利方程的知识讲解把一个乒乓球放在倒置的漏斗中间(图8-29),向漏斗口吹气,会把乒乓球吹跑吗?实际正好相反,乒乓球会贴在漏斗上不掉下来.平行地竖放两张纸,向它们中间吹气,会把两张纸吹开吗?实际正好相反,两张纸会贴近(图8-30).怎样解释上述现象呢?现象中涉及空气的流动.你可能不会想到,解释上述现象,跟说明飞机能够上天,用的是同一个道理,这就是流动的流体中压强和流速的关系.通常把液体和气体统称流体。
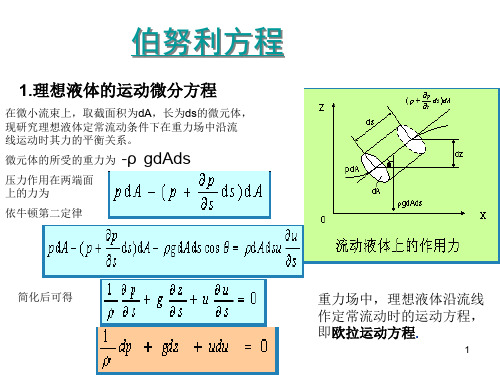
这一节把功能关系应用到流动的流体中,推导压强和流速的关系.研究流体的流动,是一门复杂的学问.初步进行研究,需要作一些限定,采用简单的物理模型,这就是理想流体的定常流动.理想流体液体不容易被压缩,在不十分精确的研究中可以认为液体是不可压缩的.气体容易被压缩,但在研究流动的气体时,如果气体的密度没有发生显著的改变,也可以认为气体是不可压缩的.流体流动时,速度不同的各层流体之间有摩擦力,也就是说,流体具有粘滞性.不同的流体,粘滞性不同.油类的粘滞性较大,水、酒精的粘滞性较小,气体的粘滞性更小.研究粘滞性小的流体,在有些情况下可以认为流体没有粘滞性.不可压缩的、没有粘滞性的流体,称为理想流体.定常流动观察一段河床比较平缓的河水的流动,你可以看到河水平静地流着,过一会儿再看,河水还是那样平静地流着,各处的流速没有什么变化.河水不断地流走,可是这段河水的流动状态没有改变.河水的这种流动就是定常流动.流体质点经过空间各点的流速虽然可以不同,但如果空间每一点的流速不随时间而改变,这样的流动就叫做定常流动.自来水管中的水流,石油管道中石油的流动,都可以看作定常流动.流体的流动可以用流线形象地表示.在定常流动中,流线表示流体质点的运动轨迹.图8-31是液体流过圆柱体时流线的分布.AB处液体流过的横截面积大,CD处液体流过的横截面积小,液体在CD处流得急,流速大.AB处的流线疏,CD处的流线密.这样,从流线的分布可以知道流速的大小.流线疏的地方,流速小;流线密的地方,流速大.伯努利方程现在研究理想流体做定常流动时,流体中压强和流速的关系.图8-32表示一个细管,其中流体由左向右流动.在管的a1处和a2处用横截面截出一段流体,即a1处和a2处之间的流体,作为研究对象.a1处的横截面积为S1,流速为v1,高度为h1.a1处左边的流体对研究对象的压强为p1,方向垂直于S1向右.a2处的横截面积为S2,流速为v2,高度为h2.a2处右边的流体对研究对象的压强为p2,方向垂直于S2向左.经过很短的时间间隔Δt,这段流体的左端S1由a1移到b1,右端S2由a2移到b2.两端移动的距离分别为Δl1和Δl2.左端流入的流体体积为ΔV1=S1Δl1,右端流出的流体体积为ΔV2=S2Δl2,理想流体是不可压缩的,流入和流出的体积相等,ΔV1=ΔV2,记为ΔV.现在考虑左右两端的力对这段流体所做的功.作用在左端的力F1=p1S1,所做的功W1=F1Δl1=p1S1Δl1=p1ΔV.作用在右端的力F2=p2S2,所做的功W2=-F2Δl2=-p2S2Δl2=-p2ΔV.外力所做的总功W=W1+W2=(p1-p2)ΔV.(1)外力做功使这段流体的机械能发生改变.初状态的机械能是a1到a2这段流体的机械能E1,末状态的机械能是b1到b2这段流体的机械能E2.由b1到a2这一段,经过时间Δt,虽然流体有所更换,但由于我们研究的是理想流体的定常流动,流体的密度ρ和各点的流速v没有改变,动能和重力势能都没有改变,所以这一段的机械能没有改变.这样,机械能的改变E2-E1就等于流出的那部分流体的机械能减去流入的那部分流体的机械能.力势能为mgh2=ρgh2ΔV.机械能的改变为右边对这段液体的的作用力向左,而这段液体的位移向右,所以功是负值。
伯努利方程的应用实际液体的流动 (1)

8.3 8.8 13
影响液体和气体流动性的因素是不同的。
在国际单位制中黏度的单位是Pas (帕秒)。黏度也 常用P (泊)作单位
1 P = 0.1 Pa s
17
二、 黏性流体的运动规律
p1
1 2
2 v1
gh1 p2
1 2
2 v2
gh2 w
黏性流体作稳定流动时所遵从的规律。 如果黏性流体沿着粗细均匀的管道作定常流动
vr Re
21
由层流过渡到湍流的雷诺数,称为临界雷诺数 Rec 。圆形管道的临界雷诺数Rec在1000 ~ 1500的 范围内。 当流速的值使雷诺数Re处于临界值Rec时,此时 的流速就是临界流速,大小为
Rec vc r
如果流速从低于vc增大到高于vc,那么流动将 会从层流转变为湍流。
黏性流体在水平放置的圆形截面的管道中作层流时, 算得流量 为
p1 p2 4 QV ( )r 8 l
l 和 r 分别是管道的长度和半径。上式称为泊肃叶定律。
流阻 如果令 R f 8l ,那么上式可写成: 4
R
P P 1P 2 Q Rf Rf
20
*四、湍流和雷诺数 (Turbulent flow ) 湍流 流体中沿垂直于管轴方向的速度分量的 不规则流动。 实验表明,发生湍流的临界流速与雷诺数 Re 相对应。 雷诺数
若流体密度为,小球密度为,半径为r,速率为 v,则小球所受的三个力平衡,即 23
4 3 4 3 r g 6 r v r g 3 3
由此可得小球下落的速率
2r v ( ) g 9
假如测出速率v,可求出液体的黏度 ; 若流体的 黏度已知, v已测出,可求得小球(或液滴)的半径。
伯努利方程
p c T v
t
51
二、空穴现象(气穴 )
• 1. 定义:由于压力降到某一值,而有气泡产生的现象称之为气
穴现象。
• 2. 原因:局部压力降低(漩涡、涡流)。
• 3. 后果:减少流量,引起流量、压力波动,使容积效率降低。
•
破坏连续性和动态性能,产生振动、噪声、冲击,
47
一、液压冲击
4. 冲击压力
1)冲击现象描述 2)冲击压力计算
根据动量方程
如果流速v0不是降到零,而是降到
v1,则上式变为: p c(v0 v1 ) c4v8
49
3)非完全冲击情况下的冲击压力
p c T v
t
50
3)非完全冲击情况下的冲击压力
• 关闭阀门时间 t T 2时l 称为完全冲击, t>T时为非完全冲击。 c
8
(一)理想液体的伯努利方程 ——能量方程
• 1. 压力所做的功
9
(一)理想液体的伯努利方程 ——能量方程
• 2. 重力所做之功 • 以水平面为基准面。
10
(一)理想液体的伯努利方程 ——能量方程
• 3. 动能变化 在稳定流动中,AB段液体的动能是不变的, AB段运动到AB段时动能的增量仅是AA段液 体移到BB段动能的变化,故动能的增量为:
6)适用于不可压缩流体,=const(对于气体在v<50m/s时也可
按该式计算,如果v>50m/s且要求精度较高时,则应按可压缩 流体的伯努利方程计算,这时要计算气体的内能)。 7)基准面是水平面。
19
伯努利方程的应用例题
• 2. 应用举例 例:图3-8为文氏流量计
第4章 伯努利方程

dK dt
d dt
V
v dV
F
由于外力有质量力和表面力之分,故上式右边的等式可写为
d
dt
v dV
V
fdV
V
S
p n dS
得控制体的动量积分方程
v
V t
dV
S v vndS
fdV
V
S p n dS
3. 水流对喷嘴的作用力
喷嘴
F ( p1 pa ) A1 q(v2 v1)
F ( p1 pa ) A1 q(v2 v1)
由连续方程得
q(v2 v1) v22 A2 (1 A2 / A1)
由伯努利方程
p1
g
v12 2g
p2
g
v
2 2
2g
,
p2
pa
得
p1
pa
1 2
v22
1
A2 A1
v2
单位重量流体的动能 流速水头
2g
z v2 p 总机械能 2g g
总水头
(速度水头) (压强水头) (位置水头)
平面流场(忽略重力作用)
v2 + p C
2
方程表明:沿流线速度和压强的变化是相互制约的,流速高的点上压强低,流 速低的点上压强高。
思考
1. 轿车高速行驶时,为何感觉车身变轻?
4.1.2 理想流体总流的伯努利方程
)
2gh
原理:测量时将静压孔和总压孔感受到 的压强分别和差压计的两个入口相连, 在差压计上可以读出总压和静压之差, 从而求得被测点的流速。
4.4 文丘里流量计 —— 测量管道中的流量
5.2 理想流体的稳定流动

17
5.2 理想流体的稳定流动
理想流体
对理想流体的两个假定:
(1)流体的密度 为常量,即认为流体不可压
缩,也就是认为压强 P 变化如此微小和缓慢,
相应的密度变化完全可以忽略,此时的物态方程 成为不必要。
(2)流体如此之稀,黏滞性可以完全不考虑。
完全不可压缩的,没有粘滞性的流体,称理想流体。
实际中,若流体的流速不大,粘滞性较小,体
PA
1 2
vA2
ghA
PC
1 2
vC 2
ghC
PA PC P0,vA 0
ghA
1 2
vC 2
ghC
vC 2g(hA hC ) 2gh2
15
取B-C流线,应用伯努力方程,有:
PB
1 2
vB 2
ghB
PC
1 2vC 2ghCvB vC,PC P0
PB ghB P0 ghC
PB p0 g(hC hB ) p0 g(h1 h2)
令:a1b1 l1 a2b2 l2
则: V1 S1l1
v2
(流入体积)
v1
V2 S2l2
对理想流体的定常流动:
(流出体积)
V1 V2 V
6
因为没有粘滞性和耗散,运用机械能守恒定 律分析可知,对流管内作定常流动的流体,考 察其能量的变化时,只需计算两端体积元的能 量差。
对动能的变化:
Ek
gH
1 2
(
S12 S22
1)v12
因此体积流量为:
H
v1 S1
v2
S2
Q v1S1 S1S2
2 gH S12 S22
13
伯努利方程

伯努利方程Bernoulli equation流体在忽略粘性损失的流动中,流线上任意两点的压力势能、动能与位势能之和保持不变。
这个理论是由瑞士数学家丹尼尔第一·伯努利在1738年提出的,当时被称为伯努利原理。
后人又将重力场中欧拉方程在定常流动时沿流线的积分称为伯努利积分,将重力场中无粘性流体定常绝热流动的能量方程称为伯努利定理。
这些统称为伯努利方程,是流体动力学基本方程之一。
流体宏观运动机械能守恒原理的数学表达式。
1738年瑞士数学家D.伯努利在《水动力学──关于流体中力和运动的说明》中提出了这一方程。
它可由理想流体运动方程(即欧拉方程)在定态流动条件下沿流线积分得出;也可由热力学第一定律导出。
它是一维流动问题中的一个主要关系式,在分析不可压缩流体的定态流动时十分重要,常用于确定流动过程中速度和压力之间的相互关系。
方程的形式对于不可压缩的理想流体,密度不随压力而变化,可得:式中Z为距离基准面的高度;p为静压力;u为流体速度;ρ为流体密度;g为重力加速度。
方程中的每一项均为单位质量流体所具有的机械能,其单位为N·m/kg,式中左侧三项,依次称为位能项、静压能项和动能项。
方程表明三种能量可以相互转换,但总和不变。
当流体在水平管道中流动时Z不变,上式可简化为:此式表述了流速与压力之间的关系:流速大处压力小,流速小处压力大。
对于单位重量流体,取管道的1、2两截面为基准,则方程的形式成为:式中每一项均为单位重量流体的能量,具有长度的因次,三项依次称为位头、静压头和动压头(速度头)。
方程的应用伯努利方程阐明的位能、动能、静压能相互转换的原理,可用来分析计算一些实际问题,例如:①计算流体从小孔流出的流速设在容器中盛有液体,液面维持不变,距液面下h处的容器壁面上开有一小孔,液体在重力作用下自小孔流出。
据伯努利方程可以计算出液体由小孔流出时的平均流速为:式中Cd为孔流系数,其值由实验确定,约为0.61~0.62;g为重力加速度。
12理想流体的定常流动
2 机械能的变化量
势能的变化量:∆ Ep = mg∆h = ρg ∆V (h2 - h1) 动能的变化量:∆ Ek = ∆ m (v2/2) =ρ∆V(v22 - v21)/2 根据功能原理,则有: A = ∆Ep + ∆ Ek (p1-p2) ∆V= ρg ∆V (h2-h1) +ρ∆V(v22-v21)/2
【问题】
( 1)
v ds v ds v ds 1 1 2 2 3 3
?
3
1 2
( 2)
v毛细管 v动脉
?
四、 伯努利方程能量守恒定律在流体力学中的应用
理想液体伯努利方程的推导
理想液体伯努利方程
1 外力对液体所做的功 A = p1S1v1 ∆ t - p2S2v2 ∆ t = (p1-p2) ∆V
整理后得理想液体伯努利方程为: p1 +ρg h1 +ρv12 / 2 = p2+ρg h2 +ρv22/2
或 p+ρg h+ v2 ρ/2= C(C为常数)
理想流体在管道中稳定流动时,同一管道内任 一截面上的总能量应该相等。
理想液体伯努利方程的物理意义
在密闭管道内作定常流动的理想流 体具有三种形式的能量,即压力能、势 能和动能。在流动过程中,三种能量之 间可以互相转化,但各个过流断面上三 种能量之和恒为定值。
于极为次要的地位,就可以看成理想流体.
2.流线与流管 流线——曲线上的每一点的切线方向和位于该点 处流体质元的速度方向一致.流线不会相交。
v1
1
v2
2
3
v3
流管——通过流体内部某一截面的流线围成的管子.
一般流线分布随时间改变,流迹并不与流线重合. 由于流线不会相交,流管内、外的流体不会穿越管壁。
大学物理伯努利方程及其应用
即流体从小孔流出的速度与流体质量元由液面处自由下落到小孔处的流
速大小相等。
虹吸管
左图是利用虹吸管从水库引水的示意图。
B A
hA
hB
虹吸管粗细均匀,选取 A、C 作为参考点。
水库表面远大于虹吸管截面,由连续性原理可
C
知
hc
v A,所0 以此例实质为小孔流速问题
v 2g(hA hC )
如果hA-hB<0 ,管内流速没有意义。如果管口比水库面高,在没有外界帮
选d 点所在平面为参考平面,对a 、d 两
h1 ab
h2
点应用伯努力方程,有
d
g (h2
h1 )
1 2
vd2
解得
vd 2gh2 h1
因b、c、d 各点处于截面积相同的同一流管中,所以
由连续性原理,有:
对于a、b 两点,有 对于a、c 两点,有
得:
vb vc vd 2gh2 h1
pb p0
S2
A2 F2v2t P2S2v2t P2V Δt
P1
h2
由功能原理 : A Ek E p 即
S1
h1
( P1
PP12)12Vv1212(vg22h1
v12 )V
P2
1 2
g(h2 h1)V
v22 gh2
或 P 1 v 2 gh C
2
上式即为伯努利方程的数学表达式。
二、伯努利方程的意义
求 (1)管2、3、4的流量; (2)管2、3、4的流速; (3)管1、4中的压强差.
2
v2
1
v1
4
v4
3
v3
解 (1)由连续性原理知 Q4= Q1 = 900cm3•s-1
大学物理--流体的运动
⑸在流量一定的情况下,细管和粗管哪个容易发生湍流?
血压测量原理
生理流动
人体中时刻存在着各种生理流动,对生命和健康最
重要的是血液循环与呼吸系统 . 健康人体的血管和气管 等流动管道都具有良好的弹性,管壁可以吸收扰动能量, 起着稳定流场的作用,因而生理流动的临界雷诺数(由层 流转变为湍流时的雷诺数 )要远远超过刚性管流的临界
雷诺数.
人体主动脉按直径不同 , 其雷诺数约在 1000 ~1500, 在正常情况下 , 血流仍保持层流状态 . 在气 管和支气管中气体的流动也是类似的,正常呼吸时, 气体一直保持层流状态 , 只有当深呼吸或咳嗽时 , 才会发生湍流 , 此时 , 雷诺数峰值可高达不可思议 的50000,在相同雷诺数条件下,层流的摩擦阻力和 能量损耗要远远低于湍流,而湍流中的物质交换和 化学反应又比层流充分得多.难怪力学专家会发出 惊叹:人体已经发展成为近乎最优化的系统.
第一节
理想流体的定常流动
一、理想流体(ideal fluid)
实际流体:具有流动性(fluidity);
黏滞性(viscosity);
可压缩性(compressibility)等
理想流体:绝对不可压缩,完全没有黏滞性的流体。
----物理模型 ,是实际流体的近似或抽象。 模型方法:模型法的意义;适用范围。
二、定常流动(steady flow)
1.流场的概念
2.定常流动
一般流动:v(x、y、z、t)
定常流动: v ( x、y、z) 3.流线和流管 1) 为了形象地描述流体的流动情况,在流体流过的空 间作许多曲线,曲线上每一点的切线方向和流经该处的 流体粒子的速度方向一致-----流线。
定常流动的流线特点:
⑴流体的动能的变化
程守洙《普通物理学》(第6版)(上册)笔记和课后习题(含考研真题)详解(3-5章)【圣才出品】
5 / 127
圣才电子书 十万种考研考证电子书、题库视频学习平台
四、定轴转动刚体的角动量定理和角动量守恒定律 1.刚体的角动量 设刚体绕 z 轴转动,则刚体绕定轴的角动量为
2.定轴转动刚体的角动量定理 (1)角动量定理的微分形式 刚体所受到的对某给定轴的总外力矩等于刚体对该轴的角动量的时间变化率.
二、力矩 转动惯量 定轴转动定律 1.力矩 力矩是指力的作用点相对给定点的位矢 r 与力 F 的矢积.对于定轴转动,r 是力作用点 相对于转动轴的位矢. (1)力 F 对 O 点的力矩 M0
M0=r×F
(2)力 F 对转轴 Oz 的力矩
图 3-1 力矩
2 / 127
圣才电子书 十万种考研考证电子书、题库视频学习平台
4.转动惯量 (1)转动惯量的定义 转动惯量是转动中惯性大小的量度,且
(2)转动惯量的积分形式
积分式中 dm 是质元的质量,r 是质元到转轴的距离. (3)平行轴定理 刚体对任一转轴的转动惯量等于刚体对通过质心并与该轴平行的轴的转动惯量 JC 加上 刚体质量与两轴间距离 h 的二次方的乘积. (4)刚体转动惯量大小的决定因素
圣才电子书 十万种考研考证电子书、题库视频学习平台
第 3 章 刚体和流体的运动
3.1 复习笔记
一、刚体模型及其运动 1.力学分析方法 对物体复杂运动的研究,一般的力学分析方法可归纳为: (1)突出主要矛盾,撇开次要因素,建立理想模型; (2)将质点系化整为零,以质点或质元为研究对象,作为突破口; (3)根据受力情况,正确地画出受力图; (4)根据已知条件或初始条件,选用所需的基本原理、定律,列出方程式; (5)根据要求,求解方程,统一变量,积零为整,用积分法求出结果; (6)讨论分析所得结果,检验是否正确. 2.刚体 刚体是一种特殊的质点系,无论在多大外力的作用下,系统内任意两质点间的距离始终 保持不变. 3.平动和转动 (1)平动 平动是指当刚体运动时,刚体内任何一条给定的直线,在运动中方向始终保持不变的运 动. 在平动中,各个质点在同一段时间内位移相同,且具有相同的速度和加速度. (2)转动
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
b两点的压强都是大气 压pa=pb=p0.由伯努利 方程,得
1 2
vb2
p0
gh
p0
式中ρ是水的密度,由此求出
vb 2gh
即管口流速和物体从高度h处自由落下的速度相等. 流量是单位时间内从管口流出的流体体积,常用Q 表示,根据这个定义,可得
Q Svb S 2gh
A P1S1V1 P2 S2V2 t
因为流体被认为不可压缩。所以a1b1和a2b2两小段流体
的体积S1v1t和S2v2t必然相等,用V表示,则上式可
写成
A P1 P2 V
其次,计算这段流体在流动中能量的变化对于稳定
流动来说,在b1a2间的流体的动能和势能是不改变的。
由此,就能量的变化来说,可以看成是原先在a1b1处的
流管:在流体中任何一束流线都可形成流管[图 (b)].
三、伯努利方程
伯努利方程是流体动力学的基本定律,它说明了
理想流体在管道中作稳定流动时,流体中某点的压 强p、流速v和高度h三个量之间的关系.
下面用功能原理导出伯努利方程。
如图所示,我们研 究管道中一段流体的运 动。设在某一时刻,这 段流体在a1a2位置,经 过极短时间t后,这段 流体达到b1b2位置
二、定常流动
定常流动:流体流动时,其中任一质元流过不同地 点的流速不尽相同,而且流经同一地点,其流速也 会随时间而变.但在某些常见的情况下,尽管流体 内各处的流速不同,而各处的流速却不随时间而变 化,这种流动称为定常流动.
流线:为了描述流体的运动,可在流体中作一系列曲 线,使曲线上任一点的切线方向都与该点处流体质元 的速度方向一致.这种曲线称为流线[图 (a)]
例题3-11 水电站常用水库出水管道处水流的动 能来发电.出水管道的直径与管道到水库水面高 度h相比为很小,管道截面积为S.试求出水处水 流的流速和流量。
解:把水看作理想流体.在水库中出水管道很小,
水流作定常流动.如图所示,在出水管中取一条流 线ab.在水面和管口这两点处的流速分别为va和vb.在 大水库小管道的情况下,水面的流速va远比管口的 的小,可以忽略不计, 即va=0.取管口处高度为
在一些实际问题中,当可压缩性和黏滞性只是 影响运动的次要因素时,可把流体看作绝对不可压 缩,且完全没有黏性的理想流体.
当理想流体流动时,由于忽略了黏性力,所以 流体各部分之间也不存在这种切向力,流动流体仍 然具有静止流体内的压强的特点,即压力总是垂直 于作用面的.
流体动压强:流体在流动时内部的压强称为流体动 压强.
*§3-6 理想流体模型 定常流动 伯努利方程
一、理想流体模型
流体:液体和气体都具有流动性,统称为流体。
流体特点:流体各部分很容易发生相对运动,因而没 有固定的形状,其形状随容器的形状而异.液体不易 被压缩,具有一定的体积,能形成自由表面;气体易 被压缩,没有固定的体积,不存在自由表面,可弥漫 于整个容器内的空间.
因为时间t极短,所以a1b1和a2b2是两段极短的位移, 在每段极短的位移中,压强p、截面积S和流速v都可看 作不变。设p1、S1、v1和p2、S2、v2分别是a1b1与a2b2处 流体的压强、截面积和流速,则后面流体的作用力是 p1S1,位移是v1 t,所作的正功是p1S1v1 t ,而前面 流体作用力作的负功是-p2S2v2 t ,由此,外力的总 功是:
流体,在时间t内移到了a2b2处,由此而引起的能量增
量是
E2 E1
(
1 2
m
v2 2
mgh2
)
(
1 2
mv12
mgh1)
V [( 1
2
v2 2
gh2 )
(1 2
v12
gh1 )]
从功能原理得
( p1
p2 )V
V
[(
1 2
v
2
2
gh2
)
(1 2ຫໍສະໝຸດ v12gh1 )]
整理后得
p1
1 2
v12
gh1
p2
例题3-12 测流量的文特利 流量计如图所示.若已知 截面S1和S2的大小以及流 体密度ρ,由两根竖直向 上的玻璃管内流体的高度 差h,即可求出流量Q.
解:设管道中为理想流体作定常流动,由伯努利方程,
得
1 2
v12
p1
1 2
v22
P2
因p1-p2=ρgh,又根据连续性方程,有
由此解得
S1v1 S2v2
a1 b1
p2 S2
v
1
h1
a2 b2
v h2p2 S2 2
现在计算在流动过程中,外力对这段流体所作的功。 假设流体没有粘性,管壁对它没有摩擦力,那么,管壁 对这段流体的作用力垂直于它的流动方向,因而不作功。 所以流动过程中,除了重力之外,只有在它前后的流体 对它作功。在它后面的流体推它前进,这个作用力作正 功;在它前面的流体阻碍它前进,这个作用力作负功。
1 2
v
2
2
gh2
这就是伯努利方程,它表明在同一管道中任何一点处, 流体每单位体积的动能和势能以及该处压强之和是个 常量。在工程上,上式常写成
p v2 h 常量
g 2g
p
g
、v 2 2g
、h
三项都相当于长度,分别
叫做压力头、速度头、水头。
所以伯努利方程表明在同一管道的任一处,压 力头、速度头、水头之和是一常量,对作稳定 流动的理想流体,用这个方程对确定流体内部 压力和流速有很大的实际意义,在水利、造船、 航空等工程部门有广泛的应用。
v1
S2 S1
v2
S2
2gh S12 S22
于是求出流量为
Q S1v1 S1S2
2gh S12 S22
选择进入下一节 §3-0 教学基本要求 §3-1 刚体模型及其运动 §3-2 力矩 转动惯量 定轴转动定律 §3-3 定轴转动中的功能关系 §3-4 定轴转动刚体的角动量定律和角动量守恒定律 §3-5 进动 §3-6 理想流体模型 定常流动 伯努利方程 §3-7 牛顿力学的内在随机性 混沌
