普通物理学教程力学课后答案高等教育出版社第七章-刚体力学习题解答
大学物理刚体力学习题讲解

(A) 只有(1)是正确的.
(B)
(B) (1) 、(2)正确,(3) 、(4) 错误. (C) (1)、(2) 、(3) 都正确,(4)错误. (D) (1) 、(2) 、(3) 、(4) 都正确.
M=L×F |M|=|L|×|F|sinθ
2. 一轻绳绕在有水平轴的定滑轮上,滑轮的转动惯量为J,绳下
4. 一作定轴转动的物体,对转轴的转动惯量J= 3.0 kg·m2,角速度0=6.0 rad/s.现对物体加一 恒定的制动力矩M =-12 N·m,当物体的角速度 减慢到=2.0 rad/s时,物体已转过了角度 =
4.0rad
M=Jβ
2as=v`2-v2 2βθ= 2 -02
5. 质量为m1, m2 ( m1 > m2) 的两物体,通过一定滑轮用绳
6. 一长为1 m的均匀直棒可绕过 其一端且与棒垂直的水平光滑固 定轴转动.抬起另一端使棒向上 与水平面成60°,然后无初转速 地将棒释放.已知棒对轴的转动
惯量为1/3ml3,其中m和l分别为
棒的质量和长度.求: (1) 放手时棒的角加速度; (2) 棒转到水平位置时的角
加速度.
l m g
O 60°
端挂一物体.物体所受重力为P,滑轮的角加速度为.若将物体
去掉而以与P相等的力直接向下拉绳子,滑轮的角加速度将
(A) 不变. (B) 变小.
(C) 变大. (D) 如何变化无法判断.
[ C]
①物体状态at=rβ (P-atm)r=Jβ ②拉力情况下Pr=Jβ
挂重物时,mg-T= ma =mRβ, TR =J, P=mg
5. 解:由人和转台系统的角动量守恒
J11 + J22 = 0 其中 J1=75×4 kg·m2 =300 kg·m2,1=v/r =0.5 rad / s J2=3000 kg•m2
大学物理课后习题答案 第七章

Q
RT1
ln
V2 V1
8.31 400 ln 0.005 0.001
5.35 103 J
(2) 根据卡诺循环的效率公式可得
1 T2 A净 T1 Q吸
A净
(1
T2 T1
)Q吸
(1
300 ) 5.35 103 400
1.34 103 J
(3)由能量守恒 Q吸 A净 Q放 可得
Pa Va )
1 2 (Pb
Pa ) (Vb
Va )
9.5 102 J
A 100 10.5% Q吸 950
B
C 2 V (L)
62
大学物理上习题册参考解答
10、一定质量理想气体(摩尔热容比为 γ)的某循环过程的 T-V 图如下,其中 CA 为绝
热过程,状态 A(T1,V1)和状态 B(T2,V2)为已知,试问:
RT2
ln
VA VB
R(T1 T2) ln
VA VB
T2 T1 T2
14、一台家用冰箱放在室温为 300K 的房间内,做一盘 2.09105 J 的热量。设冰箱为理想卡诺制冷机。 (1)求做一盘冰块所需要的功;
℃的冰块需从冷冻室取走
(2)若此冰箱能以 2.09102 J / s 的速率取出热量,求冰箱的电功率。
mR mR
60
大学物理上习题册参考解答
6、某理想气体在 P-V 图上等温线与绝热线相交于 A
点(如图所示)。 已知 A 点的压强 P1=2×105Pa,体积 V1=0.5 P ×10-3m3 ,而且 A 点处等温线的斜率与绝热线斜率之比为
0.714,现使气体从 A 点绝热膨胀至 B 点,其体积 V2=1×10-3m3。
课堂习题与练习题 第七章 刚体的平面运动_ppt课件

理论力学电子教程
第七章 刚体的平面运动
由上可得,平面运动随基 点平动的运动规律与基点的选 择有关,而绕基点转动的规律
与基点选取无关。 即 、与
基点选取无关
理论力学电子教程
第七章 刚体的平面运动
第二节
M
平面图形内各点速度的求解
M
车轮作平面运动
连杆AB作平面运动
齿轮A作平面运动
这些作平面运动的刚体,其上任一点的速度和加速度如何求?
理论力学电子教程
第七章 刚体的平面运动
【思考与讨论】
如图平面机构,由四根杆依次铰接而成。已知AB=BC=2r, CD=DE=r,AB 杆与ED杆分别以匀角速度1 和2 绕A、E 轴转动。在图示瞬时AB 与CD 铅直、BC 与 DE水平,试求该 瞬时 BC 杆转动的角速度。
B
C
2
1
D
E
A
理论力学电子教程
(2)绕基点 A 的转动(相对运动)。
y
S
y' B A x'
x
O
理论力学电子教程
第七章 刚体的平面运动
因此,平面图形内任意一点B 的运动也是这两种运动的 合成,可用点的速度合成定理来计算B 点的速度。 取A为基点, 将动系固结于A点,动系作平移。 取B为动点, 则B点的运动可视为牵连运动为平移和相对 运动为圆周运动的合成。 牵连运动为平移,则
理论力学电子教程
第七章 刚体的平面运动
刚体的平面运动可简化为平面图形在其自 身平面内的运动。
理论力学电子教程
第七章 刚体的平面运动
二、平面运动方程
为了确定代表平面运动刚体的平面图形的位置,我线段OM的位置可 用O点的坐标和AB与x轴夹 角表示.因此图形S 的位
力学第七章练习题

3解题例如例题5—5 如图5—9所示。
弹簧的质量忽略不计,而倔强系数6.11=k 牛顿/米。
绳子质量忽略不计且不可伸长。
滑轮的半径=R 10厘米,绕其抽转动的转动惯量01.0=I 千克.2米。
空气阻力不计,求质量1=m 千克的物体从静止开始(此时弹簧无伸长)落下1=h 米时的速度大小(h v )。
己知 m N k /6.11=,cm R 10= ,201.0m kg I ⋅=,m h 1=,kg m 1=求 h v例题5一6 一均匀棒长4.0=l 米,质量1=M 千克,可绕通过其上端O 的水平轴转动,质量01.0=m 千克的弹片以速度200=v 米/秒射入棒中,射入处离O 点为米〔图5-11〕。
求棒与弹片一起转动时的角速度ω,及转过的角度θ。
l 、M 、m 、弹片射入处求ω、θ角动量与刚体转动练习题一. 选择题1. 人造地球卫星绕地球做椭圆轨道运动,卫星轨道近地点和远地点分别为 A 和 B 。
用 L 和 Ek 分别表示对地心的角动量及其动能的瞬时值,那么应有.,)(kB kA B A E E L L A >>.,)(kB kA B A E E L L B <=.,)(kB kA B A E E L L C >=.,)(kB kA B A E E L L D << 解:由角动量守恒 B A L L = 由机械能守恒,因为势能 pB pA E E < .kB kA E E >∴答案 :(C)2. 由一半径为 R 的水平圆转台,可绕通过其中心的竖直固定光滑轴转动,转动惯量为 J ,开始时转台以匀角速度ωo 转动,此时有一质量为 m 的人站在转台中心,随后人沿半径向外跑去,当人到达转台边缘时,转台的角速度为图5—9.)(02ωmR J J A + .)()(02ωRm J J B + .)(02ωmR J C .)(0ωD 解:由角动量守恒 ωω)(020mR J J +=+.02ωωmR J J +=∴ 答案 :(A)3. 如下图,一静止的均匀细棒,长为 L 、质量为 M ,可绕通过棒的端点且垂直于棒长的光滑固定轴 O 在水平面内转动,转动惯量为1/3 ML2. 一质量为 m 、速率为 v 的子弹在水平面内沿与棒垂直的方向射入并穿入棒的自由端,设穿过棒后子弹的速率为1/2 v , 那么此时棒的角速度应为.)(ML mv A .23)(ML mv B .35)(ML mv C .47)(MLmv D 解:由角动量守恒 ω23121ML vl m mvl +⋅= .23ML mv =∴ω 答案 :(B )4. 关于力矩有以下几种说法:〔1〕对某个定轴而言,内力矩不会改变刚体的角动量。
大学物理 刚体力学基础习题思考题及答案

习题55-1.如图,一轻绳跨过两个质量为m 、半径为r 的均匀圆盘状定滑轮,绳的两端分别挂着质量为m 2和m 的重物,绳与滑轮间无相对滑动,滑轮轴光滑,两个定滑轮的转动惯量均为2/2mr ,将由两个定滑轮以及质量为m 2和m 的重物组成的系统从静止释放,求重物的加速度和两滑轮之间绳内的张力。
解:受力分析如图,可建立方程:ma T mg 222=-┄① ma mg T =-1┄②2()T T r J β-=┄③βJ r T T =-)(1┄④ βr a = ,2/2J mr =┄⑤联立,解得:g a 41=,mg T 811= 。
5-2.如图所示,一均匀细杆长为l ,质量为m ,平放在摩擦系数为μ的水平桌面上,设开始时杆以角速度0ω绕过中心O 且垂直与桌面的轴转动,试求:(1)作用于杆的摩擦力矩;(2)经过多长时间杆才会停止转动。
解:(1)设杆的线密度为:lm =λ,在杆上取一小质元dm d x λ=,有微元摩擦力:d f dmg gd x μμλ==,微元摩擦力矩:d M g xd x μλ=,考虑对称性,有摩擦力矩:20124l M g xd x mgl μλμ==⎰; (2)根据转动定律d M J Jdtωβ==,有:000t Mdt Jd ωω-=⎰⎰, 2011412mglt m l μω-=-,∴03l t g ωμ=。
或利用:0M t J J ωω-=-,考虑到0ω=,2112J ml =, 有:03l t gωμ=。
5-3.如图所示,一个质量为m 的物体与绕在定滑轮上的绳子相联,绳子的质量可以忽略,它与定滑轮之间无滑动。
假设定滑轮质量为TM 、半径为R ,其转动惯量为2/2MR ,试求该物体由静止开始下落的过程中,下落速度与时间的关系。
解:受力分析如图,可建立方程:m g T ma -=┄①βJ TR =┄②a R β= ,212J mR =┄③ 联立,解得:22mg a M m =+,2Mmg T M m=+, 考虑到dv a dt =,∴0022v t mg dv dt M m=+⎰⎰,有:22mg t v M m =+。
第七章 刚体动力学(讲义)

MO = ∑ MO ( Fi ) = ∑ (ri × Fi )
i =1 i =1
n
n
注意,主矩的的计算与参考点的选取有关。例如,将参考点由 O 改成 O′ ,于是
MO = ∑ ri × Fi = ∑
i =1 i =1
n
n
(ri′ + OO′) × Fi = ∑ (ri′ × Fi ) + OO′ × ∑ Fi
R = ∑ Fi
i =1
n
这是个自由矢量,它只给出矢量的大小和方向,不过问作用点的位置。 对力系的矩也可作类似的讨论。对于共点力系,合力的矩等于各个力对同一点的矩的矢量 和,即
MO ( F) = r × F = r × ∑ Fi = ∑ (r × Fi )
i =1 i =1
n
n
一般的力系中不一定存在合力,因此也就谈不上求合力的矩。但是每个力相对于同一参考 点的力矩是矢量,我们可以求这些矢量的和,并称为主矩,记为 MO ,即有
(II)刚体绕质心的转动:
dLc = ∑ ric × Fi (对质心的角动量定理) dt i
第一个式子求质心运动等同于质点动力学,可以解出刚体的平动运动部分(三个方程解三个运 动变量) 。第二个式子又可求出刚体的转动角速度 ω ( L 与 ω 有一定的关系) ,于是刚体的运动 就完全确定了。由角动量定理求刚体的转动角速度是重点讨论的内容。 7.2 作用在刚体上的力和力矩 通常矢量指的是所谓自由矢量(free vector) :只有大小和方向,它可以平行自由移动。 作为物理量的矢量则不然,例如,力矢量 F ,为了完全确定这个力,还要说明力的作用点, 若用 r 表示作用点的话,则要有两个矢量 F 和 r ,这个力才完全被确定下来。这种矢量被称为定 位矢量(bound vector) 。除了力矢量是定位矢量外,质点的速度和加速度等也是定位矢量的例 子。 还有一种矢量,称为滑动矢量(sliding vector) ,它可在包含该矢量的一直线上自由移动。 例如,作用在刚体上的力(见下面的讨论) 。
(彩色版第七版)理论力学哈工大课后题答案
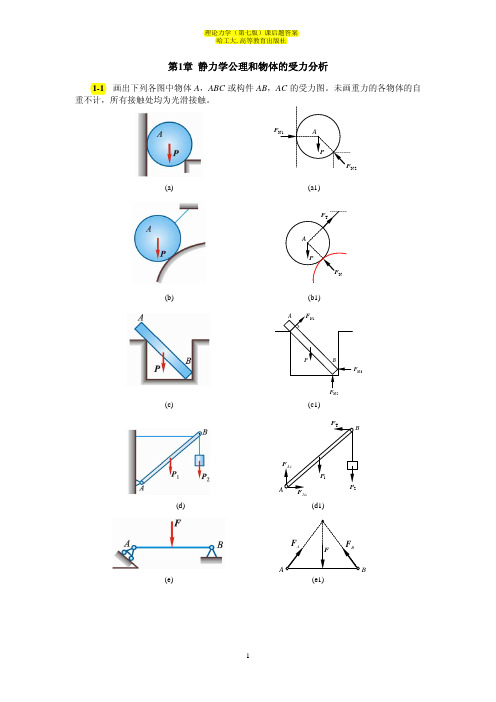
第1章 静力学公理和物体的受力分析1-1 画出下列各图中物体A ,ABC 或构件AB ,AC 的受力图。
未画重力的各物体的自重不计,所有接触处均为光滑接触。
2F(a)(a1)(b) (b1)2N F 3N(c) (c1)Ax(d) (d1)B(e) (e1)Bq(f) (f1)(g)1F 2(h)(h1)Ax(i)(i1)(j)(j1)F(k) (k1)BA F FF ′ (l) (l2) (l3)图1-11-2画出下列每个标注字符的物体的受力图。
题图中未画重力的各物体的自重不计,所有接触处均为光滑接触。
22N(a1)2AxFAx(a2)3N(b)(b1)N3′(b2) (b3)1N2AxF(c)(c1)1N2N2Ax(c2)(c3)(d) (d1)CDy(d2)(d3)CxBxByF By′(e) (e1)(e2) (e3)ByBxAx(f) (f1)AxBx F′(f2)(f3)FB(g) (g1)BCx′F(g3)(h)(h1)FFAxC(i) (i1) (i2)F(i3)(i4)AyFFFCy (j) (j1)(j2) 2TFDx3TEyFCyEx′(j3) (j4) (j5)BBDECyF(k)(k1)BBCx (k2) (k3) DEA1F(l) (l1) (l2)A C E(l3) (l4)或CDxFEyFEy(l2)’(l3)’ (l4)’F′(m)(m1)EADFH2FAD′(m2) (m3)BN(n)q3N(n2)G(o)(o1)BADB(o2) (o3) (o4)图1-2第2章 平面汇交力系与平面力偶系2-1 铆接薄板在孔心A ,B 和C 处受3个力作用,如图2-1a 所示。
N 1001=F ,沿铅直方向;N 503=F ,沿水平方向,并通过点A ;N 502=F ,力的作用线也通过点A ,尺寸如图。
求此力系的合力。
(a)(b)图2-1解 (1) 几何法作力多边形abcd ,其封闭边ad 即确定了合力F R 的大小和方向。
普通物理学(第七版)

教学资源
《普通物理学(第七版)》电子教案提供了PowerPoint格式的文件 。
《普通物理学(第七版)》网络课程结构安排与主教材相同,覆盖所有的知识点,包括基础知识、例题、习 题等模块,为教师和学生开展网上学习提供完整的课程内容和动画、图形等多媒体资源 。
教材特色
《普通物理学(第七版)》在修订过程中继承了原书的特色,体系未有大的变化,尽量做到选材精当,论述 严谨,行文简明。修订中对经典物理内容进行了精简和深化,以增强现代的观点和信息,对近代物理内容进行了 选取和通俗化,以加强学习新知识的基础,并适当介绍了现代工程技术的新发展和新动态 。
该教材上册由高等教育出版社于2016年5月24日出版 ,下册由高等教育出版社于2016年7月19日出版 。
内容简介
《普通物理学(第七版)》本书分为上、下两册,上册主要内容包括运动和力、运动的守恒量和守恒定律、 刚体和流体的运动、相对论基础、气体动理论、热力学基础、静止电荷的电场、恒定电流的磁场、电磁感应电磁 场理论,共九章;下册主要内容包括机械振动和电磁振荡、机械波和电磁波、光学、早期量子论和量子力学基础、 激光和固体的量子理论简介、原子核物理和粒子物理简介,共六章。
作者简介
程守洙:江苏南京人。1930年毕业于金陵大学物理系(1952年并入南京大学物理系)。曾任金陵大学讲师、 副教授 。
江之永:同济大学教授,旌德江村人,中共党员。1930年毕业于震旦大学工学院,历任光华大学教授、暨南 大学教授、理学院代院长,同济大学数学力学系主任,上海市物理学会第二、三届副理事长。从事物理学教材建 设和教学法研究 。
该书分上、下两册出版,上册共九章,包括力学、热学、电场和磁场;下册共六章,包括振动、波动、光学 和量子物理。
成书过程
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第七章刚体力学习题解答7.1.2 汽车发动机的转速在12s 内由1200rev/min 增加到3000rev/min.⑴假设转动是匀加速转动,求角加速度。
⑵在此时间内,发动机转了多少转?解:⑴21260/2)12003000(/7.15s rad t===-∆∆πωβ⑵rad 27.152)60/2)(12003000(21039.26222202⨯===∆⨯--πβωωθ对应的转数=42010214.3239.262≈⨯=⨯∆πθ7.1.3 某发动机飞轮在时间间隔t 内的角位移为):,:(43s t rad ct bt at θθ-+=。
求t 时刻的角速度和角加速度。
解:23212643ct bt ct bt a dtd dtd -==-+==ωθβω7.1.4 半径为0.1m 的圆盘在铅直平面内转动,在圆盘平面内建立o-xy 坐标系,原点在轴上,x 和y 轴沿水平和铅直向上的方向。
边缘上一点A 当t=0时恰好在x 轴上,该点的角坐标满足θ=1.2t+t 2 (θ:rad,t:s)。
⑴t=0时,⑵自t=0开始转45º时,⑶转过90º时,A 点的速度和加速度在x 和y 轴上的投影。
解:0.222.1==+==dtd dtd t ωθβω⑴t=0时,s m R v v y x /12.01.02.10,2.1=⨯====ωω2222/2.01.00.2/144.01.0/12.0/sm R a a s m R v a a y y n x =⨯===-=-=-=-=βτ⑵θ=π/4时,由θ=1.2t+t 2,求得t=0.47s,∴ω=1.2+2t=2.14rad/ssm R v s m R v y x /15.02/21.014.245sin /15.02/21.014.245cos =⨯⨯=︒=-=⨯⨯-=︒-=ωω222222222222/182.0)14.20.2(1.0)(45sin 45sin 45sin /465.0)14.20.2(1.0)(45cos 45cos 45cos s m R R R a s m R R R a y x -=-⨯=-︒=︒-︒=-=+⨯-=+︒-=︒-︒-=ωβωβωβωβ⑶θ=π/2时,由θ=1.2t+t 2,求得t=0.7895s,ω=1.2+2t=2.78rad/s2222/77.01.078.2/2.01.00.20/278.01.078.2s m R a s m R a v s m R v y x y x -=⨯-=-=-=⨯-=-==-=⨯-=-=ωβω7.1.5 钢制炉门由两个各长1.5m 的平行臂AB 和CD 支承,以角速率ω=10rad/s 逆时针转动,求臂与铅直成45º时门中心G 的速度和加速度。
解:因炉门在铅直面内作平动,所以门中心G 的速度、加速度与B 点或D 点相同,而B 、D 两点作匀速圆周运动,因此s m AB v v B G /155.110=⨯===ω,方向指向右下方,与水平方向成45º;222/1505.110s m AB a a B G =⨯===ω,方向指向右上方,与水平方向成45º7.1.6 收割机拨禾轮上面通常装4到 6个压板,拨禾轮一边旋转,一边随收割机前进。
压板转到下方才发挥作用,一方面把农作物压向切割器,一方面把切下来 的作物铺放在收割台上,因此要求压板运动到下方时相对于作物的速度与收割机前进方向相反。
已知收割机前进速率为 1.2m/s ,拨禾轮直径1.5m ,转速22rev/min,求压板运动到最低点挤压作物的速度。
解:拨禾轮的运动是平面运动,其上任一点的速度等于拨禾轮轮心C 随收割机前进的平动速度加上拨禾轮绕轮心转动的速度。
压板运动到最低点时,其转动速度方向与收割机前进速度方向相反,压板相对地面(即农作物)的速度s m R v v c /53.02.125.160222-=⨯-=-=⨯πω负号表示压板挤压作物的速度方向与收割机前进方向相反。
7.1.7飞机沿水平方向飞行,螺旋桨尖端所在半径为150cm ,发动机转速2000rev/min. ⑴桨尖相对于飞机的线速率等于多少?⑵若飞机以250km/h 的速率飞行,计算桨尖相对地面速度的大小,并定性说明桨尖的轨迹。
解:⑴桨尖相对飞机的速度:s m r v /3145.1'6022000=⨯==⨯πω⑵桨尖相对地面的速度:机地v v v+=',飞机相对地面的速度与螺旋桨相对飞机的速度总是垂直的,s m v /4.696060102503==⨯⨯机地所以,s m v v v /6.3214.69314'2222≈+=+=机地显然,桨尖相对地面的运动轨迹为螺旋线7.1.8桑塔纳汽车时速为166km/h ,车轮滚动半径为0.26m ,发动机转速与驱动轮转速比为0.909, 问发动机转速为每分多少转?解:设车轮半径为R=0.26m ,发动机转速为n 1, 驱动轮转速为n 2, 汽车速度为v=166km/h。
显然,汽车前进的速度就是驱动轮边缘的线速度,909.0/2212Rn Rn v ππ==,所以:min /1054.1/1024.93426.014.3210166909.02909.013rev h rev n R v ⨯=⨯===⨯⨯⨯⨯π7.2.2 在下面两种情况下求直圆锥体的总质量和质心位置。
⑴圆锥体为匀质;⑵密度为h 的函数:ρ=ρ0(1-h/L ),ρ0为正常数。
解:建立图示坐标o-x,据对称性分析,质心必在x 轴上,在x 坐标处取一厚为dx 的质元 dm=ρπr 2dx ,∵r/a=x/L ,r=ax/L ∴ dm=ρπa 2x 2dx/L 2⑴圆锥体为匀质,即ρ为常数,总质量:L a dx x dm m LLa 2310222ρπρπ===⎰⎰质心:L dx x x LL L a L dx x a dmxdm c 430333//32232==⎰=⎰⎰=⎰ρπρπ⑵x LL xL L h 0)1()1(00ρρρρ=-=-=-总质量:⎰⎰===L a dx x dm m LL a 204103320πρπρ质心:⎰==⎰⎰=LL dmxdmc L dx x x 0544447.2.3 长度为L 的匀质杆,令其竖直地立于光滑的桌面上,然后放开手,由于杆不可能绝对沿铅直方向,故随即到下。
求杆子的上端点运动的轨迹(选定坐标系,并求出轨迹的方程式)。
解:设杆在o-xy 平面内运动。
因杆 在运动过程中,只受竖直向上的支承力和竖直向下的重力的作用,在水平方向不受外力作用,∴v cx =0,a cx =0,即质心C 无水平方向的移动,只能逆着y 轴作加速直线运动,直到倒在桌面上。
取杆的上端点的坐标为x,y ,匀质杆的质心在其几何中心,由图示的任一瞬间的几何关系可知:4x 2+y 2=L 2(x ≥0,y ≥0)7.3.1 ⑴用积分法证明:质量为m 常为l 的匀质细杆对通过中心且与杆垂直的轴线的转动惯量等于2121ml ;⑵用积分法证明:质量为m 半径为R 的匀质薄圆盘对通过中心且在盘面内的轴线的转动惯量等于241mR证明:⑴取图示坐标,在坐标x 处取一线元,dx dm lm=,它对y 轴的转动惯量为:dx x dI lm 2=,整个细杆对y 轴的转动惯量:21218832/2/332/2/2)(|33ml x dx xI l l lm l l lm l l lm =+===--⎰x⑵在坐标x 处取细杆状质元,dx x R dx x R dm R mR m 22222222-=-⋅=ππ它对x 轴的转动惯量:dx x R x R dm x R dm dI R m2/322322*********)()()2(2-=-=-=π整个圆盘对x 轴的转动惯量:⎰--=RRR m dx x R I 2/32232)(2π 为了能求出积分,作如下变换:θθθd R dx R x sin ,cos -==θθθ332/3222/32222/322sin )sin ()cos ()(R R R R x R ==-=-代入上式:⎰⎰=-=ππππθθθθθ043203332sin )sin (sin 22d d R RI mR R m据三角函数公式:22cos 1cos ,22cos 1sin 22θθθθ+=-=)4cos 2cos 2()2cos 21()2cos 2cos 21()(sin 21234124cos 141241222cos 14θθθθθθθθ+-=+-=+-==∴+- 24108102360810023621234132)|4sin |2sin (44cos 22cos )4cos 2cos 2(222mR d d d d I mR mR mR =+-=⎥⎦⎤⎢⎣⎡+-=+-=⎰⎰⎰⎰ππππππππθθπθθθθθθθθ7.3.2 图示实验用的摆,l=0.92m,r=0.08m,m l =4.9kg,m r =24.5kg,近似认为圆形部分为匀质圆盘,长杆部分为匀质细杆。
求对过悬点且与盘面垂直的轴线的转动惯量。
解:摆对o 轴的转动惯量I 等于杆对o 轴的转动 惯量I l 加上圆盘对o 轴的转动惯量I r ,即I=I l +I r .根据 平行轴定理2221112232212222113222211322(),()()4.90.9224.50.0824.5(0.920.08)26l l l l l r r r l r r I m l m m l I m r m l r I m l m r m l r kgm =+==++=+++=⨯⨯+⨯⨯++=7.3.3 在质量为M ,半径为R 的匀质圆盘上挖出半径为r 的两个圆孔,圆孔中心在半径R 的中点,求剩余部分对过大圆盘中心且与盘面垂直的轴线的转动惯量。
解:大圆盘对过圆盘中心o 且与盘面垂直的轴线(以下简称o 轴)的转动惯量为221MR I =.由于对称放置,两个小圆盘对o 轴的转动惯量相等,设为I ’,圆盘质量的面密度σ=M/πR 2,根据平行轴定理,2412222222124))(()('rM r r r I Rr M R +=+=πσπσ 设挖去两个小圆盘后,剩余部分对o 轴的转动惯量为I ”)/2('2"24222122122124R r r R M Mr MR I I I Rr M --=--=-=7.3.5一转动系统的转动惯量为I=8.0kgm 2,转速为ω=41.9rad/s ,两制动闸瓦对轮的压力都为392N ,闸瓦与轮缘间的摩擦系数为μ=0.4,轮半径为r=0.4m ,问从开始制动到静止需多长时间?解:由转动定理:s rad I I /68.15,0.84.03924.02====⨯⨯⨯τββτ制动过程可视为匀减速转动,t ∆∆=/ωβs t 67.268.15/9.41/==∆=∆βω7.3.6 匀质杆可绕支点o 转动,当与杆垂直的冲力作用某点A 时,支点o 对杆的作用力并不因此冲力之作用而发生变化,则A 点称为打击中心。
