四边形竞赛试题一
初二几何竞赛试题及答案

初二几何竞赛试题及答案一、选择题(每题3分,共30分)1. 下列哪个选项是直角三角形的判定条件?A. 两边之和大于第三边B. 两边之差小于第三边C. 两边之和等于第三边D. 两边之和小于第三边答案:A2. 一个等腰三角形的底角是40°,那么顶角是多少度?A. 100°B. 80°C. 60°D. 120°答案:A3. 如果一个三角形的三个内角都是60°,那么这个三角形是:A. 等腰三角形B. 等边三角形C. 直角三角形D. 等腰直角三角形答案:B4. 一个圆的半径是5cm,那么它的周长是多少厘米?A. 10πB. 15πC. 20πD. 25π答案:C5. 一个矩形的长是宽的两倍,如果宽是3cm,那么矩形的面积是多少平方厘米?A. 9B. 12C. 18D. 24答案:C6. 下列哪个选项是平行四边形的性质?A. 对角线相等B. 对边相等C. 对角线互相垂直D. 对边互相垂直答案:B7. 一个正方形的对角线长度是5cm,那么它的边长是多少厘米?A. 2.5B. 3.5C. 4D. 5答案:C8. 一个圆的直径是10cm,那么它的面积是多少平方厘米?A. 25πB. 50πC. 100πD. 200π答案:C9. 一个等腰梯形的上底是6cm,下底是10cm,高是4cm,那么它的面积是多少平方厘米?A. 12B. 24C. 36D. 48答案:B10. 如果一个三角形的两边长分别是3cm和4cm,那么第三边的长度可能是:A. 1cmB. 2cmC. 5cmD. 7cm答案:C二、填空题(每题4分,共20分)1. 一个直角三角形的两条直角边长分别是3cm和4cm,那么斜边的长度是_________cm。
答案:52. 一个等腰三角形的顶角是30°,那么它的底角是_________°。
答案:753. 一个圆的半径是7cm,那么它的面积是_________平方厘米。
四年级下册数学竞赛试题-几何.风筝模型和梯形蝴蝶定理C级.学生版-全国通用

6风筝模型和梯形蝴蝶定理例题精讲【例11【巩固1【例21C、、/如图,四边形被两条对角线分成4个三角形,其中三个三角形的面积已知,求:⑴三角形BGC的面积;(2) AG:GC在^ABC中-B D=2:1,DC如图,平行四边形是2、4、4 和6.=?AE=I:3,求OB=?EC OEABCD的对角线交于0点,△ CEF、△ OEF、△ ODF、△ BOE的面积依次求:⑴求△ OCF的面积;⑵求△ GCE的面积.D【巩固】如右上图,已知 BO=2DO C0=5AO 阴影部分的面积和是 11平方厘米,求四边形 ABCD 的面积。
那么三角形DBE 的面积是O如图,边长为1的正方形ABCD 中,BE =2EC , CF =FD ,求三角形AEG 的面积.如图,长方形ABCD 中,BE: EC =2:3,DF :FC =1:2,三角形DFG 的面积为2平方厘米,求 长方形ABCD 的面积.如图,在 MBC 中,已知M 、N 分别在边AC 、BC 上,BM 与AN 相交于0 ,若AAOM 、虫ABO和人BON 的面积分别是3、2、1,则人MNC 的面积是如图4,在三角形 ABC 中,已知三角形 ADE 三角形DCE 三角形BCD 的面积分别是 89、28、26,-J f -I ”【例3】【巩固】【例4】 【巩固】CB【例5】已知ABCD是平行四边形,B C:CE=3:2,三角形ODE的面积为6平方厘米。
贝9阴影部分的面积是平方厘米。
AB E【巩固】在梯形ABCD中,上底长5厘米,下底长10厘米,S郎OC=20平方厘米,则梯形ABCD的面积是平方厘米。
【例6】如下图,一个长方形被一些直线分成了若干个小块,已知三角形ADG的面积是11,三角形BCH 的面积是23,求四边形EGFH的面积.【巩固】如图,长方形中,若三角形1的面积与三角形3的面积比为4比5,四边形2的面积为36,则三角形1的面积为在下图的正方形 ABCD 中,E 是BC 边的中点,AE 与BD 相交于F 点,三角形BEF 的面积为1如图所示,BD 、CF 将长方形ABCD 分成4块,心DEF 的面积是4平方厘米,ACED 的面积是6 平方厘米.问:四边形 ABEF 的面积是多少平方厘米?如图, MBC 是等腰直角三角形,DEFG 是正方形,线段 AB 与CD 相交于K 点.已知正方形DEFG 的面积48, AK : KB =1:3,则虫BKD 的面积是多少?如图所示,ABCD 是梯形,AADE 面积是1.8,心ABF 的面积是9,也BCF 的面积是27 .那么阴影 MEC 面积是多少?【例7】 平方厘米,那么正方形 ABCD 面积是平方厘米.【巩固】【例8】【巩固】方厘米,则四边形 PMON 勺面积是平方厘米。
八年级数学竞赛例题专题讲解14:多边形的边与角 含答案

专题14 多边形的边与角阅读与思考主要是指多边形的边、内外角、对角线、凸多边形、凹多边形等基本概念和多边形内角和定理、外角和定理,其中多边形内、外角和定理是解有关多边形问题的基础.多边形的许多性质与问题往往可以利用三角形来说明、解决,将多边形问题转化为三角形问题是解多边形问.题的基本策略,转化的方法是连对角线或向外补形.多边形的内角和是随着多边形的边数变化而变化的,但外角和却总是不变的,所以,我们常以外角和的“不变”来制约内角和的“变”,把内角问题转化为外角问题来处理,这是解多边形相关问题的常用技巧.例题与求解【例1】两个凸多边形,它们的边长之和为12,对角线的条数之和为19,那么这两个多边形的边数分别是____和____.(“希望杯”邀请赛试题)解题思路:设两个凸多边形分别有m,n条边,分别引出(3)2m m-,(3)2n n-条对角线,由此得m,n方程组.【例2】凸边形有且只有3个钝角,那么n的最大值是()A.5 B.6 C.7 D.8解题思路:运用钝角、锐角概念,建立关于n的不等式,通过求解不等式逼近求解.【例3】凸n边形除去一个内角外,其余内角和为2570°,求n的值.(山东省竞赛试题)解题思路:利用n边形内角和公式,以及边数n为大于等于3的自然数这一要求,推出该角大小,进而求出n的值.录入:王云峰【例4】如图,凸八边形ABCDEFGH 的八个内角都相等,边AB ,BC ,CD ,DE ,EF ,FG 的长分为7,4,2,5,6,2,求该八边形的周长. (全国通讯赛试题)解题思路:该八边形每一内角均为135°,每一外角为45°,可将八边形问题转化为特殊三角形解决、特殊四边形加以解决.【例5】如图所示,小华从M 点出发,沿直线前进10米后,向左转20°,再沿直线前进10米后,又向左转20°,…这样走下去,他第一次回到出发地M 时,行走了多少米?解题思路:试着将图形画完,你也许就知道答案了.能力训练A 级1.如图,凸四边形有___个;∠A +∠B +∠C +∠D +∠E +∠F +∠G =___.(重庆市竞赛试题)A DE FG HM2.如图,凸四边形ABCD 的四边AB ,BC ,CD 和DA 的长分别为3,4,12和13,∠ABC =90°,则四边形ABCD 的面积为___.3.如图,∠A +∠B +∠C +∠D +∠E +∠F +∠G =___.4.如图,ABCD 是凸四边形,则x 的取值范围是___..5.一个凸多边形的每一内角都等于140°,那么,从这个多边形的一个顶点出发的对角线的条数是( )A .9条B .8条C .7条D .6条(“祖冲之杯”邀请赛试题)6.—个凸n 边形的内角和小于1999°,那么n 的最大值是( )(全国初中联赛试题)A .11B .12C .13D .147.如图,是一个正方形桌面,如果把桌面砍下一个角后,桌面还剩( )个角.A .5个B .5个或3个C .5个或3个或4个D .4个 8.—个凸n 边形,除一个内角外,其余1n 个内角的和为2400°,则n 的值是( )A .15B .16C .17D .不能确定9.如图,在四边形ABCD 中,AB =AD =8,∠A =60°,∠D =150°,四边形周长为32,求BC 和DC 的长.A BCD EFG 第1题 A BC D 第2题 AB D EFG 第3题 A B C D24x 第4题 第7题 AB CD10.—个凸n边形的最小内角为95°,其他内角依次增加10°,求n的值.(“希望杯”邀请赛试题)11.平面上有A,B,C,D四点,其中任何三点都不在一直线上,求证:在△ABC,△ABD,△ACD,△BDC中至少有—个三角形的内角不超过45°.(江苏省竞赛试题)12.我们常见到如图那样图案的地面,它们分别是全用正方形或全用正六边形形状的材料铺成的,这样形状的材料能铺成平整的、无空隙的地面.问:(1)像上面那样铺地面,能否全用正五边形的材料,为什么?(2)你能不能另外想出一个用一种多边形(不一定是正多边形)的材料铺地的方案?把你想到的方案画成草图.(3)请你再画出一个用两种不同的正多边形材料铺地的草图.(安徽省中考试题)B级1.一个正m边形恰好被正n边形围住(无重叠、无间隙,如图所示是m=4,n=8的情况),若m =10,则n=____.2.如图,六边形ABCDEF 中,∠A =∠B =∠C =∠D =∠E =∠F ,且AB +BC =11,F A -CD =3,则BC +DE =____.(北京市竞赛试题)3.如图,延长凸五边形A 1A 2A 3A 4A 5的各边相交得到五个角:∠B 1,∠B 2,∠B 3,∠B 4,∠B 5,它们的和等于___.若延长凸n 边形(n ≥5)的各边相交,则得到的n 个角的和等于____.(第十二届“希望杯”邀请赛试题)4.如图,在四边形ABCD 中,AB=4BC =1,CD =3,∠B =135°,∠C =90°,则∠D =( )A .60°B .67.5°C .75°D .不能确定(重庆市竞赛试题)5.如图,已知O 是四边形ABCD 内一点,OA =OB =OC ,∠ABC =∠ADC =70°,则∠DAO +∠DCO 的大小是( )A .70°B .110°C .140°D .150°6.在一个多边形中,除了两个内角外,其余内角之和为2002°,则这个多边形的边数为( )A .12B .12或13C .14D .14或15(江苏省竞赛试题)7.一个凸十一边形由若干个边长为1的正方形或正三角形无重叠、无间隙地拼成,求此凸十一边形各个内角大小,并画出这样的凸十一边形的草图.(全国通讯赛试题)第1题 ABC D EF 第2题 1A 1B 2A 2B 3B 4B 5B 3A 4A 5A 第3题 AB CD 第4题 O ABC D 第5题8.一块地能被n 块相同的正方形地砖所覆盖,如果使用较小的相同正方形地砖,那么需n +76块这样的地砖才能覆盖该块地,已知n 及地砖的边长都是整数,求n 的值.(上海市竞赛试题)9.设有一个边长为1的正三角形,记作A 1如下左图,将A 1的每条边三等分,在中间的线段上各向形外作正三角形,去掉中间的线段后得到的图形记作A 2(如下中图);将A 2的每条边三等分,并重复上述过程,所得到的图形记作A 3(如下右图);再将A 3的每条边三等分,并重复上述过程,所得到的图形记作 A 4,求A 4的周长.(全国初中数学联赛试题)10.在日常生活中,观察各种建筑物的地板,就能发现地板常用各种正多边形地砖铺砌成美丽的图案.也就是说,使用给定的某些正多边形,能够拼成一个平面图形,既不留下一丝空白,又不互相重叠(在几何里叫作平面镶嵌),这显然与正多边形的内角大小有关,当围绕一点拼在一起的几个多边形的内角加在一起恰好组成一个周角(360°)时,就拼成了一个平面图形.(1)请根据下列图形,填写表中空格:1A 2A 3A(3)从正三角形、正四边形、正六边形中选一种,再在其他正多边形中选一种,请画出用这两种不同的正多边形镶嵌成的一个平面图形(草图);并探索这两种正多边形共能镶嵌成几种不同的平面图形.说明你的理由.(陕西省中考试题)。
2020-2021学年全国初中数学竞赛试题(多份)及答案
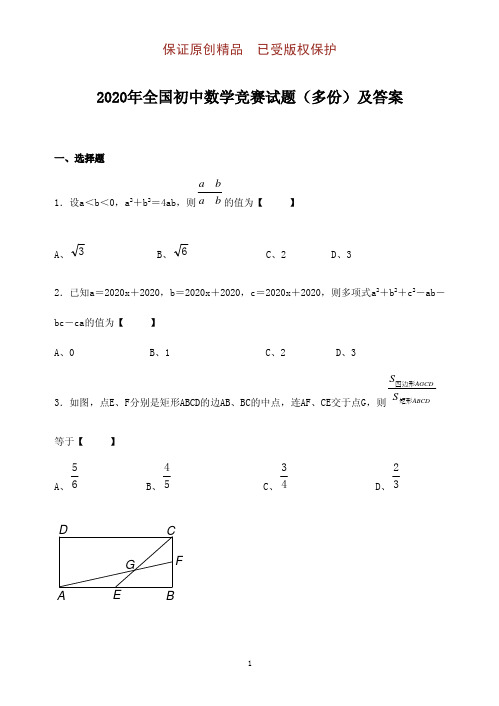
保证原创精品 已受版权保护2020年全国初中数学竞赛试题(多份)及答案一、选择题1.设a <b <0,a 2+b 2=4ab ,则b a ba 的值为【 】A 、3B 、6C 、2D 、32.已知a =2020x +2020,b =2020x +2020,c =2020x +2020,则多项式a 2+b 2+c 2-ab -bc -ca 的值为【 】A 、0B 、1C 、2D 、33.如图,点E 、F 分别是矩形ABCD 的边AB 、BC 的中点,连AF 、CE 交于点G ,则ABCDAGCDS S 矩形四边形等于【 】A 、65B 、54C 、43D 、32ABC DEF G保证原创精品 已受版权保护4.设a 、b 、c 为实数,x =a 2-2b +3,y =b 2-2c +3,z =c 2-2a +3,则x 、y 、z 中至少有一个值【 】A 、大于0B 、等于0C 、不大于0D 、小于05.设关于x 的方程ax 2+(a +2)x +9a =0,有两个不等的实数根x 1、x 2,且x 1<1<x 2,那么a 的取值范围是【 】A 、72<a <52 B 、a >52 C 、a <72 D 、112<a <06.A 1A 2A 3…A 9是一个正九边形,A 1A 2=a ,A 1A 3=b ,则A 1A 5等于【 】A 、22b a B 、22b ab a C 、b a 21D 、a +b二、填空题7.设x 1、x 2是关于x 的一元二次方程x 2+ax +a =2的两个实数根,则(x 1-2x 2)(x 2-2x 1)的最大值为 。
8.已知a 、b 为抛物线y =(x -c)(x -c -d)-2与x 轴交点的横坐标,a <b ,则bc c a 的值为 。
9.如图,在△ABC 中,∠ABC =600,点P 是△ABC 内的一点,使得∠APB =∠BPC =∠CPA ,且PA =8,PC =6,则PB = 。
山东初中数学竞赛试题及答案__六份

D.不能确定,与AC/AB的大小有关
6.甲、乙两人同时从同一地点出发,相背而行,1小时后他们分别到达各自的终 点A与B.若仍从原地出发,互换彼此的目的地,则甲在乙到达A之后35分钟到达B .那么,甲的速度与乙的速度之比为 A 3:5 B. 4:3 C. 4:5 ( D.3:4 )
7.在全体实数中引进一种新的运算*,其规定如下: (1)对任意实数a、b,有a*b=(a+1)·(b-1); (2)对任意实数a,有a*2==a*a
1999年山东省初中数学竞赛试题 .....................................................................1 2000年山东省初中数学竞赛试题 .....................................................................5 2001年山东省初中数学竞赛试题 .....................................................................7 2002年山东省初中数学竞赛试题 ...................................................................11 2003年山东数学竞赛试题 ...............................................................................14 2004年山东省初中数学竞赛试题 ...................................................................17
15.(1)不难验证,如图所示填法满足.s1,s2,…s8都大于或等于12.
六年级数学竞赛试题

六年级数学竞赛试题数学邀请赛(第一部分)填空题(1至11题每小题5分,第12题8分)1、一个数先加3,再除以3,然后减去5,再乘以4,结果是56,这个数是_______。
2、一个盖着瓶盖的瓶子里面装着一些水(如下图所示),请你根据图中标明的数据,计算瓶子的容积是_________cm³。
3、六年级某班学生中有13的学生年龄为13岁,有的学生年龄为12岁,其余学生年龄为11岁,164这个班学生的平均年龄是__________岁。
4、将25克白糖放入空杯中,倒入100克白开水,充分搅拌后,喝去一半糖水。
又加入36克白开水,若使杯中的糖水和原来的一样甜,需要加入_______克白糖。
5、六年级一班的所有同学都分别参加了课外体育小组和唱歌小组,有的同学还同时参加了两个小组。
若参加两个小组的人数是参加体育小组人数的12,是参加歌唱小组人数的,这个班只参59加体育小组与参加唱歌小组的人数之比是________。
6、熊猫妈妈的小宝宝——小熊猫今年2岁了,过若干年以后,当小熊猫和熊猫妈妈当年年龄一样大时,熊猫妈妈已经18岁了。
熊猫妈妈今年是_______岁。
7、果园收购一批苹果,按质量分为三等,最好的苹果为一等,每千克售价3.6元;其次是尔等苹果。
每千克售价2.8元;最次的是三等苹果每千克售价2.1元。
这三种苹果的数量之比为2:3:1。
若将这三种苹果混在一起出售,每千克定价________元比较适宜。
8、某班学生不超过60,在一次数学测验中,分数不低于90分的人数占1,得80----89分的人数占711,得70-----79分的人数占,那么得70分以下的有______人。
329、有一列数,按照下列规律排列:1,2,2,3,3,3,4,4,4,4,5,5,5,5,5,6,6,6,6,6,6,7,……这列数的第200个数是__________.10、某个五位数加上20万并且3倍以后,其结果正好与该五位数的右端增加一个数字2的得数相等,这个五位数是___________。
初中数学竞赛第十九讲平行截割(含答案)

第十九讲 平行截割平行线是初中平面几何中基本而重要的图形,平行线能改变角的位置并传递角,可“送”线段到恰当处,完成等积变形,当一组平行线截两条直线时就得到比例线段,平行线分线段成比例定理是研究比例线段、相似形的重要理论.利用、挖掘、创造平行线,是运用平行线分线段成比例定理解题的关键,另一方面,需要熟悉并善于从复杂图形中分解或构造如下形如“E ”、“A ”型或“X ”型的基本图形:例题求解【例1】如图,已知在平行四边形ABCD 中,M 、N 为AB 的三等分点,DM 、DN 分别交AC 于P 、Q 两点,则AP :PQ :QC= .(2001年河北省初中数学创新与知识应用竞赛试题)思路点拨 图中有形如“X ”型的基本图形,建立含AP ,PQ ,QC 的比例式,并把AP ,PQ ,QC 用同一条线段的代数式表示.【例2】如图,已知在△ABC 中,AE :EB=1:3,BD :DC=2:1,AD 与CE 相交于F ,则FDAF FC EF 的值为( ) A .21 B .1 C .23 D .2。
(江苏省泰州市中考题)思路点拨 已知条件没有平行线,需恰当作平行线,构造基本图形,产生含FC EF ,FD AF 的比例线段,并设法沟通已知比例式与未知比例式的联系.【例3】 如图,BD 、BA ,分别是∠ADC 与它的邻补角∠ABP 的平分线,AE ⊥BE ,AD ⊥BD ,E 、D 为垂足.(1)求证:四边形AEBD 为矩形;(2)若AD AE =3,F 、G 分别为AE 、AD 上的点,FG 交AB 于点H ,且3=AGAF ,求证:△AHG 是等腰三角形.(2003年厦门市中考题)思路点拨 对于(2),由比例线段导出平行线,证明∠HAG=∠AHG .【例4】 如图,梯形ABCD 中,AD ∥BC ,AB =DC .(上海市闽行区中考题)(1)如果P 、E 、F 分别是BC 、AC 、BD 的中点,求证:AB=PE+PF ;(2)如果P 是BC 上的任意一点(中点除外),PE ∥AB ,PF ∥DC ,那么AB=PE+PF 这个结论还成立吗?如果成立,请证明;如果不成立,说明理由.思路点拨 对于(2),先假设结论成立,从平行线出发证明AB=PC+PF ,即需证明1=+ABPF AB PE ,将线段和差问题的证明转化为与比例线段有关问题的证明. 注 若题设条件无平行线,需作平行线.而作平行线要考虑好过哪一点作平行线,一般是由比的两条线段启发而得的,其目的是构造基本图形.平行线分线段成比例定理是证明比例线段的常用依据之一,比例线段丰富了我们研究几何问题的方法,主要体现在:(1)利用比例线段求线段的长度;(2)运用比例线段证明线段相等,线段和差倍分关系、两直线平行等问题.【例5】如图,在四边形ABCD 中,AC 与BD 相交于点O ,直线l 平行于BD ,且与AB 、DC 、BC 、AD 及AC 的延长线分别相交于点M 、N 、R 、S 和P ,求证:PM ×PN=PR ×PS 。
初一几何竞赛试题及答案

初一几何竞赛试题及答案一、选择题(每题5分,共20分)1. 下列哪个选项是矩形的性质?A. 对角线相等B. 对边平行且相等C. 四个角都是直角D. 所有选项都是答案:D2. 一个三角形的内角和是多少度?A. 90度B. 180度C. 360度D. 720度答案:B3. 如果一个角是另一个角的两倍,且它们的和为180度,那么较小的角是多少度?A. 60度B. 90度C. 120度D. 30度答案:A4. 一个圆的半径是5厘米,那么它的周长是多少?A. 10π厘米B. 15π厘米C. 20π厘米D. 25π厘米答案:C二、填空题(每题5分,共20分)1. 一个等腰三角形的底角是50度,那么它的顶角是______度。
答案:80度2. 如果一个圆的直径是10厘米,那么它的半径是______厘米。
答案:5厘米3. 一个平行四边形的对角线互相平分,那么这个平行四边形是______。
答案:矩形4. 一个正三角形的每个内角是______度。
答案:60度三、解答题(每题15分,共30分)1. 已知一个直角三角形的两个直角边长分别为3厘米和4厘米,求斜边的长度。
答案:根据勾股定理,直角三角形的斜边长度c可以通过以下公式计算:\[ c = \sqrt{a^2 + b^2} \]其中a和b是直角边的长度。
将3厘米和4厘米代入公式中,得到:\[ c = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5 \text{厘米} \]2. 一个等腰三角形的底边长为6厘米,底边上的高为4厘米,求等腰三角形的周长。
答案:首先,我们需要求出等腰三角形的两个等边的长度。
由于底边上的高将底边平分,我们可以将等腰三角形分为两个直角三角形,每个直角三角形的底边长为3厘米(6厘米的一半),高为4厘米。
根据勾股定理,我们可以求出等边的长度:\[ a = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5 \text{厘米} \]因此,等腰三角形的两个等边的长度都是5厘米。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
【例1】如图,四边形ABCD有4个直角三角形拼凑而成,它们的公共顶点为0,已知4人08、480口 △COD的面积分别为20、10、16,求4AOD的面积。(1992年北京市“迎春杯”竞赛题)
【注释】求三角形的面积,通常需要求出底和高,当这两个值不易求出时,常把它们的积作为一个整 体,设法求出它们的积。 【例2】如图,求NA+NB+NC+ND+NE+NF+NG的度数。(1999年重庆市竞赛题)
【注释】求凹多边形的内角和,常利用四边形和三角形的内角和进行计算,有事需要添加辅助线,将 其转化为求一个凸多边形的和或一个凸多边形和一个三角形的内角和,如本题连接BF、CE,则所求的 值等于四边形ABFG的内角和加上4DCE的内角和。
【例3】如图,在四边形ABCD中,NB=ND=90°,NA=60°, AB=4, AD=5,求BC的值。(1993年“祖 CD
冲之杯”邀请赛试题)
【注释】有些几何题,按原有的图形很难求解,可根据图形的特点,将原图形补成特殊图形,利用特 殊图形的性质进行求解。 【例4】(1)是否存在这样的四边形,它的4条边依次是1、2、4、7? (2)是否存在这样的四边形,它的一组对角是直角,其中一个直角的两条边分别为3、4,另一个直 角的边为6? 【注释】探索存在型问题是指在一定条件下,判断是否存在某个结论。解答这类问题,先假设结论存 在,从假设出发,根据题设条件及有关性质进行推理论证,若推出矛盾,则不定假设,若推出合理的 结果,则说明假设正确。这种方法叫“假设法”。 【例5】如图,在四边形ABCD中,AB=AD=8,NA=60°,ND=150°,四边形ABCD的周长为32,求BC 和CD的长。 【注释】本题求最值的方法称为配方法,即欲求一个量的最大值或最小值,可先用一个量或两个量
表 示这个量,然后对列出的代数式进行配方,从而确定最大值或最小值。 【针对训练】 【1】如图,A、B、C 在一条直线上,FA±AC, FG±BE, DE±BE, DCLBC,且NF=60°,求NEBC 与ND 的度数。 【注释】对于四边形,作对角线是常用的辅助线。
【例6】如图,在四边形ABCD中,AC、BD相交于OADOC的面积Si=4,AA°B的面积{二64,求四边 形ABCD的面积的最小值。(第十一届“希望杯”邀请赛培训题)
【2】如图,求NA+NB+NC+ND+NE+NF+NG的度数。(1994年“祖冲之杯”邀请赛试题)
【3】是否存在这样的四边形,它的一组对角分别为60°、120°,且60°角的两边均为5,120°角的一边为6?
【4】如图,在四边形ABCD中,AD=DC,ZADC=ZABC=90°, DELAB于E。若四边形ABCD的面积为8, 求DE的长。(1996年四川省竞赛题)
【5】在四边形ABCD中,AB=2, BC=4, CD=7,求AD的取值范围。 【例 1】已知:四边形 ABCD,从(1) AB〃DC; (2) AB=DC; (3) AD〃BC; (4) AD=BC; (5)/A=/C; (6)/B=/D中取出两个条件加以组合,能推出四边形ABCD是平行四边形的有哪几种情形?请具体 写出这些组合。(1998年江苏省竞赛题)
【注释】解四边形问题,常需要判定其形状,要熟记判定定理;由于判定定理比较多,易混易忘,可 从边、角、对角线3个方面加以记忆。 【例2】凸四边形ABCD中,AB〃CD,且AB+BC=CD+AD。求证:ABCD是平行四边形。(1990年芜湖市竞 赛题)
【6】如图,在四边形 ABCD 中,AC 平分/BAD, CELAB 于 E,NADC=135°, AE=- (AD+AB), BC=2。 2
c c 求BE的长。 的性质证明的方法。 【例5】如图,边长为a的菱形ABCD中,NDAB=60°, E是异于A、D两点的动点,F是CD上的动点, 满足AE+CF=a。证明:不
论E、F怎样移动,^BEF总是正三角形。(1990年合肥市竞赛题) 【例3】平面上有三个正△ABD、^ACE、^BCF,两两共有一个顶点。求证:CD与EF互相平分。(1990 年芜湖市竞赛题) 【例4】在Rt^ABC中,NACB=90°, CDLAB于D, AE平分NBAC,交CD于K,交BC于E, F是BE上 一点,且BF二CE。求证:FK〃AB。(大连市第八届“育英杯”竞赛题)
【注释】对于平行四边形问题,常将其转化为三角形问题解决。解题时要注意利用平行四边形的性质, 这些性质往往为解题提供必要的条件。 【例6】矩形ABCD中,AB=20cm, BC=10cm。若在AC、AB上各取一点M、N,使BM+MN的值最小,求这 个最小值。(1998年北京市竞赛题) 【例7】设P为直角等腰三角形ABC斜边AB上任意一点,PELAC于点E, PFLBC于点F, PGLEF于G, 延长GP并在其延长线上取一点D,使得PD二PC。求证:BCLBD且BC二BD。
【注释】对于求证线段相等,角相等,线段互相平行,两线平行,两线垂直等问题,常先判定出某个 四边形是平行四边形或特殊的平行四边形,再根据其性质进行证明。这种证明方法往往优于用三角形 【例8】如图,4ABC是正三角形,△4户£的三条边A1B1、B1C1、C1A1交4ABC各边分别于C2、C3,A2、 A , B、B。已知AC二CB二BC ,且CC2+BB2=AA2。请证明:AB,CA。(2002年北京市数学竞赛复赛 3 2
3 232323 232323 11 11 题)
【针对训练】 【1】下面有4个命题:①一组对边相等,一组对角相等的四边形是平行四边形;②一组对边相等且一 条对角线平分另一条对角线的四边形是平行四边形;③一组对角相等且这一组对角的顶点所连接的对 角线平分另一条对角线的四边形是平行四边形;④一组对角相等且这一组对角的顶点所连接的对角线 被另一条对角线平分的四边形是平行四边形。其中,正确命题的个数是( )(1988年全国联赛试 题)
A、1 B、2 C、3 D、4
【2】菱形ABCD的对角线AC与BD相交于O,NABCW90°,则图中共有全等三角形( ) A、4 对 B、6 对 C、8 对 D、12 对
【3】如图,AB〃CD〃EF, AD〃BC, AC平分/BAD且与EF相交于O,那么图中与NAOE相等的角(不包 括NAOE)总共有( )(1996年荆沙市竞赛题)
A、6个 B、4个 C、3个 D、5个
【4】四边形的4条边长分别是a、b、c、d,其中a、c为对边,且满足a2+b2+c2+d2=2ab+2cd,则这个 四边形一定是( )(1995年“希望杯”邀请赛试题) A、两组对角分别相等的四边形 B、平行四边形 C、对角线互相垂直的四边形 D、对角线长相等的四边形 【5】如图,在DABCD中,NABC=75°, AFLBC于F, AF交BD于E,若DE=2AB,则NAED的大小是 __ 。 (1998年“希望杯”邀请赛试题)
【6】矩形纸片ABCD, AB=6, BC=8,将纸片折叠使得A与C重合,则折痕EF的长为—。(1995年河 北省竞赛题) 【7】如图,P为DABCD内一点,过P点分别作AB、AD的平行线,交DABCD于E、F、G、H四点,若 S33, SPFCG=5,则“PBD二——。(1998年北京市竞赛题)
【8】如图,P为矩形外一点,PC=3,PB=4,PA=5,则PD=。(1998年河北省竞赛题) 【9】如图,有一湖的湖岸在AB之间呈一段圆形劣弧,AB之间的直线距离不能直接测得;为了得到AB 之间的距离,请你用测角仪和量尺,在岸边设计出三种不同类型的测量方案(分别画出图形)并求出 AB间的距离(经测量得到的线段的长的数据用a或b或c等表示,角度用a或B等表示)。(1999年河 北省竞赛题)
【10】如图,在DABCD中,以AC为边长在两侧各作一个正△ACP,AACQ。试证BPDQ为平行四边形。
【11】如图,矩形ABCD、BFDE中,AB=BF。求证:CF±MNO 【12】在DABCD 中,BC=2AB, M 为 AD 的中点,CELAB 于 E。求证:NDME=3NMEA。
【14】如图,在等腰4ABC中,AB=AC,延长边AB到点D,延长边CA到点E,连接DE,恰有AD二BC二CE二DE。 求证:NBAC=100°。(2001年北京市数学竞赛试
题)
【13】P为四边形ABCD的两边AD、BC的延长线的交点,过P作线段EF,使PE=PF。求证:不论EF的 长度与位置如何变化,线段AE、BF的中点连线恒经过某一定
点。
第三节 梯形的判定和中位线定理 【知识点拨】 1、梯形的定义:一组对边平行,另一组对边不平行的四边形。 2、等腰梯形的性质与判定 性质定理:等腰梯形在同一底上的两个角相等。 判定定理:在同一底上两个角相等的梯形是等腰梯形。 3、梯形中位线定理:梯形中位线平行于两底,且等于两底和的一半。 对于梯形的问题,往往是通过作辅助线,将梯形问题转化成三角形或平行四边形问题来解决。常用 的辅助线如下: 【赛题精选】 【例1】已知£、F、G分别是AB、BC、CA的中点,ADLBC于D。求证:四边形EFDG是等腰梯形。
【说明】一组对边平行的四边形可能是梯形,还可能是平行四边形!因此,要证明一个四边形是梯形, 必须证这个四边形的另一组对边不平行,证明一组对边不平行的方法有: (1)证明四边形的一组对边平行且不相等,则这个四边形不是平行四边形,因而另一组对边不平行;
(2)利用经过直线外一点有且只有一条直线与这条直线平行,而经过这点的其它直线与这条直线不平 行进行证明。
【说明】以上介绍的几种辅助线要知道,还应通过做题总结出何时作何种辅助线。如本题在结论中有
两底的和或题设中有关于对角线的条件,辅助线常作对角线的平行线。 【例 4】如图,在梯形 ABCD 中,AD〃BC,NB=30°,NC=60°, E、M、F、N 分别是 AB、BC、CD、AD 的中点,已知BC=7, MN=3,求EF的值。(1997年全国联赛试题) 【说明】对于涉及梯形的两底角互余问题,常将其转化为直角三角形问题。本题有辅助线还可过点N
分别作AB、AC的平行线,证MN=1 (BC-AD)即可。 2
【例5】在等腰梯形ABCD中,CD〃AB,对角线AC、BD相交于O,NACD=60°,点S、P、Q分别是OD、 OA、BC的中点。 (1)求证:4PQS是等边三角形。 (2)若 AB=5, CD=3,求4PQS 的面积。
【例2】已知一个梯形的四条边的长分别是1、2、3、4,求此梯形的面积。(2000年全国联赛试题) 【例3】如图,在梯形ABCD中,AD〃BC, AB二DC, ACLBD 于 E, BD二BC。求证:2CE=AD+BC。
