第三节 定积分在物理学上的应用
高等数学教学大纲

高等数学教学大纲第一部分:使用说明一、课程编号:10113001二、课程性质与特点:高等数学是一门重要的基础课程。
它不仅有严谨的逻辑推理、论证的自身完美理论体系,又是其它学科(特别是理工科)广泛应用并推动其的最具活力的工具。
本课程学习的主要内容是:矢量代数和空间解析几何;单元、多元函数的微积分;曲线积分和曲面积分;矢量分析与场论;级数与傅立叶级数;微分方程等。
三、在专业教学计划中的地位和作用:高等数学是物理学专业的必修课程,是实行专业理论学习的基础工具,渗透了现代数学的思想、语言和方法,引用了一些数学记号,增加了在科学技术方面的应用,为培养学生的能力和研究素养奠定良好的基础,同时也为进一步深入的理论研究提供了基本的数学研究工具。
四、教学目的:1、使学生既能系统地学习高等数学的基础理论知识,又能使学生具有较强的计算技能,以及解决问题分析问题的能力。
2、培养学生具有认真、严谨的学习科学态度,良好的学习方法和学风。
3、培养学生具有辩证的、科学的思维方法和能力。
五、学时与学分本课程总计137学时,8学分,每周4/5学时。
六、教学方法:1、课堂讲授应着重概念、思维逻辑方法的讲述,定理、公式的提出着重讲解意义,论证的思路及其几何解译和应用.要精讲多练,侧重培养学生的计算技能和解决问题的能力。
2、教材中的某些内容,教师可以根据实际情况组织学生自学或进行讨论式教学.3、注意各教学环节间的衔接,加强批改和辅导答疑。
七、考核方式考试课程。
平时考核与期末考试相结合。
平时考核:作业和出勤占10%,期中闭卷考试占10%期末考试:闭卷笔答,成绩占80%。
八、教材及主要参考书目(一)教材同济大学应用数学系主编《高等数学》上、下册(第五版)高等教育出版社, 2002年7月(二)参考书目李文主编,《高等数学辅导及教材习题解析》,朝华出版社2005年8月第二部分:课程内容第一章函数与极限教学目的与要求:正确理解函数、反函数、复合函数,基本初等函数概念;会求函数的定义域,能判别函数的单调性、奇偶性;掌握数列、函数极限的概念及其性质;会求各种函数的极限;明确极限和无穷小的关系、无穷小的阶及无穷大的概念;掌握函数连续性概念及闭区间上连续函数的性质;会求函数的间断点及连续区间。
工科数学分析基础

6/27
微元的求法
记Q( x)为分布在区间[a, x] ( x ∈[a,b])的量Q,则
∫ Q( x) =
x
f (t)dt
( x ∈[a,b]),
a
dQ = f ( x)dx
ΔQ = dQ + o(dx)
求微元dQ, 就是寻求与 dx成线性关系的 Adx , 且使
ΔQ − Adx = o(dx).
2010-11-22
16/27
特别 , 当考虑连续曲线段 y = f ( x) (a ≤ x ≤ b)绕 x 轴
轴旋转一周围成 π[ f ( x)]2 dx a
当考虑连续曲线段
yy oo aa x bb xx
x = ϕ( y) (c ≤ y ≤ d )
5
x
dw = π ⋅ 32 ⋅ dx ⋅ 9.8 ⋅ x = 88.2π x ⋅ dx,
w
=
∫ 5 88.2π 0
⋅ x ⋅ dx
≈
3462
(千焦).
定积分的应用
2010-11-22
20/27
例 2 一个横放着的圆柱形水桶,桶内盛有半桶水,设桶的底
半径为 R,水的比重为γ ,计算桶的一端面上所受的压力.
3
定积分的应用
2010-11-22
8/27
实际问题中,如何求得非均匀连续分布量的微分?
(1)针对所给问题,分析非均匀产生的原因,它往往是 由于某一相关量 f 变动所引起的。
(2)确定如何将其局部量均匀化从而可以利用乘法得到 此局部量的线性形式的近似值.
通常是通过对 f 以不变代变来得到。
这样得到的近似值往往就是所需要的微分,而不必也 难以逐一加以验证.
高等数学上册第六章课件.ppt

4
AdA ( y 4 12 y 2 ) d y
2
18
(8 , 4)
x
第二节 定积分在几何中的应用
例
求由摆线
的一拱与 x 轴所围平面图形的面积 .
解
2π
dAA
ydx 0 a (1 cos t ) a (1 cos t ) d t
a
2
4a
X -型绕x轴旋转所围成的立体的体积:
y 2 ( x)
b
b
Vx π ( x)dx π ( x)dx
a
b
2
2
a
2
1
2
2
y 1 ( x)
π [2 ( x) 1 ( x)]dx
a
a
bx
Y-型绕y轴旋转所围成的立体的体积:
d
Vy π [ g g ]dy
2
5 3 1 π
32π a sin u du 32π a 5π 2 a3
0
6 4 2 2
3
2
6
3
第二节 定积分在几何中的应用
y
x x2 ( y )
2a
绕 y 轴旋转而成的体积为
π
π a 2 (t sin t ) 2 a sin t d t
2π
o
πa
πa
4 2 2
2
所围图形的
(利用对称性)
d
o
2a x
第二节 定积分在几何中的应用
心形线(外摆线的一种)
2
2
2
x y ax a x y
2
即 r a(1 cos )
上交大微积分教学课件 第五章定积分及其应用

最小值, 则
•性质9(定积分中值定理) 如果函数f(x)在闭区间[a, b]上连
续, 则在积分区间[a, b]上至少存在一个点 , 使下式成立:
·性质10设函数f(x)在区间[a, b]上连续,则
a
f
(x)dx
0,
a
a
2 0 f (x)dx,
(f (x)是奇函数); (f (x)是偶函数).
第二节 微积分基本定理
则该曲线弧长L为
L r2( ) r2( ) d
注意:弧长计算公式中的下限一定要小于上限.
*三、定积分在物理上的应用
1.变力沿直线做功
由物理学知道,如果物体在作直线运动的
过程中有一个不变的力F 作用在这物体上,且
这力的方向与物体的运动方向一致,那么,在
Oa
A(x) bx
y c, y dV π d 2 ( y)dy. c
y
平行截面面积已知的立体体积
❖ 有一立体被垂直于x轴的平面相截,被截体积 位于 x a和 x b的两平面之间,而且它被垂 直于x轴的平面所截的截面积是x的已知连续 函数 A(x) ,其立体的体积为
b
V a A(x) d x
(1)分割: T1t0<t1<t2< <tn1<tnT2, tititi1;
(2)近似: 物体在时间段[ti1, ti]内所经过的路程近似为
Siv(i)ti ( ti1< i<ti );
(3)求和: 物体在时间段[T1, T2]内所经过的路程近似为
n
S v( i )ti ;
i 1
(4)取极限: 记max{t1, t2,, tn}, 物体所经过的路程为
取 ε 0 ,如果极限 lim b f (x)dx 存在,则称此极限为函 ε0 a
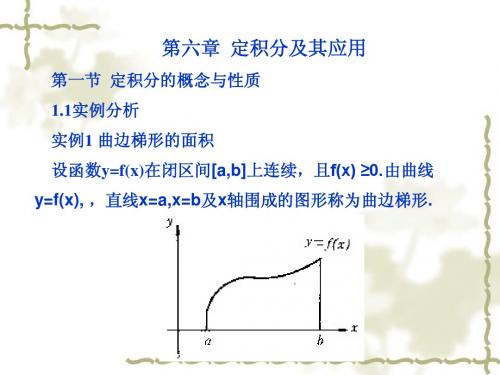
第六章 定积分及其应用
称为定积分的换元公式. 称为定积分的换元公式
定理2.4 设u(x),v(x)在区间 在区间[a,b]上有连续导数,则 上有连续导数, 定理 在区间 上有连续导数
∫ u( x) v′( x) dx = u( x)v( x)
a
b
b a
− ∫ u ′( x ) v ( x ) dx.
a
b
称为定积分的分部积分公式. 称为定积分的分部积分公式 例2 计算下列定积分
注: (1)定积分仅与被积函数及积分区间有关 , 而与积分变量 定积分仅与被积函数及积分区间有关 用什么字母表示无关.即 用什么字母表示无关 即
∫
b
a
f ( x ) d x = ∫ f (t ) d t = ∫ f (u ) d u.
a a
b
b
(2)定积分的几何意义 定积分的几何意义: 定积分的几何意义
A=∫
b
1
1 1 dx = − 2 x x
1
1 = 1− . b
b
性质2 被积函数中的常数因子可以提到积分号的前面,即 性质 被积函数中的常数因子可以提到积分号的前面,
∫
b
a
k f ( x ) dx = k ∫ f ( x ) dx
a
b
性质3 如果积分区间[a,b]被分点 分成区间 被分点c分成区间 性质 如果积分区间 被分点 分成区间[a,c]和[c,b],则 和 则
s ≈ ∑ v(ξ i ) ∆ t , (λ = max ∆ t i ).
i =1 1≤ i ≤ n n
(2)近似求和: )近似求和: (3)取极限: )取极限:
s = lim ∑ v (ξ i ) ∆ t i
定积分的定义和性质

i 1
i 1
i 1
n
i 1
i n
2
1 n
1 n3
n
i 1
i
2
1 n3
n(n
1)(2n 6
1)
1 6
1
1 n
2
1 n
,
0 n ,
1 x2dx lim n
0
0 i1
i
2xi
lim
证:
b
kf ( x)dx
a
n
n
lim kf
λ0 i1
(i )xi
limk
λ0 i1
f
(i )xi
n
k
lim
λ0 i1
f
(i
)xi
b
k f ( x)dx. a
性质2
b[ a
f
(x)
g( x)]dx
b
a
f
( x)dx
b
a
g(
x
)dx
证:
a
f (x)dx 2
a
f (x)dx
a
0
例1 利用定积分的几何意义计算0R R2 x2dx。
解:根据定积分的几何意义知, 此定积分是以R为
半径的圆面积的四分之一
故
Y
R 0
R2 x2dx R2。 4
O
y R2 x2
R
X
2
例2 计算 sin xdx
定积分的定义和性质
1 6
1
1 n
2
1 n
,
0 n ,
1 x2dx lim n
0
0 i1
i
2xi
lim
n
1 6
1
1 n
2
1 n
1。 3
证明 设函数f (x)在[0,1]上连续,且取正值,证:
lim n
在每个小区间[ xi1, xi ] 上任取一点i,
y
y f ( x)( 0)
以 [ xi1, xi ]为底,f (i )
f (i )
为高的小矩形面积为
Ai f (i )xi
则曲边梯形面积
n
A f (i )xi
i 1
o a b x x1 x2
xi1 xi
a o
=曲边梯形的面积的负值;
A
bx
b x
y f (x)
3、一般情况下
ab f ( x)dx是介于 函数 f ( x) 图形, x 轴及两条
直线 x a, x b 之间的各部分面积的代数和。 在 x 轴上方的面积取正号;在 x 轴下方的面 积取负号。
ab f ( x)dx A1 A2 A3 A4
第一类间断点,则 f ( x)在[a,b]上可积。
定理3 若函数f ( x)在[a,b]上单调有界,则 f ( x)
在[a, b]上可积。
三、定积分的几何意义
1、当 f ( x) 0时,
y
y f (x)
b
a
f
(
x)dx
A
高等数学 上下册5_1 定积分的概念和性质-精选文档
我们知道,矩形的高是不变的,它的面积可按公式 矩 形 面 积 =高 × 底 定 义 和 计 算 .而 曲 边 梯 形 在 底 边 上 各 点 处 的 高 f (x) 在 区 间 a,b上 是 变 动 的 , 故 它 的 面 积 不 能 直 接 按 上 述 公 式 定 义 和 计 算 .然 而 ,由 于 曲 边 梯 形 的 高 f (x) 在 区 间a,b 上 是 连 续 变 f (x) 的 变 化 将 是 很 小 化的,在 a,b 的 一 个 很 小 子 区 间 上 , 的 ,近 似 于 不 变 . 因 此 ,如 果 把 区 间 a,b 划 分 为 许 多 小 区 间 , 在 区 的 实 每个小区间上用其中某一点处的高来近似代替同一个小 间上的窄曲边梯形的变动的高,那么,每个窄曲边梯形 面 积 就 可 以 近 似 地 看 成 这 样 得 到 的 窄 矩 形 .基 于 这 一 事 ,我们通过如下的步骤来计算曲边梯形的面积: 第 一 步 : 分 割 .在 区 间 a,b 内 任 意 插 入 n 1 个 分 点 : a x 0 x1 x 2 xi xn b
第 二 步 : 近 似 .即 “ 以 不 变 代 变 ” , 在 小 区 间 [x ,x i 1 i] 上
f( [x ,x 任 取 一 点 以 该 点 处 的 力 替 小 区 间 的 i , i)代 i 1 i] 上
f (x ), [x ,x W 变 力 则 区 间 所 作 的 功 近 似 值 i 1 i ]上 i 有
把区间 a , b 分 割 成 n 个 小 区 间 [ x i 1 , x i ]( i = 1 , 2 ,
,n )
A = A i f ( i ) x i .
i 1 i 1
第六章定积分的应用面积旋转体积
第六章 定积分的应用定积分是求某种总量的一种数学模型,它在几何学、物理学、经济学、社会学等多方面都有着广泛的应用,显示了它的巨大魅力. 因此,我们在学习的过程中,不仅要掌握计算某些实际问题的公式,更重要的还在于深刻领会用定积分解决实际问题的基本思想和分析方法——元素法,不断积累和提高数学的应用能力.本章中我们将应用上一章学过的定积分理论来分析和解决一些几何、物理中的问题。
第一节 定积分的元素法复习引入:前一章讨论过的曲边梯形的面积问题,步骤是:(1)分割(2)近似代替(3)求和(4)求极限。
分析:主要是第二步,应用上为简便起见,省略下标i ,用A ∆表示任一小区间[x ,x+dx]上的窄曲边梯形的面积,A=∑A ∆.A ∆≈f(x)dx ,记面积元素为dA=f(x)dx ,于是A ≈∑f(x)dx ,则A=lim ∑f(x)dx=⎰badx x f )(.一般地,如果某一实际问题中的所求量U 符合下列条件: (1) U 是与一个变量的变化区间有关的量;(2)所求总量U 关于区间],[b a 应具有可加性,即如果把区间],[b a 分成许多部分区间, 则U 相应地分成许多部分量, 而U 等于所有部分量U ∆之和. 这一要求是由定积分概念本身所决定的;(3)部分量U ∆的近似值可表示为)(i f ξi x ∆.将所求量U (总量)表示为定积分的方法通常叫做元素法,这个方法的主要步骤如下: (1) 由分割写出微元 根据具体问题,选取一个积分变量,例如x 为积分变量,并确定它的变化区间],[b a ,任取],[b a 的一个区间微元],[dx x x +,求出相应于这个区间微元上部分量U ∆的近似值,即求出所求总量U 的微元(元素) dx x f dU )(=;(2) 由微元写出积分 根据dx x f dU )(=写出表示总量U 的定积分⎰⎰==bab adx x f dU U )(.注意:使用元素法的关键是正确给出部分量U ∆的近似表达式dx x f )(,即使得U dU dx x f ∆≈=)(. 在通常情况下,要检验dx x f U )(-∆是否为dx 的高阶无穷小并非易事,因此,在实际应用要注意dx x f dU )(=的合理性.不过,已有许多微元的取法已经确定是正确的,如平面面积微元可以看成矩形面积,旋转体体积微元可以看成圆柱体体积等。
考研数学一、二、三大纲详解
考研数学一、二、三大纲详解(教材分析)(共19页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--高等数学考研指定教材:同济大学数学系主编《高等数学》(上下册)(第六版)第一章函数与极限 (7天)(考小题)学习内容复习知识点与对应习题大纲要求第一节:映射与函数(一般章节)函数的概念,常见的函数(有界函数、奇函数与偶函数、单调函数、周期函数)、复合函数、反函数、初等函数具体概念和形式.(集合、映射不用看;双曲正弦,双曲余弦,双曲正切不用看)习题1-1:4,5,6,7,8,9,13,15,16(重点)1.理解函数的概念,掌握函数的表示法,并会建立应用问题中的函数关系.2.了解函数的有界性、单调性、周期性和奇偶性.3.理解复合函数及分段函数的概念,了解反函数及隐函数的概念.4.掌握基本初等函数的性质及其图形,了解初等函数的概念.5.理解极限的概念,理解函数左极限与右极限的概念,以及函数极限存在与左、右极限之间的关系.6.掌握极限的性质及四则运算法则.7.掌握极限存在的两个准则,并会利用它们求极限,掌握利用两个重要极限求极第二节:数列的极限(一般章节)数列定义,数列极限的性质(唯一性、有界性、保号性 )(本节用极限定义证明极限的题目考纲不作要求,可不看,如P26例1,例2,例3,定理1,2,3的证明都不作要求,但要理解;定理4不用看)习题1-2:1第三节:函数的极限(一般章节)函数极限的基本性质(不等式性质、极限的保号性、极限的唯一性、函数极限的函数局部有界性,函数极限与数列极限的关系等) P33(例4,例5)(例7不用做,定理2,3的证明不用看,定理4不用看)习题1-3:1,2,3,4第四节:无穷大与无穷小(重要)无穷小与无穷大的定义,它们之间的关系,以及与极限的关系(无穷小重要,无穷大了解)(例2不用看,定理2不用证明)习题1-4:1,6第五节:极限的运算法则(掌握)极限的运算法则(6个定理以及一些推论)(注意运算法则的前提条件是否各自极限存在)(定理1,2的证明理解,推论1,2,3,定理6的证明不用看)P46(例3,例4),P47(例6)习题1-5:1,2,3,4,5(重点)第六节:极限存在准则(理解)两个重要极限(要牢记在心,要注意极限成立的条件,不要混淆,应熟悉等价表达式,要会证明两个重要极限),函数极限的存在问题(夹两个重要极限(重要)逼定理、单调有界数列必有极限),利用函数极限求数列极限,利用夹逼法则求极限,求递归数列的极限(准则1的证明理解,第一个重要极限的证明一定要会,另一个重要极限的证明不用看,柯西存在准则不用看)P51(例1)习题1-6:1,2,4限的方法.8.理解无穷小量、无穷大量的概念,掌握无穷小量的比较方法,会用等价无穷小量求极限.9.理解函数连续性的概念(含左连续与右连续),会判别函数间断点的类型.10.了解连续函数的性质和初等函数的连续性,理解闭区间上连续函数的性质(有界性、最大值和最小值定理、介值定理),并会应用这些性质.第七节:无穷小的比较(重要)无穷小阶的概念(同阶无穷小、等价无穷小、高阶无穷小、k阶无穷小),重要的等价无穷小(尤其重要,一定要烂熟于心)以及它们的重要性质和确定方法(定理1,2的证明理解)P57(例1)P58(例5)习题1-7:全做第八节:函数的连续性与间断点(重要,基本必考小题)函数的连续性,间断点的定义与分类(第一类间断点与第二类间断点),判断函数的连续性(连续性的四则运算法则,复合函数的连续性,反函数的连续性)和间断点的类型。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第三节 定积分在物理学上的应用
1. 在高为5cm, 底半径为3cm的圆柱形水池中盛满了水, 现将水从池顶全部抽出, 问需做多少功?
2. 有一长为1m的木桩埋在泥土中, 它的上端刚巧与地面相齐. 为了要把木桩拔出, 必须沿木桩方向使
力. 已知所使的力F(x) = 50(1 x)(单位为N), 其中x为木桩已拔出部分的长, 求把木桩全部拔出所作的功.
3. 用铁锤将一铁钉击入木板. 设木板对铁钉的阻力和铁钉击入木板的深度成正比, 在击第一次时, 将
铁钉击入1cm, 如果铁锤每次打击铁钉所做的功相等, 问铁锤击第二次时, 铁钉又被击入多少厘米?
4. 一底为8cm、高为6cm的等腰三角形片, 铅直地沉没在水中, 顶在上, 底在下且与水面平行, 而顶离
水面3cm, 试求它每面所受的压力.
5. 设有一半径为R、中心角为 的圆弧形细棒, 其线密度为常数. 在圆心处有一质量为m的质点M.
试求这细棒对质点M的引力.
