正式 28.1锐角三角函数课件(人教版九下)
合集下载
人教版九年级数学下册第二十八章《28-1 锐角三角函数》优质课课件(共25张PPT)
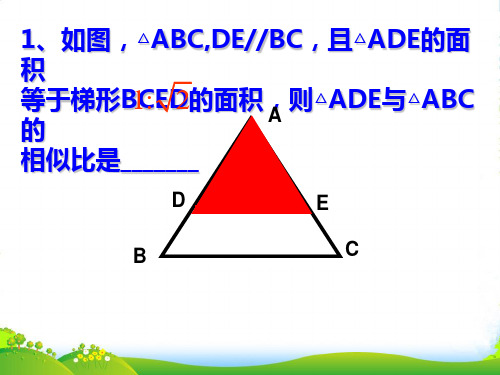
1、如图,△ABC,DE//BC,且△ADE的面
积
等于梯形B1C:ED2的面积,则△ADE与△ABC
的
A
相似比是_______
D
E
B
C
2、如图,△ABC,DE// FG// BC ,且△ADE的面积,梯 形FBCG的面积,梯形DFGE的面积均相等,
则△ADE与△ABC的相似比是1__:___3__;
100倍,sinA的值(C )
1
A.扩大100倍
B.缩小 1 0 0
C.不变
D.不能确定
3.如图 A 300
B
1
3 则 sinA=___2___ .
C 7
1.在平面直角平面坐标系中,已知点A(3,0) 和B(0,-4),则sin∠OAB等于__4_/5_
2.在Rt△ABC中,∠C=900,AD是BC边上的
B
5
5
A
DC
练一练
1.判断对错:
1) 如图
BC
(1) sinA=
(√ )
AB
B
BC (2)sinB= A B
(×)
10m
6m
(3)sinA=0.6m (×) A
C
sinA是一个比值(注意比的顺序),无单位;
(4)SinB=0.8 (√ )
2)如图,sinA=
B C ( ×)
AB
练一练
2.在Rt△ABC中,锐角A的对边和斜边同时扩大
A
1:3:5
D F B
E G C
•11、即使是普通孩子,只要教育得法,也会成为不平凡的人。 •12、首先是教师品格的陶冶,行为的教育,然后才是专门知识和技能的训练。 •13、儿童是中心,教育的措施便围绕他们而组织起来。 •14、孩子在快乐的时候,他学习任何东西都比较容易。 •15、生活即教育,社会即学校,教学做合一。 •16、当在学校所学的一切全都忘记之后,还剩下来的才是教育。2021年10月19日星期二2021/10/192021/10/192021/10/19 •17、播种行为,可以收获习惯;播种习惯,可以收获性格;播种性格,可以收获命运。2021年10月 2021/10/192021/10/192021/10/1910/19/2021 •18、我们发现了儿童有创造力,认识了儿童有创造力,就须进一步把儿童的创造力解放出来2021/10/192021/10/19October 19, 2021 •19、人自身有一种力量,用许多方式按照本人意愿控制和影响这种力量,一旦他这样做,就会影响到对他的教育和对他发生作用的环境。 2021/10/192021/10/192021/10/192021/10/19
积
等于梯形B1C:ED2的面积,则△ADE与△ABC
的
A
相似比是_______
D
E
B
C
2、如图,△ABC,DE// FG// BC ,且△ADE的面积,梯 形FBCG的面积,梯形DFGE的面积均相等,
则△ADE与△ABC的相似比是1__:___3__;
100倍,sinA的值(C )
1
A.扩大100倍
B.缩小 1 0 0
C.不变
D.不能确定
3.如图 A 300
B
1
3 则 sinA=___2___ .
C 7
1.在平面直角平面坐标系中,已知点A(3,0) 和B(0,-4),则sin∠OAB等于__4_/5_
2.在Rt△ABC中,∠C=900,AD是BC边上的
B
5
5
A
DC
练一练
1.判断对错:
1) 如图
BC
(1) sinA=
(√ )
AB
B
BC (2)sinB= A B
(×)
10m
6m
(3)sinA=0.6m (×) A
C
sinA是一个比值(注意比的顺序),无单位;
(4)SinB=0.8 (√ )
2)如图,sinA=
B C ( ×)
AB
练一练
2.在Rt△ABC中,锐角A的对边和斜边同时扩大
A
1:3:5
D F B
E G C
•11、即使是普通孩子,只要教育得法,也会成为不平凡的人。 •12、首先是教师品格的陶冶,行为的教育,然后才是专门知识和技能的训练。 •13、儿童是中心,教育的措施便围绕他们而组织起来。 •14、孩子在快乐的时候,他学习任何东西都比较容易。 •15、生活即教育,社会即学校,教学做合一。 •16、当在学校所学的一切全都忘记之后,还剩下来的才是教育。2021年10月19日星期二2021/10/192021/10/192021/10/19 •17、播种行为,可以收获习惯;播种习惯,可以收获性格;播种性格,可以收获命运。2021年10月 2021/10/192021/10/192021/10/1910/19/2021 •18、我们发现了儿童有创造力,认识了儿童有创造力,就须进一步把儿童的创造力解放出来2021/10/192021/10/19October 19, 2021 •19、人自身有一种力量,用许多方式按照本人意愿控制和影响这种力量,一旦他这样做,就会影响到对他的教育和对他发生作用的环境。 2021/10/192021/10/192021/10/192021/10/19
人教版九年级数学下册 第28.1 _锐角三角函数 第3课时 特殊角的三角函数值(共46张PPT)

7.(中考·庆阳)在△ABC 中,若角 A,B 满足|cos A- 23|+(1- tanB)2=0,则∠C 的大小是( D ) A.45° B.60° C.75° D.105°
8.若△ABC 中,sinA=cos B= 22,则下列最确切的结论是( C ) A.△ABC 是直角三角形 B.△ABC 是等腰三角形 C.△ABC 是等腰直角三角形 D.△ABC 是锐角三角形
tan A =
∠A的对边
∠A的邻边
AC . AB
B
∠A
斜边
的
对
边
A ∠A 的邻边 C
1. 对于sinα与tanα,角度越大,函数值越 大 ; 对于cosα,角度越大,函数值越 小 .
2. 互余的两角之间的三角函数关系: 若∠A+∠B=90°,则sinA = cosB,cosA = sinB, tanA ·tanB = 1 .
cos 30 3a 3 ,
60°
2a 2
tan 30 a 3 .
30°
3a 3
∴ sin 60 3a 3 , 2a 2
cos 60 a 1, 2a 2
tan 60 3a 3. a
60°
30°
设两条直角边长为 a,则斜边长 = a2 a2 2a.
∴ sin 45 a 2 , 2a 2
14.如图,在△ABC 中,∠C=90°,点 D 在 AC 上.已知∠BDC =45°,BD=10 2,AB=20,求∠A 的度数. 解:∵∠BDC=45°,∠C=90°, ∴△BCD 为等腰直角三角形,∴BC=CD. ∵BD=10 2,∴BC=10. ∵AB=20,∴sin A=BACB=1200=12. ∵∠A 为锐角,∴∠A=30°.
九年级数学下册课件-28.1 锐角三角函数9-人教版

解:如图,设点 A (3,0),连接 PA .
在Rt△APO中,由勾股定理得
OP OA2 AP2 32 42 5.
因此 sin AP 4 .
OP 5
方法总结:结合平面直角坐标系求某角的正
ቤተ መጻሕፍቲ ባይዱ
弦函数值,一般过已知点向x轴或y轴作垂线,
构造直角三角形,再结合勾股定理求解.
α
A (3,0)
课堂小结
人教版九年级数学第二十八章第一节
28.1 正弦函数
正弦定义: 如图,在 Rt△ABC 中,∠C=90°,我 们把锐角 A 的对边与斜边的比叫做∠A的正弦,记 作 sin A 即
∠A的对边
sin A = 斜边
a. c
例如,当∠A=30°时,我们有
斜边 c
B a
对边
sin A sin 30 1 ; 2
正弦函数的概念
在 Rt△ABC 中,∠C=90°,我们把 锐角 A 的对边与斜边的比叫做∠A的 正弦,记作 sin A 即
斜边 c
sin
A
=
∠A的对边
斜边
a. c
Ab
B a 对边
C
感谢大家的收看,谢谢!
A bC
当∠A=45°时,我们有 sin A sin 45 2 . 2
练一练
1. 判断对错 BC
sinA = AB BC
sinA = AC BC
sinB = AB sinA =0.6 m sinB =0.8
B
(√ )
10m
6m
( ×) A
C
(×)
(×) (√ )
例1. 如图,在平面直角坐标系内有一点 P (3,4),连 接 OP,求 OP 与 x 轴正方向所夹锐角 α 的正弦值.
初中数学人教版九年级下册:求锐角三角函数值-教学课件

则
a
√3a
自 主 探究 45°角的三角函数值
设两条直角边长为a, 则斜边长为 √2a.
归纳提炼
30°、45°、60°角的正弦值、余弦值和正切值如下表:
锐角A 锐角三角 函数
30° 45° 60°
sin A
2
3
2
2
2
cos A tan A
3 2
3 3
1
√3
学以致用
例 1求下列各式的值:
(1)cos²30°+tan30°·sin60°;
28.1锐角三角函数(第三课时)
年 级:九年级下册 学 科:初中数学(人教版)
想一想
请同学们拿出自己的学习工具——一副三角 尺.这两块三角尺中有几个不同的锐角? 这几个锐角的正弦值、余弦值和正切值各是多少?
自 主 探 究 30°、60°角的三角函数值
设30°所对的直角边长为a, 那么斜边长为2a, 另一条直角边长为 √(2a)²-a²=√3a.
∴∠A=45°.
A
学以致用
例 2 (2)如图,AO 是圆锥的高,OB 是底面半径,AO=√3 OB, 求a的度数. (2)在图中,
∴a=60°.
1.求下列各式的值:
(1)1-2sin30°cos60°; (2)3 tan30°-tan 45°+2sin60°.
解(1)1-2sin30°cos60°(2)3 tan30°-tan 45°+2sin60°
2
2
√3 √2
1 -
2
2
2
tan A
√3
3
1 √3
如图,在Rt△ABC中,三角形 的三边分别记为a,b²,
对任意锐角α,cos²a+sin²a=1 均成立.
a
√3a
自 主 探究 45°角的三角函数值
设两条直角边长为a, 则斜边长为 √2a.
归纳提炼
30°、45°、60°角的正弦值、余弦值和正切值如下表:
锐角A 锐角三角 函数
30° 45° 60°
sin A
2
3
2
2
2
cos A tan A
3 2
3 3
1
√3
学以致用
例 1求下列各式的值:
(1)cos²30°+tan30°·sin60°;
28.1锐角三角函数(第三课时)
年 级:九年级下册 学 科:初中数学(人教版)
想一想
请同学们拿出自己的学习工具——一副三角 尺.这两块三角尺中有几个不同的锐角? 这几个锐角的正弦值、余弦值和正切值各是多少?
自 主 探 究 30°、60°角的三角函数值
设30°所对的直角边长为a, 那么斜边长为2a, 另一条直角边长为 √(2a)²-a²=√3a.
∴∠A=45°.
A
学以致用
例 2 (2)如图,AO 是圆锥的高,OB 是底面半径,AO=√3 OB, 求a的度数. (2)在图中,
∴a=60°.
1.求下列各式的值:
(1)1-2sin30°cos60°; (2)3 tan30°-tan 45°+2sin60°.
解(1)1-2sin30°cos60°(2)3 tan30°-tan 45°+2sin60°
2
2
√3 √2
1 -
2
2
2
tan A
√3
3
1 √3
如图,在Rt△ABC中,三角形 的三边分别记为a,b²,
对任意锐角α,cos²a+sin²a=1 均成立.
人教版九年级数学下册28.1 锐角三角函数(2)课件(16张ppt)

又∵ OA=OB
∴
ta∠ nAP=O OA =6=3 PA8 4
• 上交作业:教科书第68页
习题28.1第1,2题(只 做与余弦、正切函数有 关的部分),第4,6 题.
• 课后作业:“学生用书” 的课后作业部分.
•不习惯读书进修的人,常会自满于现状,觉得再没有什么事情需要学习,于是他们不进则退。经验丰富的人读书用两只眼睛,一只眼睛看到纸面上的话,另 一眼睛看到纸的背面。2022年4月9日星期六2022/4/92022/4/92022/4/9 •书籍是屹立在时间的汪洋大海中的灯塔。2022年4月2022/4/92022/4/92022/4/94/9/2022 •正确的略读可使人用很少的时间接触大量的文献,并挑选出有意义的部分。2022/4/92022/4/9April 9, 2022 •书籍是屹立在时间的汪洋大海中的灯塔。
余 弦 1.在Rt△ABC中,∠C=90°,当锐角A确定 、 时,∠A的对边与斜边的比就随之确定.此 正 时,其他边之间的比是否也随之确定?为 切 什么? 的 定 义
合作探究 达成目标
点一:锐角A的余弦和正切的概念的形成
2.在Rt△ABC中,∠C=90°,我们把∠A的
邻
∠A的余
余 弦 、 正
切
边 记与 作斜 _c_o边_s_A的__比,叫即做_s=_i_n___A____∠—__弦—A____—的斜__—__邻—边__—__边__—__—___=____bc ___;_, ∠A的正切
2.对于锐角A的每一个确定的值,sinA有唯 一确定的值与它对应,所以sinA是A的函数. 同样地,_c_o_s_A_,__ta_n_A__也是A的函数.
3.锐角A的_正__弦____、__余__弦___、_正__切____都 叫做∠A的锐角三角函数.
∴
ta∠ nAP=O OA =6=3 PA8 4
• 上交作业:教科书第68页
习题28.1第1,2题(只 做与余弦、正切函数有 关的部分),第4,6 题.
• 课后作业:“学生用书” 的课后作业部分.
•不习惯读书进修的人,常会自满于现状,觉得再没有什么事情需要学习,于是他们不进则退。经验丰富的人读书用两只眼睛,一只眼睛看到纸面上的话,另 一眼睛看到纸的背面。2022年4月9日星期六2022/4/92022/4/92022/4/9 •书籍是屹立在时间的汪洋大海中的灯塔。2022年4月2022/4/92022/4/92022/4/94/9/2022 •正确的略读可使人用很少的时间接触大量的文献,并挑选出有意义的部分。2022/4/92022/4/9April 9, 2022 •书籍是屹立在时间的汪洋大海中的灯塔。
余 弦 1.在Rt△ABC中,∠C=90°,当锐角A确定 、 时,∠A的对边与斜边的比就随之确定.此 正 时,其他边之间的比是否也随之确定?为 切 什么? 的 定 义
合作探究 达成目标
点一:锐角A的余弦和正切的概念的形成
2.在Rt△ABC中,∠C=90°,我们把∠A的
邻
∠A的余
余 弦 、 正
切
边 记与 作斜 _c_o边_s_A的__比,叫即做_s=_i_n___A____∠—__弦—A____—的斜__—__邻—边__—__边__—__—___=____bc ___;_, ∠A的正切
2.对于锐角A的每一个确定的值,sinA有唯 一确定的值与它对应,所以sinA是A的函数. 同样地,_c_o_s_A_,__ta_n_A__也是A的函数.
3.锐角A的_正__弦____、__余__弦___、_正__切____都 叫做∠A的锐角三角函数.
28.1 锐角三角函数 课件 2023-2024学年人教版数学九年级下册

21k3k=21313,cos A=AACB=
3k =3 13k
13 13 .
例3 已知关于x的方程x2-5x·sin α+1=0的一个根为2+ 3 ,且α为锐角, 求cos α.
解:设方程的另一个根为x2,则(2+ 3 )x2=1,
∴x2=2- 3 . 根据根与系数的关系,得5sin α=(2+
B
?3
A
4C
图(1)
B
5
13
C
?
A
图(2)
例2
如图,在矩形ABCD中,DE⊥AC于点E.设∠ADE=α且sin α=
4 5
,
AB=4,求AD的长.
解:∵∠ADE+∠DAC=90°,∠DAC+∠BAC=90°,
∴∠ADE=∠BAC,
∴sin α=sin ∠BAC=BACC=45.
设AC=5x,BC=4x,则AB=3x=4,
3
)+(2-
3
),解得sin
α=
4 5
.
设锐角α所在的直角三角形的对边长为4k(k>0),则斜边长为5k,邻边长为
3k, ∴cos α=35kk=35.
练习
1.教材P65练习第1,2题.
2.如图,点A为∠α边上的任意一点,过点A作AC⊥BC于点C,过点C作 CD⊥AB于点D,下列用线段比表示cos α的值,错误的是( C )
二、教学重难点
重点 掌握30°,45°,60°角的三角函数值,能够用它们进行计算.
难点 理解30°,45°,60°角的三角函数值的探索过程.
三、教学设计
活动1 新课导入
在前面我们已经得到sin
30°=
1 2
,sin 45°=
人教版九年级数学下册28.1 锐角三角函数(2)课件(16张ppt)
又∵ OA=OB
∴
ta∠ nAP=O OA =6=3 PA8 4
• 上交作业:教科书第68页
习题28.1第1,2题(只 做与余弦、正切函数有 关的部分),第4,6 题.
• 课后作业:“学生用书” 的课后作业部分.
28.1 锐角三角函数
第2课时 锐角的余弦与正切
创设情景 明确目标 我们是怎样定义直角三角形中一个锐角的正弦的?
1.在RT△ABC中,∠C =90°,我们把锐角A 的对边与斜边的比叫做∠A的正弦(sine), 记作sinA,
即sinA = A的对边 = a .
斜边
c
创设情景 明确目标
2.分别求出图中∠A,∠B的正弦值.
A. sinA= 5 ;
13
B.sinA = 12
13
C.tanA= 13 ;
12
D. cosA= 5
12
4.如图:P是∠的边OA上一点,
且P点的坐标为(3,4),则
cos α 、tan α 的值.
cosα= 3 tanα= 4
5
3
总结梳理 内化目标
1.在Rt△ABC中,∠C=90°,我们把∠A的邻 边与斜边的比叫做______∠__A_的__余__弦_______, 记作_c_o_s_A__,即_s_i_n_A_=__—_∠—_A—_的斜_—_—邻边_—_边—__—_—__=__bc _; 把∠A的对边与邻边的比叫做_∠__A_的__正__切___, 记作_t_a_n_A____,即_t_a_n_A_=__—∠∠_—_AA_—的的_—_对邻—_—_边边_—_—_—__=_ba _.
解:由勾股定理得 AC AB 2 BC 2 102 62 8, 因 此 sin A B C 6 3 ,
∴
ta∠ nAP=O OA =6=3 PA8 4
• 上交作业:教科书第68页
习题28.1第1,2题(只 做与余弦、正切函数有 关的部分),第4,6 题.
• 课后作业:“学生用书” 的课后作业部分.
28.1 锐角三角函数
第2课时 锐角的余弦与正切
创设情景 明确目标 我们是怎样定义直角三角形中一个锐角的正弦的?
1.在RT△ABC中,∠C =90°,我们把锐角A 的对边与斜边的比叫做∠A的正弦(sine), 记作sinA,
即sinA = A的对边 = a .
斜边
c
创设情景 明确目标
2.分别求出图中∠A,∠B的正弦值.
A. sinA= 5 ;
13
B.sinA = 12
13
C.tanA= 13 ;
12
D. cosA= 5
12
4.如图:P是∠的边OA上一点,
且P点的坐标为(3,4),则
cos α 、tan α 的值.
cosα= 3 tanα= 4
5
3
总结梳理 内化目标
1.在Rt△ABC中,∠C=90°,我们把∠A的邻 边与斜边的比叫做______∠__A_的__余__弦_______, 记作_c_o_s_A__,即_s_i_n_A_=__—_∠—_A—_的斜_—_—邻边_—_边—__—_—__=__bc _; 把∠A的对边与邻边的比叫做_∠__A_的__正__切___, 记作_t_a_n_A____,即_t_a_n_A_=__—∠∠_—_AA_—的的_—_对邻—_—_边边_—_—_—__=_ba _.
解:由勾股定理得 AC AB 2 BC 2 102 62 8, 因 此 sin A B C 6 3 ,
数学:28.1锐角三角函数(2)课件(人教新课标九年级下)
例题示范
3 例2 如图,在Rt△ABC中,∠C=90°,BC=6,sinA= 5 ,求 cosA、tanB的值.
B
解:∵
BC sin A AB
A
6
BC 5 AB 6 10 sin A 3
又
C
AC AB 2 BC 2 10 2 62 8
AC 4 AC 4 cos A , tan B AB 5 BC 3
2. 在Rt△ABC中,如果各边长都扩大2倍,那么锐角A的正弦值、余 弦值和正切值有什么变化? 解:设各边长分别为a、b、c,∠A的三个三角函数分别为
a b a sin A , cos A , tan A c c b
则扩大2倍后三边分别为2a、2b、2c
B
2a a sin A 2c c 2b b cos A 2c c 2a a tan A 2b b
2、sinA、 cosA、tanA是一个比值(数值)。
3、sinA、 cosA 、tanA的大小只与∠A的大小 有关,而与直角三角形的边长无关。
课后作业
课时作业本 P76—P83
独立完成作业的良好习惯,
是成长过程中的良师益友。
中考语录
中考是一场跳高比赛,取胜关 键在于你起跳时对大地用力多少!
结束寄语
试一试:
下图中∠ACB=90°,CD⊥AB,垂足为D。指出∠A和∠B 的对边、邻边。 B D (1) tanA =
(BC )
= CD (AD) AC
A
C
(2) tanB=
(AC )
BC
= CD ( BD)
试一试:
如图,在Rt△ABC中,锐角A的邻边和斜边同时 扩大100倍,tanA的值( C ) A.扩大100倍 B.缩小100倍 C.不变 D.不能确定
数学:28.1锐角三角函数(第3课时) 课件(人教版九年级下)
tan
45
2 2 1 22
=0
例4 (1)如图,在Rt△ABC中,∠C=90°,
AB 6, BC 3 ,
B
Hale Waihona Puke 求∠A的度数.63
解: (1)在图中,
A
C
sin A BC 3 2 AB 6 2
A 45
(2)如图,已知圆锥的高AO等于圆锥 的底面半径OB的3 倍,求 a . 解: (2)在图中,
tan a AO 3OB 3 OB OB
A OB
a 60
练习
1. 求下列各式的值:
(1)1-2 sin30°cos30°
(2)3tan30°-tan45°+2sin60°
(3)
1
cos 60 sin 60
1 tan 30
解: (1)1-2 sin30°cos30°
12 1 3 22
1 3 2
活动1
两块三角尺中有几个不同的锐 角?分别求出这几个锐角的正 弦值、余弦值和正切值.
60°
30° 45°
45°
设30°所对的直角边长为a,那么斜边长为2a
另一条直角边长= 2a2 a2 3a
sin 30 a 1 2a 2
30°
cos 30 3a 3 2a 2
tan 30 a 3 3a 3
A
C
21
AB AC2 BC2
2
2
21 7 28 2 7
sin A BC 7 1 AB 2 7 2
∴ A=30°
∠B = 90°- ∠ A = 90°-30°= 60°
sin 60 3a 3 2a 2
cos 60 a 1
2a 2
60°
九年级数学下册课件-28.1 锐角三角函数10-人教版
D.不能确定
┌
5.已知∠A,∠B为锐角
A
C
(1)若∠A=∠B,则tanA tanB;
(2)若tanA=tanB,则∠A ∠B.
随堂练习 15
八仙过海,尽显才能 6.如图, ∠C=90°CD⊥AB.
驶向胜利 的彼岸
C
( ) ( )( )
tan A
(
)(
)(
.
)
A
┌ DB
7.在上图中,若BD=6,CD=12.求tanB的值.
(4).如图 (2) tan B 4 ( ).
3
(5).如图 (2) tan A 0.75( ).
老师期望:你能从 中悟出点东西.
随堂练习 14
八仙过海,尽显才能
驶向胜利 的彼岸
4.如图,在Rt△ABC中,锐角A的对边和邻边同时
扩大20倍,tanB的值( )
B
A.扩大20倍 B.缩小20倍
C.不变
直挂云帆 济沧海
例1 下图表示两个自动扶梯,那一个自动扶梯比
较陡?
甲
13m α
5m ┌
乙 6m ┐ 8m β
解:甲梯中, tan
5 5. 132 52 12
老师提示: 生活中,常用
乙梯中, tan 6 3 .
一个锐ห้องสมุดไป่ตู้的正
84
∵tanβ>tanα,∴乙梯更陡.
切表示梯子的
倾斜程度.
议一议 11
用数学去解释生活
驶向胜利 的彼岸
如图,正切也经常用来描述山坡的坡度.例如,
有一山坡在水平方向上每前进100m就升高60m,
那么山坡的坡度i(即tanα)就是:
老师提示:
