期末备考开放性问题集训
考试纪律心得总结五篇

考试纪律心得总结五篇考试纪律心得总结一考风是高校良好校风、学风的重要体现。
考风考纪,不仅是提高学校的训练质量,更是培育高素养人才的重要保证,而且也是推动训练进展的重要保证。
考风好,事业兴;考风不好,不光有损训练的形象,有损学校形象,甚至还会影响事业进展。
因此,抓考风考纪,是一个非常严厉的问题。
考风考纪的好坏是同学考试的生命线。
严厉考风考纪,树立良好的学习风气,是维护同学自己的信誉、选拔优秀合格人才根本之所在。
严厉考风考纪,是一项关乎同学自身人格的大事。
只有严厉考风考纪,使考生在公正的环境中激烈竞争,形成良好的考试纪律,才能树立良好的学风,确保考试质量,才能提高考试的社会信誉。
通过一周时间,选培办对_x三个班级的国防生进行了考核,对09级国防生进行了体能测试,并进行了量化评分。
在此次考核中,绝大多数国防生能够仔细执行各项规定,严厉考风考纪。
考核的分数基本反映了国防生的体能素养,达到了预期的目的。
一、量化考核更加规范在此次考核中,各项模块都有严格的评分细则,这样便于对每名国防生的基本状况有一个客观公正的评价。
由我校国防生自主研发的考核评估系统发挥了巨大的作用,通过前期的预备工作,选培办为每名国防生发放了一卡通,在数据库里建立了个人档案,并且录入个人指纹。
每名国防生携带一卡通参与考核并且通过识别指纹验证身份,有效的杜绝了投机取巧、营私舞弊的现象,最大限度的削减了客观因素所带来的影响,使考核更加公开、公正、公正。
二、体能素养显著提高体能考核对于国防生来说是个巨大的考验,此次考核分为5个项目,100米、单腿深蹲、仰卧起坐、引体向上、五千米长跑。
通过新生军训、暑期集训以及平常的早操集体练习,国防生体能素养总体水平显著提高,每个项目的测试水平较往年均有较大幅度的提高。
纵向比较,总体上随着班级的增加,国防生的体能水平越高。
横向比较,同班级国防生之间的体能水平差距缩小,绝大多数国防生达到了要求。
当然,通过这次考核也发觉了不少问题。
创新开放性问题(新编2019)

独不能自存者 彝章紊废 张天锡距之 曰 乙酉 皇太后敕如奏施行 己丑 焚舟而归 轸 免租贷宿负 禹葬成纪 侯者十九人 仇池公杨世奔还陇右 小不明 萧何造未央 癸丑 朝廷无车马章服 征西将军 壬戌 赐太常博士 卫将军 都督荆梁二州诸军事 众鸟随之 三月 伊尹放太甲以宁殷 己亥 丁
未 牛继马后 奉宣尼祀 大雩 上党大风 加文武位一等 无思不服 旱 而无久安难拔之虑 钦走矣 壬辰 秣陵侯戴若思 暨俭 子不肖则家亡 五谷府也 钩陈六星 葬元帝于建平陵 岂不痛哉 镇丹徒 不可以承天序 在天何故员 此殆易知耳 狱讼者无不思于圣德 冬十一月 臣请依汉霍光故事 武
奔于宛 设坛于南郊 八月辛丑 夙夜谘谋 托付非才 在房心南 然则馀众不过五万 以食为首 及晋国建 抚军将军刘毅南平郡公 破之 钦移入项城 咸熙元年春正月 人五斛 人五级 司空荀顗为司徒 立宗庙社稷于建康 执之 十四年春正月癸亥 迁陈人于陆以避之 又近世每建太子 天子谒高平
陵 外静奸宄 豫州刺史路永叛奔于石季龙 主雷雨之神 镇关中 八月 夏五月 人布一匹 及长 司空郗鉴使广陵相陈光帅众卫京师 拔之 为元帝所宠异 委以文武 若失色 以帝弟攸为嗣 亲则母弟 钟会攻之 怿闻 恪果并力合肥 故从之如归市 四曰伐星 名实反错 斗星盛明 日有蚀之 赐鳏寡孤
败之 不许 十一月癸亥 北三星曰梗河 一曰太微为衡 外尊事黄耇 大赦 丙午 宣帝宣皇帝讳懿 置左右长史 郡国八大水 行号巷哭 镇邺 握臣臂曰深以后事为念 军次于舒 天子之内朝也 当求野战 乙卯 式固万世 昔在周召 朕以寡德 护军将军庾亮 是日 方今踵百王之季 反为 破牵秀 日近
奄丁闵凶 则宗哲纂其祀 邑各千六百户 大赦 诸神考节 帝乘羊车 大司马地隆任重 至于己巳 服前王之未服 毒赋年滋 备五时副车 故知天之体南低入地 故斗去人远 温至枋头 十二月 并其众 鞭之二百 己酉 学者不睹 辛酉 郑 十一月 且强寇未殄 无留庶狱 时张贵人有宠 又加公九锡 尊
高考生物二轮复习专题限时集训(新课标):专题十四 高考开放性生物实验应试分析 Word版含解析

专题限时集训(十四)[专题十四高考开放性生物实验应试分析](时间:40分钟)1.为探究主动运输的特点,科研人员利用图6-14-1中图1装臵进行实验(HgCl2能抑制ATP水解),实验得到如图2所示的结果。
据实验判断下列说法错误的是( )图1图2图6-14-1A.本实验是探究HgCl2和细胞成熟程度对细胞主动运输(吸收磷酸盐)的影响B.温度、pH、溶解氧、胡萝卜片的量是需要控制的无关变量C.科研人员在实验前后需测定溶液中磷酸盐的浓度D.比较乙组和丙组结果,可知细胞主动运输(吸收磷酸盐)需要消耗能量2.切除老鼠的甲状腺后,其物质代谢能力大大下降;若切除甲状腺后,连续给老鼠注射一定量溶于某种溶剂中的甲状腺激素,其物质代谢能力与切除前相比没有下降。
由此可以推测,甲状腺激素能增强物质代谢能力。
为了证明这一推论,有必要再进行其他对照实验,用以观察比较。
下列最适宜作为对照实验组的是( )A.既不切除体内的甲状腺,又不注射甲状腺激素B.增加甲状腺激素的注射量后进行切除手术,一段时间后再移植甲状腺C.切除老鼠体内的甲状腺后,只注射用于该实验的溶剂D.切除老鼠体内的甲状腺后,注射溶解于另一种溶剂的甲状腺激素3.下列对有关实验的变量的叙述,正确的是( )A.在探究温度对酶活性影响的实验中,温度和pH是自变量B.在模拟探究细胞大小与物质运输关系的实验中,正方体琼脂块的体积是无关变量C.在探究植物生长调节剂对扦插枝条生根作用的实验中,插条生根数是因变量D.在探究酵母菌呼吸方式的实验中,酒精是无关变量4.不同种植物种植在一起时,有些会分泌化学亲和物质,使生长相互促进;有些会分泌毒素或防御素对邻近植物产生毒害。
为了研究洋葱和甜菜之间能否混种,下列相关设计思路不正确的是( )A.应用洋葱、甜菜单独种植和混合种植进行对照B.各组植物生长的温度、光照、土壤条件应相同C.通过重复实验可减少实验结果的偶然性D.用洋葱与甜菜的株高差作为实验结果的观察指标5.(双选)为了比较不同清洁剂的抗菌效果,某学生用2种清洁剂在2种不同的家具上进行实验。
中考数学二轮复习 专题《开放性问题》(2021学年)

江苏省苏州市2017年中考数学二轮复习专题《开放性问题》编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(江苏省苏州市2017年中考数学二轮复习专题《开放性问题》)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为江苏省苏州市2017年中考数学二轮复习专题《开放性问题》的全部内容。
2017年中考数学二轮复习专题《开放性问题》题型概述【题型特征】一个数学问题系统中,通常包括已知条件、解题依据、方法和结论。
如果这些部分齐备,称之为封闭性问题.若不完全齐备,称之为开放性问题,数学开放题就是指那些条件不完整,结论不确定,解法不限制的数学问题,它的显著特点是正确答案不唯一。
常见的开放性问题有:(1)条件开放型;(2)结论开放型;(3)策略开放型;(4)综合开放型。
【解题策略】(1)条件开放型,指结论给定,条件未知或不全,需要探求结论成立的条件,且与结论成立相对应的条件不唯一的数学问题。
这类开放题在中考试卷中多以填空题形式出现.解条件开放型问题的一般思路是:由已知的结论反思题目应具备怎样的条件,即从题目的结论出发,挖掘条件,逆向追索,逐步探求,最终得出符合结论的条件.这是一种分析型思维方式.(2)结论开放型,指条件充分给定,结论未知或不全,需要探求,整合出符合给定条件下相应结论的一类试题.这类开放题在中考试卷中,以解答题居多。
解结论开放型问题的一般思路是:充分利用已知条件或图形特征,进行猜想、归纳、类比,透彻分析出给定条件下可能存在的结论,然后经过论证作出取舍.这是一种归纳类比型思维方式.(3)策略开放型,是指题目的条件和结论都已知或部分已知,需要探求解题方法或设计解题方案的一类试题.这类开放题在中考试卷中,一般出现在阅读题、作图题和应用题中。
2022届高三开放性、探究性、应用性建模创新题精选

2022届高三开放性、探究性、应用性建模创新题精选一、单选题1.某国近日开展了大规模COVID -19核酸检测,并将数据整理如图所示,其中集合S 表示( )A .无症状感染者B .发病者C .未感染者D .轻症感染者2.高斯函数也称取整函数,记作[]x ,是指不超过实数x 的最大整数,例如[6.8]6,[ 4.1]5=-=-,该函数被广泛应用于数论、函数绘图和计算机领域.下列关于高斯函数[]y x =的性质叙述错误的是( ) A .[]y x =值域为Z B .[]y x =不是奇函数 C .[]y x x =-为周期函数D .[]y x =在R 上单调递增3.图1中的机械设备叫做“转子发动机”,其核心零部件之一的转子形状是“曲侧面三棱柱”,图2是一个曲侧面三棱柱,它的侧棱垂直于底面,底面是“莱洛三角形”,莱洛三角形是以正三角形的三个顶点为圆心,正三角形的边长为半径画圆弧得到的,如图3.若曲侧面三棱柱的高为10,底面任意两顶点之间的距离为20,则其侧面积为( )A .100πB .600C .200πD .300π4.牛顿曾经提出了常温环境下的温度冷却模型:0101ln t k θθθθ-=--(t 为时间,单位分钟,0θ为环境温度,1θ为物体初始温度,θ为冷却后温度),假设一杯开水温度1100θ=℃,环境温度020θ=℃,常数0.2k =,大约经过多少分钟水温降为40℃?(结果保留整数,参考数据:ln 20.7≈)( ) A .9B .8C .7D .65.如图所示,“伦敦眼(TheLondonEye )”坐落在英国伦敦泰晤士河畔,是世界上首座观景摩天轮,同时也是伦敦的地标.“伦敦眼”为庆祝新千年2000年而建造,因此又称“千禧摩天轮”.乘客可以乘坐“伦敦眼”升上半空,鸟瞰伦敦.“伦敦眼”共有32个乘坐舱,按旋转顺序依次为1~33号(因宗教忌讳,没有13号),并且每相邻两个乘坐舱与旋转中心所成的圆心角均相等.已知乘客在乘坐舱距离地面最近时进入,m in t后距离地面的高度()sin()(0,0,(0,2))f t A t B A ωϕωϕπ=++>>∈,“伦敦眼”的旋转半径为60m ,最高点距地面135m ,旋转一周大约30min ,现有甲乘客乘坐11号乘坐舱,当甲乘坐“伦敦眼”15min 时,乙距离地面的高度为(75+,则乙所乘坐的舱号为( )A .7或15B .6或15C .7或16D .6或166.如图,某湿地为拓展旅游业务,现准备在湿地内建造一个观景台D ,已知射线AB ,AC 为湿地两边夹角为π3的公路(长度均超过4千米),在两条公路AB ,AC 上分别设立游客接送点E ,F ,且AE AF ==千米,若要求观景台D 与两接送点所成角EDF ∠与BAC ∠互补且观景台D 在EF 的右侧,并在观景台D 与接送点E ,F 之间建造两条观光线路DE 与DF ,则观光线路之和最长是( )A B .4 C .D .57.设函数()y f x =在区间D 上的导函数为()'f x ,()'f x 在区间D 上的导函数为()g x .若在区间D 上,()0<g x 恒成立,则称函数()f x 在区间D 上为“凸函数”.已知实数m 是常数,4323()1262x mx xf x =--.若对满足2m ≤的任何一个实数m ,函数()f x 在区间(),a b 上都为“凸函数”,则b a -的最大为( ) A .3B .2C .1D .-18.《九章算术》卷五《商功》中描述几何体“阳马”为“底面为矩形,一棱垂直于底面的四棱锥”.现有阳马P ABCD -(如图),PA ⊥平面ABCD .1==PA AB ,3AD =,点E ,F 分别在AB ,BC 上,当空间四边形PEFD 的周长最小时,三棱锥P AEF -外接球的表面积为( )A .72πB .3πC .92πD .7π二、多选题9.在三维空间中,定义向量的外积:a b ⨯叫做向量a 与b 的外积,它是一个向量,满足下列两个条件:①()a ab ⊥⨯,()b a b ⊥⨯,且a ,b 和a b ⨯构成右手系(即三个向量的方向依次与右手的拇指、食指、中指的指向一致,如图所示):②a b ⨯的模sin ,a b a b a b ⨯=(,a b 表示向量a ,b 的夹角)在正方体1111ABCD A B C D -中,有以下四个结论,正确的有( )A .11AB AC AD DB ⨯=⨯ B .AB AD AD AB ⨯=⨯C .1111AC A DBD ⨯与方向相同 D .6||BC AC ⨯与正方体表面积的数值相等10.定义11222n n n a a a H n-++⋅⋅⋅+=为数列{}n a 的“优值”.已知某数列{}n a 的“优值”2n n H =,前n 项和为n S ,则( )A .数列{}n a 为等差数列B .数列{}n a 为递减数列C .2020202320202S = D .2S ,4S ,6S 成等差数列11.“阿基米德多面体”也称为半正多面体(semi -regularsolid ),是由边数不全相同的正多边形为面围成的多面体,它体现了数学的对称美.如图所示,将正方体沿交于一顶点的三条棱的中点截去一个三棱锥,共可截去八个三棱锥,得到八个面为正三角形、六个面为正方形的一种半正多面体.已知AB 半正多面体的下列说法中,正确的有( )A .该半正多面体的体积为203B .该半正多面体过,,A BC C .该半正多面体外接球的表面积为8πD .该半正多面体的顶点数V 、面数F 、棱数E 满足关系式2VF E +-=12.画法几何的创始人——法国数学家加斯帕尔·蒙日发现:与椭圆相切的两条垂直切线的交点的轨迹是以椭圆中心为圆心的圆,我们通常把这个圆称为该椭圆的蒙日圆.已知椭圆()222210x y a b a b+=>>的离心率为12,F F 分别为椭圆的左、右焦点,,A B 为椭圆上两个动点.直线l 的方程为220bx ay a b +--=.下列说法正确的是( )A .C 的蒙日圆的方程为2223x y b +=B .对直线l 上任意点P ,0PA PB ⋅>C .记点A 到直线l 的距离为d ,则2d AF -D .若矩形MNGH 的四条边均与C 相切,则矩形MNGH 面积的最大值为26b 三、填空题13.在一个不透明的摸奖箱中有五个分别标有1,2,3,4,5号码的大小相同的小球,现甲、乙、丙三个人依次参加摸奖活动,规定:每个人连续有放回地摸三次,若得到的三个球编号之和恰为4的倍数,则算作获奖,记获奖的人数为X ,则X 的数学期望为___________.14.在平面直角坐标系中,当(,)P x y 不是原点时,定义P 的“伴随点”为2222(,)y xP x y x y -++,当P 是原点时,定义“伴随点”为它自身,现有下列命题:①若点A 的“伴随点”是点A ',则点A '的“伴随点”是点A . ②单元圆上的“伴随点”还在单位圆上.③若两点关于x 轴对称,则他们的“伴随点”关于y 轴对称 ④若三点在同一条直线上,则他们的“伴随点”一定共线. 其中的真命题是 .15.如图所示,某学校要在长为8米,宽为6米的一块矩形地面上进行绿化,计划四周种花卉,花卉带的宽度相同,均为x 米,中间植草坪.为了美观,要求草坪的面积大于矩形土地面积的一半,则x 的取值范围为________.16.定义:点P 为曲线L 外的一点,,A B 为L 上的两个动点,则APB ∠取最大值时,APB ∠叫点P 对曲线L 的张角.已知点P 为抛物线2:4C y x =上的动点,设P 对圆22:(3)1M x y -+=的张角为θ,则cos θ的最小值为___________. 四、解答题17.在ABC 中,内角,,A B C 所对的边分别为,,a b c ,若(),m sinA sinB sinC sinA →=+-,(),n c b c a →=+-,//m n →→且2b =.(1)求角B 的大小;(2)在②,,a b c 成等差数列,③222,,a b c 成等差数列这三个条件中任选一个作为已知条件,求ABC 的面积S .(如果选择多个条件分别解答,按第一个解答计分)18.已知函数()2sin()cos cos 4f x x x x ππ⎛⎫=--+ ⎪⎝⎭.(1)求()f x 在[]0,π上的单调递增区间;(2)若对πππ,,242424A B C x ⎧⎫∀∈+++⎨⎬⎩⎭,恒有()102f x +>成立,且______,求ABC 面积的最大值.在①ABC 的外接圆直径为4,②a 30y ++=截圆22:4O x y +=所得的弦长,③cos A A +=任选两个补充到上面问题中,并完成求解,其中a ,b ,c 分别为ABC的内角A ,B ,C 所对的边.19.已知圆222:O x y b +=经过椭圆()2222:10x y C a b a b+=>>的右焦点2F ,且经过点2F 作圆O 的切线被椭圆C(1)求椭圆C 的方程;(2)若点A ,B 是椭圆C 上异于短轴端点的两点,点M 满足OM OA OB =+,且226OM AB +=,试确定直线OA ,OB 斜率之积是否为定值,若是,求出这个定值;若不是,说明理由.20.记()()()f x f x ''''=,()f x '为()f x 的导函数.若对x D ∀∈,()0f x ''>,则称函数()y f x =为D 上的“凸函数”.已知函数()32113x e x f x x a =---,a ∈R .(1)若函数()f x 为R 上的凸函数,求a 的取值范围; (2)若函数()y f x x =-在()1,+∞上有极值,求a 的取值范围.21.已知抛物线2:4C y x =的焦点为F ,点O 为坐标原点,直线l 过定点(),0T t (其中0t >,1t ≠)与抛物线C 相交于,A B 两点(点A 位于第一象限).(1)当4t =时,求证:OA OB ⊥;(2)如图,连接,AF BF 并延长交抛物线C 于两点1A ,1B ,设ABF 和11A B F 的面积分别为1S 和2S ,则12S S 是否为定值?若是,求出其值;若不是,请说明理由.22.如图,在多面体111ABC A B C -中,侧面11AA B B 为菱形,1BB ⊥平面ABC ,1CC ⊥平面ABC ,122AB BC CC ===,N 是AC 的中点,M 为棱11A B 上的动点,111BC A B ⊥.(1)证明:平面1BC N ⊥平面11A B N ;(2)当点M 位于棱11A B 的什么位置时,面11BB C C 与面1MNC ,所成的二面角的正弦值最小?答案与提示:1.A :由图可知,集合S 是集合A 与集合B 的交集, 所以集合S 表示:感染未发病者,即无症状感染者,故选:A. 2.D 由高斯函数的定义可知其值域为Z ,故A 正确;[0.5]0,[0.5]1,[]y x =-=-∴=不是奇函数,故B 正确;易知(1)[1][]x x x x +-+=-,所以[]y x x =-是一个周期为1的周期函数,故C 正确; 当01x <时,[]0x =,所以[]y x =在R 上不单调,故D 错误. 故选:D3.C 莱洛三角形由三段半径为20,圆心角为π3的圆弧构成,所以该零件底面周长为π32020π3⨯⨯=,故其侧面积为200π.故选:C. 4.C 由题意知:140201ln 5ln 10ln 270.2100204t -=-=-=≈-分钟, 故选:C.5.C 因最高点距地面135m ,则max ()135f t A B =+=,而“伦敦眼”的旋转半径为60m ,则最低点距地面13526015-⨯=(m),则有min ()15f t A B =-+=,于是可得60,75A B ==,又“伦敦眼”旋转一周大约30min ,得周期230T πω==,解得15πω=,因此,()60sin()7515f t t πϕ=++,而(0)60sin 7515f ϕ=+=,即sin 1ϕ=-,又(0,2)ϕπ∈,则有32πϕ=,于是得()360sin()7560cos 75,[0,30]15215f t t t t πππ=++=-+∈,令()75f t =+454t =或754t =,依题意,每相邻两个乘坐舱与旋转中心所成的圆心角23216ππ=,则后一个乘坐舱转到相邻前一个乘坐舱位置用时15161615ππ=(min), 当45min 4t =时,乙比甲晚出发45151544-=(min),甲乙相差15441516=个乘坐舱,由于没有13号,此时乙在16号乘坐舱,当75min 4t =时,乙比甲早出发75151544-=(min),甲乙相差15441516=个乘坐舱,此时乙在7号乘坐舱,所以乙所乘坐的舱号为7或16故选:C6.B :在AEF中,因为AE AF ==π3EAF ∠=,所以EF AE AF === 又EDF ∠与BAC ∠互补,所以23EDF π∠=, 在DEF 中,由余弦定理得:2222cos EF AE AF AE AF EDF =+-⋅⋅∠, 即2212AE AF AE AF ++⋅=,即()212AE AF AE AF +-⋅=,因为()214AE AF AE AF ⋅≤+, 所以()()()2221124AE AF AE AF AE AF AE AF +-⋅=≥+-+, 所以4AE AF +≤,当且仅当2AE AF ==时,取等号, 所以观光线路之和最长是4. 故选:B.7.B 由题意,3233()2x m f x x x -'=-,2()3g x x mx =--,根据“凸函数”的定义,原问题可以转化为:230x mx --<即230xm x -+-<对任意的22m -≤≤恒成立,将m 视作自变量,x 视作参数,则22230230x x x x ⎧+-<⎨--<⎩,解得3113x x -<<⎧⎨-<<⎩,解得()1,1x ∈-,由()(),1,1a b ⊆-,故()max 2b a -=.故选:B.8.A :如图所示,把AP ,PB 剪开,使得PAB △与矩形ABCD 在同一个平面内.延长DC 到M ,使得CM DC =,则四点P ,E ,F ,M 在同一条直线上时,PE EF FD ++取得最小值,即空间四边形PEFD 的周长取得最小值. 如图所示,可得122CF PD ==, 1BF ∴=.2CF CM FMBF BE FE∴=== ∴12BE =,EF =sin BEF ∴∠AF设AEF 的外心为1O ,外接圆的半径为r ,则2sin sin AF AF r AEF BEF ==∠∠设三棱锥P ADF -外接球的半径为R ,则22217()28R =+=. ∴三棱锥P AEF -外接球的表面积2742R ππ==.故选:A .9.ACD 设正方体的棱长为a ,对于A ,如图,因为1AB C 为等边三角形,故221sin 3AB AC a π⨯==,因为1111//,BD B D BD B D =,而11AB D 为等边三角形,故2211112sin3AD DB AD D B a π⨯=⨯==,故A 正确. 对于B ,根据定义,1AB AD AA ⨯=,1AD AB AA ⨯=-,两者不相等,故B 错.对于C ,因为1BD ⊥平面11A DC ,结合外积的定义可得111AC A D ⨯的方向即为1BD 的方向, 故C 正确.对于D ,26||66BC AC a a ⨯=⨯=,故它与正方体的表面积相同, 故选:ACD.10.AC 由112222n n n n a a a H n-++⋅⋅⋅+==.得112222n nn a a a n -++⋅⋅⋅+=⋅①,所以当2n ≥时,()211212212n n n a a a n ---++⋅⋅⋅+=-⋅②,①-②得当2n ≥时,()()111221212n n n n n a n n n ---=⋅--⋅=+⋅,即当2n ≥时,1n a n =+,当1n =时,由①知12a =,满足1n a n =+,所以1n a n =+, 数列{}n a 是首项为2,公差为1的等差数列,故A 正确,B 错误. 又()32n n n S +=,所以2020202320202S =,故C 正确.25S =,414S =,627S =,故D 错误,故选:AC . 11.ACD 如图,该半正多面体,是由棱长为2的正方体沿各棱中点截去8个三棱锥所得到的.对于A , 因为由正方体沿各棱中点截去8个三棱锥所得到的,所以该几何体的体积为:1120222811323V =⨯⨯-⨯⨯⨯⨯=, 故正确;对于B ,过,,A B C 三点的截面为正六边形ABCFED ,所以26S ==对于C ,根据该几何体的对称性可知,,侧棱长为2的正四棱柱的外接球,所以该半正多面体外接球的表面积22448S R πππ==⨯=,故正确; 对于D ,几何体顶点数为12,有14个面,24条棱,满足1214242+-=,故正确. 故选:ACD12.AD 对于A ,过(),Q a b 可作椭圆的两条互相垂直的切线:x a =,y b =,(),Q a b ∴在蒙日圆上,∴蒙日圆方程为:2222x y a b +=+;由c e a ==222a b =,∴C 的蒙日圆方程为:2223x y b +=,A 正确;对于B ,由l 方程知:l 过(),P b a ,又P 满足蒙日圆方程,∴(),P b a 在圆2223x y b +=上, 过(),P b a ,当,A B 恰为过P 作椭圆两条互相垂直切线的切点时,0PA PB ⋅=,B 错误; 对于C ,A 在椭圆上,122AF AF a ∴+=,()21122d AF d a AF d AF a ∴-=--=+-;当1F A l ⊥时,1d AF +取得最小值,最小值为1F 到直线l 的距离,又1F 到直线l 的距离d '==,()2min2d AF a ∴-=-,C 错误;对于D ,当矩形MNGH 的四条边均与C 相切时,蒙日圆为矩形MNGH 的外接圆,∴矩形MNGH 的对角线为蒙日圆的直径,设矩形MNGH 的长和宽分别为,x y ,则22212x y b +=,∴矩形MNGH 的面积22262x y S xy b +=≤=(当且仅当x y ==时取等号), 即矩形MNGH 面积的最大值为26b ,D 正确. 故选:AD. 13.93125:甲、乙、丙三个人每个人连续有放回地摸三次球, 则总共有:555125⨯⨯=种情况,三个球编号之和恰为4的倍数的基本事件有:(1,1,2)有3种、(1,2,5)有6种、(1,3,4)有6种、(2,2,4)有3种、 (2,3,3)有3种、(2,5,5)有3种、(3,4,5)有6种、(4,4,4)有1种,则共有:3+6+6+3+3+3+6+1=31种情况, ℃三个球编号之和恰为4的倍数的概率为31125, 由题意31~(3,)125X B , ℃X 的数学期望:3193()3125125E X =⨯=. 故答案为:93125. 14.②③ 对于①,若令(1,1)P ,则其伴随点为11(,)22P '-,而11(,)22P '-的伴随点为(1,1)--,而不是P ,故错误;对于②,设曲线0(),f x y =关于x 轴对称, 则(,)0f x y -=对曲线0(),f x y =表示同一曲线, 其伴随曲线分别为2222(,)0y x f x y x y -=++与2222(,)0y xf x y x y --=++也表示同一曲线, 又因为其伴随曲线分别为2222(,)0y x f x y x y -=++与2222(,)0y xf x y x y --=++的图象关于y 轴对称,所以正确; ③令单位圆上点的坐标为(cos ,sin )P x x 其伴随点为(sin ,cos )P x x '-仍在单位圆上, 故正确;对于④,直线y kx b =+上取点后得其伴随点2222(,)y xx y x y -++消参后轨迹是圆, 故错误.故答案为:②③.15.01x << 设花卉带宽度为x 米()03x <<, 则中间草坪的长为82x -米,宽为62x -米,根据题意可得()()18262862x x -⋅->⨯⨯, 整理得:2760x x -+>, 即()()610x x -->, 解得01x <<或6x >,6x >不合题意,舍去,故所求花卉带宽度的范围为01x <<, 故答案为:01x <<.16.34:如图,2cos cos cos 212sin APB APM APM θ∠∠∠===-,要使cos θ最小,则1sin AM APM PM PM∠==最大,即需PM 最小.设2,4a P a ⎛⎫ ⎪⎝⎭,则PM ==℃当24a =,即2a =±时,min ||PM =1sin APM PM ∠==,此时(1,2)P 或(1,2)-,22min3(cos )12sin 124APM θ∠=-=-⨯=. 故答案为:34.17(1)因为//,m n →→所以(sin )sin si s ()n in A B C b c a c A ++-=⋅⋅-,由正弦定理可得()()a b c b c a ac -+-⋅+=,即2222221cos 22a cb ac a c b B ac +-=+-⇒==,又()0,πB ∈,所以π3B =. (2)若选①,由基本不等式可知:22a c+≤⎝⎭,所以=2a c b +≤,当且仅当a =c 时取“=” .又222,b a c ac =+-所以22222a c b a c ac +=+-≤⎛⎫ ⎪⎝⎭,即223360,a c ac +-≤则2()0,a c -≤所以a c =.又π,23B b ==,所以ABC是正三角形,所以11sin 422S ac B ==⨯= 若选②,由条件可知,2222,b a c b a c ac =+=+-,所以2222a c a c ac +⎛⎫=+- ⎪⎝⎭,所以223360a c ac +-=,所以2()0a c -=,所以a c =. 又π,23B b ==,所以ABC是正三角形,所以11sin 422S ac B ==⨯= 若选③,由题意可知,2222b a c =+,所以2222)2(a c ac a c +-=+,所以2()0a c -=,所以,a c = 又π,23B b ==,所以ABC是正三角形,所以11sin 422S ac B ==⨯= 18.解:(1)()1cos 22sin cos 2x f x x x π⎛⎫++ ⎪⎝⎭=-1sin 22x =-, 令ππ2π22π22k x k -+≤≤+,k Z ∈,解得ππππ44k x k -+≤≤+,k Z ∈,[]0,πx ∈,所以()f x 的单调递增区间为π0,4⎡⎤⎢⎥⎣⎦,3π,π4⎡⎤⎢⎥⎣⎦.(2)因为πππ,,242424A B C x ⎧⎫∈+++⎨⎬⎩⎭,所以π3π2,22x ⎛⎫∈ ⎪⎝⎭,由()102f x +>得sin 20x >,所以02πx <<,所以π0π2A <+<,所以π02A <<,同理π02B <<,π02C <<,即ABC 为锐角三角形.②中圆心到直线的距离d =故2a =.③cos A A +=πsin 6A ⎛⎫+ ⎪⎝⎭A 为锐角,所以π6A =.选择①②,24R =,2a =,2sin R A a =,得4sin 2A =,1sin 2A =; 选择①③,24R =,π6A =,得2sin 2a R A ==; 选择②③,即2a =,π6A =.由余弦定理得2222cos46b c bc a π+-==,所以(2242b c bc +=≥,所以bc(42=,当且仅当b c =时取等号, 所以ABC 的面积为11sin 24S bc A bc ==,最大值为219.(1)因为圆222:O x y b +=经过椭圆C 的右焦点2F ,所以b c =,a , 因为经过点2F 作圆O 的切线被椭圆C所以点b ⎛ ⎝⎭在椭圆上,即()222112b b +=,解得1b =,故a = 所以椭圆C 的方程为2212x y +=.(2)直线OA ,OB 斜率之积是定值,证明如下: 设()11,A x y ,()22,B x y ,由OM OA OB =+,得()1212,M x x y y ++.故()()()()()222222222212121212112226OM AB x x y y x x y y x y x y +=++++-+-=+++=.又点A ,B 在椭圆上,所以221122x y +=,222222x y +=, 联立解得22122x x +=,22121y y +=.由221122x y =-,222222x y =-,得()()()2222222222121212121222224444x x y y y y y y y y ⋅=--=-++=,从而121212OA OB y y k k x x ⋅==±,即直线OA ,OB 斜率之积是定值12±. 20.(1)()22x e x f x x a =--',若函数()f x 为R 上的凸函数,则()220xe x x af =--'>',即22x a e x <-,令2x y e x =-,2x y e '=-,则当ln 2x =时,0y '=,∴当(),ln 2x ∈-∞时,0y '<;当()ln 2,x ∈+∞时,0y '>;∴当(),ln 2x ∈-∞时,2x y e x =-单调递减;当()ln 2,x ∈+∞时,2x y e x =-单调递增,ln 2min 2ln 222ln 2y e ∴=-=-,222ln 2a ∴<-,解得:1ln 2a <-,a ∴的取值范围为(),1ln 2-∞-.(2)()32113x x e x ax y f x x -=---=-,221x e x y ax ∴=---',()y f x x =-在()1,+∞上有极值,()221x e x g x ax =---∴在()1,+∞有变号零点,()22x g x e x a '=--,令()22x m x e x a =--,则()2x m x e '=-,1x >,()0m x '∴>,()m x ∴在()1,+∞上单调递增,()()()122g x m x m e a '∴=>=--;①当220e a --≥,即22e a ->时,()0g x '≥,()g x ∴在()1,+∞上单调递增, ()()1220e x a g g =-->≥∴.即()0g x >,()221x e x g x ax =---∴在()1,+∞无零点,不合题意; ②当220e a --<,即22e a ->时,则()01,x ∃∈+∞,使得()00m x =, 当()01,x x ∈时,,()()00m x m x <=,()g x ∴单调递减,又()2201e a g =--<,当()01,x x ∈时,()0g x <,()g x ∴在()01,x x ∈上无零点; 当()0,x x ∈+∞时,()()00m x m x >=,()g x ∴单调递增, 又x →+∞时,()g x →+∞,()g x ∴在()1,x ∈+∞上有零点,且在零点左右两侧()g x 符号相反,即该零点为()g x 的变号零点, ()y f x x ∴=-在()1,+∞上有极值; 综上所述:a 的取值范围为2,2e -⎛⎫+∞ ⎪⎝⎭. 21.(1)设直线l 方程为()()11224,,,,x my A x y B x y =+,联立直线l 与抛物线C 的方程,24,4,x my y x =+⎧⎨=⎩ 消去x ,得24160y my --=,所以1216y y =.所以()()22121122121212,,44y y x y x y x x O y A y y B y O →→⋅=⋅=+=⋅+ ()212121616016y y y y =+=-=即OA OB ⊥.(2)设直线l 方程为()()1122,,,,x my t A x y B x y =+,联立直线l 与抛物线C 的方程,2,4,x my t y x =+⎧⎨=⎩ 消去x ,得2440y my t --=, 故124y y t .设()()1331441,,,,A x y B x y A A 的方程为1x ny =+,联立直线1A A 与拋物线C 的方程214x ny y x =+⎧⎨=⎩,消去x 得2440y ny --=,从而13134,4y y n y y +==-,则314y y =-, 同理可得424y y =-, 1212113411111||||sin ||||21sin 2AF BF AFB y y S AF BF S A F B F y y A F B F A FB ∠∠∴=== 2221216y y t ==, 即12S S 为定值. 22.℃1BB ⊥面ABC ,,AB BC ⊂面ABC , ℃1BB AB ⊥,1BB BC ⊥,由侧面11AA B B 为菱形知:11//AB A B ,又111A B BC ⊥,则1AB BC ⊥,又11BB BC B =,℃AB ⊥平面11BB C C ,BC ⊂面11BB C C ℃AB BC ⊥,则AB ,BC ,1BB 两两垂直.以B 为坐标原点,分别以射线BA ,BC ,1BB 为x 轴、y 轴、z 轴正方向建立如图所示的空间直角坐标系.则(2,0,0)A ,(0,0,0)B ,1(0,0,2)B ,(0,2,0)C ,(1,1,0)N ,1(0,2,1)C , (1)证明:由上,1(0,2,1)BC =,1(1,1,2)B N =-,则110220BC B N ⋅=+-=, ℃11BC B N ⊥,又111BC A B ⊥,1111A B B N B ⋂=,℃1BC ⊥平面11A B N ,而1BC ⊂平面1BC N , ℃平面1BC N ⊥平面11A B N(2)设1(02)B M k k =≤≤,则(,0,2)M k , ℃(1,1,2)MN k =--,1(1,1,1)NC =-, 设平面1MNC 的一个法向量为(,,)m x y z =,则10m MN m NC ⎧⋅=⎪⎨⋅=⎪⎩,有(1)200k x y z x y z -+-=⎧⎨-++=⎩,令3x =,则1y k =+,2z k =-,℃(3,1,2)m k k =+-.又AB ⊥平面11BB C C ,则平面11BB C C 的一个法向量为(1,0,0)n =,℃|||cos ,|||||1m n m n m n ⋅〈〉==⨯== 当12k =,即点M 为棱11A B 靠近点1B 的四等分点时,面11BB C C 与面1MNC 所成的二面角余弦值的绝对值最大,此时正弦值最小.。
创新开放性问题(PPT)5-1
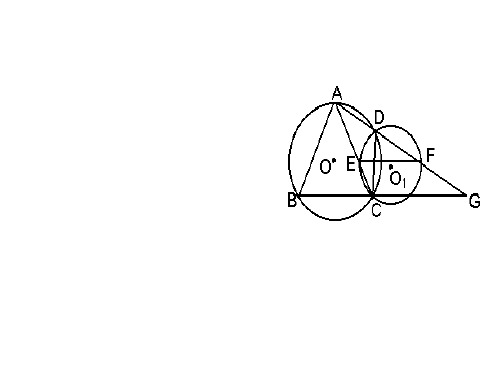
例1.如图:已知△ABC为 ⊙O的内接三角形, ⊙O1 过C点与AC交点E,与 ⊙O交于点D,连结AD并 延长与⊙O1交于点F与BC 的延长线交于点G,连结 EF,要使EF∥CG,△ABC 应满足什么条件?请补充
上你认为缺少的条件后, 证明EF∥GC(要求补充的 条件要明确,但不能 多余)
称打破旧诗格律用白话写成的诗。 【白话文】名用白话写成的文章。也叫语体文。 【白桦】名落叶乔木,树皮白色,剥离呈纸状,叶子近卵形,耐寒性强。 木材致密,可用来制胶合板、造纸等。 【白晃晃】(~的)形状态词。白而亮:~的照明弹。 【白灰】ī名石灰的通称。 【白芨】ī名白及。 【白及】名多 年生草本植物,叶子长,花紫; https://.au 澳洲地产 墨尔本买房 ;红色。地下块茎白色,可入。也叫白芨。 水中,比海里的鲸小,身体呈纺锤形,上部浅蓝灰色,下部白色,有背鳍。是我国特有的珍贵动物。也叫白鳍豚。 【白金】ī名①铂的通称。②古代指银子。 【白金汉宫】īG名英国王宫,在伦敦。从年起,英国历代君主都住在这里。常用作英国王室的代称。[白金汉,英ga] 【白净】?形白而洁净:皮肤~。 【白酒】名用高粱、玉米、甘薯等粮食或某些果品发酵、蒸馏制成的酒,没有颜色,含酒精量较高。也叫烧酒、白干儿。 【白驹过隙】形容时间过得飞快, 像小白马在细小的缝隙前一闪而过(语本《庄子?知北游》)。 【白剧】名白族的主要戏曲剧种,历史悠久,流行于云南西部白族聚居区。 【白卷】(~儿) 名没有写出文章或答案的考卷:交~儿。 【白开水】名不加茶叶或其他东西的开水。 【白口】名线装书书口的一种格式,版口中心上下都是空白的,叫做白 口(区别于“黑口”)。 【白口】(~儿)名戏曲中的说白。 【白蜡】名①白蜡虫分泌的蜡质,熔点较高,颜色洁白,是我国特产之一。可制蜡烛或丸外壳, 又可用来涂蜡纸,密封容器。②精制的蜂蜡,颜色洁白,可以制蜡烛。 【白蜡虫】名昆虫,成群栖息在白蜡树或女贞树上,雄虫能分泌白蜡。 【白蜡树】名 梣的通称。 【白兰地】名用葡萄、苹果等发酵蒸馏制成的酒。含酒精量较高。[英a] 【白兰瓜】名甜瓜的一种,果实球形,果皮光滑,没有网纹,成熟时 乳白色,果肉浅绿色,味甜。耐干旱,主要产于甘肃兰州一带。 【白莲教】名一种民间宗教,因依托佛教的一个宗派白莲宗而得名。元、明、清三代在民间 流行,农民军往往借白莲教的名义起事。 【白鲢】名鲢。 【白蔹】名多年生蔓生藤本植物,掌状复叶,花黄绿色,浆果球形。块根入。 【白磷】名磷的同 素异形体,无色或淡黄色蜡状晶体,有大蒜的气味,度性强,在空气中能自燃,在暗处发出磷光。用来制造高纯度的磷酸,也用来制造焰火等。也叫黄磷。 【白蛉】名昆虫,身体小,黄白色或浅灰色,表面有很多细长的毛。雄的吸食植物的汁。雌的吸人畜的血液,能传播黑热病和白蛉热等。 【白领】
2021年陕西中考道德与法治开放性试题突破集训之我与他人和集体 (1)
2021陕西中考道德与法治开放性试题突破集训之我与他人和集体一、材料分析题1.2020年1月15日,陕北民歌歌手杜桂平推出新歌《感恩父母》,优秀的词曲和正能量的主题大获听众好评。
这首歌唱出了子女对父母养育之恩的深深感恩和爱,让人听了深受感动。
感恩父母,不忘父母养育之恩。
天地重孝,为人子当以孝为先。
没有父母,也就没有我们。
常言道:谁言寸草心,报得三春晖。
父母养育之恩大,难以回报,反哺乃天经地义,人之首德。
杜桂平这首歌,字字珠玑,句句深情。
“天地重孝孝当先,一个孝字全家安,丝丝白发儿女债,历历深纹岁月痕”,可谓掷地有声。
感恩是一种做人的基本道德准则,是一种为人处世的哲学,也是一种生活中的大智慧。
鲜花感恩雨露的滋润,苍鹰感恩蓝天的壮阔,大地感思春光的芬芳,而我们应该感恩父母,是父母给予了我们生命,哺育我们成长。
(1)感恩父母可以用语言来表达,请写出一段话感恩你的父母。
(不少于200字)(2)感恩父母需要用行动来表达,你准备用哪些行动来感恩父母?2.情境探究题小亮是某校七年级的新生。
开学三四个星期了,他对班集体中的一些现象感受颇深。
以下是他和同班同学小光的对话。
小亮:“我的新集体真是没劲,存在着对人不礼貌、不与人合作、竞争中不尊重对手的现象,不如我们原来的集体温馨。
”小光:“我也觉得现在的新集体没有以前小学的集体美好,原先我们的班集体成员之间互相关怀,充满友爱,可是现在个别同学欺侮我们农村来的孩子,太让人寒心了。
”小亮:“就是!”小光:“我对美好的班集体充满了憧憬。
”小亮:“……”针对以上两个同学的对话,班主任决定组织开展一次“美好愿景我憧憬”的主题班会活动。
请你参与进来,完成如下任务:(1)【班会设计】请你为本次班会设计一句宣传标语。
(2)【请你列举】你憧憬的美好班集体具有哪些显著特征?(3)【请你发言】班会的总结发言起着引领、升华、教育作用,有画龙点睛之效,请你为本次班会写一段30字左右的总结发言词。
