数学物理方程试题
研究生数理方程期末试题-10-11-1-A-答案
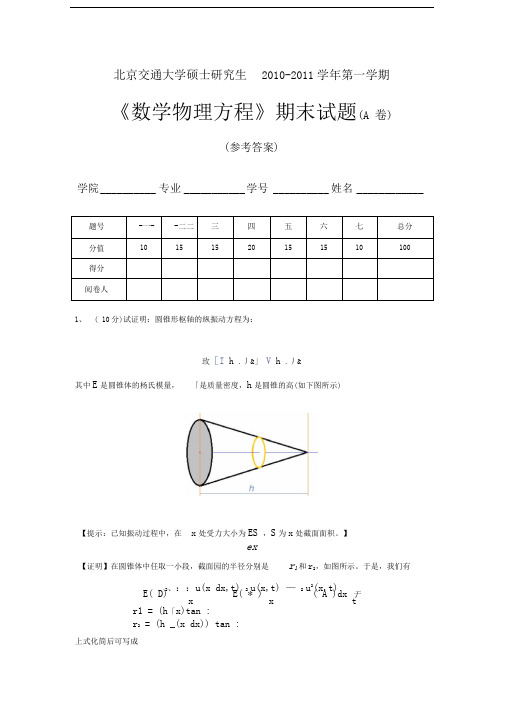
北京交通大学硕士研究生2010-2011学年第一学期《数学物理方程》期末试题(A 卷)(参考答案)学院__________ 专业___________ 学号 __________ 姓名____________1、( 10分)试证明:圆锥形枢轴的纵振动方程为:玫[I h .丿&」V h .丿&其中E是圆锥体的杨氏模量,「是质量密度,h是圆锥的高(如下图所示)【提示:已知振动过程中,在x处受力大小为ES ,S为x处截面面积。
】ex【证明】在圆锥体中任取一小段,截面园的半径分别是r1和r2,如图所示。
于是,我们有2、::u(x dx,t) 2 u(x,t) — 2 u2(x,t)E( D) E( * ) ( A )dx 于x x t r1 = (h「x)tan :r2= (h _(x dx)) tan :上式化简后可写成22::U(X,t)2::u(x,t) 2, ;u (x,t)E[(h -x)卜亠 & -(h -'X) 〔x J - - (h -'X)dx 2从而有E ::[(^x)2;:U(x ,t)H-(^x)2::u2(x,t) .x :X:t 或成2::[(1「)2汽("]“2(1「)小叩).xh ::x h ;:t其中a^E,证明完毕。
2、 (20分)考虑横截面为矩形的散热片, 它的一边y=b 处于较高温度U ,其它三边y=0.x = 0和x = a 则处于冷却介质中,因而保持较低的温度 u o 。
试求该截面上的稳定温度分布u(x,y),即求解以下定解问题:u|y 卫二 %, u|y 生二 U, 0 x a. 【提示:可以令u(x, y)二u 0 v(x, y),然后再用分离变量方法求解。
】【解】令u(x, y) v(x, y),则原定解问题变为Wl x£=0, V=0, 0cy <b;v|y/0, v|y 子U _u °,0 x a.分离变量:f 2\dU;:2U=0, 0 : x : a, 0 : y : b;y=0, 0 : x :: a, 0 : y : b;■ 2y »2 -2v(x,y) =X(x)Y(y)代入方程得到关于X和Y的常微分方程以及关于X的定解条件:X X = 0,X(0) =0,X(a) =0;Y - Y =0可以判定,特征值(n =1,,2,3J||)特征函数n 二X(x) = X n(x) =C n S in—x (n=1,,2,3JI|)利用特征值、可以求得丫(y) =Y n(y) =A n e叨B n^;y(n = 1,,2,3,l|l) 于是求得特征解n r n iy n,1V n(x,y)=(代e= B n e^ )sin x (n =1,,2,3JI|)a形式解为n -y _j-y门二v(x, y)二為V n(x, y)二為(A n e~ B n e^ )sin x吕 3r Q Qv(x,0)=迟(An+B n)sinO0 bv(x,b)八(A n e吗B n en =1pg na )sin——x 二U -u0得到A nB n =0八也如二 4 “,、A e aB e a(U - u。
数学物理方程与特殊函数试题及答案

数学物理方程与特殊函数试题及答案猜你喜欢: 1. 2. 3. 4. 5.数学物理方程与特殊函数是一门专业性比拟强的课程,要学好这门课程,同学们还是要用心去学才能学好数学物理方程与特殊函数。
下面是给大家的数学物理方程与特殊函数试题及答案,欢送大家学习参考。
1.对于一般的二阶线性偏微分方程0(1) 它的特征方程为,假设在域内ACB那么此域内称(1) 椭圆型假设在域内B那么此域内称(1)为抛物型假设在域内 B 那么此域内称(1)为双曲型。
2. 第一类格林公式第二类格林公式 . 已那么 ;而函数按1xP的展开式4.一维热传导方程可用差分方程似代替。
二维拉普拉斯方程可用差分方0 近似代替。
5. 勒让德多项式的正交性???。
二.用别离变量法求?的解。
(15分) 解:用别离变量法求解,先设满足边界条件且是变量被别离形式的特解为tTxXtxu?代入方程(1)上式左端不含有x,右端不含有t,从而得到两个线性常微分方程解(6)得 x由(2)得,及相应的固有函数为xlnBxXnn?sin? 7?? ,再由(5)得,? 由(7),(8)得由(1),(3)得又由(3) 得所以,原定解问题的解为?三.求方程? 的解。
(15分) 解:对(1)两端积分的通解为任意二阶可导函数,令(4)满足(2),(3)得解之得6(5),(6)代入(4)得u 四.求柯西问题的解。
(12分) 解;先确定所给方程的特征线。
为此,写出它的特征方程 dy2-2dxdy-3dx20 它的两族积分曲线为作特征变换4?经过变换原方程化它的通解为中21ff 是两个任意二次连续可微的函数。
方程(1)的通解为由(2。
数学物理方程习题

值使得u(Q)在A点得邻域中调和. 16.设P 为常系数线性偏微分算子,且有基本解E (x), 满足singsuppE = {0}则P 为亚椭圆的。 (Thm6.3.2) 第七章热传导方程 1.求解热传导算子的基本解 2.求解热传导方程的Cauchy问题 { ∂u − a2 ∆u = f (x, t) t > 0 ∂t u(x, t)|t=0 = φ(x) 3.求解热传导方程的初边值问题. {
∑ 1 ξ α ∂ α uP α (x, η ) α ! α
是一个重要的公式,称为推广的莱布尼茨公式.又以后对任一函数F (x, ξ )恒
β α 记F(β ) (x, ξ ) = ∂x ∂ξ F (x, ξ ),即下标表示对x求导,上标表示对ξ 求导. (α)
8.设有C ∞ (R)函数列{fn (x)}满足 1
d2 dx2 d + dx
α, α ∈ R .
2 + ∂r , 其中r =
第六章Laplace方程
n −1 ∂r r 3
√ 2 x2 1 + ... + xn
2.设开集Ω ⊂ R 有界,边界∂ Ω光滑,u(x) ∈ C 2 (Ω) ∩ C 1 (Ω), Q ∈ Ω 证明 ∫ 1 ∂u ∫ ∫ ∆u u ∂ ( 1 )ds − 41 u(Q) = 41 ds − 41 dx π ∂ Ω r ∂n π ∂ Ω ∂n r π Ω r 3.证明球面平均值公式,球体平均值公式 4.证明调和函数的极值原理 5.利用极值原理证明以下Dirichlet问题的唯一性和稳定性 ∆u = 0 u|∂ Ω = f 6.利用Green函数求解上半平面的Dirichlet问题 ∆u(x, y ) = 0 y > 0 u|y=0 = f (x) 7.利用Green函数求解圆Ω上的Dirichlet问题 ∆u = 0 u|∂ Ω = f (x) ¯ ∩ C 2 (Ω), 证明: 8.设Ω = BR (Q)(以Q为心、 R为半径的开圆域), u ∈ C (Ω) ∫∫ ∫∫∫ 1 (1).u(Q) = 4πR )∆udx. u(P )dSp + 41 (1 − 1 2 π r ∂BR (Q) BR (Q) R ∫ ∫ 1 (2).若∆u ≥ 0, 则u(Ω) ≤ 4πR2 u(P )dSp . ∂BR (Q) 9.证明第一格林公式 ∫ ∫ u
数学物理方程复习

一、填空题1、物理规律反映同一类物理现象的共同规律,称为___________。
2、在给定条件下求解数学物理方程,叫作____________________。
3、方程20tt xx u a u -=称为_________方程4、方程20t xx u a u -=称为_________方程5、静电场的电场强度E是无旋的,可用数学表示为_____________。
6、方程0j Ñ×=称为_____________的连续性方程。
7、第二类边界条件,就是______________________________________。
8、第一类边界条件,就是______________________________________。
9、00(0,)(0,)x x u x t u x t -=+称为所研究物理量u 的_____________。
10、00(0,)(0,)u x t u x t -=+称为所研究物理量u 的_____________。
11、对于两个自变量的偏微分方程,可分为双曲型、________和椭圆型。
12、对于两个自变量的偏微分方程,可分为双曲型、抛物线型和________。
13、分离变数过程中所引入的常数l 不能为_____________。
14、方程中,特定的数值l 叫作本征值,相应的解叫作_____________。
15、分离变数法的关键是________________________代入微分方程。
16、非齐次振动方程可采用______________和冲量定理法求解。
17、处理非齐次边界条件时,处理非齐次边界条件时,可利用叠加原理,可利用叠加原理,可利用叠加原理,把非齐次边界条件问题转化另一把非齐次边界条件问题转化另一_________的齐次边界条件问题。
18、处理非齐次边界条件时,处理非齐次边界条件时,可利用叠加原理,可利用叠加原理,可利用叠加原理,把非齐次边界条件问题转化另一把非齐次边界条件问题转化另一_________的齐次边界条件问题。
中国海洋大学 数学物理方程答案{其中一套试题}

本人能力有限,仅供参考,不保证全对一、1、线性偏微分方程2、线性偏微分方程3、非线性偏微分方程4、非线性偏微分方程二、1、201∆=-⨯=-0y yy<双曲型0y=抛物型y>椭圆型02、222∆=-=抛物型()0xy x y3、22∆=-++⨯=>双曲型(cos)(3sin)140x x4、2222200∆=-=-<椭圆型x y x y三、见第二章第二节“三、相关概念”四、五、定解问题222,0,0(,0)(),0(,)(0,)0,0,0u ua x l t t x u x x x l u l t u t t x ϕ⎧∂∂=<<>⎪∂∂⎪⎪=≤≤⎨⎪∂⎪==>∂⎪⎩下面用分离变量法求解 令(,)()()u x t X x T t =,则`2``XT a X T = (1)(0,)(0)()0u t X T t == (2)`(,)()()0u l t X l T t x∂==∂ (3) ```2T X a T Xλ==- (4) ``0X X λ+= (5)当20λβ=-<时 x x X Ae Be ββ-=+ 代入(2)(3)得0A B ==无意义 当0λ=时 X A x B =+代入(2)(3)得0A B ==无意义 当20λβ=> sin cos X A x B x ββ=+代入(2)(3)得0B = cos 0A x β= (6)0A ≠则cos 0l β=得21,0,1,2,2n n n lβπ+== (7) 221,0,1,2,2n n n l λπ+⎛⎫== ⎪⎝⎭(8)21sin,0,1,2,2n n n X A x n lπ+== (9) `20T a T λ+= (10)将(8)代入(10)得2`22102nn n T a T l π+⎛⎫+= ⎪⎝⎭(11)22212n a t l n n T B eπ+⎛⎫- ⎪⎝⎭= (12)故22222121222121sinsin22n n a t a t l l n n n n n n n n u X T A B ex C e x llππππ++⎛⎫⎛⎫-- ⎪ ⎪⎝⎭⎝⎭++=== (13) 222120021sin2n a t l n n n n n u u C ex lππ+⎛⎫∞∞- ⎪⎝⎭==+==∑∑ (14) 021(,0)sin()2n n n u x C x x lπϕ∞=+==∑ (15) 故方程的解为22212021sin2n a t l n n n n n u u C ex lππ+⎛⎫∞∞- ⎪⎝⎭==+==∑∑,其中nC 满足方程21sin()2n n n C x x lπϕ∞=+=∑。
数学物理方程题库

()()22221211*********cos 3sin 0cos 3sin 40.2cos 2cos 2sin x x y a a a x x xx y x −−+−=∆=−=−++=>⎧⎪==−⎪⎨⎪==−−⎪⎩=−xx xy yy y ,指出下列方程的类型并化为标准形式。
1) u u u u 解:方程的判别式所以方程为双曲型。
dy dx该方程的一组特征微分方程为dy dx 积分得到特征曲线为1112222211122222111222sin 2sin 2sin 2sin 2sin 082x c c y x xy x x c c y x xy x xy x x U U UB a a a x x x y y x y y a a x x y ξηξηξηξηξηξηξηξξ+=−+⎧⎧⇒⎨⎨=−−+=++⎩⎩−+⎧⎨=++⎩∂∂∂++=∂∂∂∂⎛⎞∂∂∂∂∂∂∂∂=+++=−⎜⎟∂∂∂∂∂∂∂∂⎝⎠∂∂=+∂∂∂1211121=于是令此时原方程可以转化为2A A 其中,A A ()()2221222211122212222sin 2sin 00a b y xy y B a a a b y xx x y y yU U Uu u u ξξηηηηξηξηξηξηξηξηξη∂∂++=−−∂∂∂∂∂∂=+++=−−∂∂∂∂∂∂∂∂++=∂∂∂∂⎛⎞∂∂∂++=⎜⎟∂∂∂∂⎝⎠1所以16y+sinx y+sinx +由于y+sinx=,所以上式可以变为关于,得标准方程2+32()22222121122121122211122200.,().02xy y a a a xy x y a y a xyy cx c x x u u uB a a x x y ξηηξηηηη++=∆=−=−=====∂∂∂++=∂∂∂∂∂∂⎛⎞=++⎜⎟∂∂∂⎝⎠2xx xy yy 221122) x u u u 解:方程的判别式所以方程为抛物型。
数学物理方程模拟题(考前打印)
数学与统计学院2007年12月一. (20分) 判断下面方程的类型并通过自变量的变换将其化为标准型二. (15) 利用叠加原理, 齐次化原理(Duhamel 原理) 叙述如下弦振动方程Cauchy 问题的求解过程, 并写出解的表达式.三. (20分) 用傅里叶(Fourier) 变换法求解如下一维热传导方程四. (20分) 用分离变量法求解弦振动方程的初边值问题五. (15分) 对受摩擦力作用且具有固定端点的有界弦振动,满足方程其中常数, 证明其能量是减少的,并由此证明方程的初边值问题解的唯一性.六. (10分) 设为平面上的有界区域, 其边界充分光滑, 考虑方程其中, 为Laplace算子. (1) 证明: 如果是方程的解, 那么, 不能在内部取正的最大值, 也不能在内部取负的最小值; (2) 证明: 上述方程的第一边值问题最多只有一个解.数学与统计学院2007年12月一. 1. (7分) 将方程化成标准型.2. (8分) 求解定解问题二. (15分) 求下述问题的形式解三. (20分) 设是定解问题的古典解, 其中为有界区域, 为其边界, 为外法线方向, , 为已知函数, 且, , 为正常数. 求证在上必有.四. 1. (5分) 写出下述热传导方程初边值问题的解的表达式, 其中为光滑函数, .2. (10分) 证明当时, 上述问题的解关于一致地收敛于零.五. (20分) 证明双曲型方程混合问题解的唯一性, 其中, , 为上的连续函数.六. (15分) 设是以原点为中心, 以为半径的圆域, 在中调和, 且在中一阶连续可微. 试证:数学与统计学院2007年12月一. (18分) (1) 判断下述方程的类型并将其化为标准型:;(2) 判断下述方程类型并求其通解, 其中为常数, 且.二. (18分) 求解下述定解问题三. (18分) 求下述Cauchy 问题的解四. (16分) 设为下述定解问题之解试证明: (1) 当适当大时, ”能量”积分为的单调不增函数; (2) 当时, 能量积分.五. (12分) 求解其中, , 表示单位球边界上的外法向导数.六. (16分) (1) 记为中以原点为中心、以为半径的球, 表示的闭包, 设, 且在中调和, 试证明:, .(2) 利用(1) 证明在全空间中有界的调和函数一定是常数.数学与统计学院2007年12月注意: 以下各题中的小题是分别计分的, 如不能完成上面的小题, 也可以直接完成下面小题.一. (20%) 给出定解问题(P)(i) 作未知函数代换, 其中是新的未知函数, 是待定函数, 使得定解问题(P) 化为关于的定解问题(Q), 而且边界条件是齐次的.(ii) 设(P) 的边界条件是齐次的(即), 求(P) 的解.二. (30%) 给出定解问题(P)(1)(2)(i) 判断方程(1) 的类型;(ii) 通过自变量的变换, 化(1) 为标准型;(iii) 求方程(1) 的通解;(iv) 求(P) 的解.三. (20%) 设区域(i) 求的Laplace 方程第一边值问题的Green 函数;(ii) 求解边值问题其中函数连续, 且有界.四. (30%) 考虑初边值问题(P)其中常数, .(i) 证明: 如果, 则, 其中, , ().(ii) 用上述极值原理证明: (P) 最多只有一个解.(iii) 用能量方法证明: (P) 最多只有一个解.数学与统计学院2007年12月注意: 以下各大题中每小题是独立的, 不回答前面的小题也可以回答后面的小题, 每题都占总分的20%.一. 1. 推导弦振动方程的通解.2. 证明方程(, 为常数) 的通解可以表示为其中, 为任意的二次连续可微函数二. 考虑以下初边值问题1. 引入新的未知函数, 将(P) 化为边界条件是齐次的初边值问题.2. 如果, , 求解问题(P). (问题(P) 中,是常数).三. 用能量方法证明以下初边值问题最多只有一个解其中, , , 是区域的边界, 且充分光滑.四. 设是平面上的有界区域, 其边界充分光滑. 考虑方程其中常数, 是Laplace 算子.1. 证明: 如果是方程的解, 那么, 不能在内部取正的最大值, 也不能在内部取负的最小值.2. 证明: 上述方程的第一边值问题最多只有一个解.3. 如果, 上述两个命题是否成立? 为什么?五. 考虑以下初边值问题:且.1. 写出区域求解Laplace 方程第一边值问题的Green 函数.2. 推导(P) 的解(不必证明).数学与统计学院2008年12月一. (9分) 试写出数学物理方程中常遇到的三类方程.二. (20分) 用分离变量法求解如下弦振动方程初边值问题的解三. (20分) 设, 分别是下述两个定解问题的解那么是定解问题的解.四. (15分) 导出(写出过程)如下热传导方程柯西问题解的表达式:五. (16分) 验证函数满足二维Poisson 方程.六. (20分) 非线性因子与耗散因子相互作用的基本数学物理模型可用如下方程表达这里为粘性系数. 设方程有型如, 的行波解(为波速), 并且满足, , . 请给出解的解析表达式. (注: , .)数学与统计学院2008年12月一. 设为分片光滑的有界区域, 是其边界. , 为上的二次可微的光滑函数. 则有如下格林公式成立其中为体积元素, 是的外法线方向, 是上的面积元素. 利用上述格林式说明1) (20分) 设函数为以曲面为边界的区域内是调和的, 在上有连续的一阶偏导数, 则2) (10分) Laplace 方程的第二边值问题即Neumann 内问题有解的必要条件为.二. (20分) 今有一弦, 其两端固定在坐标轴上和处, 在开始的一瞬间, 它的形状是一条以过点的铅垂线为对称轴的抛物线,其顶点的纵坐标为. 假定没有初速度. 试用付氏法求解弦振动方程. 提示: 先求抛物线的表达式.三. (20分) 用分离变量法求解狄利克雷(Dirichlet) 问题其中, 为已知正常数, 且.四. (20分) 有一两端无界的轴, 其初始温度为试说明轴上温度分布为这里为扩散系数.五. (10分) 说明拉普拉斯算子在球坐标下, 可以写成数学与统计学院2008年12月一. 设为分片光滑的有界区域, 是其边界. , 为上的二次可微的光滑函数. 则有如下格林公式成立其中为体积元素, 是的外法线方向, 是上的面积元素. 利用上述格林式说明1) (20分) 设函数为以曲面为边界的区域内是调和的, 在上有连续的一阶偏导数, 则2) (20分) Laplace 方程的第二边值问题即Neumann 内问题有解的必要条件为.二. (15分) 求下述问题的形式解二. (20分) 用分离变量法求解如下弦振动方程初边值问题的解三. (20分) 非线性与色散相互作用的基本数学物理模型可用如下方程表达这里为色散系数. 设方程有型如, 的行波解(为波速), 并且满足, . 请给出解的解析表达式. (注: , .)四. (20分) 验证函数满足二维Poisson 方程.数学与统计学院2008年12月一. (20分) 说明拉普拉斯算子在球坐标下, 可以写成二. (20分) 用分离变量法求解狄利克雷(Dirichlet) 问题其中, 为已知正常数, 且.三. (20分) 用分离变量法求解如下弦振动方程初边值问题的解四. (20分) 设, 分别是下述两个定解问题的解那么是定解问题的解.五. (20分) 非线性与色散相互作用的基本数学物理模型可用如下方程表达这里为色散系数. 设方程有型如, 的行波解(为波速), 并且满足, . 请给出解的解析表达式. (注: , .)数学与统计学院2008年12月总分100 分, 每题20 分, 共五题. 考试时间180 分钟.一. 用分离变量法求下列定解问题的解:二. 用分离变量法求解由下述调和方程的第一边界问题所描述的矩形平板上的稳定温度分布三. 如果有一长度为的均匀细棒, 其周围以及两端, 处均为绝热, 初始温度分布为, 问以后时刻的温度分布如何? 且证明当等于常数时, 恒有.提示: 考虑如下初边值问题四. 举例说明在二维调和方程的狄利克莱问题中, 如对解不加在无穷远处为有界的限制, 那么定解问题的解就不是唯一的.提示: 设为单位圆外 (其中) 区域, 此问题对应狄利克莱外问题的定解问题五. 对齐次方程的初值问题的解可表达为证明:a) 如果初始条件在轴的区间上发生变化, 那么对应的解在区间的影响区域以外不发生变化;b) 在轴区间上所给的初始条件唯一地确定区间的决定区域中解的数值.数学与统计学院2008年12月一. (20分) 用分离变量法求下列定解问题的解:二. 设为分片光滑的有界区域, 是其边界. , 为上的二次可微的光滑函数. 则有如下格林公式成立其中为体积元素, 是的外法线方向, 是上的面积元素. 利用上述格林式说明1) (20分) 设函数为以曲面为边界的区域内是调和的, 在上有连续的一阶偏导数, 则2) (20分) Laplace 方程的第二边值问题即Neumann 内问题有解的必要条件为.三. (20分) 用分离变量法求解如下弦振动方程初边值问题的解四. (20分) 描述耗散的基本数学物理模型可用如下方程表达这里为耗散系数. 设方程有型如, 的行波解(为波速), 并且满足, . 请给出解的解析表达式. (注: , .)。
数学物理方程 练习题
)( )
a12 a22
ξx ξy
,
)( )
a12 a22
ηx ηy
,
)( )
a12 a22
ηx ηy
,
故
(
)(
)
a11 a12
a12 a22
=J
a11 a12
a12 a22
JT,
齐海涛 (SDU)
数学物理方程
2012-10-3 4 / 39
二阶线性方程的分类
而判别式
△=
a11 a12
a12 a22
xy < 0 时, 方程为双曲型. (4) 当 xy > 0 时, 方程为抛物型; 当 xy ≤ 0 时, 方程为双曲型. (5) 系数矩阵为不定型, 且非退化, 故方程为双曲型.
齐海涛 (SDU)
数学物理方程
2012-10-3 7 / 39
二阶线性方程的分类
.E.xample 1.3
化下列方程为标准形式: 1. uxx + 4uxy + 5uyy + ux + 2uy = 0; 2. x2uxx + 2xyuxy + y2uyy = 0; 3. uxx + yuyy = 0; 4. uxx − 2 cos xuxy − (3 + sin2 x)uyy − yuy = 0;
1. 二阶线性方程的分类 2. 二阶线性方程的特征理论 3. 三类方程的比较 4. 先验估计
齐海涛 (SDU)
数学物理方程
2012-10-3 3 / 39
二阶线性方程的分类
.E.xample 1.1
证明: 两个自变量的二阶线性方程经过自变量的可逆变换后, 其类型不会改 .变, 即变换后 △ = a212 − a11a12 的符号不变.
数学物理方程_ 复习
复 习题型一、根据物理过程写出相应的定解问题。
习题一、1,2, 例1、长度为 l 的弦左端开始时自由,以后受到强度为sin A t ω的力的作用,右端系在弹性系数为k 的弹性支承上面;初始位移为(),x ϕ初始速度为().x ψ试写出相应的定解问题。
解 这是弦的自由振动,其位移函数(,)u x t 满足2,tt xx u a u = 其中2Ta ρ=.由于左端开始时自由,以后受到强度为sin A t ω的力的作用,所以(0,0)0,(0,)sin 0,0,x x u Tu t A t t ω=+=>因此 sin (0,),0.x A tu t t Tω=-≥ 又右端系在弹性系数为k 的弹性支承上面,所以 (,)(,)0,x Tu l t ku l t --= 即 (,)(,)0.x Tu l t ku l t +=而初始条件为 0(),().t tt ux u x ϕψ====因此,相应的定解问题为200,0,0,sin (0,),(,)(,)0,0.(),().tt xx xx t t t u a u x l t A t u t Tu l t ku l t t T u x u x ωϕψ==⎧=<<>⎪⎪=-+=≥⎨⎪==⎪⎩例2、一长为 l 的均匀细杆,侧面绝热,一端放入0o C 水中,另一端裹以石棉,杆的初始温度为(),x ϕ 试写出杆的温度分布函数所满足的定解问题。
题型二、求特征值问题。
例3、求下列特征值问题的特征值和特征函数.(1)''()()0,(0)()0X x X x X X l λ⎧+=⎨==⎩(2)''()()0,'(0)()0X x X x X X l λ⎧+=⎨==⎩(3)''()()0,(0)'()0X x X x X X l λ⎧+=⎨==⎩(4)''()()0,'(0)'()0X x X x X X l λ⎧+=⎨==⎩(4)''()()0,()(2)θλθθθπΦ+Φ=⎧⎨Φ=Φ+⎩题型三、用分离变量法求齐次方程齐次边界条件的定解问题。
数理方程期末试题14~15A(另一版本)
u x=0 = 0
t =0
=
sin
πx 10
,
0 < x < 10,t > 0
u x=10 = 0 ∂u = 0 ∂t t=0
解 设该定解问题的解为 u( x,t ) = X ( x )T( t )
则 T ′′( t ) = X ''( x ) = −λ T(t ) X( x )
T ′′( t ) + λT ( t ) = 0
cr n + dr−n
∂u
∂t
=
a2
∂2u ∂x2
+
A
7、定解问题
∂u = B ∂x x=0
u t =0
= cos π x l
0 ≤ x ≤ l,t ≥ 0
∂u = C ∂x x=l
,A, B,C 均为常数,
要想选用函数代换 u(x,t) = V (x,t) +W (x) 将方程和边界条件都化
阶贝塞尔函数
Jn (x)
=
∞
( −1)m
m=0
xn+2m 2n+2m m! Γ( n +
m +1)
,
∫R 0
rJ
n
(
µm(n R
)
r
)
J
n
(
µm(n R
)
r)dr
=
R2 2
J
( 2
n−1
µ(mn
)
)=
R2 2
J
( 2
n+1
µ(mn
)
)。
第 3 页 共 10 页
13、勒让德方程可表示为 ( 1 −
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数学物理方程试题(杨春)
一、化方程为标准形(10分)
22
20xxxyyyxyxuxyuyuxuyu
二、分离变量法求定解问题(10分)
2
22
sincos,(0,0)(0,)3,(,)64(,0)31,(,0)sinttxxtuauxxxltllutultxuxuxxll
三、一无限长导体圆柱壳,半径为a,把它充电到电势12,(0),(2)vvv,求
圆柱壳内电场中的电势分布(用分离变量法求解)(15分)
数学物理方程试题答案及评分标准
一、
解:222221211220aaaxyxy,方程属于抛物型………1分
特征方程为:22220dydyxxyydxdx,得dyydxx…..1分
令
y
x
y
…….1分
2
101xyxyyQxx
………..1分
11121112
2
12221222
00
0TaaaaQQaaaay
……….2分
10bLC……. 1分 2
bLCy
……. 1分
0Cf
………1分
1
uu
………1分
二、解:令(,)(,)()uxtVxtWx…….1分
将其代入定解问题可以得到:
2
,(0,0)(0,)0,(,)0.....(1)4(,0)31(),(,0)sinttxxtVaVxltVtVltxVxWxVxxll
1分
2
22
()sincos0(2)(0)3,()6aWxxxllWWl
1分
(2)的解为:2224()sin3132lxWxxall 2分
对于(1),由分离变量法可得一般解为
1(,)cossinsinnnnnatnatnxVxtablll
……………………….2分
由初始条件可求得:
2
22
444(,)cossinsin324lalatx
Vxttalall
2分
所以,原定解问题的解为:
22
2222
4444(,)cossinsinsin3132432lalatxlx
uxttxalallall
1分。
三、解:由于圆柱壳无限长,所以可以作为二维问题处理。在柱内无自由电荷,
所以柱内电势满足拉普拉斯方程。定解问题为:
2
1
2
0,(0,02),(0)(,),(2)(,2)(,),(0,)uavuavuuu
3分
令(,)()()uR得:
0
与20RRR…………………….1分
固有值问题为:
0(2)()
,求得固有值为:2(0,1,2,....)mm
固有函数为:()cossinAmBm
…………………………………2分
22
0RRmR
的解为:
000
()lnRCD
,()(0)mmmmmRCDm……………2分
于是定解问题的一般解为:
001(,)lncossinmmmmmm
muCDAmBmCD
……1分
由有限性条件得:00mDD………………..1分
01(,)cossinmmm
muCAmBm
………………….1分
22
12
012
0
122vvCvdvd
22
1201coscos0m
Avmdvmd
3分
22
12
1201sinsin1(1)mm
vvBvmdvmdm
所以定解问题的解为:
1212
1(,)1(1)sin2mmmvvvvumm
或
21121202sin21(,)221nnvvnvvuna
……………..1分
