高级数理逻辑第四章
交大数理逻辑课件数理逻辑和集合论复习提纲

4.使用推理规则证明: P(QR),S∨P, Q S R
《数理逻辑》样卷
六.应用题(共20分)
1. 甲、乙、丙、丁四人参加考试,有人问他们,谁的成绩最 好,甲说:“不是我”,乙说:“是丁”,丙说:“是乙”, 丁说:“不是我”.四人的回答只有一人符合实际,问是 谁的成绩最好,若只有一人成绩最好,他是谁?
A.A=B
B.BA
C.AB
D.A≠B
8.下列一阶谓词公式中,是逻辑有效 式的是____________。
A. x(F(x) G(x))
B. xF(x) xF(x)
C. Байду номын сангаасF(x,y) R(x,y)) R(x,y)
D. xyF(x,y) xyF(x,y)
9.设 f:B→C, g:A→B. 则下面命 题是错误的是___________。
第11章 函 数
11.1 函数 11.2 函数的合成和函数的逆
第12章 集合的基数
12.2 集合的等势 12.3 有限集合与无限集合 12.4 集合的基数
试题结构
卷面
一. 选择题(10%) 二. 填空题(20%) 三. 判断题(10%) 四. 运算题(20%) 五. 证明题(20%) 六. 应用题(20%)
《数理逻辑》样卷
6.设A、B是集合,右图的文氏图的 阴影部分的区域可用________表 达式表示
A. A∩B B. A∪B
C. A-B D. (A∪B)-(A∩B)
7.集合A和B定义如下,则它们之间 满足_________关系。
《逻辑学》第四章(精简版)

复合判断的负判断及其等值转换
3.不相容选言判断的负判断及其等值式 p∨· q←→( p ∧ q ) ∨ ( p ∧ q )
例如:并非本案的作案人要么是张某,要么是王某, 就等于断定:或者本案的作案人既是张某,又是王某;
或者本案的作案人既不是张某,也不是王某。
复合判断的负判断及其等值转换
4.充分条件假言判断的负判断及其等值式 p→q←→p∧q
假言判断的真值表
pq
++ +- -+ --
pq
+ - + +
pq
+ + - +
pq
+ - - +
假言判断的等值转换
1.如果p是q的充分条件,那么q是p的必要条件 2.如果p是q的必要条件,那么q是p的充分条件 3.如果p是q的充分条件,那么非p是非q的必要条件 4.如果p是q的必要条件,那么非p是非q的充分条件
相容选言判断
断定若干可能的事物情况中至少有一种存在 (也可能同时存在)的复合判断。
联结词常用:“或”、“或者”表示。 逻辑形式为:或者p,或者q 数理逻辑符号表示为:p∨q 其中,“∨”读作“析取”
相容选言判断的逻辑性质
相容选言判断的逻辑性质是由其逻辑联结词的性质决定 的,“或者”是表示几种事物情况至少有一种存在的联结词。
②被告人否认犯罪事实,或是由于态度不老实,或是由于根本不存在这个 犯罪事实。
选言判断由选言肢和选言联结项两部分组成。
选言肢: p、q、r…… 选言联结项:或者 ……或者;要么……要么;
选言判断的种类
在选言判断中,各个肢判断所反映的事物情况有的可以 并存,有的不能并存。
选言判断
肢判断能否并存 相容选言判断 不相容选言判断
复合判断的负判断及其等值转换
高级数理逻辑04

4一阶谓词逻辑4.1 一阶谓词逻辑的基本概念4.1.1命题逻辑的局限性命题逻辑中的原子命题是最小的研究单元,不再进行深入研究。
因此,命题逻辑对现实世界的描述能力是有限的。
1、例如:所有自然数都大于它的素数 A ∀x(A(x)→y∃(P(x,y) ∧Q(y)))A(2100)→y∃(P(2100,y) ∧Q(y))∀x(A(x)→y∃(P(y,x) ∧Q(y)))2100是自然数B A(2100)2100有大于它的素数C y∃(P(y, 2100) ∧Q(y))对于这个现实中的例子,用命题逻辑无法描述。
因为,用命题逻辑来描述,第一个句子是一个原子命题、二三句同样是原子命题。
而这些原子命题之间无法建立关联关系。
因此,每一个前题都是单一的命题,没有联结词。
所以用命题逻辑描述它不能进行推理。
然而上述推理是正确的,是现实中存在的现象。
2、再例如:所有实数的平方是非负的A-是实数B3-的平方是非负的C34.1.2一阶谓词逻辑1、概述一阶谓词逻辑解决了上述问题,能够对原子命题进行分割和更细致的研究工作。
●个体域:任何一门科学都有其研究对象,这些对象的集合称为个体域。
个体域即论域包含所描述问题域中的常元和变元。
P(x)●函词:个体上可以进行运算,能够产生新的个体。
这些运算被称为函数,在一阶谓词里被称为的函词(函数)。
F(x,y)=x*y●谓词:我们在研究个体的时候,主要研究个体的性质。
这些有关个体性质的描述称为谓词。
Q(y), P(x,y) ::x<y●量词:关于个体性质,不一定是对全体的个体的都成立。
有的对一个范围内成立,有离散的几个个体成立,有的对全部都成立。
为了描述这种范围特征,一阶谓词引入了量词。
2、谓词和函词●谓词定义:谓词表示个体性质和关系的语言成分。
它附带放置对象的空位,只有空位被填充对象,谓词才有意义。
没有被填充对象的谓词,称为谓词命名式;相反为谓词填式。
谓词后面的空位个数为谓词的元数。
谓词是一个体域上的n元关系。
数理逻辑41

第四章命题演算的一致性﹑完全性与公理的独立性4.1 命题演算的一致性和完全性*命题演算是一公理系统. 公理系统的作用在于, 从一些公理和推演规则出发, 把某一范围的真命题推演出来.*一方面我们希望, 从它能推演出较多的真命题, 希望能够完全, 能够把某一范围里的真命题完全推演出来.*另一方面, 我们也要求, 从它不能推演出我们所不要的东西, 特别是逻辑矛盾.这是所谓的完全性和一致性问题. 是否完全和是否一致, 是公理系统的两个重要问题.*推演和证明: 推演一词含义较广, 而证明一词含义较狭. 在第三章里, 我们引入了一些推演规则, 在 3.7节也定义了什么是证明. 一般说来, 推演的前提可以是任何公式或任何命题(如3.10节), 证明的根据则是一公理系统的公理(如:3.6―3.9节). 只有从公理可推演的公式或命题才是可证的, 才是定理.一. 命题演算的一致性*一个理论里如果存在逻辑矛盾, 这个理论就是不正确的. 无矛盾性, 也就是一致性, 是公理系统首先要满足的条件. 1. 一致性的几种定义:(1) 一致性的古典定义: 一个公理系统是一致的, 当且仅当, 不存在任何公式A, A和┐A都在这系统里可证.(2) 一致性的语义定义: 一个公理系统是一致的, 当且仅当,在这系统里可证的公式都是真的.*由于A和┐A不能同真, 故该系统没有逻辑矛盾.(3) 一致性的语法定义: 一个公理系统是一致的, 当且仅当, 并非任一合式公式都在这系统里可证.*如果任一公式都在系统里可证, 当然A和┐A也都在系统里可证, 因之系统按古典意义是不一致的.2. 一致性定理一致性定理一: 命题演算是语义一致的. 命题演算的定理都是重言式.证明的主要论证是:(1) 命题演算的公理都是重言式.(2) 应用命题演算的推演规则, 从重言式只能得到重言式.因之可得结论: 命题演算的定理都是重言式.逐步说明如下:(1) 命题演算的公理都是重言式.由3.3节的真值表可证4个公理都是重言式.(2) 命题演算共有三个推演规则: 代入, 分离和定义置换. 现分别加以说明.(甲) 应用代入规则, 从重言式只能得到重言式.设φ(p)为一重言式, 其中含有命题变项p. 由于φ(p)为重言式, 故不论p取值真或假, φ(p)皆为真. 真值表如下: p φ(p)0 11 1再设A为任一公式, 根据代入规则, 以A代入p后得φ(A), 而φ不变. 由于不论A如何复杂, 其值不外乎真或假, 而φ(p)是重言式, 因之, φ(A)的值都是真的. 真值表如下:A φ(A)0 11 1可以看出, φ(A)也是一重言式.(乙) 应用分离规则, 从重言式只能得到重言式.设A和A→B皆为重言式, 则它们的值常真, 在→的真值表中A B A→B0 0 10 1 11 0 01 1 1只有在第4种情况下, A和A→B同时为真, 而在这情况下, B 也为真. 如果A和A→B为重言式, 则它们的值常真, 那么B 的值也必为常真. 因之, B也是重言式.(丙) 应用定义置换规则, 从重言式只能得到重言式.由2.1节例2.4的真值表(5), (6)及德•摩根律(自己验证), 可知定义A∧B⇔┐(┐A∨┐B), A→B⇔┐A∨B,A↔B⇔(A→B)∧(B→A)的左右两方真值相同. 置换不改变真值, 置换后所得的公式和原公式真值也相同. 所以, 如原公式为重言式, 置换后的结果还是一个重言式.根据以上结果, 可知命题演算的定理都是重言式.一致性定理二: 命题演算是语法一致的. 并非任一公式都是命题演算的定理.证明: 既然一切定理都是重言式, 那么, 非重言式, 例如:p∨q 就不是定理.一致性定理三: 命题演算在古典意义下是一致的. 对于任一公式A, A和┐A不能都是命题演算的定理.证明: 对任一公式A, 有时A和┐A都不是重言式, 例如:┐p∨q和┐(┐p∨q). 则A和┐A都不是命题演算的定理. 若A是重言式, 则┐A为矛盾式, 因而不是重言式, 则A是定理, 而┐A不是定理. 因而, 命题演算是古典意义下一致的.二. 命题演算的完全性*关于公理系统的另一个重要问题是, 它能不能包括某一范围里的一切真命题, 是不是完全的. 虽然有些公理系统是完全的, 很多公理系统却是不完全的. 但是即使不完全, 公理化方法和公理系统仍然是数学科学的有力工具, 有重要的价值.1. 完全性的几种定义:(1) 完全性的语义定义: 一公理系统是完全的, 当且仅当, 一切属于某一特定范围内的真命题都是在这系统里可证的. (2) 完全性的语法定义: 一公理系统是完全的, 当且仅当, 如果把一个推演不出的公式作为公理, 其结果, 所得的系统就是不一致的.(3) 完全性的古典定义: 一公理系统是完全的, 当且仅当, 对任一合式公式A而言, 或者A是可证的, 或者┐A是可证的. *这种意义下的完全性是针对着某种公理系统而言的, 在这种系统里, 合式公式中没有自由变项. 命题演算不是这种公理系数. 在这种意义下, 命题演算不是完全的. 例如:┐p∨q 和┐(┐p∨q) 都在命题演算中不可证.2. 完全性定理完全性定理一: 命题演算在语义意义下是完全的. 一切重言式在命题演算里都是可证的.证明: 设A为一重言式.A有一合取范式. 设A的合取范式为B, B也是一重言式, 并且B为B1∧B2∧…∧B nB i (1≤i≤n)是简单析取, B i必是重言式.因之, 每一B i里必有一变项π, 并且π和┐π都作为B i的支命题出现. 每一B i都具有形式π∨┐π∨C .由定理4, p∨┐p可证, 再由附加规则, p∨┐p∨q 可证.所以, 由代入规则可知, 每一B i都可证.根据定理├p→(q→p∧q), B1∧B2∧…∧B n可证. 所以, B可证.B是A的范式, 是从A根据置换规则得到的. 如果B可证, 则A也可证.可见, 如A是重言式, 则A可证.凡重言式皆可证, 故命题演算是完全的.*这个完全性定理也提供了一个有效的证明方法.完全性定理二: 命题演算在语法意义下是完全的. 如果把一不可证的公式作为公理, 其结果将是不一致的.证明: 设A在命题演算里不可证.因凡重言式皆可证, 所以A不是重言式.设B为A的合取范式, 则B不是重言式.设B = B1∧B2∧…∧B n , 则有一B i (1≤i≤n), B i不是重言式. 所以, 在B i里, 不可能有一变项π, π和┐π都作为B i 的支命题出现. B i的支命题中, 虽然有些是否定的, 有些是肯定的, 但是命题变项不相同. 例如: p∨┐q∨┐r∨s .假若把A作为公理, 因B是A的范式, 则B可证. 所以, 根据定理├p∧q→p, B i可证.如以p代入B i中的肯定支命题, 以┐p代入B i中前面带有否定符的命题变项, 例如: 在p∨┐q∨┐r∨s中进行这样的代入, 则可得p∨┐┐p∨┐┐p∨p销去双重否定, 则得一命题变项的析取, 例如:p∨p∨p∨p所以, 如果B i可证, 则p∨p∨…∨p可证.根据公理1, ├p∨p→p, 则p可证.如p可证, 则p为一定理. 即├p . 如果A代入p, 可得├A. 如再用┐A代入p, 又可得├┐A . 如p可证, 则A 和┐A皆可证. 这是逻辑矛盾.所以, 如将一不可证的公式作为公理, 则将导致逻辑矛盾. 可见命题演算具有语法意义下的完全性.4.2 公理的独立性1. 独立性的意义: 一公式集合M是独立的, 如果M中的任一公式A都不能根据给定的推演规则从M中其它公式推演出来.*对于一公理系统的诸公理, 我们希望它们是独立的. 作为出发点的诸公理最好是缺一不可, 任何一个公理都不能从其它公理推演出来.*独立性和一致性不同, 和完全性也有所不同, 一公理系统的诸公理, 其中即使有不独立的, 也不能算是很大的缺点. 2. 算术解释方法:为了证明独立性, 我们通常采用一种算术解释方法. 以下先说明什么是算术解释方法及其可以作独立性证明的理由.设给定一公式集合{A1, A2, A3, A4}和两个推演规则R1和R2. 求证: 根据R1和R2, A4对于{A1, A2, A3}是独立的.我们先从反面着想, 假若A4不独立, 它可以从{A1, A2, A3}根据R1和R2推出. 那么, 下面的断定必然成立: 对于任一性质φ而言, 如果(1) A1, A2, A3都有性质φ,(2) 应用R1和R2, 从有性质φ的公式只能得到有性质φ的公式, 那么,(3) A4必有性质φ.根据以下断定, 假若存在着一性质φ, 并且(1) A1, A2, A3都有性质φ,(2) 应用R1和R2, 从有性质φ的公式只能得到有性质φ的公式,但是(3) A4没有性质φ.那么, 这样一个φ的存在就充分说明了, 应用R1和R2从{A1, A2, A3}不可能推演出A4, A4是独立的.采用解释方法要求我们能够发现一种解释, 这种解释与A1, A2, A3, A4以及R1和R2里的符号以特定的意义, 从而产生独立性证明所需要的性质φ.由于通常采用的解释是赋予变项和公式以数值, 所以这种方法被称为算术解释方法.3. 独立性证明:(一) 独立性证明一: 命题演算的公理1不能从公理2, 3, 4用推演规则推演出来.算术解释: 给予命题演算的原始符号如下解释.(1) 命题变项p, q, r, s, p1, …等可以有三个值: 0, 1, 2 .(2) 初始联结词的数值表如下:A ┐A AB A∨B0 1 0 0 01 0 0 1 02 2 0 2 01 0 01 1 11 2 22 0 02 1 22 2 0根据这种解释, 可有以下结果:(1) 公理2, 3, 4的值常为0. 数值表从略.(2) 应用推演规则, 从数值常为0的公式只能得到数值常为0的公式. 关于代入和定义置换的说明如下.φ(p)中p被代以A,得φ(A). 无论A多复杂, 它只取值0, 1, 2, 相当于p取值0, 1, 2, φ(p)(公理2, 3, 4或它们的推论)取值始终为0, 故φ(A)取值常为0.定义置换也类似. 定义两边A B同时取值0或1或2.在φ(A)中用B置换A得φ(B), 由于在任一解释下B与A等值, 故φ(B)与φ(A)等值.以下证明分离规则:A B ┐A A→B(┐A∨B)0 0 1 00 1 1 10 2 1 21 0 0 01 1 0 01 2 0 02 0 2 02 1 2 22 2 2 0从表上可以看出, 当A和A→B的数值皆为0时, B的值也是0. 所以, 如A和A→B的值常为0, 则B的值也常为0. 应用分离规则, 从公理2, 3, 4只能得到其值常为0的公式.*此处的“数值常为0”,就是独立性证明所需要的性质φ.公理1如果不是独立的, 是可以推出的, 它的数值也必常为0. 但公理1的数值不常为0.(见下表).p p∨p ┐(p∨p) ┐(p∨p)∨p0 0 1 01 1 0 02 0 1 2可见公理1不能从其它公理推出.(二) 独立性证明二: 公理2不能从公理1, 3, 4用推演规则推出.算术解释:(1) 命题变项有四个值: 0, 1, 2, 3 .(2) ┐和∨的数值解释, 用等式表示为:(甲)┐0=1, ┐1=0, ┐2=3, ┐3=2 .(乙) 0∨0=0∨1=0∨2=0∨3=01∨1=1∨2=1∨3=12∨2=2∨3=23∨3=3交换律对∨适用.根据这种解释, 公理1, 3, 4的值常为0或2, 推演规则也传递“等于0或2”这性质, 但公理2并不常“等于0或2”. 当p取值2, q取值1时,p→p∨q的值为2→2∨1=┐2∨(2∨1)=3∨1=1 .所以公理2是独立的.(三)独立性证明三: 公理3不能从公理1, 2, 4用推演规则推出.此处算术解释是:(1) 命题变项有四个值: 0, 1, 2, 3 .(2) ┐和∨的数值解释, 用等式表示为:(甲) ┐0=1, ┐1=0, ┐2=0, ┐3=2(乙) 0∨0=0∨1=1∨0=0∨2=2∨0=0∨3=3∨0=01∨1=1,1∨2=2∨1=2,1∨3=3∨1=32∨3=0,3∨2=3,2∨2=2,3∨3=3根据这个解释, 公理1, 2, 4的值常为0, 推演规则传递“常为0”的性质. 但公理3的值不常为0.当p取值2, q取值3时, 公理3的值为3.(四) 独立性证明四: 公理4不能从公理1, 2, 3用推演规则推出.在此我们用以下的算术解释.(1) 命题变项有四个值: 0, 1, 2, 3 .(2) ┐和∨的数值解释为:(甲) ┐0=1, ┐1=0, ┐2=3, ┐3=0 .(乙) 0∨0=0∨1=1∨0=0∨2=2∨0=0∨3=3∨0=01∨1=1,1∨2=2∨1=2,1∨3=3∨1=32∨2=2,2∨3=3∨2=0,3∨3=3 .根据这个解释, 公理1, 2, 3以及从它们推演出来的公式, 其值都常为0, 而公理4的值不常为0. 当p取值2, q取值2,r取值2时, 公理4的值为2.作业:1. 在自然推理系统P中, 证明以下推理:今天下雨或明天后天都下雨, 明天不下雨或后天不下雨而今天下雨. 可以推出“今天下雨”.2. 在自然推理系统P中, 证明以下推理:如果李敏来通信工程学院, 若王军不生病, 则王军一定去看望李敏. 如果李敏出差到南京, 那么李敏一定来通信工程学院. 王军没有生病. 所以, 如果李敏出差到南京, 王军一定去看望李敏.3. 在自然推理系统P中, 证明以下推理:前提: B∧C, (B C)→(H∨G)结论: G∨H .4. 在自然推理系统P中, 证明以下推理:前提: P→Q, (┐Q∨R)∧┐R, ┐(┐P∧S)结论: ┐S .。
北师大施翔辉数理逻辑答案HW-04

Solutions for Assignment♯41.Prove Theorem2.13.Solution:By Lemma2.11,it is enough to check the claim of uniqueness.(a)Suppose thatφ=P i(τ1...τn)andφ=P j(σ1...σn).P i and P j both occur as thefirst symbol inφand hence are equal.Consequently n=m=π(P i).Thenτ1andσ1must be equal,as neither can be a proper initial segment of the other.By induction on i less than or equal to n,for each i,τi is equal toσi,as required.(b)Suppose thatφ=(τ1ˆ=τ2)andφ=(σ1ˆ=σ2).Sinceτ1andσ1are terms,they must be equal,as neither can be a proper initial segment of the other.By the same reason,τ2=σ2.(c)Suppose thatφ=(¬ψ)andφ=(¬θ),ψandθare formulas.By Lemma2.12,ψmust be equaltoθ,as neither can be a proper initial segment of the other.(d)Suppose thatφ=(ψ1→ψ2)andφ=(θ1→θ2).Since bothψ1andθ1belong to L,by Lemma2.12,neither can be a proper initial segment of the other,they must be equal.As in the case ofnegation,it follows thatψ2andθ2are also equal.(e)Suppose thatφ=(∀x iψ)andφ=(∀x jθ).The occurrence of x i and x j withφhave the sameelement and therefore are equal.It follows thatφandθare also equal.2.Consider the set of sequences defined as in Definition2.6except that the last clause is changed toread,“Ifφ∈L and x i is a variable symbol,then∀x iφis an element of L”in which the parentheses are omitted.Is this set uniquely readable?Solution:The set is uniquely readable.It is enough to prove an analog of Lemma2.12:Ifφ∈L,then no proper initial segment ofφis an element of L.We just need to change a bit in thefinal part of the proof as follows: Consider the case whenφis∀x iφ1.Ifψis an initial segment ofφ,thenψmust be of the form ∀x iψ1,asφandψmust have the samefirst two symbols.But then induction applies toφ1,andψ1 must equalφ1.It follows thatφis equal toψ.3.Consider the set of sequences defined as in Definition2.6except that the fourth clause is changed to read,“Ifφ1andφ2are elements of L,thenφ1→φ2is an element of L”in which the parentheses are omitted.Is this set uniquely readable?Solution:The set is not uniquely readable.For example,φ1→φ2→φ3can be read asφ=((φ1→φ2)→φ3)andψ=(φ1→(φ2→φ3)).Butφ=ψ.4.Let A be a language with one binary relation symbol.Give an example of a sentenceφin this language and L A-structures M1and M2such that M1⊨φand M2⊭φ.Solution:Let R be a binary relation symbol,and letφ=∃x∀y¬(y<x).M1=(N,<)and M2=(R,<). Then M1⊨φif and only if x is the smallest number in N if and only if x=0.M2⊨φif and only if x is the smallest number in R.But this is impossible.Hence M2⊭φ.5.Do there exist an L A-structure M,an M-assignmentν,and an L A-formulaφsuch that(M,ν)⊨φand(M,ν)⊨(¬φ)?Do there exist such M andνsuch that(M,ν)⊭φand(M,ν)⊭(¬φ)?Solution:(a)There doesn’t exist such M,ν,φsuch that(M,ν)⊨φand(M,ν)⊨(¬φ).By definition,(M,ν)⊨(¬φ)if and only if(M,ν)⊭φ.By induction onϕ,φand(¬φ)can’t be satisfied by (M,ν)at the same time.(b)There doesn’t exist such M,ν,φsuch that(M,ν)⊭φand(M,ν)⊭(¬φ).By definition,(M,ν)⊭φif and only if(M,ν)⊨(¬φ).By induction onϕ,(M,ν)⊭φand(M,ν)⊭(¬φ)can’t happen at the same time.。
数理逻辑-大纲
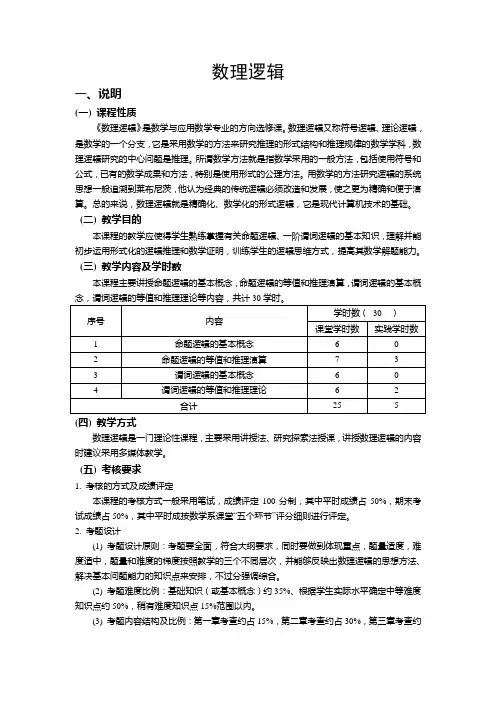
数理逻辑一、说明(一) 课程性质《数理逻辑》是数学与应用数学专业的方向选修课。
数理逻辑又称符号逻辑、理论逻辑,是数学的一个分支,它是采用数学的方法来研究推理的形式结构和推理规律的数学学科,数理逻辑研究的中心问题是推理。
所谓数学方法就是指数学采用的一般方法,包括使用符号和公式,已有的数学成果和方法,特别是使用形式的公理方法。
用数学的方法研究逻辑的系统思想一般追溯到莱布尼茨,他认为经典的传统逻辑必须改造和发展,使之更为精确和便于演算。
总的来说,数理逻辑就是精确化、数学化的形式逻辑,它是现代计算机技术的基础。
(二) 教学目的本课程的教学应使得学生熟练掌握有关命题逻辑、一阶谓词逻辑的基本知识,理解并能初步运用形式化的逻辑推理和数学证明,训练学生的逻辑思维方式,提高其数学解题能力。
(三) 教学内容及学时数本课程主要讲授命题逻辑的基本概念,命题逻辑的等值和推理演算,谓词逻辑的基本概念,谓词逻辑的等值和推理理论等内容,共计30学时。
序号内容学时数(30 )课堂学时数实践学时数1 命题逻辑的基本概念 6 02 命题逻辑的等值和推理演算7 33 谓词逻辑的基本概念 6 04 谓词逻辑的等值和推理理论 6 2合计25 5 (四) 教学方式数理逻辑是一门理论性课程,主要采用讲授法、研究探索法授课,讲授数理逻辑的内容时建议采用多媒体教学。
(五) 考核要求1. 考核的方式及成绩评定本课程的考核方式一般采用笔试,成绩评定100分制,其中平时成绩占50%,期末考试成绩占50%,其中平时成按数学系课堂“五个环节”评分细则进行评定。
2. 考题设计(1) 考题设计原则:考题要全面,符合大纲要求,同时要做到体现重点,题量适度,难度适中,题量和难度的梯度按照教学的三个不同层次,并能够反映出数理逻辑的思想方法、解决基本问题能力的知识点来安排,不过分强调综合。
(2) 考题难度比例:基础知识(或基本概念)约35%、根据学生实际水平确定中等难度知识点约50%,稍有难度知识点15%范围以内。
高级数理逻辑第4讲分析
4一阶谓词逻辑4.1 一阶谓词逻辑的基本概念4.1.1命题逻辑的局限性命题逻辑中的原子命题是最小的研究单元,不再进行深入研究。
因此,命题逻辑对现实世界的描述能力是有限的。
1、例如:所有自然数都大于它的素数 A ∀x(A(x)→y∃(P(x,y) ∧Q(y)))A(2100)→y∃(P(2100,y) ∧Q(y))∀x(A(x)→y∃(P(y,x) ∧Q(y)))2100是自然数B A(2100)2100有大于它的素数C y∃(P(y, 2100) ∧Q(y))对于这个现实中的例子,用命题逻辑无法描述。
因为,用命题逻辑来描述,第一个句子是一个原子命题、二三句同样是原子命题。
而这些原子命题之间无法建立关联关系。
因此,每一个前题都是单一的命题,没有联结词。
所以用命题逻辑描述它不能进行推理。
然而上述推理是正确的,是现实中存在的现象。
2、再例如:所有实数的平方是非负的A-是实数B3-的平方是非负的C34.1.2一阶谓词逻辑1、概述一阶谓词逻辑解决了上述问题,能够对原子命题进行分割和更细致的研究工作。
●个体域:任何一门科学都有其研究对象,这些对象的集合称为个体域。
个体域即论域包含所描述问题域中的常元和变元。
P(x)●函词:个体上可以进行运算,能够产生新的个体。
这些运算被称为函数,在一阶谓词里被称为的函词(函数)。
F(x,y)=x*y●谓词:我们在研究个体的时候,主要研究个体的性质。
这些有关个体性质的描述称为谓词。
Q(y), P(x,y) ::x<y●量词:关于个体性质,不一定是对全体的个体的都成立。
有的对一个范围内成立,有离散的几个个体成立,有的对全部都成立。
为了描述这种范围特征,一阶谓词引入了量词。
2、谓词和函词●谓词定义:谓词表示个体性质和关系的语言成分。
它附带放置对象的空位,只有空位被填充对象,谓词才有意义。
没有被填充对象的谓词,称为谓词命名式;相反为谓词填式。
谓词后面的空位个数为谓词的元数。
谓词是一个体域上的n元关系。
《高级数理逻辑》课件
介绍基于高级数理逻辑研究的智 能推理算法,让计算机更高效地 进行推理和判断。
多值逻辑及其应用
多值逻辑概述
介绍多值逻辑的概念、基本原理以及与二值逻 辑的区别。
多值逻辑在人工智能中的应用
深入研究多值逻辑在自然语言处理、机器学习 和智能系统中的应用,以提高其智能水平。
多值逻辑在计算机科学中的应用
探索多值逻辑在计算机编程、信息理论和密码 学等方面的应用。
模型检验方法
介绍基于多值逻辑的模型检验方法及其应用, 以确保系统或软件的正确性。
模态逻辑理论及扩展
1
经典模态逻辑
2
探讨经典模态逻辑的语法、语义、推理
规则及其应用。
3
非经典模态逻辑
4
介绍非经典模态逻辑,如增长逻辑、其 他模态逻辑和拓扑逻辑等,并探讨其应
用。
模态逻辑概述
介绍模态逻辑的基本概念、语言和语义。
二阶逻辑理论及应用
1 二阶逻辑概述
介绍二阶逻辑中的语法、 语义和推理规则。
Hale Waihona Puke 2 二阶逻辑的应用探讨二阶逻辑在模型论、 计算机科学和数学中的应 用。
3 高维逻辑
介绍高维逻辑的概念、语 言和语义,以及它在数学、 物理学和哲学中的应用。
可计算论概述及相关定理
可计算性理论
介绍可计算性理论和计算模型, 如图灵机、λ演算和递归函数等。
动态模态逻辑
研究模态逻辑中时间、知识和行动等概 念的语义和推理规则。
一阶逻辑及其扩展
概述
介绍一阶逻辑中的语法、语义和 推理规则。
一阶逻辑扩展
研究一阶逻辑的拓展,如高阶逻 辑、无限值逻辑和时态逻辑等, 并探讨其应用。
程序语言理论
介绍一阶逻辑在程序语言理论中 的应用,包括程序设计、程序分 析和验证等。
数理逻辑
9.1 命题
定义9.1命题:凡能分辨真、假的语句称命题。 定义 命题:凡能分辨真、假的语句称命题。 命题 定义9.2 原子命题:一命题凡不能分解为更简单的 原子命题: 定义 命题称原子命题或简称原子。 命题称原子命题或简称原子。 定义9.3命题常量 具有确定真值的命题,它可用T 命题常量: 定义 命题常量:具有确定真值的命题,它可用 表示, 或F表示,称命题常量或命题常元。 表示 称命题常量或命题常元。 定义9.4命题变量 命题变量: 为其变域的命题, 定义 命题变量:以 T,F为其变域的命题,并可 , 为其变域的命题 用命题标识符表示之。称命题变量或称命题变元。 用命题标识符表示之。称命题变量或称命题变元。
第9章 命题逻辑 章
(3)自然语言中的联结词的衡量标准不完全是其真 值表; 值表 ; 但命题逻辑中的联结词的衡量标准则是真值 因此, 联结词的唯一衡量标准是其真值表, 表 。 因此 , 联结词的唯一衡量标准是其真值表 , 而 不是由自然语言的一些日常语义确定。 不是由自然语言的一些日常语义确定。
9.3 命题公式
2
第9章 命题逻辑 章
9.2命题联结词
定义9.5复合命题 : 定义 复合命题: 由原子命题通过联结词所构成 复合命题 的命题称复合命题。 的命题称复合命题。 (1)否定 否定 否定联结词是一元联结词, 否定联结词是一元联结词,它的作用对象仅为一个 命题。 命题 。 否定联结词作用于一个命题后使该命题出现 相反的语义。 如有命题: 今天下雨, 相反的语义 。 如有命题 : 今天下雨 , 而加上否定联 结词后即成为:今天不下雨。 结词后即成为:今天不下雨。 在命题逻辑中将此联结词予以符号化, 在命题逻辑中将此联结词予以符号化,并建立符号 体系如下: 体系如下:
《数理逻辑》第四章
马琦 2010.10.16 maqi08@非形式化命题演算基本要素 真值指派 逻辑推理 等价性 p,q,r,…~,∧,∨,→,↔, A,B,C,… 真值表 重言式:对任意变元真值都取T。
论证形式的有效性语句形式演算系统 L~,→,( , ) , p1, p2, p3,… 合式公式,公理,演绎规则 重言式:对每一赋值都取T。
定理和证明(推演和后承)论证形式是有效的当且仅当相应的命题形式是重言式。
重言式是定理,定理是重言式。
论证形式是有效一阶语言 L基本要素 真值指派 x1,x2,…,a1,a2,…, Ain, fin, (,),,,~,→,∀ 解释:变元域以及其他元素的指定。
赋值:对变元的指定。
重言式:L L中重言式的代换实例。
逻辑推理 等价性 逻辑有效:对每一解释都是真的。
逻辑有效的。
重言式是逻辑有效 逻辑有效形式系统KLL的合式公式,公理,规则定理和证明(推演和后承) 定理是逻辑有效的。
逻辑有效的是定理。
公理• 设A,B,C是L的任意wf.,下列为KL的公理。
• (K1) (A→(B→A)) • (K2) (A→(B→C))→((A→B)→(A→C)) • (K3) (~A→~B)→(B→A)) • (K4) ((∀xi)A→A)),xi不在A中自由出现。
• (K5) ((∀xi)A(xi)→A(t))),A(xi)是L的wf.,而 L的项 t 对A(xi)中的 xi 是自由的。
• (K6) ((∀xi)(A→B)→(A→(∀xi)B)),若A不包含变元xi的自由出现。
规则• (1) 分离规则,即由A和 (A→B)推出B,这里A和B是L的任意wf.。
• (2) 全称概括规则,即由 A推出 (∀xi)A,这里A是L的任意wf.,xi是任意变元。
全称概括规则证明和定理• KL中的一个证明是L的wf.序列 A1,…An,使对每一i(1≤i≤n),或者Ai是KL的公理, 或者Ai是由序列中在前的wf.用MP规则或全称概括规则而推得。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
定理
若A(u1,u2,…,un)是有效的 iff ∀x1∀x2…∀xnA(x1,x2,…,xn) 是有效的。
证明:
A(u)有效 A(u)有效 iff ¬A(u)不可满足 ¬A(u)不可满足 iff ∃x(¬A(x))不可满足 ∃x(¬A(x))不可满足 iff ¬∀xA(x)不可满足 ¬∀xA(x)不可满足 iff ∀xA(x)有效的 ∀xA(x)有效的 使用归纳证明即可。
证明:
必要性:假设A 必要性:假设A ∉ ∑。 由∑是极大协调的,则∑∪{A}是不协调的,即 是极大协调的,则∑ {A}是不协调的,即 存在存在B Form(L ,使得∑ 存在存在B∈Form(L ),使得∑├B且∑├¬B。 可得∑ 可得∑, A ├B且∑,A ├¬B。因此, ∑├ ¬A。 因此, 这与∑ 这与∑协调矛盾。 充分性:易证。
可靠性定理(一) 可靠性定理(
设∑⊆Form(L ),A∈Form(L )。 Form(L Form(L
若∑├A,则∑╞A。 ,则∑ 若Ф├A,则Ф╞A。 Ф├A,则Ф
协调性
∑⊆Form(L )是协调的,当且仅当不存在 Form(L A∈Form(L ),使得∑├A且∑├¬A。 Form(L ,使得∑
定理
若A(u1,u2,…,un)是可满足的 iff ∃x1∃x2…∃xnA(x1,x2,…,xn) 是可满足的。
证明:
A(u)可满足 A(u)可满足 iff 存在赋值v,使得A(u)v=1 存在赋值v,使得A(u) v(u/uv)=1 iff 存在赋值v,使得A(u) 存在赋值v,使得A(u) iff 存在赋值v,使得(∃xA(x))v=1 存在赋值v,使得(∃xA(x)) iff ∃xA(x)可满足 ∃xA(x)可满足 使用归纳证明即可。
引理:设∑ Form(L 是极大协调集,构作真假赋值v 引理:设∑⊆Form(L p)是极大协调集,构作真假赋值v, 使得对于任何原子公式p 使得对于任何原子公式p,pv=1当且仅当p∈ ∑。于是, =1当且仅当p 对于任何A Form(L 对于任何A∈Form(L p), Av=1当且仅当A∈ ∑。 =1当且仅当A 证明:
定理:
设∑⊆Form(L )是极大协调的。对于任何A Form(L 是极大协调的。对于任何A ∈Form(L ),¬A∈∑ iff A ∉ ∑。 Form(L
证明:
必要性:假设A 必要性:假设A∈∑。可得, ∑├A。 又因为¬ 又因为¬A∈∑,且∑├¬A 。这与∑协调矛盾。 这与∑ 充分性:因为A 充分性:因为A ∉ ∑且∑是极大协调的, ∑∪{A} 是不协调的,即存在B Form(L ,使得∑ 是不协调的,即存在B∈Form(L ),使得∑, A├B且∑,A├¬B,可得∑├¬A 。所以¬A∈∑。 ,可得∑ 。所以¬
可靠性定理(二) 可靠性定理(
设∑⊆Form(L ),A∈Form(L )。 Form(L Form(L
若∑是可满足的,则∑是协调的。 是可满足的,则∑是协调的。 若A是可满足的,则A是协调的。 是可满足的,则A是协调的。
证明:
假设∑是不协调的。即存在A Form(L 假设∑是不协调的。即存在A∈Form(L ),使得 ∑├A且∑├¬A。由可靠性定理(一),得到, ∑╞A且∑╞¬A。 因为∑是可满足的,可得,存在赋值v,使得∑ =1。 因为∑是可满足的,可得,存在赋值v,使得∑v=1。 =1,矛盾。 所以A =1且 所以Av=1且(¬A)v=1,矛盾。
极大协调性
∑⊆Form(L )是极大协调的,当且仅当 Form(L
∑是协调的。 是协调的。 对于任何A 对于任何A ∉ ∑,∑∪{A}是不协调的。 {A}是不协调的。
称∑为封闭于形式可推演性的,若对于任何 A, ∑├A蕴含A∈∑。 蕴含A
定理:
设∑⊆Form(L )是极大协调的。对于任何A Form(L 是极大协调的。对于任何A ∈Form(L ),∑├A iff A∈∑。 Form(L A∈
i)若A是原子公式,成立。 )若A ii)¬A∈ ∑ iff A ∉ ∑ iff Av=0 iff (¬A)v=1。 ii)¬A∈ =1。 iii)A∧B∈ ∑ iff A ∈ ∑且B ∈ ∑ iff Av=1且 Bv=1 iff (A ∧ B)v=1。 iii) =1且 =1。 iv) A∨B∈ ∑ iff A ∈ ∑或B ∈ ∑ iff Av=1或 Bv=1 iff (A ∨ B)v=1。 iv) =1或 =1。 v) A→B∈ ∑ iff A ∈ ∑蕴含B ∈ ∑ iff Av=1蕴含Bv=1 iff (A → 蕴含B =1蕴含B B)v=1。 =1。 vi) A↔B∈ ∑ iff A ∈ ∑等值于B ∈ ∑ iff Av=1等值于 Bv=1 iff vi) A↔B 等值于B =1等值于 (A↔B =1。 (A↔B)v=1。
定理:
∑⊆Form(L )是协调的,当且仅当存在 Form(L A∈Form(L ),使得∑├/ 。 Form(L ,使得∑ A
证明:
必要性:假设对于任何A Form(L 必要性:假设对于任何A∈Form(L ),∑├A。这 与∑是协调的相矛盾。 充分性:假设∑是不协调的,即存在B Form(L 充分性:假设∑是不协调的,即存在B∈Form(L ), 使得∑ 使得∑├B且∑├¬B。则对于任何A∈Form(L ) , 。则对于任何A Form(L ∑,¬A├B且∑,¬A ├¬B,可得到∑├A。矛盾。 ¬A├ ,可得到∑
定理:
A可满足 iff A的前束范式是可满足的 A的前束范式是可满足的 A有效 iff A的前束范式是有效的 A的前束范式是有效的
定义:
∑在论域D中可满足 iff 存在以D为论域的赋值v, 在论域D 存在以D为论域的赋值v 使得∑ =1。 使得∑v=1。 A在论域D中有效 iff 对于任何以D为论域的赋 在论域D 对于任何以D 值v,Av=1。 =1。
定理:
设∑⊆Form(L )是极大协调的。对于任何A, Form(L 是极大协调的。对于任何A B∈Form(L ),A∧B∈∑ iff A∈∑并且B∈∑。 Form(L A∈ 并且B
证明:
必要性:因为A 必要性:因为A∧B∈∑。可得, ∑├A ∧B。 进一步得到, ∑├A 且∑├ B 。所以A∈∑且 。所以A B∈∑。 充分性:因为A 充分性:因为A∈∑且B∈∑。可得,∑├A 且 。可得,∑ ∑├ B。 进一步得到, ∑├A ∧B 。所以A∧B∈∑。 。所以A
定理:设∑ Form(L 定理:设∑⊆Form(L p),A∈Form(L p),且∑为有限集。 Form(L ,且∑
若Ф╞ A,则Ф├A 。 ,则Ф├A 若∑╞A ,则∑├A 。 ,则∑
证明:
设A含不同的原子公式p1,p2,…,pn。令v1,v2是真假赋值, 含不同的原子公式p 。令v1,v2是真假赋值, 且p1v1=1, p1v2=0, p2v1= p2v2=1,piv1= piv2,i=3,…,n。由 =1, =0, =1, i=3, 引理,由于A =1,所以p 引理,由于Av1=1,所以p1,p2 ,…,An├A。由于Av2=1,所 。由于A =1,所 以¬p1,p2 ,…,An├A。可得, p1 ∨ ¬p1 ,p2 ,…,An├A, p2 ,…,An├ (p1 ∨ ¬p1 ) →A (p 又因为Ф├ 又因为Ф├ p1 ∨ ¬p1 ,所以 p2 ,…,An├ p1 ∨ ¬p1 。 可得, p2 ,…,An├ A。 再令u1,u2是真假赋值,且p =1, 再令u1,u2是真假赋值,且p1u1=1, p1u2=0, p2u1= p2u2=0,piu1= =0, =0, piu2,i=3,…,n。同理可得, ¬p2 ,…,An├ A。 i=3, 可得, A3 ,…,An├ A。 进一步指定真假赋值,可得Ф├A 进一步指定真假赋值,可得Ф├A 。
定理:
任何协调集都可扩充为极大协调集。
引理:
设A ∈Form(L p)含不同的原子公式p1,p2,…, Form(L 含不同的原子公式p pn,v是真假赋值。对于i=1,2,…,n,令 是真假赋值。对于i=1, 若piv=1,则Ai=pi;否则,Ai=¬pi。则 =1,则A ;否则,A 若Av=1,则A1,A2 ,…,An├A。 =1,则A 若Av=0,则A1,A2 ,…,An├¬A。 =0,则A
定理:
设∑⊆Form(L )是极大协调的。对于任何A,B∈Form(L ), Form(L 是极大协调的。对于任何A Form(L A∨B∈∑ iff A∈∑或B∈∑。 A∈
证明:
必要性:假设A 必要性:假设A ∉ ∑且B ∉ ∑。 可得, ¬A∈∑且¬B∈∑。 ¬B∈ 进一步可得,¬ 进一步可得,¬A ∧ ¬B∈∑, ¬(A ∨ B)∈ ∑, ∑├ ¬(A ¬B∈ ¬(A B)∈ ¬(A ∨ B) 。 又因为A 又因为A∨B∈∑, ∑├ A ∨ B。这与∑协调矛盾。 。这与∑ 充分性:因为A 充分性:因为A∈∑或B∈∑。可得,∑├A ∨B 或∑├ B 。可得,∑ ∨ A。 进一步得到, A ∨ B∈∑。
定理:
设∑⊆Form(L )是极大协调的。对于任何A, Form(L 是极大协调的。对于任何A B∈Form(L ), Form(L A→B∈∑ iff A∈∑蕴含B∈∑。 A∈ 蕴含B A↔B∈∑ iff A∈∑等值于B∈∑。 ↔B∈ A∈ 等值于B
定理:
设∑⊆Form(L )是极大协调的。对于任何A Form(L 是极大协调的。对于任何A ∈Form(L ),∑├/ iff ¬A∈∑。 Form(L A
命题逻辑的完备性定理(一) 命题逻辑的完备性定理(
设∑⊆Form(L p),A∈Form(L p)。 Form(L Form(L
若∑是协调的,则∑是可满足的。 协调的,则∑ 可满足的 若A是协调的,则A是可满足的,所以∑ 因为∑是协调的,所以∑可以扩充为极大协调集 对于任何B 。因此,可得B =1, ∑*。对于任何B∈∑, B∈∑*。因此,可得Bv=1, v是构作真假赋值。即∑是可满足的。 是构作真假赋值。即∑ 可满足的。
