2019-2020学年上学期湖南省东安县舜德学校期中考试试卷八年级数学(PDF版,无答案)
2019-2020学年第一学期八年级期中考试数学试卷含答案

2019-2020学年第一学期八年级期中考试数 学 试 卷(满分:150分;考试时间:120分钟)一、选择题(共10小题,每小题4分,满分40分) 1.下列图形中,不具有稳定性的图形是( )A .平行四边形B .等腰三角形C .直角三角形D .等边三角形 2.下列运算正确的是( ) A .1243a a a =⋅ B .()523a a = C .()632273a a = D .236a a a =÷3.下列长度的三条线段能组成三角形的是( ) A .2, 3, 4 B . 3, 6, 11 C .4, 6, 10 D . 5, 8, 14 4.一个凸多边形的内角和等于900°,则这个多边形的边数是( ) A .5 B .6 C .7 D .85.若等式22)()b a M b a +=+-(成立,则M 的值为( ) A .ab 2 B .ab 4 C .ab 4- D .-6.如图,在∠AOB 的两边上,分别取OM = ON,再分别过点M 、作OA 、OB 的垂线,交点为P ,画射线OP ,则OP 平分∠的依据是( )A .SSSB .SASC .AASD .HL7.若812+-kx x 是一个完全平方式,则k 的值为( ) A .±9B .18C .±18D .-188.已知,a , b , c 是△ABC 的三条边长,化简b a c c b a ----+的结果为( ) A .c b a 222-+ B .b a 22+ C .c 2 D .0 9.下列语句中,正确的是( )A .等腰三角形底边上的中线就是底边上的垂直平分线;B .等腰三角形的对称轴是底边上的高;C .一条线段可看作是以它的垂直平分线为对称轴的轴对称图形;D .等腰三角形的对称轴就是顶角平分线。
10.如图,在2×2的方格纸中有一个以格点为顶点的△ABC ,则 与△ABC 成轴对称且以格点为顶点的三角形共有( )个 A .3 B .4 C .5 D .6二、填空题(共6小题,每小题4分,满分24分)11.点(1,2)关于x 轴对称点的坐标是 .OCG12.已知射线OM ,以O 为圆心,任意长为半径画弧,与射线OM 交 于A ,再以点A 为圆心,AO 长为半径画弧,两弧交于点B ,画射线OB ,如图所示,则∠AOB =°.13.如图,△ABC 中,∠ACB = 90°,沿CD 折叠△CBD ,使点B恰好落在AC 边上的点E 处。
2019-2020第一学期八年级数学期中试卷(含答题卷)
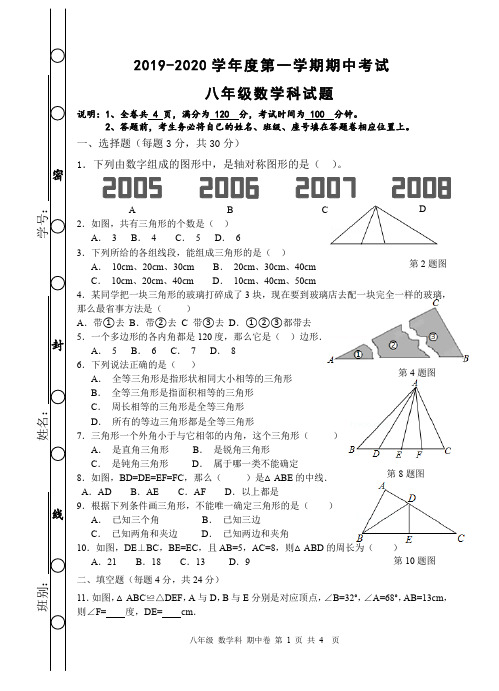
第4题图第2题图第8题图第10题图 2019-2020学年度第一学期期中考试八年级数学科试题说明:1、全卷共 4 页,满分为 120 分,考试时间为 100 分钟。
2、答题前,考生务必将自己的姓名、班级、座号填在答题卷相应位置上。
一、选择题(每题3分,共30分)1.下列由数字组成的图形中,是轴对称图形的是( )。
2.如图,共有三角形的个数是( ) A . 3 B . 4 C . 5 D . 63.下列所给的各组线段,能组成三角形的是( )A . 10cm 、20cm 、30cmB . 20cm 、30cm 、40cmC . 10cm 、20cm 、40cmD . 10cm 、40cm 、50cm4.某同学把一块三角形的玻璃打碎成了3块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事方法是( )A .带①去B .带②去C 带③去D .①②③都带去 5.一个多边形的各内角都是120度,那么它是( )边形. A . 5 B . 6 C . 7 D . 8 6.下列说法正确的是( )A . 全等三角形是指形状相同大小相等的三角形B . 全等三角形是指面积相等的三角形C . 周长相等的三角形是全等三角形D . 所有的等边三角形都是全等三角形7.三角形一个外角小于与它相邻的内角,这个三角形( ) A . 是直角三角形 B . 是锐角三角形C . 是钝角三角形D . 属于哪一类不能确定8.如图,BD=DE=EF=FC ,那么( )是△ABE 的中线.A .ADB .AEC .AFD .以上都是9.根据下列条件画三角形,不能唯一确定三角形的是( ) A . 已知三个角 B . 已知三边C . 已知两角和夹边D . 已知两边和夹角10.如图,DE ⊥BC ,BE=EC ,且AB=5,AC=8,则△ABD 的周长为( )A .21B .18C .13D .9 二、填空题(每题4分,共24分)11.如图,△ABC ≌△DEF ,A 与D ,B 与E 分别是对应顶点,∠B=32°,∠A=68°,AB=13cm ,则∠F= 度,DE= cm .ABCD第13题图12.若∠B=∠A+∠C ,则△ABC 是 . 13.如图,∠1=14.为了使一扇旧木门不变形,木工师傅在木门的背面加钉了一根 木条,这样做的道理是15在△ABC 中,AB=6,AC=8,那么BC 长的取值范围是 16.等腰三角形两内角的和是1000,则它的顶角是三、解答题(一)(每小题6分,共18分) 17、如图:(1)作出与△ABC 关于x 轴对称的图形△A 1B 1C 1;(2)若图中一个小正方形边长为一个单位长度,请写出各点的坐标:A 1__________;B 1__________;C 1__________.18.一个多边形的内角和是它的外角和的4倍,求这个多边形的边数.19.若一个等腰三角形的两边长分别是3cm 和5cm ,求它的周长.第11题图第14题图20. 如图,已知D为△ABC边BC延长线上一点,DF⊥AB于F交AC于E,∠A=35°,∠D=42°,求∠ACD的度数.第20题图21.如图,AB=AC,AD=AE,∠1=∠2,求证:BD=CE.第21题图22.如图,AC⊥BC,BD⊥AD,垂足分别为C,D,AC=BD.求证:BC=AD.第22题图23、如图所示,等边三角形ABC中,D为AC边的中点,E为BC延长线上一点,CE=CD,DM⊥BC于M,求证:M是BE的中点.24.如图,AB与CD相交于点O,∠ACO=∠BDO,OC=OD,CE是△ACO的角平分线.请你先作∠ODB的角平分线DF(用尺规作图,不要求写出作法与证明,但要保留作图痕迹);再证明CE=DF.第24题图25.如图,在△ABC中,AD为∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,△ABC 面积是28cm2,AB=20cm,AC=8cm,求DE的长.第25题图2019-2020学年度第一学期期中考试八年级 数学 答题卡一、选择题(每题3分,共30分)二、填空题(每题4分,共24分)11.∠F= 度,DE= cm 12.△ABC 是 13.∠1=14.道理是 15.BC 长的取值范围是 16.顶角是三、解答题(一)(每小题6分,共18分)17.(1) 作出与△ABC 关于x 轴对称的图形△A 1B 1C 1(2)写出各点的坐标:A 1 ;B 1;C 1 .18.19.四、解答题(二)(每小题7分,共21分)20.21.第20题图第21题图22.五、解答题(三)(每小题9分,共27分)23.第22题图24.25.第25题图第24题图。
2019-2020学年度八上期中数学考试试卷
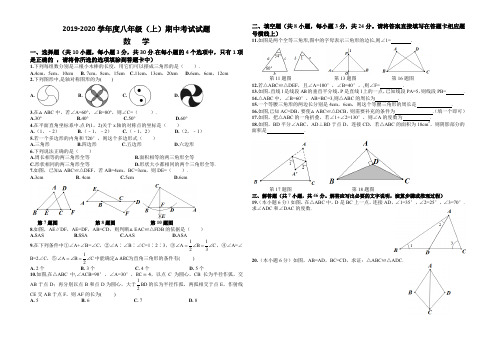
2019-2020学年度八年级(上)期中考试试题数 学一、选择题(共10小题,每小题3分,共30分.在每小题的4个选项中,只有1项是正确的 ,请将你所选的选项填涂到答题卡中)1.下列每组数分别是三根小木棒的长度,用它们可以摆成三角形的是( ).A.4cm ,5cm ,10cmB. 7cm ,8cm ,15cmC.11cm ,13cm ,20cmD.6cm ,6cm ,12cm 2.下列图形中,是轴对称图形的为( ) A.B.C.D.3.在△ABC 中,若∠A=60°,∠B=80°,则∠C=( ). A.30° B.40° C.50° D.60°4.在平面直角坐标系中 点P(1,2)关于x 轴的对称点的坐标是( )A.(1,﹣2)B.(﹣1,﹣2)C.(﹣1,2)D.(2,﹣1) 5.若一个多边形的内角和720°,则这个多边形式( )A.三角形B.四边形C.五边形D.六边形 6.下列说法正确的是( )A.周长相等的两三角形全等B.面积相等的两三角形全等C.形状相同的两三角形全等D.形状大小都相同的两个三角形全等. 7.如图,已知△ABC ≌△DEF ,若AB=4cm ,BC=3cm ,则DE=( ). A.3cm B. 4cm C.5cm D.6cm第7题图 第8题图 第10题图8.如图,AE ∥DF ,AE=DF ,AB=CD ,则判断△EAC ≌△FDB 的依据是( ) A.SAS B.SSA C.AAS D.ASA9.在下列条件中①∠A+∠B=∠C ,②∠A ∶∠B ∶∠C=1∶2∶3,③C 31B 21A ∠=∠=∠,④∠A=∠B=2∠C ,⑤C 21B A ∠=∠=∠中能确定△ 为直角三角形的条件有( )A. 2个B. 3个C. 4个D. 5个 10.如图,在△ABC 中,∠ACB=90°,∠A=30°, ,以点C 为圆心,CB 长为半径作弧,交AB 于点D ;再分别以点B 和点D 为圆心,大于BD 21的长为半径作弧,两弧相交于点E ,作射线CE 交AB 于点F ,则AF 的长为( ) A. 5 B. 6 C. 7 D. 8二、填空题(共8小题,每小题3分,共24分。
2019-2020学年八年级数学上学期期中原创卷A卷(湖南)(考试版)【测试范围:湘教版八上第1~3章】

x 1.若分式 x 3 有意义,则 x 的取值范围是
A.x>3
B.x<3
C.x≠3
D.x=3
2.下列四个实数最小的是
A.-1 3.3 的平方根是
B.- 2
C.0
D.1
A.± 3
4.下列说法不正确的是 A.0 的平方根是 0 C.-1 的立方根是±1
5. (2a2b3c1)2 的结果是
B.9
19.(本小题满分 6 分)(1)计算: 14 16 ( 1 )2 | 3|3 ; 2
(2)已知 2(x1)250,求 x 的值.
20.(本小题满分 6 分)先化简,再求值: ( 2x 3 1) x2 2x 1 ,然后从 0,1,2 三个数中选择一个
x2
x2
C.5 cm,13 cm,12 cm
7.解分式方程
x
1
1
2
3 1
x
,去分母得
A.1 2(x 1) 3
D.2 cm,7 cm,4 cm
B.1 2(x 1) 3
C.1 2x 2 3
D.1 2x 2 3
8.下列命题是假命题的是
A.实数与数轴上的点一一对应 B.如果两个数的绝对值相等,那么这两个数必定也相等
(1)当∠BAD=60°,求∠CDE 的度数;
(2)当点 D 在 BC(点 B、C 除外)边上运动时,求证:∠BAD=2∠CDE.
24.(本小题满分 9 分)如图,在方格纸中,△PQR 的三个顶点及 A,B,C,D,E 五个点都在小方格的 顶点上.现以 A,B,C,D,E 中的三个点为顶点画三角形. (1)在图 1 中画出一个三角形与△PQR 全等; (2)在图 2 中画出一个三角形与△PQR 面积相等但不全等.
2019-2020学年上学期湖南省东安县舜德学校期中考试试卷八年级数学

2019年下期八年级数学期中考试试卷(时间: 120分钟 满分: 150 分)一、选择题(每小题3分,共30分)1. 在2a -,b a ,213a b ,22ab -,3x ,14x +, 2x y p-中,分式共有( ) A .2个 B .3个 C .4个 D .5个2. 下列各组中的三条线段能组成三角形的是( )A .3,4,8B .5,6,11C .5,6,10D .4,4,83. 下列各题中,所求的最简公分母,错误的是( )A .13x 与26a x最简公分母是26x B .2313a b 与2313a b c 最简公分母是233a b c C .1m n +与1m n -最简公分母是22m n - D .()1a x y -与()1b y x -最简公分母是()()ab x y y x -- 4. 如图,将三角尺的直角项点放在直线a 上,//a b ,150??,260??,则3Ð的度数为( )A .50°B .60°C .70°D .80°5. 下列式子:①()2124--=-;②231a a a -?;③22133a a -=;④47.02100.0000702-?其中正确的式子有( )A .1个B .2个C .3个D .4个6. 如图,D 是线段AB ,BC 垂直平分线的交点,若150ABC ??,则ADC Ð的大小是( )A .60°B .70°C .75°D .80°7. 甲、乙两班学生参加植树造林.已知甲班每天比乙班少植2棵树,甲班植60棵树所用天数与乙班植70棵树所用天数相等.若设甲班每天植树x 棵,则根据题意列出方程正确的是( )A .60702x x =+B .60702xx =+ C .60702x x =- D .60702x x =- 8. 如图所示,E 是等边ABC D 中AC 边上的点,1=2行,BE CD =, 则对ADE D 的形状判断最准确的是( )A .等腰三角形B .等边三角形C .不等边三角形D .不能确定形状9. 若21025y =,则10y -等于( )A .15B .1625C .15或15-D .12510. 到ABC D 的三个顶点的距离相等的点是ABC D 的( )A .三条中线的交点B .三条角平分线的交点C .三条高的交点D .三边垂直平分线的交点二、填空题(每小题3分,共24分)11. 分式11x +有意义的条件是__________. 12. 把命题“三个角都相等的三角形是等边三角形”改写成“如果…,那么…”的形式是__________________________________________________.13. 微电子技术的不断进步,使半导体材料的精细加工尺寸大幅度缩小,某种电子元件的面积大约为0.0000007平方毫米,用科学记数法表示为__________平方毫米.14. 如图,已知AB AE =,BAD CAE ??,要使ABC AED D @D ,还需添加一个条件,这个条件可以是 .15. 一个等腰三角形的一条边长为6,一个外角为120°,则这个三角形的周长为 .16. 当a = 时,关于x 的方程2354ax a x +=-的解是1. 17. 如图,AOB Ð是一个钢架,且15AOB ??,为了使钢架更加牢固,需在内部添加一些钢管EF ,FG ,GH ,…, 添加的钢管长度都与OE 相等,则最多能添加这样的钢管______ 根。
2019-2020学年湘教版八年级数学上册期中测试卷(含答案)

2019-2020学年八年级数学上册期中测试题一.单选题(共10题;共30分)1.若分式方程+1=m有增根,则这个增根的值为()A. 1B. 3C. -3D. 3或-32.某商店销售一批服装,每件售价150元,可获利25%,求这种服装的成本价.设这种服装的成本价为x元,则得到方程( )A. B. 150-x=25% C. x=150×25% D. 25%x=1503.若分式的值为0,则x的值是()A. x=3B. x=0C. x=-3D. x=-44.工人师傅砌门时,如图所示,常用木条EF固定矩形木框ABCD,使其不变形,这是利用()A. 两点之间线段最短B. 三角形的稳定性C. 垂线段最短D. 两直线平行,内错角相等5.下列命题正确的是()A. 垂直于半径的直线一定是圆的切线B. 正三角形绕其中心旋转180°后能与原图形重合是必然事件C. 有一组对边平行,一组对角相等的四边形是平行四边形D. 四个角都是直角的四边形是正方形6.如图,已知△ABC中,AC<BC,分别以点A、点B为圆心,大于AB长为半径作弧,两弧交于点D、点E;作直线DE交BC边于点P,连接AP.根据以上作图过程得出下列结论,其中不一定正确的是()A. PA+PC=BCB. PA=PBC. DE⊥ABD. PA=PC7.如图,AB∥DE,AF=DC,若要证明△ABC≌△DEF,还需补充的条件是()A. AC=DFB. AB=DEC. ∠A=∠DD. BC=EF8.如图所示,在△ABC中,AC⊥BC,AE为∠BAC的平分线,DE⊥AB,AB=7cm,AC=3cm,则BD等于()A. 1cmB. 2cmC. 3cmD. 4cm9.如图,在△ABC中,∠C=90°,点E是AC上的点,且∠1=∠2,DE垂直平分AB,垂足是D,如果EC=3cm,则AE等于()A. 3cmB. 4cmC. 6cmD. 9cm10.下列分式中是最简分式的是()A. B. C. D.二.填空题(共8题;共26分)11.若m+n=1,mn=2,则的值为________ .12.关于x的方程=无解,则m的值是________ .13.若关于x的方程=2的解为正数,则m的取值范围是________ .14.如图所示,∠C=∠D=90°,可使用“HL”判定Rt△ABC与Rt△ABD全等,则应添加一个条件是________15.系数化成整数且结果化为最简分式:=________.16.分式,当x=________时分式的值为零.17.如图,△ABC≌△ADE,BC的延长线经过点E,交AD于F,∠ACB=∠AED=105°,∠CAD=10°,∠B=50°,则∠EAB=________°,∠DEF=________°.18.如图,△ABC≌△DEF,A与D,B与E分别是对应顶点,∠B=60°,∠A=68°,AB=13cm,则∠F=________度,DE=________cm.三.解答题(共4题;共24分)19.若0<x<1,且求的值.20.如图1,Rt△ABC中,∠ACB=90°,点D、E在边AB上,且AD=AC,BE=BC,求∠DCE的度数;(2)如图2,在△ABC中,∠ACB=40°,点D、E在直线AB上,且AD=AC,BE=BC,则∠DCE的度数;(3)在△ABC中,∠ACB=n°(0<n<180°),点D、E在直线AB上,且AD=AC,BE=BC,求∠DCE的度数(直接写出答案,用含n的式子表示).21.如图,试求∠A+∠B+∠C+∠D+∠E的度数.22.四边形ABCD中,AD=BC,BE=DF,AE⊥BD,CF⊥BD,垂足分别为E、F.(1)求证:△ADE≌△CBF;(2)若AC与BD相交于点O,求证:AO=CO.四.综合题(共2题;共20分)23.如图,线段AC∥x轴,点B在第四象限,AO平分∠BAC,AB交x轴于G,连OB,OC.(1)判断△AOG的形状,并证明;(2)如图1,若BO=CO且OG平分∠BOC,求证:OA⊥OB;(3)如图2,在(2)的条件下,点M为AO上的一点,且∠ACM=45°,若点B(1,﹣2),求M的坐标.24.在△ABC中,∠C>∠B,AE平分∠BAC.(1)如图(1),AD⊥BC于D,若∠C=75°,∠B=35°,求∠EAD;(2)如图(1),AD⊥BC于D,猜想∠EAD与∠B,∠C有什么数量关系?请说明你的理由;(3)如图(2),F为AE上一点,FD⊥BC于D,这时∠EFD与∠B、∠C又有什么数量关系?________;(不用证明)(4)如图(3),F为AE的延长线上的一点,FD⊥BC于D,这时∠AFD与∠B、∠C又有什么数量关系?________.(不用证明)答案解析一.单选题1.【答案】C【考点】分式方程的增根【解析】【分析】根据分式方程的增根的定义得出x+3=0,求出即可.【解答】∵分式方程+1=m有增根,∴x+3=0,∴x=-3,即-3是分式方程的增根,故选C.【点评】本题考查了对分式方程的增根的定义的理解和运用,能根据题意得出方程x+3=0是解此题的关键,题目比较典型,难度不大2.【答案】A【考点】由实际问题抽象出分式方程【解析】【分析】利润率=利润÷成本=(售价-成本)÷成本.等量关系为:(售价-成本)÷成本=25%.【解答】利润为:150-x,利润率为:(150-x)÷x.所列方程为:=25%.故选A.【点评】本题主要考查的知识点是利润率,利润率是利润占成本的比例.3.【答案】A【考点】分式的值为零的条件【解析】【分析】根据分式的值为零的条件可以求出x的值.【解答】由分式的值为零的条件得x-3=0,x+4≠0,由x-3=0,得x=3,由x+4≠0,得x≠-4.综上,得x=3,分式的值为0.故选:A.【点评】考查了分式的值为零的条件.若分式的值为零,需同时具备两个条件:(1)分子为0;(2)分母不为0.这两个条件缺一不可.4.【答案】B【考点】三角形的稳定性【解析】【解答】如图所示:常用木条EF固定矩形木框ABCD,使其不变形,这是利用三角形的稳定性.故选:B【分析】三角形具有稳定性,其它多边形不具有稳定性,把多边形分割成三角形则多边形的形状就不会改变.5.【答案】C【考点】命题与定理【解析】【解答】解:A、过半径的外端点且垂直于半径的直线一定是圆的切线,所以A选项错误;B、正三角形绕其中心旋转180°后能与原图形重合是不可能事件,所以B选项错误;C、有一组对边平行,一组对角相等的四边形是平行四边形,所以C选项正确;D、四个角都是直角的四边形是矩形,所以D选项错误.故选C.【分析】根据切线的判定定理对A进行判断;根据不可能事件的定义和正三角形的性质对B进行判断;根据平行四边形的判定方法对C进行判断;根据矩形的判定方法对D进行判断.6.【答案】D【考点】作图—基本作图【解析】【解答】解:由作图可得:DE是AB的垂直平分线,∵DE是AB的垂直平分线,∴AP=BP,DE⊥AB,∴AP+CP=BP+CP=BC,故A、B、C选项结论正确;∵P在AB的垂直平分线上,∴AP和PC不一定相等,故D选项结论不一定正确,故选:D.【分析】根据作图过程可得DE是AB的垂直平分线,根据线段垂直平分线的定义和性质可得AP=BP,DE ⊥AB,利用等量代换可证得PA+PC=BC.但是AP和PC不一定相等.7.【答案】B【考点】全等三角形的判定【解析】【解答】解:AB=DE,理由是:∵AB∥DE,∴∠A=∠D,∵AF=DC,∴AF+FC=DC+FC,∴AC=DF,在△ABC和△DEF中∴△ABC≌△DEF(SAS),即选项B正确,选项A、C、D都不能推出△ABC≌△DEF,即选项A、C、D都错误,故选B.【分析】根据平行线的性质得出∠A=∠D,求出AC=DF,根据全等三角形的判定定理逐个判断即可.8.【答案】D【考点】角平分线的性质【解析】【解答】解:∵AC⊥BC,AE为∠BAC的平分线,DE⊥AB,∴CE=DE,在Rt△ACE和Rt△ADE中,,∴Rt△ACE≌Rt△ADE(HL),∴AD=AC,∵AB=7cm,AC=3cm,∴BD=AB﹣AD=AB﹣AC=7﹣3=4cm.故选:D.【分析】根据角平分线上的点到角的两边的距离相等可得CE=DE,再利用“HL”证明Rt△ACE和Rt△ADE全等,根据全等三角形对应边相等可得AD=AC,然后利用BD=AB﹣AD代入数据进行计算即可得解.9.【答案】C【考点】线段垂直平分线的性质,含30度角的直角三角形【解析】【解答】解:∵DE垂直平分AB,∴AE=BE,∴∠2=∠A,∵∠1=∠2,∴∠A=∠1=∠2,∵∠C=90°,∴∠A=∠1=∠2=30°,∵∠1=∠2,ED⊥AB,∠C=90°,∴CE=DE=3cm,在Rt△ADE中,∠ADE=90°,∠A=30°,∴AE=2DE=6cm,故选C.【分析】求出AE=BE,推出∠A=∠1=∠2=30°,求出DE=CE=3cm,根据含30度角的直角三角形性质求出即可.10.【答案】A【考点】最简分式【解析】【解答】解:A、的分子、分母都不能再分解,且不能约分,是最简分式;B、;C、= ;D、;故选A.【分析】最简分式的标准是分子,分母中不含有公因式,不能再约分.判断的方法是把分子、分母分解因式,并且观察有无互为相反数的因式,这样的因式可以通过符号变化化为相同的因式从而进行约分.二.填空题11.【答案】12【考点】分式的加减法【解析】【解答】解:∵m+n=1,mn=2,∴原式=m+nmn=12.故答案为:12【分析】原式通分并利用同分母分式的加法法则计算,将m+n与mn的值代入计算即可求出值.12.【答案】1或0【考点】分式方程的解【解析】【解答】解:去分母得mx=3,∵x=3时,最简公分母x﹣3=0,此时整式方程的解是原方程的增根,∴当x=3时,原方程无解,此时3m=3,解得m=1,当m=0时,整式方程无解∴m的值为1或0时,方程无解.故答案为:1或0.【分析】先把分式方程化为整式方程得到mx=3,由于关于x的分式方程mxx-3=3x-3无解,当x=3时,最简公分母x﹣3=0,将x=3代入方程mx=3,解得m=1,当m=0时,方程也无解.13.【答案】m<6且m≠0【考点】分式方程的解【解析】【解答】解:∵关于x的方程2x-2+x+m2-x=2有解,∴x﹣2≠0,∴x≠2,去分母得:2﹣x﹣m=2(x﹣﹣2),即x=2﹣m3 ,根据题意得:2﹣m3>0且2﹣m3≠2,解得:m<6且m≠0.故答案是:m<6且m≠0.【分析】首先解方程求得方程的解,根据方程的解是正数,即可得到一个关于m的不等式,从而求得m 的范围.14.【答案】AC=AD【考点】直角三角形全等的判定【解析】【解答】解:条件是AC=AD,∵∠C=∠D=90°,在Rt△ABC和Rt△ABD中∴Rt△ABC≌Rt△ABD(HL),故答案为:AC=AD.【分析】此题是一道开放型的题目,答案不唯一,还可以是BC=BD.15.【答案】【考点】分式的基本性质,最简分式【解析】【解答】解:系数化成整数:= .故答案是:.【分析】根据分式的基本性质解答.16.【答案】-3【考点】分式的值为零的条件【解析】【解答】解:由分子x2﹣9=0解得:x=±3.而x=3时,分母x﹣3=3﹣3=0,分式没有意义;x=﹣3时,分母x﹣3=﹣3﹣3=﹣6≠0,所以x=﹣3.故答案为﹣3.【分析】要使分式的值为0,必须分式分子的值为0并且分母的值不为0.17.【答案】60;35【考点】全等三角形的性质【解析】【解答】解:如图,∵∠ACB=105°,∠B=50°,∴∠CAB=180°﹣∠B﹣∠ACB=180°﹣50°﹣105°=25°.又∵△ABC≌△ADE,∴∠EAD=∠CAB=25°.又∵∠EAB=∠EAD+∠CAD+∠CAB,∠CAD=10°,∴∠EAB=25°+10°+25°=60°,即∠EAB=60°.∴∠AEB=180°﹣∠EAB﹣∠B=180°﹣60°﹣50°=70°,∴∠DEF=∠AED﹣∠AEB=105°﹣70°=35°.故答案是:60;35.【分析】由△ACB的内角和定理求得∠CAB=25°;然后由全等三角形的对应角相等得到∠EAD=∠CAB=25°.则结合已知条件易求∠EAB的度数;最后利用△AEB的内角和是180度和图形来求∠EDF的度数.18.【答案】52;13【考点】全等三角形的性质【解析】【解答】解:∵∠B=60°,∠A=68°,∴∠ACB=180°﹣68°﹣60°=52°,∵△ABC≌△DEF,∴∠F=∠ACB=52°,DE=AB=13cm.故答案为:52,13.【分析】根据三角形内角和定理可得∠ACB=180°﹣68°﹣60°=52°,再根据全等三角形的性质可得∠F=∠ACB=52°,DE=AB=13cm.三.解答题19.【答案】解:∵x+1x=6,∴(x﹣1x)2=(x+1x)2﹣4=36﹣4=32,∴x﹣1x=±42,又∵0<x<1,∴x﹣1x=﹣42.故答案为﹣42.【考点】分式的值【解析】【分析】首先由x+1x=6,x•1x=1,运用完全平方公式得出(x﹣1x)2=(x+1x)2﹣4,再结合已知条件0<x<1,即可求出x﹣1x的值.20.【答案】解:(1)∵AD=AC,BC=BE,∴∠ACD=∠ADC,∠BCE=∠BEC,∴∠ACD=(180°﹣∠A)÷2,∠BCE=(180°﹣∠B)÷2,∵∠A+∠B=90°,∴∠ACD+∠BCE=180°﹣(∠A+∠B)÷2=180°﹣45°=135°,∴∠DCE=∠ACD+∠BCE﹣∠ACB=135°﹣90°=45°;(2)∵AD=AC,BC=BE,∴∠ACD=∠ADC,∠BCE=∠BEC,∴∠ACD=(180°﹣∠CAD)÷2,∠BCE=(180°﹣∠CBE)÷2,∵∠CAD+∠CBE=180°﹣∠CAB+180°﹣∠ABC=360°﹣(180°﹣∠ACB)=180°+40°=220°,∴∠ACD+∠BCE=(180°﹣∠CAD)÷2+(180°﹣∠CBE)÷2=180°﹣(∠CAD+∠CBE)÷2=180°﹣220°÷2=70°,∴∠DCE=∠ACD+∠BCE+∠ACB=70°+40°=110°.故答案为110°;(3)分四种情况进行讨论:①点D、E在边AB上,∵AD=AC,BC=BE,∴∠ACD=∠ADC,∠BCE=∠BEC,∴∠ACD=(180°﹣∠A)÷2,∠BCE=(180°﹣∠B)÷2,∵∠A+∠B=180°﹣n°,∴∠ACD+∠BCE=180°﹣(∠A+∠B)÷2=180°﹣90°+n°=90°+n°,∴∠DCE=∠ACD+∠BCE﹣∠ACB=90°+n°﹣n°=90°﹣n°;②点D在BA延长线上,点E在AB延长线上,∵AD=AC,BC=BE,∴∠ACD=∠ADC,∠BCE=∠BEC,∴∠ACD=(180°﹣∠CAD)÷2,∠BCE=(180°﹣∠CBE)÷2,∵∠CAD+∠CBE=180°﹣∠CAB+180°﹣∠ABC=360°﹣(180°﹣∠ACB)=180°+n°,∴∠ACD+∠BCE=(180°﹣∠CAD)÷2+(180°﹣∠CBE)÷2=180°﹣(∠CAD+∠CBE)÷2=180°﹣90°﹣n°=90°﹣n°,∴∠DCE=∠ACD+∠BCE+∠ACB=90°﹣n°+n°=90°+n°;③如图1,点D在边AB上,点E在AB延长线上,∵AD=AC,BC=BE,∴∠ACD=∠ADC,∠BCE=∠BEC,∴∠ACD=(180°﹣∠CAD)÷2,∠BCE=(180°﹣∠CBE)÷2,∵∠CBE=∠CAD+∠ACB=∠CAD+n°,∴∠CAD﹣∠CBE=﹣n°,∴∠DCE=∠DCB+∠BCE=∠ACB﹣∠ACD+∠BCE=n°﹣(180°﹣∠CAD)÷2+(180°﹣∠CBE)÷2=n°+(∠CAD ﹣∠CBE)÷2=n°﹣n°=n°;④如图2,点D在BA延长线上,点E在边AB上,∵AD=AC,BC=BE,∴∠ACD=∠ADC,∠BCE=∠BEC,∴∠ACD=(180°﹣∠CAD)÷2,∠BCE=(180°﹣∠CBE)÷2,∵∠CAD=∠CBE+∠ACB=∠CBE+n°,∴∠CBE﹣∠CAD=﹣n°,∴∠DCE=∠DCA+∠ACE=∠ACD+∠ACB﹣∠BCE=n°+(180°﹣∠CAD)÷2﹣(180°﹣∠CBE)÷2=n°+(∠CBE ﹣∠CAD)÷2=n°﹣n°=n°.【考点】等腰三角形的性质【解析】【分析】(1)由AD=AC,BC=BE,根据等边对等角得出∠ACD=∠ADC,∠BCE=∠BEC,再利用三角形内角和定理得出∠ACD=(180°﹣∠A)÷2,∠BCE=(180°﹣∠B)÷2,而∠A+∠B=90°,那么求出∠ACD+∠BCE=135°,则∠DCE=∠ACD+∠BCE﹣∠ACB=90°;(2)由AD=AC,BC=BE,根据等边对等角得出∠ACD=∠ADC,∠BCE=∠BEC,再利用三角形内角和定理得出∠ACD=(180°﹣∠CAD)÷2,∠BCE=(180°﹣∠CBE)÷2,而∠CAD+∠CBE=220°,那么求出∠ACD+∠BCE=70°,则∠DCE=∠ACD+∠BCE+∠ACB=110°;(3)分四种情况进行讨论:①点D、E在边AB上,同(1)可求出∠DCE=90°﹣n°;②点D在BA延长线上,点E在AB延长线上,同(2)可求出∠DCE=90°+n°;③点D在边AB上,点E在AB延长线上,求出∠DCE=n°;④点D在BA延长线上,点E在边AB上,求出∠DCE=n°.21.【答案】解:连结BC,∵∠E+∠D+∠EFD=∠1+∠2+∠BFC=180°,又∵∠EFD=∠BFC,∴∠E+∠D=∠1+∠2,∴∠A+∠B+∠C+∠D+∠E=∠A+∠ABD+∠ACE+∠1+∠2=∠ABC+∠A+∠ACB=180゜.【考点】三角形内角和定理【解析】【分析】连BC,根据三角形的内角和定理即可证得∠E+∠D=∠1+∠2,然后根据三角形的内角和定理即可求解.22.【答案】证明:(1)∵BE=DF,∴BE﹣EF=DF﹣EF,即BF=DE,∵AE⊥BD,CF⊥BD,∴∠AED=∠CFB=90°,在Rt△ADE与Rt△CBF中,AD=BCDE=BF,∴Rt△ADE≌Rt△CBF;(2)如图,连接AC交BD于O,∵Rt△ADE≌Rt△CBF,∴∠ADE=∠CBF,∴AD∥BC,∴四边形ABCD是平行四边形,∴AO=CO.【考点】全等三角形的判定与性质【解析】【分析】(1)根据已知条件得到BF=DE,由垂直的定义得到∠AED=∠CFB=90°,根据全等三角形的判定定理即可得到结论;(2)如图,连接AC交BD于O,根据全等三角形的性质得到∠ADE=∠CBF,由平行线的判定得到AD∥BC,根据平行四边形的性质即可得到结论.四.综合题23.【答案】(1)解:∵AO平分∠BAC,∴∠CAO=∠BAO,∵线段AC∥x轴,∴∠CAO=∠AOG,∴∠BAO=∠AOG,∴GO=GA,∴△AOG是等腰三角形(2)解:如图1,连接BC,∵BO=CO且OG平分∠BOC,∴BF=CF,∵线段AC∥x轴,∴AG=BG,由(1)得OG=AG,∴OG= AB,∴△AOB是直角三角形,∴OA⊥OB,(3)解:如图2,连接BC,由(2)有,BF=CF,BC⊥OG,∵点B(1,﹣2),∴BF=2,OF=1,在Rt△BFG中,BF=2,BG=FG+1,根据勾股定理得,(FG+1)2=FG2+4,∴FG= ,∵AC∥OG,AG=BG,∴AC=2FG=3,由(2)有,BF=CF,BC⊥OG,∵点B(1,﹣2),∴C(1,2),A(4,2),∴直线OA解析式为y= x①,延长CM交x轴于E,∵∠ACM=45°,∴∠CEO=45°,∴FE=FC=2,∴E(3,0),∵C(1,2),∴直线AE解析式为y=﹣x+3②,联立①②解得x=2,y=1,∴M(2,1).【考点】角平分线的性质,等腰三角形的性质【解析】【分析】(1)由角平分线得出∠CAO=∠BAO,由平行线得出∠CAO=∠AOG,即∠BAO=∠AOG,即可;(2)先判断出点F是BC中点,再用中位线得出AG=BG,从而判断出△AOB是直角三角形,即可;(3)先求出OG,从而求出AC,得出点A,C坐标,最后求出直线OA,CM的解析式,即可求出它们的交点坐标.24.【答案】(1)解:∵∠C=75°,∠B=35°,∴∠BAC=180°﹣∠C﹣∠B=70°,∵AE平分∠BAC,∴∠EAC= ∠BAC=35°,又∵AD⊥BC,∴∠DAC=90°﹣∠C=15°,则∠EAD=∠EAC﹣∠DAC=20°;(2)解:∵AE平分∠BAC,∴∠BAE= ∠BAC,∵∠BAC=180°﹣∠B﹣∠C,∴∠EAC= (180°﹣∠B﹣∠C)=90°﹣∠B﹣∠C,∴∠EAD=∠EAC﹣∠DAC=90°﹣∠B﹣∠C﹣(90°﹣∠C)= (∠C﹣∠B);(3)∠EFD= (∠C﹣∠B)(4)∠AFD= (∠C﹣∠B)【考点】三角形内角和定理,三角形的外角性质【解析】【解答】(3)如图②,过A作AG⊥BC于G,由(2)知,∠EAG= (∠C﹣∠B),∵AG⊥BC,∴∠AGC=90°,∵FD⊥BC,∴∠FDG=90°,∴∠AGC=∠FDG,∴FD∥AG,∴∠EFD=∠EAG,∴∠EFD= (∠C﹣∠B),故答案为:∠EFD= (∠C﹣∠B);⑷如图③,过A作AG⊥BC于G,由(1)知,∠EAG= (∠C﹣∠B),∵AG⊥BC,∠AGB=90°,∵FD⊥BC,∴∠FDC=90°,∴∠AGC=∠FDC,∴FD∥AG,∴∠AFD=∠EAG,∴∠AFD= (∠C﹣∠B),故答案为:∠AFD= (∠C﹣∠B).【分析】(1)由内角和定理得∠BAC=70°,由角平分线性质得∠EAC=35°,再根据直角三角形的性质可得∠DAC=15°,从而由∠EAD=∠EAC﹣∠DAC可得答案;(2)由AE平分∠BAC得∠BAE= ∠BAC,由∠BAC=180°﹣∠B﹣∠C得∠EAC= (180°﹣∠B﹣∠C)=90°﹣∠B﹣∠C,根据∠EAD=∠EAC﹣∠DAC可得答案;(3)AG⊥BC于G,则FD∥AG可得∠EFD=∠EAG,由(2)知∠EAG= (∠C﹣∠B),即可得答案;(4)作AG⊥BC于G,与(3)同理.。
2019-2020学年八年级数学上学期期中考试卷(考试版).doc

2019-2020学年上学期期中原创卷B卷八年级数学(考试时间:100分钟试卷满分:120分)注意事项:1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答第Ⅰ卷时,选出每小题答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
写在本试卷上无效。
3.回答第Ⅱ卷时,将答案写在答题卡上。
写在本试卷上无效。
4.考试结束后,将本试卷和答题卡一并交回。
5.考试范围:人教版第11~13章。
第Ⅰ卷一、选择题(本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一个选项是符合题目要求的)1.下列图案中,属于轴对称图形的是A .B .C .D .2.若一个三角形三个内角度数的比为2∶7∶4,那么这个三角形是A.直角三角形B.锐角三角形C.钝角三角形D.等边三角形3.已知等边三角形的边长为4,则它的高为AB.C.D.4.一个多边形的内角和是外角和的3倍,则这个多边形是A.六边形B.七边形C.八边形D.九边形5.等腰三角形的一个外角等于80°,则与它不相邻的两个内角的度数分别为A.40°,40°B.80°,20°C.50°,50°D.40°,40°或80°,20°6.如图,在△ABC中,∠BAC=56°,∠ABC=74°,BP、CP分别平分∠ABC和∠ACB,则∠BPC= A.102°B.112°C.115°D.118°7.若点A(1,2)关于x轴对称的点是B,点B关于y轴对称的点是C,则点C的坐标是A.(–1,–2)B.(–1,2)C.(1,–2)D.(–2,1)8.下列说法不正确的是A.全等三角形的对应边相等B.两角一边对应相等的两个三角形全等C.三边对应相等的两个三角形全等D.两边一角分别相等的两个三角形全等9.如图,AC⊥BE,∠A=∠E,不能判断△ABC≌△EDC的条件是A.BC=DC B.∠B=∠CDE C.AB=DE D.AC=CE10.如图,已知BD为△ABC的角平分线,EF垂直平分边BC,交BC于点E,交BD于点F,连接CF,若∠A+∠ACF=90°,则∠FCB等于A.30°B.35°C.40°D.45°第Ⅱ卷二、填空题(本大题共5小题,每小题3分,共15分)11.小明从前面的镜子里看到后面墙上挂钟的时间为2:30,则实际时间是__________.12.如图,已知在△ABC中,AD、BE、CF是△ABC的高,三条高线交于点H,则△AHC的三边上的高分别为__________.1213.如图,已知OA =a ,P 是射线ON 上一动点,∠AON =60°,当OP =__________时,△AOP 为等边三角形.14.如图,在△ABC 中,∠C =90°,AM 是∠CAB 的平分线,CM =20cm ,那么M 到AB 的距离为__________.15.已知一个等腰三角形的两条边长分别为3和8,则这个等腰三角形的周长为__________.三、解答题(本大题共8小题,共75分.解答应写出文字说明、证明过程或演算步骤)16.(本小题满分8分)如图,在△ABC 中,BC 的垂直平分线交BC 于点D ,交AB 延长线于点E ,连接CE .求证:∠BCE =∠A +∠ACB .17.(本小题满分9分)如图,A 、B 是两个蓄水池,都在河流a 的同侧,为了方便灌溉作物,要在河边建一个抽水站,将河水送到A 、B 两地,问该站建在河边什么地方,可使所修的渠道最短,试在图中确定该点.(保留作图痕迹)18.(本小题满分9分)如图,小亮从A 点出发,沿直线前进10米后向左转30度,再沿直线前进10米,又向左转30度,……,照这样走下去,他第一次回到出发点A 点时,一共走了多少米?19.(本小题满分9分)在△ABC 中,AD 平分∠BAC ,BD ⊥AD ,垂足为D ,过D 作DE ∥AC ,交AB 于E ,若AB =5,求线段DE 的长.20.(本小题满分9分)如图在平面直角坐标系中,△ABC 各顶点的坐标分别为:A (4,0),B (–1,4),C (–3,1).(1)在图中作△A ′B ′C ′使△A ′B ′C ′和△ABC 关于x 轴对称; (2)写出点A ′,B ′,C ′的坐标; (3)求△ABC 的面积.321.(本小题满分10分)如图,等边△ABC 中,点D 、E 、F 分别同时从点A 、B 、C 出发,以相同的速度在AB 、BC 、CA 上运动,连接DE 、EF 、DF .证明:△DEF 是等边三角形;22.(本小题满分10分)如图,在五边形ABCDE 中,∠BCD =∠EDC =90°,BC =ED ,AC =AD . (1)求证:△ABC ≌△AED ;(2)当∠B =140°时,求∠BAE 的度数.23.(本小题满分11分)如果一个三角形能被一条线段分割成两个等腰三角形,那么称这条线段为这个三角形的特异线,称这个三角形为特异三角形.(1)如图1,△ABC 中,∠B =2∠C ,线段AC 的垂直平分线交AC 于点D ,交BC 于点E .求证:AE 是△ABC 的一条特异线;(2)如图2,若△ABC 是特异三角形,∠A =30°,∠B 为钝角,求出所有可能的∠B 的度数.。
2019--2020学年八年级上学期期中数学考试试题与答案

2019-2020学年第一学期期中测试八年级数学试题2019年10月(本试卷共25小题,4页,满分100分,附加题20分另计。
考试用时120分钟,不得使用....计算器)一、选择题(本题共10题,每小题2分,满分20分,在每小题给出的四个选项中,只有一项是正确的)1.下列选项中的三条线段长能组成三角形的是(*)A.2,2,6B. 1,2,3C. 4,5,6D. 8,3,22.下列选项中的汽车品牌标志图,不.是轴对称图形的是(*)3.如图,在Rt△ABC中,∠B=90°,D是BC延长线上一点,∠ACD=130°,则∠A等于(*)A.40°B. 50°C. 65°D. 90°4.若一个三角形三个内角度数的比为1:2:3,则其内角度数最大的是(*)A.60°B. 90°C. 120°D. 无法判断5.在平面直角坐标系xoy中,点P(2,1)关于y轴对称的点的坐标是(*)A.(﹣2,0)B.(﹣2,1)C.(﹣2,﹣1)D.(2,﹣1)6. 三角形内部一点到三边的距离相等,则该点是(*)A.三条高线的交点B.三条中线的交点C.三条角平分线的交点D.三边垂直平分线的交点7.已知等腰三角形的一边长为4,另一边长为8,则它的周长是(*)A.12 B.16 C.20 D.16或208.如图,把矩形ABCD沿直线EF折叠,若∠1=20°,则∠2=(*)A.80°B.70°C.40°D.20°9.如图,四边形ABCD,∠BDC=108°,若点D在AB、AC的垂直平分线上,则∠B+∠C大小为(*)A.108°B.126°C.120°D.132°10.如图,等腰三角形ABC的底边BC长为4,面积是20,腰AC的垂直平分线EF分别交AC,AB边于E,F点.若点D为BC边的中点,点M为线段EF上一动点,则△CDM周长的最小值为(*)A.12B.8C.10D.14二、填空题(本题有6个小题,每小题2分,共12分)11.一个多边形的每一个外角均为30°,那么这个多边形的边数是__*__.12. 已知点A(a,2)和B(-3,b),点A和点B关于x轴对称,则a+b= _*_.13.如图,△AEB≌△DFC,AE⊥CB,DF⊥BC,垂足分别为E、F,且AE=DF,若∠C=28°,则∠A=___*___.14.如图,△ABC 中,AB=AC,CB=CD,AD=DE=EC,,则∠A=_*___.15.如图,点A,B,C在同一直线上,在这条直线同侧作等边△ABD和等边△BCE,连接AE和CD,交点为M,AE交BD于点P,CD交BE于点Q,连接PQ、BM,有4个结论:①CM平分∠BME②△DQB≌△ABP,③∠EAC=30°,④PQ//AC,请将所有正确结论的序号填在横线上___*__.16.如图∠BAC内部一点P,边AB与AC上动点M、N,∠BAC=36°,当△PMN周长最小时,∠MPN=__*__。
