欧拉稳定推导(2020年整理).pdf
欧拉公式的推导

03
欧拉公式的证明
利用三角函数的性质进行证明
总结词
利用三角函数的周期性和对称性,通 过一系列的等式变换,推导出欧拉公 式。
详细描述
首先,利用三角函数的周期性和对称 性,将角函数转化为指数形式。然 后,通过一系列的等式变换,将指数 形式转化为欧拉公式。
利用复数的性质进行证明
总结词
利用复数的共轭和模的性质,通过代数运算 和等式变换,推导出欧拉公式。
快速傅里叶变换(FFT)
欧拉公式在快速傅里叶变换算法中有重要应用, 该算法用于信号处理和频谱分析等领域。
加密算法的实现
欧拉公式可以用于实现一些加密算法,例如 RSA公钥加密算法。
并行计算中的向量旋转
在并行计算中,欧拉公式可以用于实现向量的旋转操作,提高计算效率。
THANKS
感谢观看
欧拉公式的应用场景
01
在物理学中,欧拉公式被广泛应用于波动方程、电磁学、量子 力学等领域。
02
在工程学中,欧拉公式被用于信号处理、控制系统等领域。
在金融学中,欧拉公式被用于计算复利、评估风险等。
03
02
欧拉公式的推导过程
利用三角函数的性质进行推导
总结词
利用三角函数的周期性和对称性,通过一系列的恒等变换,推导出欧拉公式。
04
欧拉公式的变种和推广
欧拉恒等式
总结词
欧拉恒等式是数学中一个重要的恒等式,它 表示三角函数和指数函数之间的关系。
详细描述
欧拉恒等式是数学中一个重要的恒等式,它 表示三角函数和指数函数之间的关系。这个 恒等式在数学分析、复变函数、微分方程等 领域有着广泛的应用。通过欧拉恒等式,我 们可以将三角函数转化为指数函数,从而简
欧拉公式推到

欧拉公式推到欧拉公式是数学史上最重要的数学公式之一,各种数学研究中都能有所体现,全面地描述出复杂的问题。
欧拉公式有很多不同的推导版本,但最终的结果都是一样的。
欧拉公式的最简单推导方式是极坐标形式,以下是极坐标推导欧拉公式的步骤:1.考虑椭圆:将椭圆的方程用极坐标形式(r,θ)表示,此时椭圆的标准方程可以表示为:r^2=a^2*cos(2θ)其中a是椭圆的长轴,θ为极坐标角。
2.算椭圆面积:椭圆的面积可以用定积分的方式求解,可以得到: A=πa^23.欧拉公式计算椭圆面积:根据欧拉公式,椭圆的面积可以表示为:A=∫r^2dθ4.椭圆方程代入:将上面求得的椭圆方程代入上面欧拉公式中,可以得到:A=∫a^2*cos(2θ) dθ5.积分:将上面求得的积分,通过积分变换和分部积分,最终可以得到:A=πa^26.比两种求解方式:将上面积分推导求得的椭圆面积A,与定积分求得的椭圆面积A进行比较,可以发现两者相等,即:A=πa^2由此可以证明欧拉公式的正确性。
在实际的数学应用中,欧拉公式可以用来求解很多复杂的问题,从而辅助解决实际的应用问题。
例如,欧拉公式可以用来求解椭圆的周长,确定多边形的面积,求解曲线的长度,以及解决积分变换的问题等。
定积分也是数学研究中一个非常重要的概念,其可以用来求解面积、体积等,运用定积分也可以得出欧拉公式,下面是定积分求解欧拉公式的步骤:1.虑椭圆:将椭圆的方程用定积分形式表示,此时椭圆的标准方程可以表示为:x^2+y^2=a^2其中a是椭圆的长轴。
2.算椭圆面积:椭圆的面积可以用定积分的方式求解,可以得到: A=∫∫1/2adxdy3.欧拉公式计算椭圆面积:根据欧拉公式,椭圆的面积可以表示为:A=∫r^2dθ4.椭圆方程代入:将上面求得的椭圆方程代入上面欧拉公式中,可以得到:A=∫a^2*cos(2θ) dθ5.积分:将上面求得的积分,通过积分变换和分部积分,最终可以得到:A=πa^26.比两种求解方式:将上面积分推导求得的椭圆面积A,与定积分求得的椭圆面积A进行比较,可以发现两者相等,即:A=πa^2由此可以证明欧拉公式的正确性。
欧拉恒等式推导全过程

欧拉恒等式推导全过程欧拉恒等式是数学中的一个重要公式,它建立了三角函数与复数指数函数之间的关系。
这个恒等式由欧拉在18世纪提出,是复数和三角函数理论中的基石之一。
欧拉恒等式的形式为:e^(iθ) = cos(θ) + i*sin(θ)其中,e 是自然对数的底数,i 是虚数单位,θ是任意实数。
为了推导欧拉恒等式,我们可以从泰勒级数展开开始。
首先,我们知道 e^x 的泰勒级数为:e^x = 1 + x/1! + x^2/2! + x^3/3! + ...对于 e^(iθ),我们可以将 x 替换为 iθ,得到:e^(iθ) = 1 + (iθ)/1! + (iθ)^2/2! + (iθ)^3/3! + ...接下来,我们分别计算每一项的值。
第一项是 1,第二项是 iθ,第三项是 (iθ)^2 = -θ^2(因为 i^2 = -1),第四项是 (iθ)^3 = -iθ^3(因为 i^3 = -i),以此类推。
将这些项重新组合,我们得到:e^(iθ) = 1 - θ^2/2! + θ^4/4! - ... + i(θ - θ^3/3! + θ^5/5! - ...)观察上面的表达式,我们可以发现实部和虚部分别是 cos(θ) 和 sin(θ) 的泰勒级数展开。
这是因为 cos(θ) 和 sin(θ) 的泰勒级数分别是:cos(θ) = 1 - θ^2/2! + θ^4/4! - ...sin(θ) = θ - θ^3/3! + θ^5/5! - ...因此,我们可以得出结论:e^(iθ) = cos(θ) + i*sin(θ)这就是欧拉恒等式的完整推导过程。
它建立了三角函数和复数指数函数之间的联系,为复数和三角函数的理论和应用提供了强大的工具。
欧拉公式推导
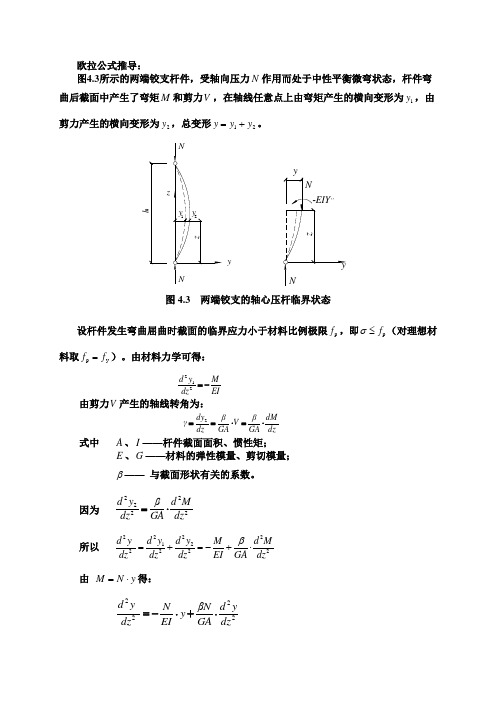
欧拉公式推导:图4.3所示的两端铰支杆件,受轴向压力N 作用而处于中性平衡微弯状态,杆件弯曲后截面中产生了弯矩M 和剪力V ,在轴线任意点上由弯矩产生的横向变形为1y ,由剪力产生的横向变形为2y ,总变形21y y y +=。
y图4.3 两端铰支的轴心压杆临界状态设杆件发生弯曲屈曲时截面的临界应力小于材料比例极限p f ,即p f ≤σ(对理想材料取y p f f =)。
由材料力学可得:EI M dz y d -=212 由剪力V 产生的轴线转角为:dz dM GA V GA dzdy ⋅=⋅==ββγ2 式中 A 、I ——杆件截面面积、惯性矩;E 、G ——材料的弹性模量、剪切模量; β—— 与截面形状有关的系数。
因为 22222dz M d GA dz y d ⋅=β 所以 2222122222d y d y d y M d M dz dz dz EI GA dzβ=+=-+⋅ 由 y N M ⋅=得:2222dzy d GA N y EI N dz yd ⋅+⋅-=β01=⋅+⎪⎭⎫ ⎝⎛-''y EIN GA N y β 令 ⎪⎭⎫ ⎝⎛-=GA N EI Nk β12得常系数线性二阶齐次方程 20y k y ''+=其通解为:sin cos y A kz B kz =+由边界条件:;0,0==y z 0=B ,kz A y sin =。
再由0,==y l z 得:0sin =kl A上式成立的条件是0=A 或0sin =kl ,其中0=A 表示杆件不出现任何变形,与杆件微弯的假设不符。
由0sin =kl ,得πn kl =(=n 1,2,3…),取最小值=n 1,得π=kl ,即2221N k N l EI GA πβ==⎛⎫- ⎪⎝⎭由此式解出N ,即为中性平衡的临界力cr N12222222211Ι11γππβππ⋅+⋅=⋅+⋅=lΕΙl ΕGA l ΕΙl ΕΙN cr (4.6) 临界状态时杆件截面的平均应力称为临界应力cr σ1222211γλπλπσ⋅+⋅==ΕΑΕA N cr cr (4.7)式中 1γ——单位剪力时杆件的轴线转角,)/(1GA βγ=;l ——两端铰支杆得长度;λ——杆件的长细比,i l /=λ;i ——杆件截面对应于屈曲轴的回转半径,A I i /=。
欧拉静平稳方程

欧拉静平稳方程为了进一步研究流体静平稳规律和流体内部静压强散布规律,咱们先运用牛顿第二定律成立流体静平稳方程.图 2-3从静止流体中取一微小六面体,其表面与坐标平面平行,边长别离为dx dy dz 、、(参见图2—3).从上一节的讨论中明白,作用在流体上的力有质量力和表面力. 关于所取的微元体,作用在其上的质量力为s dF R dxdydz ρ=,其中dxdydZ ρ是微元体的质量.在静止流体中,不存在切向力,表面力中仅有压力. 由于流体中遍地的压强不同,即压强是空间坐标的函数,(,,)p p x y z =. 因此作用在微元体各个面上的压力不同,其合力可由六个面上的压力按向量相加而得.设微元体中心C 点(,,)x y z 的压强为p ,那么微元体六个面上的压强可用泰勒级数将压强在C 点展开而得,例如,微元体左面的压强为 ()2L L x P dy p p y y p y y ∂∂=+-=-∂∂ 展开时略去了二阶以上微量,因为取极限时,这些项将趋于零. 一样,微元体右面的压强为 ()2R R p p dyp p y y p y y ∂∂=+-=+∂∂ 图2—3 上表示了y 方向两个面上的压力作用. 每一个力是三项的乘积,第一项为哪一项压强的大小,第二项是表面积,第三项是单位坐标向量,图上也说明了每一个力都指向作用面. 用一样方式能够写出其它面上的作使劲. 这些表面力的合力为 ()()()()()()22s p dx p dxd F p dxdy i p dydz i x x ∂∂=-++-∂∂ ()()()()()()22p dy p yp dzdx j p dzdx j y y ∂∂∂+-++-∂∂ ()()()()()()22p dz p dzp dxdy k p dxdy k z z ∂∂+-++-∂∂ 化简后为()S p p pdF i j k dxdydz x y z∂∂∂=-++∂∂∂ (a )括号中的项称为压强梯度,并写作gradp 或p ∇. 在直角坐标系中()()p p p gradp p ij k i j k p x y z x y z∂∂∂∂∂∂≡∇≡++≡++∂∂∂∂∂∂ (2—4) 梯度grad 或∇可看做是一个向量运算符:对标量取梯度后取得向量.采纳梯度符号后,式(a )可写成()S dF p dxdydz =-∇从而 SdF p dxdydz∇=-上式说明,压强梯度是单位体积流体所受表面力的负值.组合表面力和质量力,能够取得作用在微元体上的总作使劲为()B S dF dF dF pR p dxdydz =+=-∇在静止流体中,流体加速度为零. 于是,依照牛顿第二定律,作用在微元体上的作使劲应平稳,即0dF =于是取得 0pR p -∇= (2—5)从式(2—5)的导出进程能够看出其中各项的物理意义,第一项为哪一项单位体积流体所受的质量力,第二项是单位体积流体所受的表面力.将式(2—5)投影到各坐标轴,可得三个标量方程000p pX x ppY y p pZ z∂-=∂∂-=∂∂-=∂ (2—6) 式(2—5)和式(2—6)是由欧拉在1775年第一导出的,因此通常称它为欧拉静平稳方程. 它表示了流体在质量力和表面力作用下的平稳条件.将微分方程组(2—6)中各式别离乘以,dx dy 和dz 后相加,那么得()p p p p Xdx Ydy Zdz dx dy dz x y z∂∂∂++=++∂∂∂ 上式右边是压力函数p 的全微分dp ,因此上式又可写成()dp p Xdx Ydy Zdz =++ (2—7)若是所讨论的流体是不可紧缩的,那么因式(2—7)左侧是全微分,那么右边也应是某个函数的全微分,令此函数为(,,)U x y z ,于是有()U U U dp pdU p dx dy dz x y z∂∂∂==++∂∂∂ (2—8) 比较式(2—7)和式(2—8),能够看出,,U U U X Y Z x y z∂∂∂===∂∂∂ (2—9) 和 dU Xdx Ydy Zdz =++式(2—9)说明了函数U 与质量力之间的关系.为了弄清U 函数的物理意义,咱们做如下分析. 在流体中取一点A ,假设将该点流体移动dl 距离(参见图2—4),dl 在座标方向的分量别离为,dx dy 和dz ,那么质量力对单位质量流体所作的功为R dl Xdx Ydy Zdz =++那个值恰好等于U 函数的增量. 另一方面,它也是单位质量 图 2-4流体的势能(位能)的转变量. 因此,函数(,,)U x y z 反映了单位质量流体的势能. 因此称U 为势函数或力函数. 而且得出如下结论:质量力有势是不可压流体静止的必要条件.运动微分方程粘性流体运动微分方程的推导方式和理想流体的欧拉方程推导方式相同,仅在作使劲中显现切向表面力。
流体力学_纳维尔斯托克斯_欧拉方程的推导

一、流体力学基本公式公式的含义:质量守恒、动量守恒、能量守恒()0D V Dtρδ=(0.1)()D VUV f Dtρδδρδτ=+(0.2)()()()2/2D V e U V f U U V q Dtρδδρδτδρ+=⋅+⋅+(0.3)将(0.1)式应用于(0.2)、(0.3)两式可得()()()()()()()()()2222/2/2/2/2 D VU D V DU DU U V V V f Dt Dt Dt Dt D V e U D e U D V e U V Dt Dt Dt D e U V V f U U V q Dt V f ρδρδρδρδδρδτρδρδρδρδδρδτδρδρ=+==+++=+++==⋅+⋅+=+ ()U U V q δττδδρ⎧⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⋅+⋅+⎩即DU f Dt V δτδρ=+()2/2D e U U f U q DtV V δττδδρδρ+⎛⎫⋅=+⋅++ ⎪⎝⎭而(0.1)式本身作如下简化:()()()()00D V D D V V DtDt DtD V D D U Dt VDt Dt ρδρδδρδρρρρδ=+=+=+∇⋅=那么三个控制方程可以表示为()20/2D U DtDUf Dt V D e U U f U q Dt V V ρρδτδρδττδδρδρ⎧⎪+∇⋅=⎪⎪⎪=+⎨⎪⎪+⎛⎫⋅⎪=+⋅++ ⎪⎪⎝⎭⎩(0.4)将()()()D U Dtt∂=+⋅∇∂ 应用于(0.4)式,可以得到()0U t ρρ∂+∇⋅=∂ (0.5)U U U f t V δτδρ∂+⋅∇=+∂(0.6)()()22/2/2e U U U e U f U q t V V δττδδρδρ∂+⎛⎫⋅+⋅∇+=+⋅++ ⎪∂⎝⎭(0.7)将(0.6)式代入(0.7)式化简,可得()()()()2222/2/2/2/2e U U e U t U e U e U U t t U U U U U qt V ρρρτδρδρ⎛⎫∂+ ⎪+⋅∇+ ⎪∂⎝⎭⎛⎫∂∂⎛⎫ ⎪=+⋅∇++⋅∇ ⎪ ⎪∂∂⎝⎭⎝⎭⎛⎫∂⋅=+⋅∇⋅++ ⎪∂⎝⎭其中,()()()()()2/2/21122i i i i i i i i U U U U U U U U U U U ttt t t t∂⎛⎫∂∂∂∂∂==+==⋅ ⎪∂∂∂∂∂∂⎝⎭()()21/22j j j i i j i iU U U U U U U U U U U x x ∂∂⋅∇===⋅∇⋅∂∂所以e U U e q t V τδδρ∂⋅+⋅∇=+∂(0.8)于是,三个控制方程化简为()0U t U U U f t V e U U e qtV ρρδτδρτδδρ⎧∂+∇⋅=⎪∂⎪⎪∂⎪+⋅∇=+⎨∂⎪⎪∂⋅⎪+⋅∇=+∂⎪⎩(0.9)其中,τ为剪应力对微元体的力,故()1,2,31,2,31,2,31,2,31111ij i i j k ij i i i i j ki j j ij j k ij i ij i i j k i j T dx e dx dx T x e TV dx dx dx x U T dx dx dx U x U T T U V dx dx dx x δτδρρρρτδδρρρρ====∂⎧⎪∂∂⎪===∇⋅∂⎪⎪⎨∂⎪⎪∂∂⋅===⋅∇⋅⎪∂⎪⎩∑∑ 所以,三个控制方程最终可以写为()()011U t U U U f T t e U e T U qtρρρρ⎧∂+∇⋅=⎪∂⎪⎪∂+⋅∇=+∇⋅⎨∂⎪⎪∂+⋅∇=⋅∇⋅+⎪∂⎩(0.10)其中,T 为微元体受到的表面应力()22j ki ij kk ij ij ij k j i u u u T p S S p x xx λδμμδμ⎛⎫∂⎛⎫∂∂=-++=--++ ⎪ ⎪ ⎪∂∂∂⎝⎭⎝⎭即()()2T p U I U U μμ=--∇⋅+∇+∇(0.11)将(0.11)代入(0.10)式可以得到()()()()()()2323011U t U U U f p U U U te U e p U I U U U q tρρμμρμμρ⎧∂+∇⋅=⎪∂⎪⎪∂⎡⎤+⋅∇=+∇--∇⋅+∇⋅∇+∇⎨⎣⎦∂⎪⎪∂⎡⎤+⋅∇=--∇⋅+∇+∇⋅∇⋅+⎪⎣⎦∂⎩(0.12)将(0.12)式写为张量形式()2222323011i i j j ii i j i j i i j j i j j j j j i i j i j i i U t x U U U U U p U f t x x x x x x x x U U U U U e U e p q t x x x x x ρρμμρμμρ⎧∂∂⎪+=⎪∂∂⎪⎡⎤⎛⎫⎛⎫⎪∂∂∂∂∂∂⎪+=+--++⎢⎥ ⎪ ⎪⎨ ⎪ ⎪∂∂∂∂∂∂∂∂∂⎢⎥⎪⎝⎭⎝⎭⎣⎦⎪⎡⎤⎛⎫⎛⎫∂∂∂∂∂∂⎪+⋅∇=--+++⎢⎥ ⎪ ⎪⎪ ⎪ ⎪∂∂∂∂∂∂⎢⎥⎝⎭⎝⎭⎪⎣⎦⎩(0.13) 再将(0.13)式写为分量形式,得()()()222222222220 113 113x y u v w t x y z u u u u u v w tx y z p u v w u u u f x x x y z xy z v v v v u v w t x y z p u v w v v f y y x y z x y ρρρρμμρμμρ∂∂∂∂+++=∂∂∂∂∂∂∂∂+++∂∂∂∂⎡⎤⎛⎫⎛⎫∂∂∂∂∂∂∂∂=+-++++++⎢⎥⎪ ⎪∂∂∂∂∂∂∂∂⎝⎭⎝⎭⎣⎦∂∂∂∂+++∂∂∂∂⎛⎫∂∂∂∂∂∂∂∂=+-++++++ ⎪∂∂∂∂∂∂∂⎝⎭222222223113 2z v z w w w wu v w tx y z p u v w w w w f z z x y z x y z e e e e u v w t x y z p u v w u v w x y z x y z u μμρνρν⎡⎤⎛⎫⎢⎥⎪∂⎝⎭⎣⎦∂∂∂∂+++∂∂∂∂⎡⎤⎛⎫⎛⎫∂∂∂∂∂∂∂∂=+-++++++⎢⎥⎪ ⎪∂∂∂∂∂∂∂∂⎝⎭⎝⎭⎣⎦∂∂∂∂+++∂∂∂∂⎛⎫⎛⎫⎛⎫∂∂∂∂∂∂=--++++ ⎪ ⎪ ⎪∂∂∂∂∂∂⎝⎭⎝⎭⎝⎭∂+∂222222+v w u v u w v w q x y z y x z x z y ⎧⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫∂∂∂∂∂∂∂∂⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪++++++++ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎪ ⎪ ⎪∂∂∂∂∂∂∂∂⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎪⎝⎭⎩(0.14)当流体不可压缩时,ρ为常数,(0.14)式可以化简为22222222222222220111x y z u v w x y z u u u u pu u u u v wf t x y z x x y z v v v v p v v v u v w f t x y z y x y z w w w w pw w uv w f t x y z z x y μρμρμρ∂∂∂++=∂∂∂⎡⎤⎛⎫∂∂∂∂∂∂∂∂+++=+-+++⎢⎥ ⎪∂∂∂∂∂∂∂∂⎝⎭⎣⎦⎡⎤⎛⎫∂∂∂∂∂∂∂∂+++=+-+++⎢⎥ ⎪∂∂∂∂∂∂∂∂⎝⎭⎣⎦∂∂∂∂∂∂∂∂+++=+-+++∂∂∂∂∂∂∂22w z ⎧⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎡⎤⎛⎫⎪⎢⎥ ⎪∂⎝⎭⎪⎣⎦⎩(0.15)此时方程已经封闭,最后一个方程不需要再给出。
欧拉定理证明

欧拉定理证明第1篇:证明欧拉定理证明:(1)令Zn = {x1, x2,..., xφ(n)},S = {a * x1 mod n, a * x2 mod n,..., a * xφ(n)mod n},则 Zn = S。
#① 因为 a 与 n 互质,xi(1 ≤ i ≤ φ(n))与 n 互质,所以 a * xi 与n 互质,所以a * xi mod n ∈ Zn。
#② 若i ≠ j,那么xi ≠ xj,且由 a, n互质可得a * xi mod n ≠ a * xj mod n(消去律)。
(2)aφ(n)* x1 * x2 *...* xφ(n)mod n≡(a * x1)*(a * x2)*...*(a * xφ(n))mod n ≡(a * x1 mod n)*(a * x2 mod n)*...*(a * xφ(n)mod n)mod n ≡ x1 * x2 *...* xφ(n)mod n 对比等式的左右两端,因为xi(1 ≤ i ≤ φ(n))与 n 互质,所以aφ(n)≡ 1 mod n(消去律)。
欧拉函数是数论中很重要的一个函数,欧拉函数是指:对于一个正整数 n,小于 n 且和 n 互质的正整数(包括 1)的个数,记作φ(n)。
完全余数集合:定义小于 n 且和 n 互质的数构成的集合为 Zn,称呼这个集合为 n 的完全余数集合。
显然 |Zn| =φ(n)。
有关性质:对于素数 p,φ(p)= p-1。
对于两个不同素数 p,q,它们的乘积 n = p * q 满足φ(n)=(p-1)*(q-1)。
这是因为Zn = {1, 2, 3,..., n{p, 2p,...,(q{q, 2q,...,(p1)1)1)=(p-1)*(q-1)=φ(p)* φ(q)。
消去律:如果 gcd(c,p)= 1,则ac ≡ bc mod p ⇒ a ≡ b mod p 第2篇:欧拉定理欧拉定理欧拉定理认识欧拉欧拉,瑞士数学家,13岁进巴塞尔大学读书,得到著名数学家贝努利的精心指导.欧拉是科学史上最多产的一位杰出的数学家,他从19岁开始发表论文,直到76岁,他那不倦的一生,共写下了886本书籍和论文,其中在世时发表了700多篇论文。
欧拉公式——数理之美

欧拉公式——数理之美欧拉公式是数学中的一个重要结果,也被称为数理之美的典范之一。
它以独特而简洁的形式展现了数学中的几个重要常数和基本运算之间的关系。
下面将按照列表的方式详细介绍欧拉公式。
1. 定义与主要形式欧拉公式最常见的形式为e^ix = cos(x) + isin(x),这里e表示自然对数的底数,i是虚数单位,x是任意实数。
这个形式是欧拉公式的特殊情况,其中的三个基本数学常数e、i和π(圆周率)都被纳入其中。
2. 证明与推导欧拉公式的证明可以通过泰勒级数展开得到。
泰勒级数是一种将函数展开成无穷项幂级数的方法。
通过对指数函数exp(x)进行泰勒级数展开,结合三角函数的泰勒级数展开,可以得到欧拉公式的形式。
3. 欧拉公式的几何解释欧拉公式可以通过欧拉公式定义的复数表示在复平面上呈现出的运动,具有非常美妙的几何解释。
复数e^ix在复平面上的实部和虚部分别对应于x轴上的余弦函数值和y轴上的正弦函数值,这样欧拉公式就将三角函数与指数函数联系在了一起。
4. 欧拉公式在物理学中的应用欧拉公式在物理学中有广泛的应用。
例如,在量子力学中,欧拉公式与薛定谔方程的解之间存在关联,使得它成为描述微观粒子行为的基本工具之一。
此外,在电工学和信号处理中,欧拉公式也被广泛地应用于交流电路的分析和信号的频域处理中。
5. 欧拉公式的数学意义欧拉公式从数学的角度深刻地揭示了三角函数、指数函数和复数之间的内在联系。
它将看似无关的数学概念统一起来,形成一个简洁而完整的表达式,揭示了数学中的一种美妙的对称性和秩序。
总结:欧拉公式是数学中的一个重要结果,它以独特而简洁的形式展现了数学中的几个重要常数和基本运算之间的关系。
它的几何解释和在物理学中的应用给了它更加丰富的含义。
欧拉公式的发现和证明不仅是数学的壮举,更是反映了数学中的那种美丽与优雅。
通过欧拉公式,我们可以看到数学世界的统一和内在的连接,这是数理之美的一个鲜明例证。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
力作用时最大挠度放大系数。 将 tgu 展成幂级数
tgu=u +u3 3+2u5 15+17u 7 315 +
将 u = kl 2 = 2
P PE
可改写为
代入,则式( 3. 9 )
图 3.5 跨中集中荷载作用的压弯构件
ymax
=
y0
1 + 0.987(P
PE ) + 0.986(P
) PE 2
对理想的两端简支的双轴对称工形截面压弯构件,在两端作用有轴线压力 P 和使构件 产生同向曲率变形的弯矩 M,如果在其侧向有足够的支撑 (如图 3.1(b)),构件将发生平 面内的弯曲失稳,其荷载―挠度曲线如图 3.2(a)中曲线 a,失稳的极限荷载为 Pu,属于极 值点失稳。
图 3.1 两端简支理想压弯构件
上式是恒等式,故 c1=q∕(2P) ,c2= -ql ∕(2P) ,c3= -EIq∕P2
方程( 3. 1 )对应的齐次线性方程 y″+k2y =0 的通解可写作 y =Asin kχ+Bcos kχ,则
方程( 3. 1 ) 的通解为 y= Asin kχ+Bcos kχ+ qχ2∕(2P)-q l χ∕(2P)-EIq/ P2
下面仅讨论两端铰接受轴向压力和平面内横向荷载共同作用的弹性压弯构件的内力与 变形性能。
学海无涯
1. 横向均布荷载作用的压弯构件 图 3.4(a)所示为在均布荷载 q 作用下两端铰接的压弯构件。假定材料完全弹性,取图 3.
4(c)所示隔离体,在距左端 x 处截面的内力矩 M f = −EIy ,外力矩 M e = Py + qx (l − x) 2 ,平
弯曲失稳一般在弹塑性阶段出现,而弯扭失稳可能发生在弹性阶段,也可能出现在弹塑 性阶段。
3. 1 压弯构件平面内失稳
对压弯构件,当弯矩作用平面外有足够多支撑可以避免发生弯扭失稳时,若失稳则只可 能发生平面内弯曲失稳。
学海无涯
当用弹性理论分析理想压弯构件的荷载挠度关系,可以得到图 3. 3 中的二阶弹性曲线 b, 它以轴心受压弯构件的分岔点荷载 PE 处引出的水平线 a 为渐近线。
实际压弯构件存在初始缺陷(残余应力﹑几何缺陷),材料为弹塑性体。如按弹塑性理论 分析,荷载挠度曲线将是图中曲线 OABC。曲线上 A 点标志着杆件中点截面边缘开始屈服, 对应的荷载为 Pe,随后塑性向截面内部发展,构件变形快速增加,形成 OAB 上升段,构件 处于稳定平衡状态;B 点为曲线的极值点,对应的荷载 Pu 为构件在弯矩作用平面内失稳的 极限荷载;到达 B 点以后,由于弹性区缩小到导致构件抵抗力矩的增加小于外力矩的增加程 度,出现下降段 BC,构件处于不稳定平衡状态。由失稳全过程可以看出实际压弯构件在弯 矩作用平面内的弯曲失稳属于二阶弹塑性分析的极值点失稳,不能用弹性理论和平衡微分方 程求解极限荷载 Pu,而可用数值积分法通过得出荷载挠度曲线后求得极限荷载。
图 3.6 压弯构件弯曲失稳的塑性区分布
压弯构件的极限荷载求解比较困难,一般情况下可用数值积分法得到数值解,但如果截 面形状比较简单,不考虑初弯曲和较复杂的残余应力分布影响时,经简化后也可用解析法得 到近似解。
学海无涯
表 3.1 等效弯矩系数 m 值
1. 解析法 对于轴压力 P 和两端相同弯矩 M 共同作用的两端简支压弯构件(图 3.7),用 Jezek 解 析法[18]求解可以求出精确度比较高的极限荷载。其假设为: (1) 材料为理想的弹塑性体; (2) 构件的变形曲线为正弦曲线的一个半波。 图 3.7a 是矩形截面的压弯构件,在轴力 P 和端弯矩 M 共同作用下,平面内弹塑性弯曲 失稳时构件截面的塑性有两种类型:只出现在受压区,如图 3.7b 阴影部分所示,截面弹性
P PE
则式( 3. 4 )可写成
ymax
=
y0
1 + 1.034(P
PE )+1.0038(P
) PE 2
+
y0
1 1− P
PE
=
(3.5)
式中 Am =1/(1− P / PE )是最大挠度的放大系数。
构件中点的最大弯矩为
M max =ql2
8
+
Pymax
=
M
0
1+
1.028 P PE 1− P PE
EIy + Py = −Qx 2
学海无涯
令 k 2 = P (EI) ,则
通解为
y + k 2 y = −Qx (2EI )
y = Asin kx + Bcoskx − Qx (2P)
引入边界条件 y(0)=0 , y(l 2)= 0, 得 B = 0, A = Q sec (kl 2), 则通解
由应变图知曲率
(3.19) (3.20)
学海无涯
( ) = y + t = y + t = 2 Py − P
he
Ehe
Ebhe2
根据变形曲线假定,挠曲线为
(3.21)
y = sin (x l)
(3.22)
中央截面处的曲率为
= −y(l 2) = v 2 / l 2
(3.23)
由式(3.21)式( 3. 22 )知
ymax
=
ql 4 16 EIu 4
1− cosu cosu
−
ql 4 32 EIu 2
=
(3.4)
式中: y0 =5ql4 (384EI )
支梁的最大挠度,即当 得的最大挠度。式( 3. 4 ) 轴线压力后最大挠度的放
12(2 sec u − u 2 − 2)
y0
5u 4
是均布荷载作用下简
= mM 1 − P PE
= Am M 0
Am y0 (3.6)
式中 M 0 = ql2 8 是均布荷载作用下简支梁跨中的最大弯矩; m 为等效弯矩系数; Am 为弯矩 放大系数,用以考虑轴压力 P 产生的二阶效应。
2. 横向集中荷载作用的压弯构件 由图 3.5(c)知,当 0< x l 2 时,平衡方程为
区高度为 he ,细长构件常属此类;另一类为受压、受拉区均出现塑性区,图 3.7e 所示,短
粗构件常属此类。 下面分别加以讨论: 1)第一种情况:塑性区仅出现在受压区(图 3.7b) 图 3.7c﹑图 3.7d 分别为第 1 种情况截面的应变和应力图。由应力图可以分别得出轴线
方向力和力矩的平衡方程:
图 3.2 压弯构件荷载变形曲线
如果在侧向没有设置支撑(如图 3.1(c)),则构件在荷载 P 未达到平面内极限荷载 Pu
时,可能发生弯扭失稳,即在弯矩作用平面内产生挠度 v,在平面外剪心产生位移u,并绕 纵轴产生扭转角 (如图 3.1(d)),其荷载-变形曲线如图 3.2(b)中曲线 b,属于分支 点失稳,失稳的分荷载为 Pyw, ,且 Pyw <Pu。
衡方程为
EIy + Py = qx(l − x) 2
令 k 2 = P EI ,则
y + k 2 y = qx(x − l)
2EI 方程 (3. 1)的特解可写作 y = c1 x 2 + c2 x + c3 ,代入方程( 3. 1 ) ,有
(3.1)
(Pc1 − q 2)x2 + (Pc2 + ql 2)x + Pc3 + 2EIc1 = 0
学海无涯
( ) ( ) P
= y A −
1 2
y
+t
bhe
或
y
+t
=
2
Py − bhe
P
(3.18)
图 3.7 矩形截面压弯构件中央截面的应变和应力
( ) M
+
Pv =
1 2
y
+t
bhe
h 2
−
he 3
由上式可解出弹性区高度
3h 3(M + P )
he = 2 − Py − P
式中, Py = A y ,表示轴心受压时全截面屈服压力。
P0 A
+
P0 0
(1 − P0 PE )W
=
fy
(3.15)
因为 P0 = Af y ( 为轴心压杆稳定系数),则由式( 3. 15 )得
0
=
1
− 11 −
Af y PE
W A
将式( 3. 16 )代入( 3. 14 ),整理得由边缘纤维屈服导出的相关公式
P A
+
W
(1
−
mM P
PE ) =
2Pk
y = Q sec kl sec kx − kx
2Pk 2
(3.7) (3.8)
令 u = kl 2, 当 x = l 2 时,跨中最大挠度为
ym a x
=
Ql 4Pu
(tgu
−
u)
=
Ql 3 48EI
3 u3
(tgu
−
u)
=
y0
3(tgu −
u3
u)
(3.9)
式中 y0 = Ql 3 (48EI )是集中荷载 Q 作用在跨中时简支梁的最大挠度,3(tgu − u) u3 是有轴压
式中 M 0 = Ql 4 是集中荷载作用下简支梁最大弯矩; m 为等效弯矩系数;弯矩放大系数
Am
1− 0.2 P PE 1− P PE
。
对于弹性压弯构件,根据各种荷载作用和支撑情况,可以计算出跨中弯矩 Mmax的表达 通式
M
max
=
1
−
mM P PE
(3.12)
再考虑初始缺陷的影响,假定各种缺陷的等效初弯曲呈跨中挠度为 0 的正弦曲线,则在任
