5_5 定积分在几何学上的应用
定积分在几何和物理中的应用

定积分在几何和物理中的应用定积分是高等数学中非常重要的一个概念,它可以用于计算曲线、曲面的面积或体积,还可以应用到物理学、工程学中。
在本文中,我们将着重探讨定积分在几何和物理中的应用。
一、计算面积我们首先来看一个简单的例子,如果我们想要计算一个曲线所围成的面积,我们需要怎么做呢?假设曲线为y=f(x),我们可以将这条曲线分成若干个无限小的小矩形,每个小矩形的宽度为Δx,高度为函数值f(x),则该小矩形的面积为f(x)Δx。
我们将所有小矩形的面积相加,得到所求的曲线面积S:S=∫a^b f(x) dx其中a和b分别是曲线的起点和终点。
这里的∫符号代表积分符号,具体的计算方法不在本文中详细说明。
二、计算体积在物理学中,我们经常需要计算物体的体积,定积分也可以帮助我们实现这一目的。
比如我们需要计算一个旋转曲线所围成的立体体积,我们可以依然使用之前的方法将其分解成无限小的小圆柱体积,每个小圆柱的体积可以表示为:V=π[f(x)]^2dx我们将所有小圆柱的体积相加,得到所求的立体体积V:V=∫a^b π[f(x)]^2dx三、计算重心和质心在物理学中,重心和质心是非常重要的概念。
对于一个平面图形或者一个立体体形,它的重心和质心分别表示为:重心:(∫xdS)/(∫dS)质心:(∫xdm)/(∫dm)这里的dS和dm分别表示面元和质量元,x则表示距离中心的距离。
我们可以通过对图形进行分割并使用定积分来计算重心和质心。
四、积分在物理学中的应用定积分在物理学中的应用非常广泛,比如我们可以使用它来计算弹性势能、动能、功、功率等物理量。
举一个简单的例子,假设质量为m的物体从高度为h处自由落下,当它下落到高度为y 时,它的速度为v,我们可以使用动能和势能的转化关系求出v,设重力加速度为g,则它下落过程中失去的重力势能为mgh-mgy,同时增加的动能为(1/2)mv^2,因此:mgh-mgy=(1/2)mv^2v=sqrt(2g(h-y))我们可以使用定积分来求解物体在过程中的运动状态,以及计算其他物理量的值。
定积分在几何学上的应用

一、平面图形的面积
1. 直角坐标情形
y y f (x)
设曲线
与直线
及 x 轴所围曲 边梯形面积为 A , 则
o
a
x
x
dbx
x
dA f (x) dx
b
A a f (x) dx
y y f1(x) y f2 (x)
右图所示图形面积为
b
A a f1(x) f2 (x) dx
A 40 y d x
利用椭圆的参数方程
x y
a cos t b sin t
(0 t 2 )
y b
o xxdxa x
应用定积分换元法得
4
ab
12
2
ab
4ab 2 sin 2 t dt 0
当 a = b 时得圆面积公式
一、平面图形的面积
2. 极坐标情形
求由曲线
及
围成的曲边扇形的面积 .
在区间
2
(1
1 y 2 ) 2d y 1 (2 y)2 d y 0
内容小结
1. 平面图形的面积 直角坐标方程
边界方程 极坐标方程
2. 已知平行截面面面积函数的立体体积
旋转体的体积 绕x轴: 绕y轴:
上任取小区间
则对应该小区间上曲边扇形面积的近似值为
dA 1 ( ) 2 d
2
所求曲边扇形的面积为
r ( ) d
A 1 2 ( ) d 2
x
一、平面图形的面积
例 计算阿基米德螺线 到 2 所围图形面积 .
解:
A 2 1 (a )2 d
02
a2 2
13
3
定积分的应用

定积分的应用定积分是微积分中的重要内容之一,经常被应用于实际问题的解决中。
本文将从三个方面来论述定积分的应用。
一、定积分在几何中的应用首先,定积分可以用于求曲线下面的面积。
以 y=f(x) 为例,若f(x)>0,则曲线 y=f(x) 与 x 轴的两点 a、b 组成的图形的面积为S=∫baf(x)dx这时,可以将曲线 y=f(x) 分成许多小块,每块宽度为Δx,高度为 f(xi),从而可以得到其面积为ΔS=f(xi)Δx因此,当Δx 趋于 0 时,所有小块的面积之和就等于图形的面积,即∑ΔS→S因此,用定积分就可以求出图形的面积。
其次,定积分还可以用于求旋转体的体积。
以曲线 y=f(x) 在 x 轴上旋转360°为例,其体积为V=π∫baf(x)^2dx这里,π为圆周率。
最后,定积分还可以用于求某些奇特图形的长、面积等等。
二、定积分在物理中的应用物理中也有许多问题可以通过定积分来解决。
比如,运动问题中的速度、加速度,可以通过位移的变化来求得。
若某运动物体的速度为 v(t),则其位移 s(t) 为s(t)=∫v(t)dt同样,若某运动物体的加速度为 a(t),速度为 v(t),则其位移为s(t)=∫v(t)dt=∫a(t)dt最后,定积分还可以用于求密度、质量等物理量。
三、定积分在工程中的应用定积分在工程中的应用也非常广泛。
比如,在流体力学中,对于一条管道中的液体,可以通过惯性和重力等因素,求出其中液体的流量和压力。
而这些流量和压力可以通过定积分计算得出。
在电学中,电量、电荷、电流和电势等都可以通过定积分来求解。
在结构设计中,定积分也常常被用来计算约束力、杠杆比例等。
总之,定积分在几何、物理和工程等领域中都有着广泛应用。
熟练地掌握定积分的方法和应用,对于科学研究和实际问题的解决都有着非常积极的帮助。
定积分的应用

图1-1图1-2定积分的应用微积分学是微分学和积分学的统称,它的创立,被誉为“人类精神的最高胜利”。
在数学史上,它的发展为现代数学做出了不朽的功绩。
恩格斯曾经指出:微积分是变量数学最重要的部分,是数学的一个重要的分支,它实现带科学技术以及自然科学的各个分支中被广泛应用的最重要的数学工具。
凡是复杂图形的研究,化学反映过程的分析,物理方面的应用,以及弹道﹑气象的计算,人造卫星轨迹的计算,运动状态的分析等等,都要用得到微积分。
正是由于微积分的广泛的应用,才使得我们人类在数学﹑科学技术﹑经济等方面得到了长足的发展,解决了许多的困难。
以下将讲述一下定积分在数学﹑经济﹑工程﹑医学﹑物理方面的中的一些应用。
1 定积分的概念的提出1.1问题的提出曲边梯形的面积(如图1)所谓曲边梯形,是指由直线a x =、b x =(b a <),x 轴及连续曲线)(x f y =(0)(≥x f )所围成的图形。
其中x 轴上区间],[b a 称为底边,曲线)(x f y =称为曲边。
不妨假定0)(≥x f ,下面来求曲边梯形的面积。
由于cx f ≠)((],[b a x ∈)无法用矩形面积公式来计算,但根据连续性,任两点],[,21b a x x ∈ ,12x x -很小时,)(1x f ,)(2x f 间的图形变化不大,即点1x 、点2x 处高度差别不大。
于是可用如下方法求曲边梯形的面积。
(1) 分割 用直线1x x =,2x x =,1-=n x x (b x x x a n <<<<<-121 )将整个曲边梯形任意分割成n 个小曲边梯形,区间上分点为:b x x x x x a n n =<<<<<=-1210这里取0x a =,n x b =。
区间],[b a 被分割成n 个小区间],[1i i x x -,用i x ∆表示小区间],[1i i x x -的长度,i S ∆表示第i 块曲边梯形的面积,),,2,1(n i =,整个曲边梯形的面积S 等于n 个小曲边梯形的面积之和,即∑=∆=ni i S S 1(2)近似代替: 对每个小曲边梯形,它的高仍是变化的,但区间长度i x ∆很小时,每个小曲边梯形各点处的高度变化不大,所以用小矩形面积近似代替小曲边梯形的面积,就是,在第i 个小区间],[1i i x x -上任取一点i ξ,用以],[1i i x x -为底,)(i f ξ为高的小矩形面积i i x f ∆)(ξ,近似代替这个小曲边梯形的面积(图1-1), 即i i i x f S ∆≈∆)(ξ.(3)求和 整个曲边梯形面积的近似值为 n 个小矩形面积之和,即n S S S S ∆++∆+∆= 21=∆++∆+∆≈n n x f x f x f )()()(2211ξξξ ini ix f ∆∑=)(1ξ上式由于分割不同,i ξ选取不同是不一样的,即近似值与分割及i ξ选取有关(图1-2)。
第十周周一高等数学の5-定积分在几何物理上的应用广义积分
x
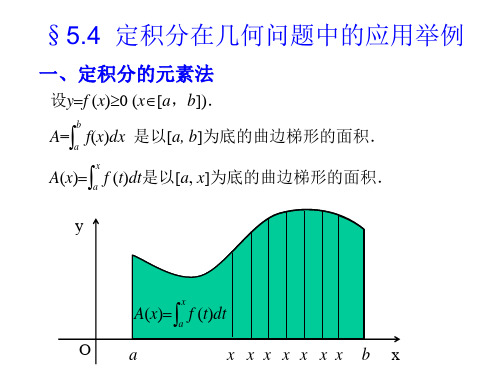
设曲线弧由直角坐标方程 yf(x) (axb)给出,其中f(x)在区 间[a,b]上具有一阶连续导数,则
ds 1 y2dx ,s b 1 y2dx . a
讨论:
(1)设曲线弧由参数方程
x
y
(t), (t)
( t )给出,其中
(t)、(t)在[,]上具有连续导数, 问弧长元素ds和弧长 s 各
2
2
1
1a
ab
b2
2(1(1cocso2st2)td)tdt11
a
ab·b·
11
a ab b..
22 0 0
2 2 2 24 4
A 4A1 a b.
2. 极坐标的情形
•曲边扇形及曲边扇形的面积元素:
由曲线r()及射线 , 围成的图形称为曲边扇形.
•曲边扇形的面积元素:
dA 1 [()] 2d .
a2 (1 cos )2 a2 sin 2 d 2a sin d .
2
所求弧长为
s
2 2a sin d
0
2
2a[2
cos
2
]02
8a .
y
2a
O
a
2 a
x
3. 极坐标的情形
设曲线弧由极坐标方程
r = r() ( ) 给出,其中r()在[,]上具有连续导数. 由直角坐标与极坐标的关系可得
是什么?
(2)设曲线弧由极坐标方程r = r() ( )给出,其中r() 在[,]上具有连续导数, 问弧长元素ds和弧长 s 各是什么?
) Ds MO MP ,
ds MP dx2 dy2 ,
直角坐标系下 y f x,
P
O
dy
定积分在几何学上的应用

解 解 直角三角形斜边的直线方程为 y
r V ( x)2 dx 0 h
h
r x. h
r 2 1
1 h [ x3 ]0 hr 2 . 3 h2 3
首页
上页
返回
下页
结束
铃
旋转体的体积: b [ f (x)]2 dx . V a 例7 计算由椭圆
2 x2 y 2 1 所成的图形绕x轴旋转而成的 2 a b
V [ f ( x)]2 dx .
a b
首页
上页
返回
下页
结束
铃
旋转体的体积: b [ f (x)]2 dx . V a 例6 连接坐标原点O及点P(h, r)的直线、直线xh及x轴围 成一个直角三角形. 将它绕x轴旋转构成一个底半径为r、高 为h的圆锥体. 计算这圆锥体的体积.
ds a 2 (1 cos )2 a 2 sin 2 d 2a sin
2
d .
于是所求弧长为
s
2 0
2a sin
2
d
2
2a[2 cos ]0 8a. 2
首页 上页 返回 下页 结束 铃
曲线yf(x)(axb)的弧长: s
a
b
1 y2 dx .
S 4 ydx .
0 a
2
y2
因为椭圆的参数方程为 xacost, ybsint, 所以
S 4 ydx 4b sin td ((acostt) S 4 ydx 4 b sin td a cos )
00
22
aa
00
4ab sin 2 tdt 2ab 2 (1 cos2t)dt
第五章 定积分的几何应用

) ( r r
d
例 5
求双纽线 a cos 2 所围平面图形
2 2
的面积.
解 由对称性知总面 积=4倍第一象限 部分面积
A 4A1
y x
2 a 2 cos 2
A 40
4
1 2 a cos 2d a 2 . 2
例 6 求心形线r a(1 cos )所围平面图形的 面积 (a 0).
小结
求在直角坐标系下、参数方程形式 下、极坐标系下平面图形的面积. 求旋转体的体积
(注意恰当的选择积分变量有助于简化 积分运算)
思考题
1. 设 曲 线 y f ( x ) 过 原 点 及 点( 2,3) , 且 f ( x ) 为单调函数,并具有连续导数,今在曲线 上任取一点作两坐标轴的平行线,其中一条平 行线与 x 轴和曲线 y f ( x ) 围成的面积是另一 条平行线与 y 轴和曲线 y f ( x ) 围成的面积的 两倍,求曲线方程.
练习题答案 32 一、1、1; 2、 ; 3、2; 3 1 1 4、y ; 5、 e 2 ; 6、 . e 2 3 7 2 二、1、 ln 2 ; 2、 ; 3、 a ; 2 6 5 3 2 2 4、3a ; 5、 ; 6、 a . 2 4 9 e 8 2 三、 . 四、 . 五、 a . 4 2 3
其上相应的窄条左、右曲边分别为 1 2 x y ,x y4 2 4 1 2 A ( y 4 y )dy 18 2 2
由此可见在面积计算中应根据平面区域的具体 特征恰当地选择积分变量找出相应的面积微元可使 计算简化
上述问题的一般情况是
d
y
x ( y)
定积分在几何计算中的应用

定积分在几何计算中的应用定积分是高等数学中的一个重要概念,它在几何计算中有着广泛的应用。
在几何学中,定积分可以用来计算曲线的长度、曲面的面积、体积等等。
下面我们就来看看定积分在几何计算中的应用。
定积分可以用来计算曲线的长度。
对于一条曲线,我们可以将其分成无数个小段,然后对每个小段的长度进行求和,最终得到整条曲线的长度。
这个过程可以用定积分来表示,即:L = ∫a^b √(1+(dy/dx)^2) dx其中,a和b分别表示曲线的起点和终点,dy/dx表示曲线在每个点的斜率。
这个式子的意义是,将曲线分成无数个小段,每个小段的长度为√(1+(dy/dx)^2) dx,然后对所有小段的长度进行求和,最终得到整条曲线的长度。
定积分可以用来计算曲面的面积。
对于一个曲面,我们可以将其分成无数个小面元,然后对每个小面元的面积进行求和,最终得到整个曲面的面积。
这个过程可以用定积分来表示,即:S = ∫∫D √(1+(∂z/∂x)^2+(∂z/∂y)^2) dxdy其中,D表示曲面的投影区域,z表示曲面在每个点的高度,∂z/∂x和∂z/∂y分别表示曲面在每个点在x和y方向上的斜率。
这个式子的意义是,将曲面分成无数个小面元,每个小面元的面积为√(1+(∂z/∂x)^2+(∂z/∂y)^2) dxdy,然后对所有小面元的面积进行求和,最终得到整个曲面的面积。
定积分可以用来计算体积。
对于一个立体图形,我们可以将其分成无数个小体元,然后对每个小体元的体积进行求和,最终得到整个立体图形的体积。
这个过程可以用定积分来表示,即:V = ∫∫∫E dxdydz其中,E表示立体图形的空间区域。
这个式子的意义是,将立体图形分成无数个小体元,每个小体元的体积为dxdydz,然后对所有小体元的体积进行求和,最终得到整个立体图形的体积。
定积分在几何计算中有着广泛的应用,可以用来计算曲线的长度、曲面的面积、体积等等。
这些应用不仅在数学中有着重要的意义,也在实际生活中有着广泛的应用,例如在建筑设计、工程计算等领域中都有着重要的作用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三、已知平行截面面积函数的立体体积
设所给立体垂直于x 轴的截面面积为A(x),
上连续, 则对应于小区间
的体积元素为
d V A( x) d x
因此所求立体体积为
V A( x) d x
a
b
A(x)
a
x
b
x
特别 , 当考虑连续曲线段
轴旋转一周围成的立体体积时, 有
V [ f ( x)] dx
a b
x dx
b x
y y f1 ( x) y f 2 ( x)
右下图所示图形面积为
A f1 ( x) f 2 ( x) dx
a
b
o
axxdx
b x
例1. 计算两条抛物线 所围图形的面积 . 解: 由
得交点 (0 , 0) , (1, 1)
在第一象限所围
y
y2 x
2
(1,1)
2
a
b
y
y f (x)
当考虑连续曲线段
o
a
x
b
x
y
绕 y 轴旋转一周围成的立体体积时,
有
V [ ( y )] d y
2
c
d
d y c o
x ( y)
x
例6. 计算由椭圆 转而成的椭球体的体积.
所围图形绕 x 轴旋转而
y
解: 方法1 利用直角坐标方程
b
o
则
x
ax
V 2 y 2 dx
3 a sin 6 0
t t d t (令 u ) 2 2
y
2a
绕 y 轴旋转而成的体积为
o
x x2 ( y ) x x1 ( y )
a
2 a x
0 3 2 a (t sin t ) 2 sin td t
0
2 注意上下限 ! a (t sin t ) 2 a sin t d t 2 2 a (t sin t ) 2 a sin t d t
ox
y
R
x
思考: 可否选择 y 作积分变量 ?
此时截面面积函数是什么 ?
如何用定积分表示体积 ?
提示:
y
A( y ) 2 x y tan
2 tan y R 2 y 2
2 2 2 tan y R y d y V
0 R
o
( x, y ) R x
四、平面曲线的弧长
0
a
(利用对称性)
b2 a 2 2 2 (a x 2 ) dx a 0 b2 2 1 3 a 4 2 2 a x x ab 2 3 0 3 a
方法2 利用椭圆参数方程
则
V 2 y 2 dx 2 ab 2 sin 3t d t
0
(sh x) ch x
例10. 计算摆线
的弧长 . 解: ds
y
一拱
(d x)2 dt
dy 2 (d t )
dt
o
2 a x
a 2 (1 cos t ) 2 a 2 sin 2 t d t
a 2(1 cos t ) d t t 2a sin dt 2 2 t 2 cos t 2 s 2a sin d t 2a 0 2 2 0 8a
3. 已知平行截面面面积函数的立体体积
旋转体的体积 绕 x 轴 : A( x) y 2 绕 y 轴 : A( x) 2 x y
(柱壳法)
思考与练习
用定积分表示图中阴影部分的面积 A 及边界长 s .
提示: 交点为(1, 1) , (9 , 3) , 以 x 为积分变量 , 则要分
弧长元素(弧微分) :
ds [ x( )]2 [ y ( )]2 d
r 2 ( ) r 2 ( ) d
因此所求弧长
(自己验证)
s
r 2 ( ) r 2 ( ) d
例9. 两根电线杆之间的电线, 由于其本身的重量, 下垂 y 成悬链线 . 悬链线方程为 c x y c ch (b x b) c b o bx 求这一段弧长 .
注
说明:
y
x xdx
柱面面积 柱壳体积
2
a(t sin t ) a (1 cos t )
2 a(t sin t ) a 2 (1 cos t ) 2 d t
0
2
t 8 (t sin t ) sin d t 2 t 令u 2
4
3 2 a 0
o
y x4
(2 , 2)
x
d A ( y 4 1 y 2 ) dy A 2
2
4
18
例3. 求椭圆
所围图形的面积 .
解: 利用对称性 , 有 d A y dx
y
A 4 y d x
0
a
b
利用椭圆的参数方程 x a cos t (0 t 2 ) y b sin t 应用定积分
x x dx
o
y x2
x 1 x d x
x
1 3
例2. 计算抛物线 y 2 x 与直线 y x 4 所围图形
2
的面积 . 解: 由 得交点
(2 , 2) , (8 , 4)
则有
y yd y y
y 2 2x
(8 , 4)
为简便计算, 选取 y 作积分变量,
定义: 若在弧 AB 上任意作内接折线 , 当折线段的最大
边长 →0 时, 折线的长度趋向于一个确定的极限 , 则称
此极限为曲线弧 AB 的弧长 , 即
n
y
M i 1
Mi
s lim M i 1M i 0
i 1
并称此曲线弧为可求长的.
A M0
B Mn
x
o
(证明略)
定理: 任意光滑曲线弧都是可求长的.
(1) 曲线弧由直角坐标方程给出:
弧长元素(弧微分) :
ds (dx) (d y )
2
2
y
(P168)
ds
y f (x)
1 y2 d x
因此所求弧长
s
b
a b
2 d x 1 y
o a
xxdx b x
1 f 2 ( x) d x
a
(2) 曲线弧由参数方程给出:
第五节 定积分在几何学上的应用
一、 定积分的元素法 二、 平面图形的面积 三、 平面曲线的弧长 四、已知平行截面面积函数的 立体体积 五、 旋转体的侧面积
一、定积分的元素法 1、什么问题可以用定积分解决 ?
1) 所求量 U 是与区间[a , b]上的某分布 f (x) 有关的
一个整体量 ;
2) U 对区间 [a , b] 具有可加性 , 即可通过
16
3 a 0
(2u sin 2u ) sin 4 u d u
2 3 2 4 16 a (2v sin 2v) cos v d v
令v u
2
偶函数
奇函数
例8. 一平面经过半径为R 的圆柱体的底圆中心 , 并
与底面交成 角, 计算该平面截圆柱体所得立体的体积 . 解: 如图所示取坐标系, 则圆的方程为 x2 y 2 R2 垂直于x 轴 的截面是直角三角形, 其面积为 1 2 2 A( x) ( R x ) tan ( R x R) 2 利用对称性 R1 V 2 ( R 2 x 2 ) tan d x 0 2 1 3 R 2 2 tan R x x 0 3
a
2 2 ab 1 3 4 ab 2 3
2
4 3 特别当b = a 时, 就得半径为a 的球体的体积 a . 3
例7. 计算摆线
的一拱与 y=0
所围成的图形分别绕 x 轴 , y 轴旋转而成的立体体积 .
解: 绕 x 轴旋转而成的体积为
y
Vx
2 a 0
0
y dx
2
y
o
2
2
a
2 a x
a (1 cos t ) a(1 cos t ) d t
2
利用对称性
2
3 a (1 cos t )3 d t 0
16
3
32 a 3 2 sin 6 u d u 32 0 2 3
5 a
5 3 1 a 6 4 2 2
0
1 2 d
内容小结
1. 平面图形的面积 直角坐标方程 边界方程 参数方程 极坐标方程 2. 平面曲线的弧长
上下限按顺时针方向 确定
弧微分: d s (d x) 2 (d y ) 2 注意: 求弧长时积分上
下限必须上大下小
直角坐标方程 曲线方程 参数方程方程
极坐标方程 d s r 2 ( ) r 2 ( ) d
o xxdx a x
4 a b 1 ab
2 2
4ab 2 sin 2 t dt
0
当 a = b 时得圆面积公式
一般地 , 当曲边梯形的曲边由参数方程
给出时, 按顺时针方向规定起点和终点的参数值
则曲边梯形面积
2. 极坐标情形
求由曲线 围成的曲边扇形的面积 . 在区间 上任取小区间 则对应该小区间上曲边扇形面积的近似值为 及
这种分析方法称为元素法 (或微元分析法) 元素的几何形状常取为: 条, 带, 段, 环, 扇, 片, 壳 等
