2-2变压器的负载运行
变压器并联运行的负载分配原理
变压器并联运行的负载分配原理
变压器并联运行是一种提高电力系统稳定性和可靠性的常用方法，但在实际应用中，如何合理地分配负载却是一个关键问题。
以下是变压器并联运行的负载分配原理。
1. 同等负载分配原则
当变压器容量和变比相同，且运行条件相同时，应采取同等负载分配原则。
即将负载平均分配到每个变压器上，以达到共同工作的目的。
这种方式能有效避免变压器过载或欠载的情况，保证变压器并联运行的稳定性和可靠性。
2. 不等负载分配原则
当变压器容量或变比不同，或者运行条件不同，应采取不等负载分配原则。
即根据变压器的容量和运行条件的不同，合理分配负载。
这种方式能实现变压器的最大利用，同时保证其正常运行。
3. 优先级分配原则
当变压器容量和变比相同，但运行条件不同时，应采取优先级分配原则。
即将负载分配到运行条件较好的变压器上，以保证系统的稳定性和可靠性。
4. 临时负载分配原则
在特殊情况下，如设备维护、故障处理等，可采取临时负载分配原则。
即将一个变压器的全部或部分负载转移到另一个变压器上，以保证供电的连续性和稳定性。
总之，变压器并联运行的负载分配原理应根据变压器的容量、变
比和运行条件等因素进行合理分配，以保证系统的稳定性和可靠性。
2.2变压器的负载运行
1、变压器带负载运行时，当负载增大（不考虑漏抗压降），则一次电流将，空载电流。
2、变压器带负载运行，当负载增大，则其铜损耗，铁损耗。
3、变压器由空载到满载，下列各物理量将如何变化（忽略漏抗压降），，，，。
4、变压器一次侧接额定电压，二次侧接纯电阻性负载，则从一次侧输入的功率。
（A）只含有有功功率；（B）只含有感性无功功率；（C）既含有有功功率又含有感性无功功率；（D）既含有有功功率又含有容性无功功率。
5、变压器负载时，一次磁动势为，一次漏磁通为，一次漏抗为；变压器空载时，一次磁动势为，一次漏磁通为，一次漏抗为，它们的关系是。
（A）；（B）；（C）；（D）。
6、变压器负载（）增加时，从理论上讲，其主磁通。
（A）稍增大；（B）稍减小；（C）增大很多；（D）减小很多。
7、电源电压一定时，试分析当变压器负载（）增加时，如何变化？8、电源电压降低对变压器铁心饱和程度，励磁电流，励磁阻抗，铁耗和铜耗等有何影响？9、简述变压器空载和负载时，励磁磁动势有何不同？10、画出变压器的“T”形、近似和简化等效电路。
11、画出变压器简化等效电路和简化向量图。
12、画出变压器短路时的等效电路，并画出与之对应的向量图。
1、增大不变2、增大不变3、不变不变不变增大4、（C）5、（B）6、（B）7、答：降低。
由外特性曲线知，随负载电流（）增大而下降。
增大。
负载越大，越大，由磁动势平衡方程式知，就越大。
不变。
大小与负载大小基本无关。
不变。
因电源电压不变，磁路饱和情况不变，故不变。
不变。
因漏磁路不饱和，。
8、答：铁心饱和程度降低。
，降低，减少，故饱和程度降低。
励磁电流减少。
由磁化曲线知，励磁电流随磁通减少而减少。
励磁阻抗增大。
励磁阻抗随饱和程度下降而增大。
铜耗减小。
电压降低，，减小，故铜耗减小。
铁耗减小。
，故铁耗减小。
9、答：，空载时I2=0，，所以空载时励磁磁动势仅为一次空载磁动势。
负载时，，励磁磁动势为一、二次的合成磁动势。
10、省略。
变压器的空载运行及负载运行
N1I0 N1 I0 N1 I1L N2 I2
N1 I1L - N2 I2
其中I1L远远大于I0，大部分用来抵抗副边电流引起的磁通量变化。
当负载运行时可认为I1L=I1。
I1
I2 k
或 I1 I2
1 k
N2 N1
k为变压器变比
一、二次电流比近似与匝数成反 比。可见匝数不同，不仅能改变 电压，同时也能改变电流。
产业信息
中国变压器设备-尤其是特种变压器-已 走向世界成为“中国制造” 品牌
谢谢聆听
P0 = PFe + Pcu ≈ PFe
铁损耗分量
铁损耗分量：符号为I10P，供给铁磁材料 铁损（磁滞和涡流损耗），为有功分量
Part 2 空载运行分析
思考
如果误将变压器高低压侧接反，会发生什么异常现象？
变压器低压侧如果接到高压电源上，则铁心主磁 通Φm会增加，磁路饱和程度增加，因而励磁电流I0大 大增加，有可能烧毁线圈（励磁电流随磁路饱和程度 增加而急剧增大）
单相变压器空载运行示意图
Part 2 空载运行分析
空载电流的作用与组成
I10 I10Q I10P
励磁分量
励磁分量：符号为I10Q，用来建立主磁 通，相位与主磁通相同，为无功分量
变压器空载运行时，只从电源吸收少量有功功率P0， 用来供给铁心中铁损PFe和少量绕组铜损Pcu=R1I102 （可忽略不计）。容量越大，空载功率P0越小
Part 3 变压器的负载运行
变压器作用 通过对变压器负载运行的分析，可以清楚地看出变压器具有变电压、 变电流、变阻抗的作用。
• 变换电压 U1/U2≈E1/E2=k=N1/N2
• 变换电流 I1/I2≈N2/N1=1/k
变压器运行性能
流主。磁对通已 经和制铁成心的磁变路压的器磁，化曲i线的大小和波形取决于 f (i )
当磁路不饱和时，磁化曲线是直线，磁化电流与磁 通成正比。
若铁心中主磁通的幅值m 使磁路达到饱和,则 i
需由图解法来确定，如图2-6(a)和(b)所示。
（２）铁耗电流:
2.电压方程
u1 i10R1
e1
i10 R1
N1
d
dt
u20
e2
N2
d
dt
3.变压器的变比及变压原理
u1 e1 N1 kK u20 e2 N 2
二、主磁通和激磁电流 1．主磁通 通过铁心并与一次、二次绕组相交链的磁通，
用 表示 .
1
N1
e1dt
1 N1
2E1 sin tdt
2E1
2.绕组 定义 变压器的电路部分，用纸包或纱包的绝缘扁 线或圆线（铜或铝）绕成。 一次绕组 : 输入电能的绕组。 二次绕组: 输出电能的绕组。
高压绕组的匝数多,导线细；低压绕组的匝数少， 导线粗。
从高,低压绕组的相对位置来看,变压器的绕组可分 为同心式和交迭式。
同心式
结构 同心式绕组的高、低压绕组同心地套装 在心柱上。
视在功率的保证值 ，单位为kV或kVA。 三相变压器指三相容量之和。
额定电压 U N 铭牌规定的各个绕组在空载、指定分
接开关位置下的端电压，单位为V或kV。 三相变压器指线电压。
额称定为电额流 定电I N流，根单据位额为定A容。量和额定电压算出的电流
三相变压器指线电流。
单相变压器：
I1N
SN U1N
按照铁心的结构，变压器可分为心式和壳式两 种。
变压器第2次课(空载与负载运行)
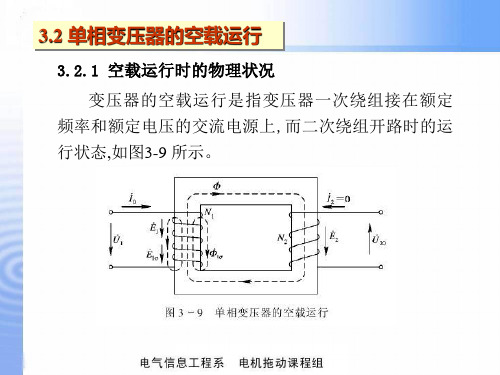
I Z I Z I Z U1 E 1 0 1 0 m 0 1 (r jX ) I (r jX ) I
0 1 1 0 m m
(3-16)
根据式 (3-16) 可画出对应的电路 , 如
图3-11 所示。
3.2.5 空载运行时的相量图 ①以 m 为参考相量
U1N/U2N=380V/220V,r1=0.14Ω ,r2=0.035Ω ， X1=0.22Ω , X2=0.055Ω , rm=30Ω ,Xm=310Ω 。一次侧加额定频率的 额定电压并保持不变,二次侧接负载阻抗ZL=(4+j3) Ω 。 试用简化等效电路计算：
(3-11)
在 电 力 变 压 器 中 , 由 于 Iμ 》IFe, 当 忽 略 IFe 时,I0≈Iμ ,因此把空载电流近似称为励磁电流。 空载电流越小越好 , 一般电力变压器 ,I0=2%～ 10%,
容量越大,I0相对越小,大型变压器I0在1％以下。
2. 空载损耗 变压器空载运行时 , 空载损耗p0 主要包括铁心损耗
同理
dΦ e2 N 2 2fN 2 m sin t 90 E2 m sin t 90 dt
e2也按正弦规律变化,但e1、e2滞后于Φ90°,且感应电动势 的有效值为 结论1
（3-7） 由上式可知,当主磁通Φ按正弦规律变化时,电动势e1、
E1m m N1 2fN1 m E1 4.44 fN1 m 2 2 2
路的电磁效应,X1=ω L1σ 由于漏磁通的路径是非铁磁性物质,磁路不会饱和, 是线性磁路 , 因此对已制成的变压器 , 漏电感Ｌ 1σ 为常 数,当频率f一定时,漏电抗X1也是常数。
2-变压器负载运行
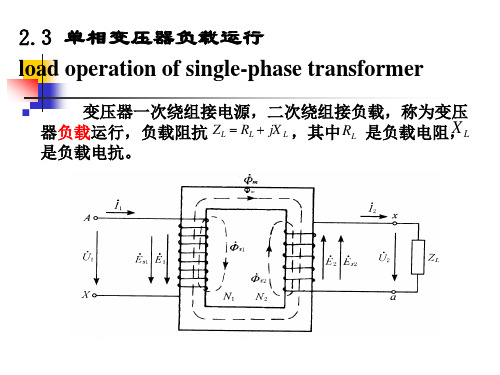
的大小
与空载运行时相比,负载时一次绕组的电流变化了,电源电压
不变,严格说来,负载时的
•
E
与空载时的不同。但在电力变压
1
器仍的然设还计是I中1N Z1I•0很U1小.仍,即存使在在U1额 E定1 由负载E1下 4运.44行fN1,I1Nm
比I0 大很多倍, 看出,空载、负
载与表运示空行。载,时其的主在磁数通值• m上的差数不值多差,仍别可很以小用,即同负一载个时符的号励I•磁0 N磁1或动势F• 0
因
，可认为 Zm
Z
' 2
Z
' L
无限Zm大而断开，于是等效电路变成了“一”型，
称为简化等效电路。如图：
单相变压器的负载运行
b.电压平衡方程式：
•
•
•
•
•
•
•
•
U1
I1
Z1
I 1 Z2'
U
' 2
I1
Z1
Z
' 2
U
' 2
I1 Zk
U
' 2
•
•
I1
I
' 2
•
•
U
' 2
Z
' L
单相变压器的负载运行
b.变压器接感性负载的相量图2-12a图：
单相变压器的负载运行
※相量图的绘制过程： 根据给定的条件不同，画法不同，但都是电压方程式 的相量图表示。
如给定U2, I2,cos2, k 及各参数，画图步骤为：
（（（（（（（1234567）））））））根画在画画画E•1 据出出出出U•2'EU超•I2•'的•20' IE••前21相和E，•1，E量•910它/加I上Z•2的' m与，上，，主I其•I•1加画磁0R夹1上出通的，I角•2'U•相R•1再m为2' I量•，0加；和再上，2为加。它j上II••超11XjI•1；2前'得X2'到得•一m 出U•个1E•。2'铁耗；角；
变压器的运行规程
变压器的运行规程一、正常运行的规定1、带负荷运行的规定1）变压器外加一次电压一般不得超过相应分接头值的5％。
2）温度的规定（１）为防止变压器油劣化过速，变压器上层油温一般不宜经常超过85℃，最高不超过95℃；（２）当主变压器负荷超过２／３或上层油温达到55℃时，自动(或手动)启动风冷装置，上层油温达到80℃时，发过温信号。
3）绝缘电阻的规定变压器电压在6kV及以上用1000—2500V摇表测量。
在接近工作温度时，每千伏工作电压不应低于1兆欧；在冷却状态下每千伏工作电压不应低于2兆欧。
4）瓦斯保护装置的运行（1）轻瓦斯保护装置应接信号，重瓦斯保护装置应接跳闸。
（2）变压器由运行改为备用时，轻重瓦斯保护照常与信号联接，以便及时发现变压器的油面下降情况，及时加油。
（3）对运行中变压器进行滤油或加油时，应将重瓦斯保护改接至信号，其它继电保护（如差动保护、复合闭锁过流）仍应投入。
等变压器完全停止排出空气气泡时，重瓦斯保护联板才能接入跳闸回路。
（4）当油面有异常升高现象时，应先将重瓦斯保护联板改至信号位置，才能打开各种放气或放油的塞子、清理呼吸器的孔眼或进行其它工作，防止瓦斯继电器误动作而跳闸。
2、变压器的巡视检查1）变压器的日常巡视检查（1）油温、油位要正常，无渗油漏油；（2）套管无裂纹、油污、放电痕迹；（3）声音正常；（4）冷却器手感温度应相近，风扇运转正常，油流及气体继电器工作正常；（5）吸湿器完好，吸附剂干燥；（6）引线接头、电缆、母线无发热迹象；（7）压力释放器，安全气道及防爆膜应完好无损；（8）气体继电器内无气体；（9）各控制箱、二次控制箱关严，无受潮；（10）变压器室门、窗、照明应完好，房屋不漏水，温度正常；2）应对变压器作定期检查，并增加以下检查内容:（1）外壳、箱沿无异常发热；（2）各部位接地良好；（3）各种标志应齐全明显；（4）各保护装置应安全良好；（5）温度表指示正常；（6）消防设施应齐全完好；（7）储油池和排油设施应保持良好状态；3）下列情况下应对变压器进行特殊巡视检查，增加巡视次数:（1）新设备或经检修的变压器在投运72h 内；（2）有较严重缺陷时；（3）气象突变（大风、大雾、大雪冰雹、寒潮等）；（4）雷雨季节，特别是雷雨后；（5）变压器急救负载运行时。
电机学 变压器2
9.2 变压器的负载运行
φ主磁通
A u1 X i1 * e1 e1σ R1
N1
*
i2 e2 e2σ
a u2 ZL x
φ1σ
φ2σ
N2
R2
N1i1
→ φ1σ
→ Fm = N1im → φ
一次绕组电压方程 dφ → e1σ = N1 1σ dt = u1 i1 R1 dφ → e1 = N1 dt
二次侧归算到一次侧后， 二次侧归算到一次侧后，二次侧的 电势和电压应乘以k倍 电流乘以1/k 电势和电压应乘以 倍，电流乘以 阻抗乘以k 倍，阻抗乘以 2倍。
2.变压器的等效电路 变压器的等效电路
归 算 后 基 本 方 程
& & & U 1 = I1Z 1σ E1 &' & ' &' ' E 2 = U 2 + I 2 Z 2σ & & &' & E1 = kE 2 = E 2 = I m Z m I + I ' = I & & & 2 m 1
1
& I
& E1
' 2
& jI1 X1σ
α 0
& &' E1 = E2
2
&' U2
' '
& U1
& &' I2 I2 R2 变压器感性负载时的相量图
&' jI2 Xz'σ
基本方程、等效电路和相量图是分析变压器运行的三种方法。 基本方程、等效电路和相量图是分析变压器运行的三种方法。基本方程概括了变 是分析变压器运行的三种方法 压器中的电磁关系，而等效电路和相量图是基本方程的另一种表达形式， 压器中的电磁关系，而等效电路和相量图是基本方程的另一种表达形式，三者是一致 的。
2-2变压器的负载运行
R1 jX 1
R
' 2
jX
' 2
′ Iɺ2
☆ “一”字型等效电路 一 不适用空载， 不适用空载，适用正常U 1 ɺ 负载运行和稳态短路。 负载运行和稳态短路。
ɺ U 2'
′ ZL
㈤ 简化等效电路
ZK = RK + jXK
′ Zk = Z1 + Z2 ′ Xk = X1 + X2 ′ Rk = R + R2 1
ɺ U1
ɺ jI1 X 1
ɺ I1 R1
ɺ − E1
ɺ' −I2
ɺ ′ ɺ′ ′ U2 = I2ZL
ɺ ' =U' + I′Z′ E2 ɺ2 ɺ2 2
ϕ1
ɺ I1
ɺ ɺ′ E1 = E2
ɺ ɺ I0 = −E1 / Zm
ɺ' I2 ϕ 2
ɺ' U2 ɺ' ' I 2 R2
ɺ' ' jI 2 X 2
ϕ0
ɺ ⋅ I − I 2 R − I 2 R − I ′ 2 R′ = U ′ ⋅ I ′ ɺ ɺ U 1 ɺ1 0 m 1 1 2 2 2 2
′ ′ ′ ′ U 1 I 1 cosϕ1 − I Rm − I R1 − I 2 R2 = U 2 I 2 cos ϕ 2
2 0 2 1 2
7、功率关系——叉乘（无功功率） 功率关系——叉乘 无功功率） 叉乘（ 7、 功率关系 、
ɺ ɺ ɺ ɺ ɺ ɺ U 1 × I 1 = ( − E1 ) × I 1 + [ I 1 ( R1 + jX 1 )] × I 1
ɺ )× (I − I′ ) + I 2 X ɺ ɺ = ( − E1 0 2 1 1 2 ɺ ′ × I′ + I 2 X =I X +E ɺ
变压器运行负荷计算公式
变压器运行负荷计算公式
变压器运行负荷计算通常涉及以下公式：
1. 容量（kVA）= 视在功率（kVAR）+ 有功功率（kW）
2. 视在功率（kVAR）= √3 × U × I
其中，U 为变压器的额定电压，I 为变压器的额定电流。
3. 有功功率（kW）= P × Cosθ
其中，P 为变压器的输出功率，Cosθ为功率因数。
4. 无功功率（kVAR）= Q × Sinθ
其中，Q 为变压器的无功功率，Sinθ为无功功率因数。
这些公式仅提供了一般的计算方法，实际的变压器运行负荷计算可能会因具体情况而有所不同。
在进行变压器运行负荷计算时，还应考虑变压器的效率、负载类型、功率因数等因素，并遵循相关的电气工程标准和规范。
如果你需要更准确和详细的计算，请咨询专业的电气工程师或相关技术人员。
变压器运行基本原理
3、试验接线如图所示。
4、处理数据
U1= U1N时的点（U1N、I0、p0）计算励磁参数:
U1 N Zm I0 p0 Rm 2 I0
X m Z m Rm
2 2
U 20 k U1N
5、试验说明以及注意事项：p28
返回
二、短路试验
1、目的：获得短路参数Zk、 Rk、 Xk。
2、方法：在高压侧加可调的低电压，低压侧短路， 测取I1N 、Uk 、pk。 3、试验接线如图所示。
由 E U，可得：
R1
E 1 E 1 U 1 I 0 R1
U1 E1 E1 I 0 R1
原方等效电路
E1 I 0 ( R1 jX 1 )
E1 j I 0 X 1
U1 E1 I 0 Z1
E2 4.44 fN1 m
'
N1 E2 E2 kE2 N2
'
3)阻抗折算： Z 2 R2 jX 2
电阻折算： 2 2 R2 I 2'2 R2' I 电抗折算： 2 2 x2 I 2'2 x2 ' I
I2 2 R2 ( ' ) R2 k 2 R2 I2 I2 2 ' x2 ( ' ) x2 k 2 x2 I2
N2
a
u20
e1
e1σ
N1
1
e2
X
E1
x
Z0
U1
Z1
I0
I0
Z m Z1
励磁阻抗
电机简答题1
0-4-3 变压器电动势和运动电动势产生的原因有什么不同？其大小与哪些因素有关？答：线圈中的感应电动势e 是由于与线圈相链的磁链ψ随时间t 变化而产生的。
线圈中磁链的变化有两个原因：一是磁通大小随时间t 变化（线圈相对磁场静止），由此产生的电动势称为变压器电动势；二是磁通本身不随时间t 变化，但线圈与磁场间有相对运动，从而引起磁链ψ随时间t 变化，由此在线圈中产生的电动势称为运动电动势。
用数学式表示时，设e 与ψ的参考方向满足右手螺旋定则，),(x i f =ψ（i 为电流，x 为位移），则R e e dtdx x dt di x dt d e +=∂∂-∂∂-=-=T ψψψ 式中，T e =dt di x ∂∂-ψ，是变压器电动势；e =dt dx x ∂∂-ψ=x v ∂∂-ψ（v 为线速度），是运动电动势。
运动电动势可形象地看成导体在均匀磁场中运动而“切割”磁感应线时产生的电动 势。
当一根长度为l 的导体在磁通密度B 大小恒定的均匀磁场中以既垂直于自身长度又垂直于B 的线速度v 运动时，导体中的感应电动势为 -Blv dx Bldx v dx d v e R e =--=-==ψ式中，ψd =Bldx -，表示导体与导线构成的回路中磁链的减少量。
e 的瞬时实际方向可用右手定则来判断。
线圈中产生的变压器电动势的大小取决于线圈磁通量的变化率，在线性情况下取决 于线圈电感和电流变化率（线圈电感又取决于线圈匝数和磁路的磁导）。
导体中产生的运动电动势的大小与磁场磁通密度大小、导体的运动速度及长度有关。
0-4-8 两个铁心线圈，它们的铁心材料、线圈匝数均相同。
若二者的磁路平均长度相等，但截面积不相等，当两个线圈中通入相等的直流电流时，哪个铁心中的磁通和磁通密度值较大？若二者的截面积相等，但磁路平均长度不等，则当两个铁心中的磁通量相同时，哪个线圈中的直流电流较大？答：(1)已知作用于磁路上的磁动势，求它产生的磁通，这属于磁路分析计算中的逆问题。
第2章单相变压器的运行原理
近于90°。因此，变压器空载时的功率因数很低，一般
cosφ0≈0.1~0.2，故应尽量避免空载运行。
第2章 单相变压器的运行原理
【例2-1】 一台三相变压器, SN=31 500 kV·A，U1N=110 kV, U2N=10.5 kV，Y、d 接法，原边绕组每相的电阻r1=1.21Ω， x1=14.45Ω，rm=1439.3 Ω，xm=14 161.3 Ω，试求：
即 Y, d 连接
k U1N 3U 2N
(2-18)
D, y 连接 Y, y连接
k 3U1N U 2N
k U1N U2N
(2-19) (2-20)
第2章 单相变压器的运行原理
2.1.4 空载时的等值电路和相量图 1. 空载时的等值电路 变压器空载运行时，既有电路，又有电和磁的相互联系，如
功功率，用来补偿铁芯中的铁损耗pFe以及极小量绕组的铜损耗
pCu
r1I
2 0
。由于空载电流I0很小，且r1也很小，故空载损耗近似
等于铁损耗，即P0≈pFe。
铁损耗pFe是交变磁通 在铁芯中造成的磁滞损耗和涡流损
耗的总和，它的测定将在2.3.1空载试验一节中进行叙述。
空载损耗一般约占变压器额定容量的0.2%~1%，由于电力变
m 一个角αFe。
第2章 单相变压器的运行原理
(4) 根据式(2-14)，在 E1 上加画与 I0 平行的 I0r1 和与 I0 垂直的 jI0 x1 ，叠加 E1、I0r1 jI0 x1 相量即得 U1 。由于 I0r1和 jI0 x1 很小，为了看清楚，图中有意将其放大了许多倍。
从例2-1
变压器的负载运行解读
（3-39）
折算后，变压器负载运行时的基本方程式组可简化为如下的方程式组
U1 E1 I1z1 E1 I0zm U2 E2 I2 z2 U2 I2 zL E2 E1 I1 I2 I0
（3-40）
变压器的负载运行(续8)
2．等效电路
在将变压器副绕组的匝数折算为
与原绕组的匝数相等后，原、副绕组
负载增加时，I2 增加，副边磁动势N1 I2N2 增加，原
边电流的负载电流分量（－
N• I2
2
）也相应增加，
N
使 的其副产边生磁的动磁势动I2N势2 ，（以－维持NN12 I• 2励）磁1 Nl电得流以分抵量消增I0 加不了
变。可见，虽然变压器的原、副边没有直接的电
路联系，但负载电流的变化也会使原边电流相应
衡方程式。
变压器的负载运行(续2)
将磁动势平衡方程式表示成电流的形式，得
I
•
I
0
(
N
2
•
I2)
（3-26）
1
N
由上式看出，变压器负1 载运行时的原边电
流 I1 是大于变压器空载运行时的原边电流 I0 的， 它由反映主磁通 m 大小的励磁电流分量 I0 和反
映负载大小的负载电流分量（－
）组成。当 N • I2 2
s
s
s
图3.9 单相变压器负载运行 时的简化等效电路
变压器的负载运行(续9)
=＝308.00V例53/111，5已V其知，负一r1＝载台0阻单.1抗相5为变，：压r2z器＝L＝的0.40数+2j43据为，。：x当S1N＝外4.06k加.V2A7电，U压，1N /为xU22N 额定值时，用简化等效电路计算原、副边电流及副边电
2台变压器负载率偏差范围
2台变压器负载率偏差范围在电力系统中，变压器是一种非常重要的电气设备，用来升降电压，实现电能传输与分配。
变压器的负载率是指变压器所承受的负荷与其额定容量之比。
负载率的偏差范围是表示变压器实际负载与额定容量之间的差异程度。
对于变压器的负载率偏差范围，国际上通常有一个统一的规定，即变压器的负载率偏差范围应在正负5%之间。
也就是说，变压器的实际负载应在额定容量的95%至105%之间。
负载率偏差范围在实际应用中具有重要的意义。
首先，控制负载率的偏差范围可以确保变压器的正常运行。
如果负载率过高或过低，都会对变压器的工作产生不良影响，甚至引发设备故障。
因此，及时调整负载率，使其处于合适的区间，是确保变压器安全运行的关键。
其次，负载率偏差范围的控制可以提高变压器的有效利用率。
将负载率控制在规定范围内，可以最大限度地发挥变压器的功效，实现能源的高效利用。
同时，通过合理调整负载率，还可以减少能源浪费，降低能源消耗，从而达到节能减排的目的。
此外，负载率偏差范围的控制还对电力系统的稳定运行起到重要作用。
在电力系统中，负载率偏差范围的变化会引起电压的波动，甚至可能导致电力系统的不稳定。
因此，通过控制负载率的偏差范围，可以提高电力系统的稳定性，保障电网的安全运行。
那么，如何控制变压器的负载率偏差范围呢？首先，需要合理规划电力配送，确保变压器的容量与负荷需求相匹配。
同时，在实际运行中，需要定期对变压器进行检测和监测，及时发现负载率的偏差，并采取相应的调整措施。
此外，还可以利用先进的电力管理技术，如智能感知、数据分析等手段，实时监控负载率的偏差情况，提前预警并进行调整。
总之，负载率偏差范围是控制变压器负载的重要指标。
合理控制负载率的偏差范围，不仅可以确保变压器的安全运行，提高能源利用率，保障电力系统的稳定性，还能够实现节能减排的目标。
因此，在电力系统运行和管理中，需要高度重视对负载率偏差范围的控制，并采取相应的措施进行监测和调整。
变压器负载运行时引起二次电压变化的原因
变压器负载运行时引起二次电压变化的原因1. 变压器基本概念首先，我们得聊聊变压器。
变压器就像电力系统中的“变身高手”，它能把高电压“变”成低电压，或者把低电压“变”成高电压，轻松解决电力传输中的各种麻烦。
想象一下，如果没有变压器，我们的电器就像没有水源的鱼，活不下去。
它们帮助我们在家里、工厂里、商店里随心所欲地用电，真是个不可或缺的小家伙。
2. 二次电压变化的原因2.1 负载变化好啦，咱们言归正传，谈谈为什么变压器在负载运行时二次电压会发生变化。
首先，负载变化就是一个大头。
在用电的时候，咱们的电器需求各不相同，比如开空调的时候，它就像个贪吃的孩子，吃得越多，变压器的负担就越重。
如果大家都在用电，那么负载就上升，电压也会有所波动。
想象一下，如果整个小区都开着空调，变压器就得拼命工作，就像一个超级奶爸，忙得不可开交。
2.2 阻抗影响接着，咱们得说说阻抗。
变压器的工作就像一场拉锯战，负载的变化引起的阻抗变化就会影响二次电压。
如果负载突然减少，就像一个突然离开的舞者，变压器的输出电压可能就会升高；反之，负载突然增加，电压就可能降低。
变压器就像在和这些负载做一场舞蹈比赛，时刻调整自己的节奏，以保持电压的稳定，真是个能屈能伸的好手。
3. 其他影响因素3.1 线损问题说到这儿，咱们不能忽视线损问题。
电流在流动的时候，就像人走在路上，总会遇到点阻碍。
这些阻碍就是线路上的损耗，电压在这个过程中就会遭殃。
线损的影响可能看似微不足道，但长时间下来就像是涓涓细流，最终汇聚成海，让电压变化变得更加明显。
3.2 温度影响最后，温度也是个大问题。
变压器在工作的时候，就像一个忙碌的小厨师，锅里烧着热汤，温度一高就容易让食材煮过头。
温度的变化会导致变压器内部的导体电阻变化，从而影响电压。
当环境温度过高时，电阻增大，电压就会下降；而温度降低时，电阻减小，电压可能上升。
变压器在这种情况下就像是个受了天气影响的情绪小孩，时刻需要调节自己的状态。
变压器工作状态
变压器工作状态变压器是一种常见的电力设备，广泛应用于电力系统中，用于改变电压的大小。
变压器的工作状态影响着其性能和效率，因此了解变压器的工作状态对于电力系统的正常运行至关重要。
一、变压器的工作状态分类根据变压器的负载情况，可以将其工作状态分为以下几种：空载、负载、过载和短路。
1. 空载状态当变压器无负载接入时，称其处于空载状态。
此时变压器的电流较小，主要是为了维持自身的损耗，保证变压器正常运行。
空载状态下，变压器的铁心损耗和漏耗较低。
2. 负载状态在负载接入变压器时，变压器处于负载状态。
根据负载的不同，可以进一步分为小负载、额定负载和大负载。
负载状态下，变压器的电流和负载功率呈正比。
3. 过载状态当变压器负载超过其额定负载时，称其处于过载状态。
在过载状态下，变压器的温度升高，可能会造成变压器的损坏。
因此，过载状态需要谨慎处理，并采取相应的保护措施，如过载保护装置的设置。
4. 短路状态当变压器的两个绕组之间出现短路故障时，称其处于短路状态。
短路状态下，变压器的电流迅速增大，可能导致变压器的损坏甚至爆炸。
因此，及时检测和修复短路故障是非常重要的。
二、变压器工作状态判断与监测方法为了确保变压器的正常工作，需要对其工作状态进行判断和监测。
以下是常用的变压器工作状态判断与监测方法：1. 温度监测变压器的温度是判断其工作状态的重要指标之一。
通过在变压器的关键位置安装温度传感器，并定期检测和记录温度，可以及时发现温度异常情况并采取相应措施。
2. 油质监测变压器内部填充绝缘油，通过定期对绝缘油的抽样分析，可以判断变压器的内部状态，如绝缘油中是否存在异常物质、电气性能是否正常等。
3. 充气压力监测变压器内部充填氮气，通过检测充气压力的变化，可以判断变压器的密封性和内部绝缘状态。
4. 电流监测通过变压器的电流变化情况，可以判断变压器的负载状况，并及时采取措施调整变压器的运行状态。
5. 振动监测变压器的振动异常可能是由内部故障引起的，通过在变压器上安装振动传感器，可以实时监测变压器的振动情况，做到早期发现和处理。
s22变压器标准
S22变压器是一种电力变压器，主要用于电力系统中的电压变换和电能传输。
S22变压器的标准主要包括以下几个方面：1. 额定容量：S22变压器的额定容量是指变压器在额定电压和额定频率下，能够稳定输出的最大功率。
额定容量通常用千伏安（kVA）表示，是选择变压器的重要参数。
2. 额定电压：S22变压器的额定电压是指变压器一次侧和二次侧的额定工作电压。
一次侧额定电压是指电源电压，二次侧额定电压是指负载所需的电压。
额定电压的选择应根据负载设备的电压要求和供电电网的电压等级来确定。
3. 额定电流：S22变压器的额定电流是指变压器在额定容量和额定电压下的满载电流。
额定电流的大小直接影响变压器的损耗和温升，因此在选择变压器时应根据负载电流的大小来选择合适的额定电流。
4. 短路阻抗：S22变压器的短路阻抗是指变压器一次侧和二次侧短路时的阻抗值。
短路阻抗的大小直接影响变压器的短路电流和短路损耗，因此在选择变压器时应根据系统短路电流的要求来选择合适的短路阻抗。
5. 空载损耗和负载损耗：S22变压器的空载损耗是指在无负载状态下，变压器内部的铁损和铜损之和。
负载损耗是指在有负载状态下，变压器输出功率与输入功率之差。
这两个参数直接影响变压器的效率和经济性，因此在选择变压器时应尽量选择低损耗的产品。
6. 绝缘等级：S22变压器的绝缘等级是指变压器绕组和铁芯之间的绝缘性能。
绝缘等级越高，变压器的安全性能越好，但成本也相应提高。
在选择变压器时，应根据系统的安全要求和经济性来选择合适的绝缘等级。
7. 冷却方式：S22变压器的冷却方式主要有自然风冷、强迫风冷、水冷等。
不同的冷却方式适用于不同的环境条件和运行要求，因此在选择变压器时应根据实际运行环境和负荷特点来选择合适的冷却方式。
8. 防护等级：S22变压器的防护等级是指变压器对外部环境的防护能力。
防护等级越高，变压器的抗干扰能力和可靠性越好，但成本也相应提高。
在选择变压器时，应根据系统的运行环境和可靠性要求来选择合适的防护等级。
变压器负载实验的实施步骤与流程解析
变压器负载实验的实施步骤与流程解析在进行变压器负载实验之前，需要明确实施步骤与流程，以保证实验的准确性和安全性。
下面将详细解析变压器负载实验的实施步骤与流程。
1. 实验目的：变压器负载实验的主要目的是测试变压器在额定负载下的性能表现，评估其稳定性和耐久性，为变压器运行和维护提供参考。
2. 实验前准备：（1）仔细阅读并理解变压器负载实验的操作规程和安全注意事项；（2）检查实验所需设备和仪器的正常工作状态，并进行必要的校准；（3）检查实验环境与条件是否符合要求，保持实验现场整洁、安全。
3. 实验装置设置：（1）连接变压器：根据实验要求，将待测试的变压器正确连接到实验装置上；（2）连接负载：根据实验设计，选择合适的负载并正确连接到变压器的输出端口；（3）设置电源参数：根据实验计划，设置电源的电压和频率参数。
4. 实验参数调整：（1）调整负载功率：根据实验计划和要求，逐步调整负载的功率，通常从零开始，然后逐渐增加，直到达到额定负载；（2）在每个功率点上，稳定一段时间，确保测量到的各项参数稳定，并记录下来。
5. 实验数据采集：（1）测量与记录：使用合适的仪器和设备，测量变压器在各个负载下的电流、电压、功率因数等参数，并记录在实验记录表格中；（2）重复实验：为了提高结果的准确性，建议对每个负载点进行多次实验，并取平均值。
6. 实验结果分析：（1）数据整理：根据记录表格，将实验得到的各项参数整理并计算得出额定负载下的性能指标；（2）结果分析：根据实验结果，对变压器的性能进行分析、评估，并与设计要求进行比较。
7. 实验总结与报告：（1）总结实验过程：根据实验过程与结果，总结实验的顺利进行以及遇到的问题与解决方法等；（2）撰写实验报告：按照所需格式撰写实验报告，包括实验背景、目的、装置设置、参数调整、数据采集、结果分析等内容。
总之，变压器负载实验的实施步骤与流程主要包括实验前准备、实验装置设置、实验参数调整、实验数据采集、实验结果分析、实验总结与报告等环节。
变压器负载率标准范围
变压器负载率标准范围变压器是一种常见的电力设备，在供电系统中发挥着重要作用。
它主要用于调整电压，改变电能的形式，或者将电能从一个回路传输到另一回路。
变压器的负载率反映了其负载状况，是电力系统运行中重要指标之一。
一般情况下，变压器的负载率应在一定范围内，并且过大或过小均会影响其正常运行。
因此，变压器的负载率必须控制在有效的范围内。
负载率的大小影响变压器的稳定性和安全性，影响变压器的使用寿命，也有影响变压器的效率，以及系统的整体运行效率。
以下是关于变压器负载率标准：1、正常负载率标准：正常负载率是指变压器能安全正常运行的负载率。
根据国家标准规定，正常负载率应在25%～100%之间，一般不宜超过85%。
2、最大短期负载率标准：最大短期负载率是指变压器短期可以承受的最大负载率。
一般最大短期负载率不宜高于正常负载率的110%～130%，变压器承受超过这一范围的长期超载会加快变压器的损耗和热老化，影响其可靠性和使用寿命，也会使变压器发生变形，从而降低变压器的性能。
3、最大长期负载率标准：最大长期负载率是指变压器所能承受的长期负载率。
由于变压器的热老化会逐渐增加，一般认为，最大长期负载率不宜高于正常负载率的90%～95%，以保证变压器的正常使用和安全运行。
以上就是有关变压器负载率标准范围的内容，变压器负载率是影响变压器正常运行的一个重要因素，必须控制在有效的范围内。
在运维变压器时，应注意控制变压器的负载率，以确保变压器的正常使用和安全运行。
变压器是电力系统中不可或缺的重要设备，它能够控制电压，改变电能形式，或者将电能从一个回路传输到另一回路。
变压器的负载率反映了变压器的负载状况，是电力系统运行中重要的指标之一，一般情况下，变压器的负载率应在一定范围内，不宜过大或过小，以保证变压器的正常使用和安全运行。
针对不同的变压器负载，变压器的负载率规定都不相同：正常负载率应在25%～100%之间，最大短期负载率不宜超过110%～130%，最大长期负载率不宜超过90%～95%。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
当仅考虑数量关系时， 当仅考虑数量关系时，一次磁动势等于二次磁 动势， 动势，即 I1N1 = I2N2 ，所以利用磁动势平衡的概 念来定性分析变压器负载运行时， 念来定性分析变压器负载运行时，可得如下结 论：电流之比等于匝数之比， 1 = I2 。 电流之比等于匝数之比， kI
2. 负载时二次电压、电流的关系 负载时二次电压、
2 2 L
& & & & & U1 = −E1 + I1Z1 = −E1 + I1(R + jX1) 1
& & &′ I1 = I0 +( −I2 )
& I1
R1
jX 1
& I0
R
' 2
jX
' 2
&′ I2
& U1
Rm
&' & E 1 = E2
&' U2
′ ZL
jX m
变压器“ T ”型等值电路
㈢ 由“T”型等效电路可得： T”型等效电路可得 型等效电路可得：
2 2 2
L
角，因为求复数阻抗比较繁，所以专业上常常把励 因为求复数阻抗比较繁， 磁支路提前。 磁支路提前。
㈣ “一”字型等效电路
变压器负载运行时， 为了简单， 变压器负载运行时，I1>>I0, 为了简单，可以忽 表现在T型等效电路上 型等效电路上， 略I0，表现在 型等效电路上，因Zm>>Z2’+ ZL’ 可以认为Z 无限大（ 很小）而断开， 可以认为 m无限大（I0很小）而断开，于是等 效电路变成了“一”字型，称为简化等效电路。 效电路变成了“ 字型，称为简化等效电路。
2
′ = k2ZL ZL
&′ & ⑷负载电压 U2 = kU2
说明： 说明：折合算法其结果不改变变压器运行的物 理本质，既不改变功率，也不影响阻抗抗角。 理本质，既不改变功率，也不影响阻抗抗角。 (证明见教材 证明见教材p27) 证明见教材 N1 一次向二次折合值为 如果 k = 则一次向二次折合值为： N2
Zk 叫短路阻抗 ， R 短路电阻， k 短路电抗 X k短路电阻，
★ 一般情况没给励磁阻抗 Zm ，只给短路阻 Zk
& U1
Rk
& &′ I1 = −I 2
jX k'
&' U2
′ ZL
抗 就用简化等值电路。
6、相量图
已知： 已知： U2 、 I2 、 ϕ2、k cos
R、 1、 '2、 '2、 m、 m R X R X 1 X
& U1
& jI1 X 1
& I1 R1
& − E1
&' −I2
& ′ &′ ′ U2 = I2ZL
& ' =U' + I′Z′ E2 &2 &2 2
ϕ1
& I1
& &′ E = E2 1
& & I0 =−E / Zm 1
&' I2 ϕ 2
&' U2 &' ' I 2 R2
&' ' jI 2 X 2
I&1
R1 jX 1
R
' 2
jX
' 2
′ I&2
☆ “一”字型等效电路 一 不适用空载， 不适用空载，适用正常U 1 & 负载运行和稳态短路。 负载运行和稳态短路。
& U 2'
′ ZL
㈤ 简化等效电路
ZK = RK + jXK
′ Zk = Z1 + Z2 ′ Xk = X1 + X2 ′ Rk = R + R2 1
& & 由 I1LN1 + I2N2 = 0 一次电流负载分量所建立
电流磁动势相平衡。 的磁动势与二次 电流磁动势相平衡。
& & & 当略去 I0时，1N1 + I2N2 = 0 I
& I & & 即一次电流达到满载时， & 当 I1 = I1N 时，即一次电流达到满载时，2 = I2N 也达到额定值 。
& & I1′ = k I1
R 1 R′ = 2 1 k
&′ & I0 = k I0
& ′ = 1U & U1 1 k
X1 ′ X1 = 2 k
Rm ′ Rm = 2 k
Xm ′ Xm = 2 k
5. 等效电路
折合后的六个基本方程式: ㈠ 折合后的六个基本方程式
& & & U1 =−E + I1Z1 1 & ′ &′ &′ ′ U2 = E2 − I2Z2 & & U′ = I′Z′
折合值： 为例。 ⑤ 折合值：二次向一次折合为例。
& N = I′N ∴ I′ = N2 I = 1 I & & & ⑴ ∵ I2 2 &2 1 2 2 2
N1 &′ E2 = − j4.44 fN1Φm ⑵电动势 & E =− j4.44 fN Φ
2 2 m
k
&′ & E2 = kE2
⑶阻抗
′ Z2 = k Z2
& ⋅ I − I 2 R − I 2 R − I ′ 2 R′ = U ′ ⋅ I ′ & & U 1 &1 0 m 1 1 2 2 2 2
′ ′ ′ ′ U 1 I 1 cosϕ1 − I Rm − I R1 − I 2 R2 = U 2 I 2 cos ϕ 2
2 0 2 1 2
7、功率关系——叉乘（无功功率） 功率关系——叉乘 无功功率） 叉乘（ 7、 功率关系 、
& E2
& & E s 2 = − jI 2 X 2
& U2
& & U2 = I2ZL
& I2
& I2N2
& Φ s2
& I 2 R2
& & & U 2 = E 2 − I 2 ( R2 + jX 2 )
4. 折合算法
目的: 使一、二次绕组“ ① 目的 a 、使一、二次绕组“有”电的连接 等效电路，这样就用电路知识来解题了。 等效电路，这样就用电路知识来解题了。 b、画相量图方便（定量画法）。 、画相量图方便（定量画法）。 解决方法（算法根据） ② 解决方法（算法根据）
& ′ &′ & ′ &′ &′ ′ &′ ′ U 2 × I 2 = E 2 × I 2 − [ I 2 ( R2 + jX 2 )] × I 2
& ′ × I ′ − I ′2 X ′ = E 2 &2 2 2
′ 2 X 2 = U 2 I 2 sin ϕ 2 ′ ′ U 1 I 1 sin ϕ − I X m − I X 1 − I 2 ′
2 0 2 1
ϕ0
& I0
& Φm
& & &′ I1 = I0 +( −I2 )
& & & U1 =−E + I1Z1 1
& &' E1 = E2
感性负载
7、功率关系——点乘（有功功率） 功率关系——点乘 有功功率） 点乘（ 7、 功率关系 、
& & & & & & U 1 ⋅ I 1 = ( − E 1 ) ⋅ I 1 + [ I 1 ( R1 + jX 1 )] ⋅ I 1
1.1 负载上电压方程
U2 = I2 ZL = I2(RL + jXL )
& & 1.2 磁动势 I1N1 和 I2N2
根据安培环路定律， 根据安培环路定律，此时一二次绕组的磁动势合 & & & & 成产生主磁通。 成产生主磁通。即 F + F = F ，其中 F为合成磁 1 2 0 0 动势。 动势。
& 不变， & 的变化。 保持 F2 不变，就不会影响 F 的变化。 1
定义： ③ 定义：保持一个绕组的磁动势不变而改变其 电流和匝数的算法称为归算法（折合算法）。 电流和匝数的算法称为归算法（折合算法）。
定义：如果保持二次绕组磁动势不变， ④ 定义：如果保持二次绕组磁动势不变，而假想
它的匝数与一次绕组匝数相同的折合算法， 它的匝数与一次绕组匝数相同的折合算法，称为二 次绕组折合成一次绕组或简称二次向一次折合。 次绕组折合成一次绕组或简称二次向一次折合。
& & & & & & U 1 × I 1 = ( − E1 ) × I 1 + [ I 1 ( R1 + jX 1 )] × I 1
& )× (I − I′ ) + I 2 X & & = ( − E1 0 2 1 1 2 & ′ × I′ + I 2 X =I X +E &
0 m 2 2 1 1
& & & U 1 = − E1 + I 1 ( R1 + jX 1 )
& I 1 R1