统计学课件第10章方差分析

合集下载

均值检验方差分析课件

消费行为
通过均值检验和方差分析，可以研究消费者行为、消费习惯、消费心理等方面的差异和变化。
产业组织
在产业组织研究中，均值检验和方差分析可用于研究企业规模、市场结构、企业绩效等方面的差异和变化。
04
均值检验与方差分析的注意事项
数据正态性的检验
总结词
在进行均值检验和方差分析之前，需要检验数据是否符合正态分布。正态分布是许多统计方法的前提假设，如果数据不满足正态分布，可能导致分析结果不准确。
详细描述
为了控制第一类错误的概率，可以采用适当的统计方法进行多重比较校正。例如，在方差分析后，可以使用多重比较校正的方法（如Tukey's HSD、Scheffé's method）来比较各组之间的差异，以减少假阳性错误。此外，还可以根据实际研究目的和数据情况选
择其他适当的统计方法进行多重比较。
适用场景
比较不同组别或不同时间点的平均值
例如比较不同班级的平均成绩、不同月份的平均销售额等。
检验总体均值的假设
例如检验某产品的平均质量是否符合标准。
计算方法
01
02
03
04
计算各组的平均值。
计算标准误差或标准差。
使用t检验或z检验等方法比较平均值。
根据p值判断是否拒绝原假设，即各组平均值相等。
05
均值检验与方差分析的软件实现
SPSS软件实现
描述性统计
SPSS提供了丰富的描述性统计功能，如均值、中位数、众数、标准差等，用于初步了解数据分布情况。
均值检验
SPSS中的“比较均值”功能可以比较两组或多组数据的均值，通过 T检验或非参数检验等方法，判断组间差异是否具有统计学显著性。
方差分析

应用统计学方差分析

3. 数据整理
对收集到的数据进行整理，包括数据筛选、缺失值处理、异常值处理等。
4. 计算统计量
根据方差分析的要求，计算样本均值、总体均值、样本方差、自由度和误差方差等统计量。
5. 检验假设
利用统计量进行假设检验，判断原假设是否成立。
6. 解读结果
根据检验结果解读方差分析的意义，并给出结论和建议。
方差分析的定义与重要性
方差分析的定义
通过比较不同组的均值，确定它们之间是否存在显著差异。它是一种有效的统计工具，用于处理多组数据，并确定这些数据组之间是否存在显著差异。
方差分析的重要性
在许多领域中，如社会科学、医学、生物学和经济学等，需要进行多组数据的比较。通过方差分析，可以更准确地评估这些数据组之间的差异，从而做出更可靠的决策和结论。
05 方差分析的局限性及注意事项
方差分析的局限性
样本量要求
方差分析要求样本量足够大，以便能够准确地估计总体参数。在样本量较小的情况下，方差分析的结果可能不准确。
异常值的影响
方差分析对异常值较为敏感，异常值的存在可能会对分析结果产生较大影响。在进行方差分析前需要进行数据清洗，剔除或处理异常值。
方差分析的假设条件
独立性
各组数据相互独立，即各组数据之间没有相互影响或关联。
正态性
各组数据的分布应符合正态分布，即数据的概率分布应呈现出钟形曲线。
同方差性
各组数据的方差应相等，即各组数据的离散程度应相似。
方差分析的统计推断
统计量计算
在方差分析中，需要计算各组数据的均值、方差和自由度等统计量。
独立性假设
方差分析基于独立观察值的假设，即各组数据之间相互独立。如果数据之间存在相关性，则会影响分析结果的准确性。

统计学之方差分析

执行方差分析
使用Python的方差分析库（如SciPy）进行方差分析，如 “scipy.stats.f_oneway()”。
查看结果
Python将输出方差分析的结果，包括F值、p值、效应量等。
THANKS FOR WATCHING
感谢您的观看
详细描述
独立性检验可以通过卡方检验、相关性检验等方法进行。如果数据不独立，需要考虑数据的相关性和因果关系等因素，以避免误导的分析结果。
06 方差分析的软件实现
SPSS软件实现
导入数据
将数据导入SPSS软件中，选择正确的数据类型和格式。
查看结果
SPSS将输出方差分析的结果，包括F值、 p值、效应量等。
03 方差分析的步骤
数据准备
01
02
03
收集数据
收集实验或调查所需的数据，确保数据来源可靠、准确。
数据筛选
对异常值、缺失值等进行处理，确保数据质量。
数据分组
根据研究目的，将数据分成不同的组或处理水平。
建立模型
确定因子
确定影响因变量的自变量或因子。
建立模型
根据因子和因变量的关系，建立合适的方差分析模型。
统计学之方差分析
目录
• 方差分析简介 • 方差分析的数学原理 • 方差分析的步骤 • 方差分析的应用场景 • 方差分析的注意事项 • 方差分析的软件实现
01 方差分析简介
方差分析的定义
• 方差分析（ANOVA）是一种统计技术，用于比较两个或多个组（或类别）的平均值差异是否显著。它通过对总体平均值的假设检验来进行数据分析，以确定不同条件或处理对观测结果是否有显著影响。
执行方差分析
在SPSS的“分析”菜单中选择“比较均值” 或“一般线性模型”中的“单变量”，然后选择需要进行方差分析的变量。

统计学第十章答案解析

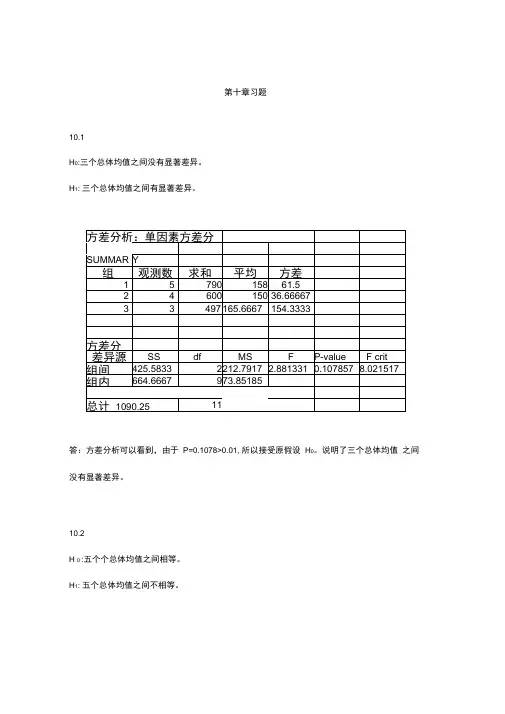
第十章习题10.1H0:三个总体均值之间没有显著差异。

H1: 三个总体均值之间有显著差异。

答：方差分析可以看到，由于P=0.1078>0.01, 所以接受原假设H0。

说明了三个总体均值之间没有显著差异。

10.2H 0 :五个个总体均值之间相等。

H1: 五个总体均值之间不相等。

P=1.02E-05<0.01, H0值之间不相等。

10.3H 0 :四台机器的装填量相等。

H1: 四台机器的装填量不相等答：方差分析可以看到，由于P=0.00068<0.01, 所以拒接原假设H0。

说明了四台机器装填量不相同。

10.4H 0 :不同层次管理者的满意度没有差异。

H1: 不同层次管理者的满意度有差异P=0.000849<0.05, H0理者的满意度有差异。

10.5H0：3 个企业生产的电池平均寿命之间没有显著差异。

H1: 3 个企业生产的电池平均寿命之间有显著差异单因素方差分析多重比较因变量: VAR00002*. 0.05答：方差分析可以看到，由于P=0.00031<0.01, 所以拒接原假设H0。

说明了不同 3 个企业生产的电池平均寿命之间有显著差异。

通过SPSS分析（1,2,3代表A,B,C公司），通过显著性对比可知道A和B以及B和C 公司有差异。

10.6H0：不同培训方式对产品组装的时间没有显著影响。

答：方差分析可以看到，由于P=0.00196<0.05, 所以拒接原假设H0。

说明了不同培训方式对产品组装的时间没有显著影响。

10.8H 0:u 1=u 2=u 3=u 4=u 5 H 1:u i (i=1,2,3,4,5) 不全相等 H 0:u 1=u 2=u 31i对于行因素， P=0.000236<0.01, 所以拒绝原假设。

说明不同供应商生产的轮胎对磨损程度有显著影响。

对于列因素， p=2.39E-06<0.01 ，所以拒绝原假设，说明不同车速对磨损程度有显著影响。

统计学方差分析

统计学方差分析方差分析（Analysis of Variance，缩写为ANOVA）是一种常用的统计学方法，广泛应用于数据分析中。

它的主要目的是用于比较多个样本群体之间的均值是否存在显著差异。

通过方差分析，可以确定因素对于不同组之间的差异程度有无显著影响。

方差分析的基本原理是将数据进行分解，并据此计算各部分之间的均方差（mean square），然后通过比较这些均方差的比值，得出各部分对总体的贡献程度，并进行显著性检验。

在方差分析中，数据通常被分为几个不同的组别，每个组别称为一个因素（factor）。

每个因素可以有不同的水平（level），例如性别因素可以有男和女两个水平。

而一个水平下的所有观测值构成一个处理（treatment）或条件（condition）。

方差分析的基本模型是一种线性模型，假设因变量与自变量之间存在线性关系。

对于单因素方差分析，它的模型可以表示为：Y=μ+α+ε其中，Y表示因变量，μ表示总体的平均值，α表示组别之间的差异，ε表示组内误差。

方差分析的目标是判断组别之间的差异（α）与组内误差（ε）的比值是否显著。

方差分析的核心思想是通过计算均方差，评估不同因素水平之间的差异是否显著。

均方差是方差与其自由度的比值，用于度量数据的离散程度。

通过计算组间均方差（MSTr）和组内均方差（MSE），我们可以得出F值，进而进行显著性检验。

F值是组间均方差与组内均方差的比值F = (MSTr / dfTr) / (MSE / dfE)其中，dfTr表示组间自由度，dfE表示组内自由度。

在统计学中，F值与显著性水平相关。

当F值大于显著性水平对应的临界值时，我们可以拒绝原假设，认为组别之间存在显著差异。

否则，我们不能拒绝原假设，即组别之间的差异不显著。

方差分析不仅可以应用于单因素情况，还可以扩展到多因素情况。

多因素方差分析可以用于研究多个自变量对因变量的影响，并评估这些自变量之间是否存在交互作用。

管理统计学10 第十章方差分析

问:不同的方案是否对汽车销售量产生影响。
星蓝海学习网
10.1 方差分析的内容和思想
10.1.1 方差分析的内容
这是一个方差分析问题。即对四种方案下的电话交易频数的均值是否相等进行检验。由于汽车是同一厂家生产的，它们的质量、外形设计、价格、内装修等所有
可能影响销售量的因素全部相同，如果检验结果 1，2，3，4
2
(xij - x)
2
(xij x j )
2
(x j x)
即
SST = SSE+SSA
关键是如何确定各离差平方的自由度:
对总离差平方和（SST）来说，它是n个离差平方之和，共同拥有一个
平均数，也就失去了一个自由度，其自由度应为n—1。因为它只有一
个约束条件，即 SST
（xij - x） 0
星蓝海学习网
10.2 单因素方差分析
10.2.2 F分布与F值的计算
对水平离差平方和（SSA）来说，它是4组水平（即四种不同方案）离差平方
(x j - x)2之和，共同拥有一个平均数，也失去1个自由度，其自由度为4-1。
用r表示组数，则有 r = 4，4－1 = r－1。它也有一个约束条件，即要求：
为了将方差分析的主要过程表现的更清楚，通常把有关计算结果列成方差分析表，如表10-3所示。
表10-3 方差分析表
星蓝海学习网
10.2 单因素方差分析
10.2.3 样本容量不等下方差分析
进行方差分析时，各个水平下的样本容量可以相同，也可以不同。进行方差分析时，可以把方差分析的因素放在列的位置，也可以放在行的位置，但通常放在列的位置。这样与计算机中数据库的结构相一致，便于计算机处理。

第十方差分析优秀课件

2、自由度的计算
dtfn1
例10-3
n k1（n相等时）
dfb k1
dwf nk dft dfb
dtf918
dbf312 dw f826
kn1 （n相等时）
3、方差（均方）的计算
St2MtS
XXt 2 SS t
dtf
df t
Sb 2MbS
XXt 2
dbf
SS b df b
Sw 2MwS
n X22 n X2 n X2
n 2 k n 2
SSbk nX nX
例10-1
学法
X
∑X ∑X2 n M
A 6 5 7 18 110 3 6
B 11 9 10 30 302 3 10
C
5 4 6 15
77 3 5
∑ －－－
63 489 9 7（Mt）
X X2 n
StSX2 nX2
X X t2 X X 2 k nXXt2 k nXXt2 k nXX2
总平方和组间平方和组内平方和
SS t SS b SS w
计算式
St S XX t2X2 nX2
SbS X X t2nX2
X2
n
Sw S XX 2X2nX2
SSt SSb
k n
2
SSt
C 80 73 70 76 82 5
D 76 74 80 78 82 5
∑
20
∑X
382 420 381 390 1573
∑X2
29276 35314 29129 30460 124179
St S 12 4 11 4 22 7 7 0 4 9 3 .5 65 2
Sb S32 8 4 22 2 5 3 02 8 312 9 1 0 25 20 7 2.3 0 50 5 Sw S 46 .52 520 .50 5262

统计学方差分析

统计学方差分析方差分析（ANOVA）是统计学中一种用于比较多个样本平均值之间差异的方法。

它能够确定因素（或者称之为自变量）对因变量的影响是否显著。

在进行方差分析时，常常使用F检验来判断不同组之间的平均值是否存在显著差异。

方差分析常被用于实验设计和自然观察研究中，特别是在多个因素同时影响因变量的情况下。

方差分析基于总体的假设，即总体的均值相等。

方差分析的目的是确定是否存在一个或多个因素对于因变量的影响。

这些因素可以是分类因素（例如不同的治疗组）或者连续因素（例如不同的剂量水平）。

方差分析通过计算组内变异和组间变异之间的比率来判断这种影响是否显著。

方差分析的基本原理是将组内变异（即观测值之间的差异）与组间变异（即组均值之间的差异）进行比较。

如果组间变异大于组内变异，那么可以推断存在一个或多个因素对于因变量的影响。

通过计算F统计量（组间均方与组内均方之比），可以判断这种影响是否显著。

方差分析有几个基本假设需要满足。

首先，观测值必须是互相独立的。

其次，观测值必须是正态分布的。

最后，方差必须是均匀的，也就是方差齐性假设。

方差分析可以分为单因素方差分析和多因素方差分析。

单因素方差分析适用于只有一个因素对因变量的影响进行研究的情况。

多因素方差分析适用于有多个因素同时对因变量进行影响的情况。

在多因素方差分析中，可以考虑因素之间的交互作用。

方差分析还可以通过进行事后多重比较来进一步研究组之间的差异。

常用的事后比较方法包括LSD（最小显著差异）方法、Tukey HSD（Tukey honestly significant difference）方法和Bonferroni校正方法等。

方差分析在实际应用中具有广泛的应用。

例如，在医学研究中，可以使用方差分析来比较不同治疗组的效果；在工程设计中，可以使用方差分析来确定不同因素对产品质量的影响；在社会科学研究中，可以使用方差分析来研究不同教育程度对工资的影响等等。

方差分析是统计学中重要的一种方法，能够帮助我们了解不同因素对因变量的影响程度。

第10章-方差分析PPT课件

2021/3/9
1.正态性的检验
各组数据的直方图峰度系数、偏度系数 Q-Q图，非参数检验
2021/3/9
2.等方差性的检验
经验方法：计算各组数据的标准差，如果最大值与最小值的比例小于2:1，则可认为是同方差的。最大值和最小值的比例等于1.83<2
Levene检验 *
N
均值标准差
第10章方差分析
2021/3/9
学习目标
掌握方差分析中的基本概念；掌握方差分析的基本思想和原理；掌握单因素、双因素方差分析的应用条件、
意义及计算方法；熟悉多重比较方法的意义及方法；掌握用Excel，spss进行方差分析的操作
方法。
2021/3/9
一、方差分析引论
为什么要进行方差分析？
2021/3/9
（续）组间方差和组内方差
组间离差平方和
k
SSA ni(xi x)2 i1
组内离差平方和
k ni
SSE
(xij xi)2
பைடு நூலகம்i1 j1
组间方差
MSA SSA k 1
2021/3/9
受因素A和随机
因素的影响
组内方差
MSE SSE nk
只受随机因素的影响
（续）方差分析的基本思想
F=
组间方差 MSA SSA k 1
组内方差 MSE SSE
nk
如果因素A的不同水平对结果没有影响，那么在组间方差中只包含有随机误差，两个方差的比值会接近1
如果不同水平对结果有影响，组间方差就会大于组内方差，组间方差与组内方差的比值就会大于1
当这个比值大到某种程度时，就可以说不同水平之间存在显著差异，或者说因素A对结果有显著影响。

方差分析-统计学原理

H0 ：a1 =a2 =…=ar =0
第三节两因素方差分析随机区组设计资料的方差分析
一、随机区组设计随机区组设计（ randomized block design ），又称配伍组设计，是配对设计的扩展。具体做法是：先按影响试验结果的非处理因素将受试对象配成区组（block），再将各区组内的受试对象随机分配到不同的处理组，各处理组分别接受不同的处理，试验结束后比较各组均数之间差别有无统计学意义，以推断处理因素的效应。
各种变异之间的关系是：
SS总 SS处理 SS区组 SS误差
其中：
v总 v处理 v区组 v误差
v区组 n 1
v误差 (n 1)(g 1)
v总 N 1 v处理 g 1
（1）总变异：反映全部试验数据间大小不等的状况，
SS总 X 2 C
方差分析的基本概念
将衡量试验结果的标志称为试验指标。将影响试验结果的条件称为因素。因素在试验中所处的不同状态称为该因素的水平。
只考察一个影响条件即因素的试验称为单因素试验，相应的方差分析称为单因素方差分析。
二、变异分解完全随机设计资料的方差分析表变异来源自由度 SS MS F 总变异
单因子方差分析的统计模型：
yij i ij , j 1, 2,..., mi , i 1, 2,..., r , 2 诸 ij 相互独立，且都服从N (0, )
模型可以改写为
yij ai ij , j 1, 2,..., mi , i 1, 2,..., r , r mi ai 0 i 1 相互独立，且都服从N(0, 2 ) ij
均数间的差异没有统计学意义；反之，如果处理有作用，则组间变异不仅包含随机误差，还有处理因素

统计学中的方差分析

统计学中的方差分析统计学是研究人类活动中涉及到随机事件和不确定性因素的科学。

方差分析（Analysis of Variance, ANOVA）是一种统计学方法，可用于比较两个或多个组之间的差异。

本文将介绍方差分析的基本概念和原理。

一、方差分析的基本概念方差分析是指基于数据的方差计算和分析，以确定比较两组或更多组数据差异的方法。

在方差分析中，被比较的组称为因素，因素又可分为单因素和多因素。

单因素方差分析包括一组数据，而多因素方差分析包括两个及以上的组数据。

方差分析的目的是确定不同组的平均值（即均数）的变异程度。

当平均数之间的差异大于各组内部个体数据的方差时，方差分析可以用来检测这种变异，而不是寻找单一的差异。

方差分析通过比较组之间的方差和误差方差来确定组之间的显著性差异性。

二、方差分析的原理方差分析的原理是基于样本和总体的假设。

以单因素方差分析为例，假设总体是由不同平均数的正态分布组成，且方差相等（即方差齐性）。

然后，从每组中随机地取样本，计算每组的均数和样本方差。

接下来，计算每组的平均数之间的方差（即组间方差）和每组内部样本方差之间的平均数（即组内方差）。

根据方差分析的原理，如果组间方差显著大于组内方差，则说明组间的差异显著，即这些组之间存在显著差异。

否则，如果组间方差与组内方差相等或组内方差超过组间方差，则说明差异不显著。

三、方差分析的步骤通常包括以下步骤：1、获取数据：数据必须充分、均匀，且符合正态分布。

2、检验方差齐性：检验各组数据的方差是否相等。

3、建立假设：建立总体假设和样本假设。

4、计算统计量：计算f值。

5、确定P值：确定P值以确定显著性水平。

6、作出结论：根据显著性水平的大小，对假设的接受或拒绝进行结论。

四、方差分析的应用方差分析应用广泛。

在医学统计学中，方差分析被用于研究不同治疗方案对患者疗效的影响。

在经济学中，方差分析用于分析不同市场条件下商品价格的波动和供求曲线变化的因素。

在生态学中，方差分析可用于分析各种生境因素对植物和动物物种多样性的影响。

方差分析课件-PPT

、、、增重表就是选用S-N-K法作均数多重两两比较得结果
增重表就是选用S-N-K法作均数多重两两比较得结果:
本例按a=0、05水准,将无显著性差异得数归为一类 (Subset for alpha=0、05)。可见
品种5、2、3得样本均数位于同一个子集( Subset )内,说明品种5、品种2、品种3得样本均数两两之间无显著差异; 品种3、4、1位于同一个Subset内,她们之间无显著差异;而品种5、2与品种4、1得样本均数有显著差异。
即三组均数间差异极显著,即不同时期切痂对大鼠肝脏 ATP含量有影响。
LSD法多重比较:
“*”显著性标注两组均数得差
•S-N-K法:本例按0、5水平,将无显著差异得均数归为一类。
•第一组与第三组为一类,无显著差异,它们与第二组之间均数差异显著。
•LSD与S-N-K法,不同得两两比较法会有不同。
如欲了解就是否达到极显著差异,需要将显著水平框中得值输入0、01。
例、为了研究烫伤后不同时间切痂对大鼠肝脏 ATP得影响,现将30只雄性大鼠随机分成3组,每组 10只:A组为烫伤对照组,B组为烫伤后24小时切痂组,C组为烫伤后96小时切痂组。全部大鼠在烫伤 168小时候处死并测量器肝脏ATP含量,结果如下。问试验3组大鼠肝脏ATP总数均数就是否相同。
该12个观察值得总得均值为91、5,标准差为34、 48。
上图为品系、剂量间均值得方差分析(F检验)结果
由表中可知,品系得F=23、771,P=0、001<0、01,差异极显著;
剂量得F=33、537,P=0、001<0、01,差异极显著。说明不同品系与不同雌激素剂量对大鼠子宫得发育均有极显著影响,故有必要进一步对品系、雌激素剂量两因素不同水平得均值进行多重比较。

统计学中的方差分析方差分解

统计学中的方差分析方差分解方差分析（analysis of variance，简称ANOVA）是一种常用的统计方法，它用于比较两个或多个组之间的差异。

在方差分析中，方差分解是一项重要的计算过程，用于将总方差分解成不同来源的方差成分，从而了解各因素对总体差异的影响程度。

1. 概述方差分析方差分解是对方差分析结果进行深入分析的一种方法。

方差分析通过比较组间变异与组内变异来评估不同组之间的差异是否显著。

而方差分解则将总体方差分解为几个基本的成分，以揭示不同因素对差异的贡献。

2. 方差分析方差分解的步骤2.1 总体方差计算首先，我们需要计算总体方差。

总体方差是整个数据集的方差，表示整体的差异程度。

2.2 组间方差计算接下来，计算组间方差。

组间方差反映了不同组之间的差异程度。

2.3 组内方差计算然后，计算组内方差。

组内方差表示同一组内部的差异程度。

2.4 方差分解通过将总体方差分解成组间方差和组内方差，我们可以计算各成分对总差异的贡献。

3. 方差分解的应用方差分解是统计学中广泛应用的一种分析方法，它在众多领域中都有重要的应用价值。

3.1 实验设计在实验设计中，方差分解可以帮助我们分析不同因素对实验结果的影响程度，从而优化实验设计。

3.2 质量控制在质量控制领域，方差分解可以帮助企业分析产品质量的差异来源，以制定相应的质量改进策略。

3.3 教育研究在教育研究中，方差分解可以用于评估不同因素对学生成绩的影响，帮助改进教学方法和教育政策。

4. 总结方差分析方差分解是统计学中一个重要的工具，它可以帮助我们理解不同因素对差异的贡献，为实验设计、质量控制和教育研究等领域提供决策支持。

总之，方差分析方差分解是统计学中的一项重要技术，通过将总方差分解成不同来源的方差成分，我们可以深入分析各因素对总体差异的影响程度。

方差分解在实验设计、质量控制和教育研究等领域都有广泛的应用，为这些领域提供了可靠的数据分析基础。

通过学习和应用方差分析方差分解的方法，我们可以更好地理解和解释数据，为决策提供科学支持。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

如果不同水平的均值间（）A有差异
10 - 19
B无差异
则不同水平间就
A会（）有系统误差
B不会
统计学方差分析的基本思想和原理
STATISTICS (第五版)
(误差平方和—SS)
1.数据的误差用平方和(sum of squares)表示
2.SST 3.组内平方和(within groups)
10 - 3
统计学
STATISTICS (第五版)
10 - 4
统计学
STATISTICS (第五版)
10 - 5
统计学什么是方差分析(ANOVA)?
STATISTICS (第五版)
(analysis of variance)
1.表面上看，是检验多个总体均值是否相等 2. 本质上，是研究变量之间的关系
统计学
STATISTICS (第五版)
第10章方差分析
10 - 1
统计学
STATISTICS (第五版)
第10章方差分析
10.1 方差分析引论 10.2 单因素方差分析
10 - 2
统计学
STATISTICS (第五版)
学习目标
1. 解释方差分析的概念 2. 解释方差分析的基本思想和原理 3. 掌握单因素方差分析的方法及应用 4. 理解多重比较的意义
3.2、分类型自变量对数值型因变量的影响
4.3、方差分析就是通过检验多个总体均值是否相等来判断分类型自变量对数值型因变量是否有显著影响
10 - 6
统计学
STATISTICS (第五版)
什么是方差分析?
(例题分析)
【例】为了对几个行业的服务质量进行评价，消费者协会在4个行业分别抽取了不同的企业作为样本。最近一年中消费者对总共23家企业投诉的次数如下表
每个行业被投诉的次数
10 - 10
统计学
STATISTICS (第五版)
方差分析中的有关术语
1.试验
▪ 这里只涉及一个因素，因此称为单因素4水平的
试验
2.总体
▪ 因素的每一个水平可以看作是一个总体
零售业、旅游业、航空公司、家电制造业是4个总体
3.样本数据
▪ 被投诉次数可以看作是从这4个总体中抽取的样
▪ 因素的同一水平下数据误差的平方和
比如，零售业被投诉次数的误差平方和
▪ 只包含随机误差
10 - 7
统计学
STATISTICS (第五版)
什么是方差分析?
(例题分析)
消费者对四个行业的投诉次数
行业
观测值零售业
旅游业
航空公司
家电制造业
1
57
68
31
44
2
66
39
49
51
3
49
29
21
65
4
40
45
34
77
5
34
56
40
58
6
53
51
7
44
10 - 8
统计学
STAT析?
(例题分析)
1.问题：
2. 4个行业之间的服务质量是否有显著差异，
3. 即“行业X”对“投诉次数Y”是否有显著影响
4.2、检验这四个行业被投诉次数的均值是否相等
5.3、结论：
6.（1）若均值相等，说明“行业”对“投诉次数”没有影响，即4个行业之间的服务质量没有显著差异；
7.（2）若均值不全相等，说明“行业”对“投诉次数 ”有影响，即它们之间的服务质量有显著差异。
10 - 15
统计学
STATISTICS
方差分析的基本思想和原理
(第五版)
1. 散点图观察不能提供充分的证据证明不同行业被投诉的次数之间有显著差异
这种差异可能是由于抽样的随机性所造成的
2. 需要有更准确的方法来检验这种差异是否显著，也就是进行方差分析
10 - 16
统计学
STATISTICS
方差分析的基本思想和原理
(第五版)
1、因为虽然我们感兴趣的是均值，但在判断均值之间是否有差异时则需要借助于方差，所以叫“方差分析”这个名字
2、进行方差分析时，需要考察数据误差的来源它是通过对数据误差来源的分析判断不同总体的均值是否相等。
10 - 17
统计学方差分析的基本思想和原理
STATISTICS (第五版)
行业
统计学方差分析的基本思想和原理
STATISTICS (第五版)
(图形分析)
1. 从散点图上可以看出
不同行业被投诉的次数有明显差异
同一个行业，不同企业被投诉的次数也明显不同
家电制造被投诉的次数较高，航空公司被投诉的次数较低
2. 行业与被投诉次数之间有一定的关系
如果行业与被投诉次数之间没有关系，那么它们被投诉的次数应该差不多相同，在散点图上所呈现的模式也就应该很接近
(两类误差)
1.随机误差： 2. 抽样的随机性所造成的
3.2、系统误差： 4. 不同总体间的系统性因素造成的
10 - 18
统计学方差分析的基本思想和原理
STATISTICS (第五版)
(误差来源及分解)
1、组内误差：来自水平内部的数据误差。仅为随机误差。
2、组间误差：来自不同水平之间的数据误差。随机误差与系统误差的总和。
10 - 9
统计学
STATISTICS (第五版)
方差分析中的有关术语
1.因素或因子(factor)
▪ 所要检验的对象
分析行业对投诉次数的影响，行业是要检验的因子
2.水平或处理(treatment)
▪ 因子的不同表现
零售业、旅游业、航空公司、家电制造业
3.观察值
▪ 在每个因素水平下得到的样本数据
▪ 因素的同一水平下数据误差的平方和
4.组间平方和(between groups)
▪ 因素的不同水平之间数据误差的平方和
10 - 20
统计学方差分析的基本思想和原理
STATISTICS (第五版)
(误差平方和—SS)
1.数据的误差用平方和(sum of squares)表示
2.组内平方和(within groups)
53
51
7
44
样本
10 - 12
数据
统计学
STATISTICS (第五版)
方差分析的基本思想和原理
10 - 13
统计学
STATISTICS (第五版)
80
方差分析的基本思想和原理
(图形分析—散点图)
60
被投诉次数
40
20
0 0
10 - 14
零售1 业
旅游2 业航空3公司家电4制造
5
不同行业被投诉次数的散点图
本数据
10 - 11
统计学
STATISTICS (第五版)
方差分析中的有关术语
(例题分析)
消费者对四个行业的投诉次数
单因素四水平
行业
因素或因子
观测值零售业
旅游业
航空公司
家电制
造业水平或处理
1
57
68
31
44
2
66
39
49
51
观测值
3
49
29
21
65
4
40
45
34
77
5
34
56
40
58
4个总体
6

统计学课件第10章方差分析

均值检验方差分析课件

应用统计学方差分析

统计学之方差分析

统计学第十章答案解析

统计学方差分析

管理统计学10 第十章 方差分析

最新人大版_贾俊平_第五版_统计学_第10章_方差分析PPT课件

第十 方差分析优秀课件

统计学方差分析

第10章-方差分析PPT课件

方差分析-统计学原理

统计学中的方差分析

方差分析课件-PPT

统计学中的方差分析方差分解

管理统计学10 第十章方差分析

第十方差分析优秀课件