云南省建水一中2012届高三10月月考理科数学试题
高2012级数学月考试题(理)及答案

高2012级第一次月考数 学 试 题(理科卷)数学试题卷共4页。
满分150分。
考试时间120分钟。
注意事项:1.答题前,务必将自己的姓名、准考证号填写在答题卡规定的位置上。
2.答选择题时,必须使用2B 铅笔将答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦擦干净后,再选涂其他答案标号。
3.答非选择题时,必须使用0.5毫米黑色签字笔,将答案书写在答题卡规定的位置上。
4.所有题目必须在答题卡上作答,在试题卷上答题无效。
第Ⅰ卷(选择题 共50分) 一.选择题:(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的) 1.函数sin 4y x =的周期是 A.2π B.2π C.4πD.4π 2.在α的终边上取一点为()3,4P -,则cos α= A.45 B.35 C.45- D.35- 3.若3cos 2α=,其中(02)απ<<,则角α所有可能的值是A.6π或116π B.6π或76π C.3π或23π D.3π或53π4.已知定义在[1,1]-上的函数()y f x =的值域为[2,0]-,则函数(cos 2)y f x =的值域为 A.[1,1]- B.[3,1]-- C.[2,0]- D.不能确定5.在等差数列{}n a 中,首项14a =-,2d =,则12345a a a a a ++++= A.0 B.10 C.-10 D.126.函数lg(sin )y x =的定义域为 A.2,22k k k Z πππ⎛⎫+∈ ⎪⎝⎭B.()2,2k k k Z πππ+∈ C.2,22k k k Z πππ⎡⎤+∈⎢⎥⎣⎦D.[]2,2k k k Z πππ+∈7.已知函数()213f x ax ax =+-的定义域是R ,则实数a 的取值范围是 A. 13a > B.13a ≤ C.120a -<< D.120a -<≤ 8.函数2cos 1y x =-2()33x ππ-≤≤的值域是 A.[]2,0- B.[]3,0- C.[]2,1- D.[]3,1- 9.函数)62sin(π+-=x y 的单调递减区间是A.2,263k k k Z ππππ⎡⎤-++∈⎢⎥⎣⎦B.52,266k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦ C.,63k k k Z ππππ⎡⎤-++∈⎢⎥⎣⎦D.5,66k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦10.已知1sin cos 5θθ+=,且θ是第二象限的角,则44sin cos θθ-= A .125 B .725- C .725± D .725第Ⅱ卷(非选择题 共100分)二.填空题(本大题共5小题,每题5分,满分25分,把答案填写在答题卡相应位置上) 11.在等比数列{}n a 中,24a =,5256a =,则公比q = . 12.54sin 28tan 45tan 62tan 36sin 22++= . 13.若3()log (1)f x x =+的反函数为1()y fx -=,则方程1()8f x -=的解x = .14.设扇形的周长为8cm ,面积为24cm ,则扇形的圆心角的弧度数是 . 15.给出下列命题:○1不等式12x≥的解集是12x x ⎧⎫≤⎨⎬⎩⎭; ○2若,αβ是第一象限角,且αβ>,则sin sin αβ>;○3tan 20tan 403tan 20tan 403++=;○4()()2sin 31f x x =+的图象可由2sin 3y x =的图象向左平移1个单位得到; ○5函数()cos 2cos sin xf x x x=-的值域是()2,2-.其中正确的命题的序号是____________________(要求写出所有正确命题的序号).三.解答题:(本大题共6小题,共75分,解答应写出文字说明,证明过程或演算步骤) 16.(本小题满分13分)已知()()tan tan sin()cos()2f x x x x x πππ⎛⎫=-++-+⎪⎝⎭. (1)化简()f x ;(2)当tan 2x =时,求()f x 的值.17. (本小题满分13分)已知3sin()5αβ+=,5cos 13β=-;且α为锐角,β为钝角. (1)求cos()αβ+和sin β; (2)求αsin 的值.18. (本小题满分13分)已知函数()sin()cos()f x x x θθ=+++的定义域为R . (1)当0θ=时,求()f x 的单调递减区间; (2)若(0,)θπ∈,当θ为何值时,()f x 为奇函数.19.(本小题满分12分)已知函数()22sin 2sin cos 3cos f x x x x x =++其中x R ∈. (1)求函数()f x 的最小正周期; (2)当0,2x π⎡⎤∈⎢⎥⎣⎦时,求()f x 的值域;20.(本小题满分12分)一般地,对于函数()y f x =,若存在0x R ∈,使00()f x x =成立,则称0x 为()f x 的不动点.若函数2()(1)1f x ax b x b =+++-其中0a ≠. (1)当1a =,2b =-时,求()f x 的不动点;(2)若对于任意实数b ,函数()f x 恒有两个相异的不动点,求a 的取值范围.21. (本小题满分12分)已知函数()44(4)f x x x x =-+≥的反函数为1()fx -,数列{}n a 满足:11a =,()11n n a f a -+=,*n N ∈,数列121321,,,,n n b b b b b b b ----是首项为1,公比为13的等比数列.(1)求证:数列{}na 为等差数列;(2)求数列{}n b 的通项公式;(3)若n n n c b a =,求数列{}n c 的前n 项和n S .数学试题参考答案2010.4.8一.选择题:ABACD BDCCD二.填空题:11.4; 12.2; 13.2; 14. 2; 15.○3、○5 三.解答题: 文16、理16解:(1)()()()cot tan sin cos f x x x x x =+-- 1sin cos x x =+---------------------6分 (2)()22sin cos 1sin cos x x f x x x =++2tan 1tan 1xx =++2271215=+=+---------------------13分 文17、理17 解:(1)0,22ππαβπ<<<<322παβπ∴<+< 又3sin()5αβ+=,5cos 13β=- 4cos()5αβ∴+=-,12sin 13β=---------------------7分 (2)由(1)可知:()()sin()sinααββ=+-354123351351365⎛⎫⎛⎫=⨯---⨯= ⎪ ⎪⎝⎭⎝⎭---------------------13分 文18解:(1)由77S =,1575S =得()17772a a +⨯=,()11515752a a +⨯= 41a =,85a =---------------------6分 (2)由(1)知:8451144a a d --=== ()()441413n a a n d n n ∴=+-=+-⨯=- 12a ∴=-()()1223152222n n a a n n n S n n +-+-∴===----------------------13分文19、理18解:(1)0θ=时,()sin cos 2sin 4f x x x x π⎛⎫=+=+ ⎪⎝⎭又由322242k x k πππππ+≤+≤+,得 52244k x k ππππ+≤≤+ ∴()f x 的单调递减区间为52,244k k ππππ⎡⎤++⎢⎥⎣⎦k Z ∈---------------------6分 (2)()2sin 4f x x πθ⎛⎫=++ ⎪⎝⎭,又若()f x 为奇函数,则(0)0f =sin 04πθ⎛⎫∴+= ⎪⎝⎭又0θπ<<,从而5444ππθπ<+< 4πθπ∴+=即34θπ∴=---------------------12分(理科13分) 文20、理19 解:(1)1cos 21cos 2()sin 2322x xf x x -+=++⨯ sin 2cos 22x x =++2sin 224x π⎛⎫=++ ⎪⎝⎭∴函数()f x 的最小正周期22T ππ==---------------------6分 (2)由(1)知:()2sin 224f x x π⎛⎫=++ ⎪⎝⎭又 0,2x π⎡⎤∈⎢⎥⎣⎦,则 52,444x πππ⎡⎤+∈⎢⎥⎣⎦ 所以 当242x ππ+=,即 8x π=时,()max 22f x =+当5244x ππ+=,即 2x π=时,()min 1f x = 所以,()f x 的值域为1,22⎡⎤+⎣⎦---------------------12分文21、理20解:(1)当1a =,2b =-时,2()3f x x x =--从而00()f x x =可化为20003x x x --=即01x =-或3所以()f x 的不动点为1-或3---------------------4分 (2)由00()f x x =可化为20010ax bx b ++-=函数()f x 恒有两个相异的不动点∴关于0x 的方程20010ax bx b ++-=恒有两不等实根从而0a ≠且()2410b a b ∆=-->对任意实数b 都成立---------------------8分即关于b 的不等式2440b ab a -+>恒成立216160a a ∴∆=-<即01a <<---------------------12分 理21(1)证明:()2()442f x x x x =-+=-由4x ≥,得()0f x ≥ 所以()21()2f x x -=+所以()211()2n n n a f a a -+==+即:12n n a a +=+故数列{}na 是以11a =为首项,2为公差的等差数列---------------------4分(2)由题意知,11b =,1113n n n b b --⎛⎫-= ⎪⎝⎭所以121321()()()n n n b b b b b b b b -=+-+-++-21111311133323n n -⎛⎫⎛⎫⎛⎫=++++=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭所以数列{}n b 的通项公式为31123n n b ⎛⎫=- ⎪⎝⎭---------------------8分 (3)由(1)得:()12121n a n n =+-=-,即:()221n a n =-由(2)得:31123n n b ⎛⎫=- ⎪⎝⎭所以()3121123n n n n c b a n ⎛⎫==-- ⎪⎝⎭12n n S c c c =+++()233135211352123333nn n ⎡-⎤⎛⎫=++++--++++⎪⎢⎥⎝⎭⎣⎦------------------10分 令23135213333n n n T -=++++ 则234111352321333333n n n n n T +--=+++++ 得:23412111112123333333n n n n T +-⎛⎫=+++++- ⎪⎝⎭ 111112113333n n n -+-⎛⎫=+-- ⎪⎝⎭ 所以113n nn T +=- 又()213521n n ++++-=所以231123n n n S n +⎛⎫=-+ ⎪⎝⎭---------------------12分。
云南省2012届高三第二次高中毕业生复习统一检测数学理试题word版.pdf

云南省2012届高三第二次高中毕业生复习统一检测数学理试题word版.pdf云南省2012年第二次高中毕业生复习统一检测数学试题(理科)本试卷分第I卷(选择题)和第II卷(非选择题)两部分,考试结束后,将本试卷和答题卡一并交回。
满分150分,考试用时120分钟。
第I卷(选择题,共60分)注意事项:1.答题前,考生务必用黑色碳素笔将自己的姓名、准考证号、考场号、座位号在答题卡上填写清楚,并认真核准条形码上的准考证号、姓名、考场号、座位号及科目,在规定的位置贴好条形码。
2.每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦擦干净后,再选涂其它答案标号,答在试卷上的答案无效。
本卷共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
一、选择题1.已知i是虚数单位,则复数等于A.B.C.D.2.已知直线与圆相交于M、N两点,则|MN|等于A.B.C.D.3.已知随机变量X服从正态分布N(0,1),在某项测量中,若X在(-1.96,1.96)内取值的概率等于0.95,则X在内取值的概率等于A.0.025B.0.05C.0.95D.0.9754.已知等于A.B.C.D.5.设由直线围成的封闭图形的面积等于S,则S等于A.B.1C.2D.π6.已知的定义域是集合P,如果,那么的最小值等于A.B.C.D.π7.在棱长为2的正方体ABCD—A1B1C1D1中,点E、F分别是棱AB、BC的中点,则点C1到平面B1EF的距离等于A.B.C.D.8.设R是实数集,平面向量,等于A.4B.C.D.9.已知的渐近线,则m等于A.B.C.D.10.已知平面向量的夹角的正切值等于的值为A.B.2C.—2D.—2,11.已知椭圆E上存在点P,在P与椭圆E的两个焦点F1、F2构成的△F1PF2中,则椭圆E的离心率等于A.B.C.D.12.已知公差不等于0的等差数列的等比中项,那么在数列中,数值最小的项是A.第4项B.第3项C.第2项D.第1项第II卷(非选择题,共90分)本卷包括必考题和选考题两部分,第(13)题~第(21)题为必考题,每个试题考生都必须作答。
云南省建水一中2012届高三9月月考--理科综合

建水一中2012届高三年级9月月考理科综合试卷本试卷分第I卷(选择题)和第II卷(非选择题)两部分,考试结束后只交答题卡。
满分300分,考试用时150分钟。
考生注意:1、答题前,考生务必用黑色碳素笔将自己的班级、姓名、准考证号在答题卡上填写清楚。
2、作答时,考生务必用黑色碳素笔将第I、II卷的答案答在答题卡上相应位置,答在试卷上的答案无效。
第Ⅰ卷(本卷共21小题,每小题6分,共126分)一、选择题:本大题共13小题,每小题6分。
在每小题给出的四个选项中,只有一项是附合题目要求的。
1.下列关于原核生物和真核生物的叙述,正确的是A.原核生物细胞不含线粒体,不能进行有氧呼吸B.真核生物细胞只进行有丝分裂,原核生物细胞只进行无丝分裂C.真核生物以DNA为遗传物质,部分原核生物以RNA为遗传物质D.真核生物细胞具有细胞膜系统(生物膜系统),有利于细胞代谢有序进行2.右图中①~④表示某细胞的部分细胞器。
下列有关叙述正确的是A.结构①是细胞生命活动所需能量的主要来源B.结构①~④中都含有大量磷脂C.此细胞不可能是植物细胞,只能是动物细胞D.该图一定是高倍光学显微镜下看到的结构3.下列与细胞内物质运输有关的叙述,正确的是A.叶绿体合成的ATP通过核孔进入细胞核B.氢离子可以通过扩散作用进入液泡内C.细胞对离子的吸收具有选择性D.人成熟红细胞吸收葡萄糖的过程消耗能量4.下列有关酶的叙述,正确的是A.酶的基本组成单位都是氨基酸B.低温、高温、过酸、过碱都会使酶永久失活的固定都需要酶的参与C.水的跨膜运输、CO2D.酶催化效率高是因为其降低活化能的作用显著5.ATP是细胞的能量“通货”,下列有关ATP的叙述正确的是A.三磷酸腺苷是生命活动的直接能源物质,其结构简式为ATPB.ATP水解失去2个磷酸基团后,剩余部分是RNA的组成单位之一C.植物细胞产生的ATP,均可用于一切生命活动D.蓝藻内产生ATP的场所有细胞质基质、线粒体以及叶绿体6.下列有关实验及显色结果的叙述,正确的是....A.水浴加热条件下,蔗糖与斐林试剂发生作用生成砖红色沉淀B.脱氧核苷酸与吡罗红发生作用呈现红色C.常温条件下,蛋白质与双缩脲试剂发生作用呈现紫色D.常温条件下,脂肪可被苏丹Ⅲ染成红色7.以节能减排为基础的低碳经济是保持社会可持续发展的战略举措,下列做法违背发展低碳经济的是 A .发展氢能和太阳能B .尽量用纯液态有机物代替水作溶剂C .提高原子利用率,发展绿色化学D .限制塑料制品的使用 8.下列能达到实验目的的是9.下列液体均处于25℃,有关叙述正确的是A .某物质的溶液p H < 7,则该物质一定是酸或强酸弱碱盐B .p H = 5.6的CH 3COOH 与CH 3COONa 混合溶液中,c(Na +) > c(CH 3COO -) C .AgCl 在同浓度的CaCl 2和NaCl 溶液中的溶解度相同D .p H = 4.5的番茄汁中c(H +)是p H = 6.5的牛奶中c(H +)的100倍 10.将NaCl 溶液滴在一块光亮清洁的铁板表面上,一段时间后发现液滴覆盖的圆周中心区(a)已被腐蚀而变暗,在液滴外沿形成棕色铁锈环(b),如图所示。
2012年高三数学10月月考试题组编含答案
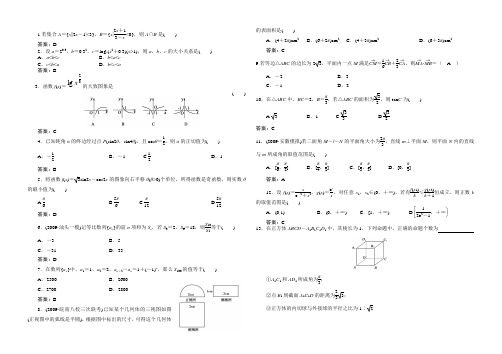
1.若集合A ={x ||2x -1|<3},B ={x |2x +13-x<0},则A ∩B 是( )答案:D2.设a =20.3,b =0.32,c =log x (x 2+0.3)(x >1),则a ,b ,c 的大小关系是( ) A .a <b <c B .b <a <c C .c <b <a D .b <c <a 答案:B 3.函数f (x )=32lg x的大致图象是( )答案:C4.已知钝角α的终边经过点P (sin2θ,sin4θ),且cos θ=12,则α的正切值为( )A .-12B .-1 C.12D .1答案:B5.将函数f (x )=3sin2x -cos2x 的图象向右平移θ(θ>0)个单位,所得函数是奇函数,则实数θ的最小值为( )A.π6B.5π6C.π12D.5π12答案:D6.(2009·汕头一模)记等比数列{a n }的前n 项和为S n ,若S 3=2,S 6=18,则S 10S 5等于( )A .-3B .5C .-31D .33答案:D7.在数列{a n }中,a 1=1,a 2=2,a n +2-a n =1+(-1)n ,那么S 100的值等于( ) A .2500 B .2600 C .2700D .2800答案:B8.(2009·皖南八校三次联考)已知某个几何体的三视图如图(正视图中的弧线是半圆),根据图中标出的尺寸,可得这个几何体的表面积是( )A .(4+2π)cm 2B .(6+2π)cm 2C .(4+3π)cm 2D .(6+3π)cm 2答案:C9.若等边△ABC 的边长为23,平面内一点M 满足CM →=16CB →+23CA →,则MA →·MB →=( A )A .-2B .3C .-1D .210.在△ABC 中,BC =2,B =π3,若△ABC 的面积为32,则tan C 为( )A. 3B .1 C.33D.32答案:C11.(2009·安徽模拟)若二面角M -l -N 的平面角大小为2π3,直线m ⊥平面M ,则平面N 内的直线与m 所成角的取值范围是( )A .[π6,π2]B .[π4,π2]C .[π3,π2]D .[0,π2]答案:A12.设f (x )=x e -2+x 2,g (x )=e x x ,对任意x 1,x 2∈(0,+∞),若有f (x 1)k ≤g (x 2)k +1恒成立,则正数k的取值范围是( )A .(0,1)B .(0,+∞)C .[1,+∞) D.⎣⎡⎭⎫12e 2-1,+∞答案:C13.在正方体ABCD -A 1B 1C 1D 1中,其棱长为1,下列命题中,正确的命题个数为①A 1C 1和AD 1所成角为π3;②点B 1到截面A 1C 1D 的距离为233;③正方体的内切球与外接球的半径之比为1∶ 214.若}{n a 是等差数列,n S 是其前n 项和,083>+a a ,09<S ,则1S ,2S ,3S ,…,n S 中最小的是5S .15.在△ABC 中,∠C 为直角,且AB BC ⋅u u u r u u u r +BC CA ⋅u u u r u u u r +CA AB ⋅u u u r u u u r=-25,则AB 的长为 .15.5.16.等给出以下结论: ①通项公式为1132-⎪⎭⎫⎝⎛⋅=n n a a 的数列一定是以1a 为首项,32为公比的等比数列;②若0cos sin >⋅θθ,则θ是第一、三象限的角;③函数xx y 2+=在()+∞,0上是单调减的;④若等差数列{n a }前n 项和为n S ,则三点⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛110,110,100,100,10,1011010010S S S 共线;⑤为了得到函数x x y 2cos 232sin 21-=的图象,可以将函数x y 2sin =的图象向右平移6π个单位长度. 其中正确的是②④⑤ .(请填写所有正确选项的序号)17. 已知△ABC 的内角A ,B ,C 所对的边分别为a ,b ,c ,且a =2,cos B =35.(1)若b =4,求sin A 的值;(2)若△ABC 的面积S △ABC =4,求b ,c 的值.解:(1)∵cos B =35>0,且0<B <π,∴sin B =1-cos 2B =45,由正弦定理得a sin A =bsin B,∴sin A =a sin Bb =2×454=25.(2)∵S △ABC =12ac sin B =4,∴12×2×c ×45=4, ∴c =5.由余弦定理得b 2=a 2+c 2-2ac cos B , ∴b =a 2+c 2-2ac cos B=22+52-2×2×5×35=17.18. (2009·潍坊二检)已知等差数列{a n }和正项等比数列{b n },a 1=b 1=1,a 3+a 5+a 7=9,a 7是b 3和b 7的等比中项.(1)求数列{a n }、{b n }的通项公式;(2)若c n =2a n ·b 2n ,求数列{c n }的前n 项和T n .解:(1)设等差数列{a n }的公差为d ,等比数列{b n }的公比为q , 由题设知a 3+a 5+a 7=9,∴3a 5=9,∴a 5=3. 则d =a 5-a 14=12,∴a n =a 1+(n -1)d =n +12.∴a 7=4.又∵a 27=b 3·b 7=16, ∴b 25=b 3·b 7=16, 又b 5>0,∴b 5=4, ∴q 4=b 5b 1=4,又q >0,∴q =2, ∴b n =b 1·qn -1=2n -12.(2)c n =2a n ·b 2n =(n +1)·2n -1, ∴T n =c 1+c 2+…+c n =2+3×2+4×22+…+(n +1)·2n -1,① 2T n =2×2+3×22+…+n ·2n -1+(n +1)·2n ,②①-②得,-T n =2+2+22+…+2n -1-(n +1)·2n =1-2n 1-2-(n +1)·2n +1=-n ·2n .∴T n =n ·2n .19.偶函数f (x )=ax 4+bx 3+cx 2+dx +e 的图象过点P (0,1),且在x =1处的切线方程为y =x -2,求y =f (x )的解析式.BCDPE解:∵f (x )的图象过点P (0,1), ∴e =1.①又∵f (x )为偶函数,∴f (-x )=f (x ).故ax 4+bx 3+cx 2+dx +e =ax 4-bx 3+cx 2-dx +e .∴b =0,d =0.② ∴f (x )=ax 4+cx 2+1.∵函数f (x )在x =1处的切线方程为y =x -2, ∴可得切点为(1,-1).∴a +c +1=-1.③ ∵f ′(1)=(4ax 3+2cx )|x =1=4a +2c , ∴4a +2c =1.④ 由③④得a =52,c =-92.∴函数y =f (x )的解析式为 f (x )=52x 4-92x 2+1.20. (2009·淄博模拟)如右图,在四棱锥S —ABCD 中,底面ABCD 是正方形,SA ⊥平面ABCD ,且SA =AB ,点E 为AB 的中点,点F 为SC 的中点.(1)求证:EF ⊥CD ;(2)求证:平面SCD ⊥平面SCE . 证明:(1)连结AC 、AF 、BF 、EF .∵SA ⊥平面ABCD ,∴AF 为Rt △SAC 斜边SC 上的中线, ∴AF =12SC .又∵ABCD 是正方形,∴CB ⊥AB .而由SA ⊥平面ABCD ,得CB ⊥SA , 又AB ∩SA =A ,∴CB ⊥平面SAB .∴CB ⊥SB , ∴BF 为Rt △SBC 斜边SC 上的中线, ∴BF =12SC .∴△AFB 为等腰三角形,EF ⊥AB . 又CD ∥AB ,∴EF ⊥CD .(2)由已知易得Rt △SAE ≌Rt △CBE ,∴SE =CE ,即△SEC 是等腰三角形,∴EF ⊥SC . 又∵SC ∩CD =C ,∴EF ⊥平面SCD . 又EF ⊂平面SCE ,∴平面SCD ⊥平面SCE .21、如图所示:正四棱锥ABCD P -中,侧棱PA 与底面ABCD 所成角的正切值为26。
云南省2012届第一次省统测超详细解析(理数)

2012年云南省第一次高中毕业生复习统一检测理科数学第1题:(1)函数)32(tan 4)(π+=x x f 的最小正周期等于(A )4π (B )3π (C )2π(D )π 解:∵)32(tan 4)(π+=x x f x 2tan 4=,∴x x f 2tan 4)(=的最小正周期为2π. 故选(C ).答题分析:1.有的考生可能是错误地记成了正弦函数的周期,故得到了错误答案22T ππ==,从而错选(D ). 2.需要强调的是:如果对三角函数的图象性质有深刻地理解,那么可以知道()4ta n (23)f x x π=+与tan (2)y x =的周期相同,因此本题不必化简函数就可以直接得出答案.第2题:抛物线022=+y x 的准线方程是(A )81=x (B )81=y (C )81-=x (D )81-=y 解:∵022=+y x ,∴y x 212-=.∵y x 212-=的准线方程是81=y ,∴抛物线022=+y x 的准线方程是81=y .故选(B ).答题分析:一些考生把抛物线的开口方向判断错了,得出了错误答案.关于抛物线的四种标准方程,务必注意它们的开口方向同方程结构的关系,关于这个知识点,历年来的各种大型考试多有所涉及,可出错的考生每次都不少!第3题:已知i 是虚数单位,i z 201220121+=,i z 312-=,那么复数221z z z =在复平面内对应的点位于(A )第一象限 (B )第二象限(C )第三象限 (D )第四象限解:∵)3(5201231)1(2012222221i i i z z z +-=-+==∴221z z z =在复平面上对应的点位于第二象限.故选(B ).答题分析:一些考生可能是复数运算有失误而导致出错.第4题:在765)1()1()1(x x x +++++的展开式中,4x 的系数等于(A )22 (B )25 (C )52 (D )55 解:∵()()()567111x x x +++++展开式中含4x 项的系数是4142435671115153555C C C ⋅+⋅+⋅=++=,∴多项式()()()567111x x x +++++中,4x 的系数等于55. 故选(D ).答题分析:本题也可以先把式子变形,再求4x 的系数.当0x ≠时,()()()53567111(1)(1)(1)=x x x x x x+-++++++-,接下来再求分子的5x 项的系数的相反数即可.这样做,在解答本题上并没有多少优势,但如果题目中的项数比较多的时候,优势就比较明显了.第5题:下图是一个几何体的三视图,其中正视图是边长为2的等边三角形,侧视图是直角边长分别为1与3的直角三角形,俯视图是半径为1的半圆,则该几何体的体积等于正视图侧视图俯视图(A )π63 (B )π33 (C )π334 (D )π21解:∵在几何体的三视图中,正视图是边长为2的等边三角形,侧视图是直角边长分别为1与3的直角三角形,俯视图是半径为1的半圆,∴此几何体是底面半径等于1,高等于3的半个圆锥.∴该几何体的体积等于π63. 故选(A ).答题分析:1.一些考生到了最后关头,忘了是半个圆锥,没有把体积除以2,所以误选B.2.由三视图还原立体图形,对学生的空间想象能力要求较高,也一直是近几年新课标高考的常考题型,在教学中要重点突破! 第6题:函数322122+---=x x x y 的极大值等于(A )51(B )1- (C )1 (D )2- 解:∵322122+---=x x x y , ∴222222)322(844322()24)(12(644+--+=+--++-+-='x x x x x x x x x x y ). ∵当2-<x 或1>x 时,0>'y ,当12<<-x 时,0<'y , ∴当2-=x 时,y 取得极大值.∴y 的极大值等于51. 故选(A ).答题分析:1.一些考生对分式函数求导不够熟练,导致了错误.2.研究分式函数的性质,通法是以导数为工具.第7题:在等比数列{}n a 中,6a 与7a 的等差中项等于48,610987654128=a a a a a a a . 如果设{}n a 的前n 项和为n S ,那么=n S(A )45-n(B )34-n(C )23-n(D )12-n解:设等比数列{}n a 的公比为q ,由已知得⎩⎨⎧=+=96)1(1285164271q q a q a ,化简得 ⎩⎨⎧=+=96)1(251661q q a q a ,解得⎩⎨⎧==211q a . ∴12-=n n S . 选(D ).答题分析:本题考查基本量方法以及方程的思想.对计算能力的考查,一直是高考数学的一个着眼点,教学中要加强对计算能力的培养,学生对常见的计算问题,如解方程组、解不等式组等要训练有素.第8题:某校对高三年级学生进行体检,并将高三男生的体重)(kg 数据进行整理后分成五组,绘制成下图所示的频率分布直方图. 如果规定,高三男生的体重结果只分偏胖、偏瘦和正常三个类型,超过kg 65属于偏胖,低于kg 55属于偏瘦.已知图中从左到右第一、第三、第四、第五小组的频率分别为25.0、2.0、1.0、05.0,第二小组的频数为400. 若该校高三男生的体重没有kg 55和kg 65,则该校高三年级的男生总数和体重正常的频率分别为(A )1000,5.0 (B )800, 5.0 (C )800, 6.0(D )1000,6.0解:由已知信息得第二小组的频率等于4.005.01.02.025.01=----,设该校高三年级的男生总数为n ,则4.0400=n,解得1000=n . 体重正常的频率分别为6.005.01.025.01=---.选(D ).答题分析:对于频率分布直方图问题,读懂题意、正确识图(统计图)是解决问题的关键.第9题:已知),(21-=,)53,(=,则向量在向量方向上的投影等于(A )557-(B )34347- (C )557 (D )34347解:∵),(21-=,)53,(=,∴7-=⋅34=34347-=. ∴向量a 在向量b 方向上的投影为34347-. 选(B ). 答题分析:1. 向量a 在向量b 方向上的投影,根据定义等于cos ,a a b 〈〉.一些考生正是通过计算模长和两向量夹角的余弦值的积来获得答案,这无疑是正确的,但加大了运算量.2. 向量a 在向量b 方向上的投影等于a b b ⋅ ,由cos ,a ba ab b⋅〈〉=可得,应理解该公式并牢牢记清楚.另一方面还可结合点积的形方面进行记忆。
云南省部分名校2012届高三数学第二次联考试题 理 新人教A版

xy O32π- 2 34π-4云南省部分名校高2012届第二次统一考试(玉溪一中、楚雄一中、昆明三中)理 科 数 学一、单项选择题(每小题5分,共60分)1.设全集{}1,2,3,4,5U =,集合{1,2,4}A =,{4,5}B =,则图中的阴影部分表示的集合为A .{}5B .{}4C .{}1,2D .{}3,52.已知非零向量a 、b 满足b a =,那么向量b a +与向量b a -的夹角为A .6π B .3π C .2π D .23π3.61()2x x -的展开式中第三项的系数是 A .154- B .154 C .15 D .52-4.圆22420x y x +-+=与直线l 相切于点(3,1)A ,则直线l 的方程为A .250x y --=B .210x y --=C .20x y --=D .40x y +-=5.某单位员工按年龄分为A ,B ,C 三组,其人数之比为5:4:1,现用分层抽样的方法从总体中抽取一个容量为20的样本,已知C 组中甲、乙二人均被抽到的概率是,451则该单位员工总数为 A .110 B .100 C .90 D .806、右边程序框图的程序执行后输出的结果是( ). A ,24, B ,25, C ,34, D ,357.已知函数sin()y A x B ωφ=++ (0,0,||2A ωφπ>><) 的周期为T ,在一个周期内的图象如图所示, 则正确的结论是( ).A.3,2A T ==πB.2,1=-=ωB开始1n =0S =10?n >输出S2n n =+S S n=+结束是 否C.4,6T φπ=π=-D.3,6A φπ== 8.将函数sin()3y x =-π的图像上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将所得图像向左平移3π个单位,则所得函数图像对应的解析式为A.1sin()26y x =-πB.1sin()23y x =-πC.1sin 2y x = D.sin(2)6y x =-π9.长方体ABCD —A 1B 1C 1D 1中,12,AB AD AA ===1D 到直线AC 的距离是 A .3 B..410. 设双曲线12222=-by a x (a >0,b >0)的一条渐近线与抛物线12+=x y 有且只有一个公共点,则双曲线的离心率为. A.45 B. 5 C. 25 D.5 11,设a ,b 是不同的直线,α、β是不同的平面,则下列命题: ①若,,//;ab a b αα⊥⊥则②若//,,;aa ααββ⊥⊥则③若βαβ⊥⊥,a ,则a ∥α④若,,,.a b a b αβαβ⊥⊥⊥⊥则其中正确命题的个数是A .0B .1C .2D .312.设函数[],0(),(1),0x x x f x f x x -≥⎧=⎨+<⎩其中][x 表示不超过x 的最大整数,如]2.1[-=-2,]2.1[=1,]1[=1,若直线y=)0(>+k k kx 与函数y=)(x f 的图象恰有三个不同的交点,则k 的取值范围是A .]31,41(B .]41,0(C .]31,41[D .)31,41[二、填空题(每小题5分,共20分)13、已知满足约束条件⎪⎩⎪⎨⎧≤≥+≥+-3005x y x y x ,则2z x y =+的最小值是14.与椭圆1422=+y x 有相同的焦点且过点P )1,2(的双曲线方程是15.一个球与一个正三棱柱的三个侧面和两个底面都相切,已知这个球的体积是π332,那么这个三棱柱的体积是 .16.对于复数=z i -1,有下面4个命题:①它在复平面上对应的点在第二象限;②它的平方是一个纯虚数;③它的模是2;④0)(22=+z z 。
云南省建水一中2012届高三数学10月月考试题 理
建水一中70届高三年级10月月考数学试卷(理)一、选择题:(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1. 复数11i+在复平面上对应的点的坐标是( )A .(1,1) B. (1,1)- C. (1,1)-- D. (1,1)- 2. 下列说法错误的是( )A .自变量取值一定时,因变量的取值带有一定随机性的两个变量之间的关系叫做相关关系;B .线性回归方程对应的直线y ^=b ^x +a ^至少经过其样本数据点(x 1,y 1), (x 2,y 2),…,(x n ,y n )中的一个点;C .在残差图中,残差点分布的带状区域的宽度越狭窄,其模型拟合的精度越高;D .在回归分析中,2R 为0.98的模型比2R 为0.80的模型拟合的效果好 3.如图,若程序框图输出的S 是126,则判断框①中应为 ( ) A .5n ≤B .6n ≤C .7n ≤D .8n ≤4.若一个三位数的十位数字比个位数字和百位数字都大,称 这个数为 “伞数”。
现从1,2,3,4,5,6这六个数字中取 3个数,组成无重复数字的三位数,其中“伞数” 有 ( ) A .120个 B .80个 C .40个 D .20个5. 若x 为三角形中的最小内角,则函数y=sinx+cosx 的值域是( ) A .,21[]22 B .]23,0( C .]2,1( D .]22,21( 6. 一个几何体按比例绘制的三视图如图所示(单位:m )则该几何体的体积为( )3m .A .37 B .29 C .27 D .49S否7.双曲线222210,0)x y a b a b-=>>(的渐近线与圆22(2)1x y +-=相切,则双曲线的离心率为( )A B .2 D .38.已知直线l :0Ax By C ++=(A ,B 不全为0),两点111(,)P x y ,222(,)P x y ,若1122()()0Ax By C Ax By C ++++>,且1122Ax By C Ax By C ++>++,则( )A .直线l 与直线P 1P 2不相交B .直线l 与线段P 2 P 1的延长线相交C .直线l 与线段P 1 P 2的延长线相交D .直线l 与线段P 1P 2相交9. 下列有关命题的说法正确的是( ) A .命题“若1,12==x x 则”的否命题为:“若1,12≠=x x 则” B .“x=-1”是“0652=--x x ”的必要不充分条件C .命题“01,2<++∈∃x x R x 使得”的否定是:“01,2<++∈∀x x R x 均有”D .命题“若y x y x sin sin ,==则”的逆否命题为真命题10.已知非零向量,,→→→a b c 满足0→→→→++=a b c ,向量,→→a b 的夹角为120,且||2||→→=b a ,则向量→→与a c 与的夹角为 ( )A .︒60B .︒90C .︒120 D . ︒15011.设=)(x f R x x x ∈+,3,当02πθ≤≤时,0)1()sin (>-+m f m f θ恒成立,则实数m 的取值范围是( )A .(0,1)B .)0,(-∞C .)21,(-∞D .)1,(-∞12.已知正六棱柱的12个顶点都在一个半径为3的球面上,当正六棱柱的体积最大(柱体体积=底面积⨯高)时,其高的值为( )A .B .CD 二、填空题(本大题共4小题,每小题5分,共20分)13.在等比数列}{n a 中,若3753)3(-=⋅⋅a a a ,则=⋅82a a .14.已知向量(1,2),(4,)a x b y →→=-=),若向量a →垂直向量b →,则yx 39+的最小值为 .15.已知函数2()321f x x x =++,若1()2()1f x dx f a =-⎰成立,则a =______________;16. 已知函数()124-+=x x f 的定义域是[]b a ,(b a ,是整数),值域是[]1,0,则满足条件的定义域的可能情况共有 种.三、解答题(本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤) 17. (本小题满分10分)已知{}n a 是等差数列,其中37618,11a a a +==. (Ⅰ)求数列{}n a 的通项公式;(Ⅱ)若数列{}n b 满足()12n n n b a n N -*=+∈ ,求数列{}n b 的前n 项和n T . 18.(本小题满分12分)函数()()()sin 0,0,f x A x b A ωϕωϕπ=++>>≤在一个周期内,当6x π=时,y 取最小值1;当23x π=时,y 取最大值3. (I)求()f x 的解析式; (II)求()f x 在区间3,2ππ⎡⎤⎢⎥⎣⎦上的最值.19. (本小题满分12分)如图,已知菱形ABCD 的边长为6,60BAD ∠=,O BD AC =⊥.将菱形ABCD 沿对角线AC 折起,使32BD =,得到三棱锥B ACD -.(Ⅰ)若点M 是棱BC 的中点,求证://OM 平面ABD ; (Ⅱ)求二面角A BD O --的余弦值; (Ⅲ)设点N 是线段BD 上一个动点,试确定N 点的位置,使得42CN =,并证明你的结论.20. (本小题满分12分)某校从参加某次知识竞赛的同学中,选取60名同学将其成绩(百分制)(均为整数)分 成6组后,得到部分频率分布直方图(如图),观察图形中的信息,回答下列问题. (Ⅰ)求分数在[70,80)内的频率,并补全这个频率分布直方图; (Ⅱ)从频率分布直方图中,估计本次考试的平均分;(Ⅲ)若从60名学生中随机抽取2人,抽到的学生成绩在[40,70)记0分,在[70,100]记1分,用X 表示抽取结束后的总记分,求X 的分布列和数学期望.M21.(本小题满分12分)已知椭圆2222:1(0)x y C a b a b+=>>过点(0,1),且离心率为32.(Ⅰ)求椭圆C 的方程;(Ⅱ),A B 为椭圆C 的左右顶点,直线:22l x =x 轴交于点D ,点P 是椭圆C 上异于,A B 的动点,直线,AP BP 分别交直线l 于,E F 两点.证明:当点P 在椭圆C 上运动时,||||DE DF ⋅恒为定值.22. (本小题满分12分)已知函数2()ln (2)f x x ax a x =-+-.(Ⅰ)若()f x 在1x =处取得极值,求a 的值;(Ⅱ)求函数()y f x =在2[,]a a 上的最大值.建水一中高70届十月月考理科数学试题答案一、 选择题 题号 123 4 5 6 7 8 9 10 11 12 答案 D B BCCCCCDBDB13.3 14.6 15.1-或1316. 5 三、解答题 17.18.解:(I)∵在一个周期内,当6x π=时,y 取最小值1;当23x π=时,y 最大值3. ∴21,2,2362T A b πππ===-=,,2T πω==,()()sin 22f x x ϕ=++, 由当23x π=时,y 最大值3得()44sin 1,2332k k Z πππϕϕπ⎛⎫+=+=+∈⎪⎝⎭526k πϕπ=-,∵ϕπ≤,∴5.6ϕπ=-()5sin 2 2.6f x x π⎛⎫=-+ ⎪⎝⎭故: (II) ∵3,2x ππ⎡⎤∈⎢⎥⎣⎦, ∴75132666x πππ≤-≤, ∴当32x π=时,()f x 取最大值52;当76x π=时,()f x 取最小值1.19. (Ⅰ)证明:因为点O 是菱形ABCD 的对角线的交点,所以O 是AC 的中点.又点M 是棱BC 的中点,所以OM 是ABC ∆的中位线,//OM AB . 因为OM ⊄平面ABD ,AB ⊂平面ABD ,所以//OM 平面ABD . (Ⅱ)解:由题意,3OB OD ==,因为32BD =所以90BOD ∠=,OB OD ⊥.又因为菱形ABCD ,所以OB AC ⊥,OD AC ⊥. 建立空间直角坐标系O xyz -,如图所示.(33,0,0),(0,3,0),A D (0,0,3)B .所以(33,0,3),(33,3,0),AB AD =-=-ABODxyzM设平面ABD 的法向量为n =(,,)x y z ,则有0,0AB AD ⎧⋅=⎪⎨⋅=⎪⎩n n 即:3330,3330x z x y ⎧-+=⎪⎨-+=⎪⎩令1x =,则3,3y z ==,所以n =(1,3,3). 因为,AC OB AC OD ⊥⊥,所以AC ⊥平面BOD . 平面BOD 的法向量与AC 平行,所以平面BOD 的法向量为0(1,0,0)=n .00017cos ,717⋅〈〉===⨯n n n n n n ,因为二面角A BD O --是锐角, 所以二面角A BD O --的余弦值为77. (Ⅲ)解:因为N 是线段BD 上一个动点,设111(,,)N x y z ,BN BD λ=,则111(,,3)(0,3,3)x y z λ-=-,所以1110,3,33x y z λλ===-, 则(0,3,33)N λλ-,(33,3,33)CN λλ=-,由42CN =得22279(33)42λλ++-=,即29920λλ-+=,解得13λ=或23λ=, 所以N 点的坐标为(0,2,1)或(0,1,2).(也可以答是线段BD 的三等分点,2BN ND =或2BN ND =)20.解:(Ⅰ)设分数在[70,80)内的频率为x,根据频率分布直方图,则有(0.01+0.015×2+0.025+0.005)×10+x=1,可得 x=0.3,所以频率分布直方图如图所示.(Ⅱ)平均分为:450.1550.15650.15750.3850.25950.0571.x =⨯+⨯+⨯+⨯+⨯+⨯=(Ⅲ)学生成绩在[40,70)的有0.4×60=24人, 在[70,100]的有0.6×60=36人,并且X 的 可能取值是0,1,2.11222436362422260606046144105(0);(1);(2).295295295C C C C P X P X P X C C C =========则 所以X 的分布列为21. 解:(Ⅰ)由题意可知,1b =,而2c a =且222a b c =+. 解得2a =,所以,椭圆的方程为2214x y +=. (Ⅱ)(2,0),(2,0)A B -.设00(,)P x y ,022x -<<,直线AP 的方程为00(2)2y y x x =++,令x =002)2y y x =+, 即00||||2)|2|y DE x =+;直线BP 的方程为00(2)2y y x x =--,令x =0y = 即00||||2)|2|y DF x =-;0000||||||||2)2)|2||2|y y DE DF x x ⋅=⋅+-2200220044|4|4y y x x ==-- 而220014x y +=,即220044y x =-,代入上式,∴||||1DE DF ⋅=,所以||||DE DF ⋅为定值1.22. 解:(Ⅰ)∵2()ln (2)f x x ax a x =-+-, ∴函数的定义域为(0,)+∞.∴2112(2)(21)(1)()2(2)ax a x x ax f x ax a x x x-+---+'=-+-==.()f x 在1x =处取得极值,即(1)(21)(1)0f a '=--+=, ∴1a =-. 当1a =-时,在1(,1)2内()0f x '<,在(1,)+∞内()0f x '>,∴EX =0×46295+1×144295+2×105295=354295.∴1x =是函数()y f x =的极小值点. ∴1a =-.(2)∵2a a < , ∴01a <<.2112(2)(21)(1)()2(2)ax a x x ax f x ax a x x x-+--+'=-+-==-∵ x ∈(0,)+∞, ∴10ax +>,∴()f x 在1(0,)2上单调递增;在1(,)2+∞上单调递减,①当102a <≤时, ()f x 在2[,]a a 单调递增,∴32max ()()ln 2f x f a a a a a ==-+-;②当21212a a ⎧>⎪⎪⎨⎪<⎪⎩,即122a <<时,()f x 在21(,)2a 单调递增,在1(,)2a 单调递减,∴max 12()()ln 21ln 22424a a a f x f -==--+=--; ③当212a ≤1a ≤<时,()f x 在2[,]a a 单调递减, ∴2532max ()()2ln 2f x f a a a a a ==-+-.综上所述,当102a <≤时,函数()y f x =在2[,]a a 上的最大值是32ln 2a a a a -+-;当122a <<时,函数()y f x =在2[,]a a 上的最大值是1ln 24a --;当2a ≥时,函数()y f x =在2[,]a a 上的最大值是5322ln 2a a a a -+-.。
云南省建水一中2012届高三数学11月月考 理
建水一中2011年11月高考适应性考试数学试卷(理工类)考试时间:2011年11月7日下午15:00 —— 17:00本试卷分第I 卷(选择题)和第II 卷(非选择题)两部分。
共150分。
考试时间120分钟。
第I 卷(选择题 共60分) 一、选择题:(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的. 每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑.)1.已知集合},1|{2R x x y y M ∈-==,}2|{2x y x N -==,则=N M ( ) A. ),1[+∞- B. ]2,1[- C. ),2[+∞ D. φ2.命题“存在04,2<-+∈a ax x R x 使”为假命题是命题“016≤≤-a ”的( ) A .充要条件B .必要不充分条件C .充分不必要条件D .既不充分也不必要条件3. 设i z -=1(i 为虚数单位),则=+z z 22 ( )A .i --1B .i +-1C .i +1D . i -14.设232555322555a b c ===(),(),(),则a , b ,c 的大小关系是 ( ) A.b >c >a B.a >b >c C.c >a >b D.a >c >b5. 已知函数()sin 3,(1,1),f x x x x =+∈-如果2(1)(1)0f a f a -+-< ,则实数a 的取值范围是( )A ()2,1 B ()()+∞-∞-,12, C ()2,-∞- D()+∞,16.设曲线11x y x +=-在点(32),处的切线与直线10ax y ++=垂直,则a =( ) A .2B .12C.2-D.12-7. 将标号为1,2,3,4,5,6的6张卡片放入3个不同的信封中.若每个信封放2张,其中标号为1,2的卡片放入同一信封,则不同的方法共有(A )12种 (B )18种 (C )36种 (D )54种8.由直线21=x ,x=2,曲线x y 1=及x 轴所围图形的面积为( ) A.2ln 2B.1ln 22C.415D.4179.函数)(x f 在定义域R 内可导,若)2()(x f x f -=,且当)1,(-∞∈x 时,0)()1(<'-x f x ,设).3(),21(),0(f c f b f a ===则( )A .c b a <<B .b a c <<C .a b c <<D .a c b <<10.对任意的实数a 、b ,记{}()max ,()a a b a b b a b ≥⎧=⎨<⎩.若{}()max (),()()F x f x g x x R =∈,其中奇函数y=f(x)在x=l 时有极小值-2,y=g(x)是正比例函数,函数()(0)y f x x =≥与函数y=g(x)的图象如图所示.则下列关于函数()y F x =的说法中,正确的是( )A.()y F x =为奇函数B.()y F x =的最小值为-2且最大值为2C.()y F x =在(3,0)-上为增函数D.()y F x =有极大值(1)F -且有极小值(0)F11. 若20112011102011)21(xa x a a x +++=- )(R x ∈,则=+++20112011221222a a a( )A .0B .-2C .-1D .212. 在体积为π34的球的表面上有A ,B ,C 三点,AB=1,BC=2,A ,C 两点的球面距离为π33,则球心到平面ABC 的距离为( )A .22B .23C .23D .1第Ⅱ卷(非选择题,共90分)二、填空题:本大题共4小题,每小题5分,共20分。
精品解析:云南省建水一中2012届高三10月月考理综(物理)试题解析
云南省建水一中2012届高三10月月考理综物理试题解析洛阳市第二中学王春旺二、选择题:本大题共8小题,每小题6分.在每小题给出的四个选项中,有的只有一项符合要求,有的有多项符合题目要求。
全部选对的得6分,选对但不全的得3分,有选错的得0分。
14.一端装有定滑轮的粗糙斜面体放在地面上,A、B两物体通过细绳连接,并处于静止状态(不计绳的质量和绳与滑轮间的摩擦),如图所示.现用水平力F作用于物体B上,缓慢拉开一小角度,此过程中斜面体与物体A仍然静止。
则下列说法正确的是A.缓慢拉开的过程中水平拉力F不变B.斜面体所受地面的支持力不变C.斜面对物体A作用力的合力变大D.物体A所受斜面体的摩擦力变小14。
B解析:用水平力F作用于物体B上,缓慢拉开一小角度的过程中,细绳中拉力增大,水平拉力F增大,选项A错误;把系统看作一个整体,竖直方向受力不变,斜面体所受地面的支持力不变,选项B正确;由于物体A仍然静止,斜面对物体A作用力的合力为零,不变,选项C错误;由于不知AB质量之间关系,在缓慢拉开的过程中,物体A所受斜面体的摩擦力如何变化不能判断,选项D错误。
15.某中学生身高1。
70m,在学校运动会上参加跳高比赛,采用背跃式,身体横着越过2.10m的横杆,获得了冠军,据此可以估算出他跳起时竖直向上的速度为:(g=10m/s2)A.7m/s B.6 m/sC.5 m/s D.3 m/s15.C解析:某中学生身高1.70m,身体横着越过2.10m的横杆,重心约上升h=1.25m,可以估算出他跳起时竖直向上的速度为v=5 m/s,选项C正确。
16.起重机的钢索将重物由地面吊到空中某个高度,其速度图像如下图1所示,则钢索拉力的功率随时间变化的图像是下图2中的16.B解析:0~t1时间内,匀加速上升,拉力大于重力,由P=Fv可知,钢索拉力的功率随时间均匀增大;在t1~t2时间内,匀速上升,拉力等于重力,由P=Fv可知,钢索拉力的功率不变;在t1时刻,拉力突变减小,钢索拉力的功率突变减小;在t2~t3时间内,匀减速上升,拉力小于重力,由P=Fv可知,钢索拉力的功率随时间均匀减小;在t2时刻,拉力突变减小,钢索拉力的功率突变减小;所以钢索拉力的功率随时间变化的图像是图B。
云南省建水一中2012届高三数学11月月考 文
建水一中高三年级11月月考数学试题(文科卷)一、选择题:(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一个选项符合题目要求的) 1.已知集合{}xx y x M 32+-==,{}|||2N x x =>,则M N = ( )A .{}|13x x <<B .{}|03x x <<C .{}|23x x <<D .{}32≤<x x2.已知12zi +=2-i (z 是z 的共轭复数),则复数z 在复平面内对应的点位于( )A .第一象限B .第二象限C .第三象限D .第四象限 3. “032>x ”是“0<x ”成立的( ) A .充分不必要条件 B .必要不充分条件C .充要条件D .既非充分也非必要条件4.已知53)4sin(=-x π,则x 2sin 的值为 ( )A .2519B .2516C .2514D .2575.若函数f(x)是定义在R 上的偶函数,在(]0,∞-上是减函数,且f(2)=0,则使得f(x)<0的x 的取值范围是( )A. ()2,2-B. ()2,∞- C . ()+∞,2 D. ()()+∞-∞-,22,6.双曲线221x p 28y -=(p>0)的左焦点F1(2P -,0),则该双曲线的离心率为( )A .1B 2C 3. 27. 一只小蜜蜂在一个棱长为4的正方体内自由飞行,若蜜蜂在飞行过程中始终保持与正方体中心的距离不超过1,称其为“安全飞行”,则蜜蜂“安全飞行”的概率为( )A. 64πB. 48πC. 16πD.12π8.如图,程序框图所进行的求和运算是( )A .12+14+16+…+120B .1+13+15+…+119 C .1+12+14+…+118 D .12+212+312+…+10129. 已知函数x y sin =的定义域为⎥⎦⎤⎢⎣⎡b ,65π,值域为⎥⎦⎤⎢⎣⎡-21,1,则65π-b 的值不可能是 A.65π B. 67π C.34πD.23π10.已知三个互不重合的平面γβα、、,且a αβ=,b αγ=,c βγ=,给出下列命题:①若c a ,b a ⊥⊥,则c b ⊥;②若P b a = 则P c a = ;③若c a ,b a ⊥⊥,则γα⊥; ④若b //a 则c //a .其中正确命题个数为 ( )A .1个B .2个C .3个D .4个11.已知直线 0634:1=+-y x l 和直线1:2-=x l ,抛物线24y x = 上一动点P 到直线12l l 和直线的距离之和的最小值是( )A .2B .3C .115D .371612.若1()1(1)f x f x +=+,当[0x ∈,1]时,()f x x =,若在区间(1-,1]内()()g x f x mx m =--有两个零点,则实数m 的取值范围是( )A .[0,1)2B .1[2,)+∞C .(0,1]2D .[0,1)3二.填空题(本大题共4小题,每小题5分,共20分) 13.已知数列{}n a 为等比数列,且64,495==a a ,则7a = ;14.直线 2x -y = 0 与圆C :(x -2)2 + (y + 1)2 = 9 交于AB 两点,则ΔABC (C 为圆心) 的面积等于_______________ .15.已知O 为坐标原点,点M 的坐标为)1,2(,点(,)N x y 的坐标x 、y 满足不等式组⎪⎩⎪⎨⎧≤≥-+≤-+1033032y y x y x . 则OM ON ⋅的取值范围是 ;16.点O 在内部且满足,则的面积与凹四边形的面积之比为 . 三、解答题:(本大题共6小题,共70分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
建水一中70届高三年级10月月考数学试卷(理)一、选择题:(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1. 复数11i +在复平面上对应的点的坐标是( )A .(1,1) B. (1,1)- C. (1,1)-- D. (1,1)- 2. 下列说法错误的是( )A .自变量取值一定时,因变量的取值带有一定随机性的两个变量之间的关系叫做相关关系;B .线性回归方程对应的直线y ^=b ^x +a ^至少经过其样本数据点(x 1,y 1), (x 2,y 2),…,(x n ,y n )中的一个点;C .在残差图中,残差点分布的带状区域的宽度越狭窄,其模型拟合的精度越高;D .在回归分析中,2R 为0.98的模型比2R 为0.80的模型拟合的效果好 3.如图,若程序框图输出的S 是126,则判断框①中应为 ( ) A .5n ≤B .6n ≤C .7n ≤D .8n ≤4.若一个三位数的十位数字比个位数字和百位数字都大,称 这个数为 “伞数”。
现从1,2,3,4,5,6这六个数字中取 3个数,组成无重复数字的三位数,其中“伞数” 有 ( ) A .120个 B .80个 C .40个 D .20个5. 若x 为三角形中的最小内角,则函数y=sinx+cosx 的值域是( ) A .,21[]22 B .]23,0( C .]2,1( D .]22,21(6. 一个几何体按比例绘制的三视图如图所示(单位:m )则该几何体的体积为( )3m .S否A .37 B .29 C .27 D .497.双曲线222210,0)x y a b ab-=>>(的渐近线与圆22(2)1x y +-=相切,则双曲线的离心率为( )A .2 D .38.已知直线l :0Ax By C ++=(A ,B 不全为0),两点111(,)P x y ,222(,)P x y ,若1122()()0Ax By C Ax By C ++++>,且1122Ax By C Ax By C++>++,则( )A .直线l 与直线P 1P 2不相交B .直线l 与线段P 2 P 1的延长线相交C .直线l 与线段P 1 P 2的延长线相交D .直线l 与线段P 1P 2相交9. 下列有关命题的说法正确的是( )A .命题“若1,12==x x 则”的否命题为:“若1,12≠=x x 则”B .“x=-1”是“0652=--x x ”的必要不充分条件C .命题“01,2<++∈∃x x R x 使得”的否定是:“01,2<++∈∀x x R x 均有”D .命题“若y x y x sin sin ,==则”的逆否命题为真命题10.已知非零向量,,→→→a b c 满足0→→→→++=a b c ,向量,→→a b 的夹角为120 ,且||2||→→=b a ,则向量→→与a c 与的夹角为 ( )A .︒60B .︒90C .︒120D . ︒15011.设=)(x f R x x x ∈+,3,当02πθ≤≤时,0)1()sin (>-+m f m f θ恒成立,则实数m 的取值范围是( )A .(0,1)B .)0,(-∞C .)21,(-∞D .)1,(-∞12.已知正六棱柱的12个顶点都在一个半径为3的球面上,当正六棱柱的体积最大(柱体体积=底面积⨯高)时,其高的值为( )A .B .C .3D 二、填空题(本大题共4小题,每小题5分,共20分)13.在等比数列}{n a 中,若3753)3(-=⋅⋅a a a ,则=⋅82a a .14.已知向量(1,2),(4,)a x b y →→=-=),若向量a →垂直向量b →,则y x 39+的最小值为 .15.已知函数2()321f x x x =++,若1()2()1f x dx f a =-⎰成立,则a =______________;16. 已知函数()124-+=x x f 的定义域是[]b a ,(b a ,是整数),值域是[]1,0,则满足条件的定义域的可能情况共有 种.三、解答题(本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤)17. (本小题满分10分)已知{}n a 是等差数列,其中37618,11a a a +==. (Ⅰ)求数列{}n a 的通项公式;(Ⅱ)若数列{}n b 满足()12n n n b a n N -*=+∈ ,求数列{}n b 的前n 项和n T . 18.(本小题满分12分)函数()()()sin 0,0,f x A x b A ωϕωϕπ=++>>≤在一个周期内,当6x π=时,y 取最小值1;当23x π=时,y 取最大值3.(I)求()f x 的解析式; (II)求()f x 在区间3,2ππ⎡⎤⎢⎥⎣⎦上的最值.19. (本小题满分12分)如图,已知菱形ABCD 的边长为6,60BAD ∠= ,O BD AC =⊥.将菱形ABCD 沿对角线AC折起,使BD =,得到三棱锥B ACD -. (Ⅰ)若点M 是棱BC 的中点,求证://OM 平面A B D ; (Ⅱ)求二面角A BD O --的余弦值; (Ⅲ)设点N 是线段B D 上一个动点,试确定N 点的位置,使得CN =并证明你的结论.M20. (本小题满分12分)某校从参加某次知识竞赛的同学中,选取60名同学将其成绩(百分制)(均为整数)分 成6组后,得到部分频率分布直方图(如图),观察图形中的信息,回答下列问题. (Ⅰ)求分数在[70,80)内的频率,并补全这个频率分布直方图; (Ⅱ)从频率分布直方图中,估计本次考试的平均分; (Ⅲ)若从60名学生中随机抽取2人,抽到的学生成绩在[40,70)记0分,在[70,100]记1分,用X 表示抽取结束后的总记分,求X 的分布列和数学期望.21.(本小题满分12分)已知椭圆2222:1(0)x y C a b ab+=>>过点(0,1),且离心率为2.(Ⅰ)求椭圆C 的方程;(Ⅱ),A B 为椭圆C 的左右顶点,直线:l x =与x 轴交于点D ,点P 是椭圆C 上异于,A B 的动点,直线,A P B P 分别交直线l 于,E F 两点.证明:当点P 在椭圆C 上运动时,||||D E D F ⋅恒为定值.22. (本小题满分12分)已知函数2()ln (2)f x x ax a x =-+-.(Ⅰ)若()f x 在1x =处取得极值,求a 的值;(Ⅱ)求函数()y f x =在2[,]a a 上的最大值.建水一中高70届十月月考理科数学试题答案一、选择题13.3 14.6 15.1-或1316. 5三、解答题 17.18.解:(I)∵在一个周期内,当6x π=时,y 取最小值1;当23x π=时,y 最大值3.∴21,2,2362T A b πππ===-=,,2T πω==,()()sin 22f x x ϕ=++,由当23x π=时,y 最大值3得()44sin 1,2332k k Zπππϕϕπ⎛⎫+=+=+∈⎪⎝⎭526k πϕπ=-,∵ϕπ≤,∴5.6ϕπ=-()5sin 2 2.6fx x π⎛⎫=-+ ⎪⎝⎭故:(II) ∵3,2x ππ⎡⎤∈⎢⎥⎣⎦, ∴75132666x πππ≤-≤,∴当32x π=时,()f x 取最大值52;当76x π=时,()f x 取最小值1.19. (Ⅰ)证明:因为点O 是菱形ABCD 的对角线的交点,所以O 是AC 的中点.又点M 是棱BC 的中点,所以OM 是ABC ∆的中位线,//OM AB .因为OM ⊄平面A B D ,A B ⊂平面A B D ,所以//OM 平面A B D . (Ⅱ)解:由题意,3OB OD ==,因为BD =所以90BO D ∠= ,OB OD ⊥.又因为菱形ABCD ,所以OB AC ⊥,OD AC ⊥. 建立空间直角坐标系O xyz -,如图所示.0,0),(0,3,0),A D (0,0,3)B .所以(0,3),(3,0),AB AD =-=-设平面A B D 的法向量为n =(,,)x y z ,则有0,0AB AD ⎧⋅=⎪⎨⋅=⎪⎩n n即:30,30z y ⎧-+=⎪⎨-+=⎪⎩令1x =,则y z ==n=(1,. 因为,AC O B AC O D ⊥⊥,所以AC ⊥平面BOD . 平面BOD 的法向量与AC 平行,所以平面BOD 的法向量为0(1,0,0)=n.0001cos ,7⋅〈〉===n n n n n n,因为二面角A BD O --是锐角,所以二面角A BD O --的余弦值为7.(Ⅲ)解:因为N 是线段B D 上一个动点,设111(,,)N x y z ,BN BD λ=,则111(,,3)(0,3,3)x y z λ-=-,所以1110,3,33x y z λλ===-, 则(0,3,33)N λλ-,3,33)C N λλ=-,由CN ==,即29920λλ-+=, 解得13λ=或23λ=,所以N 点的坐标为(0,2,1)或(0,1,2).(也可以答是线段B D 的三等分点,2BN ND = 或2BN ND =)20.解:(Ⅰ)设分数在[70,80)内的频率为x,根据频率分布直方图,则有 (0.01+0.015×2+0.025+0.005)×10+x=1,可得 x=0.3,所以频率分布直方图如图所示.(Ⅱ)平均分为:450.1550.15650.15750.3850.25950.0571.x =⨯+⨯+⨯+⨯+⨯+⨯=(Ⅲ)学生成绩在[40,70)的有0.4×60=24人, 在[70,100]的有0.6×60=36人,并且X 的 可能取值是0,1,2.11222436362422260606046144105(0);(1);(2).295295295C C C C P X P X P X CCC=========则所以X 的分布列为21. 解:(Ⅰ)由题意可知,1b =,而2c a=且222a b c =+.解得2a =,所以,椭圆的方程为2214xy +=.(Ⅱ)(2,0),(2,0)A B -.设00(,)P x y ,022x -<<, 直线AP 的方程为00(2)2y y x x =++,令x =,则002)2y y x +=+,即00||||2)|2|y D E x =+;直线B P 的方程为00(2)2y y x x =--,令x =02y x =-,即00||||2)|2|y D F x =-;0000||||||||2)2)|2||2|y y D E D F x x ⋅=+⋅+-22022044|4|4y y x x==--而220014x y +=,即220044y x =-,代入上式,∴||||1D E D F ⋅=,所以||||D E D F ⋅为定值1.∴EX =0×46295+1×144295+2×105295=354295.22. 解:(Ⅰ)∵2()ln (2)f x x ax a x =-+-, ∴函数的定义域为(0,)+∞.∴2112(2)(21)(1)()2(2)ax a xx ax f x ax a xxx-+---+'=-+-==.()f x 在1x =处取得极值,即(1)(21)(1)0f a '=--+=, ∴1a =-. 当1a =-时,在1(,1)2内()0f x '<,在(1,)+∞内()0f x '>,∴1x =是函数()y f x =的极小值点. ∴1a =-.(2)∵2a a < , ∴01a <<.2112(2)(21)(1)()2(2)ax a xx ax f x ax a xxx-+--+'=-+-==-∵ x ∈(0,)+∞, ∴10ax +>,∴()f x 在1(0,)2上单调递增;在1(,)2+∞上单调递减,①当102a <≤时, ()f x 在2[,]a a 单调递增,∴32m ax ()()ln 2f x f a a a a a ==-+-;②当21212a a ⎧>⎪⎪⎨⎪<⎪⎩,即122a <<时,()f x 在21(,)2a 单调递增,在1(,)2a 单调递减,∴m ax 12()()ln 21ln 22424a a a f x f -==--+=--;③当212a≤,即12a ≤<时,()f x 在2[,]a a 单调递减,∴2532m ax ()()2ln 2f x f a a a a a ==-+-. 综上所述,当102a <≤时,函数()y f x =在2[,]a a 上的最大值是32ln 2a a a a-+-;当122a <<时,函数()y f x =在2[,]a a 上的最大值是1ln 24a--;当2a ≥时,函数()y f x =在2[,]a a 上的最大值是5322ln 2a a a a -+-.。
